Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Feeling the strain: enhancing ionic transport in olivine phosphate cathodes for Li- and Na-ion batteries through strain effects†
Cristina
Tealdi
*a,
Jennifer
Heath
b and
M. Saiful
Islam
b
aDepartment of Chemistry, University of Pavia and INSTM, Viale Taramelli 16, 27100 Pavia, Italy. E-mail: cristina.tealdi@unipv.it
bDepartment of Chemistry, University of Bath, Bath, BA2 7AY, UK
First published on 3rd March 2016
Abstract
Olivine-type phosphates LiFePO4 and NaFePO4 are among the most widely studied cathode materials for rechargeable batteries. To improve their rate behaviour for future electronic and vehicle applications, it is vital that the Li+ and Na+ conductivities be enhanced. In this study, atomistic simulation methods (including molecular dynamics) are used to investigate the effect of lattice strain on ion transport and defect formation in olivine-type LiFePO4 and NaFePO4, as these properties are directly related to their intercalation behaviour. The results suggest that lattice strain can have a remarkable effect on the rate performance of cathode materials, with a major increase in the ionic conductivity and decrease in blocking defects at room temperature. Such understanding is important for the future optimization of high-rate cathodes for rechargeable batteries, and is relevant to the growing interest in developing thin film solid-state batteries.
1. Introduction
The successful development of next-generation lithium- and sodium-ion batteries depends to a large degree on the ability to fabricate cathode materials with superior electrochemical and mechanical properties.1–3 Cathodes based on olivine LiFePO4 have been widely studied for this purpose and continue to be important.4–6 One advantage of such polyoxyanion-type materials compared with the conventional layered transition metal oxides is that the binding of oxygen in the polyoxyanions enhances the material's stability and thus safety.6,7 Sodium-ion battery materials such as NaFePO4 have attracted increasing attention recently, largely because the high natural abundance of sodium should make them less expensive.8,9 The development of cheap and safe cathode materials is a particularly important goal in the case of large-scale batteries. However, the improvement of the rate performance of both LiFePO4 and NaFePO4 for portable electronic or electric vehicle applications will require significantly improved ionic conductivities.Previous strategies to optimize intercalation properties have mainly involved chemical doping and morphology modulation, with nanosizing and carbon coating so far proving to be the most successful approaches.10,11 The charge/discharge rate performance of olivine-type LiFePO4 has been improved by shortening the diffusion distances by preparing nanosized particles, but higher rates are required for specific applications such as electric vehicles.4 Higher energy storage capability will also require materials with faster ionic transport so that thicker electrodes can be used.5
In the case of intercalation compounds, charge/discharge rates are related to lithium and sodium diffusion kinetics which, in turn, are highly dependent upon structural and defect properties. Manipulation of lattice strain is increasingly being considered as a possible design strategy to improve the functional properties of various materials, such as superconductivity,12,13 ionic conductivity,14 ferroelectricity15 and colossal magnetoresistance.16 In particular, there has been considerable interest in the application of lattice strain in the modulation of ionic conductivity in oxide materials for solid oxide fuel cells (SOFCs).17,18 Several studies have highlighted the positive effect of tensile lattice strain on migration barriers and ion diffusion coefficients in SOFC electrolytes. Following the report of colossal ionic conductivity in epitaxial heterostructures formed by thin layers of Y/ZrO2 and SrTiO3,19 lattice strain effects on fluorite- and perovskite-type materials have been systematically studied using computational techniques.20–25 It should be noted that there is still much debate as to the nature of the charge-carriers with evidence pointing towards electronic conduction in SrTiO3.26 In contrast, the effects of mechanical strain on battery cathode materials have not been extensively considered, with only a limited number of studies to date.27–34 Shahid et al.30 report that at the nanoscale level for LiFePO4 there is an order of magnitude enhancement in the electronic (polaron) conductivity, which they attribute to lattice strain on reduction of the particle size.
Chemical or electrochemical delithiation and subsequent sodiation of the Li counterpart is currently the only known synthesis route to obtain olivine-type NaFePO4.35–38 Epitaxial deposition of thin films, and eventually strained thin films or multilayers, represents an effective strategy to stabilize metastable polymorphs under ambient conditions.39 Such strategies have not yet been explored for maricite-type NaFePO4, the thermodynamically most stable polymorph of this compound.40 Strain due to lattice mismatch may also be present at the interfaces of powder samples of intercalating materials which undergo a two-phase mechanism during intercalation, such as LiFePO4/FePO4.41
It is apparent that there are limited fundamental studies in this area comparing Li- and Na-ion systems. Here we investigate the effect of lattice strain on the ion conduction and defect properties of both LiFePO4 and NaFePO4 olivine-type cathode materials using atomistic simulation techniques. In general, the results highlight the importance of lattice strain effects as an alternative strategy to optimize the electrochemical properties of Li- and Na-ion intercalation compounds.
2. Methodology
The atomistic computational methods used in this study are well-established techniques42 (embodied in the GULP code43), and have been applied successfully to a range of polyanionic battery materials.44 They are based on the specification of a pair potential model that describes the interactions between ions within the crystal structure. For the olivine-type compounds, short-range interactions were modelled with a Buckingham potential, with an additional three-body term to describe the angle-dependent nature of the P–O–P bonds in the PO43− units (Table S1-ESI†). Potential parameters for this study were taken from previous successful work on the olivine-type phosphate systems.45,46 Ion polarisability was taken into account through the use of the well-known shell model.47 Lattice relaxation around charged defects and migrating ions was treated through the two-region Mott–Littleton scheme,48 which allows the explicit relaxation of a large number of ions (>800) to be simulated. To calculate energy barriers for Li+ or Na+ migration, the conventional hopping model for diffusion into adjacent vacancies was used.Olivine-type LiFePO4 and NaFePO4 unit cells (Pnma space group) were allowed to relax at constant pressure with zero applied strain. Subsequently, the energy minimized cells were subjected to biaxial compressive (<0%) and tensile (>0%) strains between −3% and +3% in the ab, ac and bc planes. Besides representing a physically accessible range of values, this strain range was chosen in order to avoid instabilities due to structure failure. Energy minimization of the structures with respect to the third cell parameter and all the atomic coordinates was then carried out. The strained energy-minimized structures were used as the starting configurations for ion migration and defect calculations. Similar methodology has been applied successfully to the study of SOFC oxide-ion conductors.23,25
For the MD simulations, 4 × 4 × 8 supercells with composition Li0.9FePO4 and Na0.9FePO4 were constructed and energy minimized (using the GULP code) at both zero and 3% tensile strain applied in the ac plane. Alkali ion vacancies were randomly distributed within the supercells and charge compensation was achieved through a corresponding change in the average Fe oxidation state. As in our previous MD work on LixFePO4,53 the shell model for electronic polarizability was applied to the oxygen ions (with a spring constant of 130 eV Å−2), which ensured stability of the system during the MD simulations at high temperature.
MD simulations were performed, using the DL_Poly code,49 at 500 K. Such an elevated temperature was chosen to allow both efficient thermalization of the defective solid and sufficient ionic diffusion during the simulation time span, thereby improving the statistics of the calculations. The unstrained system was first equilibrated at the desired temperature for 100 ps with a time step of 0.5 fs. The main simulation run of 750 ps was then performed in the NVT ensemble (Nose–Hoover thermostat). For the strained systems, the energy-minimized cell parameters were expanded according to the thermal expansion coefficient derived for the same composition in the absence of applied strain. Simulations in the NVT ensemble were then carried out as described above. Data analysis was performed using the Visual Molecular Dynamics package (VMD).50
3. Results and discussion
3.1 Strain effects on structures and ion conduction
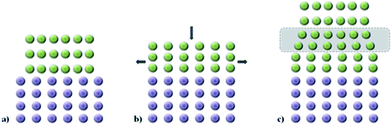
The set of interatomic potential and shell model parameters used in this study have been shown to reliably reproduce the structural features of unstrained LiFePO4 and NaFePO4, as well as their defect, transport and surface properties,45,46,50–53 providing a good starting point for our calculations. The good reproduction of the experimental structures of both LiFePO4 and NaFePO4 is shown in Table S2-ESI.†For experimental work, lattice strain in thin film samples is generated by substrate/film mismatch (i.e. differences in d spacing), as schematically shown in Fig. 1a. In the case of similar or related lattice symmetries and small mismatch values, a coherent interface is often formed. The lattice mismatch leads to in-plane tensile or compressive strain in the deposited layer. In the case of thin films deposited onto a crystalline substrate, this will be a biaxial strain. For perfectly elastic systems, the unit cell volume remains unchanged and the out-of-plane cell parameters increase or decrease as appropriate (Fig. 1b). In practice, most oxide materials have a Poisson coefficient, ν, in the range 0 < ν < 0.5,54 which means that in the case of in-plane tensile strain, the out-of-plane parameter decreases in a way such that film undergoes a net positive volume change. The effect of lattice strain due to film/substrate mismatch is restricted to thin films on the nanometre scale; in thick film samples, the strain is released as the greater distance from the film/substrate interface into the bulk of the film (Fig. 1c).
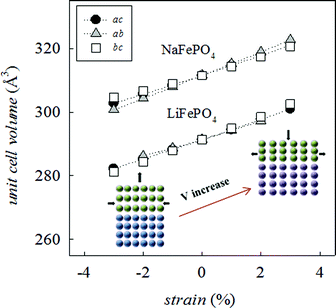
Since many electrical properties are strongly influenced by the type and number of defects and ion diffusion barriers in a crystalline material, strained systems may exhibit behaviour different from the corresponding bulk material. The application of biaxial strain on the olivine system, regardless of the plane considered, has the effect of producing a net change in unit cell volume (Fig. 2), indicative of non-ideal Poisson behaviour commonly exhibited by oxide materials.54
Li+ migration pathways in LiFePO4, as initially predicted from theoretical calculations45 and subsequently confirmed by neutron diffraction maximum entropy methods,55 zigzag along the [010] direction (path B of Fig. 3). Na+ migration in olivine-type NaFePO4 was subsequently shown to follow the same zigzag path, characterized by a lower migration barrier compared to the Li analogue (0.31 vs. 0.55 eV).46
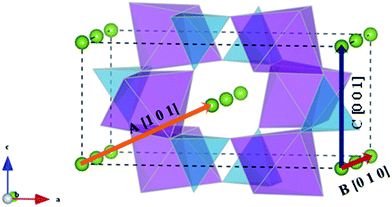 | ||
| Fig. 3 Schematic representation of the possible migration paths in olivine-type AFePO4 (A = Li+ or Na+). Blue: PO4 tetrahedra; purple: FeO6 octahedra; green: Li/Na. | ||
Fig. 4 shows the calculated migration barrier along the [010] direction as a function of applied strain for LiFePO4 and NaFePO4. For both systems, the energy barrier increases slightly along with the applied strain for the ab and bc cases. Interestingly, the migration energy decreases along with strain for the ac case, reaching a value that is approximately half the value for the unstrained system, corresponding to 3% tensile strain. The calculated migration barrier for Li+ decreases from 0.55 eV to 0.28 eV while the migration barrier for Na+ decreases from 0.37 eV to 0.16 eV. This significant reduction in migration energy with tensile strain is consistent with a previous DFT study of Lee et al.29 on olivine LiFePO4.
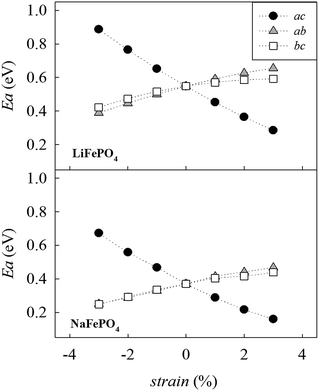 | ||
| Fig. 4 Change in the alkali-ion migration barrier along the [010] direction as a function of strain for LiFePO4 (upper panel) and NaFePO4 (lower panel). | ||
Changes in migration barrier for ion diffusion can be interpreted in terms of structural modifications. In particular, our results show a relation between the variation in migration barrier and the ion–ion hopping distance along with the applied strain. For example, in the case of LiFePO4, the Li–Li hopping distance for migration along the [010] direction decreases for the ac strained case, while it increases for the other two cases (Fig. S2a†). A decrease in ion hopping distance is expected to favour alkali-ion diffusion in the structure. Other structural parameters such as the available free volume at the saddle point position may also influence the migration barrier. Hence, the overall variation of the migration barrier along with strain is the result of a fine interplay between different structural parameters whose nature depends on the particular structure and the migration path considered (Fig. S2-ESI†).
In the olivine system, two other migration paths are potentially accessible, labelled in Fig. 3 as paths A (along the [101] direction) and C (along the [001] direction). Both paths are characterized by energy barriers >2.5 eV for the unstrained system and, as a consequence, alkali-ion transport in olivine-type materials is considered a one dimensional process. In order to determine if the dimensionality of Li+ and Na+ ion transport is affected by applied strain, the activation energies for paths A and C were calculated as a function of the applied strain. Calculated activation energies for migration along the [001] and [101] directions still remain above 2 eV for the 3% tensile strained systems (Fig. S1-ESI†) and therefore they are not comparable to the most favourable migration path running parallel to the b axis (Fig. 4). This result suggests that, even for the strained systems, Li+ and Na+ ion transport will remain a 1D diffusion process, as is found for unstrained LiFePO4 and NaFePO4.45,46
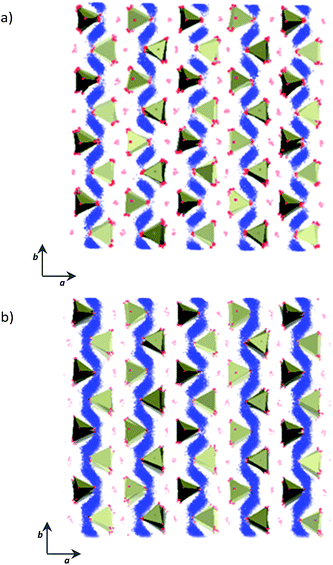
MD simulations performed on both the unstrained and the ac-plane strained systems confirmed that Li and Na ion diffusion proceeds through a zig-zag path parallel to the b-axis. The 1D and curved nature of such paths are not altered by the application of tensile strain, as shown in Fig. 5 for the Na-based system, selected as an example.
Visual analysis of Fig. 5 already indicates that the application of tensile strain has a positive effect on the alkali-ion mobility within the system showing greater Na-ion density in the trajectory plot. To better quantify such effects, Li and Na ion diffusion coefficients were derived from the slope of the mean square displacement (MSD) parameters vs. simulation time plots (Fig. 6) through the use of the following standard relation:
| 〈|ri(t) − ri(0)|2〉 = 6D + B | (1) |
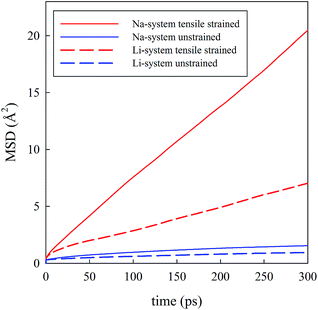 | ||
| Fig. 6 Mean square displacement (MSD) vs. time for Li0.9FePO4 (dashed lines) and Na0.9FePO4 (solid lines). | ||
| Strain (%) | D Li (cm2 s−1) | D Na (cm2 s−1) |
|---|---|---|
| 0.0 | 3.36 × 10−8 | 6.69 × 10−8 |
| 3.0 | 3.42 × 10−7 | 1.08 × 10−6 |
Analysis of the MD results indicate two main points: first, Na-ion diffusion coefficients are predicted to be higher than Li-ion diffusion coefficients in the olivine system, in line with the calculated difference in the absolute values between Na-ion and Li-ion migration barriers (Fig. 4); second, the application of tensile strain increases the alkali-ion diffusion. The predicted effect is comparable for Li and Na-based systems and, at the simulation temperature used in this study (500 K), is roughly one order of magnitude.
The overall results derived from MD simulations are in good agreement with the trend observed from static lattice simulations, i.e. tensile strain applied perpendicularly to the main diffusion direction is enhancing ion transport in the system.
Based on the calculated changes in activation energy along with strain (Fig. 4), we can estimate the change in ionic conductivity due to the application of 3% biaxial strain in the ac plane based on standard Arrhenius equations. Previous work of De Souza23 shows that with regard to oxygen diffusion in fluorite-type CeO2, ΔHmig can be conveniently approximated by the calculated activation barrier, Emig, within a certain range of applied strain. Using the values shown in Fig. 4, and approximating ΔHmig by the calculated activation barrier, Emig, we can predict an enhancement in Li+ and Na+ conductivity of approximately three orders of magnitude at room temperature. We recognize that the calculated enhancement based on MD results is significantly lower. However, a number of factors should be taken into consideration. First, MD simulations were conducted at 500 K while the estimation of conductivity increase based on the static lattice simulations result was performed at 300 K. The predicted change in activation energy along with strain (Fig. 4) suggests that differences in conductivity will be more pronounced as the temperature is reduced; for example, this has been computationally predicted20 and experimentally observed59 for oxygen diffusion in strained fluorite structures and perovskite-type materials.60 This is also in line with the predicted large effect of temperature in the exponential factor of the Arrhenius equation.
Therefore, the key conclusion of this study is that tensile biaxial strain applied in the plane perpendicular to the main diffusion path will promote alkali-ion diffusion. Even within the limits of our estimate, this is a major enhancement in ionic conductivity which should greatly improve the rate behaviour of olivine-type cathode materials. Even taking into account possible effects of interfaces (e.g. dislocations, grain boundaries and space charge regions), the ionic conductivity should undergo a significant enhancement. There are of course experimental technical challenges associated with the fabrication of epitaxial thin-films (using, for example, pulsed laser deposition) and their electrical characterisation. In particular, the evolution of dislocation defects may introduce a lower degree of strain compared to that expected on the basis of substrate/lattice mismatch. Nevertheless, our clear predictions warrant further investigation.
3.2 Strain effects on defect formation
Due to the 1D nature of alkali-ion transport in olivine-type materials, the presence of intrinsic anti-site defects (eqn (2) and (3), and Fig. 7), which involve the exchange of an Li/Na ion for a neighbouring Fe atom, can be detrimental to ion intercalation properties: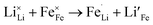 | (2) |
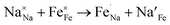 | (3) |
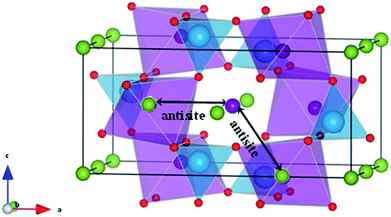 | ||
| Fig. 7 Schematic representation of two configurations of Li/Fe or Na/Fe anti-site defects in olivine-type AFePO4 (A = Li+ or Na+). | ||
Such intersite cation exchanges represent the most energetically favourable intrinsic defect in olivine-type materials.45 Their formation has been frequently observed experimentally, for example, by refinement of site occupancies in diffraction experiments61 or by direct visualization using electron microscopy methods.62 Since alkali-ion transport in olivine-type materials occurs one-dimensionally along [010], these types of defect negatively affect the intercalation properties by blocking the ion transport pathways.
In order to determine if the application of biaxial strain affects the formation energy of such defects, we calculated the energies of anti-site pair cluster formation and the binding energies for such defects as a function of strain. Fig. 8 shows the anti-site pair cluster formation energy as a function of the imposed strain in the ac plane for the LiFePO4 and NaFePO4 systems. The first point to note is that the formation of the anti-site defect for NaFePO4 is more favourable than for the Li analogue, in agreement with previous studies.46 Interestingly, the dependence of this defect formation parameter on the applied strain is more pronounced for the Na-based system. In particular, as the imposed strain increases from compressive to tensile strain, the anti-site cluster formation energy for LiFePO4 does not change greatly (Fig. 8), suggesting that strain in this system is not a crucial parameter to modulate the anti-site defect population.
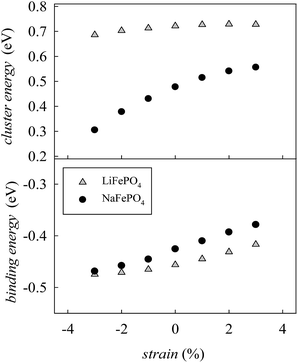 | ||
| Fig. 8 Anti-site defect energies for olivine-type AFePO4 (A = Li+ or Na+) as a function of the applied biaxial tensile/compressive strain in the ac plane; (upper) cluster formation energy (based on eqn (1) and (2)); (lower) binding energy. | ||
In contrast, the variation with strain is much more pronounced for NaFePO4, with tensile strain making the formation of anti-site defect clusters less favourable. While compressive strain increases the energy required for a Na ion to occupy an Fe site, due to size restraints with the large Na ion, the energy needed for an Fe ion to sit on a Na site is reduced to a greater extent, resulting in the predicted reduction in cluster energy. Elongation of the b-axis, caused by the application of ac strain is attributed to this change in formation energy.
Binding energies for the anti-site pair clusters were calculated as the difference between the cluster energy and the sum of the energies of the isolated defects. Negative values of binding energy imply that the cluster is bound. As shown in Fig. 8, binding energies become less negative as the applied strain increases, suggesting that tensile strain makes the Li/Na–Fe clusters less strongly bound, with a lower tendency for anti-site defect association.
Finally, the effect of strain on the anti-site cluster formation energy is negligible (LiFePO4) or positive (NaFePO4) when tensile strain in applied in the ac plane. The application of biaxial strain in directions different from the ac plane is predicted to be unfavourable for the intercalation properties of olivine-type materials since it is expected to increase the amount of anti-site defects in the system (Fig. S3-ESI†).
4. Conclusions
The effect of lattice strain on the ion conduction properties of olivine-type cathode materials for lithium- and sodium-ion batteries has been investigated using atomistic simulation techniques. Compressive or tensile strain is not found to affect the dimensionality of ion transport in either LiFePO4 or NaFePO4, which remains 1D. More importantly, the Li+ and Na+ migration barriers along the [010] direction decrease significantly when tensile strain is applied in the ac plane. It is predicted that this decrease in activation energy corresponds to a striking enhancement in ionic conductivity at room temperature. The highly positive effect of tensile strain on alkali-ion diffusion is confirmed through the use of molecular dynamics simulations. Tensile strain is also predicted to reduce the binding energies of blocking anti-site defects, and slightly increase their formation energy (especially for NaFePO4). These results suggest that tensile strain applied perpendicularly to the alkali-ion migration channels will improve the intercalation properties of olivine-type cathode materials.We recognise that interface effects (e.g. dislocations, grain boundaries and space charge regions) may influence the effective enhancement. Despite the technical challenges, related experimental work on epitaxial thin-film fabrication and their electrical characterisation would be extremely interesting.
In general, the intriguing results reported here suggest that lattice strain can lead to significant enhancements in ionic conduction and rate performance of Li- and Na-ion cathode materials. Such insights provide a framework for the future design and optimization of high-rate cathodes, and are also relevant to the development of thin-film solid-state batteries. Indeed, one of the aims of this work is to stimulate further studies on strain effects in related battery materials.
Acknowledgements
C. T. gratefully acknowledges the Cariplo Foundation and Regione Lombardia for grant 2015-0753. For a PhD studentship (J. H.) and research funding, we are grateful to the University of Bath URS scheme, the EPSRC Programme Grant on energy materials (EP/K016288/1) and the MCC/Archer consortium (EP/L000202/1).Notes and references
- B. Dunn, H. Kamath and J.-M. Tarascon, Science, 2011, 334, 928 CrossRef CAS PubMed.
- V. Etacheri, R. Marom, R. Elazari, G. Salitra and D. Aurbach, Energy Environ. Sci., 2011, 4, 3243 CAS.
- N. Yabuuchi, K. Kubota, M. Dahbi and S. Komaba, Chem. Rev., 2014, 114, 11636 CrossRef CAS PubMed.
- K. Zaghib, A. Guerfi, P. Hovington, A. Vijh, M. Trudeau, A. Mauger, J. B. Goodenough and C. M. Julien, J. Power Sources, 2013, 232, 357 CrossRef CAS.
- M. S. Whittingham, Chem. Rev., 2014, 114, 11414 CrossRef CAS PubMed.
- J. Wang and X. Sun, Energy Environ. Sci., 2015, 8, 1110 CAS.
- C. Masquelier and L. Croguennec, Chem. Rev., 2013, 113, 6552 CrossRef CAS PubMed.
- B. L. Ellis and L. F. Nazar, Curr. Opin. Solid State Mater. Sci., 2012, 16, 168 CrossRef CAS.
- S.-W. Kim, D.-H. Seo, X. Ma, G. Ceder and K. Kang, Adv. Energy Mater., 2012, 2, 710 CrossRef CAS.
- C. Delacourt, P. Poizot, S. Levasseur and C. Masquelier, Electrochem. Solid-State Lett., 2006, 9, A352 CrossRef CAS.
- H. Huang, S. C. Yin and L. F. Nazar, Electrochem. Solid-State Lett., 2001, 4, A170 CrossRef CAS.
- C. W. Hicks, D. O. Brodsky, E. A. Yelland, A. S. Gibbs, J. A. N. Bruin, M. E. Barber, S. D. Edkins, K. Nishimura, S. Yonezawa, Y. Maeno and A. P. Mackenzi, Science, 2014, 344, 283 CrossRef CAS PubMed; S. Tan, Y. Zhang, M. Xia, Z. Ye, F. Chen, X. Xie, R. Peng, D. Xu, Q. Fan, H. Xu, J. Jiang, T. Zhang, X. Lai, T. Xiang, J. Hu, B. Xie and D. Feng, Nat. Mater., 2013, 12, 634 CrossRef PubMed.
- F. Nabeshima, Y. Imai, M. Hanawa, I. Tsukada and A. Maeda, Appl. Phys. Lett., 2013, 103, 172602 CrossRef.
- N. Sata, K. Eberman, K. Eberl and J. Maier, Nature, 2000, 408, 21 CrossRef PubMed.
- J. H. Haeni, P. Irvin, W. Chang, R. Uecker, P. Reiche, Y. L. Li, S. Choudhury, W. Tian, M. E. Hawley, B. Craigo, A. K. Tagantsev, X. Q. Pan, S. K. Streiffer, L. Q. Chen, S. W. Kirchoefer, J. Levy and D. G. Schlom, Nature, 2004, 430, 758 CrossRef CAS PubMed; S. A. Harrington, J. Zhai, S. Denev, V. Gopalan, H. Wang, Z. Bi, S. A. T. Redfern, S.-H. Baek, C. W. Bark, C.-B. Eom, Q. Jia, M. E. Vickers and J. L. MacManus-Driscoll, Nat. Nanotechnol., 2011, 6, 491 CrossRef PubMed.
- A. J. Millis, T. Darling and A. Migliori, J. Appl. Phys., 1998, 83, 1588 CrossRef CAS; K. H. Ahn, T. Lookman and A. R. Bishop, Nature, 2004, 428, 401 CrossRef PubMed.
- N. Schichtel, C. Korte, D. Hesse and J. Janek, Phys. Chem. Chem. Phys., 2009, 11, 3043–3048 RSC.
- K. Wen, W. Lv and W. He, J. Mater. Chem. A, 2015, 3, 20031 CAS.
- J. Garcia-Barriocanal, A. Rivera-Calzada, M. Varela, Z. Sefrioui, E. Iborra, C. Leon, S. J. Pennycook and J. Santamaria, Science, 2008, 321, 676 CrossRef CAS PubMed.
- A. Kushima and B. Yildiz, J. Mater. Chem. A, 2010, 20, 4809 RSC.
- T. J. Pennycook, M. J. Beck, K. Varga, M. Varela, S. J. Pennycook and S. T. Pantelides, Phys. Rev. Lett., 2010, 104, 115901 CrossRef PubMed.
- M. J. D. Rushton, A. Chroneos, S. J. Skinner, J. A. Kilner and R. W. Grimes, Solid State Ionics, 2013, 230, 37 CrossRef CAS.
- R. A. De Souza, A. Ramadan and S. Horner, Energy Environ. Sci., 2012, 5, 5445 CAS.
- U. Aschauer, R. Pfenninger, S. M. Selbach, T. Grande and N. A. Spaldin, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 88, 054111 CrossRef.
- C. Tealdi and P. Mustarelli, J. Phys. Chem. C, 2014, 118, 29574 CAS.
- A. Cavallaro, M. Burriel, J. Roqueta, A. Apostolidis, A. Bernardi, A. Tarancón, R. Srinivasan, S. N. Cook, H. L. Fraser, J. A. Kilner, D. W. McComb and J. Santiso, Solid State Ionics, 2010, 181, 592 CrossRef CAS.
- H.-J. Yan, Z.-Q. Wang, B. Xu and C. Ouyang, Funct. Mater. Lett., 2012, 5, 1250037 CrossRef.
- F. Ning, S. Li, B. Xu and C. Ouyang, Solid State Ionics, 2014, 263, 46 CrossRef CAS.
- J. Lee, S. J. Pennycook and S. T. Pantelides, Appl. Phys. Lett., 2012, 101, 033901 CrossRef.
- R. Shahid and S. Murugavel, Phys. Chem. Chem. Phys., 2013, 15, 18809 RSC.
- F. Sauvage, L. Laffront, J.-M. Tarascon and E. Baudrin, J. Power Sources, 2008, 175, 495 CrossRef CAS.
- S. Laref and A. Laref, RSC Adv., 2015, 5, 35667 RSC.
- A. K. Chen, T. A. Thapa and J. Berfield, J. Power Sources, 2014, 271, 406 CrossRef.
- A. Awarke, S. Lauer, M. Wittler and S. Pischinger, Comput. Mater. Sci., 2011, 50, 871 CrossRef CAS.
- P. Moreau, D. Guyomard, J. Gaubicher and F. Boucher, Chem. Mater., 2010, 22, 4126 CrossRef CAS.
- S.-M. Oh, S.-T. Myung, J. Hassoun, B. Scrosati and Y.-K. Sun, Electrochem. Commun., 2012, 22, 149 CrossRef CAS.
- M. Casas-Cabanas, V. V. Roddatis, D. Saurel, P. Kubiak, J. Carretero-Gonzalez, V. Palomares, P. Serras and T. Rojo, J. Mater. Chem., 2012, 22, 17421 RSC.
- K. T. Lee, T. N. Ramesh, F. Nan, G. Botton and L. F. Nazar, Chem. Mater., 2011, 23, 3593 CrossRef CAS.
- A. Gupta, Curr. Opin. Solid State Mater. Sci., 1997, 2, 23 CrossRef CAS.
- B. L. Ellis, W. R. M. Makahnouk, Y. Makimura, K. Toghill and L. F. Nazar, Nat. Mater., 2007, 6, 749 CrossRef CAS PubMed.
- N. Meethong, H.-Y. Shadow Huang, S. A. Speak-man, W. Craig Carter and Y.-M. Chaing, Adv. Funct. Mater., 2007, 17, 1115 CrossRef CAS.
- C. R. A. Catlow, Computer Modelling in Inorganic Crystallography, Academic Press, San Diego, CA, 1997 Search PubMed.
- J. D. Gale, J. Chem. Soc., Faraday Trans., 1997, 93, 629 RSC; J. D. Gale and A. L. Rohl, Mol. Simul., 2003, 29, 291 CrossRef CAS.
- M. S. Islam and C. A. J. Fisher, Chem. Soc. Rev., 2014, 43, 185 RSC.
- M. S. Islam, D. J. Discroll, C. A. J. Fisher and P. R. Slater, Chem. Mater., 2005, 17, 5085 CrossRef CAS.
- R. Tripathi, S. M. Wood, M. S. Islam and L. F. Nazar, Energy Environ. Sci., 2013, 6, 2257 CAS.
- B. G. Dick and A. W. Overhauser, Phys. Rev., 1958, 112, 90 CrossRef.
- N. F. Mott and M. J. Littleton, Trans. Faraday Soc., 1938, 34, 485 RSC.
- I. T. Todorov, W. Smith, K. Trachenko and M. T. Dove, J. Mater. Chem., 2006, 16, 1911 RSC.
- W. Humphrey, A. Dalke and K. Schulten, J. Mol. Graphics, 1996, 14, 33 CrossRef CAS PubMed.
- C. A. J. Fisher and M. S. Islam, J. Mater. Chem., 2008, 18, 1209 RSC.
- A. Whiteside, C. A. J. Fisher, S. C. Parker and M. S. Islam, Phys. Chem. Chem. Phys., 2014, 16, 21788 RSC.
- C. Tealdi, C. Spreafico and P. Mustarelli, J. Mater. Chem., 2012, 22, 24870 RSC.
- G. N. Greaves, A. L. Greer, R. S. Lakes and T. Rouxel, Nat. Mater., 2011, 10, 823 CrossRef CAS PubMed.
- S. C. Nishimura, G. Kobayashi, K. Ohoyama, Y. Kanno, M. Yashima and A. Yamada, Nat. Mater., 2008, 7, 707 CrossRef CAS PubMed.
- R. Amin, P. Balaya and J. Maier, Electrochem. Solid-State Lett., 2007, 10, A13 CrossRef CAS; R. R. Chen, Y. X. Wu and X. Y. Kong, J. Power Sources, 2014, 258, 246 CrossRef; S. L. Yang, X. F. Zhou, J. G. Zhang and Z. P. Liu, J. Mater. Chem., 2010, 20, 8086 RSC.
- G. J. Shu and F. C. Chou, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 78, 052101 CrossRef.
- T. Jiang, G. Chen, A. Li, C. Wang and Y. Wei, J. Alloys Compd., 2009, 478, 604 CrossRef CAS.
- W. Shen, J. Jiang and J. L. Hertz, RSC Adv., 2014, 4, 21625 RSC.
- T. Mayeshiba and D. Morgan, Phys. Chem. Chem. Phys., 2015, 17, 2715 RSC.
- J. Chen and J. Graetz, ACS Appl. Mater. Interfaces, 2011, 3, 1380 CAS.
- S. Y. Chung, S. Y. Choi, T. Yamamoto and Y. Ikuhara, Phys. Rev. Lett., 2008, 100, 125502 CrossRef PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: List of potential parameters; comparison between calculated and experimental structures; alkali-ion migration barrier for along path A and C; formation energy for pair clusters in the case of ab and bc biaxial applied strain. See DOI: 10.1039/c5ta09418f |
| This journal is © The Royal Society of Chemistry 2016 |