Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Perpetual superhydrophobicity
Alberto
Giacomello
 *ab,
Lothar
Schimmele
b,
Siegfried
Dietrich
bc and
Mykola
Tasinkevych
*bc
*ab,
Lothar
Schimmele
b,
Siegfried
Dietrich
bc and
Mykola
Tasinkevych
*bc
aSapienza Università di Roma, Dipartimento di Ingegneria Meccanica e Aerospaziale, 00184 Rome, Italy. E-mail: alberto.giacomello@uniroma1.it; Tel: +39 06 44585200
bMax-Planck-Institut für Intelligente Systeme, 70569 Stuttgart, Germany. E-mail: miko@mf.mpg.de; Tel: +49 711 689-1949
cIV. Institut für Theoretische Physik, Universität Stuttgart, 70569 Stuttgart, Germany
First published on 7th October 2016
Abstract
A liquid droplet placed on a geometrically textured surface may take on a “suspended” state, in which the liquid wets only the top of the surface structure, while the remaining geometrical features are occupied by vapor. This superhydrophobic Cassie–Baxter state is characterized by its composite interface which is intrinsically fragile and, if subjected to certain external perturbations, may collapse into the fully wet, so-called Wenzel state. Restoring the superhydrophobic Cassie–Baxter state requires a supply of free energy to the system in order to again nucleate the vapor. Here, we use microscopic classical density functional theory in order to study the Cassie–Baxter to Wenzel and the reverse transition in widely spaced, parallel arrays of rectangular nanogrooves patterned on a hydrophobic flat surface. We demonstrate that if the width of the grooves falls below a threshold value of ca. 7 nm, which depends on the surface chemistry, the Wenzel state becomes thermodynamically unstable even at very large positive pressures, thus realizing a “perpetual” superhydrophobic Cassie–Baxter state by passive means. Building upon this finding, we demonstrate that hierarchical structures can achieve perpetual superhydrophobicity even for micron-sized geometrical textures.
1 Introduction
Superhydrophobicity refers to an important class of surface properties which include self cleaning,1 liquid repellency,2 anti-(bio)fouling, drag reduction,3etc. Superhydrophobicity is achieved by combining surface roughness and wetting properties† such that the geometrical features of the surface are filled by vapor.5 This corresponds to the so-called Cassie–Baxter state for which the liquid is in contact only with the topmost portions of the surface. This “suspended” state is fragile because the composite (solid/liquid plus liquid/vapor) interface may collapse into the fully wet Wenzel state in which the superhydrophobic properties are lost. The technological applications of superhydrophobicity are therefore severely limited by its fragility: depending on the environmental conditions and on the wetting history, a surface may or may not exhibit superhydrophobic properties. Here, we show that a class of nano-sized roughnesses is capable of destabilizing the Wenzel state thermodynamically, thus realizing virtually perpetual and robust superhydrophobicity.On rough hydrophobic surfaces the Cassie–Baxter state can be either stable or metastable depending on the thermodynamic conditions (e.g., pressure and temperature).6 The transition from the (meta)stable Cassie–Baxter state to the Wenzel state requires to overcome free energy barriers much larger than the thermal energy kBT, even for surface asperities of a few nanometers in size.7,8 These metastabilities generate strong hysteresis in the wetting and dewetting processes on such surfaces.9 On the other hand, the large free energy barriers also imply that once the system has occupied the Wenzel state, superhydrophobicity cannot be restored without supplying free energy to the system.
In order to restore superhydrophobicity from the Wenzel state the most effective strategy to date seems to be the application of an electric field to the system.10–12 Other methods include a magnetically driven Wenzel to Cassie–Baxter transition13 and heating of the surface until boiling restores the vapor pockets.14 All these active methods require special preparations of the surface and/or of the liquid as well as a free energy source; in addition, they cannot be easily applied to large surfaces.
Passive methods for restoring superhydrophobicity are in principle more economical and general than active ones. One strategy for trying to passively “stabilize” the Cassie–Baxter state is to shrink the size of surface decorations down to the nano-scale.15 For instance, by using carefully designed hydrophobic nano-textures of ca. 10 nm size it was possible to support pressures up to several tens of atmospheres before mechanical destabilization of the Cassie–Baxter state takes place at a certain critical pressure Pc.9 Verho et al. realized hierarchical structures via a regular texture (on the scale of ca. 10 μm) which is decorated by superhydrophobic silicon filaments (on the scale of 100 nm, grown on the micro-topography).16 With this two-level topography the transitions between nano- and micron-sized Cassie–Baxter states offer the opportunity that they can be reversibly switched by using either local suction (recovering the micron-sized Cassie–Baxter state from the nano-sized one) or a jet of water at low pressures (creating the nano-sized Cassie–Baxter state from the micron-sized one). Such passive approaches provide several advantages, but they do not eliminate the potential occurrence of the transition to the Wenzel state, which can always be realized by thermally activated events or pressure changes.
The aim of the present study is to introduce a completely passive method, which involves the thermodynamic destabilization of the Wenzel state over a wide range of pressures above the bulk liquid–vapor coexistence pressure. In this way, a virtually perpetual superhydrophobic Cassie–Baxter state is realized which is the only one allowed thermodynamically within that pressure range. As shown below, this can be achieved by properly choosing the surface chemistry and by scaling the size of the surface roughness, here modeled as an array of rectangular grooves, down to the nanometer range. The required size of the roughness actually depends on the contact angle of the surface; in principle the approach could work even with groove widths w of the order of 7 nm. For such surfaces, the Wenzel state can be eliminated for pressures as high as 5 atm.
The idea of eliminating the Wenzel state is based on the well-known fact that liquids have a spinodal, i.e., thermodynamic conditions for which the liquid state is unstable and disappears via cavitation. For pure liquids far from the critical point, the spinodal is observed at strongly negative pressures P (i.e., tensile stresses applied to liquid). For example, for bulk water at ambient temperature this is estimated to be around −150 MPa.17,18 However, by strongly confining the liquid it is possible to shift this spinodal to positive pressures P. This is known, e.g., for macroscopically extended hard19 and lyophobic slit pores20 (see also ref. 21–23). In ref. 20 the authors estimate that for confined water the liquid spinodal reaches, upon varying the pore width w, the bulk liquid–vapor coexistence line P0(T) at w ≈ 5 nm. Recent studies have proposed a special texture composed of a 2D square lattice of rectangular nano-pillars with added nano-particles at the centers of the lattice cells.24 Since in the fully wet Wenzel state the liquid penetrates into the surface geometric features, the following question arises: is it possible to destabilize thermodynamically the liquid confined within the surface features at positive values of the pressure by decreasing the spatial extent of the features? This would provide a means to achieve a perpetual superhydrophobic Cassie–Baxter state. The present systematic study provides a positive answer to the above question.
2 Model
Here we employ microscopic, classical density functional theory (DFT) with the aim of determining for various systems the spinodal pressure Psp of the confined liquid and the critical pressure Pc of destabilization of the Cassie–Baxter state. In particular, we study lyophobic nano-grooves of different widths (Fig. 1) and lyophobic slit pores.DFT is based on the minimization of the grand potential functional
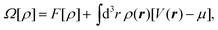 | (1) |
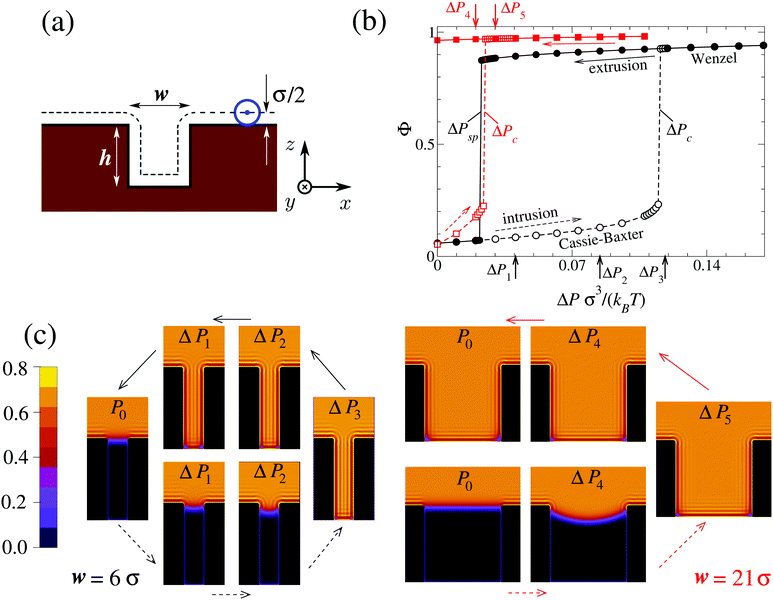
The geometry of the system is illustrated schematically in Fig. 1(a). Before introducing surface structures, the substrate occupies the lower half-space and is associated with Young's contact angle θY. For each particular system, θY is computed via independent calculations of the solid–vapor (γsv), solid–liquid (γsl), and liquid–vapor (γlv) interfacial tensions following Young's law cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θY ≡ (γsv − γsl)/γlv. In a second step, a rectangular groove of height h and width w is excavated from the solid material. Calculations of the wetting and dewetting processes in such grooves are performed using a DFT code28 applying periodic boundary conditions in the x and y directions. In these calculations the same mesh width of the computational grid has been used as in those carried out in order to determine θY. The temperature is kept fixed at T = 0.71Tc, where Tc is the critical temperature of the bulk fluid.
θY ≡ (γsv − γsl)/γlv. In a second step, a rectangular groove of height h and width w is excavated from the solid material. Calculations of the wetting and dewetting processes in such grooves are performed using a DFT code28 applying periodic boundary conditions in the x and y directions. In these calculations the same mesh width of the computational grid has been used as in those carried out in order to determine θY. The temperature is kept fixed at T = 0.71Tc, where Tc is the critical temperature of the bulk fluid.
3 Results and discussion
3.1 Pressure of the “groove”-liquid spinodal
In order to follow the metastable branch corresponding to the Cassie–Baxter (Wenzel) state at various pressures, we use initial conditions with the groove being filled with vapor (liquid). In a second step, we minimize the grand potential in eqn (1) in order to obtain ρ(r); the next point in the intrusion (extrusion) curve is obtained by initializing the system with the previous ρ(r) and increasing (decreasing) the pressure as shown by the dashed (solid) arrows in Fig. 1. Black (red) arrows correspond to w = 6σ (w = 21σ). In particular, Fig. 1(b) reports the filling fraction Φ ≡ N/(ρlVg) of the groove as a function of the pressure in the reservoir, while Fig. 1(c) shows the color-coded distribution ρ(r)σ3 which illustrates quantitatively the intrusion and extrusion processes. Here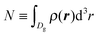 is the number of fluid particles inside the domain Dg of the groove; ρl is the bulk liquid density at the corresponding pressure and
is the number of fluid particles inside the domain Dg of the groove; ρl is the bulk liquid density at the corresponding pressure and 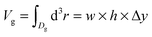 , with Δy being the groove extension in the y direction.
, with Δy being the groove extension in the y direction.
Fig. 1(b) shows that at the critical pressure Pc = ΔPc + P0 the intrusion branch jumps from the suspended Cassie–Baxter state (small Φ) to the completely filled Wenzel one (large Φ): Pc is the maximum pressure at which superhydrophobicity can survive, before it becomes mechanically unstable. It is well known that narrow grooves exhibit larger values of Pc (see the discussion below). What is more surprising in Fig. 1 is that for w = 6σ the extrusion branch jumps from the Wenzel state to the Cassie–Baxter state: this is the sought liquid spinodal pressure Psp > 0 in confinement (for w = 21σ (red) ΔPsp is negative). For P ≤ Psp, the Wenzel state is unstable and superhydrophobicity becomes perpetual.
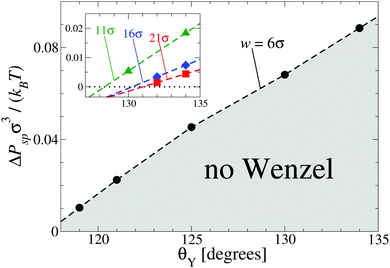
In order to understand how Psp depends on the characteristics of the surface, we performed DFT calculations similar to those leading to Fig. 1 for grooves with various widths and contact angles. The results reported in Fig. 2 show that by increasing the lyophobicity of the surface (i.e., upon increasing Young's contact angle θY) the Wenzel state can still be eliminated at ΔPsp > 0 even from increasingly wide grooves, up to w = 21σ (see red squares in Fig. 2). In summary, confinement and lyophobicity cooperate towards increasing Psp and can be engineered in order to obtain perpetual superhydrophobicity. By adopting a typical parameter value σ = 0.34 nm corresponding to the Lennard-Jones potential for Argon29 and setting T = 300 K, one can estimate that, for θY = 134°, in the case w = 6σ the Wenzel state remains eliminated up to ΔP = ΔPsp(θY) ≃ 9.3 MPa and in the case w = 21σ up to ΔP ≃ 0.5 MPa.
3.2 Grooves versus infinite slits
We now elucidate the influence of the substrate morphology on the liquid spinodal. We first calculate, via the same microscopic DFT, the (meta)stable states of the considered fluid in a slit pore of width w and confined between two infinitely extended planar walls having the same Young contact angle as the substrate from which the grooves in Fig. 1 are excavated. The slit pore calculations are performed via a 1d numerical code. In this well known case the two states to be considered are the capillary vapor and the capillary liquid.30 For θY = 121° the capillary liquid spinodal occurs at ΔPsp > 0 only for slit pores with w < 3σ (solid red line in Fig. 3(a)). In the case of grooves, however, the groove-liquid spinodal occurs at ΔPsp > 0 already for w ≲ 6σ (blue square). This demonstrates that the destabilization of the confined liquid is facilitated by the groove geometry. For the systems shown in Fig. 1 the groove height is sufficiently large to ensure that the upper portion of the groove de facto does not shift the liquid spinodal. Therefore, the density oscillations induced at the two corners at the groove bottom and at the bottom wall seem to be the main reason for the shift of the spinodal towards higher pressures as compared to a slit with the same width. It is useful to remark that this effect differs from wedge drying, because (i) θY < 135° and (ii) the presence of a single corner is insufficient to obtain ΔPsp ≥ 0 as demonstrated by the results for grooves with w > 21σ, for which ΔPsp < 0.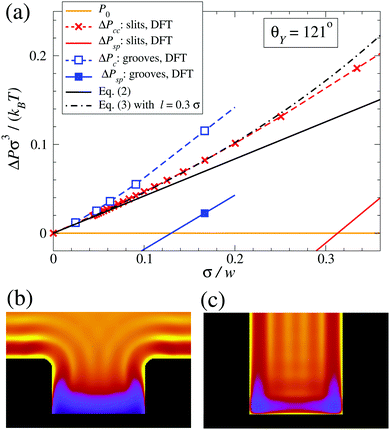 | ||
| Fig. 3 Summary of the main findings for lyophobic (θY = 121°) confined systems (rectangular grooves and slit pores). (a) Bulk liquid–vapor coexistence (orange) as well as capillary liquid and capillary vapor coexistence for slits at ΔPcc (red crosses, interpolated by the dashed red line); Kelvin–Laplace law (eqn (2), solid black line); corrected Kelvin–Laplace law with l = 0.3σ (eqn (3), dash-dotted black line). Concerning rectangular grooves, the interpolated open blue and solid blue squares represent ΔPc and ΔPsp, respectively; a second solid blue square occurs at ΔPsp < 0 and is not shown. Enlarged views of the liquid layering (b) near the top corners in the Cassie–Baxter state and (c) at the bottom corners in the Wenzel state for rectangular grooves with w = 6σ at the same pressure ΔP ≳ ΔPsp. | ||
The shift of the spinodal is caused by the strong layering in the liquid induced by the confinement (Fig. 3(c)): the layers form “interference-like” patterns within the groove, which become “destructive” for the liquid at the bottom corners. This triggers a density depletion at the bottom corners, which is further enhanced by the increased lyophobicity of the walls near the corners due to the “missing” fluid–fluid interactions at the corners as compared to a planar wall. For narrow grooves these depletion zones at the bottom corners become connected (see Fig. 3(c)) favoring the growth of a bubble and thus the formation of the Cassie–Baxter state. This mechanism has some resemblance to dewetting via the growth of unstable surface waves (see, e.g., Herminghaus et al.31). Evans and Stewart recently discussed how the local compressibility is enhanced at a lyophobic wall, thereby enhancing the density fluctuations;32 the present results suggest that the enhancement is even stronger at corners.
Another important parameter to characterize superhydrophobicity is the critical pressure Pc for which the Cassie–Baxter state ceases to be mechanically stable (Fig. 1(b)). At the macroscopic level of description Pc is determined by balancing the hydrostatic pressure, as given by the Laplace law, and the z component of the capillary forces acting upon the contact line due to the liquid–vapor surface tension γlv. In the case of rectangular grooves this force balance renders the Kelvin–Laplace law:
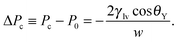 | (2) |
It is known that the Kelvin–Laplace law can be improved on the mesoscale by accounting for the formation of wetting films at the walls of the slit pore.33,34 This gives rise to the correction
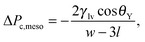 | (3) |
As shown in Fig. 3(a), the Kelvin–Laplace law, eqn (2), accurately predicts ΔPc for grooves with w ≥ 15σ. In the same range, eqn (2) also captures ΔPcc (dashed red line). For grooves and slit pores with w ≤ 15σ both ΔPc and ΔPcc, as obtained by DFT, are larger than what is predicted by eqn (2). More specifically, ΔPcc falls in between ΔPc and the Kelvin–Laplace law. By using l = 0.3σ, which is within a plausible range, as a fit parameter in eqn (3), we obtain a good agreement between ΔPcc and ΔPc,meso for w > 4σ (black dash-dotted line). In contrast to the macroscopic predictions, we find that the critical pressure ΔPc for intrusion is different from the capillary condensation pressure ΔPcc. Actually ΔPc is significantly higher than ΔPcc for small groove widths w. Before we discuss the physics behind this observation we also have to exclude potential numerical errors which could influence this result. First, ΔPcc is calculated by equating the free energies of a slit either filled with capillary liquid or with capillary vapor. Although within this treatment there is no explicit force balance at a liquid–vapor interface, the coexistence pressure, defined via the pressure in the reservoir, must be the same as one would obtain from a search for an indifferent liquid–vapor interface position in the slit. Numerics should not spoil this identity if otherwise the same conditions are chosen. A more serious source of error could be in the determination of ΔPc because the iterative computation of the fluid number densities close to the critical intrusion pressure converges very slowly. In order to ensure that metastable configurations have indeed been found and that, in the vicinity of the critical pressure, the appropriate intrusion pressure has not been missed, we carried out computations starting from distinct initial positions of the liquid–vapor interface and we increased the number of calculated pressures (see Fig. 1(b)). The error in ΔPc is estimated to be considerably smaller than the difference between ΔPc and ΔPcc.
With this we turn to the physical mechanism which can lead to the observed difference between ΔPc and ΔPcc. It has to be linked to the fact that a groove, in contrast to an infinite slit, has an open upper end and a capped bottom. Therefore, the wetting properties of a segment of a groove side wall depend on its depth in the groove, i.e., on its distance, say, from the upper corner. In a coarse picture, the wetting properties of a wall are determined by a balance of the loss of fluid–fluid interactions versus the gain in fluid–solid interactions due to the presence of the wall. For the lyophobic walls, as discussed here, one expects that the wall segments close to the upper corner are less lyophobic than an infinitely extended wall because less of the fluid–fluid interaction is replaced by the weaker fluid–solid interaction. Deeper in the groove the side wall segments become more lyophobic and, for a very deep groove, the wetting properties approach those of an infinitely extended slit. The precise characteristics of these effective properties of the wall depend on the details of the system. These generic considerations explain our observation of a partial intrusion. Liquid intrusion starting from the open upper end of the groove may progress to some depth below the open upper end where the side walls are less lyophobic, but it is stopped deeper in the groove as a result of the side walls becoming increasingly lyophobic (Fig. 3(b)). Whether the critical intrusion pressure ΔPc is larger than ΔPcc or not might depend on details of the shapes of the fluid–solid as well as of the fluid–fluid interaction. In our model the attractive part of both interactions is of the van der Waals type with, however, the fluid–fluid interaction cut off at 2.5σ. Therefore, at some distance below the upper corner of the groove the side wall of the groove becomes more lyophobic than an infinitely extended wall of the same material, because the missing fluid–solid interactions are still appreciable whereas the fluid–fluid interactions are cut off. This would lead to an enhancement of ΔPc over ΔPcc with the latter being based on the properties of infinitely extended walls. Of course intrusion into grooves is influenced additionally by specific confinement effects which become very pronounced for very small groove widths. For instance, the liquid–vapor interface at the open upper end of the groove has a structure (see Fig. 3(b)) which deviates significantly not only from that of a free liquid–vapor interface, but also from that between capillary liquid and capillary vapor deep inside the groove, which is a transient unstable configuration.
In order to summarize our remarks, deviations between ΔPcc and the Kelvin–Laplace law arise because for very narrow slits, due to various confinement effects, the force balance at a liquid–vapor interface in an infinitely extended slit cannot be reliably characterized in terms of size independent surface and interfacial tensions. Deviations between ΔPc and ΔPcc can occur because even quite deep into a groove the force balance at a liquid–vapor interface might still deviate from that in an infinitely extended slit; ΔPc is determined by the highest pressure required to push the liquid through the open upper end and further into the groove. In the present case, the two upper corners effectively enhance the lyophobicity of the groove, resulting in ΔPc > ΔPcc. In the general case, whether ΔPc is effectively enhanced over ΔPcc and to which extent will presumably depend on the detailed shapes of the fluid–solid and fluid–fluid interactions.
3.3 Hierarchical structures
In many applications, nano-structures such as those proposed here for realizing perpetual superhydrophobicity are too small to achieve effects of technological relevance. Important examples are submerged surfaces for drag reduction,3 in which slippage increases with the characteristic dimension of the texture.35 In such cases, and if it is advantageous to maximize the air volume of the Cassie–Baxter state, larger textures, say above one micrometer, should be used. Larger structures are also more resistant to mechanical wear.36 However, the composite interface associated with that scale is very fragile such that the ensuing superhydrophobic state easily breaks down into the Wenzel state, due to the very low corresponding values of ΔPc (see eqn (2)). In order to increase the stability of a composite interface, surfaces with multiscale hierarchical structures, as illustrated schematically in Fig. 4, have been suggested, e.g., in ref. 16 and 37.Here we propose the concept of perpetual superhydrophobicity, i.e., complete thermodynamic elimination of the Wenzel state, also for micron-sized geometrical textures. The basic idea is to utilize hierarchical surface structures, which exploit the perpetual superhydrophobicity of the nano-scale textures described above, in combination with the so-called wedge drying phenomenon38–40 at larger scales. Micron-sized wedges immersed in a liquid at bulk liquid–vapor coexistence, i.e., at ΔP = 0, exhibit spontaneous drying when the condition
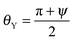 | (4) |
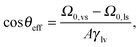 | (5) |
Within our model we computed θeffvia DFT for a nano-groove with w = 6σ, θY = 121°, and a solid fraction ϕs = 1/2 yielding θeff = 141°. This result is in fair agreement with the macroscopic estimate θCB ≃ 139° obtained by using the well-known macroscopic Cassie–Baxter equation42 cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θCB = ϕs(cos
θCB = ϕs(cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θY + 1) − 1 for describing the contact angle θCB of sessile droplets in the so-called “fakir regime”.43 In deriving this Cassie–Baxter equation, in the first step, effective solid–fluid interfacial tensions are calculated as area weighted averages of the solid–fluid and vapor–fluid interfacial tensions, which characterize the patches forming the actual surface. In the second step, these effective interfacial tensions are used in Young's law leading to the above expression for cos
θY + 1) − 1 for describing the contact angle θCB of sessile droplets in the so-called “fakir regime”.43 In deriving this Cassie–Baxter equation, in the first step, effective solid–fluid interfacial tensions are calculated as area weighted averages of the solid–fluid and vapor–fluid interfacial tensions, which characterize the patches forming the actual surface. In the second step, these effective interfacial tensions are used in Young's law leading to the above expression for cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θCB. In order to support the proposed wedge-drying mechanism for restoring the Cassie–Baxter state on the micro-scale, the nano-sized surface structure must be in the Cassie–Baxter state which is guaranteed if it is perpetual. Otherwise, once the liquid has intruded the nano-texture, a nucleus of vapor forming at the edge of a wedge cannot grow, even if it is favored thermodynamically for θY > 135°, as the result of strong pinning of the liquid–vapor interface near the intruded liquid pockets. Therefore, in this case the proposed wedge-drying mechanism becomes ineffective. In contrast to that, in the nano-sized Cassie–Baxter state this pinning is much weaker and we expect this mechanism to be effective.
θCB. In order to support the proposed wedge-drying mechanism for restoring the Cassie–Baxter state on the micro-scale, the nano-sized surface structure must be in the Cassie–Baxter state which is guaranteed if it is perpetual. Otherwise, once the liquid has intruded the nano-texture, a nucleus of vapor forming at the edge of a wedge cannot grow, even if it is favored thermodynamically for θY > 135°, as the result of strong pinning of the liquid–vapor interface near the intruded liquid pockets. Therefore, in this case the proposed wedge-drying mechanism becomes ineffective. In contrast to that, in the nano-sized Cassie–Baxter state this pinning is much weaker and we expect this mechanism to be effective.
4 Conclusions
Microscopic density functional theory has shown that the fragility of the superhydrophobic state can be entirely healed by a combination of nano-scale surface texturing (ca. 2 nm) and lyophobic coating (θY = 121°). Nanoconfinement shifts the liquid spinodal to very large pressures, up to 2.4 MPa, completely eliminating the Wenzel state over this very broad range of pressures. Thus the proposed passive strategy is expected to be robust against thermal fluctuations and abrupt changes in the liquid pressure. In addition, the critical pressure for the transition of the Cassie–Baxter state to the Wenzel state is also increased by nano-confinement, more than what can be expected based on the Kelvin–Laplace law (eqn (2)). Both effects are highly beneficial for the applications of superhydrophobicity and call for thorough wetting experiments on nano-structured surfaces. Based upon these properties of the nano-textured surfaces, hierarchical structures could be designed which would also support perpetual superhydrophobicity at the micro-scale. Here, the key requirements for the nano-textures are: (i) the occurrence of the spinodal of the nano-confined liquid at ΔPsp > 0; and (ii) sufficiently large values of the effective Cassie–Baxter contact angle.Appendix: density functional theory
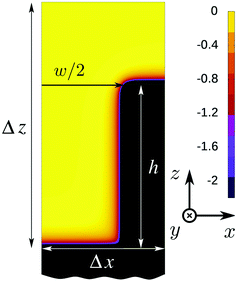
In this study we use the fundamental measure theory (FMT) due to Rosenfeld,25,26 which has been implemented into an in-house numerical code as described already elsewhere.28 Further details on this type of classical density functional theory are found in the review by Roth.27Here we describe the computational domains used for obtaining the intrusion and extrusion curves presented above. The densities have been discretized on a grid and in most calculations a mesh size of 0.05σ has been used. For comparison some computations have been repeated with a smaller mesh size of 0.025σ. From a semi-infinite wall occupying the lower half space, a parallelepipedic groove is excavated (Fig. 5). The height of the groove is fixed to the value h = 20σ while various widths are considered: w = 6σ, w = 11σ, w = 16σ, w = 21σ, and w = 41σ. Since for technical reasons we have used a 3D DFT, despite the translational invariance of the system in the y direction, our computational box has a finite extent in this direction for which we have chosen periodic boundary conditions. In order to speed up the calculations, actually only one half of the domain is considered, applying symmetric boundary conditions to the left side of the domain (see Fig. 5). To the right side also reflecting boundary conditions are applied which are equivalent to having a mirror symmetry plane along the y–z plane, i.e., we effectively treat a periodic array of grooves aligned along the y axis. The box dimensions in the x direction have been chosen such that the ridge separating the grooves has a width of 20σ. A constant number density is imposed at the top boundary of the computational box, which is equivalent to prescribing the pressure in the system far away from the wall. At the bottom boundary there is the wall.
The external substrate potential V(r) is the sum of a repulsive contribution Vrep(r) and an attractive one Vatt(r): V(r) = Vrep(r) + Vatt(r). We account for Vrep(r) in terms of a hard-sphere repulsion, chosen such that the distance of closest approach is σ/2, i.e., the radius of the fluid particles. Vrep(r) is set to infinity inside the zone of closest approach. Vatt(r) is taken as the linear superposition of the attractive part Φw of a Lennard-Jones potential between the fluid particles and the particles forming the wall with a number density ρw:
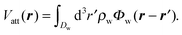 | (6) |
The pressure is calculated from the following bulk equation of state (which corresponds to the density functional which is used here):
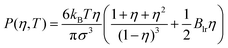 | (7) |
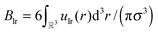 . The chemical potential μ of the reservoir can be expressed as a function of η and T:
. The chemical potential μ of the reservoir can be expressed as a function of η and T: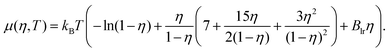 | (8) |
The density (or, equivalently, the pressure) is always chosen to lie either on the liquid side or at liquid–vapor coexistence of the bulk phase diagram. The computational domain has a total extent of Δx × Δy × Δz = (w/2 + 10σ) × 5σ × 35.5σ. This domain is discretized with 20 points per σ for a total of ca. 40 millions of points for the domain in Fig. 5.
References
- W. Barthlott and C. Neinhuis, Planta, 1997, 202, 1–8 CrossRef CAS.
- A. Tuteja, W. Choi, J. M. Mabry, G. H. McKinley and R. E. Cohen, Proc. Natl. Acad. Sci. U. S. A., 2008, 105, 18200–18205 CrossRef CAS PubMed.
- J. P. Rothstein, Annu. Rev. Fluid Mech., 2010, 42, 89–109 CrossRef.
- T. Liu and C. Kim, Science, 2014, 346, 1096–1100 CrossRef CAS PubMed.
- A. Lafuma and D. Quéré, Nat. Mater., 2003, 2, 457–460 CrossRef CAS PubMed.
- A. Giacomello, M. Chinappi, S. Meloni and C. M. Casciola, Phys. Rev. Lett., 2012, 109, 226102 CrossRef PubMed.
- T. Koishi, K. Yasuoka, S. Fujikawa, T. Ebisuzaki and X. Zeng, Proc. Natl. Acad. Sci. U. S. A., 2009, 106, 8435–8440 CrossRef CAS PubMed.
- A. Giacomello, S. Meloni, M. Chinappi and C. M. Casciola, Langmuir, 2012, 28, 10764–10772 CrossRef CAS PubMed.
- A. Checco, B. Ocko, A. Rahman, C. T. Black, M. Tasinkevych, A. Giacomello and S. Dietrich, Phys. Rev. Lett., 2014, 112, 216101 CrossRef.
- T. N. Krupenkin, J. A. Taylor, E. N. Wang, P. Kolodner, M. Hodes and T. R. Salamon, Langmuir, 2007, 23, 9128–9133 CrossRef CAS PubMed.
- R. J. Vrancken, H. Kusumaatmaja, K. Hermans, A. M. Prenen, O. Pierre-Louis, C. W. Bastiaansen and D. J. Broer, Langmuir, 2009, 26, 3335–3341 CrossRef PubMed.
- G. Manukyan, J. Oh, D. Van Den Ende, R. Lammertink and F. Mugele, Phys. Rev. Lett., 2011, 106, 014501 CrossRef CAS PubMed.
- Z. Cheng, H. Lai, N. Zhang, K. Sun and L. Jiang, J. Phys. Chem. C, 2012, 116, 18796–18802 CAS.
- G. Liu, L. Fu, A. V. Rode and V. S. Craig, Langmuir, 2011, 27, 2595–2600 CrossRef CAS PubMed.
- M. Amabili, A. Giacomello, S. Meloni and C. M. Casciola, Adv. Mater. Interfaces, 2015, 2, 1500248 CrossRef.
- T. Verho, J. T. Korhonen, L. Sainiemi, V. Jokinen, C. Bower, K. Franze, S. Franssila, P. Andrew, O. Ikkala and R. H. Ras, Proc. Natl. Acad. Sci. U. S. A., 2012, 109, 10210–10213 CrossRef CAS PubMed.
- Q. Zheng, D. J. Durben, G. H. Wolf and C. A. Angell, Science, 1991, 254, 829–832 CAS.
- M. El Mekki Azouzi, C. Ramboz, J.-F. Lenain and F. Caupin, Nat. Phys., 2013, 9, 38–41 CrossRef.
- D. Bérard, P. Attard and G. Patey, J. Chem. Phys., 1993, 98, 7236–7244 CrossRef.
- K. Lum, D. Chandler and J. D. Weeks, J. Phys. Chem. B, 1999, 103, 4570–4577 CrossRef CAS.
- D. Bratko, R. Curtis, H. Blanch and J. Prausnitz, J. Chem. Phys., 2001, 115, 3873–3877 CrossRef CAS.
- T. M. Truskett, P. G. Debenedetti and S. Torquato, J. Chem. Phys., 2001, 114, 2401–2418 CrossRef CAS.
- A. Luzar, J. Phys. Chem. B, 2004, 108, 19859–19866 CrossRef CAS.
- S. Prakash, E. Xi and A. Patel, Proc. Natl. Acad. Sci. U. S. A., 2016, 113, 5508–5513 CrossRef CAS PubMed.
- Y. Rosenfeld, Phys. Rev. Lett., 1989, 63, 980–983 CrossRef CAS PubMed.
- Y. Rosenfeld, M. Schmidt, H. Löwen and P. Tarazona, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 1997, 55, 4245–4263 CrossRef CAS.
- R. Roth, J. Phys.: Condens. Matter, 2010, 22, 063102 CrossRef PubMed.
- S. L. Singh, L. Schimmele and S. Dietrich, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2015, 91, 032405 CrossRef PubMed.
- A. Rahman, Phys. Rev., 1964, 136, A405–A411 CrossRef.
- R. Evans, U. Marini Bettolo Marconi and P. Tarazona, J. Chem. Phys., 1986, 84, 2376–2399 CrossRef CAS.
- S. Herminghaus, K. Jacobs, K. Mecke, J. Bischof, A. Fery, M. Ibn-Elhaj and S. Schlagowski, Science, 1998, 282, 916–919 CrossRef PubMed.
- R. Evans and M. C. Stewart, J. Phys.: Condens. Matter, 2015, 27, 194111 CrossRef CAS PubMed.
- B. V. Derjaguin, Acta Physicochim. URSS, 1940, 12, 181 Search PubMed.
- R. Evans and U. Marini Bettolo Marconi, Chem. Phys. Lett., 1985, 114, 415–422 CrossRef CAS.
- C. Ybert, C. Barentin, C. Cottin-Bizonne, P. Joseph and L. Bocquet, Phys. Fluids, 2007, 19, 123601 CrossRef.
- X. Tian, T. Verho and R. H. A. Ras, Science, 2016, 352, 142–143 CrossRef CAS PubMed.
- B. Bhushan, Y. C. Jung and K. Koch, Philos. Trans. R. Soc., A, 2009, 367, 1631–1672 CrossRef CAS PubMed.
- R. Roth and A. O. Parry, Mol. Phys., 2011, 109, 1159–1167 CrossRef CAS.
- R. Roth and A. O. Parry, J. Phys. Soc. Jpn., 2012, 81, SA009 CrossRef.
- A. Malijevský and A. O. Parry, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2015, 91, 052401 CrossRef PubMed.
- K. Rejmer, S. Dietrich and M. Napiórkowski, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 1999, 60, 4027–4042 CrossRef CAS.
- A. B. D. Cassie and S. Baxter, Trans. Faraday Soc., 1944, 40, 546–551 RSC.
- Z. Yoshimitsu, A. Nakajima, T. Watanabe and K. Hashimoto, Langmuir, 2002, 18, 5818–5822 CrossRef CAS.
Footnote |
| † This generally requires a Young's contact angle θY > 90°. However, special reentrant2 and doubly reentrant4 textures can achieve a “superomniphobic” behavior, i.e., they also repel liquids with θY < 90°. |
| This journal is © The Royal Society of Chemistry 2016 |