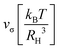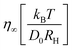DOI:
10.1039/C6SM01616B
(Paper)
Soft Matter, 2016,
12, 8825-8832
Divergence of the third harmonic stress response to oscillatory strain approaching the glass transition†
Received
15th July 2016
, Accepted 5th October 2016
First published on 7th October 2016
Abstract
The leading nonlinear stress response in a periodically strained concentrated colloidal dispersion is studied experimentally and by theory. A thermosensitive microgel dispersion serves as well-characterized glass-forming model, where the stress response at the first higher harmonic frequency (3ω for strain at frequency ω) is investigated in the limit of small amplitude. The intrinsic nonlinearity at the third harmonic exhibits a scaling behavior which has a maximum in an intermediate frequency window and diverges when approaching the glass transition. It captures the (in-) stability of the transient elastic structure. Elastic stresses in-phase with the third power of the strain dominate the scaling. Our results qualitatively differ from previously derived scaling behavior in dielectric spectroscopy of supercooled molecular liquids. This might indicate a dependence of the nonlinear response on the symmetry of the external driving under time reversal.
1 Introduction
A viscoelastic fluid exhibits an elastic stress response to a rapid deformation before flowing viscously at long times. The crossover time from elastic to viscous behavior is given by the final relaxation time τ. The origin of viscoelasticity in glass-forming systems lies in slow structural rearrangements, which require longer and longer time spans when lowering the temperature or increasing the density. Yet, while it is well established that cooperative structural processes cause the emergence of rigidity, their precise microscopic description remains unknown.1 Because the hallmark of vitrification is the change in the visco-elastic response, external fields that couple to the incipient solidity can be expected to have drastic effects. To study the nonlinear rheological response thus promises to throw light on the structural processes.
Applying oscillatory shear strain and increasing the amplitude of the deformation, a sharp transition to plastic flow was discovered in athermal particle systems.2 If thermal fluctuations are present and trigger local displacements of particles from their time-averaged sites,3 the yielding of colloidal glass requires the shear-induced breaking of cages formed by neighboring particles.4–7 Varying amplitude and frequency, studies using large amplitude oscillatory shear (LAOS) observe a rich mechanical and structural response, and have been performed in fluid8 and glass-forming states.9–11 Recently, the application of medium amplitude oscillatory shear (MAOS) has been advocated12–16 to determine the frequency-dependent spectra of the leading nonlinear response. MAOS can be considered a direct extension of the linear response approach.
Bouchaud and Biroli argued on fundamental grounds that the nonlinear response in glassy systems should be important in general.17 Alluding to the well-understood case of continuous phase transitions among equilibrium phases, they argued that nonlinear susceptibility spectra detect the long sought-after domains of cooperative motion in supercooled liquids and record their growth at the glass transition. The response at the third harmonic of the applied sinusoidal perturbation records the number of cooperatively coupled molecules, which is predicted to diverge as captured in detailed α- and β-scaling laws at the glass transition.18 These predictions were crucial for enabling nonlinear dielectric spectroscopy to test the underlying theories about cooperative dynamics.19–21
In the present contribution, we study the mechanical nonlinear susceptibility arising at the third harmonic in the stress response of a glass-forming colloidal dispersion driven by sinusoidal shear strain. Combining high-sensitivity rheological measurements on a well-characterized model glass-former with numerical and theoretical calculations in mode coupling theory (MCT), we establish that the nonlinear response function measured at the third harmonic diverges when approaching the glass transition. However, we find fundamental differences to the nonlinear response scenario predicted by Bouchaud and Biroli, and show that for the present case another class of scaling laws holds. Our experimental measurements of higher harmonic distortions in harmonically sheared colloidal dispersions rest on technical developments in Fourier transform rheology,22 including increased sensitivity,23 and the development and characterization of a colloidal model dispersion.24 Our theoretical investigations take place in the framework of MCT.25 It was developed to describe the structural relaxation in quiescent glass-forming liquids and rationalizes many phenomena observed in colloidal dispersions close to their glass transition.26 It also enters the discussion by Bouchaud and Biroli of the nonlinear spectra in supercooled molecular liquids, and its generalization to shear-driven Brownian systems27 gives the starting point for our analysis of the third harmonic response.
2 Fundamentals
2.1 Rheology
We consider the mechanical response caused by a prescribed oscillatory shear strain| | γ(t) = γ0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ωt, ωt, | (1) |
characterized by the strain amplitude γ0 and the angular frequency ω. The time-dependent shear stress σ(t) is determined by a generalized response function G(t,t′) of the material:11| | 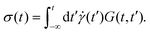 | (2) |
Here, G(t,t′) encodes the (in general strain-dependent) material response at time t to shearing at the earlier time t′. The stress signal can be Fourier-analyzed, which gives the harmonic contributions| | 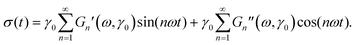 | (3) |
The in-phase (Gn′) and out-of-phase (Gn′′) moduli are the real and imaginary parts of the complex modulus Gn(ω) at the nth harmonic and arise as Fourier coefficients of the stress σ(t), which (after transient effects that are already neglected in (2)) is periodic in time with period 2π/ω. Several LAOS analysis frameworks have emerged over the years: Fourier decomposition,22 stress decomposition,28 Chebishev polynomials13 and the sequence of physical processes approach29 have been used to analyze the controlled sinusoidal strain experiment. These methods have also been adopted to stress driven experiments,13,30,31 and differences of both techniques in viscoelastic materials were discussed.32 We will focus on frequency dependent spectra because they contain important information on the competition between external driving and intrinsic viscoelastic response.17
2.2 Mode coupling theory
We require a physical model (viz. constitutive equation) for the nonlinear response function G(t,t′), which shall be taken from MCT. MCT identifies G(t,t′) as transient, strain-dependent stress auto-correlation function. Further, it assumes that stress fluctuations result from structural rearrangements, which are encoded in a transient density correlation function Φ(t,t′). The essence of the MCT approach then lies in formulating a self-consistently closed equation of motion for the density correlation function, which captures the slowing down of the internal structural dynamics by the caging of particles and the loss of memory caused by the external shear driving. The model from ref. 33 is used and solved in the Materials and methods appendix and the ESI.†
2.3 Linear response moduli
The general response simplifies in the regime of small strain amplitudes, γ0 → 0. Here the stress becomes linear in the strain and the response function turns into the equilibrium shear-stress auto-correlation function Geq according to the fluctuation dissipation relation. Because it is time-translationally invariant, Geq(t,t′) = Geq(t − t′), the shear stress in linear response varies only with the fundamental frequency of the external strain (viz. n = 1 in (3)), and the familiar storage and loss moduli of linear response are given by the one-sided Fourier-transformation of Geq(t).34
Viscoelasticity in the linear response rheological moduli is one of the hallmarks of glass-formation. In the intermediate frequency window of predominantly elastic behavior – MCT calls it β-process – the elastic modulus takes a finite value, and the loss modulus exhibits a broad minimum. MCT predicts an asymptotic scaling-law for the frequency-dependent linear moduli 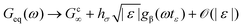 , where the parameter ε denotes the relative separation from the glass transition, which lies at ε = 0. The critical elastic constant Gc∞ measures the rigidity surviving in fluid states for high enough frequencies,3 the amplitude factor hσ links stress to structure, and the β-scaling function gβ contains the universal critical variation. It exhibits two power laws in a fluid state (ε < 0): the so-called critical law (exponent a) and the von Schweidler law (exponent −b) where a and b are material dependent.25 For the present model, a = 0.32 and b = 0.63. The β-scaling time tε diverges as a power law when approaching the glass transition, tε ∝ |ε|−1/(2a); albeit more slowly than τ ∝ |ε|−γ, with γ = (a + b)/(2ab). The β-scale can most easily be read off from the minimum in Geq′′(ω). Only for frequencies below the β-minimum, the final (or α-) relaxation commences and captures the decay of the elasticity in the fluid and the establishment of viscous flow with a finite Newtonian viscosity. The α-process shows up as a broad maximum in the loss modulus around the frequency where both moduli cross.
, where the parameter ε denotes the relative separation from the glass transition, which lies at ε = 0. The critical elastic constant Gc∞ measures the rigidity surviving in fluid states for high enough frequencies,3 the amplitude factor hσ links stress to structure, and the β-scaling function gβ contains the universal critical variation. It exhibits two power laws in a fluid state (ε < 0): the so-called critical law (exponent a) and the von Schweidler law (exponent −b) where a and b are material dependent.25 For the present model, a = 0.32 and b = 0.63. The β-scaling time tε diverges as a power law when approaching the glass transition, tε ∝ |ε|−1/(2a); albeit more slowly than τ ∝ |ε|−γ, with γ = (a + b)/(2ab). The β-scale can most easily be read off from the minimum in Geq′′(ω). Only for frequencies below the β-minimum, the final (or α-) relaxation commences and captures the decay of the elasticity in the fluid and the establishment of viscous flow with a finite Newtonian viscosity. The α-process shows up as a broad maximum in the loss modulus around the frequency where both moduli cross.
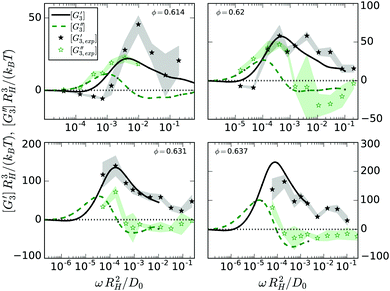
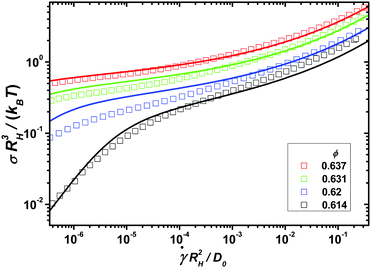
In order to identify the relevant frequency windows for the later analysis of the nonlinear response, the linear viscoelastic moduli of the model colloidal glass-forming dispersion are displayed in Fig. 1 using the hydrodynamic radius RH, the thermal energy kBT, and the diffusion coefficient at infinite dilution D0 to set the scales. Following ref. 35 we estimate the volume fractions of the measured samples as ϕ = 0.614, 0.62, 0.631 and 0.637, which are high owing to the noticeable particle size polydispersity of 17%. With increasing packing fraction, the α- and β-scaling regimes in the moduli shift to lower frequencies.
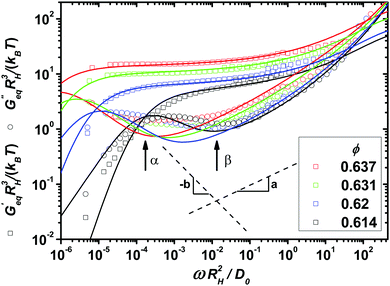 |
| | Fig. 1 Symbols represent the experimentally measured equilibrium storage and loss moduli of a model glass-forming dispersion of colloidal (near-) hard spheres at four different packing fractions ϕ approaching the glass transition. Lines show fits of the MCT model to the data using the parameters in Table 1. Labeled arrows mark the crossing of Geq′(ω) and Geq′′(ω) and the minimum in Geq′′(ω), both at ϕ = 0.614. Dashed lines indicate the two spectral power laws of MCT's β-scaling regime. | |
The schematic MCT model captures these trends reasonably. It is fitted to the linear response data following the procedure developed by ref. 35 described in the Materials and methods section, which gives the model parameters displayed in Table 1 of that section. The fit parameters provide insights into the applicability of the asymptotic laws of MCT. Asymptotically close to the transition, all changes in the spectra should be captured by the separation parameter ε = (ϕ − ϕc)/ϕc, where ϕc is the packing fraction at the glass transition. Yet, additional density dependences restrict an unambiguous application of the β-scaling law to the larger two densities.
Table 1 Parameters of the model fitted to the experimental linear moduli and flow curves shown in Fig. 1 and 8
|
T [°C] |
ϕ
|
ε
|
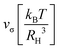
|
γ
c
|
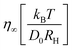
|
| 22 |
0.614 |
−1.7 × 10−3 |
60 |
0.26 |
0.361 |
| 20 |
0.62 |
−4.5 × 10−4 |
75 |
0.32 |
0.375 |
| 18 |
0.631 |
−2.4 × 10−4 |
125 |
0.29 |
0.40 |
| 15 |
0.637 |
−1.5 × 10−4 |
167 |
0.29 |
0.418 |
3 Results
3.1 Third order nonlinear response
When the amplitude of the applied sinusoidal strain is not small anymore, corrections to the linear spectra arise. Performing a straightforward Taylor expansion of the shear term in the MCT equations of motion for small but finite strain amplitude γ0, and inserting the solution into the form for the shear stress, (2) gives a correction to the linear response relation valid:
| G1(ω,γ0) = Geq(ω) + γ02[G1(ω)] + O(γ04) |
| | | G3(ω,γ0) = γ02[G3(ω)] + O(γ04), | (4) |
while all higher coefficients are negligible, Gn>3 = O(γ04). The nonlinear signal can directly be observed at the third harmonic. The MCT equations for [G1(ω)] and [G3(ω)] (our notation follows ref. 13) are solved in the Materials and methods section and in the ESI.† The amplitude of the third harmonic with respect to the first can then be studied by looking at the ratio of amplitudes36| | 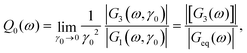 | (5) |
which becomes strain independent for γ0 → 0 and thus captures the intrinsic nonlinearity of the system.
3.2 Experimental results
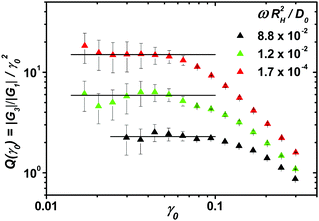
The intrinsic nonlinearity Q0(ω) of the third harmonic response measured in MAOS is shown in Fig. 2 for the same samples as in Fig. 1. Q0 exhibits a maximum which increases and moves to lower frequencies with increasing packing fraction. The position of the maximum lies close to and scales with the minimum frequency seen in Geq′′(ω); from ϕ = 0.614 to ϕ = 0.62 it shifts by about one decade to lower frequency. The intrinsic nonlinearity is maximal in the β-process window and becomes suppressed for lower frequencies during the α-process. A power law variation of the high-frequency side of the peak in Q0 with exponent a = 0.32 is compatible with the data which approximately collapse there. The small spectral range excludes similar statements below the maximum.
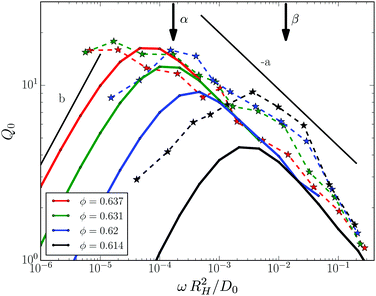 |
| | Fig. 2 Intrinsic nonlinearity Q0(ω) of the third harmonic versus rescaled frequency. Measured data are given as symbols connected by dashed lines as guides to the eye. Taylor approximation results obtained from MCT are given as solid lines with matching colors. The corresponding spectra of the linear response are given in Fig. 1, which were used to determine the model parameters (given in Table 1). Two arrows with labels mark the position of the β-process minimum and of the α-process maximum in Geq′′(ω) at ϕ = 0.614, read-off in Fig. 1. Two power laws are indicated by straight lines with exponents b and −a; see text for discussion. | |
Numerical results for Q0(ω) from MCT obtained by Taylor expansion are included with the experimental data in Fig. 2 and are given as lines. As the model parameters were fixed already, there are no adjustable parameters in the comparison of experiment and theory, which agree on the qualitative trends. Except for some mismatch in the overall amplitude, theory captures the intrinsic nonlinearity semi-quantitatively for the two lower packing fractions. For the two higher packing fractions, theory predicts a stronger variation with packing fraction than seen experimentally. This deviation in the nonlinear spectra matches the deviation already noticed in the linear spectra in Fig. 1, and may indicate a smearing of the singularity of idealized MCT well familiar from many experiments very close to the glass transition.37
3.3 Scaling laws of the third harmonic response
After having verified that the third harmonic response can be determined experimentally and follows the general frame given by theory, we turn to numerical and analytical solutions of the MCT model to discuss the nonlinearity of the third harmonic spectrum Q0 (defined in (5)) in detail. It requires to find [G3(ω)], the leading stress response at the third harmonic, when approaching the glass transition, viz. for ε → 0−.
The calculated Q0(ω,ε) in Fig. 3 exhibit a maximum, which scales with ε. The inset shows that the maximum is a feature of [G3], as the first harmonic |Geq| is monotonous in the respective frequency region. The height of the maximum diverges with 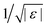 and its position shifts with 1/tε; it lies in the center of the β-process window close to the minimum of G′′. The scaling master curve (see Fig. 4a), exhibits two power laws (see ESI†). The right flank behaves as ω−a, the left as ωb. The scaling with ωb gets more pronounced upon approaching the glass transition because corrections arising from the α-process get suppressed (recall that τ diverges more strongly than tε). For frequencies smaller than the maximum, the curves for different ε collapse onto a second scaling master function valid in the α-process. Collapse in Fig. 4b holds when the frequency is rescaled by ω/|ε|γ, while the amplitude does not depend on the distance to the glass transition. Rather, the nonlinearity vanishes with decreasing frequency: the curves are proportional to ω2 for ωτ ≪ 1. This quasistatic limit, see ESI,† is included as dotted lines in Fig. 3 and 4.
and its position shifts with 1/tε; it lies in the center of the β-process window close to the minimum of G′′. The scaling master curve (see Fig. 4a), exhibits two power laws (see ESI†). The right flank behaves as ω−a, the left as ωb. The scaling with ωb gets more pronounced upon approaching the glass transition because corrections arising from the α-process get suppressed (recall that τ diverges more strongly than tε). For frequencies smaller than the maximum, the curves for different ε collapse onto a second scaling master function valid in the α-process. Collapse in Fig. 4b holds when the frequency is rescaled by ω/|ε|γ, while the amplitude does not depend on the distance to the glass transition. Rather, the nonlinearity vanishes with decreasing frequency: the curves are proportional to ω2 for ωτ ≪ 1. This quasistatic limit, see ESI,† is included as dotted lines in Fig. 3 and 4.
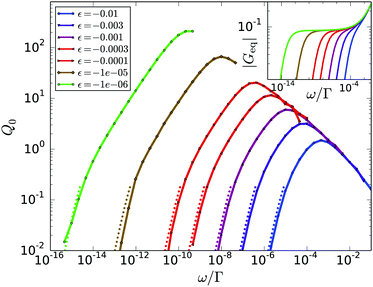 |
| | Fig. 3 Intrinsic nonlinearity Q0(ω) from MCT versus frequency ω/Γ for different distances ε to the glass transition. The small dots connected by lines indicate numerically calculated values, the lines are guides for the eyes. The cutoff of the curves is due to loss of numerical stability. The dotted lines are the corresponding quasi-static solutions valid for ω → 0. Q0 shows a maximum that is not seen in the corresponding linear response amplitudes used for normalization (see inset). | |
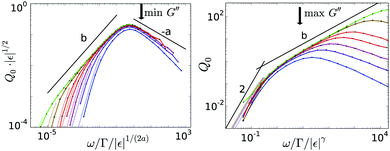 |
| | Fig. 4 Left panel: Scaling of the maximum of Q0 in the β-regime: the colored lines are the same numerical data as shown in Fig. 3, the black lines indicate the slopes of the asymptotic power laws. The height of the maximum scales with |ε|1/2, and lies in the center of the β-process window close to the minimum of G′′ (see arrow). The right flank behaves as ω−a, the left as ωb, with a = 0.32 and b = 0.69. Right panel: Scaling of Q0 in the window of the α-process: again, colored lines are the data shown originally in Fig. 3, the black lines indicate the asymptotic power law behaviors. The crossover is roughly a decade below the α-maximum of Geq′′ (see arrow). | |
3.4 Third-harmonic complex modulus
Beyond the scaling form of the amplitude, the complex third-harmonic modulus provides information on the character of the viscoelastic response.14 The elastic response proportional to the cube of the strain is given by [G3′(ω)] and the viscous response proportional to the cube of the strain rate is given by [G3′′(ω)]. The behavior we find in the α-regime of flow is generic for viscoelastic materials: [G3′′(ω)] peaks around 1/τ slightly above where [G′(ω)] changes sign from negative to positive. Yet, the behavior in the β-process window signals the breakdown of the elastic behavior. Fig. 5 shows that the elastic [G3′(ω)] dominates there, while [G3′′(ω)] has a zero-crossing and consequently is rather small. In the regime of the critical power-law, [G3′′(ω)] is strongly negative, which is absent in models without β-process.14 Interestingly, the functional shape is different also from the nonlinear conductivity in ionic systems, where the shape of the third-harmonic is discussed in hopping models.38
 |
| | Fig. 5 Elastic, [G3′(ω)], and dissipative, [G3′′(ω)], moduli at the third harmonic versus frequency; panels give data (symbols with shadings indicating error-bars) and theoretical predictions (lines) for each packing fraction as labeled. Note the different scales on the axes of the panels. | |
4 Discussion
We studied the nonlinear stress response at the third harmonic frequency of a sinusoidal perturbing strain for small amplitudes in terms of the intrinsic nonlinearity Q0. It gives the amplitude of the leading nonlinear spectrum relative to the equilibrium linear response. We find a good qualitative and quantitative agreement between the experimental and the MCT results – deviations in Q0 do not exceed a factor of two in a frequency range of over five decades. The nonlinear response diverges close to the glass transition and universal scaling laws can be derived theoretically, which rationalize the increase and shift of the measured spectra. This divergence only takes place in the β-process window, where elastic processes dominate in equilibrium, and is cut-off in the α-relaxation window at lower frequencies. Comparison with the linear response moduli shows that this is a feature of the nonlinear third harmonic, and not a property derived from the linear response moduli. The divergence of the nonlinear correction naturally limits the regime where linear response is valid. We find that this regime shrinks most quickly in the intermediate β-frequency window.
The discovered divergence of the intrinsic nonlinearity in the β-process window upon approaching the glass transition indicates the sensitivity of the incipient glass structure to the external deformation. In this frequency window characterized by the time scale tε, the dominant linear response of the stress in the material is elastic. Yet, this elastic structure has a finite life-time and is not stable with respect to thermal fluctuations; it will relax during the final α-relaxation. The external periodic strain causes large nonlinear reactions of the fragile elastic structure while it is still metastable. At lower frequencies, where the elastic structure has started to relax already by equilibrium structural processes, additional driving provided by the external straining has little effect. Thus the intrinsic nonlinearity decreases during the final (α-) relaxation and has its maximum in the β-process window.
Our results can be compared with similar nonlinear quantities derived for dielectric systems.17,18 The susceptibility χ3(ω) gives the (normalized) nonlinear response at the third harmonic frequency of the applied external electric field and thus plays an analogous role as the third-harmonic modulus [G3(ω)] under strain. The scaling of their absolute values with frequency and separation ε to the glass transition is compared in Fig. 6. (The scaling of [G3(ω)] closely follows the one of Q0 and can readily be obtained from Fig. 3.) The power-law at the critical point of MCT (at ε = 0) agrees in both response functions and is given by [G3(ω)], χ3(ω) ∝ ω−a; it diverges for ω → 0. (The different spectra at larger frequencies depend on microscopic details.) In supercooled states, for ε < 0, both response functions exhibit the critical law for frequencies in the early β-process (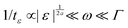 , so-called ‘critical regime’). For still lower frequencies, the dielectric nonlinearity increases during the late-β-process (‘von Schweidler regime’), while the shear modulus decreases. The maximum in the dielectric nonlinearity signals qualitatively different scaling behavior of χ3 compared to [G3] in the α-relaxation region. This has important implications for the understanding of nonlinear phenomena in driven glass-forming systems. Tarzia et al.18 consider the nonlinear response to an oscillatory field which, when applied statically, shifts the glass transition locus,39 and allows to use a generalized fluctuation dissipation relation. In the present case of shear-deformation, detailed balance does not hold and, in the case of steady shearing at constant rate, the nonergodic glass state of MCT gets melted for any shear rate.40 Thus we propose as an explanation for the differences in the observed scaling behavior that the two different scenarios of the nonlinear response under oscillatory driving show the sensitivity of the glass state to the kind of perturbing external field: whether it connects to an equilibrium state or to a nonequilibrium steady state. Future fundamental studies possibly along the lines of systematic higher order response theory41 would be very useful for broadening this insight. Especially, determining the nonlinear response under applied stress would be useful to investigate the universality of the different scaling laws found in the nonlinear oscillatory response of glass-forming systems.
, so-called ‘critical regime’). For still lower frequencies, the dielectric nonlinearity increases during the late-β-process (‘von Schweidler regime’), while the shear modulus decreases. The maximum in the dielectric nonlinearity signals qualitatively different scaling behavior of χ3 compared to [G3] in the α-relaxation region. This has important implications for the understanding of nonlinear phenomena in driven glass-forming systems. Tarzia et al.18 consider the nonlinear response to an oscillatory field which, when applied statically, shifts the glass transition locus,39 and allows to use a generalized fluctuation dissipation relation. In the present case of shear-deformation, detailed balance does not hold and, in the case of steady shearing at constant rate, the nonergodic glass state of MCT gets melted for any shear rate.40 Thus we propose as an explanation for the differences in the observed scaling behavior that the two different scenarios of the nonlinear response under oscillatory driving show the sensitivity of the glass state to the kind of perturbing external field: whether it connects to an equilibrium state or to a nonequilibrium steady state. Future fundamental studies possibly along the lines of systematic higher order response theory41 would be very useful for broadening this insight. Especially, determining the nonlinear response under applied stress would be useful to investigate the universality of the different scaling laws found in the nonlinear oscillatory response of glass-forming systems.
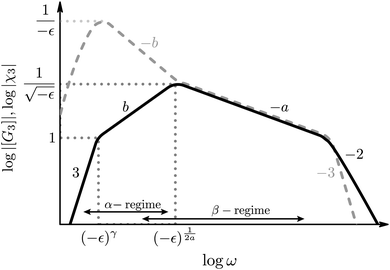 |
| | Fig. 6 Scaling of the magnitude of the third-harmonic modulus |[G3(ω)]| in sheared systems found in this paper (black solid line) in comparison to the scaling of |χ3(ω)| in dielectric systems18 (dashed grey line). The dotted lines indicate how the maxima and the shoulders of the curves scale with the distance to the glass transition ε. Only scaling behavior is shown (labeled by power-law exponents), thus, matching curves do not indicate matching values. While both nonlinear responses show the same scaling behavior ∝ ω−a at the critical point, they differ qualitatively in the α-regime. | |
A. Materials and methods
A.1 Schematic model of MCT
We determined the transient structural relaxation function Φ(t,t′) from a schematic MCT model introduced in ref. 33. It has already been used to describe LAOS11 and a few cases of simpler time-dependences.42,43 The correlator Φ(t,t′) schematically models a typical space-dependent correlation function. It depends on two time-variables, indicating the correlation of a system at time t with the system at an earlier time t′. The system at a time t is perfectly correlated with itself, Φ(t,t) = 1. A memory kernel m(t,t′), viz. a time-dependent friction kernel, encodes how much the structure can rearrange over time, or how much it is ‘stuck’ in a certain configuration. The quiescent functional ![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif) [Φ](t,s) states that the slow relaxation of the friction kernel arises from the slow structural relaxation in Φ.
[Φ](t,s) states that the slow relaxation of the friction kernel arises from the slow structural relaxation in Φ.| | 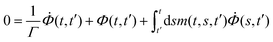 | (6) |
| | m(t,s,t′) = h(t,t′)h(t,s)![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif) [Φ](t,s) [Φ](t,s) | (7) |
| | ![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif) [Φ](t,s) = v1Φ(t,s) + v2Φ2(t,s) [Φ](t,s) = v1Φ(t,s) + v2Φ2(t,s) | (8) |
| | 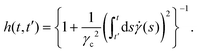 | (9) |
Given values for the parameters Γ, v1 and v2, the model can be used to calculate the equilibrium correlator without shear. In the traditional choice,11,25v2 = 2 and 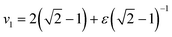 , where ε is the separation to the glass bifurcation. In flow, the complete memory function includes the external shear deformation which suppresses memory via the functions h(t,t′). This deformation triggers structural rearrangements, leading to a faster decay of the memory function. The γc enters as new parameter and sets the scale for the accumulated strain. Stress fluctuations are calculated in a mean-field-like decoupling approximation, which contains the square of the density correlator, because stress fluctuations arising from particle interactions require pairs of density fluctuations:
, where ε is the separation to the glass bifurcation. In flow, the complete memory function includes the external shear deformation which suppresses memory via the functions h(t,t′). This deformation triggers structural rearrangements, leading to a faster decay of the memory function. The γc enters as new parameter and sets the scale for the accumulated strain. Stress fluctuations are calculated in a mean-field-like decoupling approximation, which contains the square of the density correlator, because stress fluctuations arising from particle interactions require pairs of density fluctuations:| | | G(t,t′) = vσΦ2(t,t′) + η∞δ(t − t′), | (10) |
where vσ is a constant measuring the strength of stress fluctuations in the material. For the comparison with experiments, we include hydrodynamic interactions via a solvent viscosity η∞.24
A.2 Taylor expansion
For a small amplitude γ0 of the applied sinusoidal shear strain, (1), a Taylor expansion of the MCT equations of motion (6)–(9) gives for the two-time density correlator Φ(t,t′):| | Φ(t,t′) = Φeq(t − t′) + (γ0/γc)2Φω(t,t′) + O((γ0/γc)4).![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) | (11) |
With a transformation of variables to t − t′ and t + t′, we can use the periodicity 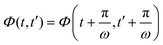 to get a Fourier series in t + t′. Because of the pure sinusoidal form of the shear strain, Fourier terms arise only for 0, ±1 in second order in strain. Using the requirement that Φ(t,t′) be real, we are left with just two Fourier terms, where the prefactors are functions of t − t′ and are given by linear integro-differential equations where the equilibrium solution enters as input; see the ESI.† The final result for the strain-dependent perturbation of the density correlator is:
to get a Fourier series in t + t′. Because of the pure sinusoidal form of the shear strain, Fourier terms arise only for 0, ±1 in second order in strain. Using the requirement that Φ(t,t′) be real, we are left with just two Fourier terms, where the prefactors are functions of t − t′ and are given by linear integro-differential equations where the equilibrium solution enters as input; see the ESI.† The final result for the strain-dependent perturbation of the density correlator is:| | | Φω(t,t′) = f0(t − t′) + eiω(t+t′)f1(t − t′) + e−iω(t+t′)f1*(t − t′). | (12) |
Inserting the Taylor solution into (10) and then into the Fourier-modes of the shear stress, (2),
| | 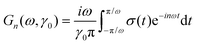 | (13) |
gives the correction to the linear response term announced in
(4). The change at the fundamental harmonic is
| | | [G1(ω)] = (2vσiω/γc2) (F{Φeq(t) f0(t)}(ω) + F{Φeq(t) f1(t)}(0)), | (14) |
and the term for the third harmonic is
| | [G3(ω)] = (2vσiω/γc2) F{Φeq(t) f1(t)}(2ω)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) . . | (15) |
Here,
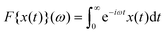
denotes the one-sided Fourier transformation. A related result to
eqn (15) was also found for the dielectric susceptibility by Tarzia
et al.18 and discussed using scaling arguments. Explicit results had previously existed for polymer melts based on reptation theory.
44 In the ESI,
† we solve the integro-differential equations for the
fi(
t) numerically, additionally, we analytically derive their scaling behavior.
A.3 Experimental aspects
For the rheological experiments we use the polydisperse suspensions of thermo-responsive core–shell particles studied in ref. 35. Details regarding the synthesis of the particles can be found in ref. 45. The suspensions' structural, thermal and linear rheological properties are well documented in ref. 35, 46 and 45. Adjusting the temperature, the particle-size and thus the packing fraction ϕ of the dispersion (viz. the fraction of the volume occupied by the particles) can readily be tuned, so that the glass transition can be studied. Because of a relative standard deviation of the radii of 17% the system does not crystallize.
The rheological experiments were conducted on a ARES-G2 (TA Instruments) strain controlled rheometer using a Couette geometry with a Peltier temperature control system. The same dispersion was measured at four temperatures, corresponding to different volume fractions; for details about the shear-protocol see the ESI.†
In Fig. 7, we present strain-amplitude measurements of the storage and loss moduli at ϕ = 0.631 for three different angular frequencies. At the third harmonic, a quadratic dependence of |G3|/|G1| on γ0 is observed as predicted by the above Taylor expansion. Therefore we reduce |G3|/|G1| to Q0 as shown in Fig. 7. This material function has been introduced by Hyun et al.36 and since then has been applied to investigate the nonlinear behavior of emulsions47 and foams,23 as well as linear48 and branched polymer melts.36 A collection of analytical expressions for Q0(ω) derived for continuum and microscopic models is available in ref. 49. Poulos et al.50 recently measured |G3|/|G1| of fluid and glassy suspensions of star polymer particles as well as sterically stabilized poly(methyl methacrylate) particles. They analyzed the frequency dependence of |G3|/|G1| at a fixed strain amplitude of γ0 = 1 and found increasing intensities for increasing frequencies in fluid samples, whereas |G3|/|G1| was shown to decrease with increasing frequency for glassy samples.
 |
| | Fig. 7 Strain amplitude dependent measurements of the sample at packing fraction ϕ = 0.631 for different reduced frequencies. The rescaled amplitude ratio of the third harmonic |G3|/|G1|/γ02 gives the intrinsic nonlinearity Q0 as plateau value for small γ0. An estimation of the reproducibility of Q0 follows from averaging three measurements with separate sample loading. It is shown as error bars indicating a relative deviation of 33%. | |
A.4 Validation of model and determination of parameters
The model parameters were determined manually by comparing the numerical solutions52 for the linear response moduli and the flow curves with the experimental data as described in ref. 35; the initial decay rate, Γ, was kept constant at the value Γ = 100(D0/RH2) determined there by high-frequency data.51 First, the separation parameter ε was adjusted to match the cross-over frequency of the experimental data and the prediction. Subsequently, the other parameters were fitted: vσ was set such that the overall magnitudes of Geq′ were matching, the critical strain, γc, was adjusted using the flow curves (Fig. 8), and the high frequency limiting viscosity, η∞, was adjusted to the moduli at high ω. The resulting parameters are shown in Table 1. Deviations of the model from the linear spectra were already seen in the investigated model dispersion and could be captured by including hopping effects.46
 |
| | Fig. 8 Symbols represent the experimentally measured flow curves for four ϕ approaching the glass transition, lines show fits of the schematic model to the data using the parameters in Table 1. | |
Acknowledgements
We thank F. Ladieu, A. Loidl, and P. Lunkenheimer for discussions. MF acknowledges the Deutsche Forschungsgemeinschaft (DFG) for partial support via FOR 1394 project P3 and in the programme ‘Freedom for Creativity’ of the Excellence Initiative. DM and MW would like to thank the DFG for financial support via SPP 1273 and WI 1911/17-1.
References
- L. Berthier and G. Biroli, Rev. Mod. Phys., 2011, 83, 587–645 CrossRef CAS.
- D. J. Pine, J. P. Gollub, J. F. Brady and A. M. Leshansky, Nature, 2005, 438, 997 CrossRef CAS PubMed.
- C. Klix, F. Ebert, F. Weysser, M. Fuchs, G. Maret and P. Keim, Phys. Rev. Lett., 2012, 109, 178301 CrossRef PubMed.
- G. Petekidis, A. Moussaid and P. N. Pusey, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2002, 66, 051402 CrossRef CAS PubMed.
- R. Besseling, E. R. Weeks, A. B. Schofield and W. C. K. Poon, Phys. Rev. Lett., 2007, 99, 028301 CrossRef CAS PubMed.
- C. P. Amann, D. Denisov, M. Dang, B. Struth, P. Schall and M. Fuchs, J. Chem. Phys., 2015, 143, 034505 CrossRef PubMed.
- N. Koumakis, J. F. Brady and G. Petekidis, Phys. Rev. Lett., 2013, 110, 178301 CrossRef CAS PubMed.
- N. Y. C. Lin, S. Goyal, X. Cheng, R. N. Zia, F. Escobedo and C. Cohen, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2013, 88, 062309 CrossRef PubMed.
- K. Miyazaki, H. M. Wyss, D. A. Weitz and D. R. Reichman, EPL, 2006, 75, 915–921 CrossRef CAS.
- H. Wyss, K. Miyazaki, J. Mattsson, Z. Hu, D. Reichman and D. Weitz, Phys. Rev. Lett., 2007, 98, 238303 CrossRef PubMed.
- J. M. Brader, M. Siebenbürger, M. Ballauff, K. Reinheimer, M. Wilhelm, S. J. Frey, F. Weysser and M. Fuchs, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2010, 82, 061401 CrossRef CAS PubMed.
- A. Kate Gurnon and N. J. Wagner, J. Rheol., 2012, 56, 333–351 CrossRef.
- R. H. Ewoldt and N. A. Bharadwaj, Rheol. Acta, 2013, 52, 201 CrossRef CAS.
- N. A. Bharadwaj and R. H. Ewoldt, J. Rheol., 2015, 59, 557–592 CrossRef CAS.
- J. W. Swan, E. M. Furst and N. J. Wagner, J. Rheol., 2014, 58, 307–337 CrossRef CAS.
- S. Kamble, A. Pandey, S. Rastogi and A. Lele, Rheol. Acta, 2013, 52, 859 CrossRef CAS.
- J.-P. Bouchaud and G. Biroli, Phys. Rev. B: Condens. Matter Mater. Phys., 2005, 72, 064204 CrossRef.
- M. Tarzia, G. Biroli, A. Lefèvre and J.-P. Bouchaud, J. Chem. Phys., 2010, 132, 054501 CrossRef PubMed.
- C. Crauste-Thibierge, C. Brun, F. Ladieu, D. L'Hôte, G. Biroli and J.-P. Bouchaud, Phys. Rev. Lett., 2010, 104, 165703 CrossRef CAS PubMed.
- T. Bauer, P. Lunkenheimer and A. Loidl, Phys. Rev. Lett., 2013, 111, 225702 CrossRef PubMed.
- S. Albert, T. Bauer, M. Michl, G. Biroli, J.-P. Bouchaud, A. Loidl, P. Lunkenheimer, R. Tourbot, C. Wiertel-Gasquet and F. Ladieu, Science, 2016, 352, 1308–1311 CrossRef CAS PubMed.
- K. Hyun, M. Wilhelm, C. O. Klein, K. S. Cho, J. G. Nam, K. H. Ahn, S. J. Lee, R. H. Ewoldt and G. H. McKinley, Prog. Polym. Sci., 2011, 36, 1697–1753 CrossRef CAS.
- M. Wilhelm, K. Reinheimer and J. Kübel, Z. Phys. Chem., 2012, 226, 547–567 CrossRef CAS.
- M. Siebenbürger, M. Fuchs and M. Ballauff, Soft Matter, 2012, 8, 4014–4024 RSC.
-
W. Götze, Complex Dynamics of Glass-Forming Liquids, A Mode-Coupling Theory, Oxford University Press, 2009 Search PubMed.
- G. L. Hunter and E. R. Weeks, Rep. Prog. Phys., 2012, 75, 066501 CrossRef PubMed.
- J. M. Brader, M. E. Cates and M. Fuchs, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2012, 86, 021403 CrossRef CAS PubMed.
- K. S. Cho, K. Hyun, K. H. Ahn and S. J. Lee, J. Rheol., 2005, 49, 747–758 CrossRef CAS.
- S. A. Rogers, J. Rheol., 2012, 56, 1129–1151 CrossRef CAS.
- J. Läuger and H. Stettin, Rheol. Acta, 2010, 49, 909–930 CrossRef.
- C. J. Dimitriou, R. H. Ewoldt and G. H. McKinley, J. Rheol., 2013, 57, 27–70 CrossRef CAS.
- R. L. Thompson, A. A. Alicke and P. R. de Souza Mendes, J. Non-Newtonian Fluid Mech., 2015, 215, 19–30 CrossRef CAS.
- J. M. Brader, T. Voigtmann, M. Fuchs, R. G. Larson and M. E. Cates, Proc. Natl. Acad. Sci. U. S. A., 2009, 106, 15186–15191 CrossRef CAS PubMed.
-
R. G. Larson, The structure and rheology of complex fluids, Oxford University Press, New York, 1999 Search PubMed.
- M. Siebenbürger, M. Fuchs, H. Winter and M. Ballauff, J. Rheol., 2009, 53, 707–726 CrossRef.
- K. Hyun and M. Wilhelm, Macromolecules, 2009, 42, 411–422 CrossRef CAS.
- Y. Yang and K. A. Nelson, Phys. Rev. Lett., 1995, 74, 4883 CrossRef CAS PubMed.
- C. Mattner, B. Roling and A. Heuer, Solid State Ionics, 2014, 261, 28–35 CrossRef CAS.
- D. L'Hôte, R. Tourbot, F. Ladieu and P. Gadige, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 90, 104202 CrossRef.
- M. Fuchs and M. E. Cates, Phys. Rev. Lett., 2002, 89, 248304 CrossRef PubMed.
- A. L. U. Basu, M. Krüger and C. Maes, Phys. Chem. Chem. Phys., 2015, 17, 6653 RSC.
- T. Voigtmann, J. M. Brader, M. Fuchs and M. E. Cates, Soft Matter, 2012, 8, 4244 RSC.
- F. Frahsa, A. K. Bhattacharjee, J. Horbach, M. Fuchs and T. Voigtmann, J. Chem. Phys., 2013, 138, 12A513 CrossRef PubMed.
- D. S. Pearson and W. E. Rochefort, J. Polym. Sci., Part B: Polym. Phys., 1982, 20, 83–98 CrossRef CAS.
- N. Dingenouts, C. Norhausen and M. Ballauff, Macromolecules, 1998, 31, 8912–8917 CrossRef CAS.
- J. J. Crassous, A. Wittemann, M. Siebenbürger, M. Schrinner, M. Drechsler and M. Ballauff, Colloid Polym. Sci., 2008, 286, 805–812 CAS.
- K. Reinheimer, M. Grosso, F. Hetzel, J. Kübel and M. Wilhelm, J. Colloid Interface Sci., 2012, 380, 201–212 CrossRef CAS PubMed.
- M. A. Cziep, M. Abbasi, M. Heck and M. Wilhelm, Macromolecules, 2016, 49, 3566–3579 CrossRef CAS.
- D. Merger, M. Abbasi, J. Merger, A. J. Giacomin, C. Saengow and M. Wilhelm, Appl. Rheol., 2016, 26, 53809 Search PubMed.
- A. S. Poulos, F. Renou, A. R. Jacob, N. Koumakis and G. Petekidis, Rheol. Acta, 2015, 54, 715 CrossRef CAS.
- J. J. Crassous, R. Régisser, M. Ballauff and N. Willenbacher, J. Rheol., 2005, 49, 851–863 CrossRef CAS.
- M. Fuchs, W. Götze, I. Hofacker and A. Latz, J. Phys.: Condens. Matter, 1991, 3, 5047 CrossRef.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c6sm01616b |
|
| This journal is © The Royal Society of Chemistry 2016 |
Click here to see how this site uses Cookies. View our privacy policy here.  Open Access Article
Open Access Article![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin
sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ωt,
ωt,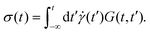
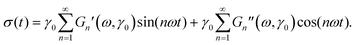
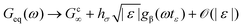 , where the parameter ε denotes the relative separation from the glass transition, which lies at ε = 0. The critical elastic constant Gc∞ measures the rigidity surviving in fluid states for high enough frequencies,3 the amplitude factor hσ links stress to structure, and the β-scaling function gβ contains the universal critical variation. It exhibits two power laws in a fluid state (ε < 0): the so-called critical law (exponent a) and the von Schweidler law (exponent −b) where a and b are material dependent.25 For the present model, a = 0.32 and b = 0.63. The β-scaling time tε diverges as a power law when approaching the glass transition, tε ∝ |ε|−1/(2a); albeit more slowly than τ ∝ |ε|−γ, with γ = (a + b)/(2ab). The β-scale can most easily be read off from the minimum in Geq′′(ω). Only for frequencies below the β-minimum, the final (or α-) relaxation commences and captures the decay of the elasticity in the fluid and the establishment of viscous flow with a finite Newtonian viscosity. The α-process shows up as a broad maximum in the loss modulus around the frequency where both moduli cross.
, where the parameter ε denotes the relative separation from the glass transition, which lies at ε = 0. The critical elastic constant Gc∞ measures the rigidity surviving in fluid states for high enough frequencies,3 the amplitude factor hσ links stress to structure, and the β-scaling function gβ contains the universal critical variation. It exhibits two power laws in a fluid state (ε < 0): the so-called critical law (exponent a) and the von Schweidler law (exponent −b) where a and b are material dependent.25 For the present model, a = 0.32 and b = 0.63. The β-scaling time tε diverges as a power law when approaching the glass transition, tε ∝ |ε|−1/(2a); albeit more slowly than τ ∝ |ε|−γ, with γ = (a + b)/(2ab). The β-scale can most easily be read off from the minimum in Geq′′(ω). Only for frequencies below the β-minimum, the final (or α-) relaxation commences and captures the decay of the elasticity in the fluid and the establishment of viscous flow with a finite Newtonian viscosity. The α-process shows up as a broad maximum in the loss modulus around the frequency where both moduli cross.
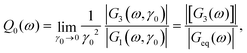

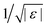 and its position shifts with 1/tε; it lies in the center of the β-process window close to the minimum of G′′. The scaling master curve (see Fig. 4a), exhibits two power laws (see ESI†). The right flank behaves as ω−a, the left as ωb. The scaling with ωb gets more pronounced upon approaching the glass transition because corrections arising from the α-process get suppressed (recall that τ diverges more strongly than tε). For frequencies smaller than the maximum, the curves for different ε collapse onto a second scaling master function valid in the α-process. Collapse in Fig. 4b holds when the frequency is rescaled by ω/|ε|γ, while the amplitude does not depend on the distance to the glass transition. Rather, the nonlinearity vanishes with decreasing frequency: the curves are proportional to ω2 for ωτ ≪ 1. This quasistatic limit, see ESI,† is included as dotted lines in Fig. 3 and 4.
and its position shifts with 1/tε; it lies in the center of the β-process window close to the minimum of G′′. The scaling master curve (see Fig. 4a), exhibits two power laws (see ESI†). The right flank behaves as ω−a, the left as ωb. The scaling with ωb gets more pronounced upon approaching the glass transition because corrections arising from the α-process get suppressed (recall that τ diverges more strongly than tε). For frequencies smaller than the maximum, the curves for different ε collapse onto a second scaling master function valid in the α-process. Collapse in Fig. 4b holds when the frequency is rescaled by ω/|ε|γ, while the amplitude does not depend on the distance to the glass transition. Rather, the nonlinearity vanishes with decreasing frequency: the curves are proportional to ω2 for ωτ ≪ 1. This quasistatic limit, see ESI,† is included as dotted lines in Fig. 3 and 4.
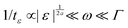 , so-called ‘critical regime’). For still lower frequencies, the dielectric nonlinearity increases during the late-β-process (‘von Schweidler regime’), while the shear modulus decreases. The maximum in the dielectric nonlinearity signals qualitatively different scaling behavior of χ3 compared to [G3] in the α-relaxation region. This has important implications for the understanding of nonlinear phenomena in driven glass-forming systems. Tarzia et al.18 consider the nonlinear response to an oscillatory field which, when applied statically, shifts the glass transition locus,39 and allows to use a generalized fluctuation dissipation relation. In the present case of shear-deformation, detailed balance does not hold and, in the case of steady shearing at constant rate, the nonergodic glass state of MCT gets melted for any shear rate.40 Thus we propose as an explanation for the differences in the observed scaling behavior that the two different scenarios of the nonlinear response under oscillatory driving show the sensitivity of the glass state to the kind of perturbing external field: whether it connects to an equilibrium state or to a nonequilibrium steady state. Future fundamental studies possibly along the lines of systematic higher order response theory41 would be very useful for broadening this insight. Especially, determining the nonlinear response under applied stress would be useful to investigate the universality of the different scaling laws found in the nonlinear oscillatory response of glass-forming systems.
, so-called ‘critical regime’). For still lower frequencies, the dielectric nonlinearity increases during the late-β-process (‘von Schweidler regime’), while the shear modulus decreases. The maximum in the dielectric nonlinearity signals qualitatively different scaling behavior of χ3 compared to [G3] in the α-relaxation region. This has important implications for the understanding of nonlinear phenomena in driven glass-forming systems. Tarzia et al.18 consider the nonlinear response to an oscillatory field which, when applied statically, shifts the glass transition locus,39 and allows to use a generalized fluctuation dissipation relation. In the present case of shear-deformation, detailed balance does not hold and, in the case of steady shearing at constant rate, the nonergodic glass state of MCT gets melted for any shear rate.40 Thus we propose as an explanation for the differences in the observed scaling behavior that the two different scenarios of the nonlinear response under oscillatory driving show the sensitivity of the glass state to the kind of perturbing external field: whether it connects to an equilibrium state or to a nonequilibrium steady state. Future fundamental studies possibly along the lines of systematic higher order response theory41 would be very useful for broadening this insight. Especially, determining the nonlinear response under applied stress would be useful to investigate the universality of the different scaling laws found in the nonlinear oscillatory response of glass-forming systems.
![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif) [Φ](t,s) states that the slow relaxation of the friction kernel arises from the slow structural relaxation in Φ.
[Φ](t,s) states that the slow relaxation of the friction kernel arises from the slow structural relaxation in Φ.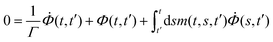
![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif) [Φ](t,s)
[Φ](t,s)![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif) [Φ](t,s) = v1Φ(t,s) + v2Φ2(t,s)
[Φ](t,s) = v1Φ(t,s) + v2Φ2(t,s)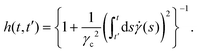
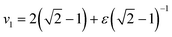 , where ε is the separation to the glass bifurcation. In flow, the complete memory function includes the external shear deformation which suppresses memory via the functions h(t,t′). This deformation triggers structural rearrangements, leading to a faster decay of the memory function. The γc enters as new parameter and sets the scale for the accumulated strain. Stress fluctuations are calculated in a mean-field-like decoupling approximation, which contains the square of the density correlator, because stress fluctuations arising from particle interactions require pairs of density fluctuations:
, where ε is the separation to the glass bifurcation. In flow, the complete memory function includes the external shear deformation which suppresses memory via the functions h(t,t′). This deformation triggers structural rearrangements, leading to a faster decay of the memory function. The γc enters as new parameter and sets the scale for the accumulated strain. Stress fluctuations are calculated in a mean-field-like decoupling approximation, which contains the square of the density correlator, because stress fluctuations arising from particle interactions require pairs of density fluctuations:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif)
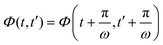 to get a Fourier series in t + t′. Because of the pure sinusoidal form of the shear strain, Fourier terms arise only for 0, ±1 in second order in strain. Using the requirement that Φ(t,t′) be real, we are left with just two Fourier terms, where the prefactors are functions of t − t′ and are given by linear integro-differential equations where the equilibrium solution enters as input; see the ESI.† The final result for the strain-dependent perturbation of the density correlator is:
to get a Fourier series in t + t′. Because of the pure sinusoidal form of the shear strain, Fourier terms arise only for 0, ±1 in second order in strain. Using the requirement that Φ(t,t′) be real, we are left with just two Fourier terms, where the prefactors are functions of t − t′ and are given by linear integro-differential equations where the equilibrium solution enters as input; see the ESI.† The final result for the strain-dependent perturbation of the density correlator is: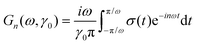
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) .
.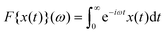 denotes the one-sided Fourier transformation. A related result to eqn (15) was also found for the dielectric susceptibility by Tarzia et al.18 and discussed using scaling arguments. Explicit results had previously existed for polymer melts based on reptation theory.44 In the ESI,† we solve the integro-differential equations for the fi(t) numerically, additionally, we analytically derive their scaling behavior.
denotes the one-sided Fourier transformation. A related result to eqn (15) was also found for the dielectric susceptibility by Tarzia et al.18 and discussed using scaling arguments. Explicit results had previously existed for polymer melts based on reptation theory.44 In the ESI,† we solve the integro-differential equations for the fi(t) numerically, additionally, we analytically derive their scaling behavior.