Off-equilibrium surface tension in miscible fluids
Domenico
Truzzolillo
* and
Luca
Cipelletti
Laboratoire Charles Coulomb (L2C), UMR 5221 CNRS-Université de Montpellier, Montpellier, France. E-mail: domenico.truzzolillo@umontpellier; Fax: +33(0)467143498; Tel: +33(0)467143589
First published on 31st May 2016
Abstract
The interfacial tension between immiscible fluids is responsible for a wealth of every-day phenomena, from the spherical shape of small drops and bubbles to the ability to walk on water of many insects. More than a century ago, physicist and mathematician D. Korteweg postulated the existence of an effective interface tension for miscible fluids, whenever a composition gradient exists, as encountered, e.g., in many flow geometries. In this mini-review, we discuss experimental work performed in the last decades that demonstrates the existence of a positive effective interface tension in a variety of systems, from molecular, near-critical liquids to complex fluids such as polymer solutions and colloidal suspensions. The various experimental strategies that have been deployed are discussed, together with their advantages and limitations. Finally, some of the key theoretical questions still open are outlined.
Luca Cipelletti is a full professor of Physics at the Université de Montpellier. After receiving a PhD degree in Physics from the University of Milan in 1997, he moved to University of Pennsylvania and Harvard University as a postdoc in the group of Prof. D. A. Weitz, before joining the Université de Montpellier in 2000. His interests range from the development of original light scattering methods and instruments to the investigation of glassy dynamics in colloidal systems and the behavior of out-of-equilibrium, driven soft matter. He authored and coauthored more than 80 articles, reviews and book chapters and coedited a book on dynamical heterogeneity and collaborates regularly with several companies in the instrumentation, food and personal care industries. |
1 Introduction
Interfacial tension is indubitably one of the most fascinating phenomena arising from the forces that act between the molecules of a liquid. The research on interfacial tension has a long history that traces back to the eighteenth century,1 continues actively in the present times, and moves further into areas of great practical interest such as biophysics and colloidal science.2–5 The origin of interfacial tension is intimately related to the compositional change that characterizes all interfaces and to the consequent stress anisotropy experienced by a portion of a liquid close to its boundary. Indeed, a molecule in the bulk experiences interactions with its neighbors that are, on average, isotropic. By contrast, the net force acting, e.g., on a molecule at the liquid–vapour interface is non-null, since there are more nearby molecules in the liquid than in the vapour. In general, when two fluids are immiscible and form an interface, a work must be done in order to bring a molecule from the bulk of one liquid to the interface, which possesses an energy density larger than the bulk. Thus, the surface behaves as if it was a stretched film or membrane under a tension, the interfacial tension.Because of interfacial tension, the surface of simple1 and complex liquids6,7 can support the weight of small objects. Insects, for example, can walk across the surface of a pond because of the surface tension of water. Surface tension also causes drops of a liquid to be spherical, since spheres minimize the surface area for a given volume; similarly, the shape of liquid jets strongly depends on the interfacial tension between the injected liquid and the surroundings. Quite generally, interfacial tension and capillary phenomena constitute an indispensable basic background for understanding hydrology, microbiology, petroleum hydrogeology, hemodynamics, multiphase transport through porous media, and many other disciplinary themes.
Scientists rationalize the numerous phenomena involving surface tension between immiscible fluids in a self-consistent framework based on a few key assumptions: the fluids that are brought in contact are at equilibrium, they are mutually saturated, the boundary between them has an infinite life time and no net interdiffusion takes place. Can these ideas be generalized to the case of miscible fluids? Is the very notion of interfacial tension still relevant in this case?
These questions are currently lively debated, as the result of systematic experimental investigations performed in the last years by several groups, who employed various experimental strategies, ranging from probing capillary waves by light scattering,8–10 to observing the shape of drops11–13 and menisci,14 and studying hydrodynamic instabilities.15,16 The interest in this topic is not purely academic: the existence of an effective surface tension, in spite of its transient character, is of great relevance in many fields, from geodynamics to polymer physics and multiphase flow, and has implications in a large number of practical applications. For example, determining the sources of instability in miscible systems and knowing under what conditions an instability or the interface breakdown will occur greatly helps in the design of fluids for extracting a host fluid from a porous medium or a piping system. Applications along these lines include oil recovery and transport, hydrology and filtration.17 Understanding interfacial processes between a contaminant and a miscible cleaning agent is important for the development of cleaning liquids for soil decontamination or for the efficient removal of a water/detergent mixture from a fabric, both processes bearing similarities to oil extraction. The effective surface tension may also play an important role at a more fundamental level, in processes at widely different length scales, from viscous fingering in a chromatography column where an injected plug of finite width moves along the column surrounded by a buffer with a different viscosity,18 to the geological scale. For the latter, Morra and Yuen19 discussed recently the important role of stresses at miscible interfaces in geodynamics, where they have implications in mantle convection, earthquakes, magma fragmentation and the dynamics of the earth core.20 A transient surface tension between two miscible phases appears also as a necessary input in the numerical simulations of miscible fluids when modeling Rayleigh–Taylor instabilities21 or Hele-Shaw flows.22,23
Traditionally, physicists have classified fluids as either miscible or immiscible, with distinct properties for each category. In the framework of a thermodynamic approach, interfacial stresses at the boundary between miscible fluids have not been taken into consideration, since at equilibrium a miscible system forms a homogeneous mixture and no interface exists. However, it is clear that such an interface can exist transiently. Quite ironically, it can be quantitatively characterized by using the same arguments introduced more than a century ago by van der Waals for a molecular-level description of the interface between immiscible fluids. Van der Waals24 was the first to recognize that an infinitely sharp interface is unphysical. He rather defined the interface between two (immiscible) fluids as a continuous region, in which there is a transition in concentration from one fluid to the other, over a thickness δ of molecular size. Fig. 1 schematically illustrates this viewpoint, showing the concentration profile at the interface of a model binary system, where concentration is expressed as the volume fraction φ of the particles of one fluid, with φ1 and φ2 the concentration in the two bulk phases.
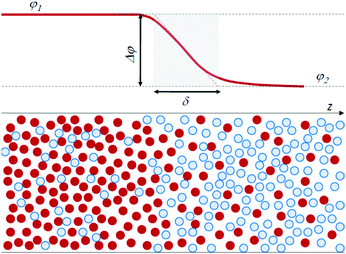 | ||
| Fig. 1 Scheme of the interface between a fluid A (red particles) and B (blue particles), with a finite thickness δ. φ is the volume fraction of the A particles. | ||
This description is also suitable for miscible fluids, as long as one recognizes that the concentration gradient is transient and will eventually fully relax once diffusion (or other mixing mechanisms) will lead to a single homogeneous phase. In practice, however, two miscible fluids brought in contact typically exhibit a well-defined transition region that can last from seconds to minutes, a time scale much larger than that of molecular motion. Modern theories leverage on this separation of time scales: by assuming local thermodynamic equilibrium,25 they extend the approach used for immiscible fluids to tackle the problem of the interface tension between miscible fluids.
The first theoretical study of the interfacial tension between miscible fluids was published in 1901, just a few years after van der Waals' paper, by the mathematician and physicist D. Korteweg,26 who argued that stresses caused by density gradients could act as an effective interfacial tension. Although Korteweg's theory was originally developed from a mechanic, rather than thermodynamic, point of view, it is now customary to recast it in the language of thermodynamics, according to which the surface tension is derived from
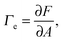 | (1) |
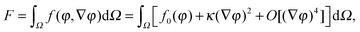 | (2) |
With these assumptions and in the simple case of a flat interface, the local part of the free energy can be integrated over the coordinates (x,y) tangential to the interface, thus obtaining F as an integral in z, the coordinate normal to the interfacial area. Taking the partial derivative of F with respect to A yields the effective interfacial tension:
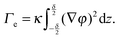 | (3) |
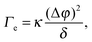 | (4) |
Before reviewing in the next sections some of the experimental work on the EIT, it's worth mentioning a very recent dynamic density functional theory (DDFT) study34 of the time-dependent, non-equilibrium interfacial tension Γe(t) for several colloidal and polymeric fluids in contact with their own solvent. The author finds Γe(t) to be proportional to (Δϕ)2, as in eqn (4), but only in the long time limit, where the interfacial tension vanishes as diffusion smears out the interface. By contrast, for short times and for particles interacting via a repulsive potential, Γe is predicted to be negative. This is a very striking result, in contrast with experiments that all report a positive EIT, as we shall discuss it in the following. Together with early reports that questioned the very existence of an EIT,35–37 this work highlights how controversial and lively this research field is, with many key questions still awaiting an answer.
2 Experiments on molecular fluids
All the earlier experiments that probed the EIT where carried on mixtures of miscible molecular fluids: only in the last years have complex fluids being introduced as suitable systems for investigating this topic. In this section we thus review works on molecular fluids, leaving complex fluids to the following section. The largest set of experiments that have suggested that an EIT is responsible for capillary forces between miscible fluids are studies of miscible drops rising or falling in a viscous medium. Joseph has conducted an extensive research in this area and has compiled a comprehensive review on the subject.38 According to him, the first report of experiments suggesting the presence of capillary forces in miscible systems tracks back to 1871, when M. Bosscha reported observations of the effect of capillarity in miscible liquids. Joseph himself has observed capillary phenomena in rising drops of nearly density matched molasses and water in glycerin.38Almost 50 years after Bosscha, H. Freundlich in his treatise on colloids and capillary chemistry (1926) cited the measurements by Quinke (1902) of a ‘dynamic tension’ between ethyl alcohol and aqueous salt solutions, which are miscible in all proportions. Freundlich discusses the different methods to measure interfacial tension between immiscible liquids and the theory behind capillary phenomena, adding that: “…the dynamic tension of liquids, when first brought into contact, is to be distinguished from the static tension, when the two liquids are mutually saturated. Not only do liquids which are not miscible in all proportion have a mutual surface tension; even two completely miscible liquids, before they have united to form one phase, exhibit a dynamical surface tension…”39
There have been many other successive reports of phenomena for which the authors invoke an interfacial tension in miscible systems. Garik et al. injected water into a CuSO4 solution or glycerin into water. They proposed that the patterns that they observed were not due to viscous fingering, but rather to an instability induced by the EIT.40 Mungall reported that miscible molten silicates form a meniscus, indicative of the existence of an interfacial tension,14 which he rationalizes with a theoretical model in terms of stresses induced by a gradient in the viscoelastic properties. Castellanos and González proposed that the wavelength selection in the electrohydrodynamic instability between miscible fluids of different conductivities can be explained by a transient interfacial tension.41 Petitjeans and Maxworthy17 conducted a study of capillary displacement to determine if an EIT exists at the transition zone between miscible fluids. Using the same experimental setup introduced by Taylor42 for immiscible fluids, based on the measurement of the average velocity of one fluid injected in a small capillary filled with the second liquid, they concluded that an EIT of 0.43 mN m−1 exists at the interface between pure glycerin and water.
Among the wide set of experimental strategies deployed to investigate miscible interfaces and their dynamics, light scattering (LS) and spinning drop tensiometry (SDT) are probably the two techniques that have yielded the more quantitative results on the EIT of a variety of miscible molecular systems. In particular, LS has been used to investigate the time dependence of the EIT, due to the smearing of the interface in miscible systems. One of the most intriguing and inspiring experiments was conducted by May and Maher.8 They considered a system of mutually saturated layers of isobutyric acid (IBA) and water. The two fluids have an upper critical solution temperature (UCST) Tc = 27.6 °C, above which they are fully miscible, while they are immiscible below Tc. The authors performed dynamic light scattering experiments to obtain the interfacial tension below Tc, by measuring the relaxation rate of the capillary waves at the interface between the two (immiscible) fluids. They then ramped up quickly the temperature just above Tc and observed that the solution still displayed a behavior indicative of the existence of an actual interface, with an EIT that relaxed with time. The experiment by May and Maher exploits two valuable features of near-critical solutions: (i) close to a critical point, interdiffusion slows down, allowing for more time to probe interfacial stresses and their evolution before the interface disappears; (ii) a sharp interface can be easily created with the system in the two-phase region of the phase diagram, thanks to the gravity-induced macroscopic phase separation. By quenching the system in the miscible region, one can then study the EIT starting from a well-defined initial condition. These considerations explain why critical mixtures have been widely studied in experiments9,10,12,43 and simulations.44
The temporal evolution of the EIT measured by May and Maher,8Γe ∝t−0.5, is qualitatively consistent with the diffusion-induced broadening of the interface, but it yields a diffusion coefficient 7 orders of magnitude smaller than expected. In ref. 8, this discrepancy is attributed to gravity, which is claimed to have a stabilizing effect on the interface. A different explanation is put forward by Cicuta et al.,9 who use static LS to investigate the non-equilibrium fluctuations occurring at the interface between two miscible phases of a near-critical aniline–cyclohexane mixture during a free-diffusion process. The authors of ref. 9 emphasize the role of the contribution to the measured scattered signal of fluctuations in bulk layers close to the interface: when this contribution is neglected, Γe may be largely overestimated. Cicuta et al. model the region separating the two fluids as two thick “bulk” layers, within which a low and linear gradient of concentration exists,45 located on either side of a thin interface layer, characterized by a steep concentration gradient. By assuming that the scattering from these layers adds up incoherently, the small-angle static scattered intensity is written as I(q) = Iint(q) + Ibulk(q), the superposition of non-equilibrium contributions due to capillary waves at the interface (Iint(q)) and density fluctuations in the bulk layers (Ibulk(q)). A linearized hydrodynamic description of the fluctuations45,46 allows the two contributions to be derived:
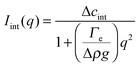 | (5) |
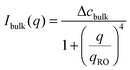 | (6) |
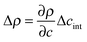 is the density difference across the interface, g is the gravitational acceleration and qRO is a rolloff wave vector characterizing the onset of gravitational stabilization at large length scales of the bulk fluctuations.47,48
is the density difference across the interface, g is the gravitational acceleration and qRO is a rolloff wave vector characterizing the onset of gravitational stabilization at large length scales of the bulk fluctuations.47,48
Eqn (5) and (6) have been used9 to fit the total scattered intensity I(q) measured at different times since the start of the remixing process of a near-critical aniline–cyclohexane mixture, yielding the effective surface tension Γe. Fig. 2 shows the measurements of ref. 9: before increasing the temperature above Tc, the system is macroscopically phase-separated and the scattered light is dominated by the contribution of the capillary waves at the interface, characterized by a distinctive high-q behavior I(q) ∼ 1/(Γq2).47 Once the system is brought in the coexistence region, the same q−2 scaling is observed at short times (t < 70 s), confirming the existence of an effective surface tension. As time proceeds, Γe decreases, because the interface smears out due to diffusion. The concomitant evolution of Γe, Δcint and Δcbulk is responsible for the evolution of the scattered patterns seen in Fig. 2. In particular, the shift from a q−2 to a q−4 large-q behavior signals the transition from a regime where the scattering is dominated by the interface capillary waves due to the EIT to a nearly homogenized mixture where only the fluctuations in the bulk layers contribute significantly to the measured intensity,48,49 making the determination of Γe impossible.
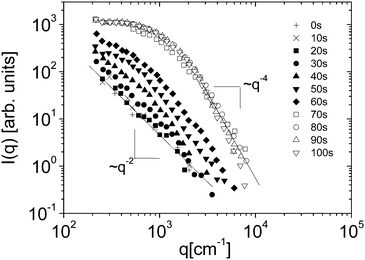 | ||
| Fig. 2 Scattered intensity I vs. scattering vector q as function of time, for an initially demixed mixture of aniline and cyclohexane, suddenly brought in the coexistence region at time t = 0. Adapted from ref. 9. | ||
The complex interplay between bulk and interface layers demonstrated by the work of Cicuta et al. highlights the difficulty of disentangling the two contributions, which ultimately limits the usefulness of LS as a probe of the EIT. An alternative, popular technique is spinning drop tensiometry (SDT). In SDT, a drop of one fluid is created in a cylindrical container filled with the second fluid. The cylinder is rotated around its axis at an angular velocity ω, which results in the deformation of the drop under the competing actions of the interfacial tension and the centrifugal acceleration (see Fig. 3A and B). More specifically, the interfacial tension may be retrieved by measuring r, the drop radius in the direction perpendicular to the axis of rotation, using Vonnegut's equation:50,51
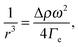 | (7) |
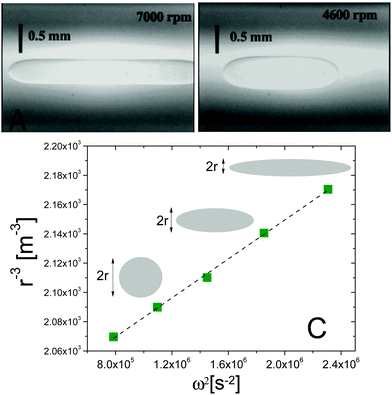 | ||
Fig. 3 Spinning drop experiments probing the interfacial tension between isobutyric acid (IBA) and water, two miscible fluids. (A and B) Images of an IBA-rich drop spun in the IBA-poor background, at 7000 and 4600 rpm, respectively. The system is brought in the miscible phase by suddenly raising T from 15 to 30 °C. (C) Inverse cube of the drop transversal radius, r−3, vs. squared spinning angular velocity ω2, for an IBA-rich drop after a temperature jump from 20 to 28.5 °C. The angular velocity was varied between 8500 and 14![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 500 rpm. The dashed line is the best linear fit to the data, whose slope yields the effective interfacial tension via the Vonnegut relation, eqn (7). Data and images are adapted with permission from ref. 12 (Copyright American Chemical Society). 500 rpm. The dashed line is the best linear fit to the data, whose slope yields the effective interfacial tension via the Vonnegut relation, eqn (7). Data and images are adapted with permission from ref. 12 (Copyright American Chemical Society). | ||
A series of very accurate SDT experiments have been performed by Pojman et al.12 on a near-critical water/IBA mixture. To demonstrate that an effective interfacial tension exists, Pojman and coworkers followed the evolution of a IBA-rich drop embedded in a IBA-poor phase, above the UCST of the mixture. Fig. 3A and B show that when decreasing ω the drop changes its shape and reduces the interface area, a clear evidence for a positive EIT. Fig. 3C shows the results of a systematic investigation of the drop transversal radius as a function of rotation speed, in the miscible phase. The data fall onto a straight line when plotting r−3vs. ω2, in excellent agreement with the behavior predicted by eqn (7). From the slope of a linear fit, a ratio EIT/Δρ of 3.7 × 103 N kg m−4 could be measured.
Spinning drop tensiometry has also been used to measure the EIT between miscible molecular fluids far from any critical point. For non-critical mixtures, diffusion is typically much faster than for near-critical fluids, which makes measurements of Γe more challenging. On the other hand, the composition of a non-critical mixture can be varied at will, contrary to near-critical mixtures. This paves the way for a systematic investigation of the Δϕ dependence of the EIT. Petitjeans11 was the first to perform such a systematic study, using spinning drop tensiometry to measure the EIT between water and aqueous solutions of glycerine. He first observed that after approximately 100 seconds drops of water reached a quasi-steady diameter when rotated in a capillary filled with pure glycerin, indicative of a positive EIT of 0.58 mN m−1. He then replaced pure glycerine by aqueous solutions of glycerine and measured the EIT as a function of the volume fraction φgly of glycerine in the background fluid. The resulting Γevs. φgly curve is shown in Fig. 4. While at the lowest glycerin concentrations the data appear overall consistent with the Γe ∝ φ2 scaling of eqn (4), a sharp increase of Γe is seen as the maximum possible concentration, φgly = 1, is approached. As we will show it in the following, this is not the only case where eqn (4) fails to fit experimental data at large φ, indicating that for large concentration gradients higher order terms of the free energy expansion, neglected in eqn (2), become relevant.
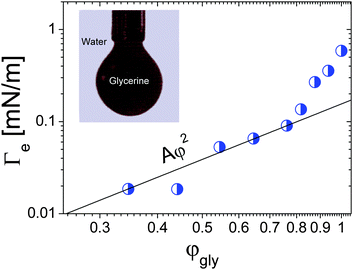 | ||
| Fig. 4 Effective interfacial tension between water and glycerine as a function of the glycerine volume fraction. The black solid lines is the best parabolic fit, as predicted by the square gradient model, in the low-φgly regime. Inset: Formation of a drop of dyed glycerine in water. Data adapted from ref. 11 (Copyright Elsevier Masson SAS. All rights reserved). | ||
As a final comment on SDT, we remark that the typical time scale of a spinning drop experiment, i.e. the time needed for a drop to reach its quasi-stationary radius, is of the order of 102 s, much larger than tD, the time for a molecule of one fluid to diffuse into the other fluid over a distance equal to its own size. For example, for water/glycerine mixtures one finds tD ≃ d2/D ≃ 4.5 × 10−9 s, where d = 2.75 Å is the diameter of a water molecule and D = 1.68 × 10−7 cm2 s−1 the diffusion coefficient of water in glycerine.17 This makes SDT unsuitable to probe the off-equilibrium interfacial tension in the t → 0 limit, especially for non-critical molecular fluids. Furthermore, we emphasize that while the drop radius and hence Γe reaches a quasi-stationary value on the time scale of about 100 s, on longer time scales the EIT keeps decreasing13 due to diffusion, similarly to what observed in the light scattering experiments discussed above.
To summarize this section, one may conclude that (i) all experiments reported here suggest that a positive interfacial tension exists between miscible molecular liquids; (ii) all standard experimental methods are confronted with various problems, mostly related to the unavoidable remixing occurring at the transition zone or, for the LS measurements, to the difficulty of separately probe interfacial and bulk properties. In the next section, we will show that most of these difficulties may be overcome by working on complex fluids and by introducing new measurement strategies.
3 Off-equilibrium interfacial tension in polymer and colloidal fluids
Colloidal and polymer suspensions may be regarded as ideal benchmark systems to investigate surface tension effects, because their interfaces may be probed in great detail down to the particle level52 by optical techniques, and because the relevant time scales are much slower and thus more easily accessible than for molecular fluids. Most of the previous works have focused on the interface between phase-separated colloidal fluids at thermodynamical equilibrium;52–55 however, colloidal suspensions are also excellent candidates for investigating off-equilibrium surface tension, since diffusion is comparatively slow in colloids or polymers, thus leaving a wider temporal window for probing the transient interface between miscible fluids.The first experimental investigation of the EIT in complex fluids miscible in all proportion has been performed by Zoltowski et al.,13 who studied drops of dodecyl-acrylate (DA) in mixtures of DA and poly(dodecyl acrylate) (PDA, molecular weight 25 kD), using a spinning drop tensiometer. After estimating the mechanical relaxation time of a drop using an immiscible analogue (1-propanol and poly(dodecyl acrylate)), they showed that the DA drops maintained a quasi-steady diameter long after this relaxation period, an observation attributed to the effect of the EIT. The EIT was found to be independent of the rotation rate above 6000 rpm, and independent of the initial drop volume; it was moreover found to increase with the difference in concentration between the monomer drop and the polymer-monomer background fluid. By measuring the thickness of the interface between the two fluids, the square gradient parameter κ was determined from eqn (4) to be on the order of 10−9 N. Note that, due to the diffusion between the two fluids, an elongated drop of DA in the spinning tensiometer has a “drop within a drop” structure, characterized by an inner and outer diameter (see Fig. 5-right panel). The interface thickness is naturally defined as the size of the region between the inner and outer diameters. Fig. 5 shows the φ dependence of the EIT retrieved from Vonnegut's relation, eqn (7), using as input either the outer or the inner diameter (panels A and B, respectively). When using the outer diameter, Γe(φPDA) does not seem to be compatible with a parabolic function at large φPDA. By contrast, the interfacial tension calculated using the inner diameter seems to be in agreement with the scaling suggested by the square gradient model, although the error bars are quite large. On the other hand, the inner diameter is found to vary along the drop profile (see Fig. 5, right panel), which is inconsistent with the assumptions of Vonnegut's theory. Thus, it seems preferable to calculate Γe from the outer diameter, the same choice adopted by Petitjeans11 in his investigation of water drops in glycerine. With this choice, the EIT between DA monomers and DA/PDA mixtures is of the order of a few 10−2 mN m−1 and appears to depart at large φ from the φ2 scaling predicted by Korteweg's law, a behavior qualitatively similar to that of the water/glycerine mixtures11 discussed in the previous section (see Fig. 4).
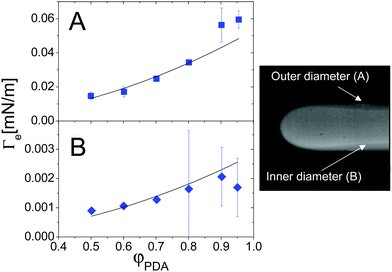 | ||
| Fig. 5 Effective interfacial tension between a DA fluid (monomer) and a DA–PDA (polymer) mixture, as a function of the polymer concentration. The EIT values have been obtained from eqn (7), either using the outer diameter (A) or the inner diameter (B). Right panel: typical image of a DA-rich drop (fluorescently labelled) in the DA/PDA background fluid, where the inner and outer diameters are clearly visible. The outer diameter is about 760 μm. Adapted with permission from ref. 13 (Copyright American Chemical Society). | ||
The experiments by Zoltowski et al.13 demonstrate the existence of a positive EIT between miscible complex fluids. Unfortunately, they also illustrate the difficulties in interpreting quantitatively the SDT measurements, due to diffusion at the interface. To overcome these difficulties, we have very recently proposed the analysis of viscous fingering instability patterns as a novel method to measure transient, low interfacial tensions.15,16 Quite generally, we argue that the direct visualization of hydrodynamic instabilities in colloidal and polymeric fluids affords the opportunity to investigate in detail the EIT of complex fluids in the t → 0 limit; it moreover allows the role of the particle structure and interparticle potential to be systematically studied.
The Saffman–Taylor instability arises when a fluid is pushed through a more viscous fluid confined between closely spaced parallel plates,56 a so-called Hele-Shaw cell. The interface between the fluids develops a hydrodynamic instability leading to the formation of finger-like patterns like the ones shown in Fig. 6, which were obtained by injecting the solvent (water) in an aqueous suspension of microgels.15 This phenomenon is called viscous fingering and is well documented, both theoretically and experimentally, when both fluids are Newtonian and immiscible.57,58 Crucially, the number of fingers observed at the onset of the fingering instability can be quantitatively related to the interfacial stresses between the two fluids, using a linear stability analysis originally developed for immiscible fluids, but also valid for miscible phases, as long as interdiffusion is negligible,15e.g. when the experiment duration is short compared to the diffusion time. More specifically, the number nA of fingers appearing at the onset of the instability can be expressed as a function of the fluids and geometrical parameter as:15
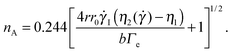 | (8) |
![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) I = 3
I = 3![[V with combining dot above]](https://www.rsc.org/images/entities/i_char_0056_0307.gif) (2πr0b2)−1 is the average shear rate at the injection hole for the imposed volume injection rate
(2πr0b2)−1 is the average shear rate at the injection hole for the imposed volume injection rate ![[V with combining dot above]](https://www.rsc.org/images/entities/i_char_0056_0307.gif) , η1 is the viscosity of the injected (less viscous) fluid, and η2(
, η1 is the viscosity of the injected (less viscous) fluid, and η2(![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) ) is the shear-rate dependent viscosity of the more viscous fluid. Eqn (8) takes into account that the more viscous fluid may be non-Newtonian; accordingly, η2 is the viscosity value at the shear rate
) is the shear-rate dependent viscosity of the more viscous fluid. Eqn (8) takes into account that the more viscous fluid may be non-Newtonian; accordingly, η2 is the viscosity value at the shear rate ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) = 4r0
= 4r0![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) I/r at the interface position.15 This is indeed the case of the patterns of Fig. 6, showing the Saffman–Taylor instability when non-Newtonian, concentrated suspensions of microgels are displaced by their solvent (water). It's worth noting that here the wavelength λ = 2πr/nA of the instability depends on the microgel concentration and the injection rate:15 this is at odd with the predictions for radial viscous fingering with zero surface tension,59 for which λ ≈ 4b independently of γI and φ. Thus, the patterns shown in Fig. 6 are indicative of a finite, positive interfacial tension between the solvent and the suspension.
I/r at the interface position.15 This is indeed the case of the patterns of Fig. 6, showing the Saffman–Taylor instability when non-Newtonian, concentrated suspensions of microgels are displaced by their solvent (water). It's worth noting that here the wavelength λ = 2πr/nA of the instability depends on the microgel concentration and the injection rate:15 this is at odd with the predictions for radial viscous fingering with zero surface tension,59 for which λ ≈ 4b independently of γI and φ. Thus, the patterns shown in Fig. 6 are indicative of a finite, positive interfacial tension between the solvent and the suspension.
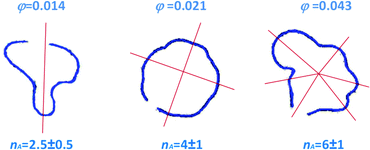 | ||
Fig. 6 Top view of the interface between the injected solvent (water) and an aqueous suspension of PNiPAM microgels confined in a Hele-Shaw cell, for various PNiPAM concentrations as indicated by the labels and a fixed shear rate at the injection hole ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) I = 570 s−1. Adapted from ref. 15. I = 570 s−1. Adapted from ref. 15. | ||
Eqn (8) has been first tested for silicon oil and water,15 a pair of Newtonian immiscible fluids for which all parameters, including Γ, are well known. Once its validity has been demonstrated, it has been used to investigate systematically the off-equilibrium interfacial tension between colloidal suspensions and their solvent. We report here the results for two different systems: the suspensions of soft microgels of ref. 15 and hard silica colloidal particles (Ludox).16
For both systems, the EIT is plotted as a function of concentration in Fig. 7. For the microgels (panel A), φ is the monomer volume fraction, which is about a factor of 20 smaller than the volume fraction occupied by the microgels, due to their high swelling. For the compact Ludox colloids (panel B), φ is the particle volume fraction. Strikingly, the behaviour of Γe depends dramatically on the kind of particles: for the microgels, Γe increases smoothly and mildly with increasing volume fraction. For the Ludox suspensions, by contrast, the EIT is smaller than for the microgels at low φ, but it increases sharply as φ increases, resulting in a growth of Γe by more than three decades over the range of the concentrations explored in our experiments.
The solid lines in Fig. 7A are parabolic fits to the data according to eqn (4), showing that for the microgels Korteweg's theory holds over the full range of φ investigated. This is consistent with the remark that the experiments of ref. 15 were performed in the low-φ, small-gradient limit, where eqn (4) is expected to be valid. As a further test of this interpretation, the square-gradient constant κ has been calculated15 by adapting existing polymer theories,60 finding
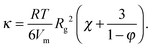 | (9) |
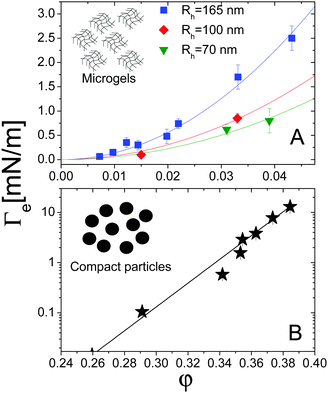 | ||
| Fig. 7 (A) Effective interfacial tension Γe between microgel suspensions and their solvent, as a function of the microgel concentration, expressed as polymer volume fraction. The lines are quadratic fits to the data for microgels with various hydrodynamic radii Rh, as shown by the legend. Data adapted from ref. 15. (B) EIT Γe between suspensions of silica particles and their solvent, as a function of the particle volume fraction. The solid line is an empirical exponential fit, as discussed in the text. Data adapted from ref. 16. | ||
For the Ludox suspensions, by contrast, the quadratic law (4) fails to fit the sharp growth of Γeversus φ. We argue that this is due to the compact nature of the silica colloids, to be contrasted with the porous, highly swollen structure of the microgels. As a consequence, a sharp composition gradient exists across the solvent-suspension interface, such that higher order terms not included in Korteweg's theory become important. One would still expect eqn (4) to hold at low enough φ; unfortunately, the viscosity contrast between diluted Ludox suspensions and their solvent is too low for this regime to be probed in our Hele-Shaw experiments. In the range of packing fractions accessible in ref. 16, the EIT of Ludox suspensions is well reproduced by an exponentially diverging law: Γe = a(exp(bφ − 1)), with a = 1.0 × 10−2 nN m−1 and b = 54.6 (solid line in Fig. 7). Ongoing work in our group focuses on investigating the physical origin of this empirical law, as well as its dependence on particle size, internal structure, and interparticle interactions.
4 Conclusions and perspectives
Although the possibility that interfacial stresses between relaxing miscible liquids act as an effective interface tension was already recognized by Korteweg26 more than a century ago, only in the last 30 years have accurate experiments been carried out to quantify such EIT and understand the physical mechanism at its origin. All the experiments reviewed here demonstrate the existence of a positive interfacial tension between miscible liquids, for near-critical, conventional, molecular and complex fluids alike. The magnitude of the EIT is far from being negligible, at least in the short time limit, before diffusion smears out significantly the concentration profile. For example, for the microgel and colloidal suspensions of Fig. 7Γe ranges from a fraction of mN m−1 up to more than 10 mN m−1, the same order of magnitude as the usual interfacial tension between, e.g., water and oil (about 40 mN m−1).Various experimental strategies have been used to measure the EIT. Standard methods tailored for low interfacial tensions like spinning drop tensiometry and light scattering have been proven to be very valuable, although they are limited respectively by mixing and by the difficulty to distinguish between light scattered by the bulk fluids and by the interfacial region. Such complications can be overcome by the visual analysis of the patterns formed in the Saffman–Taylor instability. This method allows for fast experiments (duration texp ≤ 0.1 s); when coupled to the choice of complex fluids such as colloid and polymer suspensions, it gives access to the EIT in the t → 0 limit, before diffusion takes place. As a drawback of this new method, it should be mentioned that the kinetics of the interfacial stresses cannot be investigated, contrary to the case of light scattering. Future work may help identifying new geometries where the EIT can be studied as a function of time, and for arbitrary fluid compositions.
This mini review has focussed essentially on experimental work. This is not merely the result of the taste and the inclinations of its authors: it also reflects the state of the art, with very few theoretical works devoted to this topic. Urgent questions concern the functional form of Γe(φ) beyond the Korteweg regime, its dependence on the fluid parameters (particle internal structure and interactions), and, at an even more fundamental level, the very sign of the EIT in complex fluids.
It is a pleasure to acknowledge several illuminating discussions with P. Petitjeans and J. A. Pojman. We thank our coworkers C. Dupas and S. Mora, with whom we have shared the pleasure of investigating the EIT.
Note added after first publication
This article replaces the version published on the 31st of May 2016, which contained errors in references 10, 21–23, 34, 43, 45 and 46.References
- J. Rowlinson and B. Widom, Molecular Theory of Capillarity, Clarendon, Oxford, 1982 Search PubMed.
- P.-G. de Gennes, F. Brochard-Wyart and D. Queré, Capillarity and Wetting Phenomena: Drops, Bubbles, Pearls, Waves, Springer-Verlag, Berlin, 2004 Search PubMed.
- O. H. Samuli Ollila, A. Lamberg, M. Lehtivaara, A. Koivuniemi and I. Vattulainen, Biophys. J., 2012, 103, 1236–1244 CrossRef PubMed.
- L. D. Zarzar, V. Sresht, E. M. Sletten, J. A. Kalow, D. Blankschtein and T. M. Swager, Nature, 2015, 518, 520–524 CrossRef CAS PubMed.
- E. Pennisi, Science, 2014, 343, 1194–1197 CrossRef CAS PubMed.
- P.-G. de Gennes, Scaling concepts in polymer physics, Cornell University Press, Ithaca and London, 1979 Search PubMed.
- S. Mora, C. Maurini, T. Phou, J.-M. Fromental, B. Audoly and Y. Pomeau, Phys. Rev. Lett., 2013, 111, 114301 CrossRef PubMed.
- S. E. May and J. V. Maher, Phys. Rev. Lett., 1991, 67, 2013 CrossRef CAS PubMed.
- P. Cicuta, A. Vailati and M. Giglio, Appl. Opt., 2001, 40, 4140–4145 CrossRef CAS PubMed.
- L. Lacaze, P. Guenoun, D. Beysens, M. Delsanti, P. Petitjeans and P. Kurowski, Phys. Rev. E, 2010, 82, 041606 CrossRef PubMed.
- P. Petitjeans, Cr. R. Acad. Sci. Paris, 1996, 322, 673 CAS.
- J. A. Pojman, C. Whitmore, M. L. Turco Liveri, R. Lombardo, J. Marszalek, R. Parker and B. Zoltowski, Langmuir, 2006, 22, 2569–2577 CrossRef CAS PubMed.
- B. Zoltowski, Y. Chekanov, J. Masere, J. A. Pojman and V. Volpert, Langmuir, 2007, 23, 5522–5531 CrossRef CAS PubMed.
- J. E. Mungall, Phys. Rev. Lett., 1994, 73, 288 CrossRef CAS PubMed.
- D. Truzzolillo, S. Mora, C. Dupas and L. Cipelletti, Phys. Rev. Lett., 2014, 112, 128303 CrossRef PubMed.
- D. Truzzolillo, V. Roger, C. Dupas, S. Mora and L. Cipelletti, J. Phys.: Condens. Matter, 2015, 27, 194103 CrossRef CAS PubMed.
- P. Petitjeans and T. Maxworthy, J. Fluid Mech., 1996, 326, 37 CrossRef CAS.
- S. Swernath, B. Malengier and S. Pushpavanam, Chem. Eng. Sci., 2010, 65, 2284–2291 CrossRef CAS.
- G. Morra and D. A. Yuen, Geophys. Res. Lett., 2008, 35, L07304 CrossRef.
- A. Souriau and G. Poupinet, Phys. Earth Planet. Inter., 1991, 68, 183–199 CrossRef.
- X. F. Liu, E. George, W. G. Bo and J. Glimm, Phys. Rev. E, 2006, 73, 056301 CrossRef PubMed.
- C.-Y. Chen, C.-W. Huang, H. Gadêlha and J. A. Miranda, Phys. Rev. E, 2008, 78, 016306 CrossRef PubMed.
- E. O. Dias and J. A. Miranda, Phys. Rev. E, 2013, 88, 013016 CrossRef PubMed.
- J. E. van der Waals, Z. Phys. Chem., 1894, 13, 657 Search PubMed.
- S. Kjelstrup and D. Bedeaux, Non-equilibrium thermodynamics of heterogeneous systems, World Scientific Publishing Co. Pte. Ltd, Singapore, 2008 Search PubMed.
- D. Korteweg, Arch. Neerl. Sci. Exactes Nat., 1901, 6, 1–24 CAS.
- N. Bessonov, J. A. Pojman and V. Volpert, J. Eng. Math., 2004, 49, 321–338 CrossRef.
- J. A. Pojman, Y. Chekanov, N. Wyatt, V. Bessonov and V. Volpert, Microgravity Sci. Technol., 2009, 21, 225–237 CrossRef CAS.
- J. W. Cahn and J. E. Hilliard, J. Chem. Phys., 1958, 28, 258–267 CrossRef CAS.
- D. A. Cogswell and W. C. Carter, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2011, 83, 061602 CrossRef PubMed.
- Y. B. Zeldovich, Zh. Fiz. Khim. (in Russian), 1949, 23, 931–935 CAS.
- P. G. Smith, T. G. M. Van den Ven and S. G. Mason, J. Colloid Interface Sci., 1981, 80, 302–303 CrossRef CAS.
- H. T. Davis, Numerical Simulation and Oil Recovery, Springer-Verlag, Berlin, 1988, p. 105 Search PubMed.
- M. Bier, Phys. Rev. E, 2015, 92, 042128 CrossRef PubMed.
- L. Paterson, Phys. Fluids, 1985, 28, 26–30 CrossRef.
- J. Nittmann, G. Daccord and H. E. Stanley, Nature, 1985, 314, 141–144 CrossRef CAS.
- J. Nittmann and H. E. Stanley, Nature, 1986, 321, 663–668 CrossRef.
- D. D. Joseph, Eur. J. Mech. B, 1990, 9, 595 Search PubMed.
- H. Freundlich, Colloid and Capillary Chemistry, Mathuen & Co Ltd, 1926 Search PubMed.
- P. Garik, J. Hetrick, B. Orr, D. Barkey and E. Ben-Jacob, Phys. Rev. Lett., 1991, 66, 1606–1609 CrossRef CAS PubMed.
- A. Castellanos and A. González, Phys. Fluids A, 1992, 4, 1307–1309 CrossRef CAS.
- G. I. Taylor, J. Fluid Mech., 1961, 10, 161 CrossRef.
- D. Vlad and J. Maher, Phys. Rev. E, 1999, 59, 476 CrossRef CAS.
- W.-J. Ma, P. Keblinski, A. Maritan, J. Koplik and J. R. Banavar, Phys. Rev. Lett., 1993, 71, 3465 CrossRef CAS PubMed.
- A. Cicuta, P. Vailati and M. Giglio, Phys. Rev. E, 2000, 62, 4920–4926 CrossRef.
- A. Vailati and M. Giglio, Phys. Rev. E, 1998, 58, 4361–4371 CrossRef CAS.
- L. I. Mandelstamm, Ann. Phys., 1913, 41, 609–624 CrossRef.
- A. Vailati and M. Giglio, Phys. Rev. Lett., 1996, 77, 1484–1487 CrossRef CAS PubMed.
- A. Vailati and M. Giglio, Nature, 1997, 390, 262–265 CrossRef CAS.
- B. Vonnegut, Rev. Sci. Instrum., 1942, 13, 6–9 CrossRef CAS.
- J. C. Slattery and J.-D. Chen, J. Colloid Interface Sci., 1978, 64, 371–373 CrossRef.
- D. G. A. L. Aarts, M. Schmidt and H. N. W. Lekkerkerker, Science, 2004, 304, 847 CrossRef CAS PubMed.
- E. H. A. de Hoog and H. N. W. Lekkerkerker, J. Phys. Chem. B, 1999, 103, 5274–5279 CrossRef CAS.
- H. Lekkerkerker, V. Villeneuve, J. Folter, M. Schmidt, Y. Hennequin, D. Bonn, J. Indekeu and D. Aarts, Eur. Phys. J. B, 2008, 64, 341–347 CrossRef CAS.
- S. A. Setu, I. Zacharoudiou, G. J. Davies, D. Bartolo, S. Moulinet, A. A. Louis, J. M. Yeomans and D. G. A. L. Aarts, Soft Matter, 2013, 9, 10599–10605 RSC.
- P. Saffman and G. I. Taylor, Proc. R. Soc. London, Ser. A, 1958, 245, 312 CrossRef CAS.
- D. Bensimon, L. P. Kadanoff, S. Liang, B. I. Shraiman and C. Tang, Rev. Mod. Phys., 1986, 58, 977 CrossRef.
- R. Chuoke, P. Van Meurs and C. Van der Pol, Petrol. Trans. AIME, 1959, 216, 188 Search PubMed.
- L. Paterson, Phys. Fluids, 1985, 28, 26 CrossRef.
- N. P. Balsara and E. B. Nauman, J. Polym. Sci., Polym. Phys. Ed., 1988, 26, 1077–1086 CrossRef CAS.
| This journal is © The Royal Society of Chemistry 2017 |

