Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Drainage dynamics of thin liquid foam films containing soft PNiPAM microgels: influence of the cross-linking density and concentration†
L.
Keal
ab,
V.
Lapeyre
c,
V.
Ravaine
c,
V.
Schmitt
d and
C.
Monteux
*ab
aÉcole Supérieure de Physique et de Chimie Industrielles de la Ville de Paris (ESPCI), ParisTech, PSL Research University, Sciences et Ingénierie de la Matière Molle (SIMM), CNRS UMR 7615, 10 rue Vauquelin, F-75231 Paris cedex 05, France. E-mail: cecile.monteux@espci.fr
bSorbonne-Universités, UPMC Univ Paris 06, SIMM, 10 rue Vauquelin, F-75231 Paris cedex 05, France
cUniversité de Bordeaux, Institut des Sciences Moléculaires, ENSCBP, 16 Av. Pey Berland, 33607 Pessac Cedex, France
dUniversité de Bordeaux, Centre de Recherche Paul Pascal, 115 Av. A. Schweitzer, 33600 Pessac, France
First published on 22nd June 2016
Abstract
We investigate the drainage dynamics of thin liquid foam films containing PNiPAM microgel suspensions with two cross-linking densities (1.5 and 5 mol% BIS) and at two microgel concentrations (0.1 and 1% wt). For this purpose, we use a thin-film pressure balance apparatus that can apply a controlled and sudden hydrostatic pressure on a film, and record the subsequent film thinning as a function of time. Once the film thickness has reached a stationary value, we test the adhesion between the interfaces of the film by reducing the pressure and measuring the angle between the film and the meniscus. This angle increases on reduction of pressure for adhesive films, which resists the separation of their interfaces. Non-adhesive films separate easily, and the meniscus angle stays constant. At a low microgel concentration, the more densely cross-linked microgels (5 mol% BIS) tend to drain into more adhesive films than the more loosely cross-linked particles (1.5 mol% BIS). The adhesion results from particles that bridge the two air–water interfaces of the film and are shared between them. In these cases, the film, which is initially stabilized by a bilayer of microgel particles, rearrange to a state where the microgels bridge the interfaces. These results are discussed and compared with previous studies at a low concentration of microgels, which have shown that emulsions stabilized with densely cross-linked microgels are more adhesive and less resistant to mechanical stresses than those obtained with lower cross-linking densities. In addition, micron-scale depleted zones with no microgels are observed in the films stabilized with the 5 mol% BIS particles, which eventually lead to the rupture of the films. At 1% wt, the films drain slowly, are not adhesive and have the thickness of a bilayer of microgel; while at 0.1% wt, the films have the thickness of a monolayer of microgel, are adhesive and show bridging. From the thin liquid foam film thicknesses we extract a rough estimation of the radii of adsorbed particles in the thick films before applying the pressure. Our results are consistent with particles being adsorbed in a spread conformation for the 0.1% wt sample and in a compressed conformation for the 1% wt sample. In line with previous studies on emulsions, we conclude that a larger surface coverage may reduce rearrangements, thus preventing bridging.
Introduction
Poly(N-isopropylacrylamide) (PNiPAM) thermoresponsive or pH sensitive microgel particles have recently been shown to be promising systems to stabilise responsive emulsions.1–7 These particles are surface active and spontaneously adsorb to liquid interfaces. The stability of microgel-stabilised emulsions depend on their cross-linking density,7,8 protonated state,1,2 and temperature.5,9 In contrast, electrostatics has neither impact on the microgel organization at the oil–water interface nor on emulsion stability.10 The mechanisms for emulsion stabilisation and destabilisation are not well understood and are the subject of intense research, the results of which have been summarized in recent reviews.11–13 Recent studies have focused on the adsorption kinetics and conformation of particles in emulsions and at model interfaces. Unlike the usual hard colloidal particles, soft microgel particles can deform as they adsorb at interfaces and their conformation is theoretically governed by a balance between bulk elasticity and surface tension.14,15 Experimentally, the cryo-SEM images of emulsion droplets have shown that PNiPAM microgel particles can spread as they adsorb at the oil–water interface at a low surface coverage and adopt a ‘fried-egg’ structure.6–8,16,17 This conformation is due to the fact that the cross-linking density of these microgels is not homogeneous and decreases toward the periphery of the particles. Therefore, they have a core–shell structure where the core is more strongly cross-linked and less deformable than the corona, which is composed of dangling PNiPAM arms. Moreover, Geisel et al. showed experimentally that the hydrated cores protrude into the oil phase.18,19 As the cross-linking density of such microgels decreases (more deformable microgels), it has been shown that their packing at droplet interfaces (center-to-center distance) does not vary, whereas the interpenetration of the dangling chains increases.7,8Several studies have focused on the spontaneous adsorption of microgels in model geometries, using particle tracking techniques at a flat interface,21,22 the pendant drop method5,22–26 or Langmuir trough experiments.25–27 Interestingly, particle tracking studies performed recently showed that the particles eventually form clusters,20,21 the origin of which is still unknown. Spontaneous adsorption studies have revealed the influence of the microgel concentration on the adsorption kinetics.22,25,26,28 At high microgel concentrations the adsorption kinetics are very fast leading to large decreases in the interfacial tension and consequently to high surface pressures. In turn, the adsorption kinetics and concentration control the conformation of the particles. At low surface pressures the microgel particles reach a ‘spread’ conformation, while at high surface pressures the microgels are forced into more densely packed layers.25
The conformation of the particles influences their interpenetration and, therefore, the surface viscoelasticity as well as the stability of emulsions with respect to handling. By combining Langmuir trough compressions and oscillating bubble experiments, Pinaud et al. have found that at a low surface coverage the surface dilational elasticity is low as the particles are far from each other in a spread conformation.25 As the surface coverage increases, particles come into contact and the surface dilational elasticity reaches the maximum as particles become interpenetrated; at larger surface compressions the surface dilational elasticity decreases because some polymer segments of the particles can partially desorb upon compression. The role of cross-linking density on the dilational elasticity and compressibility of the layers is not trivial. Pinaud et al.25 found that the cross-linking density influences the compressibility only at large compressions. Consistently, the dilational elasticity of microgel layers, which is obtained at low deformations using the pendant drop method, was shown not to depend on the cross-linking density.25 However Geisel et al.29 studied the compression of core–shell and hollow shell microgel particles in a Langmuir trough and found that at low compressions, the cross-linking density decreases the compressibility of the layers, while at large compressions, larger cross-linking densities favour large compression elasticity. This nontrivial behaviour is due to a competition between desorption of polymer segments at low compression and network deformation at large compression. Brugger et al. performed surface elasticity measurements of interfaces covered with microgels composed of NiPAM and acrylamide monomers which are charged at high pH and uncharged at low pH.23 They found that the surface shear and dilational elasticity is larger at high pH when the particles are charged and the microgels are partially interconnected, providing a soft gel-like interface.
The conformation of the microgel particles also plays a role in the behaviour of thin liquid films and bridging phenomena in emulsions. The studies performed on emulsions stabilised by microgels have revealed that such emulsions often exhibit adhesion between drops arising from bridging of the surfaces of two neighbouring drops by particles shared between the two droplet interfaces, as evidenced by Cryo-SEM experiments. This adhesion depends on numerous factors such as:
(i) the cross-linking density: at a fixed microgel size, the more cross-linked the microgels the more adhesive the drops.8
(ii) the microgel size: the larger the microgel the more adhesive the drops.30
(iii) the stirring energy: a higher energy input favours adhesion.31
All these parameters have been proposed to merge into a single proposition: “adhesion is promoted by a low polymer density and the existence of polymer density fluctuations parallel to the surface”.13
To our knowledge, the dynamics of thin-liquid film drainage which leads to these bridged layers of particles has never been studied in great detail. In this study, to complete the previous studies performed either on emulsions or on single model air–water or oil–water interfaces, we seek insight into films. We investigate the drainage dynamics of horizontal aqueous thin liquid films suspended in air (i.e. foam films) prepared using microgel suspensions at varying concentrations and cross-linking densities under controlled increments of hydrostatic pressure. We chose to investigate thin liquid foam films rather than emulsion films (water films suspended in oil) because they are easier to investigate experimentally. However, we show in this article that the behaviour of these suspended foam films is very similar to emulsion films observed in situ in emulsions.
The cross-linking densities of 1.5 and 5 mol% have been chosen because of the very different adhesion angle between drops. We chose two microgel concentrations (0.1 and 1% wt) in order to investigate two significantly different adsorption kinetics. We found that the particle concentration has a strong influence on the drainage dynamics. At the lowest concentration, the thin films tend to drain faster and show adhesion between the interfaces while at a larger concentration the films reach larger thicknesses and are less likely to show bridging. Calculations based on the film thickness enable the extraction of a rough estimation of the conformation of the particles, i.e. their adsorbed radius at air–water interfaces. We show that at 0.1% wt the particles are in a spread conformation while at 1% wt the particles are in a compressed conformation. Consequently, the 1% wt sample tends to drain slowly and forms very stable bilayers while the 0.1% wt films are adhesive and show bridging, which is favoured by the low surface coverage. Moreover, we found that for a given concentration the microgels with larger cross linking density tend to drain faster and form more adhesive thin-liquid films than less cross-linked microgels. At the lowest concentration and highest cross-linking density, we observe micrometric zones which are depleted of microgels. As a consequence, at rest the films made with highly cross-linked microgels are less stable than those made with the less cross-linked particles.
Experimental
Materials
The microgels were synthesized by aqueous free-radical precipitation polymerization of N-isopropylacrylamide and N,N′-methylenebisacrylamide, according to the procedure described in ref. 7. Microgels were then characterized by dynamic light scattering. Two batches of microgels having different cross-linking densities were produced. The microgels with 1.5 mol% BIS have a hydrodynamic diameter of 770 nm at 25 °C and 260 nm in the collapsed state. The microgels with 5 mol% BIS have a hydrodynamic diameter of 660 at 25 °C and 280 nm in the collapsed state. To produce fluorescent microgels, acryloyl fluorescein (0.1% wt with respect to NiPAM) was introduced in the polymerization reaction.Methods
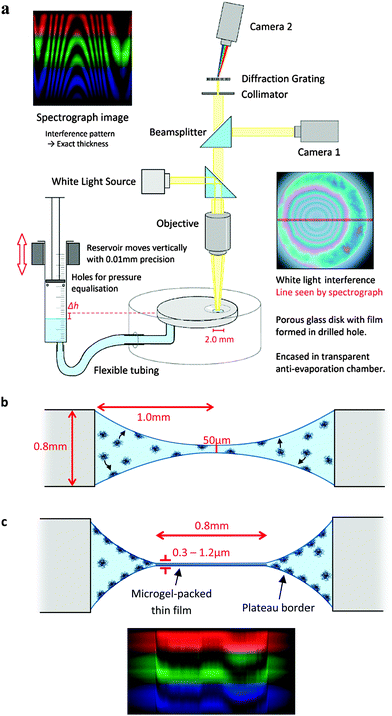
The experimental apparatus was adapted from the thin-film pressure balance apparatus as described by Mysels and Jones,32 modified to be more suitable for films with poor stability. Films were formed within a 2.0 mm diameter, 0.8 mm height hole, drilled into a porous glass plate, as shown in Fig. 1. The plate is attached to a vertical 8 mm syringe with tubing, which acts as a reservoir. Small holes open the syringe to balance the air pressure inside with that upon the film. The syringe is mounted on a micrometer adjustable vertical plate such that its height, and hence the hydrostatic pressure upon the film, can be precisely adjusted. The disk is encased in a humidified plastic chamber to prevent evaporation. The temperature of the room is controlled through air conditioning, and set at 21 ± 0.5 °C.The pressure imposed upon the film is given by Π = Δρgh, where Δρ is the density difference between the solution and air, g is gravitational acceleration and h is the vertical distance between the surface of the reservoir and the film. The diameter of the reservoir is much larger than the capillary length of the solution such that the curvature of its interface does not contribute significantly to the pressure. The volume of solution drained by the application of pressure has a negligible effect upon the volume within the reservoir. In all experiments reported here the applied pressure Π was 15 Pa.
Above the film a reflected light microscope is mounted, with a white light lamp illuminating the film. Reflected light from the film is then split by a beam splitter into both a colour video camera (Cyberlink PL-B776U) and a spectrograph (Specim V8E) connected to another video camera. The spectrograph provides the wavelength-dependent intensity for a line across the image. The wavelengths of the maxima and minima of interference occur at 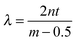 and
and 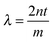 , respectively, where n is the refractive index of the solution, t the thickness and m = 1, 2, 3,…. The refractive index of the solution is calculated according to a linear combination by the concentration of the wavelength-dependent refractive index of pure water33 and pure PNiPAM.34 As explained in SI1 in the ESI†, as the microgel particles have been shown to be incompressible35 and their refractive index is close to that of water, their deformation and change in concentration in the film during drainage has no significant contribution to the overall refractive index of the film, and hence on the thickness measurement. The thickness profile of the film is attained by finding the maxima and minima.
, respectively, where n is the refractive index of the solution, t the thickness and m = 1, 2, 3,…. The refractive index of the solution is calculated according to a linear combination by the concentration of the wavelength-dependent refractive index of pure water33 and pure PNiPAM.34 As explained in SI1 in the ESI†, as the microgel particles have been shown to be incompressible35 and their refractive index is close to that of water, their deformation and change in concentration in the film during drainage has no significant contribution to the overall refractive index of the film, and hence on the thickness measurement. The thickness profile of the film is attained by finding the maxima and minima.
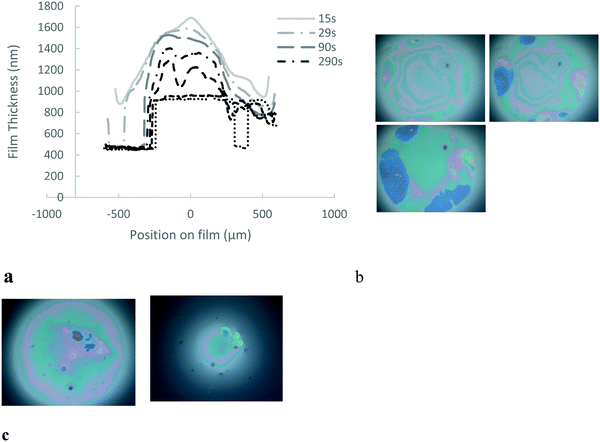
The experimental procedure begins with the formation of a film in the hole with a drop from a pipette. The initial film is set at 50 μm thickness, at which the surface is non-interacting (Fig. 1b). The system is allowed a set adsorption time for microgels to diffuse and adsorb to the surface. Unless otherwise specified, the adsorption time for 1% wt was 20 minutes and for 0.1% wt 40 minutes, chosen to allow sufficient diffusion time, based on ref. 25. Then, the hydrostatic pressure is applied in one step and the film begins to drain (Fig. 1c). Once drainage is complete, the adhesion between the interfaces is tested. In order to do this, the hydrostatic pressure is removed from the film to re-swell the film.
Measurements of the contact angle in the Plateau border begin with interferometric measurement of the thickness of the plateau border by the film edge using a 100× microscope objective (Olympus LM PlanFI 100×/0.80) and a spectrometer. A linear profile is fitted to these measurements and the angle this line makes with the horizontal plane is equal to 2θadh.
For films with a symmetrically centred dimple, interferometric measurements give the film thickness profile of the central line. By modelling the dimple as two spherical caps resting on a cylindrical volume with the thickness of the surrounding film, the model profile is fitted to the measured profile and the volume of the model system is calculated. For films in which the dimple is asymmetrically placed but still within the line measured using the spectrometer, the distance of the centre of the dimple from the spectrometer line is measured in the video microscope image, and introduced as a parameter of the model.
Film drainage experiments of microgels labelled with a small quantity of fluorescein were performed as described above for non-labelled microgels, however with a filter cube (Olympus U-MWIBA3) in the light path to select excitation and observation wavelengths at 460–495 and 510–550 nm, respectively. The presence of fluorescein in the microgels had no observable effect on their behaviour.
Results
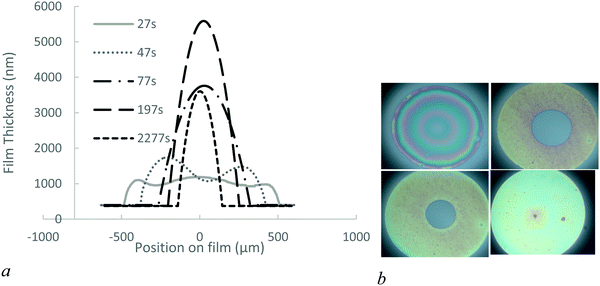
1. Behaviour of the 1.5 mol% BIS microgels
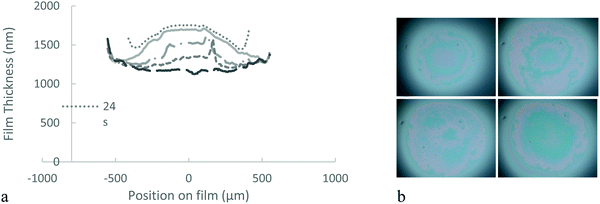
We investigate the drainage dynamics of foam films made with 1.5 mol% BIS microgels at two particle concentrations, 0.1 and 1% wt. The 1% wt foam films drain in approximately 1500 s to reach a film of thickness 1070 nm (Fig. 2). In the first stage, the films form a ‘dimple’, a spherical cap, which becomes thinner over time. Dimples are known to form because of the pressure gradient in the thin liquid foam films during drainage36,37 as the pressure is larger in the centre of the films than on the edge.In the case of the 1.5 mol% BIS microgels at 0.1% wt, we find that shortly after applying the pressure a thin liquid foam film of a uniform thickness of 340 nm invades the film and traps a spherical dimple (Fig. 3). This symmetric dimple drains into the 340 nm thin barrier ring in 1500 s. Symmetric drainage is usually observed when a high surface viscosity stabilises thin liquid films.36,37 After 2200 s, the foam film thickness becomes homogeneous.
The large difference in thickness, 1070 nm versus 340 nm, obtained at high and low concentrations, respectively, could be caused by a possible transition from bilayer to monolayer of microgels in the film in the case of low concentration, i.e. a monolayer of microgels that bridge the interfaces. As bridging is known to induce adhesion between the interfaces, we probe in the following section, the adhesion between the interfaces by reducing the applied pressure back to zero.
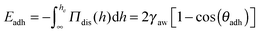 | (1) |
As shown in Table 1 and Fig. 4a and b, in the case of the 1% wt sample, we find that the meniscus recedes immediately and the adhesion angle, which is initially equal to 0.1° before the pressure reduction, remains constant after the pressure is reduced. We note that the contact angles that we measure are of the same order of magnitude as those commonly obtained for thin-liquid films standing in air.38 For the 0.1% wt sample (Fig. 4c and d), the initial contact angle θadh is 2° (Table 1). Shortly after decreasing the pressure, the meniscus remains pinned until the contact angle increases to 6° and then starts receding. From this adhesion angle, using eqn (1), taking γaw ∼ 40 mN m−1,21 we deduce that the energy of adhesion per unit surface is of the order of 0.5 mJ m−2.
| 1.5 mol% BIS | 5 mol% BIS | |||
|---|---|---|---|---|
| 0.1% wt | 1% wt | 0.1% wt | 1% wt | |
| Thickness (nm) | 340 | 1200 | 400 | 900 |
| θ adh (°) | 6 | 0.1 | 8 | 0.1 |
| E adh (mJ m−2) | 0.5 | ∼0 | 1 | ∼0 |
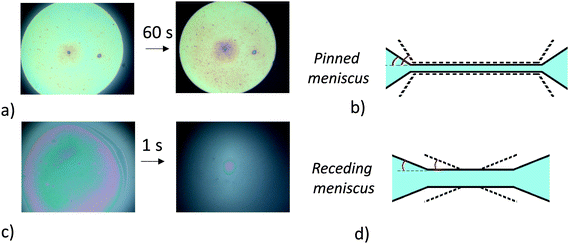 | ||
| Fig. 4 Photographic images and schematic diagrams of thin liquid foams films during adhesion test for 1.5% mol BIS microgels. (a) and (b) 0.1% wt sample. (c) and (d) 1% wt sample. | ||
From these measurements, we conclude that a lower concentration promotes adhesion between the two interfaces of the film and that the microgel particles probably bridge the interfaces of the film in the case of the 0.1% wt sample. These results are consistent with Destribats's study,8 which reported partial bridging between emulsion droplets in the case of 1.5 mol% BIS microgels. Their Cryo-SEM images show that micron-sized regions of various thicknesses coexist within the films corresponding to monolayers and bilayers. Although we measure a larger angle between the interfaces for the 0.1% wt sample, we do not have enough spatial resolution to determine whether the film is composed of a uniform monolayer of particles or whether both configurations coexist.
2. Behaviour of the 5 mol% BIS microgels at concentrations of 0.1 and 1% wt
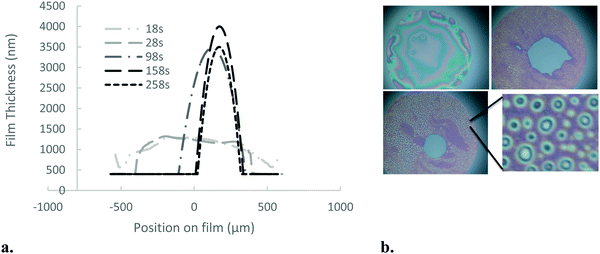 | ||
| Fig. 5 (a) Drainage dynamics and thickness profile for the 5 mol% BIS microgels at concentration 0.1% wt. (b) White light images of the thin-liquid films as a function of time for 18, 100, 1300 s. | ||
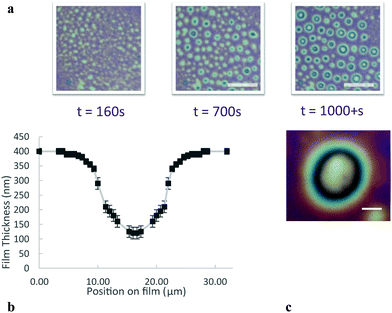
For more densely cross-linked microgels, the film thickness is much less homogenous than the microgels with lower cross-linking density; immediately after nucleation of the 400 nm film, its thickness varies by tens of nm in regions a few μm across, visible as the white and red texturing in Fig. 5. Over longer times, however, this inhomogeneity becomes much more pronounced through a process resembling spinodal decomposition,39,40 where thinner (whiter) spots deepen and occasionally coalesce on the film, eventually forming much larger thin circular zones, as demonstrated in Fig. 6a. After several hundred seconds, the larger zones (20 μm diameter) can be as thin as 110 nm in their centres. The profile of a thin zone measured using a 100× objective is shown in Fig. 6b. Once these thin zones appear in the film breakage is more likely.
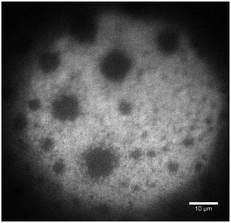
To determine whether microgel particles are present in these thinner zones, we performed fluorescence measurements using fluorescent microgels and a high-sensitivity camera. As shown in Fig. 7 the fluorescence intensity is very low in the thin zones, whereas microgels can be individually resolved at their edges. There are therefore no microgels in the 110 nm region. These depleted zones could lower the life time of the present foam film as the film is no more protected against rupture by microgels. Also, the transient stability of these zones can be explained by the fact that to empty these zones, the water has to drain slowly through the microgel compressed particle layer around.
Unlike the 1.5 mol% BIS microgel foam films, under the same experimental conditions, the 5 mol% BIS microgel foam films can exhibit two possible surface behaviours consistent with different surface concentrations (see SI3, ESI†). The lack of homogeneity in the film thickness probably reflects the lack of homogeneity in the packing density of the two single air–water interfaces, which are forced into contact to produce thin foam films upon pressure application. Such gradients in packing density may appear during the adsorption time and probably remain stable because the Brownian motion of these microgel particles is very slow at interfaces21 and they tend to form clusters at liquid interfaces.20,21
Adhesion experiments performed on the 0.1% wt films show that the angle, θadh, increases from 2.7 to 8° as the pressure is released illustrating the adhesion phenomenon between the interfaces. From the value of the angle we find an adhesion energy of ∼1 mJ m−2, which is two times larger than the one measured for the 1.5 mol% BIS microgels, showing that increasing the cross-linking density leads to an increase of the adhesion energy. This observation on a single foam film is again similar to the observation of Destribats et al.8 on emulsions. We note that our adhesion energies are an order of magnitude lower than the ones we can estimate from Destribats's adhesion angles measured between emulsions droplets. However, in their study they used much smaller particle concentrations and their emulsification process involved a high shear force which favoured the spread conformation and bridging.
3. Influence of the cross-linking density on the dimple drainage dynamics for the 0.1% wt samples
Fig. 9 presents the time evolution of the volume of the draining dimple trapped in the microgel adhesive thin liquid foam films for the 5 mol% BIS and 1.5 mol% BIS microgels at 0.1% wt. We find that the dimple drains faster for the 5 mol% BIS microgels than for the 1.5 mol% BIS microgels. From the drainage dynamics, we can estimate a global permeability of the microgel layer surrounding the dimple using Darcy's law, which describes the flow of liquids in porous media under a given pressure difference. Here, we consider the flow of water from the dimple to the meniscus, through the flat film of uniform thickness, in a cylindrical geometry,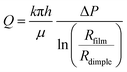 | (2) |
4. Discussion on the influence of the cross-linking density and concentration on the drainage dynamics, film thickness and bridging phenomenon
– The microgel concentration controls the adhesion between the thin liquid foam film interfaces. The lower microgel concentration film shows bridging and has a thickness of one monolayer. Conversely, we did not observe adhesion or bridging at the larger concentration. In the latter case, the films have the thickness of a bilayer.
– The more densely cross-linked microgels lead to larger adhesion angles (2.7 to 8° versus 2 to 6° at the low cross-linking density). The more densely cross-linked microgels drain more quickly, tend to present depleted zones that grow over time and lead to more unstable films.
These results present striking similarities with previous observations made for water in oil thin films observed in situ in emulsions.
– Bridging is observed for emulsions prepared in the limited coalescence regime, i.e. in a particle poor regime where the particles are in a spread conformation at interfaces. Under these conditions, bridging is favoured for more cross-linked microgels.
– The stability of emulsions with respect to handling is lower for more cross-linked microgels because of a lower lateral interpenetration and more protruding microgels in the water phase as they are less deformable. Consistently, in our study, the foam films made with the more cross linked 5 mol% BIS microgels at low concentration are thicker.
– At the larger concentrations, microgels spread to a lesser extent and are in a more compressed conformation. The connection between droplets is less probable and non adhesive bilayers are observed.
There is a fascinating similarity between the two types of interfaces and systems, i.e. air–water interfaces in a single thin liquid foam film and oil–water interfaces in emulsions, although the interfacial tensions involved are a bit different. Such a resemblance between a model foam film and a collection of emulsion films is rare. This is even more surprising as the process used to produce these two types of interfaces is very different. A strong shear energy is used to produce emulsions unlike the foam films in the thin-film pressure balance set-up. In fact the structure of the layers, such as the percentage of bridging particles in an adhesive film, may be different for both systems. We expect more particles bridging in the case of emulsions as a strong stirring energy favours a spread conformation. However, these two parameters, surface tension and stirring energy, do not seem to influence the variation in films' behaviour with respect to parameters such as cross-linking density and particle concentration.
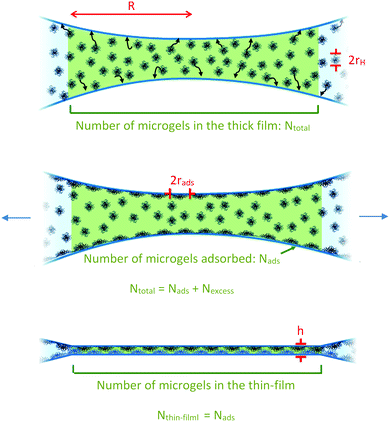
First, using a confocal microscope, we measured the number of particles per unit volume in the thick film cbulk (see SI2, ESI†) and deduce Ntotal, the total number of particles in the thick film for the 0.1 and 1% wt samples.
| Ntotal = cbulk × Vthick-film | (3) |
Then, we estimate the order of magnitude for the number of particles in the thin liquid foam film, Nthin-film, from the thickness of the film, assuming a perfect packing of the particles in the film (volume fraction equal to 1) and that the particles are incompressible,35i.e. they maintain a constant volume as they adsorb, as follows:
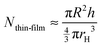 | (4) |
We then consider that the number of microgels in the thin liquid foam film, Nthin-film, is equal to the number of particles initially adsorbed, Nads, at the two interfaces of the film of radius R before applying the pressure. We therefore assume that excess of particles in the thick film are ejected into the Plateau borders during the drainage. Therefore, we write
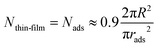 | (5) |
From eqn (5), we deduce the expression for rads:
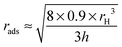 | (6) |
| 1.5 mol% BIS | 5 mol% BIS | |||
|---|---|---|---|---|
| 0.1% wt | 1% wt | 0.1% wt | 1% wt | |
| N total | 2 × 107 | 2 × 108 | 2 × 107 | 2 × 108 |
| N ads = Nthin-film | 106 | 4 × 106 | 2 × 106 | 5 × 106 |
| r ads | 635 nm | 337 nm | 453 nm | 302 nm |
| r ads/rH = 1.64 | r ads/rH = 0.87 | r ads/rH = 1.39 | r ads/rH = 0.93 | |
For the 0.1% wt sample, rads is larger than the hydrodynamic radius of the particles meaning that the particles are in a spread conformation. At this low concentration, the 1.5 mol% BIS microgels spread to a larger extent than the 5 mol% BIS microgels, because of their smaller network elasticity, ultimately leading to thinner films (400 versus 340 nm) as the pressure is applied.
For the 1% wt sample, for both cross-linking densities, rads, is lower than the hydrodynamic radius of the particles, corresponding to the so-called ‘compressed’ state in ref. 25, where the particles deform and stretch perpendicular to the interface.
As shown in Table 2, we find that the number of particles available in the thick films for the 0.1 and 1% wt samples is respectively one and two orders of magnitude larger than Nads and Nthin-film. This means that in all cases, there is a large number of particles in excess in the films, which are ejected in the plateau borders during drainage. Therefore, the large difference in surface coverage for the 0.1% wt and 1% wt samples cannot be accounted for by a large difference in the number of particles available.
We therefore learn from this simple calculation that the large difference in surface coverage for both concentrations cannot be due to the difference in the number of available particles in the thick film.
As stated by Geisel et al.24 the conformation of the particles at the interface results from a balance between adsorption dynamics and spreading/compression dynamics of the particles. In the 0.1% wt case, adsorption is slower than in the 1% wt case. Therefore, particles have more time to spread at short times. Later, for new particles to adsorb, previously adsorbed particles have to compress to make space for incoming particles, which is unfavourable because of the elasticity of the particles. For the 1% wt case, the adsorption dynamics are much faster, more particles reach the interface at the same time, and therefore, particles may not have time to spread on the interface before touching each other. Because of the driving force for particle spreading, i.e. the increase of the contact of PNiPAM segments with the interface, the particles may spread into each other at longer times, causing a stronger interpenetration of the particles dangling arms. Therefore, the adsorption kinetics may influence the degree of interpenetration of the particles.
In our case, we clearly see that increasing the cross-linking density favours the bridging phenomenon. As we apply the pressure to force the two air–water interfaces to produce a thin film, the network elasticity of the particles probably plays a role as more rigid particles prefer rearranging to form a monolayer than compressing, while softer particles can compress more easily into a squeezed bilayer. Therefore, there is no direct correlation between small-amplitude dilational rheology measurements and the bridging phenomenon. However, performing large compressions in Langmuir trough experiments is an indirect way of predicting the behaviour of deformable particles under large deformation, which is involved in the bridging phenomenon.
Let us now briefly highlight the fact that the larger cross-linking density microgels present a less symmetric dimple than the less cross-linked particles. Asymmetric dimples are known to be linked to a lower surface shear elasticity. Here, the lower interpenetration between the dangling arms for the 5 mol% BIS microgels probably favours a low shear viscosity. Owing to the low interpenetration and low spreading, the microgels are mobile enough to rearrange and provide space for particles to bridge.
To summarize, combining low shear viscosity and large compression elasticity at large deformation is correlated to easier bridging. In addition, the ability of the 5 mol% BIS microgels to rearrange in the films probably enables the depletion phenomenon observed for the 0.1% wt samples which leads to very unstable films.
Conclusion
We have investigated the drainage dynamics of thin-liquid films containing PNiPAM microgel suspensions with two cross-linking densities (1.5 and 5 mol% BIS) and at two concentrations (0.1 and 1% wt). At 1% wt, the films drain slowly, are not adhesive and have the thickness of a bilayer, while at 0.1% wt the films have the thickness of a monolayer, are adhesive and show bridging. From the thin liquid foam film thicknesses, we provide a rough estimation of the radii of adsorbed particles in the thick films before applying the pressure. Our results are consistent with particles being adsorbed in a spread conformation for the 0.1% wt sample and in a compressed conformation for the 1% wt sample. In line with previous studies on emulsions, we conclude that a larger surface coverage helps stabilize non adhesive bilayers, while a lower surface coverage favours bridging and adhesive films. At low concentrations, a dimple is trapped in the thin films and slowly drains through the bridged film. From its drainage dynamics, we deduce the permeability of the bridged layer and find that it is consistent with water flowing around the particles during drainage rather than through the polymer network of the particles.Moreover, we find that the cross-linking density has a strong influence on the film dynamics. Films made with the 5 mol% BIS microgels drain faster, show bridging as well as a larger adhesion energy. Particle bridging in thin liquid foam films can be compared to previously observed bridging in emulsions. This makes emulsions unstable against shear. This effect of bridging on Pickering emulsion stability not only holds for microgel-stabilized emulsions, but is a more general phenomenon also observed for hard colloidal particles.41 However, in the case of Pickering emulsions stabilized by microgels, this effect cannot be distinguished from another contribution arising from the particle deformability. Indeed, under shear, new contacts between drops are formed and involve microgels originally located at free interfaces. The ability of these microgels to flatten and to interpenetrate has been proposed to provide sufficient elasticity to prevent coalescence. Thus, microgels with the higher cross-linking density are less prone to such interpenetration while promoting bridging. The ability of the 5 mol% BIS microgels to bridge thin foam or emulsion films to a larger extent compared to the 1.5 mol% BIS probably explains why emulsions prepared with 5 mol% BIS microgels are unstable under mechanical disturbance.8 Moreover, for the 5 mol% BIS microgels at 0.1% wt, depleted zones appear in the films, while this phenomenon does not occur for the 1.5 mol% BIS microgels. These depleted zones are more likely to lead to the rupture of the thin liquid foam films at rest as they are not protected against coalescence. This phenomenon is probably favoured by a low interpenetration between the particles and a low surface coverage.
Acknowledgements
CM acknowledges the Marie Curie Initial Training Network Soft Matter at Aqueous Interfaces, ITN SOMATAI for funding L. K's PhD thesis as well as D. Vlassopoulos for helpful discussions and G. Tessier for his suggestions and help with the use of a spectrometer.References
- B. Brugger, B. A. Rosen and W. Richtering, Microgels as Stimuli-Responsive Stabilizers for Emulsions, Langmuir, 2008, 24, 12202–12208 CrossRef CAS PubMed.
- T. Ngai, S. H. Behrens and H. Auweter, Novel emulsions stabilized by pH and temperature sensitive microgels, Chem. Commun., 2005, 331, 10.1039/b412330a.
- T. Ngai, H. Auweter and S. H. Behrens, Environmental Responsiveness of Microgel Particles and Particle-Stabilized Emulsions, Macromolecules, 2006, 39, 8171–8177 CrossRef CAS.
- M. Destribats, et al., Pickering Emulsions Stabilized by Soft Microgels: Influence of the Emulsification Process on Particle Interfacial Organization and Emulsion Properties, Langmuir, 2013, 29, 12367–12374 CrossRef CAS PubMed.
- C. Monteux, et al., Poly(N -isopropylacrylamide) Microgels at the Oil–Water Interface: Interfacial Properties as a Function of Temperature, Langmuir, 2010, 26, 13839–13846 CrossRef CAS PubMed.
- H. Monteillet, et al., Ultrastrong Anchoring Yet Barrier-Free Adsorption of Composite Microgels at Liquid Interfaces, Adv. Mater. Interfaces, 2014, 1, 1300121 CrossRef.
- M. Destribats, et al., Soft microgels as Pickering emulsion stabilisers: role of particle deformability, Soft Matter, 2011, 7, 7689 RSC.
- M. Destribats, et al., Origin and Control of Adhesion between Emulsion Drops Stabilized by Thermally Sensitive Soft Colloidal Particles, Langmuir, 2012, 28, 3744–3755 CrossRef CAS PubMed.
- Z. Li, W. Richtering and T. Ngai, Poly(N-isopropylacrylamide) microgels at the oil–water interface: temperature effect, Soft Matter, 2014, 10, 6182–6191 RSC.
- P. Massé, E. Sellier, V. Schmitt and V. Ravaine, Impact of Electrostatics on the Adsorption of Microgels at the Interface of Pickering Emulsions, Langmuir, 2014, 30, 14745–14756 CrossRef PubMed.
- W. Richtering, Responsive Emulsions Stabilized by Stimuli-Sensitive Microgels: Emulsions with Special Non-Pickering Properties, Langmuir, 2012, 28, 17218–17229 CrossRef CAS PubMed.
- O. S. Deshmukh, D. van den Ende, M. C. Stuart, F. Mugele and M. H. G. Duits, Hard and soft colloids at fluid interfaces: Adsorption, interactions, assembly & rheology, Adv. Colloid Interface Sci., 2015, 222, 215–227 CrossRef CAS PubMed.
- V. Schmitt and V. Ravaine, Surface compaction versus stretching in Pickering emulsions stabilised by microgels, Curr. Opin. Colloid Interface Sci., 2013, 18, 532–541 CrossRef CAS.
- R. W. Style, L. Isa and E. R. Dufresne, Adsorption of soft particles at fluid interfaces, Soft Matter, 2015, 11, 7412–7419 RSC.
- H. Mehrabian, J. Harting and J. H. Snoeijer, Soft particles at a fluid interface, Soft Matter, 2016, 12, 1062–1073 RSC.
- M. Kwok and T. Ngai, A confocal microscopy study of micron-sized poly(N-isopropylacrylamide) microgel particles at the oil–water interface and anisotopic flattening of highly swollen microgel, J. Colloid Interface Sci., 2016, 461, 409–418 CrossRef CAS PubMed.
- B. Brugger, S. Rütten, K.-H. Phan, M. Möller and W. Richtering, The Colloidal Suprastructure of Smart Microgels at Oil-Water Interfaces, Angew. Chem., Int. Ed., 2009, 48, 3978–3981 CrossRef CAS PubMed.
- K. Geisel, K. Henzler, P. Guttmann and W. Richtering, New Insight into Microgel-Stabilized Emulsions Using Transmission X-ray Microscopy: Nonuniform Deformation and Arrangement of Microgels at Liquid Interfaces, Langmuir, 2015, 31, 83–89 CrossRef CAS PubMed.
- K. Geisel, L. Isa and W. Richtering, Unraveling the 3D Localization and Deformation of Responsive Microgels at Oil/Water Interfaces: A Step Forward in Understanding Soft Emulsion Stabilizers, Langmuir, 2012, 28, 15770–15776 CrossRef CAS PubMed.
- S. Huang, et al., Microgels at the Water/Oil Interface: in situ Observation of Structural Aging and Two-Dimensional Magnetic Bead Microrheology, Langmuir, 2016, 32, 712–722 CrossRef CAS PubMed.
- Y. Cohin, et al., Tracking the interfacial dynamics of PNiPAM soft microgels particles adsorbed at the air–water interface and in thin liquid films, Rheol. Acta, 2013, 52, 445–454 CrossRef CAS.
- J. Zhang and R. Pelton, Poly(N -isopropylacrylamide) Microgels at the Air–Water Interface, Langmuir, 1999, 15, 8032–8036 CrossRef CAS.
- B. Brugger, J. Vermant and W. Richtering, Interfacial layers of stimuli-responsive poly-(N-isopropylacrylamide-co-methacrylicacid) (PNIPAM-co-MAA) microgels characterized by interfacial rheology and compression isotherms, Phys. Chem. Chem. Phys., 2010, 12, 14573 RSC.
- K. Geisel, W. Richtering and L. Isa, Highly ordered 2D microgel arrays: compression versus self-assembly, Soft Matter, 2014, 10, 7968–7976 RSC.
- F. Pinaud, et al., Adsorption of microgels at an oil–water interface: correlation between packing and 2D elasticity, Soft Matter, 2014, 10, 6963–6974 RSC.
- O. S. Deshmukh, et al., Equation of state and adsorption dynamics of soft microgel particles at an air–water interface, Soft Matter, 2014, 10, 7045–7050 RSC.
- K. Geisel, L. Isa and W. Richtering, The Compressibility of pH-Sensitive Microgels at the Oil-Water Interface: Higher Charge Leads to Less Repulsion, Angew. Chem., Int. Ed., 2014, 53, 4905–4909 CrossRef CAS PubMed.
- Z. Li, K. Geisel, W. Richtering and T. Ngai, Poly(N-isopropylacrylamide) microgels at the oil–water interface: adsorption kinetics, Soft Matter, 2013, 9, 9939 RSC.
- K. Geisel, A. A. Rudov, I. I. Potemkin and W. Richtering, Hollow and Core–Shell Microgels at Oil–Water Interfaces: Spreading of Soft Particles Reduces the Compressibility of the Monolayer., Langmuir, 2015, 31, 13145–13154 CrossRef CAS PubMed.
- M. Destribats, et al., Impact of pNIPAMMicrogel Size on Its Ability To Stabilize Pickering Emulsions, Langmuir, 2014, 30, 1768–1777 CrossRef CAS PubMed.
- M. Destribats, et al., Pickering Emulsions Stabilized by Soft Microgels: Influence of the Emulsification Process on Particle Interfacial Organization and Emulsion Properties, Langmuir, 2013, 29, 12367–12374 CrossRef CAS PubMed.
- K. J. Mysels and M. N. Jones, Direct measurement of the variation of double-layer repulsion with distance, Discuss. Faraday Soc., 1966, 42, 42 RSC.
- M. Daimon and A. Masumura, Measurement of the refractive index of distilled water from the near-infrared region to the ultraviolet region, Appl. Opt., 2007, 46, 3811 CrossRef PubMed.
- M. Philipp, et al., Molecular versus macroscopic perspective on the demixing transition of aqueous PNIPAM solutions by studying the dual character of the refractive index, Soft Matter, 2014, 10, 7297 RSC.
- K. N. Nordstrom, et al., Centrifugal compression of soft particle packings: theory and experiment, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2010, 82, 041403 CrossRef CAS PubMed.
- J.-L. Joye, G. J. Hirasaki and C. A. Miller, Asymmetric Drainage in Foam Films, Langmuir, 1994, 10, 3174–3179 CrossRef CAS.
- J. L. Joye, G. J. Hirasaki and C. A. Miller, Dimple formation and behavior during axisymmetrical foam film drainage, Langmuir, 1992, 8, 3083–3092 CrossRef CAS.
- I. B. Ivanov, Thin Liquid Films: Fundamentals and Applications, M. Dekker, 1988 Search PubMed.
- C. Stubenrauch, D. Kashchiev and R. Strey, Phase diagrams of nonionic foam films: construction by means of disjoining pressure versus thickness curves, J. Colloid Interface Sci., 2004, 280, 244–255 CrossRef CAS PubMed.
- C. Stubenrauch and R. Strey, Phase Diagrams of Nonionic Foam Films: New Interpretation of Disjoining Pressure vs Thickness Curves, Langmuir, 2004, 20, 5185–5188 CrossRef CAS PubMed.
- D. J. French, P. Taylor, J. Fowler and P. S. Clegg, Making and breaking bridges in a Pickering emulsion, J. Colloid Interface Sci., 2015, 441, 30–38 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c6sm00873a |
| This journal is © The Royal Society of Chemistry 2017 |