 Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Sub-nanometre mapping of the aquaporin–water interface using multifrequency atomic force microscopy†
Maria
Ricci
a,
Roy A.
Quinlan
*b and
Kislon
Voïtchovsky
*c
aBiological and Soft Systems, Cavendish Laboratory, Cambridge University, Cambridge, UK
bSchool of Biological and Biomedical Sciences, Durham University, Durham, UK. E-mail: r.a.quinlan@durham.ac.uk
cDepartment of Physics, Durham University, Durham, UK. E-mail: kislon.voitchovsky@durham.ac.uk
First published on 16th June 2016
Abstract
Aquaporins are integral membrane proteins that regulate the transport of water and small molecules in and out of the cell. In eye lens tissue, circulation of water, ions and metabolites is ensured by a microcirculation system in which aquaporin-0 (AQP0) plays a central role. AQP0 allows water to flow beyond the diffusion limit through lens membranes. AQP0 naturally arranges in a square lattice. The malfunction of AQP0 is related to numerous diseases such as cataracts. Despite considerable research into its structure, function and dynamics, the interface between the protein and the surrounding liquid and the effect of the lattice arrangement on the behaviour of water at the interface with the membrane are still not fully understood. Here we use a multifrequency atomic force microscopy (AFM) approach to map both the liquid at the interface with AQP0 and the protein itself with sub-nanometer resolution. Imaging using the fundamental eigenmode of the AFM cantilever probes mainly the interfacial water at the surface of the membrane. The results highlight a well-defined region that surrounds AQP0 tetramers and where water exhibits a higher affinity for the protein. Imaging in the second eigenmode is dominated by the mechanical response of the protein and provides sub-molecular details of the protein surface and the sub-surface structure. The relationship between modes and harmonics is also examined.
Introduction
The eye lens plays a key role in vision: it refracts incident light and focuses it onto the retina where detection occurs. In order to achieve this task, the eye lens must remain transparent to visible light. This unique characteristic is ensured by the unusual and highly specialised arrangement of the lens constituting cells1,2 and their components.3,4 The developed lens is not vascularised as most other tissues in the body.5 Instead, the microcirculation of water, ions and metabolites is ensured by a network of protein channels that interconnect the cells.6,7 There are two main types of channels: aquaporin 0 (AQP0), which accounts for more than 50% of all proteins in the lens membrane,8 and connexins (Cx), the second most abundant protein in the plasma membrane (∼10%).9,10 Both proteins can interact with each other.11 AQP0 is a tetrameric protein with each sub-unit composed of six transmembrane α-helices forming a channel.12 The AQP0 tetramers naturally assemble in a characteristic square lattice in the membrane.12,13 The AQP0 channel is remarkably efficient, allowing water flow rates that surpass the diffusion limit.14–17 Deletion of the protein8,18,19 can lead to several types of cataracts, the main cause of blindness in developing countries.8 Given its importance, considerable research efforts have been dedicated to the investigation of AQP0 structure,13,20–24 function,17,20,25,26 evolution27 and the role it plays in the development of eye pathologies.8Despite a large body of results, a complete picture of the working protein is still lacking,16,17,20,26,28 partly because little is known about the behaviour of the liquid near and at its surface under physiological conditions. It is now well established that water molecules and ions surrounding proteins play an important role in their function29,30 and can significantly impact their efficiency.31 In the case of AQP0, theoretical and simulation-based studies contributed significantly to the explanation of its exceptional water flow rate through the channel.14,15,17 There are however still significant unanswered questions regarding its function; AQP0 serves both as a water channel and as a junction between adjacent fibre cells so as to ensure a tight extracellular space.12,58 To date, it is not clear whether these two functions represent distinct permanent states for the protein. Different crystal structures obtained by electron diffraction13,22–24 suggest that AQP0 does not conduct water in junctional conformation, but computer simulations20,32 contradict this view. The rate at which water flows through AQP0 is also a complex issue; individual AQP0 exhibits lower permeability than other aquaporins,33 but the characteristic tetrameric arrangement into a square lattice can support cooperative function and enhance permeability.26 Given the need for a global, membrane-level understanding of the AQP0 function, comprehensive computer-based approaches tend to be prohibitively expensive. Experimentally, techniques able to probe the water behaviour locally and on that scale are scarce, and little data are available.
Recent advances in the field of atomic force microscopy34 (AFM) have made it possible to map nanoscale variations in the structure and behaviour of hydration water at the interface with soft and hard surfaces,35–43 in particular the local density42,44,45 and affinity of water for the surface.46–48 The technique relies on short-range hydration forces to enhance resolution, but most results to date are on synthetic systems such as simple lipid bilayers or crystalline solids. In parallel, development in the field of multifrequency AFM has opened novel approaches to map the mechanical properties of soft materials in solution,49–54 including native cell membranes.55,56 Multifrequency approaches tend to achieve lower spatial resolution than approaches mapping interfacial water due to a need for high imaging amplitudes that prevent exploitation of the local hydration forces.
Previous studies have investigated native lens membranes using contact-mode AFM in solution and at room temperature, providing sub-molecular images of the proteins and their assembly into the membrane.57–60 The results highlighted striking differences between healthy and afflicted membranes, providing unique insights into both sub- and supra-molecular characteristics of cataract.57,59,61 Force mapping of the membrane's mechanical properties62 also revealed interesting variations between different protein domains that could be related to the membrane's function.
Here we use multifrequency amplitude-modulation AFM (AM-AFM) to investigate the surface of bovine lens membranes in solution with sub-molecular resolution. We show that when operated in the first vibration eigenmode, the phase images are particularly sensitive to the hydration structure of the membrane, effectively providing maps of the local affinity of the water for the membrane's surface. Regions located between AQP0 tetramers appear to form small ‘islands’ with a particularly strong water affinity. When operating the AFM in its second eigenmode, the tip probes the membrane itself and sub-molecular details of the AQP0 are visible in topography, but with no significant information in the phase. We also explore the transfer of energy and information between harmonics and sub-harmonics of the different eigenmodes.
The biological significance of the hydration structure identified is discussed in terms of AQP0 function and efficiency. The possibilities and limitations offered by our experimental approach are also discussed.
Experimental
Sample preparation
Fresh bovine lens membranes were prepared using a sequential extraction method.63,64 Briefly, lenses were decapsulated and stirred on ice for 20–30 min at a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 weight to volume ratio of extraction buffer (10 mM Sodium phosphate pH 7.4; 150 mM NaCl, 5 mM EDTA). The hydrodissected lens material was poured off leaving behind the residual lens, which became completely dissociated with longer stirring times. The separated lens material was Dounce homogenised. The membrane-enriched fraction was then separated from the soluble protein fraction by centrifugation (Beckman JA20 rotor; 20
2 weight to volume ratio of extraction buffer (10 mM Sodium phosphate pH 7.4; 150 mM NaCl, 5 mM EDTA). The hydrodissected lens material was poured off leaving behind the residual lens, which became completely dissociated with longer stirring times. The separated lens material was Dounce homogenised. The membrane-enriched fraction was then separated from the soluble protein fraction by centrifugation (Beckman JA20 rotor; 20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 rpm at 4 °C for 20 min). The pellet, containing the lens membranes, was Dounce homogenised once more to resuspend the membranes, and extracted again with the same buffer. This process of resuspension, stirring on ice and centrifugation was repeated with the following buffers: 10 mM Sodium phosphate pH 7.4, 1.5 M KCl, 5 mM EDTA; 10 mM ammonium bicarbonate, 1 mM EDTA; 10 mM sodium phosphate pH 7.4, 8 M urea, 5 mM EDTA; 0.1 M sodium hydroxide. Finally, the lens membranes were washed once more in extraction buffer and then resuspended in the same containing 0.01% (w/v) sodium azide and stored at 4 °C.
000 rpm at 4 °C for 20 min). The pellet, containing the lens membranes, was Dounce homogenised once more to resuspend the membranes, and extracted again with the same buffer. This process of resuspension, stirring on ice and centrifugation was repeated with the following buffers: 10 mM Sodium phosphate pH 7.4, 1.5 M KCl, 5 mM EDTA; 10 mM ammonium bicarbonate, 1 mM EDTA; 10 mM sodium phosphate pH 7.4, 8 M urea, 5 mM EDTA; 0.1 M sodium hydroxide. Finally, the lens membranes were washed once more in extraction buffer and then resuspended in the same containing 0.01% (w/v) sodium azide and stored at 4 °C.
Preparation of the AFM samples was done using a procedure similar to that described by Buzhynskyy et al.59 In short, a drop (10 μL) of inner lens membrane solution was dissolved in 30 μL of adsorption buffer (25 mM MgCl2, 150 mM KCl, 10 mM Tris–HCl, pH 7.4) and allowed to incubate at room temperature for 10 min on a freshly cleaved mica disc (SPI supplies, West Chester, PA, USA). The sample was then gently rinsed with 2 mL of imaging buffer (150 mM KCl, 10 mM Tris–HCl, pH 7.4). The sample was immediately mounted on the AFM scanner and used for imaging. If necessary, more imaging buffer was added. All the chemicals used for the buffers were purchased from Sigma-Aldrich (Sigma-Aldrich, St. Louis, Missouri, USA) and dissolved into ultrapure water (Milli-Q, 18.2 ΩM, <5 ppm organics, Merck-Millipore, Billerica, MA, USA).
Atomic force microscopy
All AFM data were acquired on a Cypher ES system (Asylum Research, Santa Barbara, CA, USA) with the sample and the cantilever/tip fully immersed in the imaging solution. The cantilever (RC800 PSA, Olympus, Tokyo, Japan) was oscillated using photothermal excitation (blueDrive) for more accuracy and stability. The spring constants of the first and second eigenmodes of the cantilever were determined to be k1 ≈ 0.38 N m−1 and k2 ≈ 13 N m−1 respectively, calibrated using the thermal spectrum method65,66 and taking into account the difference in optical lever sensitivities (InvOLS) between the modes. The experiments were conducted with the cantilever oscillating at a single frequency vd and the amplitude/phase recorded simultaneously both at vd and at a different frequency vs. The driving frequency vd was always set to coincide with the first or second vibration eigenmode of the cantilever while vs was recorded at a harmonic or sub-harmonic of vd.Imaging was conducted in AM with the feedback operating at vd. When operated in AM, the cantilever is oscillated externally at a specific frequency (here by photothermal excitation) resulting in the tip vibrating with a free amplitude Af in the liquid when far away from the surface of the sample. When the tip is brought in close vicinity to the surface, the vibration amplitude is reduced due to the tip interacting with the sample. During imaging, the tip scans across the sample while a feedback loop maintains a set amplitude As constant by continuously readjusting the average tip-sample distance. Topographic information is obtained from the corrections applied by the feedback loop. The phase lag φ between the driving and measured oscillations can vary freely and is recorded at each pixel of the imaged sample. For simplicity, imaging with the driving frequency vd set in the first and second eigenmode is hereafter referred to as AM1-AFM and AM2-AFM, respectively. In this work relatively small imaging amplitudes As (typically As < 1 nm) were used, with setpoint values defined as S = A/Af as high as possible. Most images were acquired with setpoint S > 0.9 so as to better preserve the membrane. Under these imaging conditions the imaging is dominated by short range interactions that allow for high resolution in liquid.29,37,40,46,47,67
Amplitude and phase versus distance curves were carried out on the membrane under conditions identical to imaging. Since several studies have examined the energy transferred to higher harmonics from the first eigenmode,53,55,67–69 here we only focused on curves acquired with the cantilever driven in its second eigenmode.70
Results and discussion
Imaging with first eigenmode excitation
Representative AM1-AFM images of AQP0 regions of the lens membrane extracellular surface are presented in Fig. 1. At low magnification, the characteristic square AQP0 lattice is already clearly visible in topography with occasional Cx near edges (Fig. 1a), characteristic of healthy lens membranes.57 The AQP0 lattice is non-junctional. Some substructure can be distinguished in each AQP0 tetramer, better evidenced at higher magnification (Fig. 1b). A comparison with the calculated solvent-accessible surface of the lattice confirms that the sub-molecular details are resolved (Fig. 1d), although the fragile and flexible inter-helical loops57,58 induce some imaging variability between different tetramers. Distinction between junctional23 and non-junctional22 conformations is not possible without image processing.58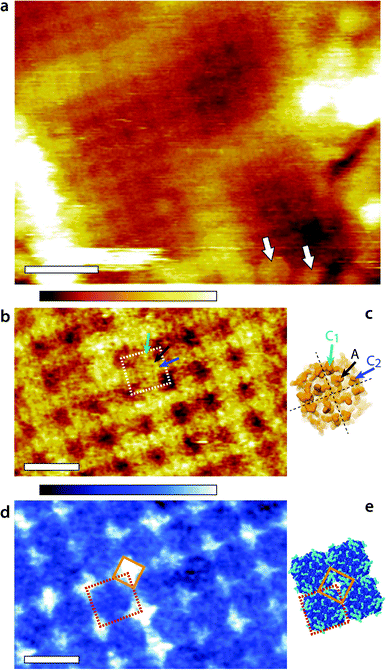 | ||
| Fig. 1 Fragment of the lens membrane extracellular surface imaged by AM1-AFM in solution. A topographic image of the large region of the fragment (a) shows the characteristic AQP0 square lattice with Cx near the edges (arrows). Some sub-molecular details of the AQP0 are already visible. Higher magnification of the AQP0 lattice reveals different sub-molecular details in topography (b) and in phase (d). In each case, a tetrameric AQP0 assembly is highlighted with a dashed square. The topographic image is similar to high-resolution topographs obtained in contact-mode AFM57,58 and the visible protrusion can be explained by the inter-helical loops A (black arrow), C1 (green arrow) and C2 (blue arrow). The image has not been symmetrized and the sub-molecular features are faint. For comparison, the same loops are shown on the calculated van-der Waals surface of an AQP0 tetramer (c). Only the most prominent parts of the extracellular surface are visible and the protein sub-structure becomes progressively more transparent when moving deeper inside the membrane. The dashed black lines separate the four AQP0 monomers and the arrows point the different loops on a single monomer. The AFM phase image (d) exhibits a characteristic diamond-shaped lattice (orange diamond) that does not match any topographical feature. Instead, it can explain the local hydration landscape (e), where the hydrophilic regions (light blue) of the calculated protein solvent-accessible surface match the observed phase pattern. All images are acquired by applying a feedback on the oscillation amplitude of the cantilever driven at the frequency of the first eigenmode of vibration (20 kHz). The scale bars are 20 nm (a) and 10 nm (b and d). The colour scale bars represent a total height variation of 6 nm (a) and 0.9 nm (b) and a phase variation of 10° (d). The structures in (c) and (e) were calculated using Jmol71 and assembled freely (e) from the 2B6P Protein Data Bank structure22 of non-junctional AQP0. | ||
The phase image (Fig. 1d) exhibits a distinct contrast from the corresponding topographic image (Fig. 1b), indicating that the phase carries novel information that is not related to topographic features or tip-scanning effects. The AQP0 lattice is clearly resolved, but only hints of the extracellular tetrameric substructure are visible. The most striking feature is the diamond-shaped contrast visible near the edges of tetramers (orange diamond in Fig. 1d). This contrast shows a good degree of agreement with the calculated hydrophilicity map of the membrane (Fig. 1e). In Fig. 1e the hydrophobic residues appear dark blue while the hydrophilic (polar and charged) residues are shown in light blue. Most of the hydrophilic residues are concentrated in locations at the edge of the AQP0 tetramers and arranged to coincide with the bright diamond-shaped contrast in phase.
The occasional hydrophilic residues located near the centre of the tetramer are much less visible in phase, but could explain the faint contrast variations observed over the same area. Previous studies have shown that when operated under the conditions similar to those used here, the AM-AFM phase is directly related to the local affinity of the water for the surface.46–48 The present results show that the approach remains valid on soft biological membranes, potentially opening novel avenues to study local nanoscale hydration effects at biointerfaces. A direct comparison between Fig. 1d and e should however be made with caution: first the calculated surface does not take into account the different relative degree of hydrophilicity of each residue and its likely influence on the surrounding solvent. Second, the AFM measurement is dynamic in nature with water forced towards and along the membrane during each tip oscillation.48 The phase image represents the energy necessary to carry out this task, which is related to the static, local water-sample affinity.46 The phase image therefore carries information about the ease water molecules move along the surface of the membrane. In distinct regions near the edges of tetramers (orange diamond in Fig. 1d and e), this motion is substantially hampered. These regions therefore act as ‘guiding walls’ potentially favouring a vertical motion of the water towards the channel entrance.
Imaging with second eigenmode excitation
The imaging was then conducted in AM2-AFM over the same area. The results are presented in Fig. 2. The topographic image (Fig. 2a) shows many sub-molecular features of the AQP0 tetramer, with an apparent resolution substantially higher than that achieved in AM1-AFM (Fig. 1b). Direct identification of the different features is however not straightforward and it is useful to compare the AFM image with the expected membrane surface calculated from its crystallographic structure. The 3M9I Protein Data Bank structure24 reflects the tetramers reconstituted into E. coli lipids, and hence represents a good model for the whole AQP0 lattice when symmetrized (Fig. 2b–d). Direct comparison between Fig. 2a and b suggests the identification of the well-known57,58 C1 and C2 inter-helical loops (black ellipse) as well as the A-loops (corners of the central black square). More details are visible in the region near the edges of the highlighted tetramer, with features oriented parallel to the sides of the central square (black arrows). These features correspond to parts of the protein located deeper in the membrane (Fig. 2b), and their orientation suggests that they are related to the alpha helices 4–6, near the periphery of the tetramer. These helices are tilted in a direction consistent with the AFM observations (Fig. 2c), especially deeper in the membrane (Fig. 2d). For the tip to reach these features, it must exert a higher pressure on the membrane, but the fact that it can resolve them in such detail suggests that the protein is not damaged by imaging.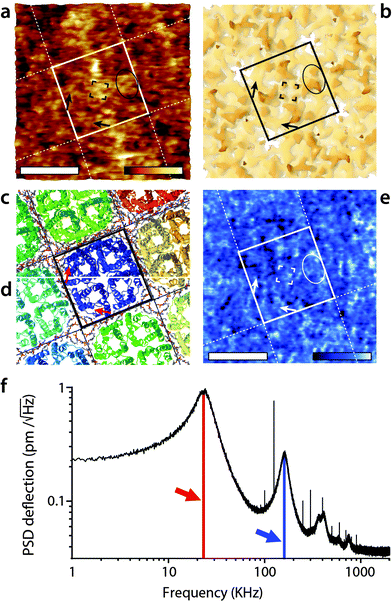 | ||
| Fig. 2 High-resolution imaging of the AQP0 by AM2-AFM in solution. The topographic image (a) reveals fine details of the protein (square) with many sub-structure features (protrusions) visible down to sub-nanometre details. The AFM image can be compared with the calculated van der Waals surface of the crystal structure comprising both AQP0 tetramers and inter-tetramer lipids24 (b). The C1- and C2-inter-helical loops can be identified (black ellipse) as well as the A-loop (four corners of the central black square). Additional features coinciding with part of the protein lying deeper in the membrane (black arrows) are also visible, suggesting the tip to press on the proteins while imaging. Since it was not possible to calculate a mechanically compressed structure for AQP0, a ribbon representation is given for the top of the extracellular surface (c) and at a cut 1 nm below the surface (d). The black arrow in (a and b) is shown in red in (c and d) and indicates that the features coincide with the position of the alpha-helices 4–6, located near the outer part of the tetramer (c and d). The AFM phase image (e) shows local variations correlated with topography, but no clear pattern is visible. The density spectrum (or thermal spectrum) of the cantilever vertical deflection as a function of frequency (e) highlights maxima corresponding to the first (red arrow) and second vibration eigenmode (blue arrow). Here, the cantilever oscillation and feedback are driven at the frequency of the second eigenmode of vibration (168 kHz). The scale bars are 5 nm (a and e). The colour scale bars represent a topographic variation of 1.2 nm (a), and a phase variation of 8° (e). The structures in (b), (c) and (d) were calculated using Jmol71 from the 3M9I Protein Data Bank structure24 and represent the extracellular surface of the junctional assembly, reconstituted in E coli lipids. The occasional sharp spikes in (f) are due to electronic noise. | ||
When operating the AFM in AM2-AFM the effectively stiffness of the oscillating cantilever increases almost 30 times, rendering the soft imaging conditions achieved in AM1-AFM almost impossible. Instead, the tip is able to easily remove all the hydration water from the surface of the membrane at the lowest point of its oscillation cycle. As a result, the tip probes the membrane itself44,67,72 and the phase carries mostly information about the local variations in the mechanical properties of the membrane. This is consistent with the phase image obtained here (Fig. 2c), which exhibits variations on the same scale as the topography, with none of the distinctive features visible in Fig. 1d.
Given the high effective stiffness of the mode, any error in the feedback loop may deform the membrane while scanning. As a result, the sub-molecular details visible in Fig. 2a may represent a slightly distorted view of the protein. Additionally, a small local variation in the imaging conditions can significantly affect the resulting image. In Fig. 2a not all tetramers appear identical and the 4-fold symmetry of the lattice is not as clear as in Fig. 1b. The distortions are however partially mitigated by using smaller working amplitude (As ∼ 0.25 nm) compared to the first eigenmode (As ∼ 1.1 nm).
Cross-talk between eigenmodes and harmonics
When interpreting the multifrequency experiments, it is essential to take into consideration the possibility for cross-talk between the driving frequency and (sub-)harmonics that may be momentarily excited as the tip ‘impacts’ the sample during its oscillation cycle.51,55,69,72–74 This non-linear interaction allows some energy dissipated by the vibrating tip to pass to the stimulated harmonics rather than to the sample only. The process depends on the tip–sample interaction and can be exploited to derive information about the sample's viscoelastic properties,50,53,73,75 but the interpretation of the results is not straightforward.51,76 In liquid, AM-AFM has been shown to be particularly prone to such multiharmonic phenomena,55,70 including on biological membranes.53,73,77 The energy transfer is enhanced if the harmonic considered coincided with an eigenmode of the cantilever.55,78,79Here harmonic cross-talk was examined systematically during imaging both in AM1-AFM and in AM2-AFM. In each case, the same region of the membrane is repeatedly imaged in the selected mode while, for each image, the second frequency probed coincides with a harmonic or sub-harmonic of the driving frequency. Fig. 3 presents the results of the study for the imaging conducted in AM1-AFM. An example of the topographic, phase and amplitude images acquired at the driving frequency is shown, with the full set of data available in the ESI† (Fig. S1, ESI†). We note that repeated imaging of the same region may alter at time the quality of the topography (Fig. 3a) but the emphasis of the experiment being placed on the evaluation of energy transfer, we do not consider this a problem. The driving phase (Fig. 3b) exhibits a similar contrast as in Fig. 1d, confirming the validity of the imaging conditions. The amplitude (Fig. 3c), kept constant by the feedback loop, only shows small (∼0.1 nm) periodic variations due to some environmental noise. The magnitude of the induced oscillation amplitudes at lower and higher harmonics during the imaging is shown in Fig. 3d, calculated from histograms of the corresponding images (Fig. S1, ESI†).
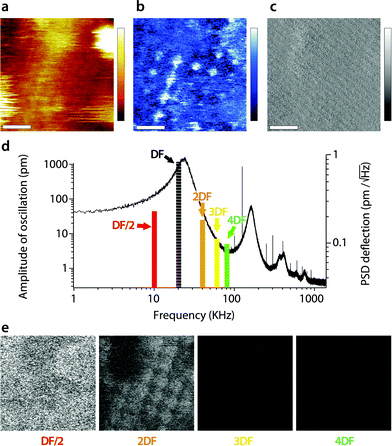 | ||
| Fig. 3 Energy transfer from the first vibration eigenmode to harmonics during high-resolution imaging. The imaging is conducted in AM1-AFM with the cantilever oscillation/feedback driven at the frequency of the first eigenmode. Data acquired at the driving frequency (DF) reveal topography (a) and phase (b) variations similar to those in Fig. 1. The amplitude (c) is kept constant by the feedback and only a faint stripy pattern due to imaging noise is visible. During the imaging, the oscillation amplitude and phase are also recorded at a different harmonic of DF. The different harmonics probed are represented as solid colour bars in (d). The height of each bar represents the average amplitude detected at the corresponding frequency (left vertical scale). Superimposed in the background is the thermal power density spectrum (right vertical scale), showing that the relative magnitude of each harmonic stimulated is consistent with its importance in the thermal spectrum. Spatial variation of the amplitude at each harmonic is shown in (e). The sub-harmonic (DF/2) only captures hints of large topographic features. Amplitude at the second harmonic (2DF) is clearly correlated with surface features, while little or nothing is visible for higher harmonics. The scale bar in (a–c) is 10 nm. The colour scale bars represent 6 nm in topography (a), 12° in phase (b) and 120 pm in amplitude (c). The grey scale in (e) represents 120 pm for all images, which shows the same area of the membrane as (a–c). The free amplitude is 1.2 nm with an imaging setpoint to a free amplitude ratio of 0.9. The full set of data (phase and amplitude for all harmonics) is shown in Fig. S1 (ESI†). | ||
As expected,53 the amplitude of the harmonics is only a fraction (<5%) of the driving amplitude, with their relative magnitude showing a similar dependence on frequency as the thermal vibration of the free cantilever. Only the second harmonic (twice the driving frequency) appears to carry some information related to molecular details of the membrane (Fig. 3e). The first sub-harmonic (half the driving frequency) shows faint features that partly correlate with the largest topographic variations of the membrane, but no molecular details are visible. The oscillation amplitudes of the third and fourth harmonics were so small (<10 pm) that no spatial information could be obtained. This indicates that the stimulation of harmonics is minimal under these imaging conditions, with only the second harmonic potentially reflecting spatial variations of the membrane's mechanical properties,79 but most of the tip vibration is dissipated directly into the hydration water which dominates the imaging both in topography and phase.38,47,67 This interpretation is further confirmed by the phase images, which did not show any sample-related information for all the frequency probed, except the driving frequency (see Fig. S1, ESI†).
A similar study was carried out in AM2-AFM, with the results presented in Fig. 4 in the same manner as in Fig. 3. As for Fig. 3, an example of topography (Fig. 4a), phase (Fig. 4b) and amplitude (Fig. 4c) at the driving frequency is shown, with the full set of data available in the ESI† (Fig. S2, ESI†). Since energy transfer to harmonics coinciding with eigenmodes tends to be enhanced,55,69 particular attention was paid to the sub-harmonic overlapping with the first eigenmode70 (Fig. 4d). Interestingly, no meaningful spatial information was found in any of the sub-harmonics, be it in the amplitude (Fig. 4e) or in phase (Fig. S2, ESI†).
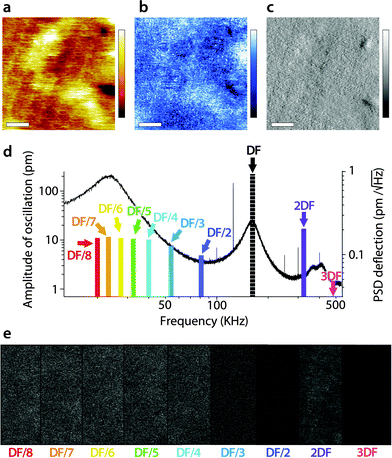 | ||
| Fig. 4 Energy transfer from the second vibration eigenmode to harmonics during high-resolution imaging. The imaging is conducted in AM2-AFM with the cantilever oscillation/feedback driven at the frequency of the second eigenmode. Data acquired at the driving frequency (DF) reveal topography (a) and phase (b) variations similar to those in Fig. 2. The amplitude (c) is kept constant by the feedback but surface features commensurate with topography are visible. The different harmonics probed are represented as solid colour bars in (d). Spatial variation of the amplitude at each harmonic is shown in (e). All amplitudes show mainly noise, apart from some faint features at 2DF, but not as clear as in Fig. 3. The scale bar in (a–c) is 10 nm. The colour scale bars represent 4 nm in topography (a), 10° in phase (b) and 30 pm in amplitude (c). The grey scale in (e) represents 30 pm for all images, which shows a fraction of the same area of the membrane as in (a–c). The free amplitude is 260 pm with an imaging setpoint to free amplitude ratio close to 0.9. The full set of data (phase and amplitude for all harmonics) is shown in Fig. S2 (ESI†). | ||
Only the second harmonics shows hints of sample-related spatial information, but much less clearly than for the first AM1-AFM. This can be explained by the lower imaging amplitude used in AM2-AFM, compared to AM1-AFM. In all cases, the phase images exhibited only apparent noise (Fig. S2, ESI†). This suggests that energy transfer from driving in the second eigenmode is negligible under these imaging conditions. Spectroscopic data acquired under similar experimental conditions confirm the observation (Fig. S3, ESI†).
General discussion
AM-AFM is extensively used to investigate soft biological membranes in liquid,29,80,81 first for its ability to preserve the delicate samples while ensuring sub-nanometre resolution images, but also for the phase that carries additional information about the sample's properties.46,53,73,82–84 Highest resolution is usually achieved using amplitudes in the order of one nanometre or less,46,47,67 typically with relatively soft cantilevers (0.1–5 N m−1).37,67,79 Working under these conditions has several consequences: first, most of the energy dissipated by the oscillating tip at the interface is transmitted to the imaged sample, with little coupling to higher harmonics.67,79 Here only the second harmonic appeared to carry meaningful information about the sample, regardless of the working eigenmode, and hence of the cantilever's effective stiffness. Second, in the first eigenmode, the vibrating cantilever does not dissipate enough energy into the interfacial liquid to fully remove the hydration water from the membrane.67 As a result, the imaging process probes mainly the interfacial liquid and the phase information reflects the ease with which the tip forces water molecules along the membranes. When working in the second eigenmode, the effective stiffness of the vibrating cantilever increases considerably and the tip easily removes the membrane's hydration layers. The resulting imaging process is therefore dominated by the structural and mechanical properties of the sample itself, and can reveal details not necessarily visible from the hydration structure (Fig. 2). This interpretation of the AM-AFM results should however be taken with caution because it relies on the assumption that the hydration water is more easily disrupted or displaced than the hydrated biomolecules themselves. Phrased in experimental terms, the assumption is that the biomembrane is ‘stiffer’ than the hydrogen-bonded network of ions and water molecules hydrating the membrane. This is not always true for biological systems where adsorbed water and ions can significantly influence bimolecular motion31 and at times even create structures that are more robust than the membrane itself.29 Nonetheless, the fact that images obtained in AM1-AFM yield phase information that correlates with the hydrophilicity map of the membrane, while AM2-AFM provides high-resolution details of the AQP0's surface indicating that our interpretation is valid. The limited cross-talk between the different harmonics also facilitates a direct association of experimental observables with the structural and mechanical properties of the membrane.From a biological point of view, the AM1-AFM results (Fig. 1) provide intriguing new insights: the behaviour of hydration water at the surface of the AQP0 lattice does not appear to correlate directly with topography except for its periodicity. This suggests a specific behaviour of the interfacial water moving at the surface of the membrane. The relevance of these findings for the membrane function cannot be explained by AFM results alone, but we can speculate on their implication for the AQP0 efficiency. It is now well recognized that the flow of water through the AQP0 channel cannot be explained by a continuum description of the water. Aquaporins allow flow rates several orders of magnitude higher than that expected from continuum fluid dynamics predictions,15,16 thanks to a largely hydrophobic channel with specific hydration water binding sites optimally placed in the channel.85 This unique hydration landscape ensures high flow efficiency85 while retaining high molecular selectivity.86 However, the entrance of the channel can strongly limit flow efficiency due to viscous dissipation effects.16 Recently, it has been shown that the hourglass-shaped entrance region of aquaporins plays a significant role in limiting this effect,16 showing aquaporins to be a highly optimized protein on every account, and not only in the channel region itself. AQP0 is less efficient in water transport than other aquaporins32,33 but still functions beyond the diffusion limit. The present results suggest that the diamond shaped regions (Fig. 1d) resisting lateral water flow along the membrane could be part of this optimisation machinery. The entrance of the channel exposed to water is relatively hydrophobic. These inter-tetramer hydrophilic regions could first play a role as a lateral flow stopper, enhancing water flow perpendicular to the membrane, along the channel's direction. From a fluid dynamics perspective, convection flow immediately parallel to the membrane's surface would be detrimental to the AQP0 efficiency considering its relatively hydrophobic surface. The existence of ‘flow stoppers’ would extend the optimisation of AQP0 into the hydration landscape of the membrane. Second, the fact that the hydration landscape follows the symmetry of tetramers suggests that it may play a role in AQP0 cooperative function,26 since the latter depends on the presence of calcium ions which tend to dramatically modify the hydration properties of interfaces upon adsorption.
Working in the second eigenmode of the cantilever also provides interesting results. Although the high effective stiffness of the vibrating cantilever can deform the protein, detailed surface features such as the more robust C1 and C2 loops can often be identified. Significantly, AM2-AFM also allows probing sub-molecular details deeper in the membrane without causing permanent damage to the protein. The fact that sub-nanometre features can be clearly resolved suggests the remarkable stability of the extracellular side of AQP0 under mechanical perturbations. Functionally, this could relate to the protein's ability to form robust inter-cellular junctions. This interpretation is supported by previous results62 which showed the gap junction to be particularly rigid.
Conclusions
In this paper, AFM has been used to investigate the surface of native AQP0 lattices in solution. Using a relatively soft cantilever operated in AM in the first eigenmode of the cantilever, we have shown that imaging provides nanoscale maps of the hydration landscape of the membrane. Given the dynamical nature of the measurement, the results effectively represent the ability of the interfacial water to flow along the membrane,48 and highlight periodic singularities located between AQP0 tetramers. We speculate that these singularities could support the channel's efficiency by minimizing shear flow immediately adjacent to the membrane, potentially helping motion of the water molecules towards the entrance of the channels. Further independent studies are however needed to confirm firstly the structure of the AQP0 lattice hydration landscape identified by AFM, and secondly the influence of this landscape on the motion of water molecules and solutes in close vicinity to the channel's entrance.Future AFM work will address the effect of adsorbed calcium ions on the structure and behaviour of lens membranes' hydration landscape. This should help determine whether the particular hydration features identified here are related to the AQP0 cooperative function.
Probing the AQP0 lattice using AM-AFM driven in the second eigenmode of the cantilever provides images of the membrane itself, capturing finer details of the AQP0 surface and sub-surface features, but potentially of a distorted protein due to the high effective stiffness of the mode.
In order to achieve high-resolution imaging, low imaging amplitudes were employed for both eigenmodes, thus preserving the sample and limiting the stimulation of higher and lower harmonics. Compared to traditional AFM, our approach has the advantage of combining measurements that usually require different experimental conditions without the need to change or re-engage the cantilever/tip. Sub-nanometre details of a biomembrane's surface and its hydration structure can be derived in the same experiment and over the same location.
Acknowledgements
We are grateful for funding from the Biotechnology and Biological Sciences Research Council (grant BB/M024830/1) (KV), the European Council (MC-CIG grant 631186) (KV), and Fight for Sight UK (RAQ). MR acknowledges the Swiss National Science Foundation for the funding of the Early Postdoc. Mobility fellowship.Notes and references
- J. R. Kuszak, R. K. Zoltoski and C. Sivertson, Exp. Eye Res., 2004, 78, 673–687 CrossRef CAS PubMed.
- S. Bassnett, Y. Shi and G. F. J. M. Vrensen, Philos. Trans. R. Soc., B, 2011, 366, 1250–1264 CrossRef PubMed.
- C. Slingsby, G. J. Wistow and A. R. Clark, Prot. Sci., 2013, 22, 367–380 CrossRef CAS PubMed.
- S. Song, A. Landsbury, R. Dahm, Y. Liu, Q. Zhang and R. A. Quinlan, J. Clin. Invest., 2009, 119, 1837–1848 CrossRef CAS PubMed.
- J. S. Zigler Jr, M. Valapala, P. Shang, S. Hose, M. F. Goldberg and D. Sinha, Biochim. Biophys. Acta, 2016, 1860, 287–298 CrossRef PubMed.
- R. T. Mathias, J. Kistler and P. Donaldson, J. Membr. Biol., 2007, 216, 1–16 CrossRef CAS PubMed.
- P. J. Donaldson, L. S. Musil and R. T. Mathias, Invest. Ophthalmol. Visual Sci., 2010, 51, 2303 Search PubMed.
- K. L. Schey, Z. Wang, J. L. Wenke and Y. Qi, Aquaporins, 2014, 1840, 1513–1523 CAS.
- V. M. Berthoud, P. J. Minogue, P. Osmolak, J. I. Snabb and E. C. Beyer, FEBS Lett., 2014, 588, 1297–1303 CrossRef CAS PubMed.
- R. T. Mathias, T. W. White and X. Gong, Physiol. Rev., 2010, 90, 179–206 CrossRef CAS PubMed.
- X. S. Yu and J. X. Jiang, J. Cell Sci., 2004, 117, 871–880 CrossRef CAS PubMed.
- A. Engel, Y. Fujiyoshi, T. Gonen and T. Walz, Curr. Opin. Struct. Biol., 2008, 18, 229–235 CrossRef CAS PubMed.
- T. Gonen, P. Sliz, J. Kistler, Y. Cheng and T. Walz, Nature, 2004, 429, 193–197 CrossRef CAS PubMed.
- M. Hashido, A. Kidera and M. Ikeguchi, Biophys. J., 2007, 93, 373–385 CrossRef CAS PubMed.
- L. Bocquet and E. Charlaix, Chem. Soc. Rev., 2010, 39, 1073 RSC.
- S. Gravelle, L. Joly, F. Detcheverry, C. Ybert, C. Cottin-Bizonne and L. Bocquet, Proc. Natl. Acad. Sci. U. S. A., 2013, 110, 16367–16372 CrossRef CAS PubMed.
- J. E. Hall and R. T. Mathias, Biophys. J., 2014, 107, 10–15 CrossRef CAS PubMed.
- S. Sindhu Kumari, N. Gupta, A. Shiels, P. G. FitzGerald, A. G. Menon, R. T. Mathias and K. Varadaraj, Biochem. Biophys. Res. Commun., 2015, 462, 339–345 CrossRef CAS PubMed.
- A. B. Chepelinsky, Handb. Exp. Pharmacol., 2009, 265–297 CAS.
- S. L. Reichow, D. M. Clemens, J. A. Freites, K. L. Németh-Cahalan, M. Heyden, D. J. Tobias, J. E. Hall and T. Gonen, Nat. Struct. Mol. Biol., 2013, 20, 1085–1092 CAS.
- R. K. Verma, N. D. Prabh and R. Sankararamakrishnan, Biochim. Biophys. Acta, 2015, 1848, 1436–1449 CrossRef CAS PubMed.
- T. Gonen, Y. Cheng, P. Sliz, Y. Hiroaki, Y. Fujiyoshi, S. C. Harrison and T. Walz, Nature, 2005, 438, 633–638 CrossRef CAS PubMed.
- W. E. C. Harries, D. Akhavan, L. J. W. Miercke, S. Khademi and R. M. Stroud, Proc. Natl. Acad. Sci. U. S. A., 2004, 101, 14045–14050 CrossRef CAS PubMed.
- R. K. Hite, Z. Li and T. Walz, EMBO J., 2010, 29, 1652–1658 CrossRef CAS PubMed.
- M. G. Gold, S. L. Reichow, S. E. O'Neill, C. R. Weisbrod, L. K. Langeberg, J. E. Bruce, T. Gonen and J. D. Scott, EMBO Mol. Med., 2011, 4, 15–26 CrossRef PubMed.
- K. L. Németh-Cahalan, D. M. Clemens and J. E. Hall, J. Gen. Physiol., 2013, 141, 287–295 CrossRef PubMed.
- R. K. Verma, A. B. Gupta and R. Sankararamakrishnan, Methods Enzymol., 2015, 557, 485–520 Search PubMed.
- K. L. Németh-Cahalan, K. Kalman and J. E. Hall, J. Gen. Physiol., 2004, 123, 573–580 CrossRef PubMed.
- S. A. Contera, K. Voitchovsky and J. F. Ryan, Nanoscale, 2010, 2, 222–229 RSC.
- K. Voïtchovsky, S. A. Contera and J. F. Ryan, Biophys. J., 2007, 93, 2024–2037 CrossRef PubMed.
- M. Grossman, B. Born, M. Heyden, D. Tworowski, G. B. Fields, I. Sagi and M. Havenith, Nat. Struct. Mol. Biol., 2011, 18, 1102–1108 CAS.
- M. Ø. Jensen, R. O. Dror, H. Xu, D. W. Borhani, I. T. Arkin, M. P. Eastwood and D. E. Shaw, Proc. Natl. Acad. Sci. U. S. A., 2008, 105, 14430–14435 CrossRef PubMed.
- B. Yang and A. S. Verkman, J. Biol. Chem., 1997, 272, 16140–16146 CrossRef CAS PubMed.
- G. Binnig, C. Quate and C. Gerber, Phys. Rev. Lett., 1986, 56, 930 CrossRef PubMed.
- T. Fukuma, M. Higgins and S. Jarvis, Phys. Rev. Lett., 2007, 98, 106101 CrossRef PubMed.
- E. T. Herruzo, H. Asakawa, T. Fukuma and R. Garcia, Nanoscale, 2013, 5, 2678–2685 RSC.
- M. Ricci, P. Spijker, F. Stellacci, J.-F. Molinari and K. Voitchovsky, Langmuir, 2013, 29, 2207–2216 CrossRef CAS PubMed.
- M. Ricci, P. Spijker and K. Voitchovsky, Nat. Commun., 2014, 5, 4400 CAS.
- K. Kobayashi, N. Oyabu, K. Kimura, S. Ido, K. Suzuki, T. Imai, K. Tagami, M. Tsukada and H. Yamada, J. Chem. Phys., 2013, 138, 184704 CrossRef PubMed.
- W. Trewby, D. Livesey and K. Voitchovsky, Soft Matter, 2016, 12, 2642–2651 RSC.
- K. Kimura, S. Ido, N. Oyabu, K. Kobayashi, Y. Hirata, T. Imai and H. Yamada, J. Chem. Phys., 2010, 132, 194705 CrossRef PubMed.
- T. Fukuma, Y. Ueda, S. Yoshioka and H. Asakawa, Phys. Rev. Lett., 2010, 104, 016101 CrossRef PubMed.
- K. H. Sheikh and S. P. Jarvis, J. Am. Chem. Soc., 2011, 133, 18296–18303 CrossRef CAS PubMed.
- H. Asakawa, S. Yoshioka, K.-I. Nishimura and T. Fukuma, ACS Nano, 2012, 6, 9013–9020 CrossRef CAS PubMed.
- K.-I. Amano, K. Suzuki, T. Fukuma, O. Takahashi and H. Onishi, J. Chem. Phys., 2013, 139, 224710 CrossRef PubMed.
- K. Voïtchovsky, J. J. Kuna, S. A. Contera, E. Tosatti and F. Stellacci, Nat. Nanotechnol., 2010, 5, 401–405 CrossRef PubMed.
- K. Voitchovsky and M. Ricci, Proc. SPIE, 2012, 8232, 82320O CrossRef.
- D. Ortiz-Young, H. C. Chiu, S. Kim, K. Voitchovsky and E. Riedo, Nat. Commun., 2013, 4, 2482 CrossRef PubMed.
- R. Garcia and R. Proksch, Eur. Polym. J., 2013, 49, 1897–1906 CrossRef CAS.
- A. Raman, S. Trigueros, A. Cartagena, A. P. Z. Stevenson, M. Susilo, E. Nauman and S. A. Contera, Nat. Nanotechnol., 2011, 6, 809–814 CrossRef CAS PubMed.
- A. Cartagena, M. Hernando-Perez, J. L. Carrascosa, P. J. de Pablo and A. Raman, Nanoscale, 2013, 5, 4729–4736 RSC.
- E. T. Herruzo, A. P. Perrino and R. Garcia, Nat. Commun., 2014, 5, 3126 Search PubMed.
- A. F. Payam, J. R. Ramos and R. Garcia, ACS Nano, 2012, 6, 4663–4670 CrossRef CAS PubMed.
- T. R. Rodríguez and R. García, Appl. Phys. Lett., 2004, 84, 449–451 CrossRef.
- X. Xu, J. Melcher, S. Basak, R. Reifenberger and A. Raman, Phys. Rev. Lett., 2009, 102, 060801 CrossRef PubMed.
- S. Patil, N. F. Martinez, J. R. Lozano and R. Garcia, J. Mol. Recognit., 2007, 20, 516–523 CrossRef CAS PubMed.
- N. Buzhynskyy, J.-F. Girmens, W. Faigle and S. Scheuring, J. Mol. Biol., 2007, 374, 162–169 CrossRef CAS PubMed.
- N. Buzhynskyy, R. K. Hite, T. Walz and S. Scheuring, EMBO Rep., 2007, 8, 51–55 CrossRef CAS PubMed.
- N. Buzhynskyy, P. Sens, F. Behar-Cohen and S. Scheuring, New J. Phys., 2011, 13, 085016 CrossRef.
- S. Scheuring, N. Buzhynskyy, S. Jaroslawski, R. P. Gonçalves, R. K. Hite and T. Walz, J. Struct. Biol., 2007, 160, 385–394 CrossRef CAS PubMed.
- S. Mangenot, N. Buzhynskyy, J.-F. Girmens and S. Scheuring, Pflügers Archiv Europ. J. Physiol., 2008, 457, 1265–1274 CrossRef PubMed.
- F. Rico, L. Picas, A. Colom, N. Buzhynskyy and S. Scheuring, Soft Matter, 2013, 9, 7866–7873 RSC.
- R. A. Quinlan, J. M. Carter, A. M. Hutcheson and D. G. Campbell, Curr. Eye Res., 1992, 11, 909–921 CrossRef CAS PubMed.
- M. D. Perng, A. Sandilands, J. Kuszak, R. Dahm, A. Wegener, A. R. Prescott and R. A. Quinlan, Methods Cell Biol., 2004, 78, 597–624 CrossRef CAS PubMed.
- J. L. Hutter and J. Bechhoefer, Rev. Sci. Instrum., 1993, 64, 1868–1873 CrossRef CAS.
- H.-J. Butt and M. Jaschke, Nanotechnology, 1995, 6, 1–7 CrossRef.
- K. Voitchovsky, Phys. Rev. E, 2013, 88, 022407 CrossRef PubMed.
- M. Stark, R. Stark, W. Heckl and R. Guckenberger, Proc. Natl. Acad. Sci. U. S. A., 2002, 99, 8473–8478 CrossRef CAS PubMed.
- R. Hillenbrand, M. Stark and R. Guckenberger, Appl. Phys. Lett., 2000, 76, 3478–3480 CrossRef CAS.
- D. Kiracofe and A. Raman, J. Appl. Phys., 2010, 107, 033506 CrossRef.
- J mol: an open-source Java viewer for chemical structures in 3D. http://www.jmol.org/.
- D. Kiracofe and A. Raman, J. Appl. Phys., 2010, 108, 034320 CrossRef.
- J. Melcher, C. Carrasco, X. Xu, J. L. Carrascosa, J. Gomez-Herrero, P. José de Pablo and A. Raman, Proc. Natl. Acad. Sci. U. S. A., 2009, 106, 13655–13660 CrossRef CAS PubMed.
- S. S. Borysov, D. Forchheimer and D. B. Haviland, Beilstein J. Nanotechnol., 2014, 5, 1899–1904 CrossRef CAS PubMed.
- M. Dong, S. Husale and O. Sahin, Nature Nanotech., 2009, 4, 514–517 CrossRef CAS PubMed.
- R. W. Stark, T. Drobek and W. M. Heckl, Appl. Phys. Lett., 1999, 74, 3296–3298 CrossRef CAS.
- J. Preiner, J. Tang, V. Pastushenko and P. Hinterdorfer, Phys. Rev. Lett., 2007, 99, 046102 CrossRef PubMed.
- S. Basak and A. Raman, Appl. Phys. Lett., 2007, 91, 064107 CrossRef.
- D. Kiracofe and A. Raman, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 86, 205405 CrossRef.
- C. A. Bippes and D. J. Müller, Rep. Prog. Phys., 2011, 74, 086601 CrossRef.
- C. Möller, M. Allen, V. Elings, A. Engel and D. Müller, Biophys. J., 1999, 77, 1150–1158 CrossRef.
- M. Stark, C. Moller, D. Muller and R. Guckenberger, Biophys. J., 2001, 80, 3009–3018 CrossRef CAS PubMed.
- J. Cleveland, B. Anczykowski, A. Schmid and V. Elings, Appl. Phys. Lett., 1998, 72, 2613–2615 CrossRef CAS.
- R. Garcia, R. Magerle and R. Perez, Nat. Mater., 2007, 6, 405–411 CrossRef CAS PubMed.
- H. Sui, B.-G. Han, J. K. Lee, P. Walian and B. K. Jap, Nature, 2001, 414, 872–878 CrossRef CAS PubMed.
- K. Murata, K. Mitsuoka, T. Hirai, T. Walz, P. Agre, J. B. Heymann, A. Engel and Y. Fujiyoshi, Nature, 2000, 407, 599–605 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c6sm00751a |
| This journal is © The Royal Society of Chemistry 2017 |
