DOI:
10.1039/C6SM00724D
(Paper)
Soft Matter, 2017,
13, 141-146
Cooperative strings in glassy nanoparticles
Received
24th March 2016
, Accepted 6th June 2016
First published on 6th June 2016
Abstract
Motivated by recent experimental results on glassy polymer nanoparticles, we develop a minimal theoretical framework for the glass transition in spherical confinement. This is accomplished using our cooperative-string model for supercooled dynamics, that was successful at recovering the bulk phenomenology and describing the thin-film anomalies. In particular, we obtain predictions for the mobile-layer thickness as a function of temperature, and for the effective glass-transition temperature as a function of the radius of the spherical nanoparticle – including the existence of a critical particle radius below which vitrification never occurs. Finally, we compare the theoretical results to experimental data on polystyrene from the recent literature, and we discuss the latter.
Introduction
As a significant part of the ongoing research towards the understanding of the glass transition,1–6 the past two decades have seen significant interest in the anomalous dynamics of thin glass-forming polymer films.7,8 In particular, the observed reductions of the glass-transition temperature in thin polymer films9–13 have been suggested to be either strongly influenced or caused by the enhanced dynamics in the free-surface region,14–18 and have triggered an intense theoretical activity.19–31 Similarly, the effect of interfaces is expected to manifest in other geometries.32,33 The simplest such case is that of polymer spherical nanoparticles,34–41 and their recent colloidal analogues.42
To our knowledge, the first report of anomalous dynamics in polymer nanoparticles is that of Sasaki et al.34 In that work, differential scanning calorimetry of aqueous dispersions of polystyrene nanospheres in the 21–274 nm radius range showed no evidence for a reduced glass-transition temperature, but instead revealed a radius-dependent value of the step in heat capacity at the glass transition. Analysis of the data suggested that this result is consistent with a near-surface region of size ∼3.8 nm not contributing to the transition. Then, Rharby used neutron scattering to measure mechanical deformations of polystyrene nanospheres individually dispersed in crosslinked polybuthylmethacrylate matrices, and deduced glass-transition temperatures that were reduced from the bulk value for nanospheres less than ∼30 nm in radius.35 Later measurements by Zhang et al.,38 and Feng et al.,40 showed reductions in the glass-transition temperature for spheres of larger radii, and with a strong dependence on the sphere coating. The latter fact is reminiscent of the strong effect even small amounts of residual surfactants can have on thin-film reductions in the glass-transition temperature, as reported by Chen and Torkelson.43 The above large disparity in observations may partially result from the much more difficult sample preparation in making dispersed nanospheres, as compared to thin films. Indeed, the presence of surfactants and/or residual monomers, and the uncertainty in final molecular weight could result in large variations between different experiments. Therefore, it appears necessary to establish a theoretical framework for the description of the glass transition in spherical confinement, and by this to enable comparisons between the observations in thin films and nanoparticles. As a remark, let us mention the existence of another theoretical attempt on nanoparticles, using a thermodynamical analogy between vitrification and crystallization.44
In this article, we utilise the cooperative-string model31 – recently developed and successfully applied to thin glassy films – for the present case of glassy nanoparticles. The general philosophy of our approach consists of combining classical free-volume and cooperativity arguments to the more recent observations of a specific string-like character of the cooperatively rearranging regions, within a minimal kinetic model allowing us to address analytically and quantitatively the confinement-induced and interfacial effects. After recalling the main ingredients of the bulk description, we turn to its modification in spherical geometry and discuss the implications for experiments. In particular, we characterize the extent of the mobile-layer region as a function of temperature, and we describe the glass-transition temperature reductions as a function of particle radius, providing predictions for experiments, including the existence of a minimal radius below which vitrification never occurs. One purpose of this work is that it allows a natural separation between the effects intrinsic to glass formation, and those related to the polymeric nature of the materials for which even the thin-film geometry12 has so far defied a proper theoretical description, despite promising ideas.45,46
Cooperative-string model
In a supercooled liquid, due to crowding and caging,47 local rearrangements seem to require the cooperative participation of a growing number of molecules as the temperature T is decreased.48,49 This was related through phenomenological arguments50,51 to the vanishing of the free volume52 needed for relaxation, and could lead to the tremendous slowing down of glassy dynamics described by the empirical time-temperature superposition.53–56 This relaxation process defines a temperature-dependent length scale ξ(T) for the cooperatively rearranging regions, and thus for glassy dynamics in the bulk.57,58 Furthermore, within some degree of polydispersity in size, numerical simulations,59–61 and experiments,62,63 suggested that those regions might take the form of unidimensional chains – the so-called cooperative strings. In a recent article,31 we developed a minimal kinetic model based on those ideas, that was successful in reproducing bulk phenomenology and in describing thin-film anomalies. Below, we reproduce the main ingredients of that model for a bulk supercooled liquid.
As a preliminary, we would like to stress an important point. For the sake of simplicity, we map the real liquid state to a simple hard-sphere liquid and thus fully neglect the enthalpic contributions in the activation barriers for relaxation. Stated differently, we assume that entropic effects are dominant in the critical slowing down of supercooled liquids. This is also what the Gibbs–DiMarzio approach to glass formation in polymers would suggest, with the underlying transition essentially determined by a vanishing of the configurational entropy.48 In fact, we are not trying to come up with a definitive and detailed theory of glassy dynamics, but rather address the much simpler question: what physics are we able to get out of the ideas of caging and cooperative motion? In particular, more than the bulk description already developed by Adam and Gibbs49 or Wolynes,58 our goal is to understand how such a minimal free-volume model will exhibit finite-size effects that are not always easily determined in other approaches.
Let us consider a dense assembly of small molecules with size λV and average intermolecular distance λ. The volume fraction is thus ϕ ∝ (λV/λ)3. A test molecule sits in a cage of volume ∼λ3, with gates of length L ∼ λ − λV. We set that a typical non-cooperative liquid-like local relaxation requires L > Lc = λc − λV, or equivalently λ to be larger than λc – the so-called onset of cooperativity, with volume fraction ϕc. Also, when λ ∼ λV, the gates are completely closed (L ∼ 0) and the system is at kinetic arrest, with volume fraction ϕV. For λV < λ < λc, the relaxation is possible but necessarily collective. It requires a random string-like cooperative motion involving at least N* − 1 neighbours of the test molecule, that provide a total space (N* − 1) L ∼ Lc − L by getting in close contact with each other. The test molecule thus sees a temporary larger gate, of length Lc, and can exit the cage. Therefore, one gets the scaling expression of the minimal number of molecules needed for a local relaxation, i.e. the so-called cooperativity:
| | 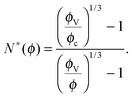 | (1) |
As expected, this expression reaches 1 at the cooperative onset
ϕc, where solitary rearrangements are allowed, and diverges at the kinetic arrest point
ϕV. Note that the bulk glass-transition point
ϕbulkg lies somewhere in between those two extreme values.
By introducing the necessity of coherence between molecular motions within a cooperative rearrangement, one showed31 that in a typical cooperative string made of N* molecules the relaxation rate τ−1 follows:
| | 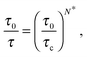 | (2) |
where
τc ∼ 1 ps is a typical liquid-like relaxation time at the cooperative onset, and
τ0 ∼ 10 fs is a molecular time scale. Our description thus naturally leads to the Adam–Gibbs phenomenology.
49 While the proposed approach does globally use free volume to correlate to dynamics, it does not necessarily mean that local regions with higher free volume are always faster in a real material, despite indications that this might be true.
64 In fact, the effect of coherence of molecular motion is at least as important as the free volume itself. If parts of the sample had a higher density, but also a higher coherence factor
τ0/
τc, then those parts may relax faster. All of this is not considered in the context of the current mean-field approach, but it does mean that we do not necessarily have to assume a strict correlation between local density and local mobility.
Since, in the temperature range considered, the thermal expansion coefficient α = −(1/ϕ)dϕ/dT of the supercooled liquid is almost constant, one has:
| | | ϕ(T) = ϕV[1 − α(T − TV)], | (3) |
where
ϕ(
TV) =
ϕV defines the Vogel temperature
TV. Therefore, our description naturally leads to the Vogel–Fulcher–Tammann time-temperature superposition
53–55 without incorporation of any enthalpic contribution, through the use of
eqn (1)–(3):
| | 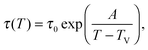 | (4) |
where
A = (
Tc −
TV)ln(
τc/
τ0), and with
ϕ(
Tc) =
ϕc by definition of the onset temperature
Tc.
As a first remark, τc/τ0 should be a constant only for hard spheres. For a real liquid, the latter dimensionless relaxation time is rather expected to follow an Arrhenius law τc/τ0 = exp(Ta/T), where kBTa is an activation energy barrier proportional to the cohesive interaction strength, and kB is the Boltzmann constant. In that case, eqn (4) would be replaced by the leading-order expression near the kinetic-arrest point:
| | 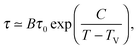 | (5) |
where
C =
Ta(
Tc −
TV)/
TV and log
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) B
B = −
C/
TV are two constants. Thus, the Vogel–Fulcher–Tammann form is still recovered asymptotically, which means, in this type of description, that the details of the enthalpic contributions are not essential to capture the critical slowing down in an ideal supercooled liquid. As a second remark, the Vogel–Fulcher–Tammann law is only valid over some temperature range, and in reality we do not expect the relaxation times to actually diverge (see
e.g.ref. 65). Our approach should rather be considered as a high-temperature approximation. The guiding idea behind that is to address the new spherical-confinement situation (see next section) using the most simple arguments, and in the bulk the Vogel–Fulcher–Tammann time-temperature superposition was the seminal approach before refinements: we thus went through the exact same admittedly-idealized path, before applying it to a novel geometry in order to extract its essential features. The low-temperature behaviour lies beyond the scope of the present minimal description, as it might involve the fine details of the real energy landscape.
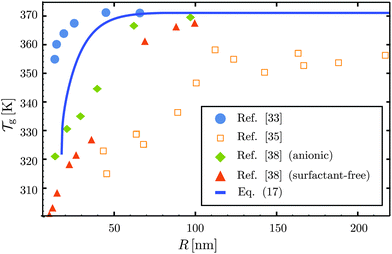
As the bulk relaxation process presented here consists of random cooperative strings involving N* molecules, one can minimally describe them through ideal random walks. The length scale ξ of the cooperatively rearranging regions is thus of the form 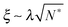 , near the kinetic arrest point. Note that if we rather use more realistic self-avoiding random walks, the exponent becomes ∼0.6 instead of 1/2 – but such a refinement would be at the cost of mathematical simplicity for the confinement effects discussed below. Invoking eqn (1) and (3), one obtains the temperature-dependent expression of the cooperativity:
, near the kinetic arrest point. Note that if we rather use more realistic self-avoiding random walks, the exponent becomes ∼0.6 instead of 1/2 – but such a refinement would be at the cost of mathematical simplicity for the confinement effects discussed below. Invoking eqn (1) and (3), one obtains the temperature-dependent expression of the cooperativity:
| | 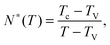 | (6) |
and thus an asymptotic expression for the associated length scale:
| | 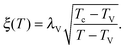 | (7) |
As a consequence of this description, the cooperative length diverges at the Vogel temperature with a −1/2 power law, and is comparable to the molecular size at the cooperative onset.
Spherical confinement
Within the context of the cooperative-string model summarized above, we now investigate the effect of confinement – a situation that arises when the system size becomes comparable to the bulk cooperative length ξ. More precisely, inspired by recent experimental results,34–41 we consider spherical nanoparticles of radius R. As illustrated in Fig. 1, the interface is a reservoir of free volume and as such it truncates the cooperative strings, leading to a higher local mobility. We therefore introduce the average local cooperativity Ns*(r, R, T), at a distance r from the center of the sphere, and at temperature T. Intuitively, if R − r is much larger than ξ, the interface is typically not reached with less than N* cooperative molecules. In contrast, when R − r becomes comparable to ξ, the cooperative strings start to feel the interface, and the effective number of cooperative molecules needed for relaxation is reduced. Lastly, as r approaches R, we expect Ns* to vanish and the relaxation to be purely liquid-like.
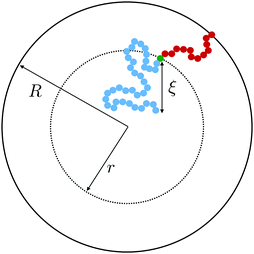 |
| | Fig. 1 Two string-like cooperative paths in a supercooled spherical nanoparticle of radius R. Relaxation of a test molecule (green) at a distance r from the sphere center can occur through either a bulk cooperative string (blue) of size ξ (eqn (7)), or a truncated string (red) touching the interface. | |
Because our minimal description of the local relaxation process relies on random cooperative strings involving N* molecules, we can use a first-passage argument in the limit of large N*, in order to determine Ns*. Before doing so, we make the following remark. The typical string length in numerical simulations is rather short.59 This is related to the fact that, due to computational time constraints, those simulations were performed at relatively high temperatures – basically near the caging onset – and thus address the onset of cooperative motion. In contrast, in experiments, such as the ones with vibrated granular beads,62 or repulsive colloids63 for instance, notably longer structures are seen. The clear advantage of working near the kinetic-arrest point is to get a Brownian description, and thus tractable analytical results using first-passage probability densities. This is an idealized asymptotic view valid only near the divergence point. But, as for critical phenomena in continuous phase transitions, it may allow to extract some universal features that might still be relevant away from the divergence point.
For that purpose, we define n0 as the number of molecular units at which a given realization of a random string reaches the interface for the first “time”. If n0 ≥ N*, the string is bulk-like; if n0 < N*, the string is truncated by the interface. Therefore, the important quantity here is the density of probability g(t) of the first-passage “time” t = n0/N* at the interface, located at dimensionless radial position R/ξ, of a 3D Brownian process starting at dimensionless radial position r/ξ, with r < R. Below, we briefly summarise the main mathematical steps allowing to obtain g(t) explicitly. The Laplace transform of g(t) can be written as:66,67
| | 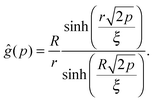 | (8) |
By using the Bromwich integral,
68 one can invert the Laplace transform through:
| | 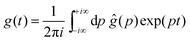 | (9) |
| | 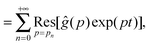 | (10) |
where
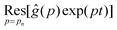
is the residue of the function
ĝ(
p)exp(
pt) around the pole:
| | 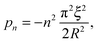 | (11) |
with
n a strictly positive integer. Note that if the numerator of the right-hand side of
eqn (8) vanishes at a given
pn, the latter is actually not a pole of
ĝ(
p), and the corresponding residue equals zero which preserves the validity of
eqn (10). Using l'Hôpital's rule,
eqn (10) can be further reformulated into the series:
| | 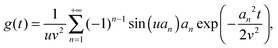 | (12) |
where we introduced
an =
nπ,
u =
r/
R, and
v =
R/
ξ, for clarity.
Knowing the first-passage probability density g(t), one can now compute the average local cooperativity Ns* by averaging the minimum between N* and n0:
| | | Ns*(r, R, T) = N*(T)〈min(1,t)〉t | (13) |
| | 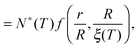 | (14) |
where 〈⋯〉
t indicates the average over all first-passage times. In the last equation, we introduced the truncation factor:
| | 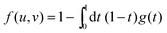 | (15) |
| | 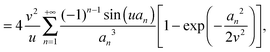 | (16) |
that takes values in the interval [0,1], and which depends on the nanoparticle radius
R, the radial location
r of the test molecule, and the bulk cooperative length
ξ.
Discussion
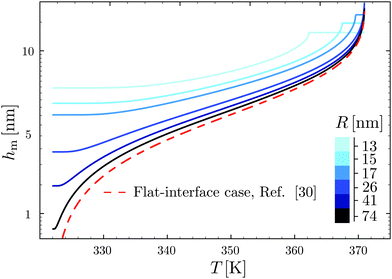
Using the results of the previous section, one can now quantify the thickness of the mobile layer near the surface of a nanoparticle. Let us consider a temperature T below the bulk glass-transition temperature Tbulkg. At the interface, the relaxation is non-cooperative or liquid-like; in contrast, deep inside the sphere the relaxation is bulk-like and the sample exhibits glassy dynamics. Therefore, there must exist a distance hm from the interface, at which the local cooperativity Ns*(R − hm, R, T) equals the bulk cooperativity at the bulk glass transition N*(Tbulkg). Invoking eqn (6), (7) and (14), one obtains:| | 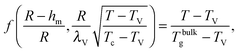 | (17) |
which implicitly defines the temperature-dependent mobile-layer thickness hm(T). The latter is plotted in Fig. 2 for several sphere radii, and with the relevant parameters for polystyrene.31,57,69,70 A number of observations can be made. First, as expected, the curves converge at large R to the flat-interface result used for the thin-film geometry.31 Secondly, hm is an increasing function of temperature, bounded by the system size R. In all cases, at the bulk glass-transition temperature Tbulkg, i.e. when all the material is liquid, hm equals the system size. Thirdly, below Tbulkg, hm is typically of the order of a few nanometers, consistent with the ∼3.8 nm estimate of Sasaki et al. for polystyrene nanospheres,34 as well as with several experimental observations on thin polystyrene films.14–18 Finally, near the Vogel temperature TV, hm saturates to a finite value that can be calculated explicitly since the cooperativity N* becomes very large (see eqn (6)) and thus the typical values of t = n0/N* are much lower than 1. In that case, f = 〈min(1,t)〉t ≃ 〈t〉t = −ĝ′(0) = (R2 − r2)/(3ξ2), according to eqn (8). Using this approximation, as well as eqn (7) and (17), one obtains the limiting value:| | 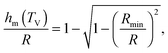 | (18) |
where 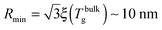 , with the parameters relevant to polystyrene.31,57,69,70 This result implies that a polystyrene nanoparticle with a nearly-free interface and a radius below a certain nanometric size remains liquid at all temperatures. Beyond its exact estimate, which might not be captured by the minimal model presented here, the existence of such a critical radius seems crucial as it might place important constraints for potential applications. On a fundamental level, the idea of a confinement-induced melting of a glass32,33 for a system size comparable to the bulk cooperative length ξ(Tbulkg) at the bulk glass transition appears to be relevant. As a last remark, note that as R diverges, hm(TV) vanishes, as in the flat-interface result used for the thin-film geometry.31
, with the parameters relevant to polystyrene.31,57,69,70 This result implies that a polystyrene nanoparticle with a nearly-free interface and a radius below a certain nanometric size remains liquid at all temperatures. Beyond its exact estimate, which might not be captured by the minimal model presented here, the existence of such a critical radius seems crucial as it might place important constraints for potential applications. On a fundamental level, the idea of a confinement-induced melting of a glass32,33 for a system size comparable to the bulk cooperative length ξ(Tbulkg) at the bulk glass transition appears to be relevant. As a last remark, note that as R diverges, hm(TV) vanishes, as in the flat-interface result used for the thin-film geometry.31
 |
| | Fig. 2 Predicted surface mobile-layer thicknesses hm of spherical polystyrene nanoparticles as a function of temperature T, according to eqn (16) and (17), for different sphere radii as indicated. We used the bulk glass-transition temperature Tbulkg = 371 K,69 and the onset temperature Tc = 463 K.57,70 We fixed the molecular size λV = 3.7 nm, and the Vogel temperature TV = 322 K, to the values previously obtained for the thin-film geometry.31 Note that we replaced the +∞ bound by 25 in eqn (16), and checked that it provides sufficiently precise numerical estimates. For comparison, the dashed line indicates the flat-interface result used for the thin-film geometry.31 | |
We can now determine the effective glass-transition temperature 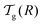 measured in nanoparticles of radius R, by using the following criterion:26,28 the transition occurs when half of the sample volume is liquid and the other half is glassy, i.e. (R − hm)/R = 2−1/3 for a sphere. Introducing
measured in nanoparticles of radius R, by using the following criterion:26,28 the transition occurs when half of the sample volume is liquid and the other half is glassy, i.e. (R − hm)/R = 2−1/3 for a sphere. Introducing 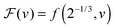 , and using eqn (17), we get:
, and using eqn (17), we get:
| | 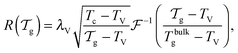 | (19) |
which implicitly defines
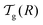
. The latter is plotted in
Fig. 3, with the relevant parameters for polystyrene,
31,57,69,70 and it is compared to experimental results from the literature.
35,37,40 Two things become immediately obvious. On one hand, it is clear and encouraging that both the model and the data show reductions in the glass-transition temperature for spherical polystyrene nanoparticles with a radius of a few tens of nanometers. On the other hand, making more detailed comparisons is simply not possible due to large scatter in the experimental data.
 |
| | Fig. 3 Comparison between experimental data (symbols) for the reduced glass-transition temperature  of spherical polystyrene nanoparticles35,37,40 of radius R, and the theory (line) given by eqn (19) – that invokes eqn (16) through of spherical polystyrene nanoparticles35,37,40 of radius R, and the theory (line) given by eqn (19) – that invokes eqn (16) through 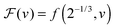 . The fixed parameters are the bulk glass-transition temperature Tbulkg = 371 K,69 and the onset temperature Tc = 463 K.57,70 The two adjustable parameters are the molecular size λV = 3.7 nm, and the Vogel temperature TV = 322 K, that were fixed to the values previously obtained for the thin-film geometry.31 Note that we replaced the +∞ bound by 25 in eqn (16), and checked that it provides sufficiently precise numerical estimates. . The fixed parameters are the bulk glass-transition temperature Tbulkg = 371 K,69 and the onset temperature Tc = 463 K.57,70 The two adjustable parameters are the molecular size λV = 3.7 nm, and the Vogel temperature TV = 322 K, that were fixed to the values previously obtained for the thin-film geometry.31 Note that we replaced the +∞ bound by 25 in eqn (16), and checked that it provides sufficiently precise numerical estimates. | |
At this point, it is important to make a few remarks. First, if we shift vertically the data of Zhang et al.,37 in order to enforce equal Tbulkg values between all studies, the general agreement to literature data becomes comparable to the thin-film case.31 Secondly, the presence of residual surfactants – a necessary ingredient in many nanosphere preparation techniques – has been shown to have a large effect on the magnitude of the glass-transition temperature reductions in thin films,43 and could thus be responsible for part of the experimental scatter. Thirdly, spherical polymer nanoparticles may well be like freestanding films, in that no part of the sample is on a substrate. It is thus fruitful here to remember the case of freestanding polystyrene thin films.12 In those samples, two different types of behaviour were observed: (i) for low molecular weights, there are reductions in the glass-transition temperature that do not depend on the molecular weight, and which are similar to the ones in supported films – well captured by our cooperative-string model;31 (ii) in contrast, for large molecular weights, the reductions in the glass-transition temperature are much more pronounced, and exhibit a dependence with molecular weight, suggesting another – polymeric – relaxation mode,45,46 still to be described theoretically in quantitative detail.
To conclude, in view of the robustness of our cooperative-string model for bulk samples and supported films,31 and given the present results and discussion, this work could be set as a theoretical framework for describing the glassy dynamics in surfactant-free monodisperse low-molecular-weight spherical nanoparticles. Beyond the radius-dependent reduction in the glass-transition temperature, the model offers a preliminary prediction on the surface mobile-layer thickness as a function of temperature, and sets the existence of a minimal sphere radius, below which vitrification never occurs. As such, our results reveal important constraints on potential applications, and may serve as a guiding tool for future fundamental studies around the glass transition, in confinement, and at interfaces.
Acknowledgements
The authors thank Raphaël Voituriez, Justin Salez, Kari Dalnoki-Veress, Ulysse Mizrahi, and Nathan Israeloff for interesting discussions. They acknowledge financial support from the ESPCI Paris Sciences Chair, the Global Station for Soft Matter – a project of Global Institution for Collaborative Research and Education at Hokkaido University – and the Perimeter Institute for Theoretical Physics. Research at Perimeter Institute is supported by the Government of Canada through Industry Canada and by the Province of Ontario through the Ministry of Economic Development & Innovation.
References
- P. W. Anderson, Science, 1995, 267, 1615 CrossRef CAS PubMed.
- G. Parisi and F. Zamponi, Rev. Mod. Phys., 2010, 82, 789 CrossRef.
- A. J. Liu and S. R. Nagel, Annu. Rev. Condens. Matter Phys., 2010, 1, 347–369 CrossRef.
-
Dynamical heterogeneities in glasses, colloids, and granular media, ed. L. Berthier, G. Biroli, J.-P. Bouchaud, L. Cipeletti and W. van Saarloos, Oxford University Press, 2010 Search PubMed.
- L. Berthier and G. Biroli, Rev. Mod. Phys., 2011, 83, 587 CrossRef CAS.
- M. D. Ediger and P. Harrowell, J. Chem. Phys., 2012, 137 Search PubMed.
- G. McKenna, Eur. Phys. J. E: Soft Matter Biol. Phys., 2003, 12, 191 CrossRef CAS PubMed.
- M. D. Ediger and J. A. Forrest, Macromolecules, 2014, 47, 471 CrossRef CAS.
- J. L. Keddie, R. A. L. Jones and R. A. Cory, Europhys. Lett., 1994, 27, 59 CrossRef CAS.
- J. A. Forrest, K. Dalnoki-Veress, J. R. Stevens and J. R. Dutcher, Phys. Rev. Lett., 1996, 77, 2002 CrossRef CAS PubMed.
- C. J. Ellison and J. M. Torkelson, Nat. Mater., 2003, 2, 695 CrossRef CAS PubMed.
- K. Dalnoki-Veress, J. A. Forrest, P. G. de Gennes and J. R. Dutcher, J. Phys., 2000, 10, Pr7 Search PubMed.
- O. Bäumchen, J. D. McGraw, J. A. Forrest and K. Dalnoki-Veress, Phys. Rev. Lett., 2012, 109, 055701 CrossRef PubMed.
- Z. Fakhraai and J. A. Forrest, Science, 2008, 319, 600 CrossRef CAS PubMed.
- M. Ilton, D. Qi and J. A. Forrest, Macromolecules, 2009, 42, 6851 CrossRef CAS.
- Z. Yang, Y. Fujii, F. K. Lee, C.-H. Lam and O. K. C. Tsui, Science, 2010, 328, 1676 CrossRef CAS PubMed.
- Y. Chai, T. Salez, J. D. McGraw, M. Benzaquen, K. Dalnoki-Veress, E. Raphaël and J. A. Forrest, Science, 2014, 343, 994 CrossRef CAS PubMed.
- W. Zhang and L. Yu, Macromolecules, 2016, 49, 731 CrossRef CAS.
- K. Ngai, A. Rizos and D. Plazek, J. Non-Cryst. Solids, 1998, 235–237, 435 CrossRef CAS.
- P. Scheidler, W. Kob and K. Binder, Europhys. Lett., 2000, 52, 277 CrossRef CAS.
- D. Long and F. Lequeux, Eur. Phys. J. E: Soft Matter Biol. Phys., 2001, 4, 371 CrossRef CAS.
- S. Herminghaus, K. Jacobs and R. Seemann, Eur. Phys. J. E: Soft Matter Biol. Phys., 2001, 5, 531 CrossRef CAS.
- F. Varnik, J. Baschnagel and K. Binder, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2002, 65, 021507 CrossRef CAS PubMed.
- J. Baschnagel and F. Varnik, J. Phys.: Condens. Matter, 2005, 17, R851 CrossRef CAS.
- J. E. G. Lipson and S. T. Milner, Eur. Phys. J. B, 2009, 72, 133 CrossRef CAS.
- J. A. Forrest, J. Chem. Phys., 2013, 139, 084702 CrossRef CAS PubMed.
- C.-H. Lam and O. K. C. Tsui, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2013, 88, 042604 CrossRef PubMed.
- J. A. Forrest and K. Dalnoki-Veress, ACS Macro Lett., 2014, 3, 310 CrossRef CAS.
- S. Mirigian and K. S. Schweizer, J. Chem. Phys., 2014, 141, 161103 CrossRef PubMed.
- P. Z. Hanakata, B. A. Pazmino Betancourt, J. F. Douglas and F. W. Starr, J. Chem. Phys., 2015, 142, 234907 CrossRef PubMed.
- T. Salez, J. Salez, K. Dalnoki-Veress, E. Raphaël and J. A. Forrest, Proc. Natl. Acad. Sci. U. S. A., 2015, 112, 8227 CrossRef CAS PubMed.
- J. Bares, Macrocmolecules, 1975, 8, 244 CrossRef CAS.
- C. L. Jackson and G. B. McKenna, J. Chem. Phys., 1990, 93, 9002 CrossRef CAS.
- T. Sasaki, A. Shimizu, T. H. Mourey, C. T. Thurau and M. D. Ediger, J. Chem. Phys., 2003, 119, 8730 CrossRef CAS.
- Y. Rharbi, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2008, 77, 031806 CrossRef PubMed.
- Y. Guo, C. Zhang, C. Lai, R. D. Priestley, M. D'Acunzi and G. Fytas, ACS Nano, 2011, 5, 5365 CrossRef CAS PubMed.
- C. Zhang, Y. Guo and R. D. Priestley, Macromolecules, 2011, 44, 4001 CrossRef CAS.
- C. Zhang, Y. Guo, K. B. Shepard and R. D. Priestley, J. Phys. Chem. Lett., 2013, 4, 431 CrossRef CAS PubMed.
- C. Zhang, V. M. Boucher, D. Cangialosi and R. D. Priestley, Polymer, 2013, 54, 230 CrossRef CAS.
- S. Feng, Z. Y. Li, R. Liu, B. Y. Mai, Q. Wu, G. D. Liang, H. Y. Gaoab and F. M. Zhu, Soft Matter, 2013, 9, 4614 RSC.
- S. Feng, Y. Chen, B. Mai, W. Wei, C. Zheng, Q. Wu, G. D. Liang, H. Y. Gaoab and F. M. Zhu, Phys. Chem. Chem. Phys., 2014, 16, 15941 RSC.
- B. Zhang and X. Cheng, Phys. Rev. Lett., 2016, 116, 098302 CrossRef PubMed.
- L. Chen and J. M. Torkelson, Polymer, 2016, 86, 226 CrossRef.
- Z. Zhang, M. Zhao and Q. Jiang, Physica B, 2001, 293, 232 CrossRef CAS.
- P.-G. de Gennes, Eur. Phys. J. E: Soft Matter Biol. Phys., 2000, 2, 201 CrossRef CAS , ISSN 1292-8941.
- S. T. Milner and J. E. G. Lipson, Macromolecules, 2010, 9865, 43 Search PubMed.
- W. Götze, Condens. Matter Phys., 1998, 1, 873 CrossRef.
- J. H. Gibbs and E. A. DiMarzio, J. Chem. Phys., 1958, 28, 373 CrossRef CAS.
- G. Adam and J. H. Gibbs, J. Chem. Phys., 1965, 43, 139 CrossRef CAS.
- A. K. Doolittle, J. Appl. Phys., 1951, 22, 1471 CrossRef CAS.
- S. F. Edwards and T. Vilgis, Phys. Scr., 1986, T13, 7 CrossRef CAS.
- M. H. Cohen and G. S. Grest, Phys. Rev. B: Condens. Matter Mater. Phys., 1979, 20, 1077 CrossRef CAS.
- H. Vogel, Phys. Z., 1921, 22, 645 CAS.
- G. S. Fulcher, J. Am. Ceram. Soc., 1925, 8, 339 CrossRef CAS.
- G. Tammann and W. Hesse, Z. Anorg. Allg. Chem., 1926, 156, 245 CrossRef.
- M. L. Williams, R. F. Landel and J. D. Ferry, J. Am. Chem. Soc., 1955, 77, 3701 CrossRef CAS.
- E. Donth, J. Polym. Sci., Part B: Polym. Phys., 1996, 34, 2881 CrossRef CAS.
- J. D. Stevenson, J. Schmalian and P. G. Wolynes, Nat. Phys., 2006, 2, 268 CrossRef CAS.
- C. Donati, J. F. Douglas, W. Kob, S. J. Plimpton, P. H. Poole and S. C. Glotzer, Phys. Rev. Lett., 1998, 80, 2338 CrossRef CAS.
- P. Pal, C. S. O'Hern, J. Blawzdziewicz, E. R. Dufresne and R. Stinchcombe, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2008, 78, 011111 CrossRef CAS PubMed.
- B. A. Pazmino Betancourt, J. F. Douglas and F. W. Starr, J. Chem. Phys., 2014, 140, 204509 CrossRef PubMed.
- A. S. Keys, A. R. Abate, S. C. Glotzer and D. J. Durian, Nat. Phys., 2007, 3, 260 CrossRef CAS.
- Z. Zhang, P. J. Yunker, P. Habdas and A. G. Yodh, Phys. Rev. Lett., 2011, 107, 208303 CrossRef PubMed.
- S. S. Schoenholz, E. D. Cubuk, D. M. Sussman, E. Kaxiras and A. J. Liu, Nat. Phys., 2016, 12, 469 CrossRef CAS.
- J. Zhao, S. L. Simon and G. B. McKenna, Nat. Commun., 2013, 4, 1783 CrossRef PubMed.
-
S. Redner, A guide to first-passage processes, Cambridge University Press, 2001 Search PubMed.
-
J. Kent, The Annals of Probability, 1978, p. 760 Search PubMed.
-
G. Arfken, Inverse Laplace Transformation, in Mathematical Methods for Physicists, Academic Press, Orlando, FL, 1985 Search PubMed.
-
M. Rubinstein and R. H. Colby, Polymer Physics, Oxford University Press, 2003 Search PubMed.
- S. Kahle, J. Korus, E. Hempel, R. Unger, S. Höring, K. Schrötter and E. Donth, Macromolecules, 1997, 30, 7214 CrossRef CAS.
|
| This journal is © The Royal Society of Chemistry 2017 |
Click here to see how this site uses Cookies. View our privacy policy here. 
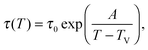
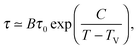
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) B = −C/TV are two constants. Thus, the Vogel–Fulcher–Tammann form is still recovered asymptotically, which means, in this type of description, that the details of the enthalpic contributions are not essential to capture the critical slowing down in an ideal supercooled liquid. As a second remark, the Vogel–Fulcher–Tammann law is only valid over some temperature range, and in reality we do not expect the relaxation times to actually diverge (see e.g.ref. 65). Our approach should rather be considered as a high-temperature approximation. The guiding idea behind that is to address the new spherical-confinement situation (see next section) using the most simple arguments, and in the bulk the Vogel–Fulcher–Tammann time-temperature superposition was the seminal approach before refinements: we thus went through the exact same admittedly-idealized path, before applying it to a novel geometry in order to extract its essential features. The low-temperature behaviour lies beyond the scope of the present minimal description, as it might involve the fine details of the real energy landscape.
B = −C/TV are two constants. Thus, the Vogel–Fulcher–Tammann form is still recovered asymptotically, which means, in this type of description, that the details of the enthalpic contributions are not essential to capture the critical slowing down in an ideal supercooled liquid. As a second remark, the Vogel–Fulcher–Tammann law is only valid over some temperature range, and in reality we do not expect the relaxation times to actually diverge (see e.g.ref. 65). Our approach should rather be considered as a high-temperature approximation. The guiding idea behind that is to address the new spherical-confinement situation (see next section) using the most simple arguments, and in the bulk the Vogel–Fulcher–Tammann time-temperature superposition was the seminal approach before refinements: we thus went through the exact same admittedly-idealized path, before applying it to a novel geometry in order to extract its essential features. The low-temperature behaviour lies beyond the scope of the present minimal description, as it might involve the fine details of the real energy landscape.
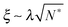 , near the kinetic arrest point. Note that if we rather use more realistic self-avoiding random walks, the exponent becomes ∼0.6 instead of 1/2 – but such a refinement would be at the cost of mathematical simplicity for the confinement effects discussed below. Invoking eqn (1) and (3), one obtains the temperature-dependent expression of the cooperativity:
, near the kinetic arrest point. Note that if we rather use more realistic self-avoiding random walks, the exponent becomes ∼0.6 instead of 1/2 – but such a refinement would be at the cost of mathematical simplicity for the confinement effects discussed below. Invoking eqn (1) and (3), one obtains the temperature-dependent expression of the cooperativity: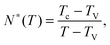
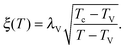

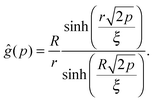
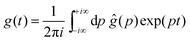
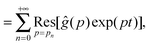
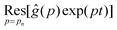 is the residue of the function ĝ(p)exp(pt) around the pole:
is the residue of the function ĝ(p)exp(pt) around the pole: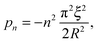
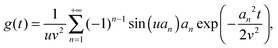
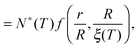
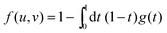
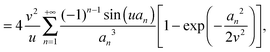
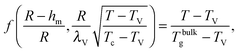
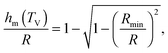
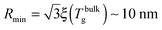 , with the parameters relevant to polystyrene.31,57,69,70 This result implies that a polystyrene nanoparticle with a nearly-free interface and a radius below a certain nanometric size remains liquid at all temperatures. Beyond its exact estimate, which might not be captured by the minimal model presented here, the existence of such a critical radius seems crucial as it might place important constraints for potential applications. On a fundamental level, the idea of a confinement-induced melting of a glass32,33 for a system size comparable to the bulk cooperative length ξ(Tbulkg) at the bulk glass transition appears to be relevant. As a last remark, note that as R diverges, hm(TV) vanishes, as in the flat-interface result used for the thin-film geometry.31
, with the parameters relevant to polystyrene.31,57,69,70 This result implies that a polystyrene nanoparticle with a nearly-free interface and a radius below a certain nanometric size remains liquid at all temperatures. Beyond its exact estimate, which might not be captured by the minimal model presented here, the existence of such a critical radius seems crucial as it might place important constraints for potential applications. On a fundamental level, the idea of a confinement-induced melting of a glass32,33 for a system size comparable to the bulk cooperative length ξ(Tbulkg) at the bulk glass transition appears to be relevant. As a last remark, note that as R diverges, hm(TV) vanishes, as in the flat-interface result used for the thin-film geometry.31

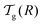 measured in nanoparticles of radius R, by using the following criterion:26,28 the transition occurs when half of the sample volume is liquid and the other half is glassy, i.e. (R − hm)/R = 2−1/3 for a sphere. Introducing
measured in nanoparticles of radius R, by using the following criterion:26,28 the transition occurs when half of the sample volume is liquid and the other half is glassy, i.e. (R − hm)/R = 2−1/3 for a sphere. Introducing 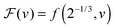 , and using eqn (17), we get:
, and using eqn (17), we get: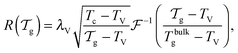
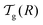 . The latter is plotted in Fig. 3, with the relevant parameters for polystyrene,31,57,69,70 and it is compared to experimental results from the literature.35,37,40 Two things become immediately obvious. On one hand, it is clear and encouraging that both the model and the data show reductions in the glass-transition temperature for spherical polystyrene nanoparticles with a radius of a few tens of nanometers. On the other hand, making more detailed comparisons is simply not possible due to large scatter in the experimental data.
. The latter is plotted in Fig. 3, with the relevant parameters for polystyrene,31,57,69,70 and it is compared to experimental results from the literature.35,37,40 Two things become immediately obvious. On one hand, it is clear and encouraging that both the model and the data show reductions in the glass-transition temperature for spherical polystyrene nanoparticles with a radius of a few tens of nanometers. On the other hand, making more detailed comparisons is simply not possible due to large scatter in the experimental data.

 of spherical polystyrene nanoparticles35,37,40 of radius R, and the theory (line) given by eqn (19) – that invokes eqn (16) through
of spherical polystyrene nanoparticles35,37,40 of radius R, and the theory (line) given by eqn (19) – that invokes eqn (16) through 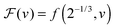 . The fixed parameters are the bulk glass-transition temperature Tbulkg = 371 K,69 and the onset temperature Tc = 463 K.57,70 The two adjustable parameters are the molecular size λV = 3.7 nm, and the Vogel temperature TV = 322 K, that were fixed to the values previously obtained for the thin-film geometry.31 Note that we replaced the +∞ bound by 25 in eqn (16), and checked that it provides sufficiently precise numerical estimates.
. The fixed parameters are the bulk glass-transition temperature Tbulkg = 371 K,69 and the onset temperature Tc = 463 K.57,70 The two adjustable parameters are the molecular size λV = 3.7 nm, and the Vogel temperature TV = 322 K, that were fixed to the values previously obtained for the thin-film geometry.31 Note that we replaced the +∞ bound by 25 in eqn (16), and checked that it provides sufficiently precise numerical estimates.