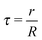DOI:
10.1039/C6SM00713A
(Paper)
Soft Matter, 2017,
13, 147-157
Topological structure prediction in binary nanoparticle superlattices
Received
23rd March 2016
, Accepted 25th April 2016
First published on 27th April 2016
Abstract
Systems of spherical nanoparticles with capping ligands have been shown to self-assemble into beautiful superlattices of fascinating structure and complexity. In this paper, I show that the spherical geometry of the nanoparticle imposes constraints on the nature of the topological defects associated with the capping ligand and that such topological defects control the structure and stability of the superlattices that can be assembled. All these considerations form the basis for the orbifold topological model (OTM) described in this paper. The model quantitatively predicts the structure of super-lattices where capping ligands are hydrocarbon chains in excellent agreement with experimental results, explains the appearance of low packing fraction lattices as equilibrium, why certain similar structures are more stable (bccAB6vs. CaB6, AuCu vs. CsCl, etc.) and many other experimental observations.
1 Introduction
Strategies for programming the self-assembly of nanoparticles consist in grafting ligands that enable the control of their interactions. DNA has proven to be a very versatile ligand, and many superlattices have been successfully assembled.1–4 Using hydrocarbons as ligands has also been a successful route for nanoparticle crystallization, both in single component5 and binary6–9 systems. While much theoretical work has been devoted to DNA programmable crystallization, see ref. 10 and 11 for recent reviews, this paper will attempt to fill the existing gap in the theoretical study of the self-assembly of nanoparticles with hydrocarbon ligands, herein called nanocrystals (NCs) into binary superlattices (BNSL).
Early studies of Murray and Sanders12 recognized the strong correlation between crystal equilibrium phases of binary micron-size particles and packing fraction in hard sphere (HS) models. Such approach has also been applied to BNSLs, where a clear but imperfect correlation between the packing fraction and equilibrium phases has been observed.6–9,13 Yet, the phase diagram of BNSLs is far more complex than the one reported for HS,14,15 as exemplified by the recent study of Boles and Talapin13 where different binary systems with similar effective NC radius (with different hydrocarbon chain length, for example) have been shown to exhibit different equilibrium phases at the same temperature and stoichiometry.
In a recent study, my group has investigated binary systems interacting with inverse power law potentials.16–18 The rationale for such study is that a sufficiently short-ranged potential should have a phase diagram whose equilibrium phases are strongly correlated to high packing fractions, and account for the flexibility of NC interactions and phonon modes. Our studies have shown that an inverse power law model provides a surprisingly successful description of the experimental results, although a few shortcomings have been noted, such as, for example, the inability to account for lattices with low packing fraction as equilibrium phases or the dominance of the CsCl over the experimentally favored AuCu lattice.
While “universal” approaches, like HS or inverse power law potentials are of great value, there is an obvious need for more microscopic models. After all, such universal models cannot predict how the ligands are organized within the lattice or what are the expected NC separations within the unit cell. Models for the interaction of two NCs with grafted polymers with tilt have been discussed before,19 but actual capping ligands in NCs contain few (less than 5) Kuhn lengths, so a description in terms of a polymer is not suitable. Still, simple but predictive microscopic models have been developed for single component systems: in ref. 20, the optimal packing model (OPM) was introduced (see Fig. 1), which provides a detailed formula for the closest separation between NCs, and correctly predicts a fcc to bcc transition for increasing ligand length. An alternative model, the overlap cone model (OCM)21–23 brings NCs much closer than predicted by OPM. Further below (see Sections 3.1 and 3.2) I provide a detailed description of these models. The beautiful results of Boles and Talapin13 have shown that two dimensional systems are well described by OPM when particles have a coordination number of six or greater while for lower coordination number results seem more consistent with the OCM. The motivation for this paper is to develop a model that can account for all these experimental results, and in this way, provide a rigorous framework for the prediction of crystal structure in general NCs systems.
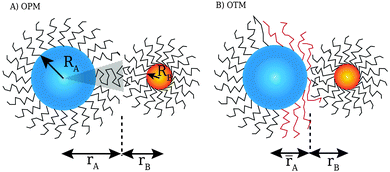 |
| | Fig. 1 Figure illustrating the assumptions of the OPM model: within the shaded cone, the ligand chain is maximally packed. If NCs come closer than predicted by OPM (![[r with combining macron]](https://www.rsc.org/images/entities/i_char_0072_0304.gif) A < rA), ligand chains must be pushed aside. This forms the basis for the OTM model discussed in this paper. A < rA), ligand chains must be pushed aside. This forms the basis for the OTM model discussed in this paper. | |
The model described in this paper is general and is applicable to spherical nanoparticles with any ligands. For the purpose of validating the model, however, special emphasis will be made to capping ligand that consist of saturated hydrocarbon chains, as those are easier to analyze theoretically and there is very detailed experimental data that can be used to validate the model. Application to other type of ligands, including the important case of hydrocarbons with some degree of unsaturation, will be left for a subsequent publication.
2 The orbifold topological model (OTM)
2.1 NC as compressible spheres
The parameters defining a single NC are the core radius R and the two properties defining the ligand: its footprint A0 and maximal length L. If the ligand consists of nH monomers (a hydrocarbon, for example), their positions are labeled as| | {![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) Hi}i=1…nH. Hi}i=1…nH. | (1) |
The volume within the NC available for a single ligand, see Fig. 1| | 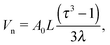 | (2) |
where it has been assumed a dense packing of ligands where the grafting density coincides with the footprint. Consideration of more sparse grafting densities may also be of interest,24 but this possibility will not be explored in this paper. The dimensionless parameters, defined in ref. 20, are
| | 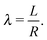 | (3) |
The actual volume occupied by the ligand is Vh = A0L. The OPM model20 assumes that for two nearest neighbor NCs, their contact ligands are occupying all the available volume, that is Vn = Vh orThe generalization of this equation to two nearest neighbor NCs (labeled k and l) is:| | | skl = rk + rl = τkRk + τlRl, | (5) |
where Ri is the radius of NC i = A, B and τi is the solution to eqn (4). With these definitions of particle radii, the ratio of two NC radii γ is defined aswhere r(A/B) is the radius of a large (A) or small (B) NC.
The monomer packing fraction (ηm) is defined as the total packing fraction, including core and ligand monomers. For a BNSL whose unit cell contains nA NC of type A and nB of type B, it is given as
| | 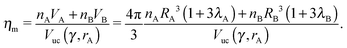 | (7) |
where
Vuc(
γ,
rA) =
Vuc(
γ)
rA3 is the volume of the unit cell. If the nearest neighbor distances are given by the OPM formula
eqn (4), then the monomer packing fraction
ηm is the same as the HS packing fraction
ηHS13| | 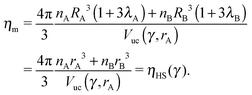 | (8) |
The free energy of the system results from a competition between the attractive van der Waals (vdW) forces and the repulsive entropic ligands. The vdW forces are approximated as two spheres of radius rk and rl in contact, whose free energy is given by25
| | 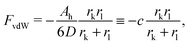 | (9) |
where
D = 0.2 (nm) (spheres in contact) and
Ah is the Hamaker constant. With these assumptions, the OPM free energy reads
| | 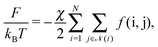 | (10) |
where
![[scr N, script letter N]](https://www.rsc.org/images/entities/char_e52d.gif)
(
i) runs over all NCs that are in physical contact with NC
i and
χ is a dimensionless coupling constant. As for the entropic hydrocarbon chain contribution, I assume that the approximation of modeling the NC as a deformable sphere already captures part of this contribution. More sophisticated free energies are available,
26 but they will not be necessary for the goals of this paper, as the limitations of the OPM model in describing BNSLs are of a different nature, as I extensively discuss below. The function
f(i,j) follows from
eqn (9)| | 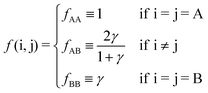 | (11) |
The definition of physical contact may include nearest neighbors, whose distance is
sij or further away neighbors at a distance
νsij, with
ν > 1. Two NCs are defined to be in contact if their mutual distance is less than their fully extended hydrocarbon chains. This condition can be stated as
| | | νijsij ≤ Ri(λi + 1) + Rj(λj + 1). | (12) |
The free energy
eqn (10) and (11) together with the constraint
eqn (12) define the free energy of the OPM model. By construction, the lattices are incompressible, and I will assume that the external pressure is zero. Thus, the chemical potential is numerically the same as the free energy.
Given the chemical potentials for all the pure phases, first the lowest chemical potential for each lattice with a given stoichiometry is determined. Then, those lattices are checked for possible phase separation against two phases X + Y, following the standard rules of thermodynamics (see for example, the formulas in ref. 17 and 18). Those lattices that survive all phase separation conditions define equilibrium.
2.2 NCs and topological defects
The closest approach within NCs would occur if the monomer packing fraction would become one ηm = 1. From eqn (7), this would correspond to a NC radius A rA′ given by| | 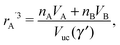 | (13) |
and a minimal separation| | | skl′ = ηHS1/3(γ′)skl, | (14) |
with skl given by the OPM formula eqn (5), which corresponds to the OCM model.23 Such model would definitely optimize the vdW attraction, but would incur, as I show below, in a prohibitively large free energy cost.
This large free energy cost is a result of inherent topological constraints. First I define a vector joining the first monomer (the one attached to the core) to the last (see notations in eqn (1))
| | 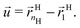 | (15) |
As clear from
Fig. 1, within the OPM model, the vector
![[u with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0075_20d1.gif)
is perpendicular to the core surface, thus defining a hedgehog structure. When interdigitation occurs the vector field
![[u with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0075_20d1.gif)
cannot be perpendicular to the surface, at least over a finite domain, as illustrated in
Fig. 2. I find it useful to consider the projection of
![[u with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0075_20d1.gif)
to the tangent plane of the sphere
thus defining a two dimensional field. When two NCs interdigitate, the
![[m with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006d_20d1.gif)
field in at least one NC will contain a topological defect located at their contact point, see
Fig. 2. If there is more than one topological defect, then there maybe neutral lines, see
Fig. 3 (left), where the ligands are perpendicular to the sphere, and the vector field
![[m with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006d_20d1.gif)
is identical to zero.
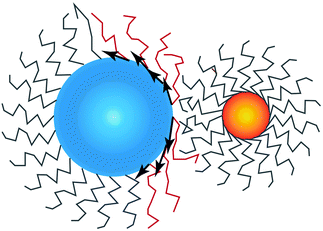 |
| | Fig. 2 Illustration on how the projection of the vector field ![[u with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0075_20d1.gif) , given by , given by ![[m with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006d_20d1.gif) as defined in eqn (16) becomes non-zero and defines a topological defect. NC A (left) has a topological index qT = 1 while NC B (right) has qT = 0. as defined in eqn (16) becomes non-zero and defines a topological defect. NC A (left) has a topological index qT = 1 while NC B (right) has qT = 0. | |
 |
| | Fig. 3 (left) Two defect separated by a neutral line. (right) Different possible defect configurations on the sphere: (A) vortices surrounded by neutral lines, where topology does not constrain the number of defects, and two types of configurations with four ½-disclinations: tetrahedral (B) and along the equator (major circle) (C). | |
I now consider the case where there are nS defects and no anti-defects, as those very quickly annihilate on the surface of a sphere.27 If the defects have charge Q = 2πp, topological constraints28 dictate that
| | 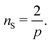 | (17) |
If defects are vortices
p = 1 then
nS = 2 and there must be two of them. The order parameter
![[u with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0075_20d1.gif)
is 3-dimensional, however, so it is possible to allocate an arbitrary number of vortices
nS > 2, circumventing
eqn (17) by separating vortices with neutral lines, as illustrated in
Fig. 3A.
It is also possible that each vortex will split into two ½ disclinations connected by a neutral line, see Fig. 3B and C. Such defect configuration has neutral lines that are much shorter than a configuration with four vortices, see Fig. 3A. It is also apparent that ½-disclinations are joined by straight neutral lines, compared to the kinks and vertices for a configuration with vortices. I will therefore assume that the cost of neutral lines is such that only ½ disclinations joined by neutral lines are possible (which includes a vortex, as the limit of two disclinations located at the same point). In this case the vector ![[m with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006d_20d1.gif) can be identified with its −
can be identified with its −![[m with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006d_20d1.gif) (as the direction can be changed along the neutral line), thus becoming an effective two dimensional nematic on a sphere, whose free energy is
(as the direction can be changed along the neutral line), thus becoming an effective two dimensional nematic on a sphere, whose free energy is
| | 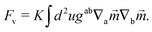 | (18) |
Here,
K is the Frank constant, and
gab and ∇
a define the differential geometry of the surface (in this case the sphere), namely the metric and the covariant derivative. In this way, nematic textures describe the tilt of the ligand chains from its normal. These nematic textures have been extensively investigated in the liquid crystal community and can be read from existing literature.
27–29
2.3 The equations defining the OTM model: topological index
I define the topological index qT of a NC as the total number of defects of its capping ligands. Considerations discussed above have served to motivate the hypothesis that the topological index of a single NC must be such that qT ≤ 4. The OTM defines the NC radius ![[r with combining macron]](https://www.rsc.org/images/entities/i_char_0072_0304.gif) A,
A, ![[r with combining macron]](https://www.rsc.org/images/entities/i_char_0072_0304.gif) B of a given NCs within a unit cell as the smallest distance that maximizes ηm with the qT ≤ 4 constraint. I note that if the topological index is qT = 0, the chains must be all perpendicular to the sphere and the closest separation between two NCs is given by the OPM result. For two isolated NCs, the topological index is not restricted and the OTM and OCM results coincide. The OTM monomer packing fraction of a given BNSL is given as
B of a given NCs within a unit cell as the smallest distance that maximizes ηm with the qT ≤ 4 constraint. I note that if the topological index is qT = 0, the chains must be all perpendicular to the sphere and the closest separation between two NCs is given by the OPM result. For two isolated NCs, the topological index is not restricted and the OTM and OCM results coincide. The OTM monomer packing fraction of a given BNSL is given as| | 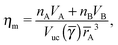 | (19) |
and satisfies ηHS(![[small gamma, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0c4.gif) ) ≤ ηm ≤ 1. The interparticle distances are also in between the OCM and OPM results, namely
) ≤ ηm ≤ 1. The interparticle distances are also in between the OCM and OPM results, namely| | skl′ ≤ ![[s with combining macron]](https://www.rsc.org/images/entities/i_char_0073_0304.gif) kl ≤ skl. kl ≤ skl. | (20) |
Thus, the OTM model predictions are always in between the OCM and OPM values and coincide only in some limits. Note that the parameter ![[small gamma, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0c4.gif) is different than γ as defined by eqn (6), and is determined by the OTM radius
is different than γ as defined by eqn (6), and is determined by the OTM radius ![[r with combining macron]](https://www.rsc.org/images/entities/i_char_0072_0304.gif) A and
A and ![[r with combining macron]](https://www.rsc.org/images/entities/i_char_0072_0304.gif) B. In the results section I show how these considerations completely determine all NCs distances, coordination numbers and the monomeric packing fraction(density). I emphasize that although for qT = 0 the NC interacting potential is two body (as it is defined by eqn (9)), for qT ≠ 0, the model includes many body effects.
B. In the results section I show how these considerations completely determine all NCs distances, coordination numbers and the monomeric packing fraction(density). I emphasize that although for qT = 0 the NC interacting potential is two body (as it is defined by eqn (9)), for qT ≠ 0, the model includes many body effects.
 |
| | Fig. 4 Color code for the lattices used. | |
3 Results
3.1 Single component phase diagram
I consider the simple lattices shown in Table 1. The chemical potential is given by eqn (10) and is computed for each value of λ. The results are shown in Fig. 5. The discrete jumps correspond to λ where the fully stretched capping ligand reaches across additional nearest neighbors as defined by eqn (5), thus increasing the coordination number q of the corresponding NC. A fcc/hcp transition to bcc is found at around λ = 0.66, as previously discussed in ref. 20. Neither fcc (q = 12) nor bcc (q = 8 + 6) can support solutions with non-trivial topological index.
Table 1 Simple lattices considered (ST: lattice type, SG: space group, S: strukturberich symbol, P: pearson symbol, A: alternative name)
| N |
ST |
SG |
S |
P |
A |
| fcc |
Simple |
Fm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m m |
A1 |
cF4 |
|
| hcp |
Simple |
P63mmc |
A3 |
hP2 |
| bcc |
Simple |
Im3m |
A2 |
cI2 |
| sc |
Simple |
Pm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m m |
Ah |
cP1 |
| cub-diamond |
Simple |
Fd![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m m |
A4 |
cF8 |
| hex-diamond |
Simple |
P63mmc |
A3′ |
hP4 |
| A15 |
Simple |
Pm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m m |
A15 |
cP8 |
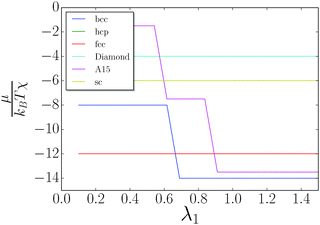 |
| | Fig. 5 Chemical potential as a function of λ. The only equilibrium phases are fcc/hcp and bcc. | |
Diamond q = 4 + 4 can support solutions with qT ≤ 4, and at sufficiently large λ such OTM solutions can be competitive with bcc. However, this possibility occurs for large λ > 1.5 (very hairy), where other considerations may apply, as single component NCs are observed to develop non-cubic unit cells.20 Investigation of large λ > 1.5 will be left for a future work.
3.2 Phase diagram of binary nanocrystals with topological index qT = 0
I will consider NCs with RA = 35 RB = 20.5 (35, 20.5) and RA = 50.1, RB = 20.5 (50.1, 20.5), units in Angstrom. The phase diagram will be computed as a function of λ1 = λA and λ2 = λB. All the lattices considered are listed in Tables 1 and 2. The calculations used the software HOODLT as it has been described elsewhere.16
For the (35, 20.5) case, the phase diagram, shown in Fig. 6, contains significant regions that include the following phases: AlB2, CaB6, NaCl, MgCu2, AuCu, NaZn13, CsCl, bccAB6 and CaCu5. Three more equilibrium phases: cubAB13, Cr3Si and Li3Bi are also found, but only in discrete points. The region λ1 ≈ λ2 corresponds to γ ∼ 0.55, which is where the HS packing fraction for AlB2 and NaZn13 becomes maximum, and indeed, those are the phases found. Similarly, λ1 ∼ 0.3, λ2 ∼ 1 corresponds to γ ∼ 0.75, where the equilibrium phases CsCl, AuCu and MgZn2 have large packing fraction. The bottom left corner of the figure corresponds to γ ∼ 0.35, where the packing fraction for bccAB6 and CaB6 is large, and those two phases compete as equilibrium phases, as it has also been pointed out experimentally.30 There is a central region (λ1 > 0.7, λ2 > 0.7) where no binary lattices exist and equilibrium corresponds to two pure A and B bcc lattices. This is a result that bcc has 14 neighbors, and when it becomes the equilibrium phase for both pure A and B, no other binary lattices within this range of λ exist with so many nearest neighbors.
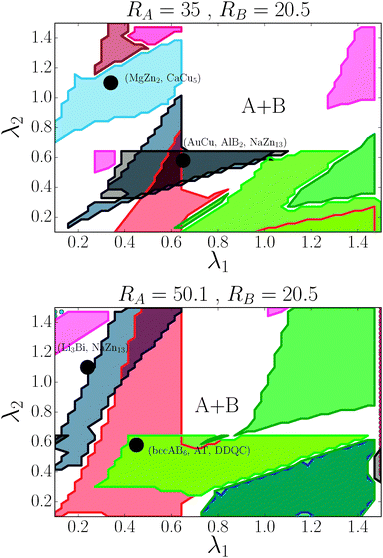 |
| | Fig. 6 Phase diagram for nanoparticles with radius RA and RB as a function of (λ1, λ2). The dots correspond to the experimental cases of ref. 13. Color codes are as shown in Fig. 4. | |
For the (50.1, 20.5) case, seven phases exist over significant regions: AlB2, CaB6, NaCl, Cr3Si, NaZn13, bccAB6 and CaCu5, and three more: AuCu, MgZn2 and cubAB13 are found in somewhat restricted points. The same correlation with HS packing fraction holds. Perhaps the most remarkable aspect is the appearance of the Cr3Si phase at around γ ∼ 0.3, competing with bccAB6. This phase is ubiquitous in DNA nanoparticle crystallization3,31 but, to my knowledge, has not been observed when the ligands are hydrocarbon chains. Compared with (35, 20.1), (50.1, 35) NCs exhibit the phases AuCu3 and Li3Bi.
The stability of the different phases is investigated in Fig. 7 and 8 and will be compared against experimental results.13 For each of the phases considered, the quantity
| | 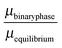 | (21) |
is shown. Here,
μbinaryphase is the chemical potential of the binary phase, and
μequilibrium is the value of the equilibrium chemical potential for the corresponding stoichiometry. Thus, the above quantity is 1 if the phase is equilibrium, and if it is not, it measures how far it is from actually becoming equilibrium. In the top figure (
λ = 0.578), AlB
2 and NaZn
13 are correctly predicted, but AuCu, which is reported experimentally, does not even exist at this packing fraction
γ as for
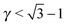
, the AuCu phase is, in reality, a CsCl.
17 The prediction for
γ = 0.77 shows only one equilibrium binary phase MgZn
2/MgCu
2 (within the free energy
eqn (10) the chemical potential is the same for both), which is among the ones reported experimentally. Two more phases: Cr
3Si and CaCu
5 are close to being equilibrium, but only the CaCu
5 phase is experimentally reported. If one where to assume, without any evidence, that the Cr
3Si might be a difficult phase to nucleate, the results seem in excellent agreement with the experiments at
γ = 0.77. It should be noted, however, that experiments for the MgZn
2 phase report a NC radius that is 15% lower than the one predicted for
qT = 0
eqn (5), clearly pointing to a more nuanced scenario than the
qT = 0 predicts.
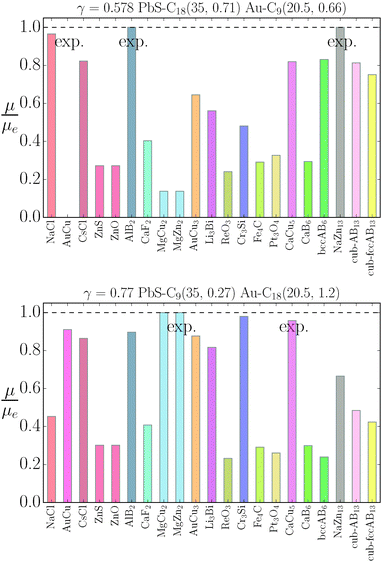 |
| | Fig. 7 Relative value of chemical potentials as defined in eqn (21). | |
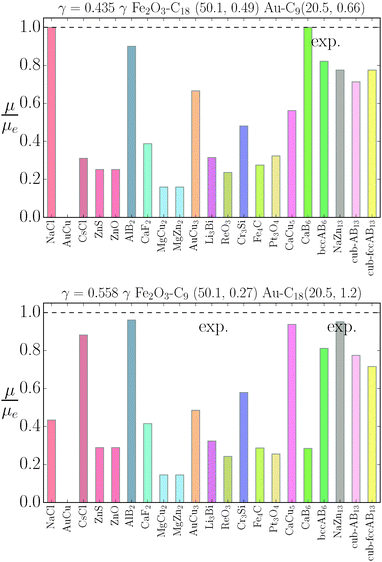 |
| | Fig. 8 Relative value of chemical potentials as defined in eqn (21). | |
The relative chemical potentials follow similar trends for γ = 0.435 and γ = 0.558, see Fig. 8. Even though at γ = 0.435 the experiment reports bccAB6 (and two other quasicrystal structures that are not investigated in this paper), the theory predicts CaB6 with bccAB6 close. As previously noticed, those two phases compete for equilibrium, but the qT = 0 clearly favors CaB6. For γ = 0.558, the experimental phases reported are NaZn13, which is very close to equilibrium, and Li3Bi, which is clearly very far from equilibrium, pointing to a clear failure of the qT = 0 assumption.
Overall, predictions for qT = 0 turn out to be in fair agreement with experiments, but a number of discrepancies are obvious. Before discussing how allowing NCs to have a non-trivial topological index may modify the overall scenario, it is worth exploring whether reasonable variations of the model eqn (10) may solve any of these pending issues. For this purpose I consider the following six potentials, with fAA = 1 (see eqn (11)):
| | 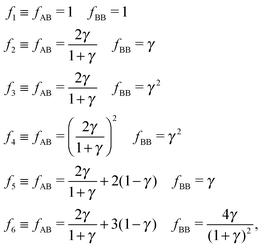 | (22) |
where the relative strength of AA, AB and BB interactions are altered. As shown in
Fig. 9 the original predictions turn out to be very robust against these variations and do not fix any of the discrepancies noted. If anything, potential
f5, which enhances the AB attractions over AA and BB does seem to fare slightly better than the other cases. At the risk of over interpreting the results, this might come from the fact that whenever two NC of different sizes come in contact, the smaller (or larger) NC may have more than one ligand in close contact, as depicted in
Fig. 1.
 |
| | Fig. 9 Relative value of chemical potentials for variations of the potential eqn (11), as defined in eqn (22). | |
3.3 Binary nanoparticle supercrystals with non-trivial topological index
A given A-NC can be nearest neighbor with qAA A-NCs and qAB B-NCs, giving a total coordination number q = qAA + qAB. Similarly, for a B NC, the total coordination number will be q = qBA + qBB. A necessary condition for BNSLs with qT ≠ 0 to exist is that at least one of the coordination numbers qAA, qAB, qBA, qBB is less or equal than four. This condition, by itself, is less restrictive than it may appear: out of the 21 binary lattices in Table 2, 18 admit, in principle, non-trivial OTM solutions, at least for a range of γ-ratios. Thus, a first prediction from OTM is that the following 3 lattices: NaCl, CsCl, CaB6 are the only ones rigorously described by the qT = 0 results discussed above.
Table 2 Binary lattices considered (ST: lattice type, SG: space group, S: strukturberich symbol, P: pearson symbol, A: alternative name)
| N |
ST |
SG |
S |
P |
A |
| NaCl |
AB |
Fm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m m |
B1 |
cF8 |
|
| AuCu |
AB |
P4/mmm |
L10 |
cP4 |
|
| CsCl |
AB |
Pm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m m |
B2 |
cP2 |
|
| ZnS |
AB |
F![[4 with combining macron]](https://www.rsc.org/images/entities/char_0034_0304.gif) 3m 3m |
B3 |
cF8 |
|
| ZnO |
AB |
P63/mc |
B4 |
hP4 |
|
| AlB2 |
AB2 |
P6/mmm |
C32 |
hP3 |
|
| CaF2 |
AB2 |
Fm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m m |
C1 |
cF12 |
|
| MgCu2 |
AB2 |
Fd![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m m |
C15 |
cF24 |
Laves |
| MgZn2 |
AB2 |
P63/mmc |
C14 |
hP12 |
Laves |
| AuCu3 |
AB3 |
Pm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m m |
L12 |
cP4 |
|
| Li3Bi |
AB3 |
Fm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m m |
|
cF16 |
|
| ReO3 |
AB3 |
Pm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m m |
D09 |
cP4 |
|
| Cr3Si |
AB3 |
Pm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) n n |
A15 |
cP8 |
|
| Fe4C |
AB4 |
P![[4 with combining macron]](https://www.rsc.org/images/entities/char_0034_0304.gif) 3m 3m |
|
cP5 |
|
| Pt3O4 |
A3B4 |
Pm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) n n |
|
cP14 |
|
| CaCu5 |
AB5 |
P6/mmm |
D2d |
hP6 |
|
| CaB6 |
AB6 |
Pm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m m |
D21 |
cP7 |
|
| bcc-AB6 |
AB6 |
Im![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m m |
|
cI14 |
Cs6C60 |
| NaZn13 |
AB13 |
Fm3c |
D23 |
cF112 |
|
| cub-AB13 |
AB13 |
Pm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m m |
|
cP14 |
|
| cub-fcc-AB13 |
AB13 |
Fm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m m |
D2f |
cF56 |
|
The detailed solution for each of the eighteen lattices considered and their free energy will be described elsewhere. Instead, I will discuss four inconsistencies that have been emphasized during the qT = 0 analysis: smaller NC radius for MgZn2, low packing fraction Li3Bi absent as an equilibrium phase, the CaB6 being slightly favored over the bccAB6 and the AuCu lattice, which does not even exist at the corresponding γ ratio.
3.3.1 MgZn2.
This lattice is described by space group P63/mmc (194) with a unit-cell of four A-particles in Wyckoff positions 4f and eight B-particles in positions 2a and 6h. If the A and B particles are hard spheres, the maximum packing fraction is reached for 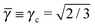 . At this value there are A–A and B–B contacts, but no A–B contacts. For
. At this value there are A–A and B–B contacts, but no A–B contacts. For ![[small gamma, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0c4.gif) < γc, the shortest separation within B-particles is given as
< γc, the shortest separation within B-particles is given as| | 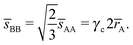 | (23) |
For ![[small gamma, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0c4.gif) < γc A–A hard spheres are in contact, with qAA = 4 and those are the NCs with qT = 4. Thus, for this lattice, OTM solutions will exist for
< γc A–A hard spheres are in contact, with qAA = 4 and those are the NCs with qT = 4. Thus, for this lattice, OTM solutions will exist for ![[small gamma, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0c4.gif) ≤ γc only.
≤ γc only.
The corresponding nematic texture (from the free energy eqn (18)) consists of four ½-disclinations sitting at the corners of a perfect tetrahedra, as shown in Fig. 3C. Because the B-particles are six coordinated their radii is given by rB (eqn (5)). Therefore, from eqn (23), the NC radius for the A-particles will satisfy
| | 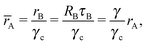 | (24) |
where
γ is always defined by
eqn (6), that is, with respect to the
qT = 0 case. Note that if
γ ≥
γc, then
![[r with combining macron]](https://www.rsc.org/images/entities/i_char_0072_0304.gif) A
A becomes
rA, as topology prevents the appearance of defects for six coordinated particles.
3.3.2 Li3Bi.
This lattice is described by space group Fm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m (225) with a unit cell of four A-particles in Wyckoff positions 4a and twelve B-particles in positions 4b and 8c. If the A and B particles are hard spheres, the maximum packing fraction is reached for
m (225) with a unit cell of four A-particles in Wyckoff positions 4a and twelve B-particles in positions 4b and 8c. If the A and B particles are hard spheres, the maximum packing fraction is reached for 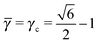 . At this value, there are A–A contacts and A–B contacts (the 4a particles touching the 8c particles). The shortest separation between A and B particles for
. At this value, there are A–A contacts and A–B contacts (the 4a particles touching the 8c particles). The shortest separation between A and B particles for ![[small gamma, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0c4.gif) > γc is given by
> γc is given by| | 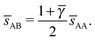 | (25) |
The smallest distance between 4a and 4b particles is also relevant and is given by| | 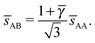 | (26) |
In this case, the NC with non-trivial topological index are the 8c and therefore those NC in Wyckoff positions 8c (and only those) have qT = 4. OTM solutions exist for ![[small gamma, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0c4.gif) > γc only. The corresponding nematic texture on each 8c NC also consists of four ½-disclinations sitting at the corners of a perfect tetrahedra. Here again, the A NC have q = 8 so their closest separation is given by the qT = 0 formulas. The smallest
> γc only. The corresponding nematic texture on each 8c NC also consists of four ½-disclinations sitting at the corners of a perfect tetrahedra. Here again, the A NC have q = 8 so their closest separation is given by the qT = 0 formulas. The smallest ![[s with combining macron]](https://www.rsc.org/images/entities/i_char_0073_0304.gif) AB distance will be given by
AB distance will be given by
| | 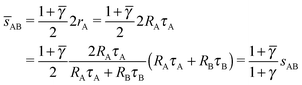 | (27) |
Since
![[small gamma, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0c4.gif)
is a free parameter, the optimal value would be
![[small gamma, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0c4.gif)
=
γc, as this is the value that brings the NC the closest. However, the 4b B-particles have
qT = 0. From
eqn (26), it follows
| | 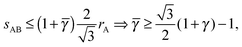 | (28) |
this lower bound determines
![[small gamma, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0c4.gif)
. The formula for the monomer packing fraction reads
| | 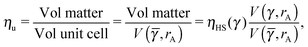 | (29) |
where
V is the volume of the corresponding unit cell.
3.3.3 bccAB6.
This lattice is described by space group Im![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m (229) with a unit cell containing two A particles in Wyckoff positions 2a and twelve B particles in Wyckoff positions 12d. If the A and B particles are hard spheres, there are two maxima of the packing fraction. The first occurs at
m (229) with a unit cell containing two A particles in Wyckoff positions 2a and twelve B particles in Wyckoff positions 12d. If the A and B particles are hard spheres, there are two maxima of the packing fraction. The first occurs at 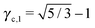 , and the second for
, and the second for 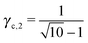 . If γc,1 <
. If γc,1 < ![[small gamma, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0c4.gif) < γc,2, the minimum A–B distance is given by
< γc,2, the minimum A–B distance is given by| | 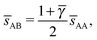 | (30) |
while for ![[small gamma, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0c4.gif) > γc,2, it is given by
> γc,2, it is given by
OTM solutions with non-trivial topological index may exist for any ![[small gamma, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0c4.gif) > γc,1. In all situations, qT = 0 for the A-particles. In the first branch γc,1 <
> γc,1. In all situations, qT = 0 for the A-particles. In the first branch γc,1 < ![[small gamma, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0c4.gif) < γc,2 the solution corresponds to B-particles with qT = 4. The four disclinations follow a distorted tetrahedra and the shortest separation among A–B NCs reads
< γc,2 the solution corresponds to B-particles with qT = 4. The four disclinations follow a distorted tetrahedra and the shortest separation among A–B NCs reads
| | 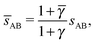 | (32) |
In this case, a further restriction exists among B-NCs, which reads
| | 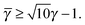 | (33) |
The monomeric packing fraction
ηu can be computed by
eqn (29), adapted to this case. There is a second branch for
![[small gamma, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0c4.gif)
>
γc,2. In that case, contacts are among B-particles, and the analysis can be done along the same lines.
3.3.4 AuCu.
This lattice is described by space group P4/mmm (123) with a unit cell of two A particles in Wyckoff positions 1a and 1b and two B-particles in Wyckoff positions 2e. If the A and B particles are hard spheres, the maximum packing fraction is reached for 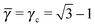 . At this value, each A particle is in contact with six other A-particles and eight B-particles, in a structure that is identical to CsCl. For
. At this value, each A particle is in contact with six other A-particles and eight B-particles, in a structure that is identical to CsCl. For ![[small gamma, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0c4.gif) > γc the shortest separation between A and B particles is given by
> γc the shortest separation between A and B particles is given by| | 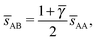 | (34) |
The smallest distance between A–A particles along the c-axis is| | 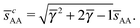 | (35) |
Each A-NC is in contact with four other A-NC while still maintaining contact with eight B NCs. Thus, the A-NCs are those with qT = 4, and OTM solutions exist for 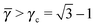 only.
only.
In this case, the nematic texture for each A-NC corresponds to four disclinations contained within a single plane on a great circle in the sphere, as shown in Fig. 3C. Although such configuration is not the minimum of the free energy eqn (18), it has been found in numerical simulations of nematics on the sphere,32 and it is a minor variation of the tetrahedral configuration obtained by stretching the neutral lines all the way till the equators, which presumably may incur in a relatively low free energy cost.
A first relation follows from the observation that two A NCs separated along the c-axis will touch each other along the north and south poles, where according to the nematic texture in Fig. 3C there is a neutral line, so ![[s with combining macron]](https://www.rsc.org/images/entities/i_char_0073_0304.gif) cAA = sAA = 2rA. Thus, from eqn (35), it follows
cAA = sAA = 2rA. Thus, from eqn (35), it follows
| | 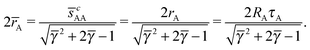 | (36) |
Another equation is obtained from noting that topology forbids disclinations for the B-NCs so their smallest possible radius is
rB. Therefore
| | ![[small gamma, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0c4.gif) ![[r with combining macron]](https://www.rsc.org/images/entities/i_char_0072_0304.gif) A ≥ rB = τBRB. A ≥ rB = τBRB. | (37) |
If I assume that the equality in the above equation holds, the pair of equations eqn (36) and (37) admit a continuous solution for 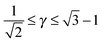 , which are shown in Fig. 10. At any other
, which are shown in Fig. 10. At any other 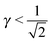 ,
, ![[small gamma, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0c4.gif) = 1, (the cubic AuCu) and the smallest A–A separation is given by
= 1, (the cubic AuCu) and the smallest A–A separation is given by
| | 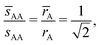 | (38) |
independently of the actual value of
γ. In this case, however, the B-NCs ligands are not fully compressed and the corresponding vdW energy is not optimal.
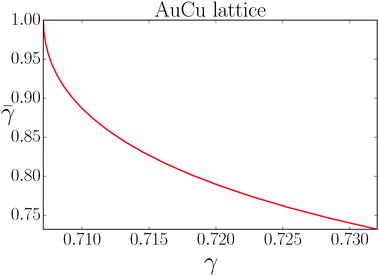 |
| | Fig. 10 Solution of the couple equations eqn (36) and (37) determining the structure of the AuCu lattice. | |
4 Comparison with experimental results
To make contact with experiments, the maximum length L of the capping ligands needs to be determined as a function of their actual chemical composition. For a ligand consisting of n saturated hydrocarbons, such length is given as| | L = nr0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos(α/2) + r1 = 0.128n + 0.2 (in nm) cos(α/2) + r1 = 0.128n + 0.2 (in nm) | (39) |
where α = 180 − 112 = 68 is the C–C angle, r0 = 0.154 is the C–C bond distance and r1 = 0.2 is the radius for an end-carbon.25 It has been argued33 that this formula tends to overestimate the maximum total hydrocarbon length. Actually, ref. 13 usedwhich predicts a slightly shorter maximum length than eqn (39). Results using both formulas will be quoted, serving the purpose of quantifying the sensitivity of the OTM in regards to maximum ligand length.
The quantities that will be compared to the experiments are the monomer packing fraction ηu and
| | ![[d with combining macron]](https://www.rsc.org/images/entities/i_char_0064_0304.gif) ij = ij = ![[s with combining macron]](https://www.rsc.org/images/entities/i_char_0073_0304.gif) ij − Ri − Rj, ij − Ri − Rj, | (41) |
which are quoted by Boles and Talapin
13 in the supplementary information Tables S3, S4, S7 and S8. When using
eqn (39) the OTM predictions will be quoted as OTM, and as OTM* when using
eqn (40). The comparison between theory and experiment is summarized in
Table 3. I now discuss each of the cases analyzed in more detail.
Table 3 Comparison between theory and experiment ηu (dimensionless) is the monomer packing fraction eqn (7). ![[d with combining macron]](https://www.rsc.org/images/entities/i_char_0064_0304.gif) ij is the quantity eqn (41) (in nm). For MgZn2 (i = A, j = B), Li3Bi (i = A, j = B), bccAB6 (i = A, j = B), AuCu (i = A, j = A). Experimental results marked with † were incorrect in the original reference and have been corrected
ij is the quantity eqn (41) (in nm). For MgZn2 (i = A, j = B), Li3Bi (i = A, j = B), bccAB6 (i = A, j = B), AuCu (i = A, j = A). Experimental results marked with † were incorrect in the original reference and have been corrected
| BNSL |
η
u
|
![[d with combining macron]](https://www.rsc.org/images/entities/i_char_0064_0304.gif) ij
ij
|
| Exp. |
OTM |
OTM* |
Exp. |
OTM |
OTM* |
| MgZn2 |
0.79 |
0.77 |
0.83 |
1.30 |
1.35 |
1.13 |
| Li3Bi |
0.88 |
0.87 |
0.86 |
0.90 |
0.98 |
1.00 |
| bccAB6 |
0.83 |
0.84 |
0.86 |
1.90 |
2.20 |
2.01 |
| AuCu |
(—)† |
>1 |
>1 |
0.05† |
0.02 |
0.01 |
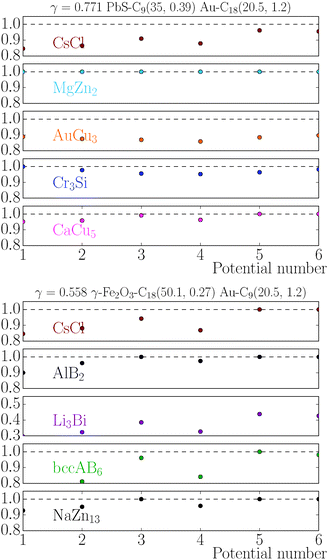
The MgZn2 is already the equilibrium phase at qT = 0, see Fig. 7, although in this case ηu = ηHS(γ = 0.77) = 0.64 and ![[d with combining macron]](https://www.rsc.org/images/entities/i_char_0064_0304.gif) AA = 1.85 (nm) in clear disagreement with the experimental results in Table 3. The solution for qT = 4 brings both results to agreement.
AA = 1.85 (nm) in clear disagreement with the experimental results in Table 3. The solution for qT = 4 brings both results to agreement.
The Li3Bi at qT = 0 has a very low monomer packing fraction ηu and it is very far from equilibrium, see Fig. 8. Even with reasonable variations of the potential, this BNSL cannot become equilibrium with a trivial topological index. The OTM solution makes use of eqn (28), which gives ![[small gamma, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0c4.gif) = 0.34, 0.35*, with results quoted in the table. As noted in experiment, the actual monomer packing fraction is very high (close to 0.9), in contrast with the nominal HS packing fraction ηHS = 0.54.
= 0.34, 0.35*, with results quoted in the table. As noted in experiment, the actual monomer packing fraction is very high (close to 0.9), in contrast with the nominal HS packing fraction ηHS = 0.54.
The bccAB6 BNSL is not the equilibrium for qT = 0, but rather, the competing CaB6 phase is. However, the latter does not admit non-trivial OTM solutions while the bccAB6 phase does. Given that the non-trivial OTM solution has much lower vdW attraction, the bccAB6 phase should become equilibrium in agreement with experiments. The results quoted in the table fully support this statement, although, admittedly, a rigorous proof will require a free energy calculation, which is not developed in this paper.
The AuCu phase at γ = 0.58 imply ![[small gamma, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0c4.gif) = 1. For this value of γ = 0.58, the ligands for the B NCs are not fully compressed, which points to some inconsistency for this solution. Within the OTM, the AuCu consists of a cubic unit cell with
= 1. For this value of γ = 0.58, the ligands for the B NCs are not fully compressed, which points to some inconsistency for this solution. Within the OTM, the AuCu consists of a cubic unit cell with ![[d with combining macron]](https://www.rsc.org/images/entities/i_char_0064_0304.gif) AA = 0.3 nm within the basal plane (perpendicular to the c-axis) and a c-axis length of 10.2 nm in reasonable agreement with the 10.6 nm value quoted by the experiment results13 (Fig. S10 in supplementary information). The resulting monomeric packing fraction is ηu > 1, which strongly suggests that ligands were lost during or before the measurement process. The PbS NCs have ligands bound to both the {111} and {100} planes, and different calculations24,34 show a much weaker binding to the latter, which may result in desorption during sample preparation after successive washing steps. Further evidence for ligand desorption is provided in ref. 7, where AuCu BNSLs are observed to display orientational core–core registry, as shown by lobes in the wide-angle electron diffraction.
AA = 0.3 nm within the basal plane (perpendicular to the c-axis) and a c-axis length of 10.2 nm in reasonable agreement with the 10.6 nm value quoted by the experiment results13 (Fig. S10 in supplementary information). The resulting monomeric packing fraction is ηu > 1, which strongly suggests that ligands were lost during or before the measurement process. The PbS NCs have ligands bound to both the {111} and {100} planes, and different calculations24,34 show a much weaker binding to the latter, which may result in desorption during sample preparation after successive washing steps. Further evidence for ligand desorption is provided in ref. 7, where AuCu BNSLs are observed to display orientational core–core registry, as shown by lobes in the wide-angle electron diffraction.
5 Conclusions
In this paper I have introduced the orbifold topological model (OTM) which recognizes the role played by the topological defects associated to the capping ligand. The model provides detailed predictions on the structure of super-lattices and quantitatively describes the experimental data with excellent precision, as summarized in Table 3. In addition, the OTM provides clear explanations for a number of experimental observations:
• Lattices with non-trivial topological index qT > 0 dominate over competing phases with qT = 0 (such as bccAB6 over CaB6 or AuCu over CsCl)
• Lattices with low hard sphere packing may become equilibrium phases with maximal monomer packing fraction ηu (such as Li3Bi).
• Ligand reorganization is a factor that may determine equilibrium in some cases (such as AuCu).
The first statement follows from the fact that CaB6 and CsCl do not admit OTM solutions with non-trivial topological index, while both AuCu and bccAB6 do, and those solutions with non-trivial topological index have a much lower van der Waals energy, which generally determines the equilibrium state.26 The second statement has been illustrated with the Li3Bi case, see Table 3. It should be noted, however, that for such low nominal packing fraction phases to become equilibrium, those phases must have a large packing fraction maximum at some other value of ![[small gamma, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0c4.gif) = γc, see discussion in Section 4.
= γc, see discussion in Section 4.
Dynamical ligands and their effect on the phase diagram has recently been investigated in ref. 35. It has been shown that for two different Ag NCs coated with the same ligand, resulting phases are consistent with the HS model predictions, while for Ag NCs each coated with a different ligand other phases: CaB6, AuCu3 and DDQC were observed. It was argued that there is an exchange of ligands between NCs and that this process stabilizes those phases not present in the HS model phase diagram. Within this scenario, low packing fraction phases are interpreted as kinetically trapped during ligand exchange. The detailed predictions of the OTM model have shown excellent agreement with the experimentally observed NC distances, see Table 3. If ligand exchange would become a dominant process, those distances would differ very significantly from those predictions and I must conclude that for the Au, PbS and Fe2O3 NCs ligand exchange is not significant, except for the AuCu (PbS and Au NC) phase. Furthermore the OTM shows that low nominal packing fraction phases (Li3Bi) do not need to be metastable and can be equilibrium. Finally, as our previous results17,18 and this paper shows, the HS model does not provide a reliable description of BNSLs, as phase diagrams depend not only on γ, but on the characteristics of the ligand also. Of course, there is always the possibility that ligand exchange may be more relevant for specific Ag NCs (similarly as found for the {100} plane for PbS), but this will need to be substantiated with detailed atomistic studies, such as ref. 34.
The OTM also provides many other predictions that should be verifiable with current experimental techniques. For example, the actual ligand textures, with the ½-disclinations and the location of neutral lines, see Fig. 3 should be visible with microscopy techniques. Other predictions, such as the detailed NC separations within the unit cell for ligands with unsaturated hydrocarbons and others36 will be discussed elsewhere.
Because of the role played by topological defects, the OTM includes many body effects whenever the topological index qT is different from zero. It also generalizes two previous models, the optimal packing model (OPM)20 and the overlap cone model (OCM).23 The OTM reduces to the OCM for two isolated nanoparticles and to the OPM when nanoparticles have trivial topological index qT = 0. It is interesting to note that the OTM for qT = 0 basically predicts the same equilibrium phases, see Fig. 6, as found with inverse power law potentials17,18 and with similar inconsistencies: absence of low packing fraction phases and the predominance of some phases such as CsCl over AuCu or CaB6 over bccAB6. This probably points out to the limitations of “universal” approaches, which cannot account for the nuances in the structure of the ligands.
Certainly, the role of topological defects, the interactions of neutral lines, see Fig. 3, and the precise structure of the corresponding ligand textures will require a more detailed and quantitative analysis. There are here other possibilities that I have not discussed in this paper. For example, how ½ disclinations might split into defects with lower charges or the role of anti-defects. Also, the case of topological index qT = 3, which may become relevant for some BNSLs, such as the NaZn13 or AlB2 and last, but not least, the necessary free energy for a rigorous quantitative analysis, will be discussed with full detail in the near future. This last part serves to emphasize the role of softness, as it has been discussed with simpler binary mixtures models of colloids.37,38
In summary, the OTM is a significant progress towards a prediction of the structure in nanoparticle superlattices and reveals fascinating relations between packing of hard spheres, lattice structure, geometry and topology.
Acknowledgements
I am indebted to M. Boles for many clarifications of the experimental results and existing literature of BNSLs. I also acknowledge interest and discussions with C. Calero, N. Horst, O. Gang, S. Mallapragada, D. Talapin and D. Vaknin. I want to thank T. Kennedy for many discussions and encouragement during the course of this work. This work is supported by the U.S. Department of Energy (DOE), Office of Science, Basic Energy Sciences, Materials, Materials Science and Engineering Division. The research was performed at the Ames Laboratory, which is operated for the US DOE by Iowa State University under contract number DE-AC02-07CH11358.
References
- S. Y. Park, A. K. R. Lytton-Jean, B. Lee, S. Weigand, G. C. Schatz and C. A. Mirkin, Nature, 2008, 451, 553–556 CrossRef CAS PubMed.
- D. Nykypanchuk, M. M. Maye, D. van der Lelie and O. Gang, Nature, 2008, 451, 549–552 CrossRef CAS PubMed.
- R. J. Macfarlane, B. Lee, M. R. Jones, N. Harris, G. C. Schatz and C. A. Mirkin, Science, 2011, 334, 204–208 CrossRef CAS PubMed.
- M. T. Casey, R. T. Scarlett, W. Benjamin Rogers, I. Jenkins, T. Sinno and J. C. Crocker, Nat. Commun., 2012, 3, 1209 CrossRef PubMed.
- R. L. Whetten, M. N. Shafigullin, J. T. Khoury, T. G. Schaaff, I. Vezmar, M. M. Alvarez and A. Wilkinson, Acc. Chem. Res., 1999, 32, 397–406 CrossRef CAS.
- E. V. Shevchenko, D. V. Talapin, N. A. Kotov, S. O'Brien and C. B. Murray, Nature, 2006, 439, 55–59 CrossRef CAS PubMed.
- E. V. Shevchenko, D. V. Talapin, C. B. Murray and S. O'Brien, J. Am. Chem. Soc., 2006, 128, 3620–3637 CrossRef CAS PubMed.
- D. V. Talapin, J.-S. Lee, M. V. Kovalenko and E. V. Shevchenko, Chem. Rev., 2009, 110, 389–458 CrossRef PubMed.
- X. Ye, J. Chen and C. B. Murray, J. Am. Chem. Soc., 2011, 133, 2613–2620 CrossRef CAS PubMed.
- C. Knorowski and A. Travesset, Curr. Opin. Solid State Mater. Sci., 2011, 15, 262–270 CrossRef CAS.
- S. Angioletti-Uberti, B. M. Mognetti and D. Frenkel, Phys. Chem. Chem. Phys., 2016, 18, 6373–6393 RSC.
- M. J. Murray and J. V. Sanders, Philos. Mag. A, 1980, 42, 721–740 CrossRef CAS.
- M. A. Boles and D. V. Talapin, J. Am. Chem. Soc., 2015, 137, 4494–4502 CrossRef CAS PubMed.
- M. D. Eldridge, P. A. Madden and D. Frenkel, Nature, 1993, 365, 35–37 CrossRef CAS.
- N. Hunt, R. Jardine and P. Bartlett, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 2000, 62, 900–913 CrossRef CAS.
- A. Travesset, J. Chem. Phys., 2014, 141, 164501 CrossRef PubMed.
- A. Travesset, Proc. Natl. Acad. Sci. U. S. A., 2015, 112, 9563–9567 CrossRef CAS PubMed.
- N. Horst and A. Travesset, J. Chem. Phys., 2016, 144, 014502 CrossRef PubMed.
- M. W. Matsen, Macromolecules, 2005, 38, 4525–4530 CrossRef CAS.
- U. Landman and W. D. Luedtke, Faraday Discuss., 2004, 125, 1–22 RSC.
- P. Schapotschnikow, R. Pool and T. J. H. Vlugt, Mol. Phys., 2007, 105, 3177–3184 CrossRef CAS.
- P. Schapotschnikow, R. Pool and T. J. H. Vlugt, Nano Lett., 2008, 8, 2930–2934 CrossRef CAS PubMed.
- P. Schapotschnikow and T. J. H. Vlugt, J. Chem. Phys., 2009, 131, 124705 CrossRef PubMed.
- S.-H. Choi, F. S. Bates and T. P. Lodge, Macromolecules, 2011, 44, 3594–3604 CrossRef CAS.
-
J. Israelachvili, Intermolecular and Surface Forces, Academic Press, London, 2000 Search PubMed.
- B. W. Goodfellow, Y. Yu, C. A. Bosoy, D.-M. Smilgies and B. A. Korgel, J. Phys. Chem. Lett., 2015, 6, 2406–2412 CrossRef CAS PubMed.
- R. L. B. Selinger, A. Konya, A. Travesset and J. V. Selinger, J. Phys. Chem. B, 2011, 115, 13989–13993 CrossRef CAS PubMed.
- D. R. Nelson, Nano Lett., 2002, 2, 1125–1129 CrossRef CAS.
- V. Vitelli and D. R. Nelson, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2006, 74, 021711 CrossRef CAS PubMed.
- Z. Chen, J. Moore, G. Radtke, H. Sirringhaus and S. O'Brien, J. Am. Chem. Soc., 2007, 129, 15702–15709 CrossRef CAS PubMed.
- T. I. Li, R. Sknepnek, R. J. Macfarlane, C. A. Mirkin and M. Olvera de la Cruz, Nano Lett., 2012, 12, 2509–2514 CrossRef CAS PubMed.
- H. Shin, M. J. Bowick and X. Xing, Phys. Rev. Lett., 2008, 101, 037802 CrossRef PubMed.
-
C. Tanford, The Hydrophobic effect: Formation of Micelles and Biological Membranes, John Wiley and Sons, 1980 Search PubMed.
- D. Zherebetskyy, M. Scheele, Y. Zhang, N. Bronstein, C. Thompson, D. Britt, M. Salmeron, P. Alivisatos and L.-W. Wang, Science, 2014, 344, 1380–1384 CrossRef CAS PubMed.
- J. Wei, N. Schaeffer and M.-P. Pileni, J. Am. Chem. Soc., 2015, 137, 14773–14784 CrossRef CAS PubMed.
- B. T. Diroll, K. M. Weigandt, D. Jishkariani, M. Cargnello, R. J. Murphy, L. A. Hough, C. B. Murray and B. Donnio, Nano Lett., 2015, 15, 8008–8012 CrossRef CAS PubMed.
- G. Cinacchi, Y. Martínez-Ratón, L. Mederos, G. Navascués, A. Tani and E. Velasco, J. Chem. Phys., 2007, 127, 214501 CrossRef PubMed.
- L. Rovigatti, N. Gnan, A. Parola and E. Zaccarelli, Soft Matter, 2015, 11, 692–700 RSC.
|
| This journal is © The Royal Society of Chemistry 2017 |
Click here to see how this site uses Cookies. View our privacy policy here. ![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) Hi}i=1…nH.
Hi}i=1…nH.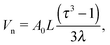
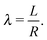
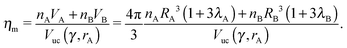
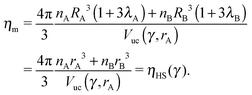
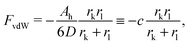
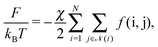
![[scr N, script letter N]](https://www.rsc.org/images/entities/char_e52d.gif) (i) runs over all NCs that are in physical contact with NC i and χ is a dimensionless coupling constant. As for the entropic hydrocarbon chain contribution, I assume that the approximation of modeling the NC as a deformable sphere already captures part of this contribution. More sophisticated free energies are available,26 but they will not be necessary for the goals of this paper, as the limitations of the OPM model in describing BNSLs are of a different nature, as I extensively discuss below. The function f(i,j) follows from eqn (9)
(i) runs over all NCs that are in physical contact with NC i and χ is a dimensionless coupling constant. As for the entropic hydrocarbon chain contribution, I assume that the approximation of modeling the NC as a deformable sphere already captures part of this contribution. More sophisticated free energies are available,26 but they will not be necessary for the goals of this paper, as the limitations of the OPM model in describing BNSLs are of a different nature, as I extensively discuss below. The function f(i,j) follows from eqn (9)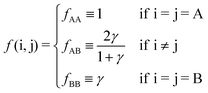
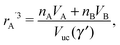
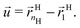
![[u with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0075_20d1.gif) is perpendicular to the core surface, thus defining a hedgehog structure. When interdigitation occurs the vector field
is perpendicular to the core surface, thus defining a hedgehog structure. When interdigitation occurs the vector field ![[u with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0075_20d1.gif) cannot be perpendicular to the surface, at least over a finite domain, as illustrated in Fig. 2. I find it useful to consider the projection of
cannot be perpendicular to the surface, at least over a finite domain, as illustrated in Fig. 2. I find it useful to consider the projection of ![[u with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0075_20d1.gif) to the tangent plane of the sphere
to the tangent plane of the sphere![[m with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006d_20d1.gif) =
= ![[scr P, script letter P]](https://www.rsc.org/images/entities/char_e52f.gif) S2
S2![[u with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0075_20d1.gif) ,
,![[m with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006d_20d1.gif) field in at least one NC will contain a topological defect located at their contact point, see Fig. 2. If there is more than one topological defect, then there maybe neutral lines, see Fig. 3 (left), where the ligands are perpendicular to the sphere, and the vector field
field in at least one NC will contain a topological defect located at their contact point, see Fig. 2. If there is more than one topological defect, then there maybe neutral lines, see Fig. 3 (left), where the ligands are perpendicular to the sphere, and the vector field ![[m with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006d_20d1.gif) is identical to zero.
is identical to zero.

![[u with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0075_20d1.gif) , given by
, given by ![[m with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006d_20d1.gif) as defined in eqn (16) becomes non-zero and defines a topological defect. NC A (left) has a topological index qT = 1 while NC B (right) has qT = 0.
as defined in eqn (16) becomes non-zero and defines a topological defect. NC A (left) has a topological index qT = 1 while NC B (right) has qT = 0.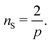
![[u with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0075_20d1.gif) is 3-dimensional, however, so it is possible to allocate an arbitrary number of vortices nS > 2, circumventing eqn (17) by separating vortices with neutral lines, as illustrated in Fig. 3A.
is 3-dimensional, however, so it is possible to allocate an arbitrary number of vortices nS > 2, circumventing eqn (17) by separating vortices with neutral lines, as illustrated in Fig. 3A.
![[m with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006d_20d1.gif) can be identified with its −
can be identified with its −![[m with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006d_20d1.gif) (as the direction can be changed along the neutral line), thus becoming an effective two dimensional nematic on a sphere, whose free energy is
(as the direction can be changed along the neutral line), thus becoming an effective two dimensional nematic on a sphere, whose free energy is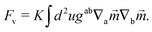
![[r with combining macron]](https://www.rsc.org/images/entities/i_char_0072_0304.gif) A,
A, ![[r with combining macron]](https://www.rsc.org/images/entities/i_char_0072_0304.gif) B of a given NCs within a unit cell as the smallest distance that maximizes ηm with the qT ≤ 4 constraint. I note that if the topological index is qT = 0, the chains must be all perpendicular to the sphere and the closest separation between two NCs is given by the OPM result. For two isolated NCs, the topological index is not restricted and the OTM and OCM results coincide. The OTM monomer packing fraction of a given BNSL is given as
B of a given NCs within a unit cell as the smallest distance that maximizes ηm with the qT ≤ 4 constraint. I note that if the topological index is qT = 0, the chains must be all perpendicular to the sphere and the closest separation between two NCs is given by the OPM result. For two isolated NCs, the topological index is not restricted and the OTM and OCM results coincide. The OTM monomer packing fraction of a given BNSL is given as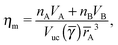
![[small gamma, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0c4.gif) ) ≤ ηm ≤ 1. The interparticle distances are also in between the OCM and OPM results, namely
) ≤ ηm ≤ 1. The interparticle distances are also in between the OCM and OPM results, namely![[s with combining macron]](https://www.rsc.org/images/entities/i_char_0073_0304.gif) kl ≤ skl.
kl ≤ skl.![[small gamma, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0c4.gif) is different than γ as defined by eqn (6), and is determined by the OTM radius
is different than γ as defined by eqn (6), and is determined by the OTM radius ![[r with combining macron]](https://www.rsc.org/images/entities/i_char_0072_0304.gif) A and
A and ![[r with combining macron]](https://www.rsc.org/images/entities/i_char_0072_0304.gif) B. In the results section I show how these considerations completely determine all NCs distances, coordination numbers and the monomeric packing fraction(density). I emphasize that although for qT = 0 the NC interacting potential is two body (as it is defined by eqn (9)), for qT ≠ 0, the model includes many body effects.
B. In the results section I show how these considerations completely determine all NCs distances, coordination numbers and the monomeric packing fraction(density). I emphasize that although for qT = 0 the NC interacting potential is two body (as it is defined by eqn (9)), for qT ≠ 0, the model includes many body effects.
![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m
m![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m
m![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m
m![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m
m
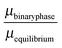
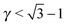 , the AuCu phase is, in reality, a CsCl.17 The prediction for γ = 0.77 shows only one equilibrium binary phase MgZn2/MgCu2 (within the free energy eqn (10) the chemical potential is the same for both), which is among the ones reported experimentally. Two more phases: Cr3Si and CaCu5 are close to being equilibrium, but only the CaCu5 phase is experimentally reported. If one where to assume, without any evidence, that the Cr3Si might be a difficult phase to nucleate, the results seem in excellent agreement with the experiments at γ = 0.77. It should be noted, however, that experiments for the MgZn2 phase report a NC radius that is 15% lower than the one predicted for qT = 0 eqn (5), clearly pointing to a more nuanced scenario than the qT = 0 predicts.
, the AuCu phase is, in reality, a CsCl.17 The prediction for γ = 0.77 shows only one equilibrium binary phase MgZn2/MgCu2 (within the free energy eqn (10) the chemical potential is the same for both), which is among the ones reported experimentally. Two more phases: Cr3Si and CaCu5 are close to being equilibrium, but only the CaCu5 phase is experimentally reported. If one where to assume, without any evidence, that the Cr3Si might be a difficult phase to nucleate, the results seem in excellent agreement with the experiments at γ = 0.77. It should be noted, however, that experiments for the MgZn2 phase report a NC radius that is 15% lower than the one predicted for qT = 0 eqn (5), clearly pointing to a more nuanced scenario than the qT = 0 predicts.


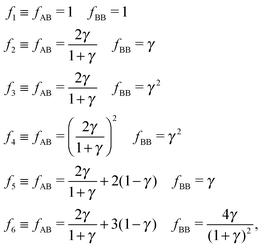

![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m
m![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m
m![[4 with combining macron]](https://www.rsc.org/images/entities/char_0034_0304.gif) 3m
3m![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m
m![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m
m![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m
m![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m
m![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m
m![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) n
n![[4 with combining macron]](https://www.rsc.org/images/entities/char_0034_0304.gif) 3m
3m![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) n
n![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m
m![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m
m![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m
m![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m
m . At this value there are A–A and B–B contacts, but no A–B contacts. For
. At this value there are A–A and B–B contacts, but no A–B contacts. For ![[small gamma, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0c4.gif) < γc, the shortest separation within B-particles is given as
< γc, the shortest separation within B-particles is given as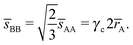
![[small gamma, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0c4.gif) < γc A–A hard spheres are in contact, with qAA = 4 and those are the NCs with qT = 4. Thus, for this lattice, OTM solutions will exist for
< γc A–A hard spheres are in contact, with qAA = 4 and those are the NCs with qT = 4. Thus, for this lattice, OTM solutions will exist for ![[small gamma, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0c4.gif) ≤ γc only.
≤ γc only.
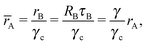
![[r with combining macron]](https://www.rsc.org/images/entities/i_char_0072_0304.gif) A becomes rA, as topology prevents the appearance of defects for six coordinated particles.
A becomes rA, as topology prevents the appearance of defects for six coordinated particles.
![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m (225) with a unit cell of four A-particles in Wyckoff positions 4a and twelve B-particles in positions 4b and 8c. If the A and B particles are hard spheres, the maximum packing fraction is reached for
m (225) with a unit cell of four A-particles in Wyckoff positions 4a and twelve B-particles in positions 4b and 8c. If the A and B particles are hard spheres, the maximum packing fraction is reached for 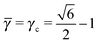 . At this value, there are A–A contacts and A–B contacts (the 4a particles touching the 8c particles). The shortest separation between A and B particles for
. At this value, there are A–A contacts and A–B contacts (the 4a particles touching the 8c particles). The shortest separation between A and B particles for ![[small gamma, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0c4.gif) > γc is given by
> γc is given by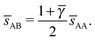
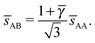
![[small gamma, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0c4.gif) > γc only. The corresponding nematic texture on each 8c NC also consists of four ½-disclinations sitting at the corners of a perfect tetrahedra. Here again, the A NC have q = 8 so their closest separation is given by the qT = 0 formulas. The smallest
> γc only. The corresponding nematic texture on each 8c NC also consists of four ½-disclinations sitting at the corners of a perfect tetrahedra. Here again, the A NC have q = 8 so their closest separation is given by the qT = 0 formulas. The smallest ![[s with combining macron]](https://www.rsc.org/images/entities/i_char_0073_0304.gif) AB distance will be given by
AB distance will be given by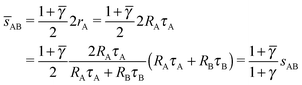
![[small gamma, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0c4.gif) is a free parameter, the optimal value would be
is a free parameter, the optimal value would be ![[small gamma, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0c4.gif) = γc, as this is the value that brings the NC the closest. However, the 4b B-particles have qT = 0. From eqn (26), it follows
= γc, as this is the value that brings the NC the closest. However, the 4b B-particles have qT = 0. From eqn (26), it follows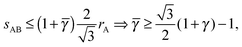
![[small gamma, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0c4.gif) . The formula for the monomer packing fraction reads
. The formula for the monomer packing fraction reads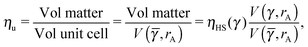
![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m (229) with a unit cell containing two A particles in Wyckoff positions 2a and twelve B particles in Wyckoff positions 12d. If the A and B particles are hard spheres, there are two maxima of the packing fraction. The first occurs at
m (229) with a unit cell containing two A particles in Wyckoff positions 2a and twelve B particles in Wyckoff positions 12d. If the A and B particles are hard spheres, there are two maxima of the packing fraction. The first occurs at 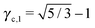 , and the second for
, and the second for 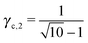 . If γc,1 <
. If γc,1 < ![[small gamma, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0c4.gif) < γc,2, the minimum A–B distance is given by
< γc,2, the minimum A–B distance is given by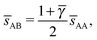
![[small gamma, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0c4.gif) > γc,2, it is given by
> γc,2, it is given by![[s with combining macron]](https://www.rsc.org/images/entities/i_char_0073_0304.gif) BB =
BB = ![[small gamma, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0c4.gif)
![[s with combining macron]](https://www.rsc.org/images/entities/i_char_0073_0304.gif) AA
AA![[small gamma, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0c4.gif) > γc,1. In all situations, qT = 0 for the A-particles. In the first branch γc,1 <
> γc,1. In all situations, qT = 0 for the A-particles. In the first branch γc,1 < ![[small gamma, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0c4.gif) < γc,2 the solution corresponds to B-particles with qT = 4. The four disclinations follow a distorted tetrahedra and the shortest separation among A–B NCs reads
< γc,2 the solution corresponds to B-particles with qT = 4. The four disclinations follow a distorted tetrahedra and the shortest separation among A–B NCs reads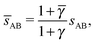
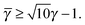
![[small gamma, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0c4.gif) > γc,2. In that case, contacts are among B-particles, and the analysis can be done along the same lines.
> γc,2. In that case, contacts are among B-particles, and the analysis can be done along the same lines.
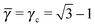 . At this value, each A particle is in contact with six other A-particles and eight B-particles, in a structure that is identical to CsCl. For
. At this value, each A particle is in contact with six other A-particles and eight B-particles, in a structure that is identical to CsCl. For ![[small gamma, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0c4.gif) > γc the shortest separation between A and B particles is given by
> γc the shortest separation between A and B particles is given by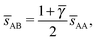
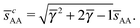
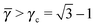 only.
only.
![[s with combining macron]](https://www.rsc.org/images/entities/i_char_0073_0304.gif) cAA = sAA = 2rA. Thus, from eqn (35), it follows
cAA = sAA = 2rA. Thus, from eqn (35), it follows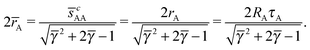
![[small gamma, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0c4.gif)
![[r with combining macron]](https://www.rsc.org/images/entities/i_char_0072_0304.gif) A ≥ rB = τBRB.
A ≥ rB = τBRB.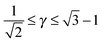 , which are shown in Fig. 10. At any other
, which are shown in Fig. 10. At any other  ,
, ![[small gamma, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0c4.gif) = 1, (the cubic AuCu) and the smallest A–A separation is given by
= 1, (the cubic AuCu) and the smallest A–A separation is given by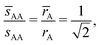

![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos(α/2) + r1 = 0.128n + 0.2 (in nm)
cos(α/2) + r1 = 0.128n + 0.2 (in nm)![[d with combining macron]](https://www.rsc.org/images/entities/i_char_0064_0304.gif) ij =
ij = ![[s with combining macron]](https://www.rsc.org/images/entities/i_char_0073_0304.gif) ij − Ri − Rj,
ij − Ri − Rj,![[d with combining macron]](https://www.rsc.org/images/entities/i_char_0064_0304.gif) ij is the quantity eqn (41) (in nm). For MgZn2 (i = A, j = B), Li3Bi (i = A, j = B), bccAB6 (i = A, j = B), AuCu (i = A, j = A). Experimental results marked with † were incorrect in the original reference and have been corrected
ij is the quantity eqn (41) (in nm). For MgZn2 (i = A, j = B), Li3Bi (i = A, j = B), bccAB6 (i = A, j = B), AuCu (i = A, j = A). Experimental results marked with † were incorrect in the original reference and have been corrected
![[d with combining macron]](https://www.rsc.org/images/entities/i_char_0064_0304.gif) ij
ij
![[d with combining macron]](https://www.rsc.org/images/entities/i_char_0064_0304.gif) AA = 1.85 (nm) in clear disagreement with the experimental results in Table 3. The solution for qT = 4 brings both results to agreement.
AA = 1.85 (nm) in clear disagreement with the experimental results in Table 3. The solution for qT = 4 brings both results to agreement.![[small gamma, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0c4.gif) = 0.34, 0.35*, with results quoted in the table. As noted in experiment, the actual monomer packing fraction is very high (close to 0.9), in contrast with the nominal HS packing fraction ηHS = 0.54.
= 0.34, 0.35*, with results quoted in the table. As noted in experiment, the actual monomer packing fraction is very high (close to 0.9), in contrast with the nominal HS packing fraction ηHS = 0.54.![[small gamma, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0c4.gif) = 1. For this value of γ = 0.58, the ligands for the B NCs are not fully compressed, which points to some inconsistency for this solution. Within the OTM, the AuCu consists of a cubic unit cell with
= 1. For this value of γ = 0.58, the ligands for the B NCs are not fully compressed, which points to some inconsistency for this solution. Within the OTM, the AuCu consists of a cubic unit cell with ![[d with combining macron]](https://www.rsc.org/images/entities/i_char_0064_0304.gif) AA = 0.3 nm within the basal plane (perpendicular to the c-axis) and a c-axis length of 10.2 nm in reasonable agreement with the 10.6 nm value quoted by the experiment results13 (Fig. S10 in supplementary information). The resulting monomeric packing fraction is ηu > 1, which strongly suggests that ligands were lost during or before the measurement process. The PbS NCs have ligands bound to both the {111} and {100} planes, and different calculations24,34 show a much weaker binding to the latter, which may result in desorption during sample preparation after successive washing steps. Further evidence for ligand desorption is provided in ref. 7, where AuCu BNSLs are observed to display orientational core–core registry, as shown by lobes in the wide-angle electron diffraction.
AA = 0.3 nm within the basal plane (perpendicular to the c-axis) and a c-axis length of 10.2 nm in reasonable agreement with the 10.6 nm value quoted by the experiment results13 (Fig. S10 in supplementary information). The resulting monomeric packing fraction is ηu > 1, which strongly suggests that ligands were lost during or before the measurement process. The PbS NCs have ligands bound to both the {111} and {100} planes, and different calculations24,34 show a much weaker binding to the latter, which may result in desorption during sample preparation after successive washing steps. Further evidence for ligand desorption is provided in ref. 7, where AuCu BNSLs are observed to display orientational core–core registry, as shown by lobes in the wide-angle electron diffraction.![[small gamma, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0c4.gif) = γc, see discussion in Section 4.
= γc, see discussion in Section 4.