Curing and viscoelasticity of vitrimers†
Frank
Snijkers
*a,
Rossana
Pasquino
b and
Alfonso
Maffezzoli
a
aDepartment of Engineering for Innovation, University of Salento, 73100 Lecce, Italy. E-mail: frank.snijkers@gmail.com
bDepartment of Chemical, Materials and Production Engineering, University of Napoli Federico II, 80125 Napoli, Italy
First published on 27th June 2016
Abstract
We present an experimental investigation of the curing kinetics and viscoelasticity for a number of “vitrimers” recently developed by Leibler and coworkers.1–3 Vitrimers are covalently crosslinked networks that can relax stress at elevated temperatures due to thermoreversible bond-exchange reactions. The chosen formulations are composed of diglycidyl ether of bisphenol A, commercial fatty acid mixtures and an appropriate catalyst. The effects of the catalyst and functionality of the curing agents on the kinetics of the curing reactions were systematically investigated using rheometry. The curing kinetics followed the Arrhenius law and the catalyst drastically accelerated the reactions. Time-temperature superposition was used to construct master curves of the small-strain amplitude oscillatory shear moduli over wide ranges of frequencies for the cured networks. Terminal relaxation was not reached in oscillatory experiments for temperatures up to 130 °C and creep and stress relaxation experiments were used to probe the long-time relaxation. The shift factors displayed a Williams–Landel–Ferry dependence on temperature which could be divided into two regions, one above 70 °C, where the dynamics appeared to be controlled by the catalyst, and one below, controlled by the monomeric friction and the free volume of the network. The moduli of the vitrimers obeyed the classical rubber theory well, indicating that the curing reactions proceeded to completion. Furthermore, we systematically and reproducibly observed a double relaxation behavior for the vitrimers, i.e. next to the rubbery plateau at high frequencies, the storage modulus displayed a secondary plateau at lower frequencies before reaching terminal relaxation at even lower frequencies. Interestingly, 70 °C was found to be the transition point in agreement with the shift factors. To the best of our knowledge, the double relaxation behavior has not been previously reported in experimental works and recent theories do not incorporate an explanation for this behavior. Consequently, future investigations concerning the viscoelasticity of other “vitrimer-chemistries” are important to assess if the double relaxation is a universal fingerprint for vitrimers or if it is specific to the here-investigated formulations based on commercial fatty acid mixtures.
I. Introduction
The interest in the effects of reversible interactions on the properties of polymers has greatly increased in recent years.1–27 The introduction of enthalpic interchain-interactions in polymers has great potential for technological applications as it provides sensitive routes to tune the physical properties and create smart materials via the manipulation of types, density and strength of interactions. The possible types of interactions vary from directional hydrogen bonding groups,4–7 to ionic aggregates8–11 and reversible covalent bonds.1–3,12–27 The classical division of polymeric materials in thermosets, with superior chemical stability, and mechanical and thermal properties, and thermoplastics, with the benefits of molten state processability and recyclability, is fading due to the possibility to bridge the gap between the two via the inclusion of reversible interactions. In terms of viscoelasticity, there are two key differences between the two classes: (1) above the glass transition temperature, thermoplastics display a certain temperature-dependent relaxation time with fluid behavior at long and elastic behavior at short times while thermosets display solid, “elastic” behavior at all accessible times and temperatures.28,29 (2) The order of magnitude of the stress relaxation modulus above the glass transition is lower for thermoplastics (of order 1 MPa or below depending on chemistry) as compared to thermosets (between 1 and 100 MPa depending on chemistry and crosslink density).28–30 Both differences relate directly to the processability of thermoplastics (1) and superior mechanical properties and stability of thermosets (2). Detailed studies of the viscoelasticity of novel materials with reversible interactions are consequently interesting as they allow for a direct assessment of the mechanical properties, relaxation and processability.Here, we focus on a subset of functional polymeric materials, so-called Covalent Adaptable Networks (CANs), i.e. crosslinked materials containing reversible covalent bonds.12,13 In the literature, several systems have been proposed following different ideas. One route concerns the inclusion of crosslinks via disulfide-bridges.14 The disulfide bonds can be reduced (to –SH) and oxidized using appropriate agents, thereby enabling a reversible control of the crosslink density and consequently processability, modulus and relaxation. Other systems are based on thermoreversible equilibrium reactions, such as the Diels–Alder reaction.15–18 In these materials, the equilibrium of the reaction (at the specific temperature) controls relaxation and processability. The materials typically “depolymerize” at elevated temperatures. Scott et al.19 showed that it is also possible to use photomediated exchange reactions (via addition-fragmentation using allyl sulfides as chain transfer agents) instead of thermoreversible equilibrium reactions to obtain CANs. Due to the existence of an intermediate state in the addition-fragmentation process, the topology of the network could rearrange upon radiation, while the network connectivity remained unaltered, i.e. without depolymerization. Later, Leibler and coworkers1–3 exploited the reversible transesterification reaction: RCOOR′ + R′′OH ⇄ RCOOR′′ + R′OH. Transesterification is known to proceed via an intermediate state, including both the original ester and the hydroxyl-function, before a new ester bond can emerge (based on the latter hydroxyl-function).1,31 Consequently, the ester bonds can exchange without breaking. The principle was proved by using epoxy networks based on di- and tri-functional carboxylic acids and diglycidyl ether of biphenol A (DGEBA).1 The exchange reactions could be thermally activated and controlled by different catalysts.3 The materials were termed “vitrimers”.1 Several other systems have been proposed since 2011 and the current state-of-the-art is reviewed in ref. 20. There are now vitrimers based on polylactide,21 epoxised soybean oil and aqueous citric acid,22 vinylogous urethane (based on transamination reactions),23 polyhydroxyurethane (transcarbamoylation),24 triazolium salts (transalkylation)25 and polybutadiene (olefin metathesis; exchange reactions of carbon–carbon double bonds).26,27 The above-mentioned studies are mainly focused on the chemistry and resulting material properties (ability to self-heal, insolubility, processing and ability to relax stress). In terms of viscoelasticity, most of the above-mentioned papers1,3,21–27 report renormalized stress relaxation curves at temperatures far above the glass transition to evidence the eventual relaxation of the networks and prove the “vitrimer-concept”. An Arrhenius-like dependence of the viscosity has typically been reported at temperatures far above the glass transition. We have only been able to find one more in-depth experimental study focused on the dynamic properties reported by Yu et al.32 They found a clear linear relation between the high temperature flow activation energy and the glass transition temperature in their study of different vitrimers based on mixtures of two curing agents, a flexible one and a more stiff one at fixed catalyst content.32 Finally, there have been several theoretical33–36 and simulation37 works concerning the dynamics, bond-exchange and self-healing of vitrimers.
In this work, we attempt to pinpoint the exact viscoelastic fingerprint of the vitrimers over wider ranges of compositions, temperatures and frequencies. To this end, we report upon an investigation of a specific set of vitrimers with systematic variations in the formulation. The chemicals, preparation and composition of the investigated samples are discussed in Section II together with the experimental methods. The results of the curing and gelation behavior of the samples and the viscoelastic master curves of the cured samples are shown in Section III. In Section IV, the experimental results are discussed and finally, in Section V, the findings are summarized.
II. Materials and methods
II.1. Materials and sample preparation
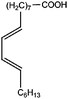
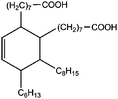
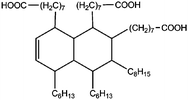
All materials are commercially available and were used as received without further purification following ref. 1–3. The resin, diglycidyl ether of bisphenol A (DGEBA), was obtained from Elantas Camattini (Italy). Grade EC01 was chosen with an epoxy equivalent molar mass between 184 and 190 g molEPOXY−1 (as certified by the manufacturer). We further used the average value of 187 g molEPOXY−1 for the calculations in Section IV. The catalyst, zinc acetate dihydrate Zn(OAc)2·2H2O, was bought from Sigma-Aldrich. As curing agents, three different types of commercial fatty acid mixtures were kindly provided by Croda Europe (the Netherlands). The three mixtures, Pripol-1040, 1025, and 1252, differ in their relative amounts of mono-, di- and tri-functional carboxylic acids, as indicated in Table 1. From left to right, Table 1 lists the commercial product number of the Pripol, the equivalent molar mass per carboxyl group, the composition of the different Pripols in percentage of mono-, di- and tri-acids, and finally the calculated mass average functionality 〈f〉 of the samples. The molecular formulas of the mono-, di- and tri-acids are shown in the last row of Table 1. All information in Table 1 was provided by the manufacturer. The molar masses Mf can be calculated from the molecular formulas and this results in 281, 561, and 842 g mol−1 for the mono-, di-, and tri-functional acids, respectively. Important to note is the discrepancy between the latter values, which all lead to a theoretical equivalent molar mass per carboxyl function of 281 g mol−1 and the experimentally determined values in column 2 (supplied by the manufacturer). This indicates that some of the fatty acids are imperfect (∼5%), possibly due to the loss of a carboxylic acid function.Following ref. 1–3, the catalyst was first solubilized in the fatty acid mixtures. The catalyst was mixed in the Pripol and slowly heated from 100 to 180 °C while vigorously stirring and increasingly strong vacuum. Acetic acid gas develops during this process indicating that the fatty acids replace the acetates as ligands of zinc. The mixture was considered ready when the gas development stopped which could take up to 6 hours. The so-prepared mixtures of Pripol with catalysts are termed Hardener-1040, 1025, and 1252. All contain 7.5 mol% of catalyst per mol COOH-groups and they are all prepared similarly. Subsequently, the hardener mixtures are mixed by hand in different proportions with the epoxy resin. For each experiment, fresh samples were prepared as the curing reaction also proceeds (very slowly) at room temperature. The thermal history has furthermore been closely controlled during the curing of the samples on the rheometer, as for these reactive materials reproducibility is intrinsically difficult.38–40
In terms of composition, we studied epoxy/acid networks at stoichiometric ratios of the carboxyl to epoxy groups of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 with the three different curing agents and also for mixtures with pure Pripol, i.e. without catalyst. The list of studied samples is shown in Table 2. The first column reports the sample code, the second the curing agent, and the third the ratio of tri-acids to epoxy groups. The first three samples with vitrimer in their coding contain 7.5 mol% catalyst per carboxyl group as discussed in Section II.1, while the last sample with Network in its coding does not contain any catalyst. Sample “vitrimer-2.10” has been investigated most extensively and can be seen as the reference sample. The sample coding indicates the composition with the numbers corresponding to the average functionalities of the Pripols (Table 1).
1 with the three different curing agents and also for mixtures with pure Pripol, i.e. without catalyst. The list of studied samples is shown in Table 2. The first column reports the sample code, the second the curing agent, and the third the ratio of tri-acids to epoxy groups. The first three samples with vitrimer in their coding contain 7.5 mol% catalyst per carboxyl group as discussed in Section II.1, while the last sample with Network in its coding does not contain any catalyst. Sample “vitrimer-2.10” has been investigated most extensively and can be seen as the reference sample. The sample coding indicates the composition with the numbers corresponding to the average functionalities of the Pripols (Table 1).
| Sample code | Hardener | TRI-f/EPOXY |
|---|---|---|
| Vitrimer-2.76 | Hardener-1040 | 0.76 to 1 |
| Vitrimer-2.10 | Hardener-1025 | 0.20 to 1 |
| Vitrimer-1.75 | Hardener-1252 | 0.11 to 1 |
| Network-2.10 | Pripol-1025 | 0.20 to 1 |
II.2. Methods: rheometry and differential scanning calorimetry
The curing kinetics and viscoelasticity were mainly studied using a stress-controlled Bohlin-rheometer (CVO 100, Malvern Instruments, UK) equipped with a forced convection oven to control temperature with an accuracy of ±0.1 °C. In some limited cases, a strain-controlled Advanced Rheometric Expansion System (ARES, TA-Instruments, USA) equipped with a 2K force-rebalanced transducer (2K-FRT) and a forced convection oven was used. Measurements were generally performed between 20 and 130 °C with some selected experiments at 150 and 170 °C. Given the relatively mild temperatures, measurements were performed in air. Homemade parallel plate geometries with a diameter of 8 mm were used and the gap size was around 1 mm in all cases.Curing was studied using dynamic oscillatory measurements with a small-strain amplitude of 1% at a fixed angular frequency of 1 rad s−1 to monitor the changes in the moduli of the samples as a function of time and temperature. Heating ramps were always performed starting from 30 °C with a heating rate of 3 °C min−1 up to the chosen curing temperature. During the heating ramp the thermal expansion of the plates was taken into account by making the appropriate changes in gap size. A relatively slow heating rate of 3 °C min−1 was chosen to ensure the thermal homogeneity of the samples while being sufficiently fast to allow them to reach their curing temperatures well before gelation. This procedure enabled a study of the effects of formulation and curing temperature on the gelation time under essentially isothermal conditions, with a negligible effect of the heating ramp.
The viscoelastic properties, i.e. the elastic G′ and loss G′′ moduli as a function of angular frequency ω, were measured using small-strain amplitude oscillatory shear measurements at different temperatures. The linearity of the measurements was checked by performing strain sweeps, i.e. measurements of the dynamic moduli as a function of strain amplitude at a fixed frequency. Also here, the gap size was adjusted to account for the thermal expansion of the plates. The resulting frequency sweeps were combined by shifting them towards a chosen reference temperature Tref to create master curves using time-temperature superposition.41 First, the moduli were shifted vertically. The vertical shift factors bT are expected to follow:41
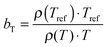 | (1) |
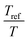 . The error introduced by neglecting the temperature dependence of the density is nevertheless small and the applied vertical shift factors were in all investigated cases between 0.8 and 1.2 over the full range. Next, the moduli were shifted along the frequency axis by a least-square minimization method using the RSI-Orchestrator software (TA-instruments, USA). At temperatures above the glass transition temperature Tg, the horizontal shift factors aT for polymers and networks can generally be described with the Williams–Landel–Ferry (WLF) equation:41
. The error introduced by neglecting the temperature dependence of the density is nevertheless small and the applied vertical shift factors were in all investigated cases between 0.8 and 1.2 over the full range. Next, the moduli were shifted along the frequency axis by a least-square minimization method using the RSI-Orchestrator software (TA-instruments, USA). At temperatures above the glass transition temperature Tg, the horizontal shift factors aT for polymers and networks can generally be described with the Williams–Landel–Ferry (WLF) equation:41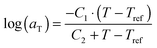 | (2) |
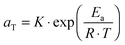 | (3) |
Terminal relaxation was not reached in the dynamic oscillatory tests and the frequency axis was extended by performing long-time stress relaxation and creep experiments. These tests generally took three hours and were performed at 130 °C. The linearity of the stress relaxation modulus was ensured by performing tests with different values for the step-strain. Generally, step-strains of 1% were found to be in the linear regime. The linearity of the creep experiments was checked by performing tests with different values for the creep stress. Stresses of order 100 Pa were found to be in the linear regime. The conversion of the relaxation modulus G(t) to the dynamic moduli was performed using NLReg.42 The conversion of the creep compliance J(t) to the dynamic moduli is known to be more problematic.43,44 We performed the conversions with both NLReg42 and the method of Schwarzl43 (as in ref. 44). The difference between the elastic modulus G′ obtained from the conversions with the one from the frequency sweep was always within 10% over the complete overlapping frequency regions. We further compared the relaxation times from the converted data (defined as the inverse crossover frequencies of G′ and G′′) with the relaxation time defined as the time at which the creep compliance has increased with 30% from its plateau value. The latter time is prone to error due to the lack of a truly constant plateau, but nevertheless, these times compare within a factor of 2. Finally, the dynamic moduli from the converted creep or stress relaxation tests were shifted to the reference temperature, using the shift factors obtained from the time-temperature superposition.
The glass transition temperatures Tg of the networks were measured after the rheological measurements using a Differential Scanning Calorimeter (DSC TW60, Shimadzu Scientific Instruments, Japan) equipped with a Peltier element. The glass transition temperatures were determined by performing several heating/cooling cycles at rates of 10 °C min−1. The measured Tg values were in the range between −15 and 25 °C and were extracted from the data obtained during the second heating ramp as the midpoints of the heat capacity changes.
III. Experimental results and discussion
III.1. Curing and gelation
Representative curing curves obtained with the Bohlin for the vitrimer-2.10 (Table 2) are shown in Fig. 1a. The elastic and loss moduli obtained at 1 rad s−1 with a strain of 1% are shown as a function of time for the vitrimer-2.10 for different curing temperatures from 90 to 150 °C. We checked the potential strain-dependence of the curing kinetics to ensure that the strain of 1% was in the linear regime. We found no strain-dependence and an identical gelation time (within 10%) for a strain of 5%. At short times, the moduli do not appear in Fig. 1a because measurements were performed with geometries with a diameter of 8 mm and, at short times, the samples were low viscous fluids, resulting in torques below the sensitivity limit of the rheometer (∼50 Pa for 8 mm plates). For this reason, the lower limit of the y-axis in Fig. 1a is set to 100 Pa. Samples were freshly prepared before each measurement. The temperature ramp was always initiated from 30 °C with a heating rate of 3 °C min−1, leading to ramp times of maximally 40 min. The samples slowly evolved from a liquid (G′′ > G′) to a gel (G′ ≈ G′′) and then to a solid state (G′ > G′′). The evolution is faster with increasing temperature. The gelation time was taken at the crossover point (G′ = G′′).38–40,45,46 This definition is only strictly valid for balanced stoichiometries as shown in the seminal works of Winter and coworkers.38–40 We always aimed to obtain balanced stoichiometries (as calculated from the functionalities of the chemicals1–3) and we hence assume that this definition is exact. The main issue with this definition is that it ignores the existence of side-reactions and “imperfections” of the commercial reagents. A variety of slow side-reactions are known for epoxy/acid compounds,2,30,47,48 although it has been reported that the addition of a catalyst, such as the one we employed, favors the main reaction of carboxylic acid on epoxy groups over the possible side-reactions.2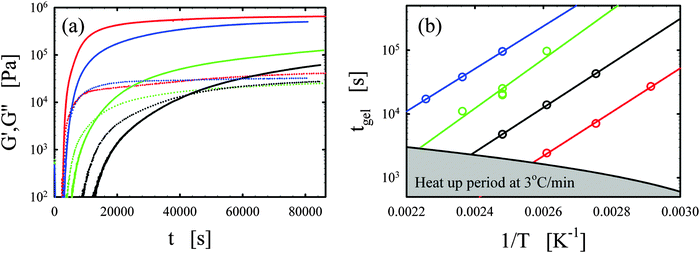 | ||
| Fig. 1 (a) Elastic G′ (full lines) and loss G′′ (dotted lines) moduli as a function of time t for different curing temperatures of 90, 110, 130, and 150 °C are shown in black, green, blue, and red, respectively for the vitrimer-2.10 (Table 2). (b) Gelation time tgel as a function of inverse curing temperature 1/T [K−1] is shown for the vitrimer-1.75 (green), vitrimer-2.10 (black), vitrimer-2.76 (red), and network-2.10 (blue) (Table 2). Lines are fits following eqn (4). | ||
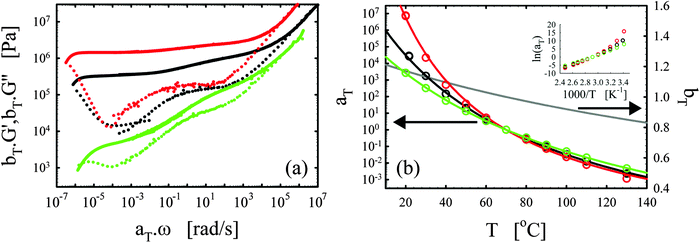
We consistently obtained the gelation time tgel for all formulations and varying curing temperatures. In some cases, the gelation point occurred below the limit of the rheometer and slight extrapolation was necessary. Extrapolation was performed by fitting straight lines to the log(G′) and log(G′′) versus time curves in the region close to the gelation point. The gelation time is plotted as a function of inverse absolute temperature in Fig. 1b. The experimental data were fitted with Arrhenius relations:45,46,48
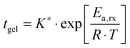 | (4) |
III.2. Viscoelasticity of the cured networks
After a certain curing period of about one day at 130 °C, the oscillatory data were collected at different temperatures and the master curves were constructed using the time-temperature superposition as discussed in Section II.2. The exact curing times are collected in the legend of Fig. 2a. Although the samples are never absolutely stable at elevated temperatures, we found that, after a curing time of one day at 130 °C, the slow remaining evolutions of the moduli over time were negligible over the long experimental time periods to obtain the master curves (about 10 hours). This is further evidenced by the reproducibility and the overlap of the converted long-time creep data with the oscillatory data and also by the overlap of frequency sweeps obtained at different points in time for the same sample at 130 °C. The results, i.e. the master curves of the storage G′ and loss G′′ moduli as a function angular frequency ω at a reference temperature Tref of 70 °C, are shown in Fig. 2a with full and dotted lines, respectively, for four different vitrimer-2.10 samples. The corresponding van Gurp-Palmen plots of the phase angle δ = arctan (G′′/G′) as a function of the complex modulus G* = (G′2 + G′′2)0.5 are shown in the ESI† (Fig. S1a). The samples did not reach their terminal relaxation regime in the frequency window (from 0.1 to 100 rad s−1) of the dynamic oscillatory tests at 130 °C. To extend the frequency axis, we performed creep experiments with the Bohlin and stress relaxation experiments with the ARES at 130 °C and we converted the resulting creep compliance J(t) and stress relaxation modulus G(t) to the dynamic moduli as discussed in Section II.2. The results were then shifted to 70 °C using the shift factors obtained from the time-temperature superposition of the oscillatory data. The results from the conversion of the creep data are shown with black dashed and dash-dotted lines and those from the conversion of the stress relaxation data with red dashed and dash-dotted lines in Fig. 2a. The reproducibility of the master curves in Fig. 2a is relatively good, but imperfect. The samples corresponding to the green and blue curves were furthermore prepared and measured several months before the ones represented by the black and red curves. Furthermore, one can observe that the full dynamic regime from the high-frequency crossover (towards the glass transition) to the low-frequency crossover (towards terminal relaxation) was captured and that it is exceptionally large, i.e. almost 14 decades in frequency. Finally, we observe a peculiar, reproducible “double relaxation behavior” with two apparent plateau moduli, one at high and one at low frequencies.
 | ||
| Fig. 2 Reproducibility of the viscoelasticity of vitrimer-2.10 (Table 2). (a) Full and dotted lines represent the master curves of the oscillatory data at Tref = 70 °C of G′ and G′′, respectively. Dashed (G′) and dash-dotted (G′′) lines result from the conversion of stress relaxation (red) and creep data (black). Samples were cured at 130 °C. Green: on Bohlin for 22.4 hours; blue: on ARES for 21.5 hours; black: on Bohlin for 23.9 hours; red: on ARES for 23.8 hours. (b) aT (symbols) and bT (dark grey line) as a function of T [°C]. The black and light grey lines are fits of the aT values with eqn (2) and (3), respectively. Inset: Arrhenius plot, ln(aT) versus 1000/T [K−1]. | ||
The horizontal aT and vertical bT shift factors as a function of temperature T [°C] are shown in Fig. 2b. The aT values were fitted with a WLF-equation (eqn (2); black line). We found a value of 9.0 for C1 and 150 °C for C2 at Tref = 70 °C. The inset in Fig. 2b shows the natural logarithm of the aT values as a function of the inverse absolute temperature [K−1]. This plot allows for a visual assessment of the validity of the Arrhenius law (eqn (3)) as Arrhenius predicts a linear dependence. One can clearly observe that Arrhenius is not valid over the full temperature range, but only for T > 70 °C. The resulting flow activation energy Ea is 120 kJ mol−1 and the fit is shown with a light grey line in Fig. 2b. The glass transition temperatures Tg of the four samples varied between 4.8 and 6.6 °C with an average and standard deviation of 6 ± 1 °C. We further used the black dataset from Fig. 2 as reference for the viscoelasticity of the vitrimer-2.10.
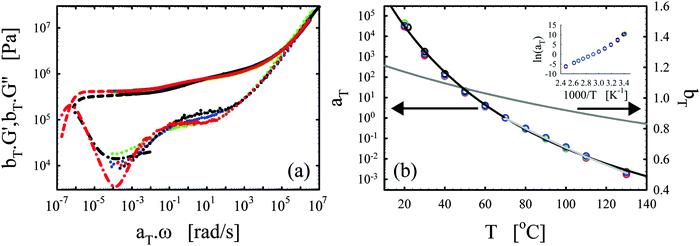
 | ||
| Fig. 3 Effects of the catalyst. (a) Master curves of G′ (full lines) and G′′ (dotted lines) as a function of ω at 70 °C for vitrimer-2.10 (cured for 23.9 hours at 130 °C) in black and network-2.10 (cured for 115 hours at 130 °C) in blue. (b) aT (symbols) and bT (grey line) as a function of T [°C]. Lines are fits of aT with eqn (2). Inset: Arrhenius plot, ln(aT) versus 1000/T [K−1]. | ||
The elastic modulus of the network-2.10 without catalyst is essentially constant over the full frequency range below the transition region (ω < 104 rad s−1), as expected for a thermoset material.28,29 The vitrimer-2.10 on the other hand displays a double relaxation behavior and a transition towards a flow regime at the lowest frequencies. One can further note that, at frequencies around ω ∼ 103 rad s−1, the elastic moduli of both samples are nearly identical as expected because the functionalities of the involved chemicals (and hence the crosslink densities) are identical. The slightly higher modulus of the network is probably a consequence of the absence of a catalyst and necessary extended curing time for the network. Under these conditions, slow side-reactions, such as the etherification of the hydroxyl group on the DGEBA with an epoxy group,2,30,48 can have a significant influence on the results. The etherification reaction indeed increases the average functionality of the epoxy resin somewhat above two, which hence leads to a higher crosslink density and modulus. For the vitrimer, the catalyst is known to suppress possible slow side-reactions.2,30,48 Examination of Fig. 3b shows that the aT values of the vitrimer-2.10 display a significantly stronger dependence on temperature above 70 °C, while below they are nearly identical to those of the network-2.10. The transition from the primary high-frequency plateau to the secondary low-frequency plateau for the vitrimer occurs also at 70 °C, i.e. around ω ∼ 1 rad s−1. Consequently, the catalyst for the transesterification reaction seems to become active around 70 °C, thereby inducing bond reversibility and dynamics in the system at higher temperatures.
The horizontal shift factors aT of the network-2.10 were fitted with a WLF-equation (eqn (2); blue line in Fig. 3b). At Tref = 70 °C, we found values of 4.4 and 93 °C for C1 and C2, respectively. The inset in Fig. 3b shows the natural logarithm of the aT values as a function of the inverse absolute temperature to allow for a visual assessment of the validity of the Arrhenius law (eqn (3)) as in Section III.2.1. Also for network-2.10, the aT values can be described with an Arrhenius equation for T > 70 °C leading to a flow activation energy Ea of 75 kJ mol−1 (compared to 120 kJ mol−1 for the vitrimer-2.10). The Tg of network-2.10 was measured to be 12 °C, slightly larger than 6 °C of the vitrimer-2.10. Tg is expected to increase with crosslink density and a “Fox-Flory”-type28 relationship between Tg and 1/S (with S the average molar mass between crosslinks) is often found over certain ranges of crosslink densities.49 The larger Tg of the network-2.10 is hence in agreement with the potential larger crosslink density.
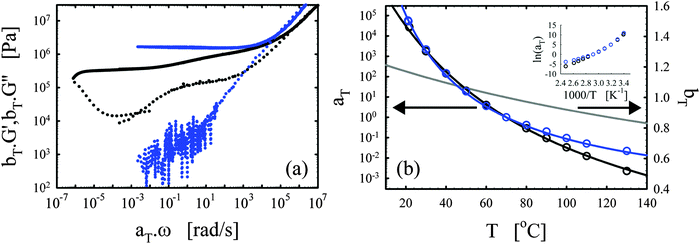
 | ||
| Fig. 4 Effects of the functionality. (a) Master curves of G′ (full lines) and G′′ (dotted lines) as a function of ω at 70 °C for the vitrimer-1.75 (green), vitrimer-2.10 (black), and vitrimer-2.76 (red) (Table 2). All were cured at 130 °C, the vitrimer-1.75 for 74.6 hours, and the vitrimer-2.10 and vitrimer-2.76 for 23.9 hours. (b) aT (symbols) and bT (grey line) as a function of T [°C]. Colored lines are fits of aT with eqn (2). Inset: Arrhenius plot, ln(aT) versus 1000/T [K−1]. | ||
Fig. 4a shows that the three samples display a transition towards terminal relaxation around a frequency of 10−6 rad s−1. Although this frequency slightly increases with crosslink density (from vitrimer-1.75 (green) to vitrimer-2.10 (black) to vitrimer-2.76 (red)), at first approximation the difference is negligible. This is in fact in agreement with expectations as the amount of catalyst is expected to be the key control parameter for the terminal relaxation.3 All three samples display a double relaxation behavior with two distinct plateau regions for G′, one at frequencies around ω ∼ 102 rad s−1 and one at frequencies around ω ∼ 10−4 rad s−1. Also this observation is, at first approximation, independent of formulation. Also the transition from the first to the second plateau around ω ∼ 10−1 rad s−1 is roughly independent of formulation. The aT values for the three samples are furthermore roughly identical at T > 70 °C, while they differ strongly at lower temperatures. It is in this respect interesting to compare Fig. 3b with Fig. 4b, in both graphs a “transition” can be observed around 70 °C. The bond-exchange reactions (controlled by the catalyst and its concentration) seem to control the temperature dependence of the viscoelasticity at T > 70 °C, while the details of the network (i.e. the functionality of the components and the resulting friction) control the temperature dependence at T < 70 °C. The aT values were fitted with WLF-equations (eqn (2); Fig. 3b). For Tref = 70 °C, we found C1 = 9.7 and C2 = 193 °C for vitrimer-1.75, C1 = 9.0 and C2 = 150 °C for vitrimer-2.10, and C1 = 7.4 and C2 = 105 °C for vitrimer-2.76. The inset in Fig. 4b shows ln(aT) as a function of 1/T [K−1] to allow for a visual assessment of the validity of the Arrhenius law (eqn (3)). Also here, for T > 70 °C, the aT values can be well-described with Arrhenius equations (eqn (3)) leading to flow activation energies Ea of 103, 120, and 130 kJ mol−1, for the vitrimer-1.75, vitrimer-2.10, and vitrimer-2.76, respectively. The Ea values hence display a slight systematic increase with functionality. The Tg values from DSC were found to be −11, 6, and 21 °C, for the vitrimer-1.75, vitrimer-2.10, and vitrimer-2.76, respectively. The variation in Tg is in agreement with the variation in crosslink density.49
IV. Discussion
The master curves of the moduli (Fig. 2a, 3a, and 4a) proof that time-temperature superposition works reasonably well for the investigated samples. A clear WLF-dependence of the shift factors is observed (Fig. 2b, 3b, and 4b). Table 3 collects some of the key observations. The sample codes are in column 1. Details of the compositions can be found in Tables 1 and 2. Column 2 shows the high-frequency plateau moduli of the samples G0,exp defined as the values of G′ at the high-frequency minima of their respective tan(δ) = G′′/G′. The values of the WLF-parameters at Tref = 70 °C are shown in columns 3 and 4. The flow-activation energies Ea as calculated using fits of the Arrhenius relations to the horizontal shift factors at T > 70 °C for the respective samples are collected in column 5. The Tg values are collected in column 6. Columns 7, 8, 9, and 10 contain the theoretical average molar mass between crosslinks S, the corresponding plateau moduli G0,the, the fractional free volume fg at Tg, and the thermal expansion of the free volume αf at Tg, respectively. Their calculation is detailed below.| Sample code | G 0,exp/105 [Pa] | C 1 [—] | C 2 [°C] | E a [kJ mol−1] | T g [°C] | S [kg mol−1] | G 0,the/105 [Pa] | f g [—] | α f × 104 [°C−1] |
|---|---|---|---|---|---|---|---|---|---|
| Vitrimer-1.75 | 2 | 9.7 | 193 | 103 | −11 | 6.6 | 4 | 0.026 | 2.3 |
| Vitrimer-2.10 | 9 ± 1 | 9.0 | 150 | 120 | 6 ± 1 | 4.4 | 7 | 0.028 | 3.2 |
| Vitrimer-2.76 | 23 | 7.4 | 105 | 130 | 21 | 1.2 | 24 | 0.031 | 5.6 |
| Network-2.10 | 15 | 4.4 | 93 | 75 | 12 | 4.4 | 7 | 0.037 | 10.6 |
Different theories exist that relate the modulus of an elastomer to its structural properties.50 Here, we utilize the most simple “Affine Network”-model from Kuhn, Wall and Flory50–52 to estimate the elastic modulus of the networks G0,the:
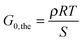 | (5) |
 | (6) |
The Tg values of the vitrimers display the expected increase with crosslink density, from vitrimer-1.75 to vitrimer-2.10 to vitrimer-2.76.49 Furthermore, network-2.10 has a higher Tg than vitrimer-2.10, for the same reasons discussed in the previous paragraph. Yu et al.32 reported a linear dependence of the high temperature flow-activation energies Ea on Tg upon systematically varying the flexibility of the curing agent. Following their work, we can note that also here the flow-activation energies of the vitrimers display a slight but systematic dependence on the glass transition temperature, and, although there are only three points, the variation can be accurately described with a linear equation (graph not shown, least-square error minimization leads to Ea = 113 + 0.847·Tg with Tg in °C and Ea in kJ mol−1). In this case, however, the difference between the vitrimers lies in the different molar mass between crosslinks as opposed to those in ref. 32 in which the flexibility of the hardener was responsible for the variation.
The fractional free volume fg (column 9 in Table 3) and the thermal expansion of the free volume αf at Tg (column 10) are calculated from the constants of the WLF-equation following ref. 41. The WLF-parameters (C1 and C2 in Table 3) are first shifted to Tg using 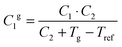 and Cg2 = C2 + Tg − Tref. Subsequently, fg and αf are calculated as:
and Cg2 = C2 + Tg − Tref. Subsequently, fg and αf are calculated as:
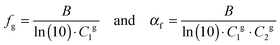 | (7) |
The relaxation time τ of the vitrimer-2.76 calculated from the data in Fig. 4a by taking the reciprocal of the low-frequency crossover (with G′ = G′′) is 3 × 106 s at 70 °C. In the literature,1,3,32 this chemistry has been investigated before, although those samples were based on a different epoxy resin and contained different amounts of catalyst. The relaxation time found in the literature1,3 was ∼3000 s at 150 °C at a catalyst content of 10% and a factor of 2 longer at 5%.3 The vitrimers studied here contain 7.5% of catalyst. Shifting our relaxation time to 150 °C using the WLF-equation leads to τ = 2000 s, slightly shorter but nevertheless of the same order as the relaxation times reported in the literature. Yu et al.32 quoted a value of 1300 s at 160 °C with a catalyst content of 5%. Shifting our time to 160 °C yields the same value, although our catalyst content is slightly different. The values for the flow-activation energies in the literature are between 70 and 90 kJ mol−1. They were obtained at high temperatures from 100 to 280 °C. We found a higher Ea of 130 kJ mol−1 with 70 < T < 130 °C for the vitrimer-2.76. The apparent flow activation energy as a function of temperature can be calculated from the WLF-equation as:41
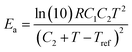 | (8) |
The shift factors of the vitrimers clearly display a WLF-dependence on temperature, as opposed to some statements (not with the observations) in the literature. In the literature, the temperature dependence of the viscosity is indeed Arrhenius-like, because the stress relaxation measurements were performed at temperatures far above Tg in agreement with our results. The WLF-dependency only becomes clear at temperatures close to Tg. The Arrhenius-like temperature dependence of the viscosity is certainly not a unique nor distinctive property of vitrimers as regular polymeric systems also become Arrhenius-like at high temperatures.41
The most distinctive observation is the double relaxation behavior of the vitrimers. We explicitly note that the double relaxation is reproducible and beyond any measure of experimental error. It furthermore becomes more pronounced upon prolonged curing, i.e. it is not a transient effect. It is clear that the double relaxation behavior occurs upon addition of the catalyst (Fig. 3) and that it is accompanied by a clear signature in the shift factors with 70 °C being the “key temperature”, i.e. above 70 °C, the catalyst-controlled bond-exchange reactions control the temperature dependence, while below 70 °C, the “common” effects related to the network structure (free volume) and monomeric friction are dominant. Double relaxation has been observed for a variety of systems: model architecturally complex polymers with a hierarchy of relaxation modes,53,54 immiscible polymer blends,55 nanocomposites,56,57 miscible binary polymer blends,58 and polymers with functional groups, like e.g. hydrogen bonding motifs.5–7,59 Although the vitrimers share several features with functional polymers, they are not strictly comparable as the segments between crosslinks have essentially no internal dynamics and are expected to relax very fast due to the bond-exchange reactions, while we observe a significant delay between the time/temperature where the catalyst becomes active and the eventual terminal relaxation of the sample. Also additional secondary interactions such as hydrogen bonds or π–π stacking do not offer an explanation for the observed double relaxation behavior because the high-frequency moduli follow the rubber theory, and, if secondary interactions were responsible, the high-frequency moduli would be higher, while the low-frequency moduli would agree with the predictions (as in ref. 59). The low-frequency moduli are however much lower. Furthermore, also network-2.10 would display a transition around 70 °C, which is not the case (see Fig. 3). The double relaxation behavior has, to the best of our knowledge, not been reported for vitrimers. The main reason is that the stress relaxation tests in the literature were performed at temperatures far above Tg and only the terminal relaxation was observed. The construction of master curves including measurements closer to Tg has not been reported. In this respect, we further note that the existing theories for the dynamics of vitrimers33–36 do not predict a double relaxation behavior and we consequently believe that some ingredients might be missing from the theories. On the other hand, future studies concerning the viscoelasticity of other “vitrimer-chemistries” should be performed to assess the universality of the double relaxation behavior.
V. Conclusions
We presented an experimental investigation of the curing kinetics and viscoelastic properties of several epoxy/carboxylic acid-based vitrimers based on commercial fatty acid mixtures. The curing kinetics followed the Arrhenius law and the catalyst drastically accelerated the reactions. Time-temperature superposition worked reasonably well for the construction of master curves for the final networks and the shift factors were described with WLF-equations. From the comparison of the different samples, the temperature dependency could be divided into two regions, one above 70 °C, where the dynamics was controlled by the bond-exchange reactions, and one below, controlled by the free volume and monomeric friction of the network itself as in regular elastomers and polymers. The vitrimers systematically and reproducibly displayed a double relaxation behavior with 70 °C being the point of transition, in agreement with the shift factors. The high-frequency moduli of the vitrimers followed the classical rubber theory, indicating that the curing reactions proceeded to completion. The vitrimers relaxed and displayed a transition to a flow regime at long times as previously reported.1–3 The origin of the double relaxation behavior of the vitrimers appeared different from the origin in other systems in the literature and we hope that the experimental results presented in this work can further stimulate both theoretical and experimental works towards the elucidation of the details of the viscoelasticity and dynamics of vitrimers. More particularly, recent theories that describe the dynamics of vitrimers do not include a two step relaxation and consequently, future investigations concerning the viscoelasticity of other “vitrimer-chemistries” are important to assess if the double relaxation is a generic fingerprint for vitrimers or if it is specific to the epoxy/carboxylic acid chemistry based on commercial fatty acid mixtures investigated here.Acknowledgements
We gratefully acknowledge Christian Olagnon, Laurent Heux, Michael Rubinstein and Dimitris Vlassopoulos for stimulating discussions. We further thank the technical support of Malvern Instruments and Croda Europe for supplying the Pripol samples.References
- D. Montarnal, M. Capelot, F. Tournilhac and L. Leibler, Science, 2011, 334, 965 CrossRef CAS PubMed.
- M. Capelot, D. Montarnal, F. Tournilhac and L. Leibler, J. Am. Chem. Soc., 2012, 134, 7664 CrossRef CAS PubMed.
- M. Capelot, M. M. Unterlass, F. Tournilhac and L. Leibler, ACS Macro Lett., 2012, 1, 789 CrossRef CAS.
- W. H. Binder and R. Zirbs, Adv. Polym. Sci., 2007, 207, 1 CrossRef CAS.
- C. L. Lewis, K. Stewart and M. Anthamatten, Macromolecules, 2014, 47, 729 CrossRef CAS.
- X. Callies, C. Vechambre, C. Fonteneau, S. Pensec, J.-M. Chenal, L. L. Chazeau, L. Bouteiller, G. Ducouret and C. Creton, Macromolecules, 2015, 48, 7320 CrossRef CAS.
- A. Shabbir, H. Goldansaz, O. Hassager, E. van Ruymbeke and N. J. Alvarez, Macromolecules, 2015, 48, 5988 CrossRef CAS.
- R. A. Register and R. K. Prud’Homme, Melt Rheology, in Ionomers: Synthesis, Structure, Properties and Applications, ed. M. R. Tant, K. A. Mauritz and G. L. Wilkes, Chapman & Hall, 1997 Search PubMed.
- Q. Chen, S. Liang, H. Shiau and R. H. Colby, ACS Macro Lett., 2013, 2, 970 CrossRef CAS.
- R. A. Weiss and H. Zhao, J. Rheol., 2009, 53, 191 CrossRef CAS.
- N. C. Zhou, C. D. Chan and K. I. Winey, Macromolecules, 2008, 41, 6134 CrossRef CAS.
- C. N. Bowman and C. J. Kloxin, Angew. Chem., Int. Ed., 2012, 51, 4272 CrossRef CAS PubMed.
- C. J. Kloxin and C. N. Bowman, Chem. Soc. Rev., 2013, 42, 7161 RSC.
- J. Kamada, K. Koynov, C. Corten, A. Juhari, J. A. Yoon, M. W. Urban, A. C. Balazs and K. Matyjaszewski, Macromolecules, 2010, 43, 4133 CrossRef CAS.
- R. J. Wojtecki, M. A. Meador and S. J. Rowan, Nat. Mater., 2011, 10, 14 CrossRef CAS PubMed.
- X. Chen, M. A. Dam, K. Ono, A. Mal, H. Shen, S. R. Nutt, K. Sheran and F. Wudl, Science, 2002, 295, 1698 CrossRef CAS PubMed.
- B. J. Adzima, H. A. Aguirre, C. J. Kloxin, T. F. Scott and C. N. Bowman, Macromolecules, 2008, 41, 9112 CrossRef CAS PubMed.
- Y. Zhang, A. A. Broekhuis and F. Picchioni, Macromolecules, 2009, 42, 1906 CrossRef CAS.
- T. F. Scott, C. N. Bowman, C. D. Wayne and A. D. Schneider, Science, 2005, 308, 1615 CrossRef CAS PubMed.
- W. Denissen, J. M. Winne and F. E. Du Prez, Chem. Sci., 2016, 7, 30 RSC.
- J. P. Brutman, P. A. Delgado and M. A. Hillmyer, ACS Macro Lett., 2014, 3, 607 CrossRef CAS.
- F. I. Altuna, V. Pettarin and R. J. J. Williams, Green Chem., 2013, 15, 3360 RSC.
- W. Denissen, G. Rivero, R. Nicolaÿ, L. Leibler, J. M. Winne and F. E. Du Prez, Adv. Funct. Mater., 2015, 25, 2451 CrossRef CAS.
- D. J. Fortman, J. P. Brutman, C. J. Cramer, M. A. Hillmyer and W. R. Dichtel, J. Am. Chem. Soc., 2015, 137, 14019 CrossRef CAS PubMed.
- M. M. Obadia, B. P. Mudraboyina, A. Serghei, D. Montarnal and E. Drockenmuller, J. Am. Chem. Soc., 2015, 137, 6078 CrossRef CAS PubMed.
- Y.-X. Lu, F. Tournilhac, L. Leibler and Z. Guan, J. Am. Chem. Soc., 2012, 134, 8424 CrossRef CAS PubMed.
- Y.-X. Lu and Z. Guan, J. Am. Chem. Soc., 2012, 134, 14226 CrossRef CAS PubMed.
- M. Rubinstein and R. H. Colby, Polymer Physics, Oxford University Press, 2003 Search PubMed.
- W. W. Graessley, Polymeric Liquids & Networks: Structure & Rheology, Garland Science, New York, 2008 Search PubMed.
- Epoxy Polymers: New Materials and Innovations, ed. J.-P. Pascault and R. J. J. Williams, Wiley, Weinheim, Germany, 2010 Search PubMed.
- J. Otera, Chem. Rev., 1993, 93, 1449 CrossRef CAS.
- K. Yu, P. Taynton, W. Zhang, M. L. Dunn and H. J. Qi, RSC Adv., 2014, 4, 48682 RSC.
- F. Smallenburg, L. Leibler and F. Sciortino, Phys. Rev. Lett., 2013, 111, 188002 CrossRef PubMed.
- E. B. Stukalin, L.-H. Cai, N. A. Kumar, L. Leibler and M. Rubinstein, Macromolecules, 2013, 46, 7525 CrossRef CAS PubMed.
- F. Meng, R. H. Pritchard and E. M. Terentjev, Macromolecules, 2016, 49, 2843 CrossRef CAS.
- R. Long, H. J. Qi and M. L. Dunn, Soft Matter, 2013, 9, 4083 RSC.
- H. Yang, K. Yu, X. Mu, X. Shi, Y. Wei, Y. Guo and H. J. Qi, Soft Matter, 2015, 11, 6305 RSC.
- H. H. Winter and F. Chambon, J. Rheol., 1986, 30, 367 CrossRef CAS.
- F. Chambon and H. H. Winter, J. Rheol., 1987, 31, 683 CrossRef CAS.
- H. H. Winter and M. Mours, Adv. Polym. Sci., 1997, 134, 165 CrossRef CAS.
- J. D. Ferry, Viscoelastic Properties of Polymers, Wiley, New York, 3rd edn, 1980 Search PubMed.
- J. Honerkamp and J. Weese, Rheol. Acta, 1993, 32, 65 CrossRef CAS.
- F. R. Schwarzl, Rheol. Acta, 1969, 8, 6 CrossRef.
- R. Pasquino, B. Zhang, R. Sigel, H. Yu, M. Öttiger, O. Bertran, C. Aleman, A. D. Schlüter and D. Vlassopoulos, Macromolecules, 2012, 45, 8813 CrossRef CAS.
- J. Ampudia, E. Larrauri, E. M. Gil, M. Rodríguez and L. M. León, J. Appl. Polym. Sci., 1999, 71, 1239 CrossRef CAS.
- J. M. Laza, C. A. Julian, E. Larrauri, M. Rodríguez and L. M. León, Polymer, 1998, 40, 35 CrossRef.
- L. Matějka, S. Pokorný and K. Dušek, Polym. Bull., 1982, 7, 123 Search PubMed.
- K. Dušek, Adv. Polym. Sci., 1986, 78, 1 CrossRef.
- E. Crawford and A. J. Lesser, J. Polym. Sci., Part B: Polym. Phys., 1998, 36, 1371 CrossRef CAS.
- M. Rubinstein and S. Panyukov, Macromolecules, 2002, 35, 6670 CrossRef CAS.
- W. Kuhn, J. Polym. Sci., 1946, 1, 380 CrossRef CAS.
- F. T. Wall and P. J. Flory, J. Chem. Phys., 1951, 19, 1435 CrossRef CAS.
- J. Roovers and W. W. Graessley, Macromolecules, 1981, 14, 766 CrossRef CAS.
- T. C. B. McLeish, Adv. Phys., 2002, 51, 1379 CrossRef CAS.
- M. Kapnistos, D. Vlassopoulos and S. H. Anastasiadis, Europhys. Lett., 1996, 34, 513 CrossRef CAS.
- P. Cassagnau, Polymer, 2003, 44, 2455 CrossRef CAS.
- J. Moll, S. K. Kumar, F. Snijkers, D. Vlassopoulos, A. Rungta, B. C. Benicewicz, E. Gomez, J. Ilavsky and R. H. Colby, ACS Macro Lett., 2013, 2, 1051 CrossRef CAS.
- E. van Ruymbeke, V. Shchetnikava, Y. Matsumiya and H. Watanabe, Macromolecules, 2014, 47, 7653 CrossRef CAS.
- L. Leibler, M. Rubinstein and R. H. Colby, Macromolecules, 1991, 24, 4701 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c6sm00707d |
| This journal is © The Royal Society of Chemistry 2017 |