 Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
On the Gaussian approximation in colloidal hard sphere fluids
Alice L.
Thorneywork
a,
Dirk G. A. L.
Aarts
a,
Jürgen
Horbach
b and
Roel P. A.
Dullens
*a
aDepartment of Chemistry, Physical and Theoretical Chemistry Laboratory, University of Oxford, South Parks Road, Oxford, OX1 3QZ, UK. E-mail: roel.dullens@chem.ox.ac.uk
bInstitut für Theoretische Physik II, Heinrich-Heine-Universität Düsseldorf, Universitätsstrasse 1, 40225 Düsseldorf, Germany
First published on 1st April 2016
Abstract
We study the behaviour of the self-intermediate scattering function and self-van Hove correlation function for quasi-two-dimensional colloidal hard sphere fluids at a range of area fractions. We compute these functions first directly from the particle coordinates and secondly from the mean squared displacement via the Gaussian approximation. This allows us to test the validity of this approximation over a range of length and time scales, where we find that the Gaussian approximation holds if the hydrodynamic limits are appropriately probed. Surprisingly, only small deviations from Gaussian behaviour are seen at intermediate times, even for dense fluids. We next consider these deviations from Gaussian behaviour firstly via the non-Gaussian parameter and secondly by considering the relaxation times of the intermediate scattering function. From these measurements we develop a scaling relation in order to directly determine the combinations of wavevectors and times at which the non-Gaussian behavior is seen. This allows for the clear identification of the hydrodynamic regimes and thus provides new insight into the crossover between long- and short-time self-diffusion.
1 Introduction
Scattering techniques have long played an important role in the study of complex fluids, where they have been used to probe a wide range of phenomena related to the structure and dynamics of systems such as colloidal fluids, polymer solutions or proteins in membranes.1–8 In scattering experiments, the central dynamic quantity is the intermediate scattering function (ISF), F(k,t) with k the wavevector, which is directly related to the fluctuations in the intensity of the scattered light as a function of time.9F(k,t) can be split into two components, which describe either the self or collective behaviour. The calculation of the self-part, Fs(k,t), allows a number of other properties to be determined indirectly, most importantly the mean squared displacement (MSD), δr2(t), and the self-diffusion coefficients.The conversion between the self-ISF obtained from scattering measurements and the MSD requires the use of the Gaussian approximation.10,11 This assumes that the self-ISF is Gaussian and related to the MSD as
| Fs(k,t) = exp(−δr2(t)k2/2d), | (1) |
For colloidal diffusion in particular, single particle transport is diffusive at both short and long times. As such, two diffusion coefficients may be defined, with two corresponding hydrodynamic limits. These are associated with Gaussian behaviour as
| Fs(k,t) = exp(−Dik2t), i = S, L, | (2) |
As the hydrodynamic limit is an asymptotic regime, for long-time self-diffusion it is only reached in the limit of very large length and long time scales. Therefore, at finite length and time scales, quantitative deviations from the asymptotic limit are seen.10 Interestingly, these deviations can be very different in magnitude for different quantities, as has been recently explored for the diffusion dynamics of different colloidal fluids.14,21,22 While the MSD in these systems shows a linear dependence on time, as expected in the hydrodynamic limit, the self-part of the van Hove correlation function, Gs(r,t), i.e. the inverse Fourier transform of Fs(k,t), displays significant deviations from a Gaussian function. This has led to suggestions that the Gaussian approximation is in fact not applicable in many systems.14,21,23 A clear method by which to determine the regimes in which the Gaussian approximation holds is, however, currently lacking.
Here, we aim to quantify deviations from the behaviour in the hydrodynamic limit by studying the full spatial and time dependence of Fs(k,t) for a quasi-two-dimensional colloidal hard sphere fluid. In particular, we firstly calculate both the Fourier space quantity, Fs(k,t), and the real-space quantities, MSD and Gs(x,t), directly from the particle coordinates as obtained from video-microscopy experiments.24–28 Secondly, we also compute Fs(k,t) and Gs(x,t) via the Gaussian approximation using the MSD. From a comparison of these results we are able to test the validity of the Gaussian approximation over a range of length and timescales and to probe the two hydrodynamic limits, corresponding to the long- and short-time self-diffusion coefficients defined for colloidal fluids. Deviations from Gaussian behaviour are quantified primarily using the non-Gaussian parameter but also through a consideration of the relaxation times of Fs(k,t). From the latter we develop a scaling relation that is used to determine directly the combinations of wavevectors and times at which the non-Gaussian behaviour is seen and to study the crossover between the two diffusive regimes.
2 Theoretical background
The self-ISF, Fs(k,t), for a system of N particles in two-dimensions may be calculated as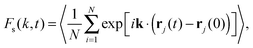 | (3) |
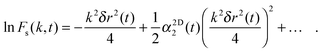 | (4) |
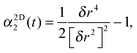 | (5) |
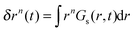 .
.
The real-space analogue of the self-ISF is the self-van Hove correlation function, Gs(r,t). The self-van Hove function corresponds to the probability that a particle, j, has moved to position rj, after a time t, given that it was at a certain position at t = 0. In analogy to the self-ISF, Gs(r,t) quantifies the time-dependent correlation of the microscopic one-particle density variable, ρ(r,t) = ∑ δ(r − rj(t))10 and for a homogeneous fluid, Gs(r,t) depends only on the absolute value of the position vector, r ≡ |r|. The self-van Hove function can also be computed separately in each spatial direction as
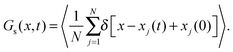 | (6) |
 | (7) |
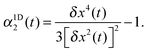 | (8) |
3 Experimental methods
Our colloidal model system is composed of melamine formaldehyde particles (Microparticles GmbH) with a hard sphere diameter of σ = 2.79 μm.31 The particles are dispersed in a 20/80 v/v% ethanol/water mixture and sediment to form a monolayer with area fraction ϕ on the base of a glass sample cell. The cell has a height of 200 μm and is cleaned before use with a 2% solution of Hellmanex. The particle mass density of 1.57 g cm−3 results in a gravitational length of 0.07 μm and thus out of plane fluctuations are negligible and the system is structurally two-dimensional. The area fraction, ϕ, is varied over a range from approximately ϕ = 0.05 to 0.66.The system is imaged at a rate of 2 frames per second for up to 30 minutes using a simple video-microscopy setup, consisting of an Olympus CKX41 inverted microscope with a 40× objective and equipped with a PixeLink CMOS camera (1280 × 1080 pixels). This image size corresponds to an area of 218 × 174 μm2 with the number of particles in the field of view varying with area fraction from approximately 460 to 3950. Standard particle tracking software32 was used to obtain particle coordinates, with an error of 12 ± 10 nm in the particle position.31 The self-ISF and self-van Hove correlation functions are calculated directly from particle coordinates from eqn (3) and (6), respectively. For Fs(k,t) values of k = |k| are chosen to range from approximately k = 2.5 to 0.1 μm−1, where the length in k-space corresponding to the particle diameter is kp = 2.25 μm−1 for the σ = 2.79 μm system. The smallest value of k chosen is larger than the minimum value of k set by the field of view, i.e. k ≈ 0.04 μm−1. The self-ISF and the self-van Hove correlation functions are also both computed from the MSD using the Gaussian approximation according to eqn (1) and (7).
4 Results and discussion
First, we consider the behaviour of the self-ISF at a variety of area fractions. In Fig. 1a and b, Fs(k,t) is shown for systems with ϕ = 0.08 and 0.66, for a range of wavevectors, k. Here, the self-ISF has been calculated both directly from particle coordinates as described by eqn (3) and from the MSDs (shown in Fig. 1c) via the Gaussian approximation as in eqn (1). Fig. 1 demonstrates a key strength of the self-ISF with respect to the MSD in that by varying k it is possible to separately probe the self-dynamics of particles over differing lengthscales. For example, here it can clearly be seen that as the value of k decreases, indicating that larger real-space lengthscales are being probed, Fs(k,t) exhibits a much slower decay. Additionally, for the system at ϕ = 0.66, slower decay of Fs(k,t) at a particular value of k is seen when compared to the system at ϕ = 0.08. This is consistent with the smaller particle displacements and thus slower particle motion seen at higher ϕ in the MSDs. The self-ISF calculated directly from the particle coordinates shows excellent agreement with Fs(k,t) calculated via the Gaussian approximation for all area fractions considered. However, small deviations are seen at long times for the system with ϕ = 0.66 at almost all values of k.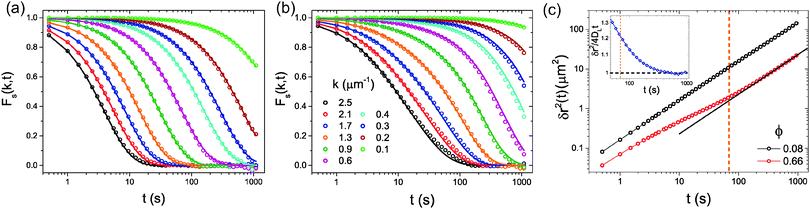 | ||
| Fig. 1 The self-ISF, Fs(k,t), as a function of time, t, and for a range of wavevectors, k, at (a) ϕ = 0.08 and (b) ϕ = 0.66. Values of k in (b) apply to both panels. Symbols show Fs(k,t) computed from eqn (3) and lines are calculated from the MSD, as shown in panel (c), using the Gaussian approximation, eqn (1). In (c) the solid line corresponds to the asymptotic slope, DL at long times for ϕ = 0.66 and the dashed vertical orange line corresponds to the time at which α1D2(t) reaches a maximum (see Fig. 2c). The inset of (c) shows the ratio δr2/4DLt at long times for the system at ϕ = 0.66 with the black dashed line indicating the long-time limit of δr2/4DLt = 1. | ||
Next, the self-van Hove functions, Gs(x,t), corresponding to the self-ISFs in Fig. 1a and b are computed using eqn (6) and are shown in Fig. 2a and b. Here, we again present data for both a direct calculation of Gs(x,t) using eqn (6) and for a calculation via the Gaussian approximation as in eqn (7). For comparable time delays, much smaller particle displacements are observed at higher ϕ. This is consistent with the slower diffusion seen at higher ϕ, which is clearly shown in the MSDs in Fig. 1c. Consistently, the Gaussian approximation is seen to be in good agreement with Gs(x,t) calculated directly from particle coordinates, however, there are deviations at intermediate times for the system at higher ϕ.
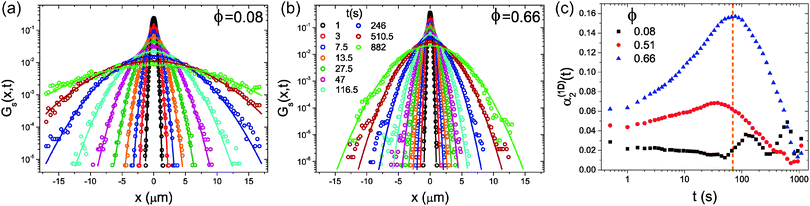 | ||
| Fig. 2 The variation of the self-van Hove function, Gs(x,t), with time at (a) ϕ = 0.08 and (b) ϕ = 0.66. Symbols show Gs(x,t) computed from eqn (6) and lines are calculated from the MSD using the Gaussian approximation, eqn (7). Values of t in (b) apply to both panels. (c) The variation in the non-Gaussian parameter, α1D2(t), with ϕ. The dashed vertical orange line indicates the time at which α1D2(t) for ϕ = 0.66 reaches a maximum. | ||
Fig. 1 and 2 illustrate the general trends in the behaviour of Fs(k,t) and Gs(x,t) with varying area fraction: in both cases, deviations from the Gaussian approximation are seen at certain values of t and k, which are small in overall magnitude, but larger for higher ϕ. This is consistent with previous results for the van Hove function from microscopy28,33 and for the intermediate scattering function in 3D from DLS measurements.1,18 This variation of the non-Gaussian behaviour can also be seen in Fig. 2c where we show the non-Gaussian parameter, α1D2(t), calculated by eqn (8) for a variety of values of ϕ. Here, α1D2(t) shows that deviations from Gaussian behaviour are largest at intermediate time and increase with increasing ϕ. However, this parameter clearly gives only an indication of the average behaviour with time, and does not provide any detailed information about the lengthscale dependence of the deviations from Gaussian behaviour.
To address the relationship between Fickian diffusion and the Gaussian approximation,14,21 we show in Fig. 1c a straight line with a gradient corresponding to the self-diffusion coefficient at long times, which appears to be in agreement with the experimental data for approximately t > 200 s. We also indicate the time at which α1D2(t) reaches a maximum, which lies close to this apparent onset of the long-time diffusive regime, seeming to indicate that we observe Fickian diffusion combined with non-Gaussian behaviour in agreement with previous reports.14,21 To probe this further, however, we consider the quantity δr2/4DLt as a function of time, which we plot in the inset of Fig. 1c. In this representation, it is clear that the MSD is in fact only slowly approaching the hydrodynamic limit for times t > 200 s, and thus our observations do not imply a failure of the Gaussian approximation, but simply that it is difficult to infer from the MSD visually whether the true, asymptotic, long-time limit has been reached.
In order to consider both the time and lengthscale dependence of the non-Gaussian contributions to Fs(k,t) and Gs(x,t) in more detail we now attempt to determine directly the combinations of wavevectors and times at which the non-Gaussian behavior is seen. To this end, we consider the relaxation time scale τA(k) at which Fs(k,t) decays to a given value A:
| A = Fs(k,t = τA(k)). | (9) |
| A = exp(−Dik2τA(k)), | (10) |
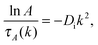 | (11) |
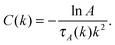 | (12) |
In Fig. 3 we show the variation of τA with k for A ranging from 0.9 to 0.1 for systems at ϕ = 0.08, 0.43, and 0.62. Here, results are considered in the form described by eqn (11) and thus the gradient is equal to −Di. As such, lines corresponding to eqn (11) computed using the short- and long-time self-diffusion coefficients measured from the MSDs34 are also shown. The comparison between the relaxation times of Fs(k,t) and the two limiting gradients set by the self-diffusion coefficients in Fig. 3a–c clearly demonstrates that there is a crossover from short to long-time behaviour with decreasing k and A. This is consistent with the fact that k is an inverse length scale and therefore relaxation times measured at higher k will reflect behaviour over shorter length scales which is naturally associated with shorter times. The value of A impacts upon the timescale probed; a longer time is required for Fs(k,t) to decay to a lower value of A, and this automatically results in a consideration of behaviour at longer times.
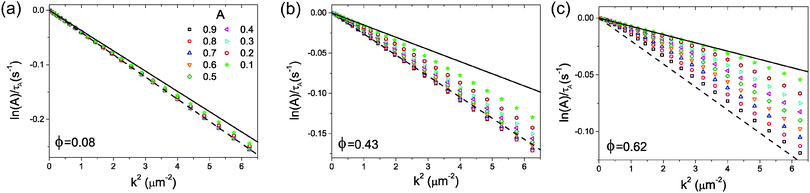 | ||
| Fig. 3 The relaxation time as defined by eqn (11) as a function of k2 shown for a range of values of A at (a) ϕ = 0.08, (b) ϕ = 0.43 and (c) ϕ = 0.62. Values of A relate to all panels. Lines show the expected gradient from an independent measurement of the self-diffusion coefficients using the MSD. Here, the dashed line is calculated from the short-time self-diffusion coefficient, DS, and the solid line from the long-time self-diffusion coefficient, DL. | ||
The dependence of τA upon A is clearly much stronger for the systems at higher ϕ. This reflects the greater difference in the magnitude of the long- and short-time self-diffusion coefficients at higher ϕ.34 Also evident is the difference in the timescales related to the short and long-time behaviour. For systems at low ϕ, a particle experiences relatively few direct interactions during a certain period of time due to the large average distance between particles. As such, the difference between the short-time and long-time diffusion coefficients, which arises from direct interactions, is relatively small, and only at very long times and length scales is the crossover to the long-time behaviour seen (see Fig. 3a). In contrast, for higher area fractions, the distance a particle must travel in order to directly interact with another particle is very short, resulting in significant number of direct interactions at short times. This both significantly reduces the value of the long-time self-diffusion coefficient relative to its short-time value, but also results in a crossover from the short- to long-time regime at much earlier time and smaller length scales. This is illustrated in Fig. 3c where ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) A/τA exhibits a gradient consistent with the long-time self-diffusion coefficient up to reasonably high values of k.
A/τA exhibits a gradient consistent with the long-time self-diffusion coefficient up to reasonably high values of k.
We now consider the trends displayed by Fig. 3 using the function C(k) defined in eqn (12). In Fig. 4a we show the variation of C(k) with k for three values of A for the system with ϕ = 0.62. For each line it is possible to determine an inflection point at a certain value of k, which we denote as k*, and these values are also indicated in Fig. 4a. The value of k* indicates a crossover point between short- and long-time behaviour, and in Fig. 4b, k* is plotted as a function of A. For all three values of ϕ, k* increases with decreasing A. This arises from the fact that the behaviour at small A corresponds to that at long times and thus long-time behaviour is seen even for large values of k. Furthermore, k* for a fixed value of A is seen to increase with ϕ, demonstrating that as the area fraction increases, the length scale associated with the crossover between short- and long-time behaviour decreases. This is due to the fact that at lower ϕ the distance between particles is much greater and thus particles must diffuse further in order for sufficient collisions to occur to reach the long-time regime.
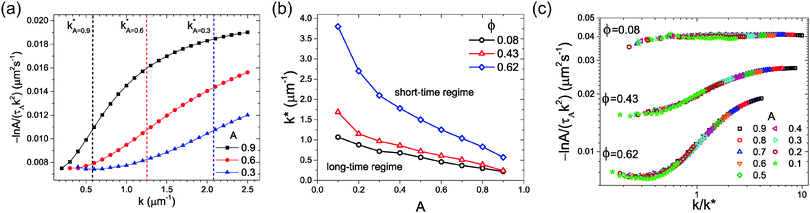 | ||
| Fig. 4 (a) The dependence of the self-diffusion coefficient viaeqn (11) on k for three different values of the parameter A at ϕ = 0.62. Vertical dashed lines indicate the value of k* for each curve. (b) The value of k* as a function of A for systems at ϕ = 0.08, 0.43 and 0.62. (c) The variation of C(k) (eqn (12)), with k rescaled by k* for ϕ = 0.08, 0.43 and 0.62. | ||
In Fig. 4c, C(k) computed for all values of A is replotted with k now rescaled by k*. This scaling relation is shown for systems with ϕ = 0.08, 0.43, and 0.62, where data for different values of A for each ϕ are seen to fall onto one master curve. Here, the presence of the long- and short-time regimes for the three different area fractions is clear, with the difference in long- and short-time behaviour seen to increase with ϕ. In addition to this, universal behaviour is seen with respect to the scaling relation at intermediate values of k close to k*. This is surprising, due to the fact that the mechanisms that govern particle motion at intermediate lengthscales, and therefore times, are complex, and expected to differ with area fraction. Importantly, it is clear that both Fig. 3 and 4 provide significantly more information regarding the nature of the crossover from long- to short-time behaviour than that available from calculation of the non-Gaussian parameter. In particular, by determining the quantity k* we are able to estimate the ranges of k for which the two hydrodynamic limits as a function of ϕ are seen.
5 Conclusions
We have computed the self-intermediate scattering function, Fs(k,t), and the self-van Hove correlation function, Gs(x,t), for a quasi-two-dimensional colloidal system, with a particular focus upon the estimation of these quantities using the Gaussian approximation. The Gaussian approximation is found to be in excellent agreement with a direct measurement of Gs(x,t) and Fs(k,t) for the full range of fluid area fractions in the relevant hydrodynamic regimes. This indicates that, in contrast to recent reports, the Gaussian approximation remains a useful tool in the discussion of particle dynamics providing that these regimes can be identified. Furthermore, the fact that deviations from Gaussian behaviour disappear in the hydrodynamic regimes suggests that reports of Fickian yet non-Gaussian diffusion may arise from measurements outside the asymptotic long-time limit.Small deviations from Gaussian behaviour are, however, found at intermediate times, and depend sensitively upon the area fraction and the wavevector at which the system is probed. These deviations are further quantified both through the non-Gaussian parameter, and more thoroughly via the relaxation times of Fs(k,t). These relaxation times for systems at all area fractions are seen to obey a scaling relation, which allows the combinations of wavevectors and times at which the non-Gaussian behavior is seen to be determined. Furthermore, as this relation approaches the long-time self-diffusion coefficient for small values of k and short-time self-diffusion coefficient for large values of k it can be used to identify the two diffusive regimes and provides new insight into the crossover between them.
Acknowledgements
We thank Thomas Skinner and Michael Juniper for useful discussions. J. H. and R. P. A. D. acknowledge the Royal Society, A. L. T. and R. P. A. D. the EPSRC and the ERC (ERC Starting Grant 279541-IMCOLMAT) for financial support.References
- W. van Megen, T. Mortensen, S. Williams and J. Müller, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 1998, 58, 6073–6085 CrossRef CAS.
- V. Michailidou, G. Petekidis, J. Swan and J. Brady, Phys. Rev. Lett., 2009, 102, 068302 CrossRef CAS PubMed.
- W. van Megen and S. M. Underwood, J. Chem. Phys., 1989, 91, 552 CrossRef CAS.
- M. M. Kops-Werkhoven and H. M. Fijnaut, J. Chem. Phys., 1981, 74, 1618 CrossRef CAS.
- B. Mos, P. Verkerk, S. Pouget, A. Van Zon, G. J. Bel, S. W. De Leeuw and C. D. Eisenbach, J. Chem. Phys., 2000, 113, 4–7 CrossRef CAS.
- J. H. Roh, V. N. Novikov, R. B. Gregory, J. E. Curtis, Z. Chowdhuri and A. P. Sokolov, Phys. Rev. Lett., 2005, 95, 1–4 CrossRef PubMed.
- U. Lehnert, V. Réat, M. Weik, G. Zacca, C. Pfister, G. Zaccai and C. Pfister, Biophys. J., 1998, 75, 1945–1952 CrossRef CAS PubMed.
- M. T. Bishop, K. H. Langley and F. E. Karasz, Macromolecules, 1989, 22, 1220–1231 CrossRef CAS.
- J. K. G. Dhont, An Introduction to Dynamics of Colloids, Elsevier, 1996 Search PubMed.
- J. P. Boon and S. Yip, Molecular Hydrodynamics, Dover Publications Inc., 1980 Search PubMed.
- J.-P. Hansen and I. R. McDonald, Theory of Simple Liquids, Academic Press, 3rd edn, 2006 Search PubMed.
- G. H. Vineyard, Phys. Rev., 1958, 110, 999–1010 CrossRef CAS.
- P. A. Egelstaff, An Introduction to the Liquid State, Oxford University Press, 1994 Search PubMed.
- G. D. J. Phillies, Soft Matter, 2015, 11, 580–586 RSC.
- J. M. Rallison and E. J. Hinch, J. Fluid Mech., 1986, 167, 131 CrossRef CAS.
- U. Balucani and M. Zoppi, Dynamics of the Liquid State, Oxford University Press, 1994 Search PubMed.
- A. Van Veluwen and H. N. W. Lekkerkerker, Phys. Rev. A: At., Mol., Opt. Phys., 1988, 38, 3758–3763 CrossRef CAS.
- W. van Megen and S. M. Underwood, J. Chem. Phys., 1988, 88, 7841 CrossRef CAS.
- R. J. A. Tough, P. N. Pusey, H. N. W. Lekkerkerker and C. Van Den Broeck, Mol. Phys., 1986, 59, 595–619 CrossRef CAS.
- W. van Megen and I. K. Snook, J. Chem. Phys., 1988, 88, 1185 CrossRef CAS.
- J. Guan, B. Wang and S. Granick, ACS Nano, 2014, 8, 3331–3336 CrossRef CAS PubMed.
- G. Kwon, B. J. Sung and A. Yethiraj, J. Phys. Chem. B, 2014, 118, 8128–8134 CrossRef CAS PubMed.
- B. Wang, S. M. Anthony, S. C. Bae and S. Granick, Proc. Natl. Acad. Sci. U. S. A., 2009, 106, 15160–15164 CrossRef CAS PubMed.
- C. A. Murray and D. G. Grier, Annu. Rev. Phys. Chem., 1996, 47, 421–462 CrossRef CAS.
- V. Prasad, D. Semwogerere and E. R. Weeks, J. Phys.: Condens. Matter, 2007, 19, 113102 CrossRef.
- J. Santana-Solano and J. L. Arauz-Lara, Phys. Rev. Lett., 2001, 87, 038302 CrossRef CAS PubMed.
- S. Mazoyer, F. Ebert, G. Maret and P. Keim, EPL, 2009, 88, 66004 CrossRef.
- A. H. Marcus, J. Schofield and S. A. Rice, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 1999, 60, 5725–5736 CrossRef CAS.
- B. R. A. Nijboer and A. Rahman, Physica, 1966, 32, 415 CrossRef.
- A. Rahman, Phys. Rev., 1964, 136, A405 CrossRef.
- A. L. Thorneywork, R. Roth, D. G. A. L. Aarts and R. P. A. Dullens, J. Chem. Phys., 2014, 140, 161106 CrossRef PubMed.
- J. C. Crocker and D. G. Grier, J. Colloid Interface Sci., 1996, 179, 298 CrossRef CAS.
- M. Carbajal-Tinoco, G. Cruz de León and J. Arauz-Lara, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 1997, 56, 6962–6969 CrossRef CAS.
- A. L. Thorneywork, R. E. Rozas, R. P. A. Dullens and J. Horbach, Phys. Rev. Lett., 2015, 115, 268301 CrossRef PubMed.
| This journal is © The Royal Society of Chemistry 2016 |
