Open Access Article
Open Access ArticleA magnetic look into the protecting layer of Au25 clusters†
Mikhail
Agrachev
a,
Sabrina
Antonello
a,
Tiziano
Dainese
a,
José A.
Gascón
b,
Fangfang
Pan
c,
Kari
Rissanen
c,
Marco
Ruzzi
a,
Alfonso
Venzo
d,
Alfonso
Zoleo
*a and
Flavio
Maran
*ab
aDepartment of Chemistry, University of Padova, via Marzolo 1, 35131 Padova, Italy. E-mail: alfonso.zoleo@unipd.it; flavio.maran@unipd.it
bDepartment of Chemistry, University of Connecticut, 55 North Eagleville Road, Storrs, 06269 Connecticut, USA
cDepartment of Chemistry, Nanoscience Center, University of Jyväskylä, P.O. Box 35, 40014 JYU, Finland
dNational Research Council, ICMATE c/o Department of Chemistry, University of Padova, via Marzolo 1, 35131 Padova, Italy
First published on 19th September 2016
Abstract
The field of molecular metal clusters protected by organothiolates is experiencing a very rapid growth. So far, however, a clear understanding of the fine interactions between the cluster core and the capping monolayer has remained elusive, despite the importance of the latter in interfacing the former to the surrounding medium. Here, we describe a very sensitive methodology that enables comprehensive assessment of these interactions. Pulse electron nuclear double resonance (ENDOR) was employed to study the interaction of the unpaired electron with the protons of the alkanethiolate ligands in four structurally related paramagnetic Au25(SR)018 clusters (R = ethyl, propyl, butyl, 2-methylpropyl). Whereas some of these structures were known, we present the first structural description of the highly symmetric Au25(SPr)018 cluster. Through knowledge of the structural data, the ENDOR signals could be successfully related to the types of ligand and the distance of the relevant protons from the central gold core. We found that orbital distribution affects atoms that can be as far as 6 Å from the icosahedral core. Simulations of the spectra provided the values of the hyperfine coupling constants. The resulting information was compared with that provided by 1H NMR spectroscopy, and molecular dynamics calculations provided useful hints to understanding differences between the ENDOR and NMR results. It is shown that the unpaired electron can be used as a very precise probe of the main structural features of the interface between the metal core and the capping ligands.
Introduction
In monolayer-protected gold clusters (MPCs) with gold cores of diameter <1.6 nm the number of Au atoms is sufficiently small to make them display molecular features. This makes the study of their fundamental properties particularly fascinating and often intriguing.1–5 Instrumental to these studies has been the possibility of preparing molecule-like gold MPCs in an atomically precise form, as assessed by mass spectrometry and single-crystal X-ray crystallography.6 The structure of Au25(SR)18 clusters, by far the most well known among molecular clusters, is based on a 13 gold-atom icosahedral core surrounded by 6 Au2(SR)3 units, with minor differences induced by the charge state (−1, 0, and +1) and the ligands,7–11 even when the linear polymer (Au25)n forms.12 Several molecular features of Au25(SR)18 clusters have been studied in detail, such as the characteristic electrochemical behavior13–15 and charge-dependent optical16 and nuclear magnetic resonance (NMR) patterns.17 Studies of their photophysical behavior,18–21 chirality,22 electron-transfer and redox-catalysis properties,23–27 have been described. Several theoretical studies have been carried out and reviewed.28–30 Whereas the as prepared anionic cluster Au25(SC2H4Ph)18− is a diamagnetic species, the corresponding, indefinitely stable neutral form Au25(SC2H4Ph)018 is paramagnetic. The effect of the unpaired electron was detected by 1H and 13C NMR at room temperature17 or electron paramagnetic resonance (EPR) at temperatures typically lower than 100 K.16,31 The Jin's group showed that the magnetic state can be switched off by reduction to diamagnetic Au25(SC2H4Ph)18−.31 Similarly, we demonstrated by both NMR17 and EPR16 that oxidation to cation Au25(SC2H4Ph)18+ generates a diamagnetic species. DFT calculations indicated that the magnetic behavior is controlled by significant splitting of the relevant orbital energy levels.17The NMR spectrum of the three charge states evidenced very profound charge-induced variations in the position and shape of the peaks.17 Most notably, some of the ligands' resonances undergo a significant downfield shift upon formation of paramagnet Au25(SR)018. This was first observed by the Murray's group32 and then perfected by us through identification of all resonances as a function of temperature or ligand type.10,12,17,26 In this context, it is important to stress that the 18 thiolated ligands present in the 6 Au2(SR)3 half-crowns (or staples) capping the central Au13 core split into a group of 12 inner and a group of 6 outer ligands. Here, inner refers to the fact that the two terminal SR groups of –(SR)–Au–(SR)–Au–(SR)– also bind to Au13, whereas outer refers to the outmost, remaining thiolate of the half-crown. 1D and 2D NMR analysis allowed distinguishing between the two ligands' families, also on a quantitative basis. There is a general consensus that the properties of molecular MPCs mostly depend on the number and relative position of the gold atoms.5,6 On the other hand, NMR evidence and corresponding DFT calculations indicated that the singly occupied molecular orbital (SOMO) spreads onto the first groups of the thiolated ligands. Very recent studies also concluded that the ligand structure/composition can be a factor affecting the optical behavior of molecular and larger MPCs.33,34 These results thus indicate that the highest occupied and the lowest unoccupied MOs (HOMOs and LUMOs) are not just limited to the Au13 core, as often implicitly assumed, but rather involve to some extent the ligands. Another example is provided by the optical spectrum of Au25 capped by thiophenolate-type ligands, which shows band shifts35 and a small decrease of the HOMO–LUMO gap compared to that of Au25 capped by alkanethiolates, for which the spectrum does not depend on the ligand length:26 this effect shows that changing the carbon type at the α position to sulfur affects the electronic properties of the cluster. The way by which the capping ligands interact with the core, the shape and spreading of the chemically relevant orbitals, and the actual environment experienced by molecules or ions penetrating the monolayer15 are expected to be crucial factors also for understanding the catalytic effects of ultrasmall clusters27 on a truly molecular basis.
Very recently, we illustrated the remarkable potentialities of pulse electron nuclear double resonance (ENDOR).10 This technique is a very sensitive way of performing ENDOR36 and is meant to characterize hyperfine coupling (A) between an unpaired electron and nuclei nearby. This interaction consists of isotropic and anisotropic parts: the former is a through-bond contribution that depends on the number and type of bonds involved, whereas the latter depends on both through-bond and through-space (electron-dipole/nuclear-dipole) interactions. In the ENDOR spectrum, a doublet of lines is associated with a magnetic nucleus with nuclear spin I = 1/2. When A < 2ν, where ν is the nucleus Larmor frequency, the doublet is centered at ν and the separation between the two lines is A. On the other hand, for A > 2ν the doublet is centered at A/2 and the separation between the two lines is 2ν. The Larmor frequency ν depends only on the magnetic field B at which the ENDOR spectrum is recorded, according to the relation ν = γIB/(2π), where γI is the nucleus gyromagnetic ratio. For larger nuclear spins, such as for 197Au whose I = 3/2, the quadrupolar and hyperfine interactions split the ENDOR lines further. This was experimentally verified in the ENDOR analysis of Au25(SEt)018.10 The hyperfine interaction between the unpaired electron and the gold atoms could be assessed quantitatively, and the ENDOR results could be nicely reproduced by density functional theory (DFT) calculations, which could be particularly precise due to the very small thiolate used.
Here, we describe a methodology and results that accurately enabled assessing the spin density and, therefore, the distribution of the SOMO in Au25(SR)018 clusters. We employed pulse ENDOR to study the interaction of the unpaired electron with the protons of the alkanethiolate ligands, an approach that was never described before. The resulting information was compared with that obtained by 1H NMR spectroscopy of how and how much the chemical shifts change when the charge state of the cluster is varied from −1 to 0. Molecular dynamics (MD) calculations provided useful hints in understanding differences between the ENDOR and NMR results. We noted that by reducing the temperature to 5 K, a pronounced increase of spin-polarization occurs. It is thus shown that the unpaired electron can be used as a particularly sensitive probe of the main structural features of the interface between the metal core and the capping ligands, leading to establish a very precise and consistent picture of these complex systems.
Experimental
Au25(SEt)18 and Au25(SBu)18 were prepared as described previously.10,12 The two new clusters, Au25(SPr)18 and Au25(SMePr)18, were synthesized and oxidized along similar lines.1H and 13C NMR spectroscopy measurements were carried out on 3 mM [n-Oct4N+][Au25(SR)18−] or Au25(SR)018 in benzene-d6 (100%, 99.96% d6, Aldrich). We used a Bruker Avance DMX-600 MHz spectrometer equipped with a 5 mm TX-1 x, y, z-gradient powered, triple resonance inverse probe operating at 599.90 (1H NMR) or 150.07 MHz (13C NMR). The temperature was controlled at 298 K with a Bruker BVT-300 automatic temperature controller. Chemical shifts are in ppm units (δ) with reference to tetramethylsilane used as an internal standard for both 1H and 13C NMR. The proton assignments were either already known or performed by 2D correlation spectroscopy (COSY), total correlation spectroscopy (TOCSY), and nuclear Overhauser enhancement spectroscopy (NOESY) experiments. 13C chemical shifts were obtained and assigned through heteronuclear multiple quantum coherence (HMQC) correlation experiments.
For ENDOR measurements, the samples consisted in 100 μl of 0.5 mM Au25(SR)018 in toluene. Each solution was introduced into the EPR sample holder, a 3 (o.d.) × 2 mm (i.d.) quartz tube, and degassed through freeze–pump–thaw cycles in a vacuum line and sealed at low pressure (5 × 10−5 torr). The samples were frozen at 80 K and then introduced in the probehead. The experiments were carried out at 5 K. 1H Pulse ENDOR measurements were carried out with a Bruker Elexsys E580 instrument equipped with a pulse ENDOR dieletric probehead and an Oxford CF935 cryostat. We used the Davies pulse sequence, with 160 ns microwave inversion pulse and 80–160 ns pulse-sequence for electron-spin echo detection. The radiofrequency pulse was 8–10 μs long and amplified with a 150 W RF Bruker amplifier. The spectra were recorded at the top of the echo detected EPR spectra (approximately 290 mT), with a RF scan ranging from 1 to 20 MHz, where the proton peaks were expected. The narrow spectral range and the long microwave pulses were chosen to spot and enhance ENDOR lines from 1H with respect to 197Au.10 ENDOR simulations were performed with a homebuilt program running on the open-source Scilab-5.5.1 calculation package [http://www.scilab.org].
Results and discussion
We used a series of related Au25(SR)0/−118 clusters. The ligands were chosen to provide a progressive variation of the chain length from two to four carbon atoms, as shown in Chart 1. The single crystal structures of the SEt and SBu protected clusters were available from previous work, whereas that of Au25(SPr)018 is described here for the first time. The effect of branching was checked by changing a hydrogen atom with a methyl group at the β position: for this ligand, 2-methyl-1-propanethiolate, we will use the notation SMePr to stress both methyl branching and that the fully extended chain length is the same as that of SPr.Starting from sulfur, the carbon atoms and associated hydrogen atoms are defined as α, β, γ, and δ; the second CH3 group of HSMePr is denoted as γ′. Monodisperse samples of the four Au25(SR)18− clusters were prepared, and the clusters were oxidized according to a method already described.10 Full characterization of the purified neutral clusters was carried out by a combination of matrix-assisted laser desorption ionization time-of-flight mass spectrometry (e.g., Fig. S1 in ESI†), UV-vis absorption spectroscopy, differential-pulse voltammetry, and 1H NMR spectroscopy techniques. Au25(SPr)18 and Au25(SMePr)18 are new clusters.
X-ray crystallography
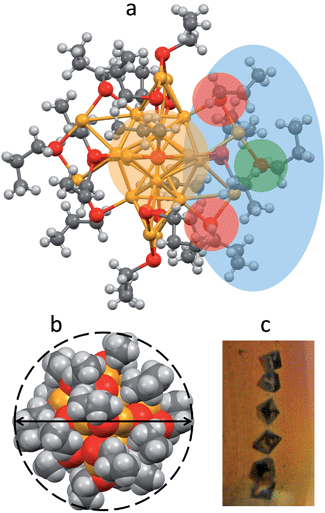
Au25(SPr)018 crystallizes (Fig. 1c) in trigonal space group P![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) , with three cluster molecules in the unit cell. This MPC is highly symmetric with a 3-fold rotoinversion axis running through the central Au atom. As for the other known Au25(SR)18 structures,7–12 the 25 gold atoms can be regarded as being formed by two shells composed by an Au13 icosahedral core, consisting of a central Au atom with 12 Au atoms directly interacting with it, and an outer shell of 12 Au atoms bound to thiolate groups to form –(SR)–Au–(SR)–Au–(SR)– motifs (Fig. 1a): The Au–Au bond-strength order is Aucentral–Auico > Auico–Auico > Auico–Austaple. These bonds correspond to average Au–Au bond lengths of 2.784, 2.927 and 3.163 Å, respectively. It is worth noting that there is a significantly shorter Auico–Auico bond (2.7746 Å) and a relatively longer Auico–Austaple bond (3.3206 Å). We found this feature also in the closely related SEt and SBu analogues.10,12 Concerning the orientation of the carbon chains with respect to the plane of the same half-crown, Au25(SPr)018 features the first case of a Au25 cluster where only alternate orientations are observed. The space-filling model (Fig. 1b) illustrates that the ligands are quite folded around the gold core, thereby forming a relatively thin monolayer, at least in the solid state. Evidence for the formation of quite thin capping monolayers was previously gathered also in solution, through electron-transfer measurements26 of a series of monodisperse Au25(SCnH2n+1)18 clusters with n varying from 2 to 18. Of particular importance for the current investigation, from the structures of Au25(SEt)018, Au25(SPr)018, and Au25(SBu)018 we could calculate the average distances (mediated over the six staples) of the corresponding hydrogen atoms for both the inner and outer ligands. In this connection, it is worth noting that the average radii (rMPC) of these three clusters nicely match those calculated from the Stokes–Einstein–Sutherland equation, D = kBT/6πηrMPC, where D is the electrochemically determined diffusion coefficient,15kB is the Boltzmann constant, and η is the solvent viscosity: for Au25(SEt)018, Au25(SPr)018, and Au25(SBu)018 we find the couple of values 8.3 and 7.8, 8.6 and 8.6, 10.2 and 9.4 Å, respectively.
, with three cluster molecules in the unit cell. This MPC is highly symmetric with a 3-fold rotoinversion axis running through the central Au atom. As for the other known Au25(SR)18 structures,7–12 the 25 gold atoms can be regarded as being formed by two shells composed by an Au13 icosahedral core, consisting of a central Au atom with 12 Au atoms directly interacting with it, and an outer shell of 12 Au atoms bound to thiolate groups to form –(SR)–Au–(SR)–Au–(SR)– motifs (Fig. 1a): The Au–Au bond-strength order is Aucentral–Auico > Auico–Auico > Auico–Austaple. These bonds correspond to average Au–Au bond lengths of 2.784, 2.927 and 3.163 Å, respectively. It is worth noting that there is a significantly shorter Auico–Auico bond (2.7746 Å) and a relatively longer Auico–Austaple bond (3.3206 Å). We found this feature also in the closely related SEt and SBu analogues.10,12 Concerning the orientation of the carbon chains with respect to the plane of the same half-crown, Au25(SPr)018 features the first case of a Au25 cluster where only alternate orientations are observed. The space-filling model (Fig. 1b) illustrates that the ligands are quite folded around the gold core, thereby forming a relatively thin monolayer, at least in the solid state. Evidence for the formation of quite thin capping monolayers was previously gathered also in solution, through electron-transfer measurements26 of a series of monodisperse Au25(SCnH2n+1)18 clusters with n varying from 2 to 18. Of particular importance for the current investigation, from the structures of Au25(SEt)018, Au25(SPr)018, and Au25(SBu)018 we could calculate the average distances (mediated over the six staples) of the corresponding hydrogen atoms for both the inner and outer ligands. In this connection, it is worth noting that the average radii (rMPC) of these three clusters nicely match those calculated from the Stokes–Einstein–Sutherland equation, D = kBT/6πηrMPC, where D is the electrochemically determined diffusion coefficient,15kB is the Boltzmann constant, and η is the solvent viscosity: for Au25(SEt)018, Au25(SPr)018, and Au25(SBu)018 we find the couple of values 8.3 and 7.8, 8.6 and 8.6, 10.2 and 9.4 Å, respectively.
NMR spectroscopy
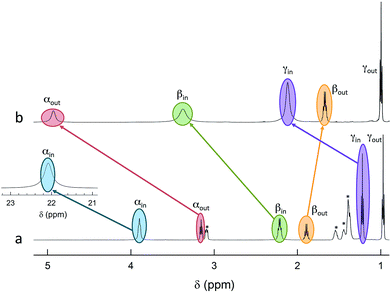
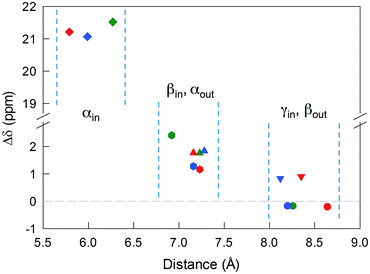
The 12 inner and the 6 outer ligands experience a different chemical environment and thus show distinct NMR spectroscopy signals. When the cluster is in its paramagnetic state, differences are enhanced, especially for those resonances related to the proton and carbon atoms closer to the gold core. We studied the spectra of the selected clusters in either charge state, using benzene-d6 as the solvent. Fig. 2 illustrates for the case of Au25(SPr)18 the most salient differences in chemical shift as one goes from the paramagnetic to the diamagnetic states. Further spectra (Fig. S2–S4†) and data are in ESI.†The most significant effect of the one-electron oxidation of the native cluster is to shift downfield the NMR peaks pertaining to the protons in positions α, β and γ (except for Au25(SEt)18, which has no γ groups) of the inner ligands, and in positions α and (to a small extent) γ of the outer ligands; instead, the β protons of the outer ligands undergo an upfield shift. For the three clusters of known crystallographic structure, the chemical shift differences (Δδ = δradical − δanion) are displayed in Fig. 3 as a function of the average distance between the central Au atom and the two or three hydrogen atoms of the specific resonance, averaged for the six half-crowns. The positive differences roughly obey an exponential dependence on distance (taking into account the error on the latter), as already commented upon for Au25(SBu)18.12 As to Au25(SMePr)18, we observed the same charge-dependent effect (Fig. S3 and S4†). The NMR shifts observed upon changing the charge state from −1 to 0 are related to the contact interaction of the nuclear magnetic moments with the unpaired electron, and can thus be taken as a measure of how far the spin density spreads outside the Au13 core.17
The Δδ values can be used to estimate the isotropic hyperfine coupling constant A according to the relationship (eqn (1)):37
| Δδ = AgβeS(S + 1)/(3ħγIkBT) | (1) |
| Ligand and position | A (kHz) | A , (MHz) | T xx , (MHz) | T yy , (MHz) | T zz , (MHz) | n |
|---|---|---|---|---|---|---|
| a From NMR measurements at 298 K, using eqn (1). b From ENDOR measurements at 5 K. c The error associated with the simulations is ca. 0.1 MHz. d T xx , Tyy, and Tzz are the main values of the anisotropic hyperfine tensor. e n is the number of equivalent nuclei corresponding to the best simulation. f Not determined: see text. g As discussed in the text, this number is affected by further contributions. | ||||||
| SEt | ||||||
| (α-CH)in | 723 | n.d.f | ||||
| (β-CH)in | 81.1 | −4.2 | −0.8 | −2.7 | 3.5 | 36 |
| (α-CH)out | 59.2 | −1.6 | −0.9 | −0.9 | 1.8 | 12 |
| (β-CH)out | −5.78 | −0.24 | −0.01 | −0.01 | 0.02 | 14g |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
||||||
| SPr | ||||||
| (α-CH)in | 713 | n.d.f | ||||
| (β-CH)in | 39.3 | −5.5 | −1.2 | −1.2 | 2.4 | 24 |
| (α-CH)out | 59.7 | −2.0 | −0.6 | −0.6 | 1.2 | 12 |
| (β-CH)out | −6.89 | −0.24 | −0.01 | −0.01 | 0.02 | 14g |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
||||||
| SBu | ||||||
| (α-CH)in | 708 | n.d.f | ||||
| (β-CH)in | 42.9 | −5.8 | −0.7 | −0.7 | 1.4 | 24 |
| (α-CH)out | 61.9 | −2.2 | −0.6 | −0.6 | 1.2 | 12 |
| (β-CH)out | −5.82 | −0.24 | −0.01 | −0.01 | 0.02 | 16g |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
||||||
| SMePr | ||||||
| (α-CH)in | 355 | n.d.f | ||||
| (β-CH)in | −4.94 | −5.5 | −1.2 | −1.2 | 2.4 | 12 |
| (α-CH)out | 63.5 | −2.8 | −0.6 | −0.6 | 1.2 | 12 |
| (β-CH)out | −10.1 | −0.22 | −0.01 | −0.01 | 0.02 | 28g |
| (γ-CH)in | 31.9 | −2.0 | −0.5 | −0.5 | 1.0 | 60 |
ENDOR
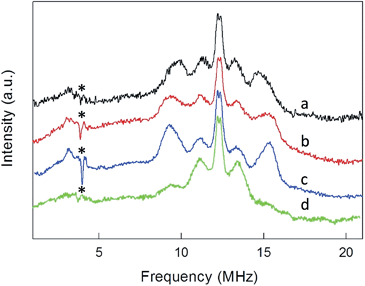
ENDOR experiments were carried out at 5 K in frozen solutions of 0.5 mM Au25(SR)018 in toluene. The spectra of the four clusters (Fig. 4) show a large background between 2 and 20 MHz due to an ENDOR line of gold atoms.10 By focusing on the region between 8 and 16 MHz, as shown in Fig. 5 for Au25(SBu)018, one can notice the presence of three symmetrical line doublets centered at the Larmor frequency ν. At a magnetic field of 0.29 T, which is the field at which ENDOR spectra were acquired, the Larmor frequency is 12.34 MHz for the protons. The three symmetric doublets are marked by brown (outer), green (middle), or black (inner) lines. Similar ENDOR spectra are observed for the other clusters capped by linear-chain thiolates, but the relative intensity ratios are different.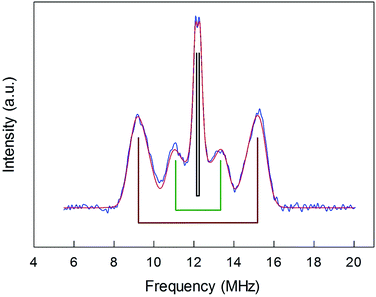 | ||
| Fig. 5 Baseline-corrected 1H-ENDOR spectrum (blue) and simulation (red) for Au25(SBu)018 in toluene at 5 K. The lines mark the outer (brown), middle (green), and inner (black) proton ENDOR doublets. | ||
The simplest case to analyze is Au25(SEt)018. The two proton types and the two ligand families generate four groups of equivalent protons: 24 (α-CH)in, 36 (β-CH)in, 12 (α-CH)out, and 18 (β-CH)out. These groups should give rise to four doublets of lines. Three doublets of lines are clearly observed and positioned symmetrically around the Larmor frequency, whereas a broad line is observed at ca. 3 MHz (Fig. 4, trace a). The latter could be attributed to the low-frequency part of a doublet of lines pertaining to the most strongly coupled protons. However, the corresponding high-frequency component, which should occur at ca. 21 MHz, is almost undetectable in the spectra (not shown). Furthermore, in the region around 3 MHz hyperfine couplings from 13C nuclei could also contribute. This makes uncertain the attribution of this feature to a proton line.
For Au25(SEt)018, the average crystallographic distance between the alkanthiolate protons and the central gold atom increases in the order 6.27 (α-CH)in, 6.92 (β-CH)in, 7.23 (α-CH)out, and 8.26 Å (β-CH)out. The (α-CH)in protons are closer to the gold cluster than the other protons and, therefore, they should give rise to the most strongly coupled doublet. In the hypothesis the 3 MHz line is a proton line, this could be related to the (α-CH)in, in keeping with the aforementioned NMR results. However, the ENDOR lines of the (α-CH)in protons could be simply undetectable, which is indeed not unusual for strongly coupled nuclei. The (β-CH)out protons are located at the largest distance from the center of the Au core and the inner lines are thus attributed to them. The distances characterizing the (β-CH)in and (α-CH)out proton groups are quite similar, in the solid state at least, and thus a direct assignment is difficult. This problem can be addressed by simulation of the ENDOR outer, middle and inner doublets. The spectrum of Au25(SEt)018 is well simulated (ESI, red line in Fig. S6†) by using the parameters shown in Table 1, in which a ratio of 36![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 12 for the intensity of the outer and middle doublets is considered. This ratio corresponds to the ratio between the nuclei (β-CH)in and (α-CH)out. The position of the doublets is also in agreement with the crystallographic relative distances from the central Au atom, which for this cluster are 6.92 vs. 7.23 Å. This allows assigning the outer, middle and inner doublets to (β-CH)in, (α-CH)out, and (β-CH)out, respectively. Regarding the (β-CH)out protons, the simulation provides a number, 14, that does not fully agree with that expected, 18. For weak couplings, however, some differences are not unusual because the ENDOR selectivity effect reduces the ENDOR line intensity, whereas the presence of the proton-free Larmor line (a single line associated with the solvent protons) could contribute to the inner doublet by increasing the line intensity.38 Depending on the prevailing effect, either a decrease or an increase in intensity may occur.
12 for the intensity of the outer and middle doublets is considered. This ratio corresponds to the ratio between the nuclei (β-CH)in and (α-CH)out. The position of the doublets is also in agreement with the crystallographic relative distances from the central Au atom, which for this cluster are 6.92 vs. 7.23 Å. This allows assigning the outer, middle and inner doublets to (β-CH)in, (α-CH)out, and (β-CH)out, respectively. Regarding the (β-CH)out protons, the simulation provides a number, 14, that does not fully agree with that expected, 18. For weak couplings, however, some differences are not unusual because the ENDOR selectivity effect reduces the ENDOR line intensity, whereas the presence of the proton-free Larmor line (a single line associated with the solvent protons) could contribute to the inner doublet by increasing the line intensity.38 Depending on the prevailing effect, either a decrease or an increase in intensity may occur.
For the other clusters, we assign the (β-CH)in and (α-CH)out doublets as for Au25(SEt)018; for (α-CH)in, the above considerations about the broad peak at 3 MHz are also valid. The crystallographic distances of the (β-CH)in and (α-CH)out groups from the cluster's center are similar, i.e., 7.23 and 7.16 Å (Au25(SPr)018), and 7.16 and 7.28 Å (Au25(SBu)018), respectively. In addition to the signals already discussed, the ENDOR spectrum of Au25(SPr)018 is liable to show a contribution also from the 36 (γ-CH)in, whose average crystallographic distance is 8.35 Å, and thus shorter than that of the (β-CH)out protons, 8.64 Å; a similar outcome is observed for Au25(SBu)018 whose values are 8.12 and 8.20 Å, respectively. However, we could still simulate the spectrum of Au25(SPr)018 well (ESI, Fig. S7†) by using for the outer and middle doublets an ENDOR intensity ratio of 24![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 12, which corresponds to the number of equivalent (β-CH)in and (α-CH)out protons. Apparently, no (γ-CH)in protons need to be taken into account. In fact, according to the NMR results, the (γ-CH)in protons could have a hyperfine coupling smaller than that of the (α-CH)out protons but still detectable. However, the room-temperature NMR data cannot be directly compared with the low-temperature ENDOR data. At room temperature, the random motion of the alkyl chain is fast, with the (γ-CH)in atoms moving often closer to the metal core than the (β-CH)in atoms, but NMR spectroscopy only probes the average contact shift. Electron-transfer26 and diffusion-coefficient15 measurements provided evidence for the ligand chains being quite mobile in solution; for example, the D values yield rMPC values smaller than the average radius of the same clusters as calculated from the crystallographic structure. At 5 K, however, whereas the ligands' motion is very limited by the frozen glassy solution, (γ-CH)in can still be present in different conformations. It is thus conceivable that the ENDOR doublet of the (γ-CH)in protons is associated with a wide conformational distribution (larger than that experienced by the β- and, even more, the α-groups) and this would cause significant line broadening and thus spreading of the signal under the outer and middle doublets.
12, which corresponds to the number of equivalent (β-CH)in and (α-CH)out protons. Apparently, no (γ-CH)in protons need to be taken into account. In fact, according to the NMR results, the (γ-CH)in protons could have a hyperfine coupling smaller than that of the (α-CH)out protons but still detectable. However, the room-temperature NMR data cannot be directly compared with the low-temperature ENDOR data. At room temperature, the random motion of the alkyl chain is fast, with the (γ-CH)in atoms moving often closer to the metal core than the (β-CH)in atoms, but NMR spectroscopy only probes the average contact shift. Electron-transfer26 and diffusion-coefficient15 measurements provided evidence for the ligand chains being quite mobile in solution; for example, the D values yield rMPC values smaller than the average radius of the same clusters as calculated from the crystallographic structure. At 5 K, however, whereas the ligands' motion is very limited by the frozen glassy solution, (γ-CH)in can still be present in different conformations. It is thus conceivable that the ENDOR doublet of the (γ-CH)in protons is associated with a wide conformational distribution (larger than that experienced by the β- and, even more, the α-groups) and this would cause significant line broadening and thus spreading of the signal under the outer and middle doublets.
To shed further light onto this issue, it is useful to compare the ENDOR spectra of Au25(SPr)018 and Au25(SMePr)018 (Fig. 6). Whereas in the latter there are 72 (γ-CH)in protons that can contribute to the spectrum, the (β-CH)in and (β-CH)out protons are only 12 and 6, respectively, i.e., one half than those in Au25(SPr)018. Fig. 6 shows that in Au25(SMePr)018 the ENDOR lines of the outer doublet are indeed significantly smaller than those of Au25(SPr)018, and this confirms that for all clusters the outer doublet is consistently associated with the (β-CH)in protons. The increase in the middle doublet is particularly worth noting. This increase is attributed to a strong contribution from the (γ-CH)in protons: compared to those in Au25(SPr)018, in Au25(SMePr)018 these protons have a narrower conformational distribution due to the steric hindrance introduced by the second methyl group. Hindrance not only makes these methyl groups less mobile but also the whole monolayer stiffer and thus the MPC radius larger. Support to this view comes from the electrochemical determination of the D value in dicholoromethane (see ESI and Fig. S5†) and, thus, rMPC value of Au25(SMePr)018: they are 5.16 × 10−6 cm2 s−1 and 10.3 Å, respectively, whereas for Au25(SPr)018 (which has the same fully extended length but more fluid chains in the monolayer) they corresponding values are 6.15 × 10−6 cm2 s−1 and 8.6 Å.15 The simulation of the ENDOR spectrum of Au25(SMePr)018 (ESI, Fig. S7†) was carried out as summarized in Table 1. The number of protons required to obtain the best fit to the inner signals is indeed significantly larger than 6, which in this specific cluster corresponds to the particularly small number of (β-CH)out protons. We note, however, that the average crystallographic distance for the (γ-CH)out protons in Au25(SPr)018 and Au25(SBu)018 is 8.9 Å and thus only slightly larger than for the (β-CH)out protons. A weak coupling is thus expected also for the (γ-CH)out protons: for Au25(SMePr)018 these protons are particularly numerous, 36, and this could make their contribution to the inner ENDOR lines quite significant. This hypothesis is reasonable but not quantifiable also because of the aforementioned problems associated with weak couplings.
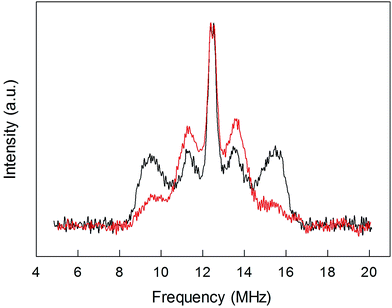 | ||
| Fig. 6 Comparison between the normalized ENDOR spectrum of Au25(SPr)018 (black line) and Au25(SMePr)018 (red line). For comparison, the spectra were normalized for the height. | ||
Regarding Au25(SBu)018 (Fig. 5), the most evident new feature is that the outer lines are higher than the middle lines. However, the number of protons causing an ENDOR line is related to the area, not to the line height. The simulation (ESI, Fig. S8†) results in a ratio of 24![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 12 between the outer and middle lines, in agreement with the attribution of the outer line to (β-CH)in and the middle line to (α-CH)out; the outer lines are just narrower than in Au25(SEt)018 and Au25(SPr)018. As for Au25(SPr)018, conformational distribution would make the contribution of the (γ-CH)in protons spread in the region pertaining to the outer and middle lines. As a matter of fact, the Stokes radius of this cluster, 9.4 Å, is smaller than that of the stiffer Au25(SMePr)018 cluster. Regarding the (β-CH)out protons, the best fit to the inner lines is obtained by using a number of protons, 16, larger than 12. Interestingly, also for Au25(SPr)018 the number is larger, 14. We believe that the reason is as already described for Au25(SMePr)018, i.e., a non vanishingly small contribution from the (γ-CH)out protons.
12 between the outer and middle lines, in agreement with the attribution of the outer line to (β-CH)in and the middle line to (α-CH)out; the outer lines are just narrower than in Au25(SEt)018 and Au25(SPr)018. As for Au25(SPr)018, conformational distribution would make the contribution of the (γ-CH)in protons spread in the region pertaining to the outer and middle lines. As a matter of fact, the Stokes radius of this cluster, 9.4 Å, is smaller than that of the stiffer Au25(SMePr)018 cluster. Regarding the (β-CH)out protons, the best fit to the inner lines is obtained by using a number of protons, 16, larger than 12. Interestingly, also for Au25(SPr)018 the number is larger, 14. We believe that the reason is as already described for Au25(SMePr)018, i.e., a non vanishingly small contribution from the (γ-CH)out protons.
Electron–nucleus interaction
The isotropic coupling is proportional to the spin density on the nucleus. The simulations of the ENDOR spectra provide both the isotropic and the anisotropic hyperfine values. The latter are mainly related to the magnetic dipole–dipole interaction between electron and nucleus, therefore providing geometrical information. This interaction can be described by three main values, Txx, Tyy and Tzz, called hyperfine tensor main values, which are specific for each nucleus.39 Here, the axes x, y, z represent a main reference system whose origin is at the center of the electron spin-distribution (in our case, the gold-cluster center). The values of Txx, Tyy and Tzz can be obtained by averaging spatially the dipole–dipole interaction over the spin distribution, according to the following equation (eqn (2)), exemplified for x: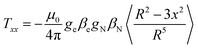 | (2) |
Table 1 shows that the various proton types are consistently in the form [−T, −T, +2T], except for (β-CH)in in Au25(SEt)018 in which a [Txx, Tyy, Tzz] form is observed, with a marked difference between Txx and Tyy. With all cautions already discussed, if we assume that the feature at 3 MHz is due to (α-CH)in protons, its A can be estimated to be around 15–20 MHz. This would be about one order of magnitude larger than the value pertaining to the (α-CH)out protons. In this connection, it is worth recalling that DFT calculations carried out for Au25(SCH2CH2Ph)018 showed that the spin density at (α-CH)in is one order of magnitude larger than at (α-CH)out.17 If we now compare the (β-CH)in and the (α-CH)out isotropic hyperfine couplings for alkanethiolates of increasing length (Table 1, third column), we note an increase in the absolute value of A, particularly in the passage from Et to Pr. This suggest that the ligands are not completely indifferent to the spin distribution in Au25(SR)018, and thus to the SOMO structure.
Another aspect regards the sign of A. According to the theory, the isotropic hyperfine coupling with a nucleus is given by (eqn (3)):
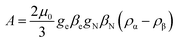 | (3) |
From the simulations, we obtain the sign with respect to [Txx, Tyy, Tzz], i.e., the pattern of the doublet does not change if we were to revert both the sign of A and [Txx, Tyy, Tzz]. However, if we assume that the anisotropic interaction is mainly dipolar, then the form of the anisotropic tensor main values is [−T, −T, +2T] with T > 0, and thus the sign of A is determined as shown in Table 1. Consequently, a negative value in A is an indication that A is mainly determined by spin-polarization through bonds, with a small contribution from direct spin density on the proton nuclei from the SOMO orbital, according to eqn (3). We can thus speculate that the increase of |A| as one goes from Et to Bu is the result of a decreasing, positive contribution to the hyperfine coupling from the direct spin-density of the SOMO, suggesting again that in the Et cluster spin-density is more diffuse toward the ligands than in the Pr or Bu cases.
We can now compare these A values with those obtained from NMR measurements and the DFT-calculated spin density values obtained previously.10,17Table 1 shows that the ENDOR parameters differ from those obtained from the NMR signals in two ways: (i) in ENDOR, the absolute values of A are significantly larger than the equivalent NMR values: 1.3–2.1 log units, except for (β-CH)in in Au25(SMePr)018 whose value is 3.0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) log units; (ii) some of the signs are different. Previous comparisons between the A values obtained from NMR and ENDOR measurements carried out in solution at the same or not very different temperature provided comparable values and the same signs for many radicals.40 Our NMR and the ENDOR experiments, however, refer to very different conditions. In a previous comparison of this kind (for an iron-sulfur cluster),41 similar NMR and ENDOR values were obtained, but the possibility that a strong temperature difference could lead to different results was also commented upon.41 Additionally, we note that compared to previous investigations focusing on quite rigid radical structures and without particularly heavy atoms, here we considered entirely new systems composed of a gold nanocore and many flexible ligands.
log units; (ii) some of the signs are different. Previous comparisons between the A values obtained from NMR and ENDOR measurements carried out in solution at the same or not very different temperature provided comparable values and the same signs for many radicals.40 Our NMR and the ENDOR experiments, however, refer to very different conditions. In a previous comparison of this kind (for an iron-sulfur cluster),41 similar NMR and ENDOR values were obtained, but the possibility that a strong temperature difference could lead to different results was also commented upon.41 Additionally, we note that compared to previous investigations focusing on quite rigid radical structures and without particularly heavy atoms, here we considered entirely new systems composed of a gold nanocore and many flexible ligands.
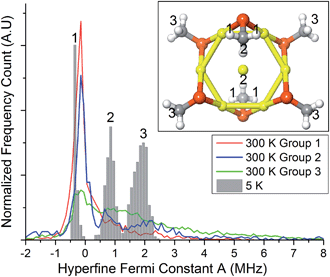
To gain insights into this aspect, we performed ab initio MD calculations by using the Atom Centered Density Matrix Propagation molecular dynamics model (ADMP),42 as implemented in Gaussian 09.43 Because a converged finite-temperature sampling is exceedingly computationally costly, we resorted to use a cluster model consisting of Au7(SCH3)6, which is paramagnetic in the neutral state (Fig. 7, inset). The model consists of a 6 Au atom ring with a central gold core atom. We performed 2 ps MD simulations at 300 and 5 K with a time step of 0.001 fs. Snapshots were collected every 1 fs, for which we evaluated the isotropic Fermi constant.
Despite its simplicity, the model contains protons with different values of A, ranging from negative to positive values. The values for protons in the group 2 and 3 (cf. inset to Fig. 7) come from the unpaired electron in the SOMO, whereas protons in groups 1 have negative values due to spin-polarization. At 300 K, thermal motion tends to reduce spin-polarization on group 1, whereas at 5 K there is a sharp distribution with a peak value (−0.35 MHz) more negative than the peak value at 300 K (−0.15 MHz). This is in qualitative agreement with the ENDOR results for (α-CH)out that show an overall decrease in the absolute value of A. Close inspection of the MD trajectories shows that at 5 K the rotation of the methyl groups is completely frozen in the global energy minimum, whereas at 300 K free rotations cause the direct effect of the spin electron and spin-polarization to roughly average out. The experimental and theoretical results thus point to the emergence, at very low temperature, of a pronounced increase in spin-polarization. These results, therefore, bring some rationale to the change in sign and magnitude observed by carrying out the hyperfine-coupling constant measurements at very different temperatures.
Conclusions
We used four structurally related paramagnetic Au25 clusters to determine how spin density and thus orbital distribution spread onto the protecting alkanethiolate ligands. The structures of two clusters were known, whereas that of the highly symmetric Au25(SPr)018 is described here for the first time. 1H NMR and ENDOR measurements proved to be very sensitive in assessing how the unpaired electron interacts with progressively more distant protons, with significant differences between the two types of ligand. Simulations provided the values of the corresponding hyperfine coupling constants. Interestingly, the experimental and MD results point to an increase of spin-polarization at very low temperature. The results show that the electron–proton interaction extends to the protons at the α, β, and γ positions, with a much stronger interaction for the ligands directly connected to the Au13 icosahedral core. We thus show for the first time that orbital distribution affects atoms that can be as far as 6 Å from the icosahedral core. This information is deemed as essential especially for properly describing the mechanisms of the many reactions already known to be catalyzed by molecular MPCs. As a final remark, we note that the strategy and methodologies here described are suitable to be applied to the study of other molecular clusters (regardless of the actual metal core composition) that already are in the form of free radicals or could generate them by electron transfer.Acknowledgements
This work was financially supported by AIRC (FM, Project 12214: Innovative Tools for cancer risk assessment and early diagnosis – 5 per mille), the Academy of Finland (KR, projects no. 263256 and 292746), and the Office of the Vice President of Research at the University of Connecticut (JG).References
- J. F. Parker, C. A. Fields-Zinna and R. W. Murray, Acc. Chem. Res., 2010, 43, 1289–1296 CrossRef CAS PubMed.
- T. Tsukuda, Bull. Chem. Soc. Jpn., 2012, 85, 151–168 CrossRef CAS.
- H. Qian, M. Zhu, Z. Wu and R. Jin, Acc. Chem. Res., 2012, 45, 1470–1479 CrossRef CAS PubMed.
- Y. Negishi, W. Kurashige, Y. Niihori and K. Nobusada, Phys. Chem. Chem. Phys., 2013, 15, 18736–18751 RSC.
- R. Jin, Nanoscale, 2015, 7, 1549–1565 RSC.
- Protected Metal Clusters: From Fundamentals to Applications, in Frontiers of Nanoscience, ed. T. Tsukuda and H. Häkkinen, Elsevier, Amsterdam, 2015, vol. 9 Search PubMed.
- M. W. Heaven, A. Dass, P. S. White, K. M. Holt and R. W. Murray, J. Am. Chem. Soc., 2008, 130, 3754–3755 CrossRef CAS PubMed.
- M. Zhu, W. T. Eckenhoff, T. Pintauer and R. Jin, J. Phys. Chem. C, 2008, 112, 14221–14224 CAS.
- M. Zhu, C. M. Aikens, F. J. Hollander, G. C. Schatz and R. Jin, J. Am. Chem. Soc., 2008, 130, 5883–5885 CrossRef CAS PubMed.
- T. Dainese, S. Antonello, J. A. Gascón, F. Pan, N. V. Perera, M. Ruzzi, A. Venzo, A. Zoleo, K. Rissanen and F. Maran, ACS Nano, 2014, 8, 3904–3912 CrossRef CAS PubMed.
- M. A. Tofanelli, K. Salorinne, T. W. Ni, S. Malola, B. Newell, B. Phillips, H. Häkkinen and C. J. Ackerson, Chem. Sci., 2016, 7, 1882–1890 RSC.
- M. De Nardi, S. Antonello, D. E. Jiang, F. Pan, K. Rissanen, M. Ruzzi, A. Venzo, A. Zoleo and F. Maran, ACS Nano, 2014, 8, 8505–8512 CrossRef CAS PubMed.
- D. Lee, R. L. Donkers, G. Wang, A. S. Harper and R. W. Murray, J. Am. Chem. Soc., 2004, 126, 6193–6199 CrossRef CAS PubMed.
- S. Antonello, T. Dainese and F. Maran, Electroanalysis, 2016 DOI:10.1002/elan.201600323.
- S. Antonello, T. Dainese, M. De Nardi, L. Perotti and F. Maran, ChemElectroChem, 2016, 3, 1237–1244 CrossRef CAS.
- S. Antonello, N. V. Perera, M. Ruzzi, J. A. Gascón and F. Maran, J. Am. Chem. Soc., 2013, 135, 15585–15594 CrossRef CAS PubMed.
- A. Venzo, S. Antonello, J. A. Gascón, I. Guryanov, R. D. Leapman, N. V. Perera, A. Sousa, M. Zamuner, A. Zanella and F. Maran, Anal. Chem., 2011, 83, 6355–6362 CrossRef CAS PubMed.
- S. H. Yau, O. Varnavski and T. Goodson III, Acc. Chem. Res., 2013, 46, 1506–1516 CrossRef CAS PubMed.
- S. Wang, X. Zhu, T. Cao and M. Zhu, Nanoscale, 2014, 6, 5777–5781 RSC.
- A. Mathew, E. Varghese, S. Choudhury, S. K. Pal and T. Pradeep, Nanoscale, 2015, 7, 14305–14315 RSC.
- X. Yuan, N. Goswami, W. Chen, Q. Yao and J. Xie, Chem. Commun., 2016, 52, 5234–5237 RSC.
- S. Knoppe and T. Bürgi, Acc. Chem. Res., 2014, 47, 1318–1326 CrossRef CAS PubMed.
- S. Antonello, A. H. Holm, E. Instuli and F. Maran, J. Am. Chem. Soc., 2007, 129, 9836–9837 CrossRef CAS PubMed.
- Z. Liu, M. Zhu, X. Meng, G. Xu and R. Jin, J. Phys. Chem. Lett., 2011, 2, 2104–2109 CrossRef CAS.
- S. Antonello, M. Hesari, F. Polo and F. Maran, Nanoscale, 2012, 4, 5333–5342 RSC.
- S. Antonello, G. Arrigoni, T. Dainese, M. De Nardi, G. Parisio, L. Perotti, A. René, A. Venzo and F. Maran, ACS Nano, 2014, 8, 2788–2795 CrossRef CAS PubMed.
- G. Li and R. Jin, Acc. Chem. Res., 2013, 46, 1749–1758 CrossRef CAS PubMed.
- J. Akola, M. Walter, R. L. Whetten, H. Häkkinen and H. Grönbeck, J. Am. Chem. Soc., 2008, 130, 3756–3757 CrossRef CAS PubMed.
- D.-E. Jiang, Nanoscale, 2013, 5, 7149–7160 RSC.
- A. Fernando, K. L. D. M. Weerawardene, N. V. Karimova and C. M. Aikens, Chem. Rev., 2015, 115, 6112–6216 CrossRef CAS PubMed.
- M. Zhu, C. M. Aikens, M. P. Hendrich, R. Gupta, H. Qian, G. C. Schatz and R. Jin, J. Am. Chem. Soc., 2009, 131, 2490–2492 CrossRef CAS PubMed.
- J. F. Parker, J.-P. Choi, W. Wang and R. W. Murray, J. Phys. Chem. C, 2008, 112, 13976–13981 CAS.
- A. Tlahuice-Flores, R. L. Whetten and M. Jose-Yacaman, J. Phys. Chem. C, 2013, 117, 20867–20875 CAS.
- S. E. Crawford, C. M. Andolina, A. M. Smith, L. E. Marbella, K. A. Johnston, P. J. Straney, M. J. Hartmann and J. E. Millstone, J. Am. Chem. Soc., 2015, 137, 14423–14429 CrossRef CAS PubMed.
- R. Guo and R. W. Murray, J. Am. Chem. Soc., 2005, 127, 12140–12143 CrossRef CAS PubMed.
- E. R. Davies, Phys. Lett. A, 1974, 47, 1–2 CrossRef CAS.
- I. Bertini, C. Luchinat and G. Parigi, Prog. Nucl. Magn. Reson. Spectrosc., 2002, 40, 249–273 CrossRef CAS.
- A. Schweiger and G. Jeschke, Principles of pulse electron paramagnetic resonance, Oxford University Press, Oxford, 2001 Search PubMed.
- J. Weil and J. R. Bolton, Electron paramagnetic resonance. Elementary Theory and Practical Applications, Wiley-Interscience, Hoboken, NJ, 2nd edn, 2007, pp. 50–51 Search PubMed.
- S. F. Nelsen, P. A. Petillo, J. De Felippis, Y. Wang, L.-J. Chen, M. J. R. Yunta and F. A. Neugebauer, J. Am. Chem. Soc., 1993, 115, 5608–5615 CrossRef CAS.
- J.-M. Mouesca, G. Rius and B. Lamotte, J. Am. Chem. Soc., 1993, 115, 4714–4731 CrossRef CAS.
- S. S. Iyengar, H. B. Schlegel, J. M. Millam, G. A. Voth, G. E. Scuseria and M. J. Frisch, J. Chem. Phys., 2001, 115, 10291–10302 CrossRef CAS.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery Jr, J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, Ö. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski, and D. J. Fox, Gaussian 9 (Revision E.01), Gaussian Inc., Wallingford, CT, 2009 Search PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: Details on the synthesis and characterization of Au25(SPr)018 and Au25(SMePr)018, full NMR spectroscopy data, electrochemistry, simulation of the ENDOR spectra, DFT calculations, and X-ray crystallography, including check CIF file. CCDC 1453036. For ESI and crystallographic data in CIF or other electronic format see DOI: 10.1039/c6sc03691k |
| This journal is © The Royal Society of Chemistry 2016 |