Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Polymorphism at 129 dictates metastable conformations of the human prion protein N-terminal β-sheet†
S. Alexis
Paz
 a,
Eric
Vanden-Eijnden
b and
Cameron F.
Abrams
a,
Eric
Vanden-Eijnden
b and
Cameron F.
Abrams
 *a
*a
aDepartment of Chemical and Biological Engineering, Drexel University, Philadelphia, PA 19104, USA. E-mail: cfa22@drexel.edu
bCourant Institute of Mathematical Sciences, New York University, New York, NY 10012, USA
First published on 30th September 2016
Abstract
We study the thermodynamic stability of the native state of the human prion protein using a new free-energy method, replica-exchange on-the-fly parameterization. This method is designed to overcome hidden-variable sampling limitations to yield nearly error-free free-energy profiles along a conformational coordinate. We confirm that all four (M129V, D178N) polymorphs have a ground-state conformation with three intact β-sheet hydrogen bonds. Additionally, they are observed to have distinct metastabilities determined by the side-chain at position 129. We rationalize these findings with reference to the prion “strain” hypothesis, which links the variety of transmissible spongiform encephalopathy phenotypes to conformationally distinct infectious prion forms and classifies distinct phenotypes of sporadic Creutzfeldt-Jakob disease based solely on the 129 polymorphism. Because such metastable structures are not easily observed in structural experiments, our approach could potentially provide new insights into the conformational origins of prion diseases and other pathologies arising from protein misfolding and aggregation.
1 Introduction
Transmissible spongiform encephalopathies (TSE's) are a collection of neurodegenerative diseases associated with the misfolding and aggregation of the prion protein (PrP). It is widely accepted that the key phenomenon in pathogenesis is the isomerization of the mostly α-helical native cellular protein (PrPC) into a β-sheet-rich misfolded conformation termed “scrapie” (PrPSc).1 The “protein-only” hypothesis maintains that this transformation is catalyzed only by PrPSc, which underlies the transmissible nature of prion diseases. However, there is an unusually large spectrum of TSE phenotypes, even within the same animal species, which is difficult to reconcile with the existence of a single PrPSc state. It has therefore been hypothesized that TSE phenotypic differences arise from different PrPSc strains which are primarily marked by conformational differences.2–9A methionine–valine polymorphism observed in codon 129 of the PRPN gene has a strong influence on susceptibility to human prion diseases.10–12 Clinical aspects and neuropathology of sporadic Creutzfeldt-Jakob disease (sCJD), which represents ∼75% of all prion disease cases,8,13,14 significantly vary depending on whether the patient is homozygous for methionine (MM), for valine (VV) or heterozygous (MV). The 129 polymorphism has acquired a central role in attempts to develop early diagnostic15,16 and phenotypic classification6,7,9,17 of sCJD. This suggests that residue 129 somehow controls which prion strains emerge in sCJD cases.3 Moreover, to date all confirmed cases of variant CJD, which, distressingly, is associated with the epidemic of bovine spongiform encephalopathy,18 correspond to MM homozygosity at codon 129,9,19 and homozygosity also seems to increase susceptibility to iatrogenic CJD.12,20 Finally, one of the most striking examples of 129's influence relates to mutation D178N, which causes genetic CJD if residue 129 is valine and Fatal Familial Insomnia (FFI) if residue 129 is methionine.17,21
The lack of a structural basis for the apparent correspondence between phenotypic and genotypic variability, especially in relation to residue 129, is a major complication in understanding the prion strain phenomenon. To begin to provide such structural insight, we focus in the contribution of the small antiparallel β strands of PrPC. This structure is of particular interest for two reasons. First, the β1 strand begins precisely at residue 129. Second, there are at least two conformational changes to PrPC that could conceivably lead to the β-sheet-driven aggregation characteristic of TSE's: (i) elongation of the loop anchored by the β1 and β2 strands to form a β-hairpin that could attach to similar hairpins in other protomers,22 and (ii) breaking of the two β strands to enable either (a) a registry of H-bonds in the β strand distinct from that in native PrPC or (b) interprotomer β-sheet assembly and further aggregation.23 In this “PrPC-breaking” hypothesis, the small PrPC β-sheet represents an energy barrier for PrPC misfolding and aggregation.
This work is based on the idea that conformational differences among difficult-to-observe metastable intermediates on the PrPC → PrPSc pathway could underlie 129's multifaceted influence. We explore this idea by direct measurement of the thermodynamics associated with the PrPC β-sheet in all-atom explicit-solvent molecular dynamics (MD) simulations. In particular, we compute the free energy along a collective variable (CV) that measures the degree of “intactness” of the set of four hydrogen bonds that define the PrPC β sheet.24,25 Like all CV's, this one is chosen to represent a process that would never spontaneously occur on limited MD timescales at any physically relevant temperature, so a direct CV-biasing method is required. Importantly, however, we show that thermodynamically comparing the mutants associated with the 129/178 polymorphs requires much higher precision (≪1 kcal mol−1) than is typically available in existing free-energy methods, due to the common problem of “hidden variables”;26,27i.e., variables not explicitly biased in the calculation are not ergodically sampled and therefore stymie sampling of the CV of interest. To meet this challenge in the study of PrPC, we report here the development of a new free-energy method termed replica-exchange on-the-fly free-energy parameterization (RE-OTFP), which seems uniquely effective at overcoming the hidden-variable problem and is able to produce free-energy profiles of high-enough precision to distinguish roles played by point mutations in the stability of the PrPC β-sheet.
This paper is organized as follows. We first present RE-OTFP in context of current methods of CV-biasing in order to explain its advantages. As calibration, we first report its performance on measuring the free energy of the β sheet in the mouse PrPC relative to other methods. We then describe the detailed simulation protocols used to simulate the four 129/178 double-mutants of human PrPC (HuPrPC). We then present and discuss our results, with particular emphasis on the role of 129 in the determination of whether a β-sheet breaking or elongation conformational phenotype is preferred.
2 Methods
2.1 Replica exchange on-the-fly parameterization
CV's are a standard way to simplify the description of complex systems. Free-energy minima in CV space correspond to metastable states, and working in CV space therefore provides a framework for identifying such states for further characterization. Projecting the 3N-dimensional configuration space of the N-atom system x ∈![[Doublestruck R]](https://www.rsc.org/images/entities/char_e175.gif) 3N onto a chosen lower-dimensional CV space z ∈
3N onto a chosen lower-dimensional CV space z ∈ ![[Doublestruck R]](https://www.rsc.org/images/entities/char_e175.gif) Mvia mapping functions θ: x ↦
Mvia mapping functions θ: x ↦ ![[Doublestruck R]](https://www.rsc.org/images/entities/char_e175.gif) M gives rise to a free-energy landscape (FEL) given by
M gives rise to a free-energy landscape (FEL) given by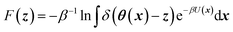 | (1) |
TAMD introduces auxiliary variables z into an MD simulation, and these are tethered to θ(x) via harmonic springs, such that 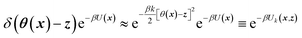 . Replacing the delta-function in eqn (1) with the Gaussian factor defines the mollified estimate of the free energy:
. Replacing the delta-function in eqn (1) with the Gaussian factor defines the mollified estimate of the free energy:
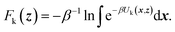 | (2) |
The equations of motion of z are tuned such they feel negative gradients in Fk(z) as if they were conservative forces; providing the z with a higher “auxiliary” temperature ![[small beta, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0c3.gif) −1 > β−1 gives them the ability to overcome free-energy barriers and therefore better sample CV space than would a projection of any finite thermal MD simulation. OTFP accumulates the estimators of ∇F(z) in a TAMD simulation and, positing a basis-function expansion of F(z), uses them to find optimal coefficients in that expansion, providing an estimate for F(z). That is, TAMD ensures good sampling of CV space by overcoming free-energy barriers and OTFP actually computes the FEL.41 A key feature in the efficiency of OTFP is that estimates of local free-energy gradients converge more quickly than does the uniformity of sampling of CV-space.
−1 > β−1 gives them the ability to overcome free-energy barriers and therefore better sample CV space than would a projection of any finite thermal MD simulation. OTFP accumulates the estimators of ∇F(z) in a TAMD simulation and, positing a basis-function expansion of F(z), uses them to find optimal coefficients in that expansion, providing an estimate for F(z). That is, TAMD ensures good sampling of CV space by overcoming free-energy barriers and OTFP actually computes the FEL.41 A key feature in the efficiency of OTFP is that estimates of local free-energy gradients converge more quickly than does the uniformity of sampling of CV-space.
Replica-exchange molecular dynamics (REMD) can be implemented on top of TAMD in the following way. Consider an artificial system built up of R replicas of a TAMD system, each replica with its own real and auxiliary temperatures. Replicas are labeled following the convention β1 > β2 > … > βR and the auxiliary temperatures can be taken arbitrarily. Let ρ(x1, z1, …, xR, zR) denote the joint distribution of the R replicas. It is given by
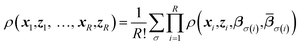 | (3) |
ρ(x,z,β,![[small beta, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0c3.gif) ) = ρ(x|z,β)ρ(z,β, ) = ρ(x|z,β)ρ(z,β,![[small beta, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0c3.gif) ) ) | (4) |
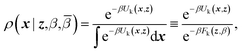 | (5) |
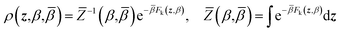 | (6) |
Eqn (4) says that the x variables are effectively at equilibrium with (i.e., adiabatically slaved to) the z variables and feel the temperature β, whereas the variables z navigate on the mollified free energy computed at temperature β, Fk(z,β), but feel the auxiliary temperature ![[small beta, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0c3.gif) . Assume now that we attempt to exchange the temperatures between replica i having positions (xi,zi) and temperatures (βi,
. Assume now that we attempt to exchange the temperatures between replica i having positions (xi,zi) and temperatures (βi,![[small beta, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0c3.gif) i), and replica j having positions (xj, zj) and temperatures (βj,
i), and replica j having positions (xj, zj) and temperatures (βj,![[small beta, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0c3.gif) j), so that, if the move is accepted, immediately after this move replica i is now at temperatures (βj,
j), so that, if the move is accepted, immediately after this move replica i is now at temperatures (βj,![[small beta, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0c3.gif) j) and replica j at temperatures (βi,
j) and replica j at temperatures (βi,![[small beta, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0c3.gif) i), with their respective positions unchanged. The metropolis acceptance probability of this move is
i), with their respective positions unchanged. The metropolis acceptance probability of this move is
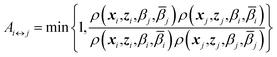 | (7) |
Using (4), the factor involving ratios of ρ's can be written explicitly
| Ai↔j = min{1,exp(Δi,j)} | (8) |
Δi,j = (βj − βi)(Uk(xj,zj) − Uk(xi,zi)) + (![[small beta, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0c3.gif) j − βj)(Fk(zj,βj) − Fk(zi,βj)) + ( j − βj)(Fk(zj,βj) − Fk(zi,βj)) + (![[small beta, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0c3.gif) i − βi)(Fk(zi,βi) − Fk(zj,βi)) i − βi)(Fk(zi,βi) − Fk(zj,βi)) | (9) |
As can be appreciated from eqn (8), the acceptance criterion requires as input the free energies at the two replica temperatures, F(z,βi) and F(z,βj), each evaluated at both points in z-space, zj and zi. We propose here to use OTFP to estimate the free energy differences needed in the acceptance criterion. As the simulation progresses, the computed FEL of each replica will be continuously refined via OTFP.
Exchange moves between adjacent replicas are attempted at regular intervals. Furthermore, many trials can be performed simultaneously: it is a common practice to consider only neighboring replicas for exchange which allows ∼R/2 independent simultaneous attempts. In each attempt, the (groups of) processors running the ith and jth replica communicate to each other their instantaneous values of zi and zj respectively. Then, each processor can compute the values of F(zj,βi) − F(zi,βi) and F(zj,βj) − F(zi,βj) as needed. One of the processors communicates back the value obtained and its instantaneous value of Uk(x,z). The other processor will use this information to compute if the exchange is accepted using eqn (8). If is accepted, only the real and auxiliary temperatures are swapped. Finally, the momenta associated with xi and xj are rescaled using the factors  and
and 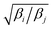 respectively.44 Since we evolve the auxiliary variables using Brownian dynamics, there is no momentum associated with them. However, if different stochastic dynamics are used, equivalent scaling factors using the auxiliary temperatures should be applied.
respectively.44 Since we evolve the auxiliary variables using Brownian dynamics, there is no momentum associated with them. However, if different stochastic dynamics are used, equivalent scaling factors using the auxiliary temperatures should be applied.
We have given the name “replica-exchange on-the-fly free-energy parameterization” (RE-OTFP) to the present combination of REMD and TAMD with OTFP. Note that the RE-OTFP has similarities with PT-WTMD.37 This becomes evident in the comparison of the acceptance rules for both methods: it is possible to shown that the two terms with the free-energy differences in eqn (9) are equivalent to the two bias terms in the acceptance rule of PT-WTMD. The analogy between RE-OTFP and PT-WTMD is not surprising, considering the similarities between OTFP and WTMD pointed out in our previous work.25 Note, however, that there is no history-dependent bias in RE-OTFP.
2.2 Simulation set-up and protocols
The number of replicas and their corresponding temperatures are important choices that can drastically affect sampling in a replica exchange simulation. Following Kone and Kofke,45 the average acceptance probability can be approximated as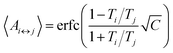 | (10) |
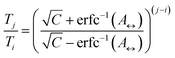 | (11) |
Another fundamental factor in the success of an RE-OTFP simulation is the choice of the auxiliary temperatures for each replica. This parameter defines the acceleration strength of each TAMD replica and will also affect the acceptance probability of the exchange between them (eqn (8)). In the present study we choose a constant auxiliary temperature ![[T with combining macron]](https://www.rsc.org/images/entities/i_char_0054_0304.gif) i = 3000 K for all replicas. This is the same auxiliary temperature using in our previous work,25 which means that the replica here at 300 K will experience the same bias as in that work. However, other choices for
i = 3000 K for all replicas. This is the same auxiliary temperature using in our previous work,25 which means that the replica here at 300 K will experience the same bias as in that work. However, other choices for ![[T with combining macron]](https://www.rsc.org/images/entities/i_char_0054_0304.gif) i are possible and will be carefully studied in future works.
i are possible and will be carefully studied in future works.
All simulations presented in this work were performed using NAMD 2.9 (ref. 47) and the CHARMM force field48 with CMAP corrections.49 The system details as well as the equilibration procedure used to obtain the initial configuration of the mouse prion protein (MoPrP) are described elsewhere.25 An analogous protocol was used for the human prion protein HuPrP-129M: after solvating the NMR structure50 (PDB ID: 1HJM), 110 ns of equilibration were run while keeping the protein fixed during the first 5 ns. Mutant D178N-129M was constructed by substituting residue 178 in this equilibrated system and was subsequently equilibrated for 50 ns. The 129-valine polymorphs were constructed substituting residue 129 in the HuPrP-129M and D178N-129M equilibrated structures and were subsequently equilibrated another 50 ns. The details of these preliminary simulations and their RMSDs are included in the ESI.†
RE-OTFP replicas were simulated in the NVT ensemble in agreement with eqn (8). The temperature was controlled using a Langevin thermostat with a damping constant of 50 ps−1. We devised a standard protocol for RE-OTFP simulations comprising four stages:
All RE-OTFP simulations of the prion protein genotypes use 1 ns of initialization, 8 ns of equilibration and 1 ns in the reset stage. The production stage involve 18 ns for MoPrP system and 28 ns for HuPrP and D178N polymorphs.
2.3 Validating RE-OTFP with alanine dipeptide
As a further validation of the present RE-OTFP method, we include in Section 3 of the ESI† the 1-D FEL reconstructions for the ψ and ϕ angles of alanine dipeptide in water. The simulation parameters for this system where identical to those used for the prion systems. The obtained profiles were compared with those obtained from 74 ns of pure REMD and showed excellent agreement.3 Results
3.1 RE-OTFP performance on mouse PrpC
We first characterize the performance of RE-OTFP by reconstructing the FEL of the β-sheet structure of the murine prion protein. The CV is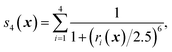 | (12) |
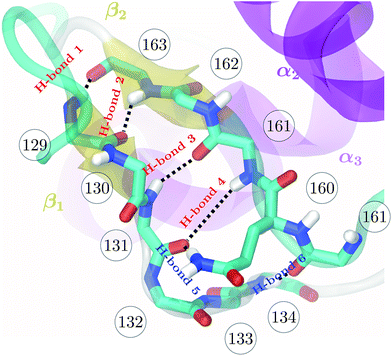 | ||
| Fig. 1 Backbone of the β-sheet structure of the mouse prion protein. Secondary structure, residue numbers and H-bonds labels are included. | ||
We performed three independent RE-OTFP simulations, each consisting of 30 replicas spanning from 295 K to 400 K and lasting 28 ns (18 ns of production). The FELs obtained were in excellent agreement among the three independent simulations, as shown in Fig. 2a for four representative temperatures. It is remarkable that this agreement persists even for the free-energy shoulder at s4 ≈ 3.2, which we showed previously suffers very large errors using WTMD and non-RE OTFP, due to hidden variables.25 In Fig. 2b we show a comparison between the FEL obtained at 300 K via RE-OTFP and the corresponding profile obtained via averaging 16 independent OTFP simulations of 60 ns each from our previous work.25 The remarkable precision observed for the RE-OTFP profiles indicates that the method is able to overcome the hidden barriers that underlie error in this region of CV space and thereby achieve high reproducibility. The dispersion of these profiles is small enough to establish that an independent RE-OTFP simulation can adequately represent the average to much less than 1 kcal mol−1. Despite the small overhead due to replica exchange, the computational effort for a single RE-OTFP simulation yielding sub-kcal errors is 840 ns (30 × 28), which is somewhat lower than the 960 ns (16 × 60) used to obtain the FEL via OTFP with errors of greater than 4 kcal mol−1.25 We show in the ESI† (Sections 3 and 5) evidence that RE-OTFP outperforms OTFP and REMD separately in both sampling the CV and overcoming hidden-variable sampling issues.
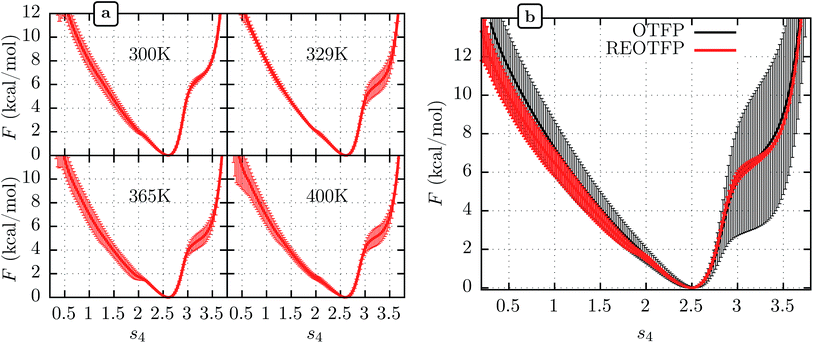 | ||
| Fig. 2 (a) Average free energy landscape (FEL) along s4 for the MoPrPC at different temperatures obtained via RE-OTFP simulations. (b) Comparison between FELs obtained via RE-OTFP and pure OTFP.25 Error bars correspond to ±one standard deviation from independent simulations (RE-OTFP, n = 3; OTFP, n = 16). | ||
The higher precision obtained via RE-OTFP relative to OTFP allows observation of finer details of the FEL's. Fig. 2a shows the averaged FEL for s4 in the MoPrPC at different temperatures. We observe that the free energy shoulder at s4 > 3 decreases with increasing temperature. This effect can be explained on the basis of the competition between H-bond 4 and H-bond 5. While the acceptor group for H-bond 4 is in the backbone of residue 131, H-bond 5 involves the side chain of residue 160. When the temperature increases, it is reasonable to expect an increase in the side-chain flexibility and thus H-bond 5 will be weakened, allowing H-bond 4 to form and contribute to s4. In the opposite direction, Fig. 2 shows the formation of a smaller shoulder near s4 ≈ 1.8 indicating destabilization of the β-sheet at high temperatures. By inspection of the corresponding configurations, we can relate this shoulder to the full detachment of H-bond 3 leading only H-bond 1 and 2 remaining intact.
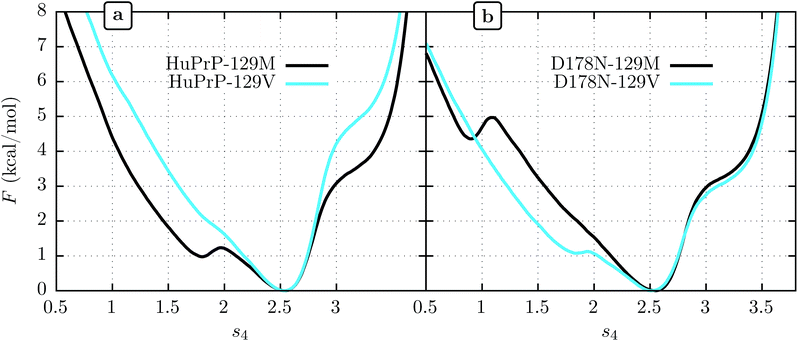
3.2 Human PrPC: effects of 129 and 178 polymorphisms on β-sheet stability
We show FEL's at physiological temperature (309 K) for the human PrPC (HuPrPC) for both M and V genotypes at position 129 in Fig. 3a. We see that in both cases the thermodynamically most stable state falls around s4 = 2.5, similar to MoPrP. However, significant differences appear in the free energy of the surrounding subdomains. While the valine genotype displays a FEL similar to that of MoPrPC, the methionine genotype shows a striking secondary free-energy minimum at s4 ≈ 1.8. In Fig. 3b we show the corresponding FEL's for the D178N mutant. Again, the most stable state in all cases is at s4 = 2.5. With the D178N mutation, however, the 129 polymorphism has the opposite effect on the metastabilities on s4 relative to WT: the valine genotype shows a secondary minimum at s4 ≈ 1.8 while the methionine genotype shows no such secondary minimum.One reasonable interpretation of the secondary minimum at s4 ≈ 1.8 is as an indicator of a propensity of the β-sheet to unfold.23 We see that the valine genotype at 129 therefore stabilizes the β-sheet in the D178 background but destabilizes it in the N178 background. Within this interpretation, a comment must be added in respect to the minimum observed at s4 ≈ 0.8 in D178N-129M (Fig. 3b). While this minimum indicates another metastable state present at low s4, it has a free energy of 4.5 kcal mol−1 above the global minimum, which implies a marginal population of near the 0.3% of the equilibrium configuration at s4 ≈ 2.5. In contrast, the secondary minima at s4 ≈ 1.8 present in D178N-129V and HuPrP-129M is expected to be more significant in the β-sheet stability because it represent nearly the 20% of the equilibrium configuration.
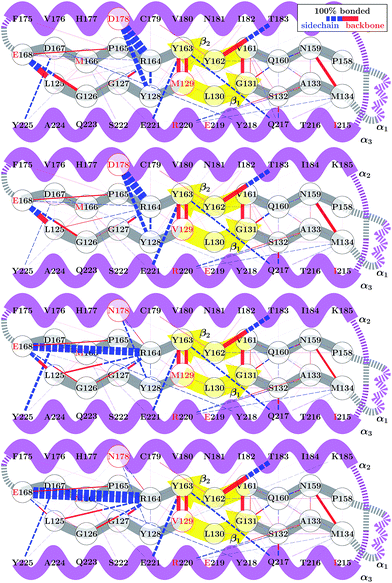
Although the 178 polymorphism has an effect on the H-bond network in the ground-state PrPC conformations, an effect of the 129 polymorphism on these states is not apparent. Fig. 4 shows the H-bond network near residue 178 for the equilibrium configurations (i.e. 2.4 < s4 < 2.6) at 309 K from the REOFTP simulations. The different line widths in the schematic represents the frequency at which we observe each H-bond at a bond distance below 2.5 Å. In the wild-type, the side chain of D178 acts as an H-bond donor and bind the side chain of R164 and Y128. After the mutation D178N is introduced, R164 forms a strong H-bond with E168 and no longer interacts with 178. However, no significant differences in the H-bond network were observed between the different 129 genotypes in the D178N mutant or in the wild-type. The same observations remain true also in the H-bond networks for s4 ≈ 1.8 (see Fig. S11 in the ESI†).
The FEL for the wild-type and mutant polymorphs predicts an equilibrium configuration of s4 ≈ 2.5 in all cases. This is in agreement with the crystal structures for D178N-M129, D178N-V129 and the three structures for HuPrP-129V reported by Lee et al.51 After adding the corresponding hydrogens to these structures we measure values of s4 = 2.57, 2.52, 2.65, 2.61 and 2.51 respectively. Nonetheless, a detailed comparison between the H-bond network from our simulations, presented in Fig. 4, and networks observed in crystal structures is not straightforward. Lee et al. observed several different configurations for the H-bond network surrounding residues 129 and 178, indicating high variability in the side-chain packing for this area.51 The present results also resemble those of Hosszu et al.,52 where the NMR and crystal structure for the two wild type polymorphs are shown to closely match.52 Furthermore, Hosszu et al. find no significant differences in local dynamics and structural stability in measurements of amide protection factors and chemical shifts, which is consistent with our present picture of the H-bond network.
4 Discussion
It has been proposed that conformational changes in the native β-sheet structure may have an important role in the PrPC → PrPSc conversion. The main reason to focus on this small structure is that this conversion should be accompanied by a large increase in the β-sheet content of PrPC. However, two seemingly contrary hypotheses arise from considering the role played by this structure: the β-sheet serves as a seed that guides the elongation as an early stage of the PrPC transformation22 or the native β-sheet must break to allow the transformation to occur.23,53 The results obtained in the present work motivate us to contribute a different hypothesis to this discussion: crossing an energetic barrier associated first with rupture of the native β-sheet or first with elongation of the native β-sheet each commit PrPC to distinct infectious PrPSc forms, and the polymorphism at 129 can favor one or the other. The minima observed at s4 ≈ 1.8 indicate that the methionine genotype seems to be more susceptible to breaking of the native β-sheet structure (Fig. 3). The FEL for the valine genotype indicates an improved native β-sheet stability at physiological temperatures, which is consistent with the idea of an elongation of the native β-sheet structure as a mechanism of conversion.Modern classification schemes for sporadic CJD phenotypes originated with Parchi et al.6–8 In this scheme, two different PrPSc types are defined, and according to patient allele at codon 129, six sporadic CJD sub-types are identified. These sub-types conform very well to the clinical and histological observations. The evidence suggests that each PrPSc type arises from different PrPSc conformations. At the same time, a strong correlation exists between the PrPSc type and the codon 129 allele. PrPSc type 1 presents in 95% of the sporadic CJD patients who are MM homozygous, whereas PrPSc type 2 was present in 86% of the patients who are either VV homozygous or MV heterozygous5,54 The idea that each polymorphism can facilitate two different ways of PrPC → PrPSc interconversion is consistent with these observations. If our hypothesis is correct, we predict that PrPSc type 1, which correlates with the M genotype, arises from a PrPC → PrPSc that proceeds by a mechanism initiated by the breaking of the PrPC native β-sheet structure, while PrPSc type 2 correlates with the V genotype and follows a PrPC → PrPSc reaction through a native β-sheet elongation mechanism.
In the most simplistic projection of this model, the misfolding of a PrPC through β-sheet breaking should lead to a PrPSc type 1 that catalyzes further β-sheet breaking. In this approach, is reasonable to consider that the recruiting of PrPSc type 1 will be significantly affected if many of the PrPC genotypes that reacts are resistant to the β-sheet breaking. The same reasoning applies to the elongation mechanism and PrPSc type 2. Here we are considering that the 129 allele is only tilting the thermodynamic balance to one or other reaction, thus an unfavorable crossing catalysis might still be possible. The observation that homozygosity is not a fully restrictive condition to prion disease might arise from this consideration.
Our hypothesis postulates the existence of a “fork” in the PrPC → PrPSc reaction mechanism that can be affected by the polymorphism 129 via its influence on the β-sheet structure stability. This idea of course does not clarify the full mechanism of PrPC → PrPSc reaction and does not gives any direct insight in the PrPSc aggregation process. Furthermore, besides the classification scheme of Parchi et al., other classification systems exist and more PrPSc types have been observed,9,55 and the existence of several PrPSc types was considered a potential cause.3 Therefore, it is reasonable to consider the possibility of other forks in the PrPC → PrPSc reaction mechanism,56 other thermodynamic/kinetic determinants in the aggregation process4 or even the action of other biomolecules in this process. Nevertheless, the results presented here might give a thermodynamic/kinetic explanation to the important influence of residue 129 in the different disease phenotypes and susceptibilities.
5 Conclusion
We have reported results of all-atom free-energy calculations assessing the stability of the native N-terminal β-sheet of native human PrPC using the new method of replica-exchange on-the-fly-parameterization (RE-OTFP). We showed unprecedentedly high precision of the free-energy landscapes (≪1 kcal mol−1) computed using RE-OTFP and illustrated that RE-OTFP is vastly cheaper on a per-unit-error basis than any current collective-variable biasing free-energy method. We compared free-energy landscapes for the four genotypes arising from the M129V/D178N polymorphs of the human PrPC, which were selected due to the singular importance of these two residues in determining variability of TSE phenotypes. Although all landscapes had the same ground state structure, which agrees with experiment for all polymorphs, we showed clear differences among these free-energy landscapes in the form of new metastabilities. This led us to hypothesize that TSE strains might originate from differences in the energetic accessibility of metastable states that select for either elongation or breaking of the native β-sheet on pathways to distinct infectious PrPSc conformations. The marginal effect of polymorphism 129 in the equilibrium configuration together with the FELs presented indicate that the study of excited PrPC configurations might lead to further insights in the prion phenotype phenomena. Finally, the precision of the FELs generating using RE-OTFP indicate that it might be the method of choice for characterizing thermodynamic stability differences of protein conformations arising from seemingly conservative mutations that do not introduce or destroy any specific interactions but nonetheless lead to distinct functional phenotypes.Acknowledgements
Direct financial support from National Science Foundation (DMR-1207389) is gratefully acknowledged. Work reported here was run on hardware supported by Drexel's University Research Computing Facility and by the Extreme Science and Engineering Discovery Environment (XSEDE),57 which is supported by National Science Foundation grant number ACI-1053575.References
- S. B. Prusiner, Proc. Natl. Acad. Sci. U. S. A., 1998, 95, 13363–13383 CrossRef CAS.
- R. Morales, K. Abid and C. Soto, Biochim. Biophys. Acta, Mol. Basis Dis., 2007, 1772, 681–691 CrossRef CAS PubMed.
- J. Collinge and A. R. Clarke, Science, 2007, 318, 930–936 CrossRef CAS PubMed.
- R. Morales, P. P. Hu, C. Duran-Aniotz, F. Moda, R. Diaz-Espinoza, B. Chen, J. Bravo-Alegria, N. Makarava, I. V. Baskakov and C. Soto, Sci. Rep., 2016, 6, 20526 CrossRef CAS PubMed.
- P. Gambetti, I. Cali, S. Notari, Q. Kong, W.-q. Zou and W. K. Surewicz, Acta Neuropathol., 2011, 121, 79–90 CrossRef CAS PubMed.
- P. Parchi, A. Giese, S. Capellari, P. Brown, W. Schulz-Schaeffer, O. Windl, I. Zerr, H. Budka, N. Kopp, P. Piccardo, S. Poser, A. Rojiani, N. Streichemberger, J. Julien, C. Vital, B. Ghetti, P. Gambetti and H. Kretzschmar, Ann. Neurol., 1999, 46, 224–233 CrossRef CAS PubMed.
- P. Parchi, R. Strammiello, S. Notari, A. Giese, J. P. M. Langeveld, A. Ladogana, I. Zerr, F. Roncaroli, P. Cras, B. Ghetti, M. Pocchiari, H. Kretzschmar and S. Capellari, Acta Neuropathol., 2009, 118, 659–671 CrossRef CAS PubMed.
- G. Puoti, A. Bizzi, G. Forloni, J. G. Safar, F. Tagliavini and P. Gambetti, Lancet Neurol., 2012, 11, 618–628 CrossRef CAS PubMed.
- J. D. F. Wadsworth and J. Collinge, Acta Neuropathol., 2011, 121, 69–77 CrossRef CAS PubMed.
- S. Mead, Science, 2003, 300, 640–643 CrossRef CAS PubMed.
- A. Aguzzi and A. M. Calella, Physiol. Rev., 2009, 89, 1105–1152 CrossRef CAS PubMed.
- M. Imran and S. Mahmood, Virol. J., 2011, 8, 559 CrossRef CAS PubMed.
- W. J. Huang, W. W. Chen and X. Zhang, Eur. Rev. Med. Pharmacol. Sci., 2015, 19, 4028–4034 Search PubMed.
- J. C. Watts, K. Giles, A. Serban, S. Patel, A. Oehler, S. Bhardwaj, S. Guan, M. D. Greicius, B. L. Miller, S. J. DeArmond, M. D. Geschwind and S. B. Prusiner, Ann. Neurol., 2015, 78, 540–553 CrossRef CAS PubMed.
- I. Zerr, K. Kallenberg, D. M. Summers, C. Romero, A. Taratuto, U. Heinemann, M. Breithaupt, D. Varges, B. Meissner, A. Ladogana, M. Schuur, S. Haik, S. J. Collins, G. H. Jansen, G. B. Stokin, J. Pimentel, E. Hewer, D. Collie, P. Smith, H. Roberts, J. P. Brandel, C. Van Duijn, M. Pocchiari, C. Begue, P. Cras, R. G. Will and P. Sanchez-Juan, Brain, 2009, 132, 2659–2668 CrossRef CAS PubMed.
- S. J. Collins, Brain, 2006, 129, 2278–2287 CrossRef CAS PubMed.
- P. Gambetti, Q. Kong, W. Zou, P. Parchi and S. G. Chen, Br. Med. Bull., 2003, 66, 213–239 CrossRef CAS PubMed.
- N. Nathanson, J. Wilesmith and C. Griot, Am. J. Epidemiol., 1997, 145, 959–969 CrossRef CAS PubMed.
- A. Maheshwari, M. Fischer, P. Gambetti, A. Parker, A. Ram, C. Soto, L. Concha-Marambio, Y. Cohen, E. D. Belay, R. A. Maddox, S. Mead, C. Goodman, J. S. Kass, L. B. Schonberger and H. M. Hussein, Emerging Infect. Dis., 2015, 21, 750–759 CrossRef PubMed.
- S. Mead, S. P. Mahal, J. Beck, T. Campbell, M. Farrall, E. Fisher and J. Collinge, Am. J. Hum. Genet., 2001, 69, 1225–1235 CrossRef CAS PubMed.
- P. Gambetti, P. Parchi, R. B. Petersen, S. G. Chen and E. Lugaresi, Brain Pathol., 1995, 5, 43–51 CrossRef CAS.
- S. Prigent and H. Rezaei, Prion, 2011, 5, 69–75 CrossRef CAS PubMed.
- A. Barducci, R. Chelli, P. Procacci, V. Schettino, F. L. Gervasio and M. Parrinello, J. Am. Chem. Soc., 2006, 128, 2705–2710 CrossRef CAS PubMed.
- A. Barducci, G. Bussi and M. Parrinello, Phys. Rev. Lett., 2008, 100, 20603 CrossRef PubMed.
- S. A. Paz and C. F. Abrams, J. Chem. Theory Comput., 2015, 11, 5024–5034 CrossRef CAS PubMed.
- L. Zheng, M. Chen and W. Yang, J. Chem. Phys., 2009, 130, 234105–234115 CrossRef PubMed.
- D. A. Pearlman and P. A. Kollman, J. Chem. Phys., 1989, 91, 7831 CrossRef CAS.
- C. F. Abrams and G. Bussi, Entropy, 2014, 16, 163–199 CrossRef.
- H. Zheng, R. K. Smith, Y.-W. Jun, C. Kisielowski, U. Dahmen and A. P. Alivisatos, Science, 2009, 324, 1309–1312 CrossRef CAS PubMed.
- L. Zheng and W. Yang, J. Chem. Theory Comput., 2012, 8, 810–823 CrossRef CAS PubMed.
- L. Zheng, M. Chen and W. Yang, Proc. Natl. Acad. Sci. U. S. A., 2008, 105, 20227–20232 CrossRef CAS PubMed.
- C. Lu, X. Li, D. Wu, L. Zheng and W. Yang, J. Chem. Theory Comput., 2016, 12, 41–52 CrossRef CAS PubMed.
- U. H. Hansmann, Chem. Phys. Lett., 1997, 281, 140–150 CrossRef CAS.
- D. J. Earl and M. W. Deem, Phys. Chem. Chem. Phys., 2005, 7, 3910–3916 RSC.
- W. Zhang, C. Wu and Y. Duan, J. Chem. Phys., 2005, 123, 1–9 Search PubMed.
- J. F. Dama, M. Parrinello and G. A. Voth, Phys. Rev. Lett., 2014, 112, 240602 CrossRef PubMed.
- M. Deighan, M. Bonomi and J. Pfaendtner, J. Chem. Theory Comput., 2012, 8, 2189–2192 CrossRef CAS PubMed.
- G. Bussi, F. L. Gervasio, A. Laio and M. Parrinello, J. Am. Chem. Soc., 2006, 128, 13435–13441 CrossRef CAS PubMed.
- E. Darve and A. Pohorille, J. Chem. Phys., 2001, 115, 9169 CrossRef CAS.
- E. Darve, D. Rodríguez-Gómez and A. Pohorille, J. Chem. Phys., 2008, 128, 144120 CrossRef PubMed.
- C. F. Abrams and E. Vanden-Eijnden, Chem. Phys. Lett., 2012, 547, 114–119 CrossRef CAS PubMed.
- L. Maragliano, A. Fischer, E. Vanden-Eijnden and G. Ciccotti, J. Chem. Phys., 2006, 125, 24106 CrossRef PubMed.
- C. F. Abrams and E. Vanden-Eijnden, Proc. Natl. Acad. Sci. U. S. A., 2010, 107, 4961–4966 CrossRef CAS PubMed.
- Y. Sugita and Y. Okamoto, Chem. Phys. Lett., 1999, 314, 141–151 CrossRef CAS.
- A. Kone and D. A. Kofke, J. Chem. Phys., 2005, 122, 1–2 CrossRef PubMed.
- N. Rathore, M. Chopra and J. J. de Pablo, J. Chem. Phys., 2005, 122, 024111 CrossRef PubMed.
- J. C. Phillips, R. Braun, W. Wang, J. Gumbart, E. Tajkhorshid, E. Villa, C. Chipot, R. D. Skeel, L. Kalé and K. Schulten, J. Comput. Chem., 2005, 26, 1781–1802 CrossRef CAS PubMed.
- A. D. MacKerell Jr, D. Bashford, M. Bellott, R. L. Dunbrack Jr, J. D. Evanseck, M. J. Field, S. Fischer, J. Gao, H. Guo, S. Ha, D. Joseph-McCarthy, L. Kuchnir, K. Kuczera, F. T. K. Lau, C. Mattos, S. Michnick, T. Ngo, D. T. Nguyen, B. Prodhom, W. E. Reiher III, B. Roux, M. Schlenkrich, J. C. Smith, R. Stote, J. Straub, M. Watanabe, J. Wiorkiewicz-Kuczera, D. Yin and M. Karplus, J. Phys. Chem. B, 1998, 102, 3586–3616 CrossRef PubMed.
- A. D. Mackerell, M. Feig and C. L. Brooks, J. Comput. Chem., 2004, 25, 1400–1415 CrossRef CAS PubMed.
- L. Calzolai and R. Zahn, J. Biol. Chem., 2003, 278, 35592–35596 CrossRef CAS PubMed.
- S. Lee, L. Antony, R. Hartmann, K. J. Knaus, K. Surewicz, W. K. Surewicz and V. C. Yee, EMBO J., 2010, 29, 251–262 CrossRef CAS PubMed.
- L. L. P. Hosszu, G. S. Jackson, C. R. Trevitt, S. Jones, M. Batchelor, D. Bhelt, K. Prodromidou, A. R. Clarke, J. P. Waltho and J. Collinge, J. Biol. Chem., 2004, 279, 28515–28521 CrossRef CAS PubMed.
- L. L. P. Hosszu, M. A. Wells, G. S. Jackson, S. Jones, M. Batchelor, A. R. Clarke, C. J. Craven, J. P. Waltho and J. Collinge, Biochemistry, 2005, 44, 16649–16657 CrossRef CAS PubMed.
- P. Parchi, R. Castellani, S. Capellari, B. Ghetti, K. Young, S. G. Chen, M. Farlow, D. W. Dickson, A. A. F. Sima, J. Q. Trojanowski, R. B. Petersen and P. Gambetti, Ann. Neurol., 1996, 39, 767–778 CrossRef CAS PubMed.
- A. F. Hill, S. Joiner, J. D. F. Wadsworth, K. C. L. Sidle, J. E. Bell, H. Budka, J. W. Ironside and J. Collinge, Brain, 2003, 126, 1333–1346 CrossRef PubMed.
- J. Garrec, I. Tavernelli and U. Rothlisberger, PLoS Comput. Biol., 2013, 9, e1003057 CAS.
- J. Towns, T. Cockerill, M. Dahan, I. Foster, K. Gaither, A. Grimshaw, V. Hazlewood, S. Lathrop, D. Lifka, G. D. Peterson, R. Roskies, J. R. Scott and N. Wilkens-Diehr, Comput. Sci. Eng., 2014, 16, 62–74 CrossRef.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c6sc03275c |
| This journal is © The Royal Society of Chemistry 2017 |