Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Sizing the role of London dispersion in the dissociation of all-meta tert-butyl hexaphenylethane†
Sören
Rösel
a,
Ciro
Balestrieri
b and
Peter R.
Schreiner
 *a
*a
aInstitute of Organic Chemistry, Justus-Liebig University, Heinrich-Buff-Ring 17, 35392 Giessen, Germany. E-mail: prs@uni-giessen.de
bDepartment of Chemical Sciences, University of Padova, Via Marzolo 1, 35131 Padova, Italy
First published on 23rd August 2016
Abstract
The structure and dynamics of enigmatic hexa(3,5-di-tert-butylphenyl)ethane was characterized via NMR spectroscopy for the first time. Our variable temperature NMR analysis demonstrates an enthalpy–entropy compensation that results in a vanishingly low dissociation energy (ΔG298d = −1.60(6) kcal mol−1). An in silico study of increasingly larger all-meta alkyl substituted hexaphenylethane derivatives (Me, iPr, tBu, Cy, 1-Ad) reveals a non-intuitive correlation between increased dimer stability with increasing steric crowding. This stabilization originates from London dispersion as expressed through the increasing polarizability of the alkyl substituents. Substitution with conformationally flexible hydrocarbon moieties, e.g., cyclohexyl, introduces large unfavourable entropy contributions. Therefore, using rigid alkyl groups like tert-butyl or adamantyl as dispersion energy donors (DED) is essential to help stabilize extraordinary bonding situations.
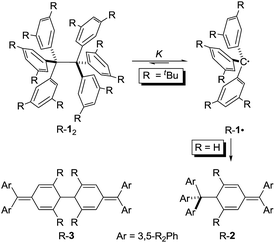
Hexaphenylethane (HPE; H-12) was long assumed to have been synthesized by Gomberg in 1900 in the context of preparing the first organic free radical, the triphenylmethyl radical (H-1·) (Scheme 1).1,2 However, it was shown in 1968 that H-12 rather corresponded to quinoid H-2.3 While steric repulsion between the phenyl moieties was readily made responsible for instability of H-12, the introduction of bulky tert-butyl groups in all meta positions, which should lead to significantly higher steric crowding, resulted in isolable hexa(3,5-di-tert-butylphenyl)ethane (tBu-12) that could even be characterized through X-ray crystal diffraction.4–6 Clearly, this questions our (conceptual) understanding of the balance of steric repulsion vs. noncovalent attraction, and a dispersion energy donor (DED) concept employing large alkyl groups may be invoked to rationalize such surprising bonding situations.7 The classic HPE system therefore seems well suited to probe this concept. Here we report on the challenging re-synthesis and the first NMR-spectroscopic characterization of tBu-12 as well on density functional theory (DFT) computations to gauge the fine balance between Pauli repulsion and London dispersion (LD) attraction.
It is quite remarkable that the structural proposal for H-12 prevailed for almost 70 years because Gomberg himself noted that “Der Körper zeigt in höchstem Maasse die Eigenschaften einer ungesättigten Verbindung” (the substance shows pronounced properties of unsaturation) and readily adds oxygen and halogens.1 He concluded: “Die oben mitgetheilten experimentellen Ergebnisse zwingen mich zu der Annahme, dass in dem ‘ungesättigten Kohlenwasserstoff’ das Radical Triphenylmethyl vorliegt” (the disclosed experimental findings force me to assume that the “unsaturated hydrocarbon” presents the radical triphenylmethyl).1 In addition, the neat colourless hydrocarbon was found to be in equilibrium with a coloured form in solution.8 This triggered an intense discussion regarding the proper structure of triphenylmethyl where, apart from the highly symmetric HPE structure,9 quinoid structures H-210 and H-311 were suggested (Scheme 1). In an early review Gomberg described an equilibrium between an associated and a free radical, the monoquinoidal structure, and HPE.12 In the following years an equilibrium between H-1· and H-12 suggested first by Flürscheim13,14 was gradually accepted and the quinoid structures vanished from the discussion, despite Gomberg mentioning later that a quinoid tautomer of H-1· causes the yellow colour of the solution.15
Notwithstanding the fact that some had misgivings regarding the correct structure of HPE,16 dimer H-12 was generally accepted until Nauta et al. reinvestigated it utilizing 1H-NMR and IR spectroscopies. These studies demonstrated that HPE adopted Jacobsen's monoquinoidal dimer H-2.3 The first computational investigation of H-12 was reported by Mislow et al. utilizing empirical force field (EFF) computations that revealed a very long central RCC of 1.64 Å in H-12 due to the repulsion between the trityl moieties.17 The D3 symmetric structure was found to be 2.6 kcal mol−1 more stable than the S6 structure. A QM/MM (ONIOM) study of 2002 favoured the S6 form and gave a BDE = 16.6 kcal mol−1 for H-12 and a central bond length of 1.72 Å.18
The first isolation of an unbridged HPE derivative was achieved by Rieker in 1978 through the introduction of tert-butyl groups in all 2- and 6-positions onto the Schlenk (tri(4-biphenyl)-methyl) radical.4,5 The previously reported introduction of tBu groups onto the trityl radical H-1· yielded tris(3,5-di-tert-butylphenyl)methyl (tBu-1·) that was found to be monomeric in benzene19 and Rieker concluded that […] steric hindering of formation of the Jacobson–Nauta structure [R-2] by incorporation of bulky groups [in meta and/or para positions], [R-1·] must then either be persistent as the monomer—or dimerize to [R-12].4,5 Indeed, “poor, colourless crystals” could be grown from the orange cyclohexane solution consisting of the first unbridged HPE derivative 1,1,1,2,2,2-hexakis(2,6-di-tert-butyl-[1,1′-biphenyl]-4-yl)ethane (tBu-42).4,5 The dimer crystallized in S6 symmetry with an astonishingly short experimental RCC of only 1.47 Å. Mislow responded with improved EFF and MNDO SCF-MO computations that gave a RCC between 1.62 and 1.68 Å.20 Finally, a central bond length of 1.67 Å was determined from a new crystal structure of tBu-12;6 magic angle spinning (MAS) nutation experiments gave RCC = 1.64–1.65 Å,21 confirming the earlier bond distance and refuting Rieker's structure. Our recent computational reinvestigation of the “HPE riddle” with the modern DFT implementations confirmed these results.22
Both H-2 and tBu-12 afford yellowish-orange, EPR active solutions, in line with very low computed dissociation energies.22 The equilibrium constants for radical formation form the dimers should therefore be accessible by variable temperature NMR spectroscopy despite Rieker's notion that “Because of the high degree of dissociation and the sensitivity of the radical towards traces of oxygen no definite proof of the structure of [tBu-12] can be obtained with 1H-NMR, 13C-NMR, and mass spectroscopy, […]”.4 The stronger magnetic fields available with current NMR spectrometers together with sophisticated techniques encouraged us to investigate the dissociation/association equilibrium of tBu-12.
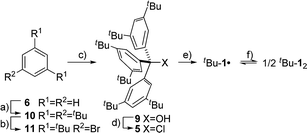
The precursor tris(3,5-di-tert-butylphenyl)methyl chloride (5) was synthesized from benzene (6) via Friedel–Crafts alkylation with tBuCl, ipso-bromination followed by lithiation at −78 °C, subsequent triple addition to diethylcarbonate and chlorination of the central methyl carbon with acetyl chloride (Scheme 2). The classic reduction of 5 to tBu-1· with silver in benzene1,21,23 under meticulous exclusion of oxygen was slow and mainly yielded bis(tri(3,5-di-tert-butylphenyl)methyl) peroxide (7). Even silver derived from reduction of silver nitrate seemed to introduce a significant amount of oxygen. Using the zinc–copper couple instead gave rapid quantitative conversion. The reduction in benzene-d6 resulted in an orange solution with a 1H-NMR spectrum that contained, besides several sharp signals, a very broad peak at δ = 1.88 ppm with a total width of 3 ppm (Fig. 1a, top). The sharp signals were assigned to 7, tris(3,5-di-tert-butylphenyl)methane (8) and tris(3,5-di-tert-butylphenyl)methanol (9) by comparison with the NMR spectra of the pure compounds (cf. ESI†). The sample gave an EPR signal featuring the known spin pattern.19,24 This, together with the known NMR lifetime broadening of organic radicals25 as well as the r−6 line width dependence of the NMR signal with respect to the radical centroid in the molecule,26 made it possible to identify the broad peak as the tert-butyl group hydrogen resonance of tBu-1·.
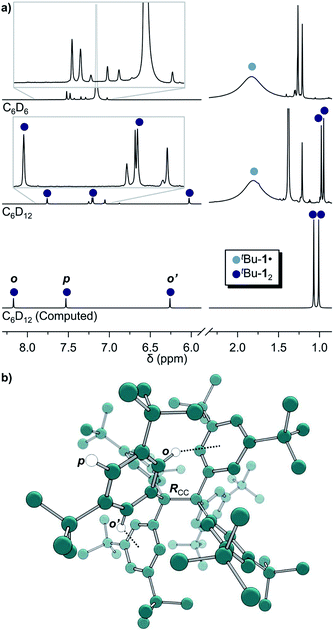 | ||
| Fig. 1 (a) 1H-NMR of tBu-1· in benzene-d6 (top) in equilibrium with tBu-12 in cyclohexane-d12 (middle) and the computed spectrum(ii) of tBu-12 (bottom); see ESI† for full spectra. (b) The structure of tBu-12 for NMR computations. Rcc: exp.4 1.67(3) Å, comp. 1.662 Å. (ii)(B3LYP-D3(BJ)/6-31G(d,p)/C-PCM:cyclohexane). | ||
The in situ radical generation in cylohexane-d12 through reduction with Zn(Cu) is slower as compared to benzene-d6 but gave the same orange solution and a similar 1H-NMR spectrum with five additional peaks at δ = 7.75, 7.19, 6.02, 0.98 and 0.95 ppm in a ratio of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 9
9![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 9, respectively (Fig. 1a, middle). This indicates a highly symmetric structure that would be incompatible with a less symmetric quinoid structure for which an allylic resonance at 5 ppm and a vinylic resonance at 6.4 ppm in a 1
9, respectively (Fig. 1a, middle). This indicates a highly symmetric structure that would be incompatible with a less symmetric quinoid structure for which an allylic resonance at 5 ppm and a vinylic resonance at 6.4 ppm in a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 ratio would be expected.3,27 The spectrum is also in excellent agreement with the B3LYP-D3(BJ)/6-31G(d,p) C-PCM:cyclohexane computed spectrum of tBu-12 (Fig. 1a, bottom).
2 ratio would be expected.3,27 The spectrum is also in excellent agreement with the B3LYP-D3(BJ)/6-31G(d,p) C-PCM:cyclohexane computed spectrum of tBu-12 (Fig. 1a, bottom).
This first 1H-NMR spectrum of an unbridged HPE derivative features a significant chemically inequivalence of the ortho or meta phenyl nuclei (for the 13C-NMR spectrum see the ESI†). The fast inversion of the local helical chirality of an individual trityl group through a two-ring flip mechanism28–30 that makes the two ortho or meta nuclei appear as a single signal at rt is blocked in tBu-12. That is, one edge of the phenyl ring points outside and the other inside towards the S6 axis. While the phenyl groups in the X-ray crystal structure are indistinguishable due to the superposition of four disordered tBu-12 arrangements,6 the computed structure (Fig. 1b) nicely features this structural difference between inside (o′) and outside (o) protons (Fig. 1a, bottom). Fortunately, the equilibrium between the tBu-1· radical and tBu-12 revealed a strong temperature dependence (Fig. 2a), allowing us to determine parameters to calculate the equilibrium constant K at a particular temperature through integration of
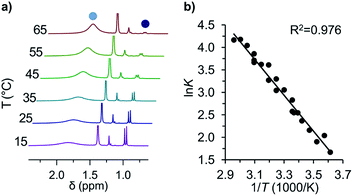 | ||
Fig. 2 (a) Variable temperature 1H-NMR spectra of the equilibrium between tBu-1· ( ) and tBu-12 ( ) and tBu-12 ( ) and (b) the corresponding van't Hoff plot (see ESI† for complete spectra). ) and (b) the corresponding van't Hoff plot (see ESI† for complete spectra). | ||
The van't Hoff plot (Fig. 2b) shows a good linear correlation and ΔG298d = −1.60(6) kcal mol−1 for the homolysis of tBu-12 into two radicals reveals a very low dissociation energy. This ΔG298d value agrees reasonably well with computational predictions of ΔG298d = −3 to +1 kcal mol−1 in cyclohexane with PWPB95-D3/TZV(2d,2p),22 and it is in the range of the weakest experimentally determined ΔG298d of −0.2(1) kcal mol−1 for a C–C single bond reported for the 2,6-di-tert-butyl-4-methoxyphenoxyl dimer (12, Fig. 3).31 As found for 12, ΔH298d of 6.1(5) kcal mol−1 is outbalanced by TΔS298d = 6.3 kcal mol−1 (298 K). We find a similar enthalpy–entropy compensation for tBu-12 with ΔH298d = 7.94(3) kcal mol−1 and TΔS298d = 9.5(3) kcal mol−1 (298 K); this compares well with other weakly bonded hydrocarbons (cf. ESI†).
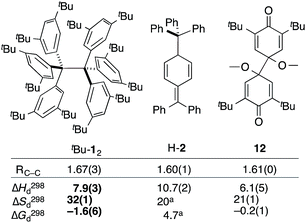 | ||
| Fig. 3 The experimental bond lengths RCC do not correlate well with the bond dissociation enthalpy, entropy, and free energy. Bond lengths given in Å, enthalpies and energies in kcal mol−1, entropies in cal K−1 mol−1. Bold numbers are from this work. aNo error given. tBu-12;6 H-2;32,3312.31 | ||
The dissociation enthalpy of tBu-12 is 2.8 kcal mol−1 smaller than the 10.7(2) kcal mol−1 ΔH298d of H-2,32 while the entropy contribution in tBu-12 is significantly larger (TΔS298d = 6.0 kcal mol−1). This is not surprising because covalent tBu-12 requires much more ordering of the tBu-groups for optimizing the LD interactions, leading to a large, counteracting ΔS contribution. This is likely to be a general phenomenon for structures with large LD contributions because the DEDs often require optimal structural alignment for maximizing the LD interactions.
Differences in LD contributions between gas phase computations and solution experiments were rationalized with a di-n-hexyl substituted Wilcox-type balance by Cockroft and co-workers.34,35 Another approach outlined here is the use of the radical dimerization energies to determine the effect of DEDs on chemical equilibria. While large, polarizable electron donor substituents stabilize the dimers and the free radicals to different degrees, the radicals are stabilized mostly by conjugation. Depending on which radical stability scale one uses, meta alkyl substitution of benzyl radicals may be slightly stabilizing36–38 or destabilizing,39,40 but it is small in all cases. That is, the increased stability of tBu-12 relative to parent H-12 must originate from the LD contributions of the tBu groups.
Does the common measure for bond strengths, the bond dissociation energy (BDE), still apply here? BDEs were initially developed on the basis of small (often diatomic) molecules for which LD is a minor component and the overall bond stability reflects the covalent bond strength. For larger, crowded molecules as R-12 the covalent bond increasingly is influenced by Pauli repulsion and LD attraction. While for H-12 LD attenuates about half of the repulsion, in tBu-12 the increased repulsion must be compensated by LD to a higher degree.41 The difference between the ΔG298d computed in the gas phase (13.7 kcal mol−1)22 and the experimental ΔG298d value measured here (−1.6 kcal mol−1) can be taken as a rough measure of the attenuation of the LD interactions in solution. As the corrections to account for LD effects are large (ca. 60 kcal mol−1),22 a significant LD contribution must therefore persist also in solution. In light of such large LD contributions (cf. Table S3†), the BDE does not seem to be a good measure for the covalent bond strength of the central bond.
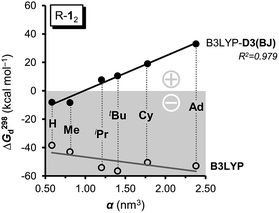
As large-scale computations including properly computed entropy terms can reproduce ΔG298d reasonably well,22 we used more approximate DFT computations to make some qualitative predictions regarding other DEDs in R-12 as model (Fig. 4). We employed the commonly used alkyl groups Me, iPr, tBu, Cy, and 1-Ad as DEDs. With up to 356 atoms in Ad-12 only DFT methods are currently feasible; these computations still take a very long time because of the very flat potentials caused by the rotations of these groups. The B3LYP42,43 functional with the Becke–Johnson damped dispersion correction D3(BJ) introduced by Grimme44,45 as well as the hybrid GGA functional M06-2X46 of Truhlar et al. were used in conjunction with a cc-pVDZ basis set (Table S3†).47 In the HPE derivatives the symmetry was restricted to the S6 point group6,18 (as experimentally observed for tBu-12) while the radical monomers tBu-1· were assumed to have C3 symmetry. The C-PCM model was employed to account for bulk solvent effects.48
First of all, the B3LYP-D3(BJ) and M06-2X results with a cc-pVDZ basis set show the same general trends but diverge significantly as the size of the DED increases (Table S3†). The M06-2X functional is in good agreement for tBu-12 but the trend is not as smooth as with B3LYP-D3(BJ).49 Still, the LD contributions are not merely minor corrections but are quite large, exceeding the magnitude of carbon–carbon bond energies for R = 1-Ad (cf. ESI†). There is a large dispersion correction even in the hitherto unobserved parent system H-12 that is predicted to dissociate with a ΔG298d of less than −5 kcal mol−1.
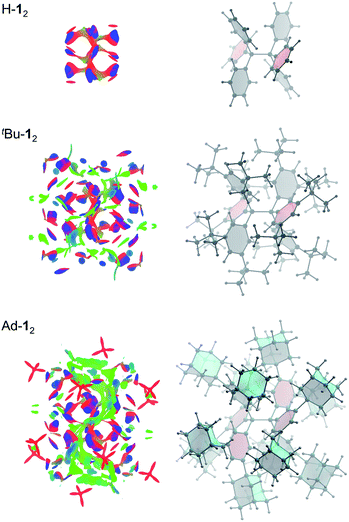
Non-covalent interactions can be visualized by plotting the reduced density gradient in regions of low electron density (NCI plot).50 This enables a qualitative analysis of the balance between repulsive and attractive contact areas. The NCI plots (Fig. 5) of H-12, tBu-12 and Ad-12 visually support the general trend obtained for ΔG298d. Parent H-12 features repulsive (red) areas between phenyl moieties within and between the trityl groups and few attractive (C–H⋯π) interactions (blue). Substitution with tBu groups leads to significant growth of both attractive and repulsive regions in the periphery of the HPE core structure but scattered weak interactions (green) also appear. Finally, Ad-12 clearly shows a dense, weakly interacting region between the substituted trityl moieties. Hence, although the 1-adamantly moieties are even larger than the tBu groups, they exhibit a huge noncovalent contact area that maximizes attractive LD interactions visually outweighing the repulsive regions.
Conclusions
We re-synthesized tBu-12, a member of the elusive class of HPE derivatives, and were able to obtain its dynamic NMR spectrum in equilibrium with the corresponding free radical tBu-1·. The dissociation free energy of ΔG298d (exp.) = −1.60(6) kcal mol−1 confirms computational pre-dictions and is composed of nearly equally large enthalpy and entropy contributions at 298 K. Computations suggest that substitutions with isopropyl and cyclohexyl DEDs also are accompanied by large unfavourable entropy contributions so that it is imperative to use rigid hydrocarbon moieties as DEDs. As a consequence, the introduction of sterically even more demanding 1-adamantyl substituents predicts an even further reduction the central bond length and a significant increase in stability as compared to tBu-12. Counterintuitively, Ad-12 should therefore be an isolable HPE derivative despite the use of even bulkier groups. Hence, large, highly polarizable and rigid hydrocarbon moieties are the most effective DEDs.Acknowledgements
We thank Bart Kahr (NY University) for making his PhD thesis available and H. Hausmann (JLU Giessen) for support with the NMR spectroscopic measurements. This work was supported by the Deutsche Forschungsgemeinschaft, Priority Program “Dispersion” (SPP 1807, Schr 597/27-1).Notes and references
- M. Gomberg, Ber. Dtsch. Chem. Ges., 1900, 33, 3150–3263 CrossRef CAS.
- M. Gomberg, J. Am. Chem. Soc., 1900, 22, 757–771 CrossRef.
- H. Lankamp, W. T. Nauta and C. MacLean, Tetrahedron Lett., 1968, 9, 249–254 CrossRef.
- M. Stein, W. Winter and A. Rieker, Angew. Chem., Int. Ed. Engl., 1978, 17, 692–694 CrossRef.
- M. Stein, W. Winter and A. Rieker, Angew. Chem., 1978, 90, 737–738 CrossRef CAS.
- B. Kahr, D. V. Engen and K. Mislow, J. Am. Chem. Soc., 1986, 108, 8305–8307 CrossRef CAS.
- S. Grimme, R. Huenerbein and S. Ehrlich, ChemPhysChem, 2011, 12, 1258 CrossRef CAS PubMed.
- J. Schmidlin, Ber. Dtsch. Chem. Ges., 1908, 41, 2471–2479 CrossRef CAS.
- A. E. Tschitschibabin, Ber. Dtsch. Chem. Ges., 1904, 37, 4709–4715 CrossRef CAS.
- P. Jacobsen, Ber. Dtsch. Chem. Ges., 1905, 38, 196–199 CrossRef.
- E. Heintschel, Ber. Dtsch. Chem. Ges., 1903, 36, 320–322 CrossRef CAS.
- M. Gomberg, J. Am. Chem. Soc., 1914, 36, 1144–1170 CrossRef.
- B. Flürscheim, J. Appl. Chem., 1905, 71, 497–539 Search PubMed.
- B. Flürscheim, Ber. Dtsch. Chem. Ges., 1908, 41, 2746–2747 CrossRef.
- M. Gomberg, Chem. Rev., 1924, 1, 91–141 CrossRef CAS.
- J. M. McBride, Tetrahedron, 1974, 30, 2009–2022 CrossRef CAS.
- W. D. Hounshell, D. A. Dougherty, J. P. Hummel and K. Mislow, J. Am. Chem. Soc., 1977, 99, 1916–1924 CrossRef CAS.
- T. Vreven and K. Morokuma, J. Phys. Chem. A, 2002, 106, 6167–6170 CrossRef CAS.
- K. Schreiner, A. Berndt and F. Baer, Mol. Phys., 1973, 26, 929–939 CrossRef CAS.
- E. Osawa, Y. Onuki and K. Mislow, J. Am. Chem. Soc., 1981, 103, 7475–7479 CrossRef CAS.
- N. Yannoni, B. Kahr and K. Mislow, J. Am. Chem. Soc., 1988, 110, 6670–6672 CrossRef CAS.
- S. Grimme and P. R. Schreiner, Angew. Chem., Int. Ed., 2011, 50, 12639–12642 CrossRef CAS PubMed.
- M. Stein and A. Rieker, Tetrahedron Lett., 1975, 16, 2123–2126 CrossRef.
- H. Sakurai, H. Umino and H. Sugiyama, J. Am. Chem. Soc., 1980, 102, 6837 CrossRef CAS.
- K. H. Hausser, H. Brunner and J. C. Jochims, Mol. Phys., 1966, 10, 253–260 CrossRef CAS.
- F. Rastrelli and A. Bagno, Chem.–Eur. J., 2009, 15, 7990–8004 CrossRef CAS PubMed.
- C. Chen, H. Lee and R. F. Jordan, Organometallics, 2010, 29, 5373–5381 CrossRef CAS.
- R. J. Kurland, I. I. Schuster and A. K. Colter, J. Am. Chem. Soc., 1965, 87, 2279–2281 CrossRef CAS.
- D. Gust and K. Mislow, J. Am. Chem. Soc., 1973, 95, 1535–1547 CrossRef CAS.
- K. Mislow, Acc. Chem. Res., 1976, 9, 26–33 CrossRef CAS.
- J. M. Wittman, R. Hayoun, W. Kaminsky, M. K. Coggins and J. M. Mayer, J. Am. Chem. Soc., 2013, 135, 12956–12959 CrossRef CAS PubMed.
- W. P. Neumann, W. Uzick and A. K. Zarkadis, J. Am. Chem. Soc., 1986, 108, 3762–3770 CrossRef CAS.
- N. S. Blom, G. Roelofsen and J. A. Kanters, Cryst. Struct. Commun., 1982, 11, 297–304 CAS.
- S. Paliwal, S. Geib and C. S. Wilcox, J. Am. Chem. Soc., 1994, 116, 4497–4498 CrossRef CAS.
- L. X. Yang, C. Adam, G. S. Nichol and S. L. Cockroft, Nat. Chem., 2013, 5, 1006–1010 CrossRef CAS PubMed.
- X. Creary, Acc. Chem. Res., 2006, 39, 761–771 CrossRef CAS PubMed.
- T. H. Fisher, S. M. Dershem and M. L. Prewitt, J. Org. Chem., 1990, 55, 1040–1043 CrossRef CAS.
- R. A. Jackson and R. Moosavi, J. Chem. Soc., Perkin Trans. 2, 1992, 885–888 RSC.
- W. Adam, H. M. Harrer, F. Kita, H.-G. Korth and W. M. Nau, J. Org. Chem., 1997, 62, 1419–1426 CrossRef CAS.
- A. M. D. P. Nicholas and D. R. Arnold, Can. J. Chem., 1986, 64, 270–276 CrossRef CAS.
- R. M. Parrish, J. F. Gonthier, C. Corminboeuf and C. D. Sherrill, J. Chem. Phys., 2015, 143, 051103/1–5 CrossRef PubMed.
- A. D. Becke, J. Chem. Phys., 1993, 98, 5648–5652 CrossRef CAS.
- C. T. Lee, W. T. Yang and R. G. Parr, Phys. Rev. B, 1988, 37, 785–789 CrossRef CAS.
- S. Grimme, S. Ehrlich and L. Goerigk, J. Comput. Chem., 2011, 32, 1456–1465 CrossRef CAS PubMed.
- S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104–154119 CrossRef PubMed.
- Y. Zhao and D. G. Truhlar, Acc. Chem. Res., 2008, 41, 157–167 CrossRef CAS PubMed.
- T. H. Dunning, J. Chem. Phys., 1989, 90, 1007–1023 CrossRef CAS.
- V. Barone and M. Cossi, J. Phys. Chem. A, 1998, 102, 1995–2001 CrossRef CAS.
- S. Grimme, A. Hansen, J. G. Brandenburg and C. Bannwarth, Chem. Rev., 2016, 116, 5105–5154 CrossRef CAS PubMed.
- J. Contreras-García, E. R. Johnson, S. Keinan, R. Chaudret, J.-P. Piquemal, D. N. Beratan and W. Yang, J. Chem. Theory Comput., 2011, 7, 625–632 CrossRef PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: Experimental procedures, spectra and computational details. See DOI: 10.1039/c6sc02727j |
| This journal is © The Royal Society of Chemistry 2017 |