Open Access Article
Open Access ArticleSize-dependence of carbon nanotube confinement in catalysis†
Jianping
Xiao
,
Xiulian
Pan
*,
Fan
Zhang
,
Haobo
Li
and
Xinhe
Bao
*
State Key Laboratory of Catalysis, Dalian Institute of Chemical Physics, Chinese Academy of Sciences, Zhongshan Road 457, Dalian 116023, P. R. China. E-mail: panxl@dicp.ac.cn; xhbao@dicp.ac.cn
First published on 5th August 2016
Abstract
An increasing number of studies have demonstrated that confinement within carbon nanotubes (CNTs) provides an effective approach for the modulation of catalysis. It was generally predicted that confinement became stronger with a decreasing diameter of CNTs. However, our present study here overturns the previous expectation: the influence on catalysis is not monotonic. Instead, it exhibits a volcano relationship with CNT diameter. Taking Pt catalyzing O2 conversion and Re catalyzing N2 conversion as probes using density functional theory, we show that only within tubes with an i.d. of ∼1 nm can the activity of metal clusters be enhanced to its maximum. Furthermore, confinement only enhances the catalytic activity of metals with strong intrinsic binding with reactants, whereas it is suppressed for those with weak binding. These findings shed further light on the fundamental effects of confinement on catalysis, and could guide more rational design of confined catalysts.
Tuning the physical and chemical properties of metal and metal oxide clusters via encapsulation within a confined nanospace of porous materials has attracted increasing attention.1 Carbon nanotubes (CNTs) with a well-defined one-dimensional channel provide an ideal model for studying confined chemistry.2 Peculiar structures were observed for a series of substances even under mild conditions, which otherwise did not exist in the bulk.3 For example, a molecular dynamics (MD) simulation showed that a CNT(6,6) with a diameter of 0.81 nm has a strong effect on water, inducing the formation of a single-file chain structure and facilitating its transport.4 Wang et al.5 further demonstrated that the structure of confined water in wider CNTs becomes more disordered towards that of bulk water. NMR using pulse-field gradient technology demonstrated that the diffusivity of water in CNTs with an i.d. of ∼2 nm is twice that in wider tubes with an i.d. of ∼6 nm.6 In addition, we also observed experimentally that the reduction of encapsulated iron oxide is facilitated more in smaller diameter nanotubes, as evidenced by a stepwise declining reduction temperature with the decreasing diameter of CNTs.7 Therefore, it was accepted that smaller CNTs would exert stronger confinement effects considering their larger curvature and more distorted sp2 hybridization.2 This has prompted wide efforts for growing smaller CNTs with diameters down to less than 0.5 nm8,9 in order to unveil more fascinating chemistry within such nanospaces.
Despite significant progress being made in the synthesis technologies of CNTs with different diameters and morphologies, experimental verification of stronger confinement in a smaller nanospace is still hampered by the availability of CNTs with diameters smaller than 1 nm in reasonable amounts and effective methods to introduce metals into such small nanotubes. Therefore, we turn to density functional theory calculations by carrying out a systematic investigation into the confinement effects in nanotubes with a wide range of inner diameters, by taking the activation and conversion of O2 and N2 catalyzed by Pt and Re, respectively, as probes. With this, we intend to elucidate the size effect of the nanospace on catalysis with particular attention to the underlying mechanism.
To assess this effect, we employed microkinetic modelling and the concept of confinement energy (Econ). Econ is defined as Econ = Eb(in) − Eb(out), as in our previous study,10 where Eb(in) and Eb(out) are the dissociative binding energies of O2 and N2 over an encapsulated metallic cluster and the same sized cluster located outside the same CNTs, respectively. Taking the CNT-encapsulated Pt catalysts as an example, which were shown experimentally with an extraordinary stability and activity in the oxidation of methylbenzene in contrast to conventional supported Pt clusters on a variety of supports.11 The catalyst with Pt clusters encapsulated within the CNT channels is denoted Pt-in, and Pt-out points to the clusters supported on the exterior walls of CNTs.
Although diffusion through nanochannels may slow down the reaction to some extent, this does not seem to offset the confinement effects on catalysis, as demonstrated by numerous studies.6,13,15,28,29 Furthermore, it was also frequently reported that molecules transported faster inside CNTs than in the bulk, e.g. N2, n-heptane9, etc. Although the precise effect of the diffusion on the exterior walls of CNTs is not known yet compared to that inside the interior channels, electronic effects can still be one of the dominant factors for catalytic performance considering the host–guest interactions. Therefore, we only considered the electronic effects in the present work in order to capture the fundamentals of confinement on catalysis. The catalytic oxidation of methylbenzene can be assumed to follow the Langmuir–Hinshelwood mechanism. O2 first adsorbs on the surface and the resulting *O2 adsorbates undergo dissociation. As the dissociation of *O2 is usually much slower than the adsorption process, the dissociation of *O2 is irreversible. Although the rate-determining step of O2 conversion may change over different catalysts,30 it was found that the optimal binding energy to allow desorption of oxygen-containing species is quite close to the optimum required for dissociation. Therefore, it is reasonable to study the trend by assuming the dissociation of *O2 as the rate-determining step. Thus, by referring to a previous report,12 the overall reaction rate at a steady state, r, can be written as:
| r = 2kP(O2)θ*2 | (1) |
We first examined the averaged Eb(O) over 10 different adsorption sites of a supported Pt42 cluster (Pt-out) on the exterior of CNT(18,0) and the same cluster encapsulated in the same CNT (Pt-in), as shown in Fig. 1. The calculated value of Eb(O) over Pt-in is −1.31 eV while it is −1.57 eV over Pt-out, indicating that the binding strength between the adsorbate, O, and the catalyst surface is weakened by 0.26 eV via encapsulation, which is defined as Econ. This is due to the stronger electronic interaction between the encapsulated Pt cluster and the interior wall of the CNT compared to the supported one. Although the confinement effect becomes weaker with decreasing size of the encapsulated Pt clusters in the same CNT, for example, confinement energies of 0.11 eV and 0.03 eV for Pt13 and Pt9 clusters, respectively, the study here by taking one specific cluster size with 9 atoms still allows us to capture a general trend in energetics. Since SWCNTs in experiments frequently contain a certain number of double-walled CNTs (DWCNTs) and triple-walled CNTs (TWCNTs), we examined the effect of the CNT wall thickness on Eb(O). Three nanotubes with the same outer diameter, namely a SWCNT(16,16), a DWCNT(10,10)@(16,16) and a TWCNT(6,6)@(10,10)@(16,16) were checked first. As shown in Table 1, Eb(O) of Pt-out is about −1.23 eV over the SWCNT and it is practically the same within the DWCNT and TWCNT. In addition, encapsulated Pt-in within three nanotubes with the same inner diameter were also examined, i.e. SWCNT(6,6), DWCNT(6,6)@(10,10), and TWCNT(6,6)@(10,10)@(16,16), which show a comparable Eb in the range of 0.07–0.08 eV. Further taking Fe-in and Fe-out as probes (Table 1) validates the negligible effect of CNT wall thickness on Eb of O2 for these metals. Therefore, we will take a SWCNT as a model in the following for the sake of simplicity in the calculations.
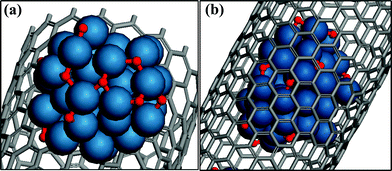 | ||
| Fig. 1 Optimized structures of (a) a Pt42 cluster supported on the outer wall of CNT(18,0) (Pt-out) and (b) a Pt42 cluster encapsulated in CNT(18,0) (Pt-in). | ||
| Location of metal clusters | SWCNT | DWCNT | TWCNT | |||
|---|---|---|---|---|---|---|
| Pt | Fe | Pt | Fe | Pt | Fe | |
| a All units are in eV. | ||||||
| Inside | 0.07 | −2.29 | 0.07 | −2.29 | 0.08 | −2.28 |
| Outside | −1.23 | −3.25 | −1.23 | −3.30 | −1.23 | −3.26 |
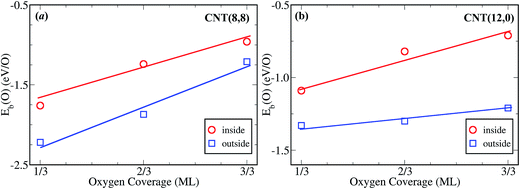
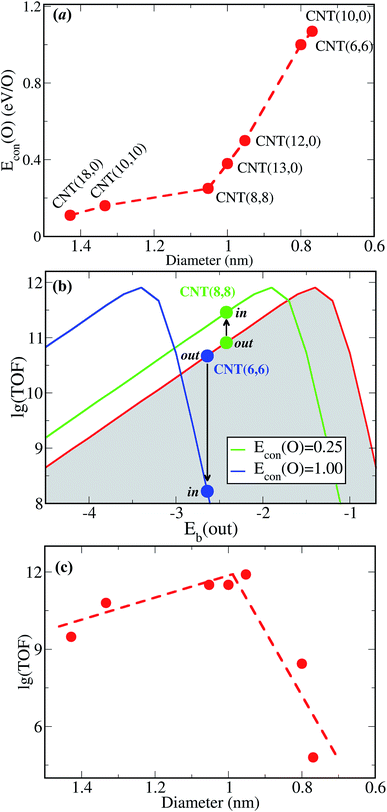
Fig. 2a shows Eb(O) over the Pt-in and Pt-out clusters as a function of coverage (θ). For a CNT(8,8), Eb(O) over Pt-out is ∼2.25 eV at a low oxygen coverage such as θ = 1/3 ML. However, when Pt clusters are placed into the channel of CNT(8,8), Eb(O) reduces by 0.5 eV due to confinement effects. This is also the case at a higher oxygen coverage, implying that it is more difficult for the encapsulated Pt to bind oxygen. Even at a coverage of 2/3 ML, Eb(O) over Pt-out is still slightly stronger (−1.87 eV) than that over Pt-in at θ = 1/3 ML (−1.76 eV). This suggests that encapsulation can protect the Pt clusters from oxidation by oxygen with respect to those exposed on the outer walls of the CNTs (Pt-out). For comparison, within a smaller nanotube CNT(12,0), Eb(O) over Pt-in is again weaker than that over Pt-out (Fig. 2b). More interestingly, Eb(O) over Pt-in at a coverage of 1/3 ML is even weaker than that over Pt-out at a full coverage (1 ML). This means that CNT(12,0) has a greater confinement strength and Pt clusters can be better protected against oxidation than in CNT(8,8). Fig. 3a shows that Econ(O) further increases with decreasing diameter, such as (6,6) and (10,0), almost monotonically as a function of the reciprocal of the diameter. This suggests that the smaller diameter of the CNTs, the more difficult it is to oxidize the encapsulated metal clusters, which is consistent with the previous findings for encapsulated Fe and Fe2O3 in a redox reaction too.7
Although Eb(O) over Pt-in clusters is weakened via encapsulation in comparison with Pt-out, the oxidation activity of the Pt-in catalyst is not suppressed, as observed experimentally. Instead, Pt-in exhibits a higher activity and stability than Pt-out in the oxidation of methylbenzene.11 This is governed mainly by the volcano relationship of catalytic activity versus Eb(O),14 as depicted by the red curve in Fig. 3b. On the left hand side of the volcano curve, oxygen binds the catalyst strongly. Strong binding usually causes a slow diffusion of reactants and more difficult desorption of products from the catalyst surface. In contrast, the catalyst on the right hand of the volcano curve usually exhibits weaker binding with oxygen. Too weak binding will lead to slow adsorption and dissociation of O2 according to the Brønsted–Evans–Polanyi-type relation.15 Thus, the optimum Eb(O) for molecular dioxygen activation can be estimated to be about −1.44 eV/O2 at T = 600 K and P = 3 MPa, according to the microkinetic model (Fig. 3b). Since Eb(O) is weakened via encapsulation in the channel of CNTs, the effective volcano curve of catalytic activity in CNTs shifts toward the metals with higher binding energies, corresponding to the green curve with a confinement energy of Econ(O) = 0.25 eV in CNT(8,8). Hence, the reaction rate on Pt-in-CNT(8,8) is estimated to be enhanced by ∼5 times with respect to that over Pt-out-CNT(8,8), consistent with the trend observed experimentally.11 By decreasing the diameter of CNTs to ∼1.0 nm, the activity of Pt-in can be further enhanced (Fig. 3c).
However, this enhancement does not proceed monotonically with further decreasing the diameter of CNTs. The activity reaches a maximum within a diameter of ∼1 nm and after further reducing the diameter, the reaction is instead inhibited, as demonstrated by the steep drop in activity within CNT(6,6) and CNT(10,0) (Fig. 3c). Their corresponding Econ(O) for encapsulated Pt is ∼1.0 and ∼1.1 eV, respectively. Obviously, this confinement is too strong and leads to overly weakened binding, with Eb(O) = −0.32 eV/O, which is much lower than the optimum −0.72 eV/O. This does not benefit the adsorption and activation of O2. As demonstrated in Fig. 3b, with this Econ(O) (corresponding to the blue curve, 1.0 eV), the turnover frequency (TOF) is significantly reduced, represented by the blue filled dots. In other words, confinement within CNT(6,6) and CNT(10,0) inhibits the oxidation, showing negative effects on the activity of Pt-in. This result overturns the common assumption that smaller tubes provide stronger confinement effects.
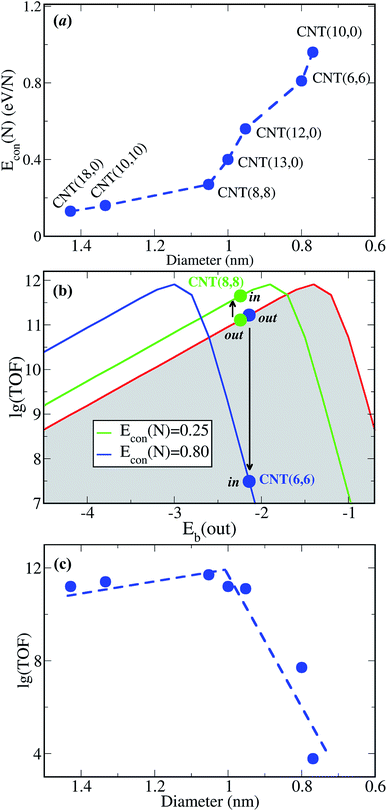
We further examined the generality of this size dependence of confinement, by taking Re as a probe, since Re is a known active metal for ammonia synthesis.18 Interestingly, the binding between N adsorbates and encapsulated Re catalysts is also weakened, as demonstrated by the positive Econ(N) of Re-in in the examined diameter range (Fig. 4a). The binding strength over Re-in becomes weaker as the CNT’s diameter reduces, as for O with Pt-in. The confinement strength on N–Re bonds is slightly weaker than O–Pt within the same CNT. The optimum diameter of CNTs for enhancing N2 conversion is estimated to be ∼1.08 nm (Fig. 4c), within which the activity can be enhanced to a maximal value.
These results further validate our previous finding of tunable catalytic activity by confinement and this can be described by the concept of confinement energy. Confinement generally makes the binding of a reactant on a catalyst weaker. Therefore, it is not desirable to introduce confinement to metals with intrinsically weak or intermediate binding strengths because this will only inhibit their activity, for example, Ru. Lowered CO conversion,10 ammonia synthesis16 or decomposition17 have been reported for the encapsulated Ru catalysts. As the Eb(N) over Ru-out is intermediate (about −1.0 eV) and the Eb(N) becomes weaker within CNTs (about −0.5 eV), resulting in the dissociation of N2 over encapsulated Ru-in being ∼1.5 times slower, agreeing with the observed inhibition of ammonia synthesis.10Eb(CO) over Ru-out is smaller than −1.44 eV, located on the right-hand side of the volcano curve too, while Eb(CO) is smaller by ∼0.5 eV over Ru-in, qualitatively consistent with experimentally measured CO adsorption heat in microcalorimetry.16 In other words, a negative confinement effect will be observed for the catalyst with weak or intermediate intrinsic reactivity.
In contrast, the catalysts which have stronger intrinsic binding with reactants will benefit from encapsulation because weakened binding facilitates desorption and consequently enhances the catalytic activity according to microkinetic modelling, as observed experimentally in CO conversion13,19 over encapsulated Fe and RhMn, and O2 activation11 over Pt-in. Thus, enhanced CO oxidation can be audaciously predicted over confined Pt, which is notorious for binding with CO too strongly and, hence, becoming poisoned. Indeed, recent experiments show that the CO oxidation reaction over Pt nanoparticles was enhanced in a confined 2D space.31 Furthermore, an appropriately sized CNT should be chosen because the confinement effect exhibits a volcano relationship with CNT diameter. Within too small nanotubes, the binding is overly weakened, and thus activation of the reaction molecules is sluggish. Consequently, the overall activity is inhibited according to the Sabatier principle20 and volcano plots.21 The optimum diameter of CNTs is identified to be about 1 nm for both O2 and N2 conversion. However, the optimum diameter may deviate from 1 nm in experiments because of inhomogeneity of the nanotubes and metal clusters. It could vary with specific reactions and chosen metal clusters as well.
With this, a simple descriptor is provided for guiding more rational design of confined catalysts. First of all, confinement only enhances the catalytic activity of metals with intrinsic strong binding with reactants. Secondly, this enhancement is size dependent, exhibiting a volcano relationship. Taking Pt catalyzing oxidation and Re catalyzing N2 conversion as probes, the activity reaches a maximal within a tube with an i.d. of around 1.0 nm. Beyond this diameter, confinement leads to a steep drop in activity due to overly weakened binding under a stronger confinement energy. More interestingly, this concept is also applicable to other confined catalysts and reactions.22–24 For example, CO oxidation was enhanced within a confinement environment generated by an extended Pt surface and two-dimensional boron nitride/graphene sheets, also due to weakened binding of CO.22,23
Computational details
All calculations were carried out using density functional theory (DFT), as implemented in the Vienna ab initio simulation package (VASP).25 The projector augmented wave (PAW) formalism26 in conjunction with the Perdew–Burke–Ernzerhof functional27 was adopted in the total energy calculations. A kinetic energy cutoff of 400 eV was chosen for the plane wave expansion and the k-point was sampled at gamma. In the geometric optimization, the calculated Hellmann–Feynman force was acquired smaller than 0.05 eV Å−1. All CNT models are periodic in the axial (z) direction, and the radial directions (x and y) are separated by a vacuum distance of ∼10 Å. In addition, we considered two representative chiralities of CNTs, i.e. armchair and zigzag. Two semiconducting CNTs (13,0) and (10,0) were also studied for comparison with other metallic ones. The dissociative binding energies of O2 and N2 over the supported and encapsulated catalysts (Fe, Ru, Pt, and Re) were calculated with an analogous definition. Taking the definition of Eb(O) as an example, the chemical potential of oxygen was referred to an O2 molecule in a vacuum. Optimized geometries are given in the ESI.†Acknowledgements
J. X. acknowledges financial support from the Outstanding Postdoctoral Award (DMTO Project) from the Dalian Institute of Chemical Physics, Chinese Academy of Science and the China Postdoctoral Science Foundation (No. 2014M551131). X. P. and X. B. acknowledge support from the Natural Science Foundation of China (21425312 and 21321002). We thank the Shanghai Supercomputer Center for computational resources.References
- (a) E. G. Derouane, J. Catal., 1986, 100, 541 CrossRef CAS; (b) P. Serp and E. Castillejos, ChemCatChem, 2010, 2, 41 CrossRef CAS.
- (a) X. Pan and X. Bao, Chem. Commun., 2008, 6271 RSC; (b) X. Pan and X. Bao, Acc. Chem. Res., 2011, 44, 553 CrossRef CAS PubMed.
- (a) O. Byl, J. C. Liu, Y. Wang, W. L. Yim, J. K. Johnson and J. T. Yates Jr, J. Am. Chem. Soc., 2006, 128, 12090 CrossRef CAS PubMed; (b) P. Kondratyuk and J. T. Yates Jr, Acc. Chem. Res., 2007, 40, 995 CrossRef CAS PubMed; (c) T. Fujimori, A. Morelos-Gómez, Z. Zhu, H. Muramatsu, R. Futamura, K. Urita, M. Terrones, T. Hayashi, M. Endo, S. Y. Hong, Y. C. Choi, D. Tománek and K. Kaneko, Nat. Commun., 2013, 4, 2162 Search PubMed; (d) F. Zhang, P. Ren, X. Pan, J. Liu, M. Li and X. Bao, Chem. Mater., 2015, 27, 1569 CrossRef CAS.
- G. Hummer, J. C. Rasaiah and J. P. Noworyta, Nature, 2001, 414, 188 CrossRef CAS PubMed.
- J. Wang, Y. Zhu, J. Zhou and X. Lu, Phys. Chem. Chem. Phys., 2004, 6, 829 RSC.
- X. Liu, X. Pan, S. Zhang, X. Han and X. Bao, Langmuir, 2014, 30, 8036 CrossRef CAS PubMed.
- W. Chen, X. Pan and X. Bao, J. Am. Chem. Soc., 2007, 129, 7421 CrossRef CAS PubMed.
- (a) N. Wang, Z. K. Tang, G. D. Li and J. S. Chen, Nature, 2000, 408, 426 CrossRef PubMed; (b) X. Zhao, Y. Liu, S. Inoue, T. Suzuki, R. O. Jones and Y. Ando, Phys. Rev. Lett., 2004, 92, 12550 Search PubMed.
- (a) G. U. Sumanasekera, C. K. W. Adu and P. C. Eklund, Phys. Rev. Lett., 2000, 85, 1096 CrossRef CAS PubMed; (b) P. Kondratyuk, Y. Wang, J. Liu, J. K. Johnson and J. T. Yates, J. Phys. Chem. C, 2007, 111, 4578 CrossRef CAS.
- J. Xiao, X. Pan, S. Guo, P. Ren and X. Bao, J. Am. Chem. Soc., 2015, 137, 477 CrossRef CAS PubMed.
- F. Zhang, F. Jiao, X. Pan, K. Gao, J. Xiao, S. Zhang and X. Bao, ACS Catal., 2015, 5, 1381 CrossRef CAS.
- T. Bligaard, J. K. Nørskov, S. Dahl, J. Matthiesen, C. H. Christensen and J. Sehested, J. Catal., 2004, 224, 206 CrossRef CAS.
- W. Chen, Z. Fan, X. Pan and X. Bao, J. Am. Chem. Soc., 2008, 130, 9414 CrossRef CAS PubMed.
- (a) J. K. Nørskov, T. Bligaard, J. Rossmeisl and C. H. Christensen, Nat. Chem., 2009, 1, 37 CrossRef PubMed; (b) J. Greeley, I. E. L. Stephens, A. S. Bondarenko, T. P. Johansson, H. A. Hansen, T. F. Jaramillo, J. Rossmeisl, I. Chorkendorff and J. K. Nørskov, Nat. Chem., 2009, 1, 552 CrossRef CAS PubMed.
- (a) J. K. Nørskov, T. Bligaard, B. Hvolbæk, F. Abild-Pedersen, I. Chorkendorff and C. H. Christensen, Chem. Soc. Rev., 2008, 37, 2163 RSC; (b) A. Michaelides, Z.-P. Liu, C. J. Zhang, A. Alavi, D. A. King and P. Hu, J. Am. Chem. Soc., 2003, 125, 3704 CrossRef CAS PubMed.
- S. Guo, X. Pan, H. Gao, Z. Yang, J. Zhao and X. Bao, Chem.–Eur. J., 2010, 16, 5379 CrossRef CAS PubMed.
- W. Zheng, J. Zhang, B. Zhu, R. Blume, Y. Zhang, K. Schlichte, R. Schlögl, F. Schueth and D. S. Su, ChemSusChem, 2010, 3, 226 CrossRef CAS PubMed.
- T. R. Munter, T. Bligaard, C. H. Christensen and J. K. Nørskov, Phys. Chem. Chem. Phys., 2008, 10, 5202 RSC.
- X. Pan, Z. Fan, W. Chen, Y. Ding, H. Luo and X. Bao, Nat. Mater., 2007, 6, 507 CrossRef CAS PubMed.
- P. Sabatier, Ber. Dtsch. Chem. Ges., 1911, 44, 1984 CrossRef CAS.
- J. K. Nørskov, F. Abild-Pedersen, F. Studt and T. Bligaard, Proc. Natl. Acad. Sci. U. S. A., 2011, 108, 937 CrossRef PubMed.
- Y. Yao, Q. Fu, Y. Zhang, X. Weng, H. Li, M. Chen, L. Jin, A. Dong, R. Mu, P. Jiang, L. Liu, H. Bluhm, Z. Liu, S. Zhang and X. Bao, Proc. Natl. Acad. Sci. U. S. A., 2014, 111, 17023 CrossRef CAS PubMed.
- Y. Zhang, X. Weng, H. Li, H. Li, M. Wei, J. Xiao, Z. Liu, M. Chen, Q. Fu and X. Bao, Nano Lett., 2015, 15, 3616 CrossRef CAS PubMed.
- H. Xiong, Y. Zhang, S. Wang, K. Liew and J. Li, J. Phys. Chem. C, 2008, 112, 9706 CAS.
- G. Kresse and J. Furthmuller, Phys. Rev. B: Condens. Matter, 1996, 54, 11169 CrossRef CAS.
- G. Kresse and D. Joubert, Phys. Rev. B: Condens. Matter, 1999, 59, 1758 CrossRef CAS.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865 CrossRef CAS PubMed.
- H. Zhang, X. Pan, X. Han, X. Liu, X. Wang, W. Shen and X. Bao, Chem. Sci., 2013, 4, 1075 RSC.
- E. Castillejos, P. J. Debouttière, L. Roiban, A. Solhy, V. Martinez, Y. Kihn, O. Ersen, K. Philippot, B. Chaudret and P. Serp, Angew. Chem., Int. Ed., 2009, 48, 2529 CrossRef CAS PubMed.
- J. Xiao, L. Kou, C. Y. Yum, T. Frauenheim and B. Yan, ACS Catal., 2015, 5, 7063 CrossRef CAS.
- L. Gao, Q. Fu, J. Li, Z. Qu and X. Bao, Carbon, 2016, 101, 324 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c6sc02298g |
| This journal is © The Royal Society of Chemistry 2017 |