Open Access Article
Open Access ArticleHow covalence breaks adsorption-energy scaling relations and solvation restores them†
Federico
Calle-Vallejo
*a,
Alexander
Krabbe
b and
Juan M.
García-Lastra
 *b
*b
aLeiden Institute of Chemistry, Leiden University, Einsteinweg 55, 2333 CC Leiden, The Netherlands. E-mail: f.calle.vallejo@chem.leidenuniv.nl
bDepartment of Energy Conversion & Storage, Technical University of Denmark, Fysikvej 309, DK-2800 Kongens Lyngby, Denmark. E-mail: jmgla@dtu.dk
First published on 5th August 2016
Abstract
It is known that breaking the scaling relations between the adsorption energies of *O, *OH, and *OOH is paramount in catalyzing more efficiently the reduction of O2 in fuel cells and its evolution in electrolyzers. Taking metalloporphyrins as a case study, we evaluate here the adsorption energies of those adsorbates on the metal centers Cr, Mn, Fe, Co, Ni and Cu, using H, F, OH, NH2, CH3, and BH2 as ring ligands. We show that covalence systematically breaks scaling relations under vacuum by strengthening certain M–OOH bonds. However, covalence modifies adsorbate solvation in solution depending on the degree of covalence of the metal–adsorbate bonds. The two effects have similar magnitudes and opposite signs, such that scaling relations are restored in solution. Thus, solvation is a crucial ingredient that must be taken into account in studies aimed at breaking scaling relations in solution. Our findings suggest that the choice of metal and ligand determines the catalytic activity within the limits imposed by scaling relations, whereas the choice of an appropriate solvent can drive such activity beyond those limits.
Introduction
Since their discovery almost a decade ago,1 adsorption-energy scaling relations have experienced rapid development2–4 that has, in turn, revolutionized the “in silico” design of catalysts.4,5 Among the numerous fields that benefit from their insight, oxygen electrocatalysis is a prominent example. For the oxygen evolution reaction (OER), scaling relations have provided a simple framework for selecting active catalysts6–9 and revealed the existence of thermodynamic limitations to the efficiency of electrolyzers related to the relative stability of the adsorbed intermediates.6,10If the OER proceeds through a mechanism in which water molecules are transformed into molecular oxygen as follows: H2O → *OH → *O → *OOH → O2, the ideal energetic separation between *OH and *OOH (where * denotes an adsorbed state) should be 2.46 eV. However, it is found to be ∼3.2 eV, estimated from the energetics of: *OH + H2O(l) → *OOH + 2(H+ + e−), regardless of the material types4,6,8–11 and the geometry of their active sites.3 Therefore, there is a substantial “scaling” overpotential ηscalingOER ≈ (3.20 − 2.46) eV/2e− ≈ 0.37 V. Note that such an overpotential is also present in the oxygen reduction reaction (ORR) in proton-exchange membrane fuel cells, at the cathode of which molecular oxygen is transformed into water.12,13 These stringent limitations make the breaking of scaling relations paramount in oxygen electrocatalysis, though only a few examples exist in which the breaking of the *OH vs. *OOH scaling is correlated with an experimental increase in catalytic activity.14,15
Given the versatility of MN4 complexes16 such as porphyrins and their high activities for the OER, the ORR and other reactions,17–20 here we evaluate whether they can break scaling relations by changing the metal centers (Cr, Mn, Fe, Co, Ni, Cu) and ring ligands (H, F, OH, CH3, NH2 and BH2). We show that Ni and Cu centers with various ligands break scaling relations under vacuum by virtue of their highly covalent bonds with *OOH. However, such covalence entails poor solvation in aqueous solution, which restores scaling relations. Thus, scaling relations must be broken in solution, where substrate–solvent–adsorbate interactions are present. This is a simple yet important conclusion in computational electrocatalysis, as solvation is normally added as an external, constant correction, regardless of the nature of the active site.11,13,15,28,29 In practice, our results suggest that a combination of high covalence and poor adsorbate–solvent interactions can be beneficial for oxygen electrocatalysis.
Methods
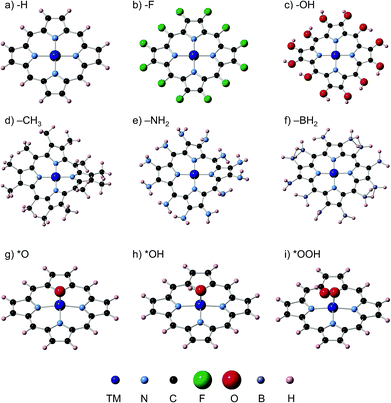
We have carried out spin unrestricted calculations of the porphyrins with and without the adsorbates and determined the most stable spin states, which can be found in the ESI, Section S4.† The spin states found are in agreement with those reported in previous studies. Fig. 1 contains typical geometric configurations of the metalloporphyrins and ligands in this study. While rings with H, F, OH and BH2 ligands are flat, NH2 and CH3 introduce large distortions. In all cases, however, the four nitrogen atoms and the metal center are in a square planar arrangement. The DFT calculations of the adsorption energies were performed using the PAW method in VASP,21,22 the RPBE exchange-correlation functional,23 and a plane-wave cut-off of 400 eV. We used the computational hydrogen electrode24 to describe proton–electron transfers and Rossmeisl et al.'s model for the ORR/OER on functionalized graphitic materials,26 which has also been used before on porphyrins,11,19 see full details in Sections S1 and S2.† The structures were optimized with the conjugate gradient method, allowing all atoms to relax in all directions until the maximum force on any atom was below 0.01 eV Å−1. Porphyrins, H2O and H2 were calculated in boxes of 20 Å × 20 Å × 20 Å, with kBT = 0.001 eV, using the gamma point only and Gaussian smearing; all energies were extrapolated to 0 K. Section S1 in the ESI† contains the DFT adsorption energies (ΔE), zero-point energies (ZPE), entropy (TS) and solvation corrections (ΔEsol) needed to calculate free energies under vacuum (ΔGvac) and in solution (ΔGsolv). We assessed the solvation corrections with the Conductor-like Screening Model (COSMO)25 to account for water–adsorbate–porphyrin interactions, following recent works.20 See further details of the COSMO and ZPE calculations in Section S3 in the ESI,† where we also provide a comparison between implicit and first-shell explicit solvation to demonstrate the suitability of the implicit method used here to capture solvation effects.Results and discussion
Fig. 2 shows the trends in adsorption energies for *O, *OH and *OOH. The trends in average adsorption energies are a function of the number of outer electrons (N) of the metal centers.7,9 Since the oxidation state of those centers in porphyrins is +2, N is 2e− less than the number of valence electrons. The error bars in Fig. 2 show the influence of the ligands on the adsorption properties. According to the figure, N is the main parameter that modulates the trends, but the porphyrin's ligands can as well change the adsorption properties substantially. For instance, the effects of F, OH, CH3, NH2 and BH2 on the binding energies of *OH are presented in Table S5.† In broad terms, F, OH, CH3 and NH2 stabilize the adsorption energies with respect to porphyrin rings with H ligands, while BH2 destabilizes them, regardless of the metal center. Thus, ligand selection is a rational way of tuning the adsorption properties of porphyrins.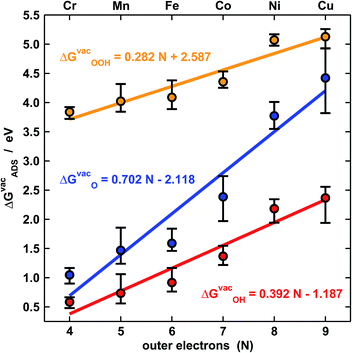 | ||
| Fig. 2 Adsorption-energy trends of *O (blue), *OH (red) and *OOH (orange) under vacuum for metal centers from Cr to Cu as a function of their number of outer electrons (N). The points are the average adsorption energies and the error bars show the energetic effect of the ligands in Fig. 1. | ||
The approximate linearity of the relations between adsorption energies and N in Fig. 2 justifies the existence of linear scaling relations between the adsorption energies themselves shown in Fig. 3a.1–3,7,9 Quantitatively speaking, combining the linear fits in Fig. 2 provides good estimates of the slopes and offsets in Fig. 3a. For instance, the ratio of the slopes for the adsorption energies of *OH (0.38) and *OOH (0.28) in Fig. 2 is equivalent to that observed at the bottom of Fig. 3a (0.79). In similar ways, one can obtain the rest of the slopes and offsets in Fig. 3a.
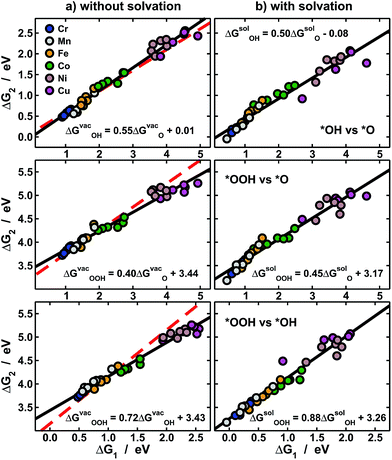 | ||
| Fig. 3 Scaling relations between the adsorption energies of *O, *OH and *OOH (a) under vacuum, and (b) solvated. In each panel linear fits (black) and their equations are provided. Top: *OH vs. *O; middle: *OOH vs. *O; bottom: *OOH vs. *OH. The red dashed lines in (a) are from ref. 11 and show that while ΔGvacO and ΔGvacOH behave normally (top), ΔGvacOOH (middle and bottom) causes large deviations in scaling relations. In (b) solvation restores the scaling relations broken under vacuum by making the slopes approach the ideal values of 0.5 and 1. | ||
The expected slope of the adsorption-energy scaling relation of *OH vs. *O (Fig. 3a, top) is 0.5,1–3 as oxygen in *OH lacks 1e− to reach the octet and *O lacks 2e−. The slope of 0.55 is, thus, in fair agreement with this prediction and our new data fit within previous trends,11,26 represented by the dashed line. Analogously, the expected slope for *OOH vs. *O is 0.5, but the one observed here is 0.40 (Fig. 3a, middle). Furthermore, the expected slope for *OOH vs. *OH is 1,1–3 as the oxygen in both *OH and *OOH lacks 1e− to reach the octet, but the observed slope is 0.72. These slopes of 0.40 and 0.72 cause deviations from the expected trends (red lines in Fig. 3a, middle and bottom) that can be as large as 0.65 eV for Ni and Cu centers. We note that smaller deviations were reported before on metal oxides from the unity slope,7,27 but their origin and implications were not discussed. The even larger deviations in this study are systematic and stem from the sizably different slopes of the relations of ΔGvacOOH and ΔGvacOH with N in Fig. 2 (0.28 vs. 0.39). In Fig. 4 and 5 we show the reason for such different slopes.
In sum, Fig. 3a indicates that the adsorption energies under vacuum of *O and *OH behave normally, while those of *OOH are anomalous. As described before, such deviations are important for OER/ORR electrocatalysis, as it is believed that the scaling between the adsorption energies of *OOH and *OH limits the performance of fuel cells and electrolyzers.3,6,7,9–11 Let us consider one exceptional site in Fig. 3a: Cu centers with CH3 ligands, which have an energetic difference of 2.55 eV between *OOH and *OH, implying that the predicted “scaling” overpotential is ηscalingOER/ORR = 0.04 V. Thus, those and several other Ni and Cu centers promise to catalyze almost reversibly the OER/ORR in view of their nearly ideal energetic differences between *OH and *OOH. However, the adsorption energies in Fig. 2 and 3a do not contain any solvation contributions, as those are traditionally added externally and are constant for all materials.11,13,15,28,29
To get a more accurate assessment of water solvation, we have used an implicit solvent model,25 the results of which appear in Fig. 3b. Interestingly, *O is substantially solvated on metalloporphyrins (−0.39 eV on average), in contrast with metal surfaces where it has no solvation.15,28,29 Moreover, for the scaling of *OH vs. *O the slope changes from 0.55 to 0.50, for *OOH vs. *O it changes from 0.40 to 0.45, and for *OOH vs. *OH it moves from 0.72 to 0.88. These changes, which make the slopes approach the values expected from electron-counting rules, are possible because the evaluated solvation contributions differ from one metal center to the next and also depend on the ring ligands, unlike traditional, constant-shift solvation corrections.11,28,29
Thus, solvation restores in aqueous solution the scalability lost under vacuum. It is important to emphasize that studies devoted to scaling relations1–3,6,10 and their breaking14,30 are usually carried out under vacuum and do not directly consider the effect of active-site-dependent solvation. In conclusion, non-scalability under vacuum is neither a necessary nor a sufficient condition to ensure high catalytic activity in solution, and actual breaking of scaling relations for electrocatalytic purposes can only be guaranteed if solvent–adsorbate–substrate interactions are properly accounted for.
It is then essential to understand why scaling relations are broken under vacuum but restored in solution. Recapping, Fig. 2 shows that adsorption energies become weaker as the metal center ranges from Cr to Cu, but the changes for those of *OOH are less pronounced than for *OH. Fig. 3a shows that this results in sizable deviations from ideality for Ni and Cu centers under vacuum. However, Fig. 3b shows that water solvation restores the lost scalability. These observations intuitively suggest that a given aspect of Ni and Cu centers makes them bind *OOH and *OH differently compared to other centers, an effect which is compensated in solution by solvation losses. In the following we will argue that this such aspect is the covalence of the bonds created by Ni and Cu with the oxygen atom in *OH and *OOH.
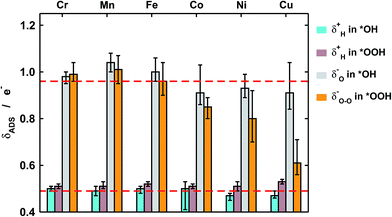
First of all, in Fig. 4 we quantify covalence in terms of the average excess charge in *OH (δOH−) and *OOH (δOOH−), calculated with Bader's method.31 The excess or lack of charge is calculated with respect to the number of valence electrons: a lack of charge of 0.5e− for H (1s1) means that 0.5e− from its valence electron has been withdrawn. Analogously, an excess charge of 1e− for O (1s2 2s2 2p4) means that in addition to its 6 valence electrons, the interaction with H and the porphyrin ring grants it an additional electron. For all metal centers with *OH and *OOH the charge depletion in the H atoms is approximately constant (∼0.5e−). Similarly, the excess charge of the O atoms in *OH is constant (∼1e−). Therefore, the charge in *OH remains approximately constant regardless of the nature of the metal center and the ligands. However, significant changes are observed for the O–O moiety in *OOH, where the excess charge decreases systematically from 1 to ∼0.65e− when the metal center varies between Cr and Cu. Thus, the covalence of the metal–oxygen bonds in *OOH, measured as a depletion of charge in the adsorbate, changes substantially, is different compared with that of metal–oxygen bonds in *OH, and is due to the O–O moiety.
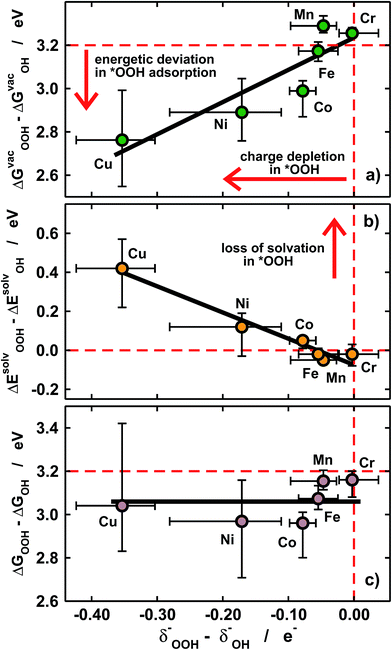
Furthermore, we show in Fig. 5a that the degree of covalence and energetic deviation for the scaling relation between *OH and *OOH are directly related. This means that covalence is responsible for the breaking of scaling relations between adsorption energies for highly covalent metal–oxygen bonds, namely those in which there is little charge transfer between active sites and adsorbates. Since the exceptions arise only for late transition metals, namely Ni and Cu, the linearity of the relations is not affected and the deviations modify only the slope.
Given that *OH and *OOH are polar chemisorbates immersed in a polar solvent (water), intuitively large covalence should cause a loss of solvation. This is what we see in Fig. 5b, where covalence lowers the solvation energies in solution for Ni and Cu centers. The magnitude of the losses in Fig. 5b is commensurate with that of the adsorption-energy deviations under vacuum for all metal centers in Fig. 5a but their signs are opposite, so that the adsorption energies in solution behave normally (see Fig. 3b) and ΔGsolvOOH − ΔGsolvOH ≈ 3.2 eV for all metal centers and ligands, as shown in Fig. 5c.
In sum, Fig. 5 supports the following simple but important methodological conclusion: if scaling relations are to be broken to improve the efficiency of (electro)catalytic reactions in solution, solvation has to be taken into account in the calculations, which is not generally the case in the state of the art.
Before closing the discussion, it is important to evaluate the impact of solvation on catalytic-activity predictions. To do so, in Fig. 6 we present volcano-type activity plots for the OER and the ORR on the porphyrins under study. Fig. 6a contains free energies in solution including only a constant-shift solvation (CSS) correction of −0.30 eV for *OH and *OOH on all centers.11,26 On the other hand, Fig. 5b contains the metal- and ligand-dependent solvation (MLS) corrections in Fig. 3b and 5 added to the free energies of *O, *OH and *OOH.
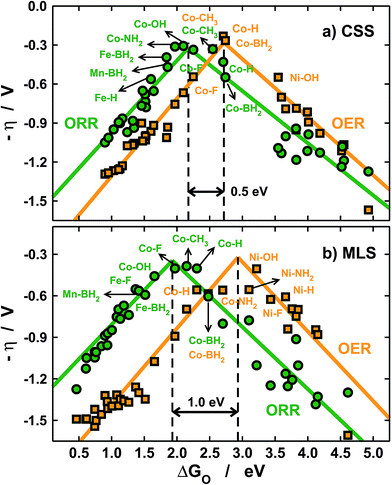 | ||
| Fig. 6 Volcano-type activity plots for the ORR (green) and the OER (orange). The overpotential (η) is plotted against the adsorption energies of *O, see Section S2 in the ESI.† (a) Using a constant-shift solvation correction (CSS) from ref. 11 and 26 and (b) using the metal- and ligand-dependent solvation corrections (MLS) calculated in this study. The black dashed lines mark the top of the OER and ORR volcanoes and show that different solvation treatments lead to different activity predictions. | ||
With the CSS and MLS approaches we find that the best catalysts for the ORR contain Co centers, and various ligands help in tuning the activity towards the top of the volcano. Note that F and BH2 enhance the ORR activity of Fe centers. For the OER, however, the predictions differ significantly. In the MLS approach Ni centers with OH and NH2 ligands are predicted to be highly active, and Co centers with BH2 and NH2 also appear to be fairly active.
Conversely, the CSS approach predicts that only Co centers are active for the OER. The predictions are similar for the ORR and different for the OER because of the reaction mechanisms (see Section S2 in the ESI†).
For the ORR, the overpotential (η) typically depends on elementary steps involving *OH and *OOH only, the solvation of which is accounted for by both the CSS and MLS methods. Conversely, for the OER the overpotential depends on steps involving *O, the solvation of which is completely neglected in the CSS approach.
Besides, the tops of the OER volcanoes are located at 2.7 (CSS) and 2.9 eV (MLS) and those of the ORR are found at 2.2 (CSS) and 1.9 eV (MLS). Therefore, in the CSS approach the separation between the OER and ORR maxima is only ∼0.5 eV, while it is nearly 1 eV in the MLS approach (see the black dashed lines in Fig. 6). These considerable differences are also due to the omission of *O solvation and lead to different predictions of bifunctional active metal centers, as the OER/ORR tops are considerably closer in the CSS approach. In any case, Co centers with ligands such as CH3 and BH2 are predicted to have similarly low overpotentials for both reactions. Importantly, this observation also suggests that a significant decrease in adsorbate solvation could lead to OER/ORR bifunctionality.
Conclusions
We have shown here that various metal centers and ring ligands can make metalloporphyrins break scaling relations, in particular those between the adsorption energies of *OH and *OOH, which are of importance for oxygen reduction and evolution. This shows that (1) flat sites made of a single metal species that binds *OH and *OOH similarly can indeed break scaling relations and (2) there is no need for the ligands to interact directly with the adsorbates in order to do so, which goes against commonly accepted ideas.10,11,26,32 This stems from the fact that covalence is in this case the factor responsible for breaking scaling relations. However, the scaling broken under vacuum is restored in water by virtue of the loss of solvation caused by high covalence as well.Methodologically speaking, this means that future studies aimed at breaking such relations in solution must take the solvent into account in the calculations. Although some examples exist, that is not a common practice in computational electrocatalysis.5,24 For instance, the importance of the solvent's dielectric constant (ε) on the ORR activity of platinum has been recently pointed out by Fortunelli et al.33 Moreover, other authors are making significant efforts to understand water solvation at pristine and stepped surfaces by including it explicitly in the calculations,34–36 while some models include solvation effects in the modelling of catalytic reactions on metallic surfaces.37–39 In spite of this burgeoning interest in solvent effects, it is not a common practice to include solvation effects in computational electrocatalysis.5,24
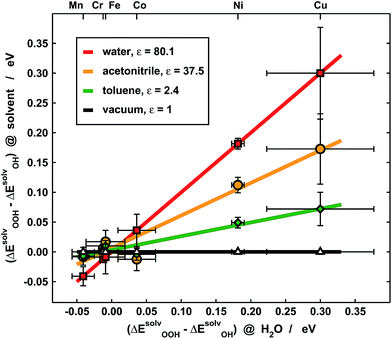
Experimentally, our results imply that poor solvent–adsorbate interactions can prove beneficial to boost the ORR/OER and avoid the solvation-mediated restoration of scaling relations. Indeed, this is exemplified in Fig. 7, where the *OOH solvation losses with respect to *OH analyzed in Fig. 5b are compared for porphyrins with –H and –F ligands in three different solvents: water (ε = 80.1), acetonitrile (ε = 37.5) and toluene (ε = 2.4). Clearly, for Cr, Mn, Fe and Co the differences are small, regardless of the solvent, and as a result of the ionic character of the metal–adsorbate bonds. However, for Ni and Cu the differences are significant due to high covalence and decrease alongside the dielectric constant of the solvent. Since small *OOH solvation losses indicate that the breaking of scaling relations under vacuum is maintained in solution, these results point toward careful solvent selection or, in more general terms, toward the creation of active sites where the interactions between solvent and adsorbates are poor, which can be achieved by means of e.g. steric hindrance.
Acknowledgements
FCV acknowledges funding from NWO, Veni project no. 722.014.009. JMGL acknowledges funding from MINECO, projects FIS2012-30996, FIS2013-46159-C3-1-P, and the Villum Foundation's Young Investigator Program, grant no. 10096. We also thank NCF with support from NWO and Niflheim for the use of their supercomputer facilities and Dr Adrien Göttle for helpful discussions.Notes and references
- F. Abild-Pedersen, J. Greeley, F. Studt, J. Rossmeisl, T. R. Munter, P. G. Moses, E. Skúlason, T. Bligaard and J. K. Nørskov, Phys. Rev. Lett., 2007, 99, 016105 CrossRef CAS PubMed.
- F. Calle-Vallejo, J. I. Martinez, J. M. Garcia-Lastra, J. Rossmeisl and M. T. M. Koper, Phys. Rev. Lett., 2012, 108, 136101 CrossRef PubMed.
- F. Calle-Vallejo, D. Loffreda, M. T. M. Koper and P. Sautet, Nat. Chem., 2015, 7, 403–410 CrossRef CAS PubMed.
- M. M. Montemore and J. W. Medlin, Catal. Sci. Technol., 2014, 4, 3748–3761 CAS.
- J. K. Norskov, T. Bligaard, J. Rossmeisl and C. H. Christensen, Nat. Chem., 2009, 1, 37–46 CrossRef CAS PubMed.
- I. C. Man, H.-Y. Su, F. Calle-Vallejo, H. A. Hansen, J. I. Martínez, N. G. Inoglu, J. Kitchin, T. F. Jaramillo, J. K. Nørskov and J. Rossmeisl, ChemCatChem, 2011, 3, 1159–1165 CrossRef CAS.
- F. Calle-Vallejo, N. G. Inoglu, H.-Y. Su, J. I. Martinez, I. C. Man, M. T. M. Koper, J. R. Kitchin and J. Rossmeisl, Chem. Sci., 2013, 4, 1245–1249 RSC.
- O. Diaz-Morales, I. Ledezma-Yanez, M. T. M. Koper and F. Calle-Vallejo, ACS Catal., 2015, 5, 5380–5387 CrossRef CAS.
- F. Calle-Vallejo, O. A. Díaz-Morales, M. J. Kolb and M. T. M. Koper, ACS Catal., 2015, 5, 869–873 CrossRef CAS.
- M. T. M. Koper, J. Electroanal. Chem., 2011, 660, 254–260 CrossRef CAS.
- F. Calle-Vallejo, J. I. Martinez, J. M. Garcia-Lastra, E. Abad and M. T. M. Koper, Surf. Sci., 2013, 607, 47–53 CrossRef CAS.
- I. E. L. Stephens, A. S. Bondarenko, U. Gronbjerg, J. Rossmeisl and I. Chorkendorff, Energy Environ. Sci., 2012, 5, 6744–6762 CAS.
- F. Calle-Vallejo, J. Tymoczko, V. Colic, Q. H. Vu, M. D. Pohl, K. Morgenstern, D. Loffreda, P. Sautet, W. Schuhmann and A. S. Bandarenka, Science, 2015, 350, 185–189 CrossRef CAS PubMed.
- N. B. Halck, V. Petrykin, P. Krtil and J. Rossmeisl, Phys. Chem. Chem. Phys., 2014, 16, 13682–13688 RSC.
- H. Li, Y. Li, M. T. M. Koper and F. Calle-Vallejo, J. Am. Chem. Soc., 2014, 136, 15694–15701 CrossRef CAS PubMed.
- J. H. Zagal, S. Griveau, K. I. Ozoemena, T. Nyokong and F. Bedioui, J. Nanosci. Nanotechnol., 2009, 9, 2201–2214 CrossRef CAS PubMed.
- D. K. Dogutan, R. McGuire Jr and D. G. Nocera, J. Am. Chem. Soc., 2011, 133, 9178–9180 CrossRef CAS PubMed.
- R. McGuire Jr, D. K. Dogutan, T. S. Teets, J. Suntivich, Y. Shao-Horn and D. G. Nocera, Chem. Sci., 2010, 1, 411–414 RSC.
- J. D. Baran, H. Grönbeck and A. Hellman, J. Am. Chem. Soc., 2014, 136, 1320–1326 CrossRef CAS PubMed.
- J. Shen, M. J. Kolb, A. J. Göttle and M. T. M. Koper, J. Phys. Chem. C, 2016, 120, 15714–15721 CAS.
- G. Kresse and J. Furthmüller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169–11186 CrossRef CAS.
- G. Kresse and D. Joubert, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758–1775 CrossRef CAS.
- B. Hammer, L. B. Hansen and J. K. Nørskov, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 7413–7421 CrossRef.
- J. K. Nørskov, J. Rossmeisl, A. Logadottir, L. Lindqvist, J. R. Kitchin, T. Bligaard and H. Jónsson, J. Phys. Chem. B, 2004, 108, 17886–17892 CrossRef.
- A. Klamt and G. Schuurmann, J. Chem. Soc., Perkin Trans. 2, 1993, 799–805 RSC.
- F. Calle-Vallejo, J. Ignacio Martinez and J. Rossmeisl, Phys. Chem. Chem. Phys., 2011, 13, 15639–15643 RSC.
- M. Bajdich, M. García-Mota, A. Vojvodic, J. K. Nørskov and A. T. Bell, J. Am. Chem. Soc., 2013, 135, 13521–13530 CrossRef CAS PubMed.
- J. Greeley, I. E. L. Stephens, A. S. Bondarenko, T. P. Johansson, H. A. Hansen, T. F. Jaramillo, J. Rossmeisl, I. Chorkendorff and J. K. Nørskov, Nat. Chem., 2009, 1, 552–556 CrossRef CAS PubMed.
- A. A. Peterson, F. Abild-Pedersen, F. Studt, J. Rossmeisl and J. K. Norskov, Energy Environ. Sci., 2010, 3, 1311–1315 CAS.
- R. Michalsky, Y.-J. Zhang, A. J. Medford and A. A. Peterson, J. Phys. Chem. C, 2014, 118, 13026–13034 CAS.
- J. I. Rodríguez, R. F. W. Bader, P. W. Ayers, C. Michel, A. W. Götz and C. Bo, Chem. Phys. Lett., 2009, 472, 149–152 CrossRef.
- A. A. Peterson and J. K. Nørskov, J. Phys. Chem. Lett., 2012, 3, 251–258 CrossRef CAS.
- A. Fortunelli, W. A. Goddard, Y. Sha, T. H. Yu, L. Sementa, G. Barcaro and O. Andreussi, Angew. Chem., Int. Ed., 2014, 53, 6669–6672 CrossRef CAS PubMed.
- S. Schnur and A. Groß, New J. Phys., 2009, 11, 125003 CrossRef.
- M. J. Kolb, J. Wermink, F. Calle-Vallejo, L. B. F. Juurlink and M. T. M. Koper, Phys. Chem. Chem. Phys., 2016, 18, 3416–3422 RSC.
- M. J. Kolb, R. G. Farber, J. Derouin, C. Badan, F. Calle-Vallejo, L. B. F. Juurlink, D. R. Killelea and M. T. M. Koper, Phys. Rev. Lett., 2016, 116, 136101 CrossRef PubMed.
- J. R. Schmidt, K. Yu and J. G. McDaniel, Acc. Chem. Res., 2015, 48, 548–556 CrossRef CAS PubMed.
- X. Nie, M. R. Esopi, M. J. Janik and A. Asthagiri, Angew. Chem., Int. Ed., 2013, 52, 2459–2462 CrossRef CAS PubMed.
- V. Tripković, E. Skúlason, S. Siahrostami, J. K. Nørskov and J. Rossmeisl, Electrochim. Acta, 2010, 55, 7975–7981 CrossRef.
Footnote |
| † Electronic supplementary information (ESI) available: Assessment of adsorption energies, models used for the oxygen evolution and reduction reactions, details of the calculations in ADF, tables with spin states, zero-point energies, solvation energies, adsorption energies and ligand effects. See DOI: 10.1039/c6sc02123a |
| This journal is © The Royal Society of Chemistry 2017 |