Mechanical oscillation of dynamic microtubule rings

Abstract

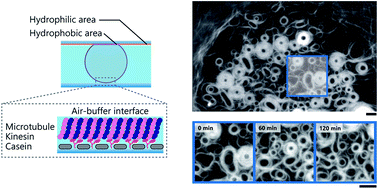
Mechanical oscillation is a ubiquitous phenomenon observed in living systems, which emerges from a wide range of well-organized self-assembled structures, and plays important roles in many biological processes. Although considerable efforts have been devoted to demonstrate the mechanical oscillation of organized structures produced through self-assembly in vitro, it has rarely been documented. Here we report the mechanical oscillation of ring-shaped structures, composed of multiple microtubule (MT) filaments, obtained through energy dissipative self-assembly of MT filaments at an air-buffer interface. The MT rings exhibit autonomous oscillation manifested through periodic changes in the size and shape. We propose the oscillation of the MT rings is attributed to mechanical feedback arising from accumulated stress induced by the driving force of the motor protein system. This work might offer new insights to our current understanding on the mechanical feedback driven oscillation of organized structures and its effect on dynamic processes in living systems.

---

Introduction

Active self-assembly is the preferred way of nature to produce ordered structures from discrete constituent components through continuous consumption of energy.^1–3 To study the formation of ordered structures through the active self-assembly process the motor protein systems actin–myosin and MT-kinesin have been widely employed in recent years.^4,5 By utilizing their ability to convert chemical energy into mechanical work, a variety of ordered structures such as asters,^6,7 vortices,⁸ density waves,⁹ rings or spools^10,11 and bundles^12,13 etc. have been achieved. Although these ordered structures exhibit dynamic organization, the mechanical oscillation, as observed in living systems, has rarely been documented for these self-assembled structures. One remarkable finding in this regard was the demonstration of cilia like beating of reconstructed MTs bundles.¹⁴ Mechanical oscillation plays crucial roles in many biological processes like growth, development, migration, etc. of living organisms.^15–17 Specific examples can be given by cell shape oscillations,^16,18 spindle oscillations during asymmetric cell division,^19,20 chromosome oscillations during mitosis,²¹ oscillations of muscle sarcomere,²² beating of cilia and flagella.^23,24 In this work, we demonstrate formation of MT rings, through active self-assembly of reconstructed MT filaments, which exhibit self-oscillation manifested by periodic expansion and contraction. To this end, MTs traveling on a kinesin coated substrate in the presence of adenosine triphosphate (ATP) were assembled into the rings at an air-buffer interface in an inert atmosphere.²⁵ The air-buffer interface allowed this transformation of the filamentous MTs into the rings through an attractive interaction induced by the surface tension.²⁶ We found the velocity of MTs at the inner and outer periphery of the rings were almost comparable. Based on this observation we propose that the oscillation of the MT rings, formed at the air-buffer interface, is driven by internal mechanical stress, i.e. the stress accumulated inside the rings due to mismatch in angular velocity at the inner and outer periphery of the rings. Recent works suggest that internal stress induced by motor protein systems works as a mechanical feedback and triggers periodic oscillation of self-assembled structures in living systems without any involvement of biochemical signals.¹⁵ Therefore, our work offers an insight in the mechanical feedback regulated oscillation of self-assembled structures, which might be beneficial in understanding the mechano-regulation of dynamic processes in living systems.

Experimental section

Tubulin purification

Tubulin was purified from porcine brain by using a high-concentration 1,4-piperazinediethanesulfonic acid (PIPES; Sigma) buffer (1 M PIPES, 20 mM EGTA, 10 mM MgCl₂; pH adjusted to 6.8).²⁷ High-molarity PIPES buffer (HMPB) and BRB80 buffer were prepared using PIPES and the pH was adjusted using KOH.

Kinesin purification

Green fluorescent protein (GFP)-fused kinesin-1 construct consisting of the first 560 amino acids (K560-GFP) were prepared as described in previously published papers, by partially modifying the expression and purification methods.²⁸

Rhodamine labeling and stoichiometric estimation

Rhodamine-labeled tubulin was prepared using tetramethylrhodamine succinimidyl ester (TAMRA-SE; Invitrogen) according to standard techniques.²⁹ The ratio of rhodamine to tubulin was 1 : 1, as determined by measuring the absorbance of the protein at 280 nm and the absorbance of tetramethylrhodamine at 555 nm.

Silanization of glass surface

First the cover glasses were treated by a UV ozone cleaning system by passing O₂ for 2 min, UV irradiation for 15 min and N₂ for 3 min. After that, the glasses and the fluorosilane agent (1H,1H,2H,2H-perfluorodecyltrichlorosilane; Wako, Japan) were placed in a desiccator under vacuum (−0.07 MPa) and kept overnight. The silanization increased the hydrophobicity of the glass surface which was confirmed by contact angle measurement. It was found that the contact angle of the silanized glass surface (∼105 ± 0.82°, average ± standard deviation) was higher compared to that of an untreated glass surface (∼54 ± 0.79°).

Formation of MT rings at an air-buffer interface

A flow cell with approximate dimensions of 2 × 9 × 0.6 mm³ (W × L × H) was prepared by placing a silanized cover glass (9 × 18 mm², Matsunami) on a glass slide (40 × 50 mm², Matsunami) where double-sided tape was used as a spacer. Before placing the silanized cover glass, it was plasma treated covering the central area by a small PDMS sheet. By the plasma irradiation the cover glass was made hydrophilic except the center area which was covered by the PDMS and as a result remained hydrophobic (Fig. S1 in the ESI†). After preparation the flow cell was filled with anti-GFP antibody solution (0.2 mg mL⁻¹), and incubate for 5 min, and washed by BRB80 buffer. Then 5 μL of 600 nM kinesin (K560-GFP) was applied and incubated for 5 min, which was followed by a wash with 15 μL wash buffer (80 mM PIPES, 1 mM EGTA, 1 mM MgCl₂, 1 mM DTT, 0.5 mg mL⁻¹ casein, 10 μM paclitaxel, 4.5 mg mL⁻¹ D-glucose, 50 U mL⁻¹ glucose oxidase, 50 U mL⁻¹ catalase). Next 5 μL of 10 μM MT solution was passed through the flow cell and incubated for 5 min. After washing with 15 μL wash buffer, ATP buffer (80 mM PIPES, 1 mM EGTA, 1 mM MgCl₂, 10 mM ATP, 10 μM paclitaxel, 2 mM trolox, 4.5 mg mL⁻¹ D-glucose, 50 U mL⁻¹ glucose oxidase, 50 U mL⁻¹ catalase) was applied into the flow cell. Then by using the air-buffer interface control system,²⁶ a micro pump (HARVARD) and a capillary tube (GL Sciences, Japan), air bubbles were created in the flow cell and allowed to settle at the center of hydrophobic area of the cover glass. After that, humid nitrogen gas was passed through the inert chamber and the existing oxygen was removed out from the chamber.²⁵ During the experiments the humidity inside the inert chamber was maintained more than ∼90%. Finally, after passing the nitrogen gas for 60 min through the chamber fluorescence microscopic observation of the MT assembly induced by the air bubble was performed. All these experiments were performed at 25 °C and the nitrogen gas was kept passing continuously through the inert chamber until the experiments were finished.

Fluorescence microscopy observation of the MT assemblies

The samples were illuminated with a 100 W mercury lamp and visualised with an epifluorescence microscope (Eclipse Ti; Nikon) using an oil-coupled Plan Apo 60 × 1.40 objective (Nikon). Filter blocks with UV-cut specifications (TRITC: EX540/25, DM565, BA606/55; GFP-HQ: EX455-485, DM495, BA500-545; Nikon) were used in the optical path of the microscope to allow visualisation of the samples while eliminating the UV portion of the radiation and minimising the harmful effects of UV radiation on the samples. Images and movies were captured using a cooled CMOS camera (Neo sCMOS; Andor) connected to a PC.

Image and movie analysis

Movies and images captured under a fluorescence microscopy were analyzed using the image analysis software ImageJ.

Measurement of roundness

In our analyses, we considered only those MT rings for which the roundness value was higher than 0.75 (Fig. S2 in the ESI†). Here we define the roundness by the equation mentioned below:³⁰

Results and discussion

In this work by employing a simple fabrication technique we have controlled the position of the air-buffer interface inside the in vitro motility assay system (Experimental section, Fig. 1a and S1 in the ESI†). The MT filaments, subjected to an air-buffer interface, were found to form stable ring-shaped assemblies.²⁶ Here by employing a high density of MTs on a kinesin coated substrate in an inert atmosphere, we demonstrated formation of the MT rings at an air-buffer interface that exhibited structural transformation with time (Fig. 1b, ESI Movie 1†). MTs moving on the kinesin coated substrate were free to come in and move out of the region covered by the air-buffer interface (air bubble). The motile MT filaments formed rings when they entered the region at the air-buffer interface. The most compelling feature of the MT rings created at the air-buffer interface is that unlike the MT assemblies demonstrated in the previous report²⁶ the active MT rings showed periodic expansion and contraction over time which constitutes their oscillating behavior. We investigated in detail the behavior of the MT rings for which we have considered only the assembled structures which meet two criteria (Experimental section and Fig. S2 in the ESI†), particularly a structure is considered a ring when the roundness was larger than 0.75. As shown by the representative fluorescence microscopy images in Fig. 1c, the MT rings were not stable, rather they continuously changed their size over time. The average radius of the MT rings fluctuated with time although neither a clear tendency nor a significant difference could be noticed (Fig. 1d and S3 in the ESI†). Since the MT rings showed continuous structural fluctuation, here we considered the change in number of the MT rings over time in a certain region of interest (ROI). Fig. 1e reveals how the number of the MT rings in a certain ROI (∼900 μm²) fluctuated with time. At this stage this change in number of the MT rings appears due to disappearance or regeneration of the MT rings with time which is evident from the ESI Movie 2.† Detailed investigation on the dynamic behavior of the MT rings revealed that the MT rings followed four different routes. As shown in the Fig. 2a–d, the MT rings adopted four different modes of transformation namely, (a) assimilation, (b) oscillation, (c) collapse and (d) differentiation. At this moment it seems these four different routes might have caused the fluctuation in number of the MT rings over time in a certain ROI (Fig. 1e). We measured the proportion of these four events at different time (Fig. 2e) which revealed that majority of the MT rings underwent the oscillation event.

Fig. 1 Schematic diagram of the experimental design used to demonstrate the formation of dynamic MT rings at an air-buffer interface (a). Fluorescence microscopy image of the MT rings prepared from filamentous MTs at the air-buffer interface (b). Time lapse fluorescence microscopy images showing dynamic reorganization of the MT rings at the air-buffer interface (c). Change in size (d) and number (e) of the MT rings with time in a specific region of interest. In (d) “n” represents the number of MT rings considered. Scale bar: 2.5 μm.

Fig. 2 Time lapse fluorescence microscopy images and corresponding schematic illustrations of the four different modes of dynamic reorganization of the MT rings at the air-buffer interface: (a) assimilation, (b) oscillation, (c) collapse and (d) differentiation. Percentage of different modes of dynamic reorganization of the MT rings at different time (e). Here, “n” represents the number of MT rings considered. Scale bar: 2.5 μm.

The four dynamic transformation modes of the MT rings are shown in Fig. 2 by the fluorescence microscopy images and schematic illustrations. In the assimilation event the MT rings were found to grow by continuous incorporation of motile MT filaments into the already formed rings, as a result of which the outer diameter and thickness (subtraction of inner diameter from the outer diameter) of the rings increased with time (Fig. 2a and ESI Movie 3†). For those MT rings that displayed the oscillation, which was the most frequent event, the diameter and thickness of the MT rings were found to constantly fluctuate. The change in diameter and thickness are evident form the time lapse fluorescence microscopy images and schematic illustrations shown in the Fig. 2b and ESI Movie 4.† In the collapse event, a sudden increase in size (inner and outer diameter) was noticed during rotation of the rings as shown in Fig. 2c and ESI Movie 5,† which was finally followed by a morphological transition of the MT rings to the filamentous state. In a differentiation event, a MT ring was found to produce two new rings (Fig. 2d and ESI movie 6†). As seen from the fluorescence microscopy images, a differentiation event took place through two phases. First a MT ring expanded which was then followed by division of the ring into two new rings.

Next we particularly considered in detail the results for the two frequently observed events, i.e. oscillation (Fig. 3a) and collapse (Fig. 3b). Both the inner and outer diameter of a MT ring fluctuated considerably over time in the oscillation event, although the change in the thickness of the MT rings was very small (Fig. 3a). For the collapse event (Fig. 3b), initially the inner diameter of a MT ring decreased drastically by 10 min after which both the inner and outer diameter were found to increase sharply at 15 min. But in contrary to the oscillation, change in the thickness of the MT rings was considerably larger for the collapse event. At the onset of expansion the thickness reached a maximum value (∼1 μm) which is suspected to trigger the transformation of the rings in the collapse event. For both the events, there seems to exist a minimum or threshold value of inner diameter which could be accounted for by the balance in bending energy and surface energy of the MT rings where the inner diameter of the rings settle at an energetically favorable state as discussed in the literature.²⁶ Therefore, we also investigated the effect of the air-buffer interface on the dynamic behavior of the gliding MTs and measured the velocity and the persistence length, which can be considered a measure of the rigidity of the MTs. Considerable decrease in the persistence length of the MTs was observed beneath the air-buffer interface (Fig. S4 in the ESI†) which can be accounted for by the condensation of counter ions and consequent decrease in surface energy of the MTs. This decrease in the surface energy explains the formation of the MT rings at the air-buffer interface.²⁶ However dynamic reorganization of the rings could not be understood by this argument.

Fig. 3 Change in inner, outer diameter and thickness of a representative MT ring with time for the oscillation (a) and collapse (b). Fluctuation in angular velocity coefficient, ΔD (open circle) of the representative MT ring as a function of time for the oscillation (c) and collapse (d). For the oscillation, a periodic change in angular velocity coefficient with time could be observed which is supported by the Fast Fourier Transform analysis of the experimental results (dotted line). Histogram of the angular velocity coefficient of MT rings for the oscillation (e) and collapse (f). Ten MT rings were considered in each case for preparing the histograms. The average angular velocity coefficient was 0.17 ± 0.05 μm⁻¹ and 0.27 ± 0.15 μm⁻¹ (average ± standard deviation) for the oscillation and collapse respectively.

Since in the oscillation and collapse event the change in thickness of the MT rings with time shows different trends, we suspect the reorganization of the rings might have been associated with mechanical frustration arising due to differences in angular velocities at the inner and outer periphery of the rings. This is plausible because the MTs moved with a constant velocity on the kinesin coated surface and internal frictions among the neighbor MT filaments within a ring structure is also likely to occur which can cause a difference in angular velocity at different regions of the MT rings. To investigate our hypothesis we measured the velocity of MTs at the most inner and outer region of the MT rings. From our measurement it was revealed that velocity of the MTs at the inner and outermost region of the rings were almost same. This outcome suggests that through sliding MTs are able to overcome the strain due to their interactions. To confirm our hypothesis further, we performed additional experiments as control where we used a strong ligand–receptor interaction i.e., streptavidin (St)–biotin (Bt) interaction to prevent the sliding of the MTs.³¹ In this case also MTs were assembled into rings, but unlike the rings produced at the air-buffer interface, MTs in those rings had no chance of sliding past each other due to strong binding between St and Bt. We prepared kymographs of MTs moving at the inner and outermost periphery of a MT ring produced by using the St–Bt interaction (Fig. S5 in the ESI†). The two kymographs clearly show a difference in MT velocity at the inner and outermost periphery of the ring. From the kymographs we found that the (linear) velocity of MTs at the inner and outermost periphery were 0.06 and 0.19 μm s⁻¹. Moreover, the velocity of MTs at the outermost periphery of the rings was comparable to that of single MT filaments gliding on kinesins. These results clearly suggests that MTs in the rings (St–Bt) are always under strain (suppression) that prevents the MTs at different regions of the rings from moving at the same velocity so as to keep the angular velocity same. To further investigate the behavior of the MT rings formed at the air-buffer interface, we measured the angular velocity coefficient, ΔD (difference in thickness divided by the product of inner and outer diameter) of the MT rings for the oscillation and collapse events. The angular velocity at the inner and outer periphery could be expressed by eqn (1) and (2) respectively, as shown below;

where, v_i, v_o are linear velocity of MTs at the inner and outer periphery of a MT ring respectively and r_i, r_o are inner and outer radius of the MT ring respectively. Therefore the difference in angular velocity is;
where, v* = 2v_i = 2v_o; D_i, D_o are inner and outer diameter of a MT ring respectively and |D_i–o| = D_i − D_o. As from our experiment the velocity of MTs at the inner and outer region of the MT rings formed at the air-buffer interface were found similar, i.e. constant, we estimated the ΔD which might be considered a measure of the difference in angular velocity at the inner and outermost periphery of the MT rings. Here, ΔD depends not only on the thickness, but also on the size of the MT rings. The results, which consider the change in ΔD with time, are shown in the Fig. 3c and d for the oscillation and collapse respectively; this result (Fig. 3c) confirms the involvement of mechanical feedback induced periodic oscillation in the dynamic reorganization of the MT rings. The histograms, shown in the Fig. 3e and f for the oscillation and collapse respectively, which were prepared by considering an ensemble of ten MT rings in each case, reveal that there is a range of ΔD for both the events. For the collapse event the range is wider than that of the oscillation event. The average values of ΔD were 0.17 ± 0.05 μm⁻¹ (average ± standard deviation) and 0.27 ± 0.15 μm⁻¹ for the oscillation and collapse events respectively and these two values are found statistically different (P < 0.01). To gain further insight of the phenomenon, we performed Fast Fourier Transform (FFT) analysis of the oscillation displayed by the MT rings. From the power spectrum obtained from the FFT analysis (Fig. S6 in the ESI†) the dominant frequency was found to be 7.33 × 10⁻³ Hz, which corresponds to a period of ∼136 s. The oscillation frequency of the MT rings are found much smaller compared to the oscillation frequency of biological structures observed in vivo e.g., cilia and flagella.^32–35 As the cellular events such as cell division and reorganization take place on a timescale of minutes or even longer, oscillation of the MT rings observed in this work might be beneficial in obtaining insight of the role of mechanical oscillation in cellular processes. We found that the oscillation frequency of the MT rings is well comparable to that of self-oscillating cilia like structures prepared from reconstructed MT bundles.¹⁴ From the above discussion, it can be concluded that the dynamic transformation of the MT rings at the air-buffer interface is the result of mechanical strain i.e., mechanical feedback which is originated due to the mismatch or difference in ΔD at different regions of the MT rings, as schematically illustrated in the Fig. 4. Perhaps different remodeling routes of the MT rings might have arisen due to the difference in ΔD values. As already mentioned, the mechanical oscillation is the mostly followed route among the four different routes observed in our work. Through the oscillation i.e., through periodic changes in the size and shape, the MT rings might have released the accumulated stress inside the structures. This oscillation process is found to be associated with decrease in the thickness of the rings which might has helped the rings avoid an energetically unfavorable state due to mismatch in angular velocity. Oscillation triggered by chemical reactions was previously reported,^33,36 but the oscillation of organized or self-assembled structures due to mechanical feedback in an in vitro system is rare. In addition to the difference in structures, the difference in mechanical instability of the MT rings and other oscillating structures should be investigated in detail in future.

Fig. 4 Schematic illustration of the oscillation mechanism of MT rings at the air-buffer interface. Here, V_MT, ω_s, ω_ex represent linear velocity of MTs, angular velocity of MT rings in the shrunk and expanded state respectively.

Conclusions

We report mechanical feedback driven oscillation of self-assembled active structures in an artificial environment. Using a reconstructed motor protein system (MT-kinesin), we demonstrated the active self-assembly of MT filaments at an air-buffer interface that formed dynamic MT rings. The MT rings exhibited continuous reorganization over time. We showed that mechanical feedback which originated due to the mismatch in angular velocity at the inner and outer periphery of the MT rings regulated the reorganization of the MT rings. The reorganization of the MT rings took place through four different routes among which mechanical oscillation was the most frequently followed one. This work might offer a better understanding on the role of mechanical feedback in mechanical oscillation and reorganization of active materials in living organisms. At the same time this work would be helpful in realizing mechanical feedback driven transformation of dynamic structures in synthetic world, which would be of great importance for the development of adaptive and responsive smart devices in future.^37–39

Acknowledgements

This work was financially supported by Grant-in-Aid for Scientific Research on Innovative Areas (grant number 24104004), and Grant-in-Aid for Scientific Research (B) (grant number 15H03706) from Japan Society for the Promotion of Science (JSPS). Discussion with Prof. Ken Nagai is gratefully acknowledged.

References

1. G. M. Whitesides and B. Grzybowski, Science, 2002, 295, 2418–2421.
2. M. Fialkowski, K. J. M. Bishop, R. Klajn, S. K. Smoukov, C. J. Campbell and B. A. Grzybowski, J. Phys. Chem. B, 2006, 110, 2482–2496.
3. D. Philp and J. F. Stoddart, Angew. Chem., Int. Ed. Engl., 1996, 35, 1154–1195.
4. A. M. R. Kabir, A. Kakugo, J. P. Gong and Y. Osada, Macromol. Biosci., 2011, 11, 1314–1324.
5. A. T. Lam, V. VanDelinder, A. M. R. Kabir, H. Hess, G. D. Bachand and A. Kakugo, Soft Matter, 2016, 12, 988–997.
6. F. J. Nedelec, T. Surrey, A. C. Maggs and S. Leibler, Nature, 1997, 389, 305–308.
7. T. Surrey, F. Nedelec, S. Leibler and E. Karsenti, Science, 2001, 292, 1167–1171.
8. Y. Sumino, K. H. Nagai, Y. Shitaka, D. Tanaka, K. Yoshikawa, H. Chate and K. Oiwa, Nature, 2012, 483, 448–452.
9. V. Schaller, C. Weber, C. Semmrich, E. Frey and A. R. Bausch, Nature, 2010, 467, 73–77.
10. A. Kakugo, A. M. R. Kabir, N. Hosoda, K. Shikinaka and J. P. Gong, Biomacromolecules, 2011, 12, 3394–3399.
11. V. Schaller, C. A. Weber, B. Hammerich, E. Frey and A. R. Bausch, Proc. Natl. Acad. Sci. U. S. A., 2011, 108, 19183–19188.
12. R. Kawamura, A. Kakugo, Y. Osada and J. P. Gong, Langmuir, 2010, 26, 533–537.
13. H. Hess, J. Clemmens, C. Brunner, R. Doot, S. Luna, K.-H. Ernst and V. Vogel, Nano Lett., 2005, 5, 629–633.
14. T. Sanchez, D. Welch, D. Nicastro and Z. Dogic, Science, 2011, 333, 456–459.
15. K. Karsten and D. Riveline, in Current topics in developmental biology, 2011, vol. 95, pp. 67–91.
16. N. Gorfinkiel, Dev. Dyn., 2015, 245, 268–275.
17. F. Jülicher, Comptes Rendus de l'Académie des Sciences-Series IV-Physics-Astrophysics 2.6, 2001, p. 849.
18. N. Gorfinkiel and G. B. Blanchard, Curr. Opin. Cell Biol., 2011, 23, 531–539.
19. S. W. Grill, K. Kruse and F. Julicher, Phys. Rev. Lett., 2005, 94, 108104.
20. C. Kozlowski, M. Srayko and F. Nedelec, Cell, 2007, 129, 499–510.
21. O. Campas and P. Sens, Phys. Rev. Lett., 2006, 97, 128102–128104.
22. S. Gunther and K. Kruse, New J. Phys., 2007, 9, 417.
23. D. Bray, in Cell Movements, Garland, New York, 1992.
24. M. Murase, in The Dynamics of Cell Motility, Wiley, New York, 1992.
25. A. M. R. Kabir, D. Inoue, A. Kakugo, A. Kamei and J. P. Gong, Langmuir, 2011, 27, 13659–13668.
26. A. M. R. Kabir, S. Wada, D. Inoue, Y. Tamura, T. Kajihara, H. Mayama, K. Sada, A. Kakugo and J. P. Gong, Soft Matter, 2012, 8, 10863–10867.
27. M. Castoldi and A. V. Popov, Protein Expression Purif., 2003, 32, 83–88.
28. R. B. Case, D. W. Pierce, H. B. Nora, L. H. Cynthia and R. D. Vale, Cell, 1997, 90, 959–966.
29. J. Peloquin, Y. Komarova and G. Borisy, Nat. Methods, 2005, 2, 299–303.
30. M. B. Mgangira, J. K. Anochie-Boateng and J. Komba, Presented at the 32nd Southern African Transport Conference (SATC 2013), South Africa, Pretoria, July 2013.
31. R. Kawamura, A. Kakugo, K. Shikinaka, Y. Osada and J. P. Gong, Biomacromolecules, 2008, 9, 2277–2282.
32. I. C. Chen, O. Kuksenok, V. V. Yashin, A. C. Balazs and K. J. V. Vliet, Adv. Funct. Mater., 2012, 22, 2535–2541.
33. A. Hilfinger, PhD Dissertation, TU Dresden, GE, 2006.
34. I. R. Gibbons, J. Cell Biol., 1981, 91, 107s.
35. C. Gadelha, B. Wickstead and K. Gull, Cell Motil. Cytoskeleton, 2007, 64, 629–643.
36. V. V. Yashin and A. C. Balazs, Science, 2006, 314, 798–801.
37. Y. Dong, C. Zhang, L. Wu, Y. Chen and Y. Hu, Macromol. Rapid Commun., 2014, 35, 1943–1948.
38. K. S. Toohey, N. R. Sottos, J. A. Lewis, J. S. Moore and S. R. White, Nat. Mater., 2007, 6, 581–585.
39. D. Suzuki, T. Kobayashi, R. Yoshida and T. Hirai, Soft Matter, 2012, 8, 11447–11449.

---

Footnotes

† Electronic supplementary information (ESI) available. See DOI: 10.1039/c6ra16613j

‡ These authors contributed equally to this work.

---