Pressure-induced phase transitions of lead iodide†
Abstract
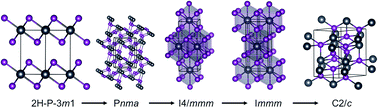
Pressure is a fundamental thermodynamic variable that can efficiently modify crystal or electronic structure leading to new material states of interest. Here we search the crystal structures of lead iodide (PbI2) up to 200 GPa using the swarm-intelligent CALYPSO structure prediction method combined with ab initio calculations. Four new stable high-pressure phases (orthorhombic Pnma, tegragonal I4/mmm, orthorhombic Immm and monoclinic C2/c) have been uncovered. A layered to three-dimensional structure transition from the ambient-pressure 2H phase to the orthorhombic Pnma phase is proposed to be taking place at ∼2.5 GPa. The newly proposed Pnma phase is a semiconductor with an indirect band gap of 1.68 eV. It is isosymmetric to the well-known cotunnite phase but with a very different bonding pattern. The semiconductor–metal transition of PbI2 occurs at ∼27.2 GPa, where the semiconducting Pnma phase transforms to the metallic I4/mmm phase due to pressure-induced broadening of both the valance and conduction bands. The metallic nature persists in the higher-pressure phases of Immm and C2/c up to about 169.1 GPa, above which PbI2 decomposes to its constituent elements. The current results represent a significant step toward the understanding of structural and electronic properties of PbI2 under compression.

 Please wait while we load your content...
Please wait while we load your content...