Unexpected superhard phases of niobium triborides: first-principles calculations

Abstract

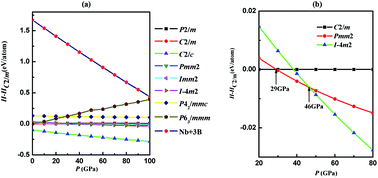
Using an unbiased structure search method based on particle-swarm optimization algorithms in combination with density functional theory calculations, we investigate the phase stability and electronic properties of NbB₃ under high pressures. By structure searching as implemented in the CALYPSO code, we obtained the most stable monoclinic phase (C2/c) and four metastable phases (P6₃/mmm, C2/m, Pmm2 and I4̄m2) for NbB₃. Under high pressure, the C2/m structure transforms to Pmm2 phase and to I4̄m2 phase at about 29 and 46 GPa, respectively. Surprisingly, the five phases of NbB₃ are all dynamically and mechanically stable at ambient conditions. The high bulk and shear modulus, and low Poisson's ratio for both phases in NbB₃, make it a promising low compressible material. Moreover, interestingly the hardness of the five phases of NbB₃ are very close to 40 GPa, in particular, the C2/m and Pmm2 phases have sufficient hardness (45 and 44 GPa, respectively), for it to be considered as a superhard material. All phases of NbB₃ with high hardness are stable due to the strong covalent bonding nature via electronic density of states and electron localization function analysis.

---

Introduction

The various applications of superhard materials in many industrial areas, such as abrasives, polishing, cutting tools, wear-resistance, protective coatings, etc., have stimulated great interest in the design and preparation of such materials.^1–4 It is generally accepted that the superhard materials, which are formed by the light elements (B, C, N and O), such as diamond,⁵ c-BN⁶ and so on. The reason for superhardness of these materials is due to the formations of strong three-dimensional covalent bonding networks.⁷ Although diamond is the hardest material known, with a measured hardness, 60–120 GPa, it reacts easily with iron-based materials. Cubic BN has a higher hardness than diamond, but it can be synthesized only under high pressure and temperature at great cost.⁸ Therefore, great efforts have been devoted to explore novel hard and ultra-incompressible materials, such as ReB₂, RuB₂, OsB₂, and so on.^9–13 These transition metal borides maybe become potential ultra-hard candidate materials. They usually possess high electron density and strong covalent bonds. Moreover, they can be synthesized under ambient pressure, which reduces the cost of synthesis.

The 4d transition metal borides have also attracted great attentions. Theoretical calculations¹⁴ have indicated that Amm2 and Cmcm phases of ZrB₄ have a high hardness of about 42 GPa, which reveal that they are potentially superhard materials. It has been theoretically proved that tungsten triboride is a better candidate material than WB₄, because WB₃ is are more stable. Boron atoms in tungsten borides W_1−xB₃ to WB_3+x, space group (P6₃/mmc)^15,16 exhibit a three-dimensional (3D) framework consisting of xy planar graphene-like layers with distorted sp² hybridization B–B bonds and possible interstitial boron atoms, contributing to its high hardness. A stable orthorhombic phase (Imma phase) TaB₃ (ref. 17) is predicted, which has a hardness of 41.2 GPa. The ground-state phases of ReB₃ and IrB₃ are predicted to have P6m2 and Amm2 phases, respectively. These crystal phases have ultra-incompressibility, and a high bulk and shear modulus.¹⁸ These results indicated that 3d, 4d TMs borides may be another choice for superhard material. According to the design principle, Nb-based borides have attracted attention because of their low cost, high hardness, high elastic modulus, and excellent thermal stability.^19,20 So far, studies of Nb–B binary compounds have focused on the structure and mechanical properties of NbB₂.^21,22 Pan et al.²³ investigated the elastic properties, theoretical hardness, and chemical bonding of Nb–B compounds with different B concentrations. Among them, the calculated hardness of Nb₂B₃ is 33.5 GPa and thus it can be considered as a potential superhard material. However, presently, the debate on the ground state structure of NbB₃ has never been solved and its physical behaviors are still controversial, possibly due to the uncertainty of its crystal structure. Therefore, resolving the crystal structure of NbB₃ has an important significance.

In the present work, the crystal structures of NbB₃ are extensively explored over a wide range of pressures (0–150 GPa) using a specifically developed particle swarm optimization (PSO) algorithm technique for crystal structure prediction.^24,25 A stable monoclinic phase C2/c and four metastable phases at ambient condition for NbB₃ have been uncovered. The stabilities of these new phases at ambient condition have been determined by elastic constants and phonon spectra. Under pressure, three of the metastable phases are found to have a phase transition. Further calculations have been performed to study the mechanical and electronic properties of all phases of NbB₃.

Computational methods

To search for potential crystal structures, the PSO technique in the Crystal Structure Analysis by Particle Swarm Optimization (CALYPSO) package^24,25 was employed at 0, 50, 100 and 150 GPa with six formula units (f.u.) in each simulation cell. The underlying ab initio structural relaxations and electronic band structure calculations used density functional theory with the Perdew–Burke–Ernzerhof (PBE) generalized gradient approximation (GGA) of the exchange–correlation energy and local density approximation (LDA),²⁶ as implemented in the VASP code.²⁷ The projector augmented wave (PAW) method was used to model the electron–ion interaction, including the 2s²2p¹, and 4d⁴5s¹ of B and Nb, respectively, in the valence space. A cutoff energy of 600 eV and a fine regular k-point grids sampling with grid spacing of 2π × 0.03 Å⁻¹ are used the plane wave expansion of the wave functions, which can ensure that all the enthalpy calculations were converged to better than 1 meV per atom. The validity of pseudopotentials used at high pressures is carefully examined with the full-potential linearized augmented plane-wave method through the WIEN2k package²⁸ (Fig. S1†). The accuracy of the total energies obtained within the framework of density functional theory is in many cases sufficient to predict the stability of structures. In phonon calculations, the interatomic force constant was calculated using a supercell approach combined with Parlinski–Li–Kawazoe method²⁹ as implemented in the PHONOPY code.³⁰ A fine relaxation with a force criterion of 10⁻⁸ eV Å⁻¹ between ions is performed at the first step of lattice dynamics calculations. The supercell size of C2/c, P6₃/mmm, C2/m, Pmm2 and I4̄m2 phases are constructed by 2 × 2 × 1, 2 × 2 × 3, 3 × 3 × 1, 3 × 3 × 1, 3 × 3 × 3, and 4 × 8 × 4, 6 × 6 × 6, 6 × 6 × 8, 6 × 6 × 6, 6 × 6 × 8 are employed as k-points, respectively.

Results and discussion

By using the evolutionary methodology of the crystal structure prediction, we have performed structure predictions for NbB₃ with variable-cell simulation cell sizes of six formula units (f.u.) at 0, 50, 100 and 150 GPa, respectively. We obtained five high pressure phases with space groups C2/c (4 f.u. per cell), P6₃/mmm (2 f.u. per cell), C2/m (2 f.u. per cell), Pmm2 (2 f.u. per cell) and I4̄m2 (1 f.u. per cell), respectively. The formation enthalpies and bond lengths are calculated by GGA only. The enthalpy–pressure relations of the candidate structures are shown in Fig. 1(a). It is very obvious that C2/c phase was energetically more favorable than other candidate phases in the wide pressure range studied. The application of a compound requires an accurate knowledge of its thermodynamic stability. For further experimental synthesis it was therefore necessary to investigate the relative stability of NbB₃. The formation enthalpies were evaluated using α phase of boron and cubic phase (Im3̄m) of Nb as the reference structures by the equation: ΔH = H(NbB₃) − H(Nb) − 3H(B). The formation enthalpy of C2/c phase is −1.769 eV per formula, and that of C2/m, P6₃/mmm, Pmm2 and I4̄m2 phases are −1.672, 1.671, −1.657 and −1.638 eV, respectively, which is slightly higher than C2/c. Therefore, the P6₃/mmm, C2/m, Pmm2 and I4̄m2 phases are metastable structures for NbB₃. For metastable phases, at higher pressures, we found the phase transition of them. The phase transition pressure can calculated from the usual condition of equal enthalpies, i.e., the pressure P at which the enthalpies, H = E + PV, of the C2/m and Pmm2 phases, Pmm2 and I4̄m2 phases are the same. Therefore, pressure drives the distortion of crystal lattice and shift of atomic positions, leading to phase transition of crystal structures. From Fig. 1(b), by the method of equal enthalpies we firstly found the phase transition pressures from C2/m to Pmm2 to I4̄m2 are 29 GPa and 46 GPa, respectively. The crystal structures are shown in Fig. 2. For the most stable crystal phase C2/c, the puckered parallel boron bilayers were tightly connected by B4 rhomboid with short side 1.745 Å and long side 1.825 Å, close to that of B–B bond distances WB₄ (1.749–1.810 Å),³¹ but shorted than that of ZrB₄ (1.801–1.829 Å),¹⁴ indicating relatively strong B–B interactions. For metastable phases P6₃/mmm and Pmm2, the conjunctional modes of their B layers are very similar, which include the a planar graphene-like boron sheet (ochre spheres in Fig. 2(b) and (d)) appearing with B–B bonds varying from 1.767 Å to 1.873 Å. In the C2/m phase, B atoms are arranged by an unusual 3D framework of interconnected square B4 units (Fig. 2(c)), which is highly similar to the C4 unit in the tetragonal body-centered allotrope (bct-C4) of carbon.³² For I4̄m2 phase, B atoms also are constituted by a B4 triangle unit, in which three B atoms located in the vertex of the triangle and another B atom is in its center. Overall, the crystal structures of NbB₃ are constructed by stacking Nb or B layers, considered as sandwich structures. All the lattice parameters of five phases of NbB₃ are showed in Table S1,† which indicated that the values obtained by GGA and LDA method are comparable.

Fig. 1 (a) Enthalpy–pressure diagrams of NbB₃; (b) the calculated enthalpies differences relative to C2/m phase of C2/m, Pmm2 and I4̄m2 phases for NbB₃ in the pressure range from 20 GPa to 80 GPa.

Fig. 2 Crystal structures of NbB₃ (a) C2/c (b) P6₃/mmm (c) C2/m (d) Pmm2 and (e) I4̄m2. The red and green balls represent Nb and B atoms, respectively.

To check the dynamical stabilities of the currently predicted phases of NbB₃, we have calculated their phonon dispersion curves using GGA method. A stable crystalline structure requires all phonon frequencies to be positive. As seen in Fig. 3, the absence of any imaginary phonon frequency in the whole Brillouin zone for five phases of NbB₃ indicate the dynamical stabilities of them at ambient pressure in the whole BZ, confirming the dynamic stability of the newly proposed crystal structures of NbB₃. It is well known that shorter bond lengths contribute to higher phonon frequencies. The phonon frequency of all the phases of NbB₃ (∼30 THz) shown in Fig. 3 indicates that there are short bond lengths in NbB₃ and their stronger interactions between Nb–B and B–B. Simultaneously, the primitive cell of the C2/c, P6₃/mmm, C2/m, Pmm2, and I4̄m2 phases contain 16, 8, 8, 8, and 4 atoms, which have 48, 24, 24, 24, and 12 phonon branches, respectively. The calculated zone center (Γ) phonon eigenvectors were used to deduce the symmetry labels of phonon modes. The vibrational modes at the zone center have their reducible representations constituted by infrared, Raman and hyper-Raman modes, which can be obtained via the Bilbao Crystallographic Server.³³ Both infrared and Raman frequencies of crystal structures for Γ point can provide useful information for future experiments to identify the predicted new phases.

Fig. 3 Phonon dispersion relations of predicted new phases of NbB₃ at ambient condition (a) C2/c (b) P6₃/mmm (c) C2/m (d) Pmm2 (e) I4̄m2.

The mechanical stability of a phase has been investigated because it is a necessary condition for the existence of a crystal. Accurate elastic constants can directly describe the response of the crystal to external stresses and are essential for many practical applications related to the mechanical properties of materials. They also provide very useful information to estimate the hardness of the material. Meanwhile, for a stable crystal, the elastic constants C_ij must satisfy the Born–Huang criterion.³⁴ For a monoclinic crystal, the independent elastic stiffness tensor consists of thirteen components C₁₁, C₂₂, C₃₃, C₄₄, C₅₅, C₆₆, C₁₂, C₁₃, C₂₃, C₁₅, C₂₅, C₃₅, and C₄₆. Its mechanical stability of monoclinic phase is given by:

C_ii > 0 (i = 1, 2, 3, 4, 5, 6), [C₁₁ + C₂₂ + C₃₃ + 2(C₁₂ + C₁₃ + C₂₃)] > 0, (C₃₃C₅₅ − C₃₅²) > 0, (C₄₄C₆₆ − C₄₆²) > 0, (C₂₂ + C₃₃ − 2C₂₃) > 0, [C₂₂(C₃₃C₅₅ − C₃₅²) + 2C₂₃C₂₅C₃₅ − C₂₃²C₅₅ − C₂₅²C₃₃] > 0, g = C₁₁C₂₂C₃₃ − C₁₁C₂₃² − C₂₂C₁₃² − C₃₃C₁₂² + 2C₁₂C₁₃C₂₃, {2(C₁₅C₂₅(C₃₃C₁₂ − C₁₃C₂₃) + C₁₅C₃₅(C₂₂C₁₃ − C₁₂C₃₃) + C₂₅C₃₅(C₁₁C₂₃ − C₁₂C₁₃)] − [C₁₅²(C₂₂C₃₃ − C₂₃²) + C₂₅²(C₁₁C₃₃ − C₁₃²) + C₃₅²(C₁₁C₂₂ − C₁₂²)] + C₅₅g > 0

For orthorhombic phase, the mechanical stability can be judged from:

C_ii > 0, i = 1, 2, 3, 4, 5, 6

C₁₁ + C₂₂ + C₃₃ + 2(C₁₂ + C₁₃ + C₂₃) > 0

C_ii + C_jj − 2C_ij > 0, (i, j = 1, 2, 3, i ≠ j)

For a stable tetragonal phase, its elastic constants should obey the following inequalities:

C₄₄ > 0, C₆₆ > 0, C₁₁ > |C₁₂|, 2C₁₃² < C₃₃(C₁₁ + C₁₂)

Therefore, we calculated the elastic constants of the five phases of NbB₃ by the strain–stress method, which are showed in Table 1 (both GGA and LDA), together with those of other transition metal triborides TMB₃ (TM = V, Ir, and Re).^17,18 We found that the elastic constants are a little larger by LDA method than GGA one. However, the differences do not affect the mechanical natures of NbB₃. As seen in Table 1, the predicted phases of NbB₃ all satisfied the mechanical stability criteria, indicating that they are mechanically stable. The obtained elastic constants of the predicted new phases of NbB₃ are competitive with those of other transition metal triborides.^17,18 As seen in Table 1, C₄₄, C₅₅, and C₆₆ for these phases are very close. C₁₁, C₂₂, and C₃₃ for these phases are larger than 400 GPa, indicating strong incompressibility along the a, b, and c-axis, respectively. The values of C₁₁ of C2/c, P6₃/mmm, and I4̄m2 phases are larger than those of C₃₃, indicating that the bond strength along the [100] direction is much stronger than that along the [001] direction. Among them, for C2/m-NbB₃, C₂₂ [716 GPa (GGA), 724 GPa (LDA)] is much larger than C₁₁ [574 GPa (GGA), 584 GPa (LDA)] and C₃₃ [577 GPa (GGA), 588 GPa (LDA)], comparable to that of c-BN, 820 GPa,³⁵ which may come from the accumulation of electron density due to the shorter B–B bond (1.744 Å). C₄₄ is an important indicator for the hardness of materials. All the studied structures have large C₄₄ values. Notably, Pmm2-NbB₃ possesses the largest C₄₄ value, indicating its relatively strong strength against shear deformation. Unfortunately, there are no experimental data available for comparisons, therefore, our results could be a reference for future studies and applications of NbB₃.

Table 1 The elastic constants of five phases of NbB₃ at zero pressure, together with other transition metal triborides^17,18

	Space group	Method	C11	C22	C33	C44	C55	C66	C12	C13	C23	Ref.
NbB3	C2/c	GGA	644	624	513	239	233	258	103	174	184	Present
		LDA	699	675	572	264	258	281	115	192	201	Present
	P63/mmm	GGA	583		438	206			110	128		Present
		LDA	589		451	211			112	127		Present
	C2/m	GGA	574	716	577	237	272	273	108	126	135	Present
		LDA	584	724	587	243	280	279	107	129	140	Present
	Pmm2	GGA	572	606	588	264	258	278	147	122	160	Present
		LDA	609	659	640	287	272	300	168	136	173	Present
	I4̄m2	GGA	601		560	213		238	155	138		Present
		LDA	661		617	238		262	173	150		Present
TaB3	Imma		561	705	620	266	262	302	166	168	80	17
ReB3	P63/mmc		665		809	217			128	123		18
	P3̄m1		613		795	194			177	122		18
IrB3	Amm2		475		486	184		164	277	120		18
	P63/mmc		398		643	164			172	223		18
	P3̄m1		556		666	131			176	147		18

---

Bulk and shear moduli are important indicators of the hardness of a material. The calculated elastic constants were used to estimate the bulk and shear modulus of ReB₃ and IrB₃ using the Voigt–Reuss–Hill (VRH) approximation.³⁶ As is known, a high bulk modulus of a material illustrates its strong ability to resist volume deformation caused by an applied load. Apparently, all the predicted phases^17,18 in Table 2 have large bulk modulus (above 255 GPa), comparable to that of TaB₃, ReB₃ and IrB₃, which indicated that they are difficult to compress. Compared with the bulk modulus, the shear modulus (G) is a much better parameter to indicate the hardness of a material. From Table 2, all the structures of NbB₃ possess high shear modulus. Among them, C2/m-NbB₃ has the largest shear modulus (251 GPa by GGA, 255 GPa by LDA), indicating that it can withstand the largest extent shear strain. Besides the bulk modulus and shear modulus, Young's modulus could also provide a good measure of the stiffness of materials. The Young's modulus E is obtained by the equation: E = (9GB)/(3B + G). Young's modulus is defined as the ratio of stress and strain, and is used to provide a measure of the stiffness of materials in the range of elastic deformation. When the value of E is larger, the material is stiffer. In the same way, C2/m phase has highest Young's modulus, and therefore will be much stiffer than the other phases studied. Hence, all predicted phases could be potentially hard materials. The value of B/G is commonly used to describe the ductility or brittleness of materials, with 1.75 as critical reference point. Higher (or lower) B/G value than 1.75 indicates that the material is ductile (or brittle).considered to be ductile (or brittle). From Table 2, the B/G values of all the phases of NbB₃ are below the critical value, implying their brittle nature. The value of the Poisson's ratio is indicative of the degree of directionality of the covalent bonds. The Poisson's ratio ν is obtained by the equation: ν = (3B − 2G)/2(3B + G). The typical ν value is 0.1 for covalent materials and 0.33 for metallic materials, respectively. The values of the Poisson's ratio of all phases for NbB₃ are smaller than 0.33, indicating that NbB₃ has covalent bond characterization. Especially, C2/m and Pmm2 phases have the close small Poisson ratio (0.162 and 0.167 by GGA), which indicated that the directionality degree of covalent bonding of C2/m and Pmm2 phases are stronger than the other phases of NbB₃. The directionality of covalent bonding plays an important role in the hardness of materials. Smaller the Poisson's ratio is, larger the hardness is. Therefore, C2/m and Pmm2 phases perhaps have higher hardness. The bulk modulus B, shear modulus G, Young modulus E, B/G, Poisson's ratio ν are all listed in Table 2. These results will provide theoretical guidance for future experimental and theoretical work.

Table 2 The isotropic bulk modulus B, shear modulus G, Young's modulus E, and the hardness H_V in unit of GPa, B/G and the Poisson's ratio ν for hexagonal, monoclinic and orthorhombic phases of NbB₃ at ambient pressure

	Space group		B	G	E	ν	B/G	HV	Ref.
NbB3	C2/c	GGA	299	231	552	0.193	1.296	38.8	Present
		LDA	329	253	590	0.193	1.296	40.8	Present
	P63/mmm	GGA	258	211	497	0.178	1.223	37.8	Present
		LDA	261	215	505	0.177	1.216	38.3	Present
	C2/m	GGA	287	251	581	0.162	1.148	43.9	Present
		LDA	291	255	593	0.161	1.141	44.3	Present
	Pmm2	GGA	291	247	578	0.169	1.181	42.7	Present
		LDA	319	267	626	0.173	1.196	44.2	Present
	I4̄m2	GGA	289	219	525	0.197	1.318	36.8	Present
		LDA	318	243	580	0.196	1.310	34.2	Present
TaB3	Imma		301	262	608	0.16	1.149	41	17
ReB3	P63/mmc		321	258	610	0.18	1.24	37	18
	P3̄m1		318	228	552	0.21	1.39	29	18
IrB3	Amm2		285	157	398	0.27	1.82	16	18
	P63/mmc		297	143	370	0.29	2.08	13	18
	P3̄m1		302	178	446	0.25	1.70	19	18

---

The hardness of a material is the intrinsic resistance to deformation when a force is applied, which depends on the loading force and the quality of the sample (i.e., the presence of defects such as vacancies and dislocations). Therefore, we estimate Vickers hardness (H_V) by an empirical model proposed by Chen et al.,³⁷ H_V = 2(k²G)^0.585 − 3 (k = G/B). The calculated hardness of five predicted phases of NbB₃ are listed in Table 2. The hardness determined by GGA and LDA methods is almost identical. The estimated hardness of 44 and 43 GPa for C2/m and Pmm2 phases, respectively, exceed 40 GPa, which can be considered as the superhard materials. Moreover, C2/m and Pmm2 phases have the largest hardness among other studied niobium borides.²³

To our knowledge, electronic structure and chemical bonding are key factors to deeper understanding the origin of hardness and elastic properties. Following, the density of states (DOS) and bond characteristic are calculated and analysed here. Fig. 4 represents the total and partial density of states of five different phases of NbB₃, and the black vertical dashed of DOS indicates the Fermi level (E_F). The obtained DOS curves show large similarities in these phases of NbB₃ as follows. It is clear that some bands are across the E_F, indicating that those phases exhibit metallic behavior. It is easy to see that the peaks below-10 eV are mainly attributed to B-s states and B-p states with a slight contribution from, Nb-p and Nb-d states. The states from −10 to 0 eV mainly originate from Nb-d and B-p orbitals with slight contributions of Nb-p and B-s. Moreover, the partial DOS profiles for both Nb-4d and B-2p are very similar in the range of −10 to 0 eV, reflecting the significant hybridization between these two orbitals. This fact also shows a strong covalent interaction between the Nb and B atoms. On the other hand, the DOS profile near E_F comes from the 4d state of Nb. The typical feature of their DOS is to have a pseudogap near Fermi level, which is the borderline between bonding and antibonding states. It should be pointed out that the E_F is lying on the pseudogap in all phases, revealing the p–d bonding states started to be saturated. The nearly full occupation of bonding states and without filling on the antibonding states leads to the high bulk modulus and shear modulus, small Poisson's ratio, and also increase the structural stabilities of NbB₃.

Fig. 4 The total and partial density of states of NbB₃ at zero pressure.

To gain more detailed insight into the bonding character of NbB₃, we have calculated the electronic localization function (ELF),³⁸ which is based on a topological analysis related to the Pauli exclusion principle. The ELF is a contour plot in real space where different contours have values ranging from 0 to 1. A region with ELF = 1 is where there is no chance of finding two electrons with the same spin. This usually occurs in places where covalent bonds or lone pairs (filled core levels) reside. An area where ELF = 0 is typical for a vacuum (no electron density) or areas between atomic orbitals. This is where electrons of like spin approach each other the closest. ELF = 0.5 for a homogeneous electron gas, with values of this order indicating regions with bonding of a metallic character. It should be noted that ELF is not a measure of electron density but is a measure of the Pauli principle, and is useful in distinguishing metallic, covalent, and ionic bonding. The contours of ELF domains for all the phases on its (100) plane except P6₃/mmm phase along the (001) plane are shown in Fig. 5. The high electron localization can be seen in the region between adjacent B and B atoms indicative of covalent bonding. Meanwhile, the ELF is very small at the Nb sites, whereas it attains local maximum values at the B sites, manifesting another covalent interaction between Nb and B atoms. Therefore, the strong covalent interaction between B–B bonds and B–Nb bonds is the main driving force for its higher bulk and shear modulus.

Fig. 5 ELF contours of the electronic localization function (ELF) of C2/c, C2/m, Pmm2, and I4̄m2 phases of NbB₃ on the (100) plane and P6₃/mmm phase on the (001) plane. The isosurface level value is 0.80.

Conclusions

In summary, we have explored the high-pressure crystal structures of NbB₃ and investigated their electronic, dynamic, and mechanical properties via the PSO algorithm combined with first-principle calculations. The predicted new phases of NbB₃ belong to monoclinic C2/c and C2/m, orthorhombic Pmm2, tetragonal I4̄m2 and hexagonal P6₃/mmm, in which C2/c is most stable crystal structure and other four phases are metastable phases. Phonon and formation enthalpy calculations have confirmed that all of the phases are dynamically stable and synthesizable under ambient conditions. Under high pressure, we found that pressure stimulates the metastable phases of NbB₃ to go through phase transition twice, from C2/m phase to Pmm2 phase at 29 GPa and Pmm2 phase to I4̄m2 phase at 46 GPa. All phases with high bulk and shear modulus, and low Poisson's ratio make NbB₃ become a promising low-compressible material. The calculated hardness of C2/c, C2/m and Pmm2 phases are 39 GPa, 45 GPa and 44 GPa, respectively, which is a potential superhard material. Moreover, the electronic density of states and electronic localization function analysis have demonstrated that the strong covalent B–B and B–Nb bonding play a key role in the incompressibility and hardness for NbB₃. Our results are encouraging for further experimental and theoretical research.

Acknowledgements

This work was financially supported by the National Natural Science Foundation of China Grant No. 11304141 and the Henan Key Teacher Project No. 2014GGJS-114.

References

1. H. Y. Chung, M. B. Weinberger, J. B. Levine, A. Kavner, J. M. Yang, S. H. Tolbert and R. B. Kaner, Science, 2007, 316, 436.
2. R. B. Kaner, J. J. Gilman and S. H. Tolbert, Science, 2005, 308, 1268.
3. B. H. Chu, D. Li, F. B. Tian, D. F. Duan, X. J. Sha, Y. Z. Lv, H. D. Zhang, B. B. Liu and T. Cui, Sci. Rep., 2015, 5, 10500.
4. V. V. Brazhkin, A. G. Lyapin and R. J. Hemley, Philos. Mag. A, 2002, 82, 231.
5. N. Mounet and N. Marzari, Phys. Rev. B: Condens. Matter Mater. Phys., 2005, 71, 205214.
6. J. C. Zheng, Phys. Rev. B: Condens. Matter Mater. Phys., 2005, 72, 052105.
7. A. L. Ivanovskii, Prog. Mater. Sci., 2012, 57, 184.
8. B. L. Jonathan, H. T. Sarah and B. K. Richard, Adv. Funct. Mater., 2009, 19, 3519.
9. R. W. Cumberland, M. B. Weinberger, J. J. Gilman, S. M. Clark, S. H. Tolbert and R. B. Kaner, J. Am. Chem. Soc., 2005, 127, 7264.
10. X. F. Hao, Y. H. Xu, Z. J. Wu, D. F. Zhou, X. J. Liu, X. Q. Cao and J. Meng, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 74, 224112.
11. H. Y. Chung, M. B. Weinberger, J. M. Yang, S. H. Tolbert and R. B. Kaner, Appl. Phys. Lett., 2008, 92, 261904.
12. M. G. Zhang, H. Y. Yan, G. T. Zhang and H. Wang, J. Phys. Chem. C, 2010, 114, 6722.
13. Q. Tao, D. Zheng, X. Zhao, Y. Chen, Q. Li, Q. Li, C. Wang, T. Cui, Y. M. Ma, X. Wang and P. Zhu, Chem. Mater., 2014, 26, 5297.
14. X. Y. Zhang, J. Q. Qin, X. W. Sun, Y. N. Xue, M. Z. Ma and R. P. Liu, Phys. Chem. Chem. Phys., 2013, 15, 20894.
15. R. Mohammadi, A. T. Lech, M. Xie, B. E. Weaver, M. T. Yeung, S. H. Tolbert and R. B. Kaner, Proc. Natl. Acad. Sci. U. S. A., 2011, 108, 10958.
16. I. Zeiringer, P. Rogl, A. Grytsiv, J. Polt, E. Bauer and G. Giester, J. Phase Equilib. Diffus., 2014, 35, 384.
17. X. Z. Zhang, E. J. Zhao and Z. J. Wu, J. Alloys Compd., 2015, 632, 37.
18. Q. Yan, Y. X. Wang, B. Wang, J. M. Yang and G. Yang, RSC Adv., 2015, 5, 25919.
19. A. Pallas and K. Larsson, J. Phys. Chem. B, 2006, 110, 5367.
20. E. Deligoz, K. Colakoglu and Y. O. Ciftci, Solid State Commun., 2010, 150, 405.
21. P. Vajeeston, P. Ravindran, C. Ravi and R. Asokamani, Phys. Rev. B: Condens. Matter Mater. Phys., 2001, 63, 045115.
22. I. R. Shein and A. L. Lvanovskii, J. Phys.: Condens. Matter, 2008, 20, 415218.
23. Y. Pan and Y. H. Lin, J. Phys. Chem. C, 2015, 119, 23175.
24. Y. Wang, J. Lv, L. Zhu and Y. Ma, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 82, 094116.
25. Y. C. Wang, J. Lv, L. Zhu and Y. M. Ma, Comput. Phys. Commun., 2012, 183, 2063.
26. D. M. Ceperley and B. J. Alder, Phys. Rev. Lett., 1980, 45, 566.
27. G. Kresse and J. Joubert, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758.
28. P. Blaha, K. Schwarz, P. Sorantin and S. B. Trickey, Comput. Phys. Commun., 1990, 59, 399.
29. K. Parlinski, Z. Q. Li and Y. Kawazoe, Phys. Rev. Lett., 1997, 78, 4063.
30. A. Togo, F. Oba and I. Tanaka, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 78, 134106.
31. M. Wang, Y. Li, T. Cui, Y. Ma and G. Zou, Appl. Phys. Lett., 2008, 93, 101905.
32. K. Umenoto, R. M. Wentzcovitch, S. Saito and T. Miyake, Phys. Rev. Lett., 2010, 104, 125504.
33. E. Kroumova, M. I. Aroyo, J. M. Perez-Mato, A. Kirov, C. Capillas, S. Ivantchev and H. Wondratschek, Phase Transform., 2003, 76, 155.
34. Z. J. Wu, E. J. Zhao, H. P. Xiang, X. F. Hao, X. J. Liu and J. Meng, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 76, 054115.
35. M. Grimsditch, E. S. Zouboulis and A. Polian, J. Appl. Phys., 1994, 76, 832.
36. R. Hill, Proc. Phys. Soc., London, Sect. A, 1952, 65, 349.
37. X. Q. Chen, H. Y. Niu, D. Z. Li and Y. Y. Li, Intermetallics, 2011, 19, 1275.
38. A. D. Becke and K. E. Edgecombe, J. Chem. Phys., 1990, 92, 5397.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/c6ra05162f

---