Two step label free particle separation in a microfluidic system using elasto-inertial focusing and magnetophoresis†
Abstract
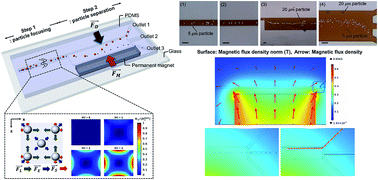
This study focuses on the separation of different sized particles and cells by employing a facile two step label free separation technique which consists of elasto-inertial particle focusing and magnetophoretic particle repulsion. The elasto-inertial force makes the objects migrate toward the centerline at the first stage, and the magnetophoretic repulsion force makes them migrate to the lateral direction depending upon their particle size at the second stage in the microchannel. An analytical calculation is carried out to predict the trajectories of different sized particles by considering hydrodynamic viscous drag and magnetophoretic repulsion forces, and this is compared to the experimental results. Numerical analyses are performed to understand the physics underlying the elasto-inertial particle focusing and the magnetophoretic particle migration.

 Please wait while we load your content...
Please wait while we load your content...