Open Access Article
Open Access ArticleA relationship between three-dimensional surface hydration structures and force distribution measured by atomic force microscopy†
Keisuke
Miyazawa
a,
Naritaka
Kobayashi
a,
Matthew
Watkins
b,
Alexander L.
Shluger
c,
Ken-ichi
Amano
d and
Takeshi
Fukuma
*ae
aDivision of Electrical Engineering and Computer Science, Kanazawa University, Kakuma-machi, Kanazawa 920-1192, Japan. E-mail: fukuma@staff.kanazawa-u.ac.jp; Fax: +81-76-234-4632; Tel: +81-76-234-4847
bSchool of Mathematics and Physics, University of Lincoln, Brayford Pool, Lincoln LN6 7TS, UK
cDepartment of Physics and Astronomy and London Centre for Nanotechnology, University College London, Gower Street, London, WC1E 6BT, UK
dDepartment of Energy and Hydrocarbon Chemistry, Graduate School of Engineering, Kyoto University, Kyoto 615-8510, Japan
eACT-C, Japan Science and Technology Agency, Honcho 4-1-9, Kawaguchi 332-0012, Japan
First published on 4th March 2016
Abstract
Hydration plays important roles in various solid–liquid interfacial phenomena. Very recently, three-dimensional scanning force microscopy (3D-SFM) has been proposed as a tool to visualise solvated surfaces and their hydration structures with lateral and vertical (sub) molecular resolution. However, the relationship between the 3D force map obtained and the equilibrium water density, ρ(r), distribution above the surface remains an open question. Here, we investigate this relationship at an interface of an inorganic mineral, fluorite, and water. The force maps measured in pure water are directly compared to force maps generated using the solvent tip approximation (STA) model and from explicit molecular dynamics simulations. The results show that the simulated STA force map describes the major features of the experimentally obtained force image. The agreement between the STA data and the experiment establishes the correspondence between the water density used as an input to the STA model and the experimental hydration structure and thus provides a tool to bridge the experimental force data and atomistic solvation structures. Further applications of this method should improve the accuracy and reliability of both interpretation of 3D-SFM force maps and atomistic simulations in a wide range of solid–liquid interfacial phenomena.
1 Introduction
Hydration plays an important role in various solid–liquid interfacial phenomena, including crystal growth,1 electrochemical reactions2 and biomolecular functions.3–5 To understand the mechanism of these processes, non-uniform water density distributions, ρ(r) (i.e. hydration structures), at solid–liquid interfaces have been intensively studied by spectroscopic methods using X-ray6 or neutron7 beam technologies, and mechanical methods such as surface force apparatus8 and atomic force microscopy (AFM).9 However, direct imaging of a hydration structure generally requires a subnanometer-scale and three-dimensional (3D) spatial resolution, which has been difficult for conventional measurement techniques. A requirement that these measurements should be relatively non-invasive, limits the application of approaches using charged particles (e.g. electron microscopy).Recently, AFM techniques for imaging a 3D force distribution at a solid–liquid interface have been proposed.10,11 In these methods, an AFM tip is scanned vertically as well as laterally in an interfacial space. During scanning, the variation of force applied to the tip, F(r), is recorded to produce a 3D F(r) image. These methods can be combined with any AFM operation modes, such as frequency modulation10,11 and amplitude modulation12 modes. However, realising the full potential of this powerful technique requires establishing the imaging mechanism and developing a practical algorithm to connect the force measurement to the water density distribution about the interface, ρ(r).
In this paper, for the first time, we make a direct comparison of two theoretical models with experimental 3D force distribution measured by AFM in aqueous solution. This has been achieved by improvements in experimental techniques and data processing, which now allow measurements to be made in pure water within 20 minutes of the sample being exposed to solution. This, in turn, allowed us to overcome the main difficulties in previous studies, which have been obtaining stable working conditions to take the measurements of the dissolving surface, and will thus greatly widen the number of systems accessible to this technique. Experimentally, it had been found to be significantly easier to work with (super-saturated) electrolyte solutions, which provide a larger signal and a more stable system.13 But, the electrolyte solution significantly complicates the theory and simulation of the system, making detailed interpretations of images unreliable. Although the influence of a tip on the intrinsic hydration structure or the presence of ions in solution can affect the 3D force distribution, as we show below, the pure water measurements allow a quantitative comparison of experimental data to forces predicted by two theoretical approaches. The resulting simple model provides a bridge between the experimental force data and atomistic solvation structures.
Atomistic simulations have been vital for our understanding and interpretation of atomic-scale AFM measurements in vacuum14 and recently in solutions.15–18 Harada and Tsukada investigated the correlation between free energy of the system and the overlap between the tip and sample hydration layers.15 They found that an attractive F(r) peak appears at the tip position where the tip and sample hydration peaks overlap each other. Watkins and Shluger investigated the changes in potential energy and entropy during a tip approach to the CaF2(111) surface.16,19 They clarified that the potential energy increase caused by the removal of water from the interface is largely compensated by the increase of entropy. Fukuma et al. performed a detailed comparison between 3D F(r) images obtained by experiments and simulation.20 They showed that subnanometer-scale F(r) contrasts mainly originate from the direct interaction between the tip apex atom and a hydration peak (i.e. localised enhanced ρ(r) distribution) just under it. These simulations, however, use specific tip models and have high computational costs. They provided deep insight into the mechanisms of imaging in solutions, but are less practical for routine interpretation of the growing number of images and 3D force distributions at the solid–liquid interface. There is a strong need for simpler, more general and efficient models.
Recently, a model describing the relationship between F(r) and ρ(r) distributions was proposed.21,22 In the model, an AFM tip is approximated by a single water molecule (we refer to water, but the model is applicable to other solvents). Namely, F(r) is approximated by the force that a water molecule would experience when it is held fixed at a specific site, r. By a statistical–mechanical approach, the relationship between F(r) and ρ(r) is derived as21,22
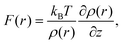 | (1) |
In this study, we investigate the relationship between F(r) and ρ(r) distributions at a fluorite–water interface by experiments, explicit MD simulation of tip–substrate force and calculations based on the STA model and conclude that the conversion of the ρ(r) image to an F(r) image by the STA model is the current best practice for image interpretation.
2. Methods
2.1 AFM experiment
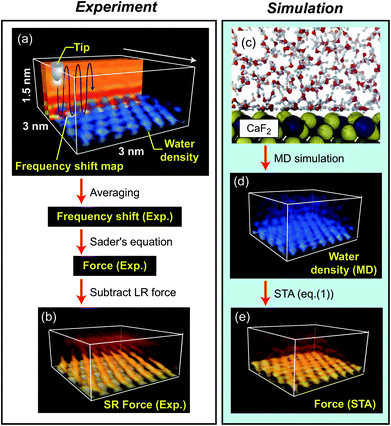
The fluorite(111) surface rapidly dissolves in water to form islands made of calcium hydroxo complexes.23 These interfacial processes prevent atomic-scale measurements after ∼20 min from the immersion of a fluorite substrate into water.24 In practice, the optical alignment of a cantilever deflection sensor and the tip coarse approach process take ∼10 min. Thus, 3D force images should be collected within ∼10 min, which is a very severe experimental condition. To overcome this difficulty, we used 3D scanning force microscopy (3D-SFM).10 In the method, we modulate the z tip position with a sine wave while the tip is laterally scanned (Fig. 2a). During the scan, Δf(r) induced by the F(r) variation is detected to form a 3D Δf(r) image. Among several Δf(r) measurement techniques proposed so far, 3D-SFM has been providing the highest imaging speed of less than 1 min per frame. This capability allows us to obtain a Δf(r) image even in a very limited experimental time window available (∼10 min) and to examine the structure of a much wider variety of solvated mineral interfaces with atomic resolution in 3D.Another problem is that force variation induced by a hydration structure in pure water is much smaller than that in an electrolyte solution. In addition, the fast imaging requires a wide bandwidth in the force detection. This leads to a lower signal-to-noise ratio (SNR). Due to these severe experimental conditions, the SNR obtained by a conventional cantilever (f0 ≃ 150 kHz) was insufficient for providing a clear atomic-scale 3D force image. To solve this problem, we used an ultra-short cantilever (USC, Nanoworld) with an f0 of 3.5 MHz in water.25 This high f0 greatly improves force sensitivity and hence enables atomic-resolution 3D Δf(r) measurements even in pure water.
Even with these efforts, an experimental condition that allows us to obtain an image showing clear atomic-scale contrast lasts only for a few tens of seconds as shown in Fig. S1 in the ESI.† As we needed to obtain a 3D Δf image in less than 20 min after the immersion of the sample into water, the thermal and mechanical drifts were not negligible. The initial swelling of the sample and cantilever holders induced by their contact with water leads to a non-linear mechanical drift. The irradiation of the laser beams for the cantilever excitation and deflection measurement initially induces a non-linear thermal drift. In addition, the dissolution of the fluorite surface changes the solution condition and hence the effective setpoint for the tip–sample distance regulation. These factors lead to the instability of the experimental conditions. To solve these problems, we focused on the image area showing atomic-scale contrasts with negligible distortion and applied an averaging filter using a pattern matching algorithm (see Fig. S1 in the ESI† for details). Although the imaging conditions were not stable, we were able to confirm the reproducibility of the main contrast features in the 3D Δf image. An example of such images is shown in Fig. S4 in the ESI.†
We converted the filtered 3D Δf image to a 3D Fexp(r) image using Sader's equation.26 From the 3D Fexp(r) image, we subtracted the long-range (LR) component (due to macroscopic effects) to obtain a 3D short-range (SR) Fexp(r) image (Fig. 2b) (see Fig. S2 in the ESI† for details). The obtained 3D SR Fexp(r) image shows clear atomic-scale contrasts, which should be directly comparable with the forces calculated by the two computational methods as the data are (i) measured in pure water and (ii) have long range macroscopic interactions subtracted out.
The AFM experiments were performed by a custom-built AFM with an ultra-low noise cantilever deflection sensor27,28 and a high stability photothermal excitation system.25,29 A commercially available phase-locked loop (PLL) circuit (OC4, SPECS) was used for oscillating a cantilever at its resonance frequency with a constant amplitude and for detecting Δf(r) induced by the F(r) variation. The AFM head was controlled with a commercially available AFM controller (ARC2, Asylum Research). We modified the control software to perform 3D force measurements. The size of the original 3D Δf(r) image was 3 × 3 × 1.5 nm3 with 64 × 64 × 256 pixels. The frequency and amplitude of the z modulation and the lateral scan speed during the 3D-SFM imaging were 195.3 Hz, 1.5 nm and 9.16 nm s−1, respectively. The whole 3D image was obtained in 53 s.
We used commercially available small cantilevers (USC-F5-k30, Nanoworld) with the following modifications.30 We removed an electron beam deposited (EBD) tip which comes with an as-purchased USC cantilever. Subsequently, we attached a silica bead with a diameter of 2 μm (43-00-203 Sicastar, Micromod) on the cantilever end. We fabricated the EBD tip with a length of approximately 500 nm and a tip apex radius of less than 10 nm using a field emission scanning electron microscope (FE-SEM) (ERA-8000FE, ELIONIX) with a 30 kV accelerating voltage on the attached silica bead. Just before the AFM experiment, we coated the cantilever with Si (30 nm) using a dc sputter coater (K575XD, Emitech). This is to remove surface contaminants on the tip apex31 as well as to prevent the dissolution of carbon from the EBD tip and the resulting contamination of the sample surface.30 The f0 and Q factor (Q) in the liquid, and the spring constant (k) of the cantilever were 3.91 MHz, 9.6 and 106.0 N m−1, respectively.
We used a fluorite(111) substrate with a size of 10 × 10 × 2 mm3 (crystal base). The substrate was glued onto a sample holder and cleaved with a razor blade. Immediately after the cleavage, we dropped 50 μL of water onto the substrate and performed AFM experiments at room temperature.
2.2 AFM simulation
Extensive details of the calculations used in this paper and discussion on the accuracy of various free energy methods, can be found in ref. 17.The ρ(r) distribution of water at a fluorite(111)–water interface was calculated by MD simulation, and is shown in Fig. 2c and d.16 From the obtained ρ(r) distribution, an F(r) map was obtained using the STA model, FSTA(r), (Fig. 2e). The force versus distance curves over special sites of the fluorite(111) surface were obtained using MD simulation with an explicit AFM tip model, FMD(r) (Fig. 2d). The free energy profiles were calculated by the free energy perturbation (FEP) method of Zwanzig32 applied to the vertical motion of an explicit tip model (a 72 ion CaF2 cluster) sampled using molecular dynamics simulation. The F(r) profiles were determined by numerical differentiation of the free energy profiles with respect to z (only the component of the force perpendicular to the interface affects the oscillation frequency of the cantilever in the mode of operation used here).
We do not know the exact atomic-scale structure of the tip end during the imaging as we do not have a method to confirm it in situ. As we coated the tip with Si, a silicon oxide cluster may be one of the possible models. However, it is highly likely that the tip was covered with CaF2 due to an accidental crash into the surface or adsorption of the dissolved ions. Similar assumptions have often been made for simulation of atomic-scale AFM imaging of ionic crystals.14,16,17,19–21,33,34 In addition, the CaF2 tip model used in this study was well tested in the previous studies.16,17,19,21 Therefore, we used the CaF2 tip model as described above.
Simulations were carried out using classical molecular dynamics as implemented in the version 4 series of the GROMACS code.35 The force-field describing CaF2 and water–CaF2 interactions was taken from de Leeuw,36 discarding polarization terms. To describe water the TIP4P/2005 model was used.37 We applied a 0.9 nm cut-off to treat non-bonded interactions and a smooth particle mesh Ewald method to treat electrostatics.38 The equations of motion were integrated using a 2 fs time step, and the LINCS algorithm was used to enforce rigid water geometries. An NPT ensemble (300 K, 1 atm) was generated using Berendsen thermostats and barostats, with time constants of 1.0 and 10.0 ps for temperature and pressure, respectively. The first 0.5 ns of the 4 ns simulations were discarded as the equilibration period.
3 Results and discussion
3.1 3D distribution of ρ(r), FSTA(r) and Fexp(r)
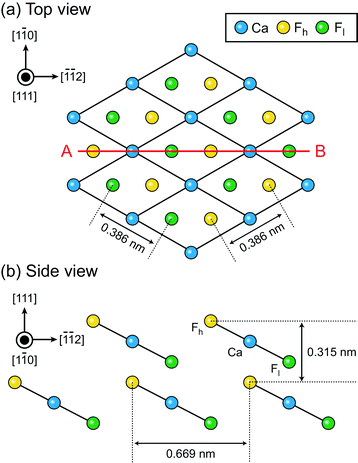
The number of solid–liquid interfaces that have been studied by atomic-level AFM simulation is very limited.15,16,18,20 The fluorite(111)–water interface is one of the few examples and hence suitable for a detailed comparison between simulation and experiments. Fluorite (CaF2) crystals are widely used for semiconductor lithography,39 other laser technologies40 and radioactivity investigations.41,42 Their growth process in an aqueous environment is important not only for the fabrication of industrial devices but also for understanding the mechanism of bio-mineralisation, formation of the tooth enamel,43,44 desalination for oil recovery45–47 and water purification.48–50 Hydration structures formed at the fluorite–water interface strongly influence ion adsorption and desorption in these processes.The fluorite(111) surface consists of hexagonally arranged Ca2+ and F− ions as shown in Fig. 1a. Among the F− ions, some are higher and the others are lower than the Ca2+ ions. Here, we refer to the former as Fh and the latter as Fl as indicated in Fig. 1b. All of the three ions (i.e. Ca, Fh and Fl) exist along line AB in Fig. 1a.
In the experiment, we obtained a 3D short-range (SR) force map, Fexp(r) (Fig. 2b). In the simulation, we calculated a ρ(r) distribution at a fluorite(111)–water interface using MD (Fig. 2c and d).16 The ρ(r) distribution was converted to a force map using the STA model, FSTA(r) (Fig. 2e). The FSTA(r) image is compared with the Fexp(r) map.
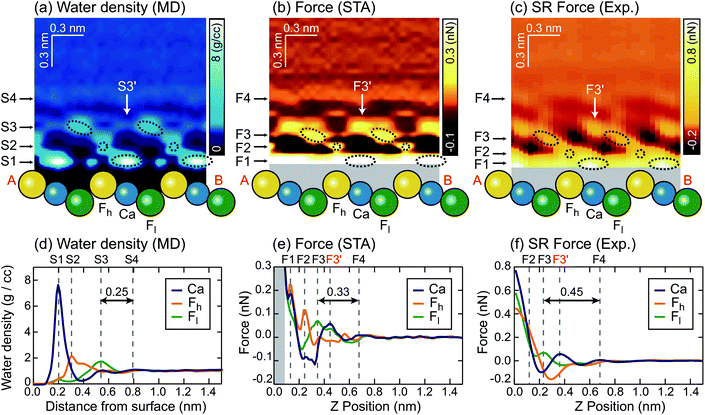
We extracted z cross sections along line A–B in Fig. 1a through the ρ(r) and F(r) distributions (Fig. 3a–c) to visualise their local distributions over the three special sites in one image. We plotted z profiles over each of the three sites for easier quantitative comparison (Fig. 3d–f).
 | ||
| Fig. 3 z cross sections of the (a) ρ(r), (b) FSTA(r) and (c) Fexp(r) images. z profiles of the (d) ρ(r), (e) FSTA(r) and (f) Fexp(r) images over Ca, Fh and Fl sites. | ||
The z cross section of the ρ(r) image (Fig. 3a) shows localised enhanced contrasts (hydration peaks) above Ca, Fh and Fl sites as indicated by the circles with dotted lines. Here, we refer to each of the hydration peaks as S1, S2 and S3, respectively, as we move away from the water–fluorite interface. Above these peaks, the image shows a layer-like enhanced contrast (hydration layer) which we will refer to as S4. The z profiles (Fig. 3d) of the ρ(r) image over Ca, Fh and Fl sites also show peaks corresponding to S1–S4. These profiles reveal that the peak corresponding to S1 is much larger than the others reflecting the strong attraction of water to the divalent cation.
3.2 Comparison between ρ(r) and Fexp(r)
We converted the ρ(r) distribution to an FSTA(r) map using the STA model (i.e.eqn (1)). Fig. 3b and e show the z cross section and z profiles of the FSTA(r) image. Eqn (1) shows that FSTA(r) is proportional to (∂ρ(r)/∂z)/ρ(r). Thus, repulsive force peaks appear at locations where ρ(r) is small but its gradient is large, namely, at a lower edge of a hydration peak. Consequently, the peak positions are shifted downwards by the ρ(r) to the FSTA(r) conversion process. Here, we define the repulsive force peaks originating from S1–S4 as F1–F4, respectively. To facilitate the comparison between the two images, the vertical position of the FSTA(r) is shifted upwards to match the S4 and F4 positions. Due to the contribution of the factor (1/ρ(r)) in eqn (1), FSTA(r) goes to infinity near the sample surface where water is sterically forbidden from approaching. In Fig. 3b and e, we indicated this z range with a grey background colour.Qualitatively, similar features appear in both the FSTA(r) and ρ(r) maps, such as the layer-like distribution of S4 and F4, and localised distributions of S1–S3 and F1–F3 over Ca, Fh and Fl sites (circles with dotted lines). The similarity of the FSTA(r) and ρ(r) maps can be understood by the observation that moving away from the surface, the ρ(r) map over each site appears, to a reasonable approximation, as a damped sinusoidal function. The sinusoidal form means that the (∂ρ(r)/∂z) factor in eqn (1) preserves the general form of the ρ(r) map, but with a quarter wavelength shift or approximately the radius of a water molecule. This result shows clearly why attempts to associate force peaks and troughs directly with water density have been broadly successful,10,11 due to the qualitative similarity between ρ(r) and FSTA(r) maps.
However, a closer examination reveals significant differences between the two functions. The force peak (F4′) originating from the secondary hydration peak over the Ca site (S3′) is strongly enhanced in the FSTA(r) image as indicated by arrows in Fig. 3a and b. Over the Ca site, the ρ(r) value at the z position between S1 and S3′ (z ≃ 0.4 nm) is as small as 0.3 g cc−1. Thus, the water density gradient ∂ρ/∂z shows a large value at z = 0.4–0.55 nm. This leads to an enhancement of the corresponding FSTA(r) peak (i.e., F3′).
A local spot showing such a small ρ(r) distribution does not generally exist near a solid surface. For example, in the case of a mica–water or a calcite–water interface, hexagonally arranged hydration peaks are closely packed to fill out the whole 3D interfacial space.10,20 Thus, there is no local site showing such a small ρ(r) and hence no clear difference between the ρ(r) and F(r) images was found in these cases. In contrast, at a fluorite–water interface, a more complicated hydration structure is formed due to the existence of the three different sites (i.e. Ca, Fh and Fl sites). These results show that the contrasts in the ρ(r) and F(r) images do not necessarily agree with each other.
Another difference is that F1–F3 in the FSTA(r) image are lower than S1–S3 in the ρ(r) image, using the S4 and F4 positions as a vertical reference. For example, the S3–S4 separation in the ρ(r) profile is 0.25 nm, while the F3–F4 separation in the FSTA profile is 0.33 nm. In general, the individual peaks in the ρ(r) profile have different shapes, and the magnitude of the peak shift caused by the conversion by eqn (1) is not constant. Therefore, peak separations in the ρ(r) and FSTA(r) maps are not necessarily the same.
This is an important finding. In previous studies, oscillatory force profiles were often attributed to a hydration force mainly due to the agreement between the size of a water molecule (0.25–0.30 nm) and the peak separations (0.2–0.4 nm).9,51–53 However, the reported variation of the force peak separation is larger than expected from the size of a water molecule. So far, these discrepancies have tentatively been attributed to the influence of ions or the invasive nature of the tip during measurements.54 In contrast, the above argument has clarified another mechanism to create such variations, even without any influence of ions in solution, with an absolutely idealised tip model.
3.3 Comparison between FSTA(r) and Fexp(r)
Similarly to the ρ(r) and FSTA(r) images, the Fexp(r) image (Fig. 3c) shows localised distributions of F1–F3 and a layer-like distribution of F4. In Fig. 3c, the vertical position of the Fexp(r) image is adjusted to match its F4 position to the S4 position of the ρ(r) image. In this case, the presence of the F4 may also provide a marker for calibrating the height of the tip above the surface.The lateral alignment of the Fexp(r) image is then adjusted to best match the 3D distribution in the FSTA(r). This is perfectly reasonable to do as we do not know which image features correspond to which surface sites a priori. In the future, it may be possible to devise numerical optimization schemes for the alignment – here we use symmetry to determine the correct slice to work with and a best judgement on the relative positions of the various maxima and minima along the slice. If the agreement between the theory and experiment is good this operation should be quite well defined. The arrangement between S1–S3 and F1–F3 is similar to that between the ρ(r) and FSTA(r) images. Moreover, the other features of the FSTA(r) image, such as an enhancement of F3′ and the lower positions of F1–F3 than S1–S3, are confirmed in the Fexp(r) image. These features can be seen more clearly in the z profiles (Fig. 3f). These profiles show that the F3–F4 separation in the Fexp(r) image (0.45 nm) is larger than the S3–S4 separation in the ρ(r) image (0.25 nm). They also show that the magnitude of the F3, F3′ and F4 peaks in the Fexp(r) image approximately agrees with that in the FSTA(r) image.
This result indicates that FSTA(r) gives a much better overall description of Fexp(r) than ρ(r), especially at larger distances from the surface. The overall shape of the force map is sufficiently detailed to allow a reliable assignment of the lateral alignment between the theory and experiment – this means that we identify the atomic sites at the surface.
3.4 Comparison between FSTA(r), Fexp(r) and FMD(r)
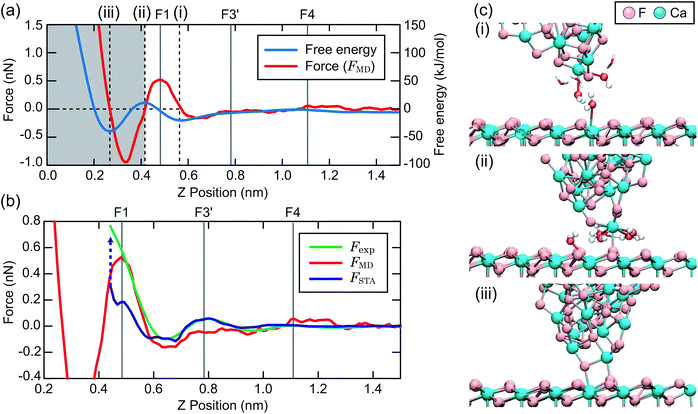
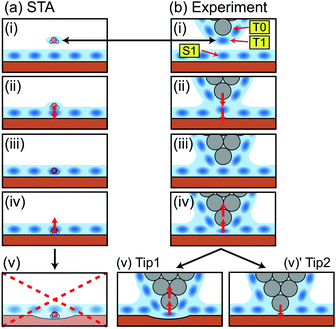
To make a connection with an atomistic picture of the measurement process, we briefly examine the results of the atomic-scale MD simulation of the tip–surface interaction in water16 and compare the results to the STA and experimental data. A previous comparison with simulations with explicit AFM tip models revealed modest agreement between the explicit modelling and the STA results.21 Nevertheless, the 3D FSTA(r) and Fexp(r) show strong similarities, as seen in the last section, possibly suggesting that the AFM tip models used were not totally realistic, rather than a breakdown of the STA model.Fig. 4a shows the free energy and FMD(r) changes during the approach of a CaF2 cluster tip model over a Ca site. The FMD(r) profile is obtained by differentiating the free energy profile with respect to z. Thus, the repulsive and attractive force peaks appear at the positions where the free energy profile shows the minimum and maximum slopes, respectively.
As the tip approaches the surface, the free energy gradually decreases to show a minimum at position (i). At this position, the first hydration peak just under the tip apex atom (T1) overlaps with S1 as indicated by the snapshot of the MD simulation in Fig. 4c(i). At this tip–sample separation, there are energetically favorable interactions for water molecules with both the tip and sample, leading to a reduction of the free energy.
With a further tip approach, the free energy increases to show a maximum at position (ii). During the tip approach process, water density continues to occupy the space between the tip and sample. It is confined compared to the minima in the free energy at (i), leading to an increase of the free energy. When the tip reaches position (ii), the tip penetrates the confined water layer and starts to directly interact with the sample surface as indicated in Fig. 4c(ii). This leads to a decrease of the free energy due to the release of the confined water as well as an attractive interaction between the tip and sample atoms.
At position (iii), the free energy is at its minimum. At this position, the confined water layer is entirely removed and multiple tip apex atoms directly interact with the surface atoms, as indicated in Fig. 4c(iii). A further tip approach leads to a sharp increase of the free energy due to the steric repulsion between the tip and sample atoms. These results show that the free energy change after the penetration of the last water layer strongly depends on the tip apex structure and properties.
Fig. 4b shows the same FMD(r) profile as shown in Fig. 4a but with a magnified scale. To compare it with the Fexp(r) and FSTA(r) profiles, we also plotted them with their z positions adjusted to match the peak positions. As we cannot determine the absolute z tip position in an experiment, it is natural to adjust the z position of the Fexp profile with respect to the others. As for FSTA(r) and FMD(r), their z positions are defined in the same way in the simulation box. Nevertheless, we needed to shift the z position of the FSTA(r) profile upwards by 0.35 nm to match the S4 and F4 positions. The origin for this z position difference is explained in the next section.
Fig. 4b shows that the FMD(r), FSTA(r) and Fexp(r) profiles are similar in the z range above S1, i.e. at distances larger than a water molecule above the surface. In contrast, we find clear differences between them in the z range below S1. In this z range, FMD(r) sharply decreases after the tip penetration of S1 and subsequently steeply increases. Thus, the FMD(r) profile shows a clear repulsive peak F1. In contrast, Fexp(r) and FSTA(r) continue to increase.
3.5 Physical reason for the agreement and disagreement between FSTA(r), Fexp(r) and FMD(r)
 | ||
| Fig. 5 Schematic models showing a relationship between the tip position and the measured force in (a) the STA model and (b) the real experiment. | ||
In a real experiment, we should consider the water tip as a hydration peak (T1) under the tip apex atom (T0) as shown in Fig. 5b(i). An attractive or repulsive force applied to T1 is directly transmitted to T0. Therefore, FSTA(r) can quantitatively agree with Fexp(r). This model explains the upward shift that we needed to apply to the FSTA(r) profile in Fig. 4b. In fact, the shifted distance (0.35 nm) approximately corresponds to the distance between T0 and T1.
As we see in Fig. 4b, the FSTA(r) profile is closer to the Fexp(r) profile (rigid tip case) than the FMD(r) profile. In our experiments, we hardly find a force profile showing a clear peak corresponding to S1. This result suggests that real tips used for atomic-scale measurements mostly correspond to a rigid one. In an experiment, a cantilever mechanically oscillates at a frequency higher than 3.5 MHz. The repeated tip approach and retraction cycles may change an unstable tip structure into a stable one. In addition, at the beginning of an imaging experiment, we often see atomic-scale contrast changes but it settles down after several scans. During this process, the tip apex structure is probably stabilised.
4 Conclusions
We have investigated the relationship between 3D hydration structures and force distributions measured by AFM at a fluorite–water interface and performed a detailed comparison between 3D images of F(r) measured by AFM, ρ(r) calculated by MD simulation, and F(r) calculated by the STA model. This comparison has been enabled by improved experimental protocols allowing accurate force maps to be obtained in less than 20 minutes in pure water.We propose that the conversion of a ρ(r) image to an F(r) image by the STA model is the current best practice for image interpretation. The converted F(r) image quantitatively illustrates the main features in the experimentally obtained F(r) image in the z range above the first hydration layer on a sample (S1). However, we should consider that F(r) calculated by the STA model represents F(r) applied to the hydration peak just under a tip apex. In addition, the STA model cannot be used for calculating a force profile in the z range below S1 (i.e. z < 0.25 nm).
Good agreement between the STA model and experimental data implies very strongly that the water density used as an input for the STA model is in good agreement with that probed experimentally by the AFM. The agreement between the STA model and experiment also implies that the experimental measurement is essentially noninvasive at larger distances from the surface. The STA model only requires the calculation of the equilibrium solvent density above the interface, which will soon be tractable using ab initio methods for simple systems.
Fig. 2 shows a practical scheme for the reconstruction of the solvent density by a joint experiment and theory. It works by the direct comparison of experimentally measured short range forces between the tip and hydration structures and the simulated force calculated from a simulated solvent density map using the STA model. Good agreement between the forces from the experiment and theory increases the reliability of both. The water density can be taken as a working model for the solvation structure at the interface where agreement between the theory and experiment is good.
The proposed method should improve the accuracy and reliability of this measurement technique and lead to its future applications in various solid–liquid interfacial studies. The greatly improved speed of measurements makes the technique applicable to a large number of systems that would have been too unstable to measure previously.
Acknowledgements
This work was supported by ACT-C, Japan Science and Technology Agency. MW and AS thank the Leverhulme trust for previous funding (grant F/07 134/CK). Via our membership of the UK's HEC Materials Chemistry Consortium, which is funded by EPSRC (EP/L000202), this work used the ARCHER UK National Supercomputing Service (http://www.archer.ac.uk).References
- P. Raiteri and J. D. Gale, J. Am. Chem. Soc., 2010, 132, 17623–17634 CrossRef CAS PubMed.
- G. Dong, P. Teo, Z. K. Wickens and R. H. Grubbs, Science, 2011, 333, 1609–1612 CrossRef CAS PubMed.
- J. Ostmeyer, S. Chakrapani, A. C. Pan, E. Perozo and B. Roux, Nature, 2013, 501, 121–124 CrossRef CAS PubMed.
- D. Krepkiy, M. Mihailescu, J. A. Freites, E. V. Schow, D. L. Worcester, K. Gawrisch, D. J. Tobias, S. H. White and K. J. Swartz, Nature, 2009, 462, 473–479 CrossRef CAS PubMed.
- M. S. Cheung, A. E. García and J. N. Onuchic, Proc. Natl. Acad. Sci. U. S. A., 2002, 99, 685–690 CrossRef CAS PubMed.
- S. Bae, R. Taylor, D. Hernández-Cruz, S. Yoon, D. Kilcoyne and P. J. M. Monteiro, J. Am. Chem. Soc., 2015, 98, 2914–2920 CAS.
- A. Vorobiev, A. Dennison, D. Chernyshov, V. Skrypnychuk, D. Barbero and A. V. Talyzin, Nanoscale, 2014, 6, 12151–12156 RSC.
- S. H. Donaldson, S. Das, M. A. Gebbie, M. Rapp, L. C. Jones, Y. Roiter, P. H. Koenig, Y. Gizaw and J. N. Israelachvili, ACS Nano, 2013, 7, 10094–10104 CrossRef CAS PubMed.
- T. Fukuma, M. J. Higgins and S. P. Jarvis, Biophys. J., 2007, 92, 3603–3609 CrossRef CAS PubMed.
- T. Fukuma, Y. Ueda, S. Yoshioka and H. Asakawa, Phys. Rev. Lett., 2010, 104, 016101 CrossRef PubMed.
- K. Kobayashi, N. Oyabu, K. Kimura, S. Ido, K. Suzuki, T. Imai, K. Tagami, M. Tsukada and H. Yamada, J. Chem. Phys., 2013, 138, 184704 CrossRef PubMed.
- E. T. Herruzo, H. Asakawa, T. Fukuma and R. Garcia, Nanoscale, 2013, 5, 2678 RSC.
- H. Imada, K. Kimura and H. Onishi, Langmuir, 2013, 29, 10744–10751 CrossRef CAS PubMed.
- A. S. Foster, C. Barth, A. L. Shluger and M. Reichling, Phys. Rev. Lett., 2001, 86, 2373–2376 CrossRef CAS PubMed.
- M. Harada and M. Tsukada, Phys. Rev. B: Condens. Matter, 2010, 82, 035414 CrossRef.
- M. Watkins and A. L. Shluger, Phys. Rev. Lett., 2010, 105, 196101 CrossRef PubMed.
- B. Reischl, M. Watkins and A. S. Foster, J. Chem. Theory Comput., 2013, 9, 600–608 CrossRef CAS PubMed.
- P. Spijker, T. Hiasa, T. Musso, R. Nishioka, H. Onishi and A. S. Foster, J. Phys. Chem. C, 2014, 118, 2058–2066 CAS.
- M. Watkins, M. L. Berkowitz and A. L. Shluger, Phys. Chem. Chem. Phys., 2011, 13, 12584–12594 RSC.
- T. Fukuma, B. Reischl, N. Kobayashi, P. Spijker, F. F. Canova, K. Miyazawa and A. S. Foster, Phys. Rev. B: Condens. Matter, 2015, 92, 155412 CrossRef.
- M. Watkins and B. Reischl, J. Chem. Phys., 2013, 138, 154703 CrossRef PubMed.
- K.-I. Amano, K. Suzuki, T. Fukuma, O. Takahashi and H. Onishi, J. Chem. Phys., 2013, 139, 224710 CrossRef PubMed.
- G. Jordan and W. Rammensee, Surf. Sci., 1997, 371, 371–380 CrossRef CAS.
- N. Kobayashi, S. Itakura, H. Asakawa and T. Fukuma, J. Phys. Chem. C, 2013, 117, 24388–24396 CAS.
- T. Fukuma, K. Onishi, N. Kobayashi, A. Matsuki and H. Asakawa, Nanotechnology, 2012, 23, 135706 CrossRef CAS PubMed.
- J. E. Sader and S. P. Jarvis, Appl. Phys. Lett., 2004, 84, 1801–1803 CrossRef CAS.
- T. Fukuma, M. Kimura, K. Kobayashi, K. Matsushige and H. Yamada, Rev. Sci. Instrum., 2005, 76, 053704 CrossRef.
- T. Fukuma and S. P. Jarvis, Rev. Sci. Instrum., 2006, 77, 043701 CrossRef.
- T. Fukuma, Rev. Sci. Instrum., 2009, 80, 023707 CrossRef PubMed.
- K. Miyazawa, H. Izumi, T. Watanabe-Nakayama, H. Asakawa and T. Fukuma, Nanotechnology, 2015, 26, 105707 CrossRef CAS PubMed.
- S. M. R. Akrami, H. Nakayachi, T. Watanabe-Nakayama, H. Asakawa and T. Fukuma, Nanotechnology, 2014, 25, 455701 CrossRef CAS PubMed.
- R. W. Zwanzig, J. Chem. Phys., 1954, 22, 1420–1426 CrossRef CAS.
- A. S. Foster, A. L. Shluger and R. M. Nieminen, Appl. Surf. Sci., 2002, 188, 306 CrossRef CAS.
- A. S. Foster, C. Barth, A. L. Shluger, R. M. Nieminen and M. Reichling, Phys. Rev. B, 2002, 66, 235417 CrossRef.
- B. Hess, C. Kutzner, D. van der Spoel and E. Lindahl, J. Chem. Theory Comput., 2008, 4, 435–447 CrossRef CAS PubMed.
- N. H. de Leeuw and T. G. Cooper, J. Mater. Chem., 2003, 13, 93–101 RSC.
- C. Vega, J. L. F. Abascal, E. Sanz, L. G. MacDowell and C. McBride, J. Phys.: Condens. Matter, 2005, 17, S3283–S3288 CrossRef CAS.
- U. Essmann, L. Perera, M. L. Berkowitz, T. Darden, H. Lee and L. G. Pedersen, J. Chem. Phys., 1995, 103, 8577–8593 CrossRef CAS.
- N. Senguttuvan, M. Aoshima, K. Sumiya and H. Ishibashi, J. Cryst. Growth, 2005, 280, 462–466 CrossRef CAS.
- I. Nicoara, M. Stef and A. Pruna, J. Cryst. Growth, 2008, 310, 1470–1475 CrossRef CAS.
- S. Wakahara, Y. Furuya, T. Yanagida, Y. Yokota, J. Pejchal, M. Sugiyama, N. Kawaguchi, D. Totsuka and A. Yoshikawa, Opt. Mater., 2012, 34, 729–732 CrossRef CAS.
- Y. Zhang, X. Xiang and W. J. Weber, Nucl. Instrum. Methods, 2008, 266, 2750–2753 CrossRef CAS.
- T. Aoba and O. Fejerskov, Crit. Rev. Oral Biol. Med., 2002, 13, 155–170 CAS.
- O. Prymak, V. Sokolova, T. Peitsch and M. Epple, Cryst. Growth Des., 2006, 6, 498–506 CAS.
- S. M. Hamza and S. K. Hamdona, J. Phys. Chem., 1991, 95, 3149–3152 CrossRef CAS.
- Z. Amjad, Langmuir, 1993, 9, 597–600 CrossRef CAS.
- C. H. de Vreugd, J. H. ter Horst, P. F. M. Durville, G. J. Witkamp and G. M. van Rosmalen, Colloids Surf., A, 1999, 154, 259–271 CrossRef CAS.
- C. Y. Tai, J. Cryst. Growth, 1999, 206, 109–118 CrossRef CAS.
- C. Y. Tai, P. C. Chen and T. M. Tsao, J. Cryst. Growth, 2006, 290, 576–584 CrossRef CAS.
- J. J. Eksteen, M. Pelser, M. S. Onyango, L. Lorenzen, C. Aldrich and G. A. Georgalli, Hydrometallurgy, 2008, 91, 104–112 CrossRef CAS.
- S. P. Jarvis, T. Uchihashi, T. Ishida, H. Tokumoto and Y. Nakayama, J. Phys. Chem. B, 2000, 104, 6091–6094 CrossRef CAS.
- T. Uchihashi, M. Higgins, Y. Nakayama, J. E. Sader and S. P. Jarvis, Nanotechnology, 2005, 16, S49–S53 CrossRef CAS.
- T. Fukuma, K. Kobayashi, K. Matsushige and H. Yamada, Appl. Phys. Lett., 2005, 87, 034101 CrossRef.
- J. Kilpatrick, S.-H. Loh and S. P. Jarvis, J. Am. Chem. Soc., 2013, 135, 2628–2634 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: Detailed explanations on data processing procedures used for preparing 3D water density and force distribution images. See DOI: 10.1039/C5NR08092D |
| This journal is © The Royal Society of Chemistry 2016 |