Pressing a spring: what does it take to maximize the energy storage in nanoporous supercapacitors?
Svyatoslav
Kondrat
ab and
Alexei A.
Kornyshev
b
aForschungszentrum Jülich, IBG-1: Biotechnology, 52425 Jülich, Germany. E-mail: s.kondrat@fz-juelich.de
bDepartment of Chemistry, Faculty of Natural Sciences, Imperial College London, SW7 2AZ, UK. E-mail: a.kornyshev@imperial.ac.uk
First published on 16th September 2015
Abstract
We discuss the nonlinear effects and efficiency of charge storage in supercapacitors with nanoporous electrodes and ionic liquids, and demonstrate that to maximize the stored energy, it may be beneficial to create ‘obstacles’ or ‘difficulties’ in charging. This can be achieved by making thermodynamically unfavourable conditions for ions inside nanopores, or more favourable outside. We show by means of Monte Carlo simulations that such ‘ionophobic’ pores store energy more efficiently and can provide equivalent or even better energy capacity. Since the recent analysis predicts much faster charging of ionophobic nanopores, we conclude that such pores offer a better option for simultaneous energy/power optimization.
Conceptual insightsSupercapacitors emerge as a promising green alternative to batteries. They store energy via fast charge accumulation in nano-thick ionic layers at the electrode/electrolyte interface. The stored energies are relatively low for microporous electrodes with wide pores, and electrodes with ultranarrow 1–2 nm sized pores are used to increase the energy density. However, such narrow pores are detrimental to the rate of charging/discharging and hence power density, the high value of which is one of the most important advantages of supercapacitors over batteries. We explore here a hypothesis on how this problem can be overcome by creating ‘ionophobic’ pores with a low or vanishing amount of an ionic liquid inside them at no applied voltage. Counter-intuitively, our analysis shows that such ionophobic nanopores can store not less but often more energy than the conventional ionophilic pores. Nanopores empty in a non-polarized state have also been shown to charge with a much faster rate. This suggests a challenging task and an exciting opportunity for materials scientists to engineer nanoporous electrodes for supercapacitors that can fulfil two dreams simultaneously – high energy and power densities, to date considered as mutually exclusive. |
Supercapacitors are energy storage devices that offer exceptionally high power densities and long cycle life but only moderate energy densities.1,2 They have numerous applications in industry, however their use is typically limited to devices which require rapid delivery or fast harvesting of electric energy, but which are not critical to accumulating a large amount of energy. Examples include storing automotive breaking energy, or supplying energy to flash lights in cameras or to car starters in hybrid vehicles.
Extensive research efforts have been dedicated to optimizing energy storage and understanding the charging mechanism in supercapacitors.3–12 Supercapacitors are composed of porous electrodes and an electrolyte medium, and store energy in a potential-driven accumulation of counterions in an electrical double layer formed at the electrode/electrolyte interface. The amount of stored energy correlates with the surface area, and its increase (per electrode volume) together with the pore size optimization has been identified as the main strategy in maximizing energy storage and capacitance.13 The maximal capacitances per electrode surface area have been observed for pores comparable in size to the diameter of a single desolvated ion.14–16 This anomalous increase of capacitance can be explained by the emergence of a superionic state in narrow conducting nanopores,17,18 where the inter-ionic interactions are exponentially screened, allowing counterions to pack more easily inside nanopores. The screening becomes stronger for narrower pores, making repulsion between counterions weaker and unbinding like charges easier. As a result, the capacitance increases with decreasing pore size.
Although well-understood now, the anomalous increase of capacitance is more surprising than it may have seemed, especially in relation to the energy storage. Indeed, by decreasing the pore size below two ion diameters, the whole layer of ions, which are potential energy carriers, is expelled from the pore; nevertheless, the stored energy shows a similar ‘anomalous’ increase in some range of pore sizes,19 which suggests more efficient energy storage by narrow nanopores. This important issue has recently been pointed out by Merlet et al.20 who have shown that indeed, the charge is stored “more efficiently” (with respect to integral capacitance) in nano confinement as compared to, e.g., at flat electrodes. This conclusion has been reached by looking at the electron counter charge on the electrode induced by an ion, in the vicinity of the ion, and observing that it is larger for higher degrees of confinement (for instance, it is larger in pockets rather than at edges).
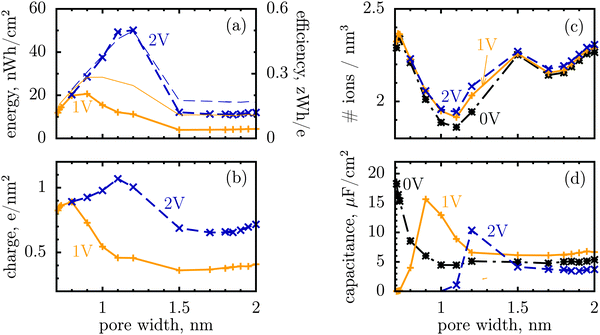
We shall look at storage efficiency from a slightly different angle, however, and define it as the average energy stored by a unit charge at a given applied voltage, i.e. ε = E/Q, where E is the total stored energy and Q the accumulated charge. In contrast to the local efficiency defined by Merlet et al., ‘our’ efficiency reflects the integral property of charge storage. Fig. 1a shows this quantity plotted as a function of pore width, and compares it with the stored energy per surface area. In line with the observation by Merlet et al., the efficiency increases as the pore becomes narrower, and hence the degree of confinement increases, but there is a maximum at some pore width, below which the efficiency starts to fall off. This maximum is very close to, but does not coincide exactly with, the maximum of the stored energy. The difference is in particular due to the variation of the accumulated charge with the pore size, as evidenced by Fig. 1b.
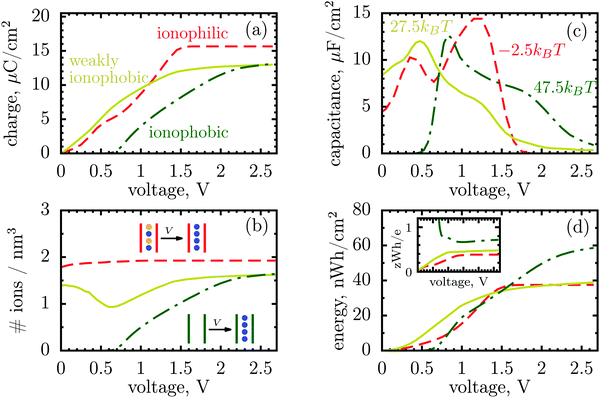
 | ||
| Fig. 1 Energy and charge storage in ionophilic pores from Monte Carlo simulations. (a) Energy per surface area stored in a nanopore versus pore width (thick lines with symbols). Storage efficiency, defined as the stored energy per accumulated charge, is shown by thin lines. (b) Accumulated net charge. (c) Total ion density (ρ) inside the nanopores. A dramatic increase of ρ below 1 nm is due to an increase in image forces promoting the ions of both signs to enter the pore. Below 1 nm the density practically does not change with voltage for voltages above 1 V, and thus charging is exclusively due to swapping of coions from the pore for the counterions from the bulk of a supercapacitor. At low voltages (or pores wider than 1 nm) charging is due to both swapping and counterion electrosorption, although the contribution from the latter is relatively weak. (d) Differential capacitance at different voltages. At low voltages (around zero volts), the capacitance increases with decreasing pore width, in line with ref. 14–16. At higher voltages, the capacitance vanishes for narrow pores because the pores are saturated with counterions. The ion diameter is 0.7 nm, and the line and color code is the same for all plots. | ||
It is a distinct feature of charging at the nanoscale that the pores become saturated with counterions when a voltage higher than a certain threshold, say V1, is applied (cf. red curve in Fig. 2a). The differential capacitance, dQ/dV, vanishes above V1, as a further increase in voltage has no effect on the accumulated charge inside the nanopores, and thus the region V > V1 does not contribute to the stored energy. Now, narrow pores can generally accommodate fewer ions than wider pores of the same length; they have therefore lower saturation voltage V1. For instance, at an applied potential of 2 V, the capacitance is non zero for pores wider than L = 1 nm but vanishes when L < 1 nm (Fig. 1d). This explains why energy and storage efficiency are lowered with the narrowing of the pores to the size of the ion diameter – this is because the charge and energy saturate.
Thus, such ultra narrow pores (below 1 nm) seem to limit the application of nanoporous supercapacitors to low voltages, at which the capacitance is nonzero. This has indeed been observed by Mysyk et al.,21 who also demonstrated, experimentally, that one way out of it is, not surprisingly, to use wider pores. Wide pores (but within two ion diameters) are also optimal for maximizing the stored energy at high voltages.19
However, there is another possibility to increase the stored energy. As discussed, the reason that the energy storage worsens with narrowing a pore is that the pore becomes saturated with counterions at relatively low voltages; making pores wider shifts the saturation to higher voltages and thus raises the stored energy. But, the saturation voltage can also be augmented by other means, for instance by reducing the affinity of pores towards ions, i.e. by making pores more ionophobic. Fig. 2 compares the ‘conventional’ (ionophilic) pore with ionophobic pores. The ionophobic pores were created in Monte Carlo simulations by making positive and large the energy of transfer of ions from the bulk of a supercapacitor into a pore,17,22 such that the pore is (almost) free of ions at no applied voltage (see Methods). Experimentally, the ionophobicity can be manipulated by functionalizing nanoporous carbons23 (see below). Adding carbon-philic surfactants24,25 or other elements to ionic liquids or using pore-affinity solvents can likewise be considered as methods for creating ionophobic pores.
Fig. 2a and c show that for ionophobic pores the saturation is indeed shifted towards higher voltages, as manifested, in particular, by a nonzero capacitance for V ≳ V1 ≈ 1.7 V, where it vanishes for the ionophilic pore. However, the capacitance of the strongly ionophobic pore vanishes, instead, at low voltages. Nevertheless, at moderate voltages the stored energies seem comparable for all pores, while the ionophobic pores clearly beat the ionophilic ones at higher voltages (Fig. 2d). A similar result has been obtained by the exact solution of the Blume–Emery–Griffiths model for charge storage in a single file pore.26
To understand this result, let us resort to a comparison of the electric energy stored in a supercapacitor with storing elastic energy by mechanical springs. Assume for simplicity a linear regime, which means a voltage-independent capacitance. Then, the energy stored in a nanopore per surface area is 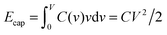 , where C is the capacitance per surface area and V the applied voltage. For a spring, there is the well known Hooke's law dF = kdx, where k is spring's stiffness, F the force and x the displacement. For the applied force F, the elastic energy stored in a compressed spring is Eelastic = F2/2k. By analogy with Ecap, the capacitance plays a role of inverse of the spring stiffness, while the force is the applied voltage. It must be emphasized however that both equations are valid only in the linear regime.
, where C is the capacitance per surface area and V the applied voltage. For a spring, there is the well known Hooke's law dF = kdx, where k is spring's stiffness, F the force and x the displacement. For the applied force F, the elastic energy stored in a compressed spring is Eelastic = F2/2k. By analogy with Ecap, the capacitance plays a role of inverse of the spring stiffness, while the force is the applied voltage. It must be emphasized however that both equations are valid only in the linear regime.
Imagine now a spring that can react only to forces larger than F0 but smaller than F1. In other words, the spring stiffness depends on the force and this dependence has the form of a rectangular function, i.e. it is infinitely large (no compression) for small and large forces, and it is finite and constant for F0 < F < F1. Then the Hooke's elastic energy for such a spring must be modified to 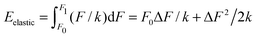 , where ΔF = F1 − F0. As evidenced by this ‘tricky’ example, the stored energy increases by F0ΔF/k when the region of ‘effective compression’ (finite k), during which the energy is actually stored, is shifted to larger applied forces while keeping the same ΔF.
, where ΔF = F1 − F0. As evidenced by this ‘tricky’ example, the stored energy increases by F0ΔF/k when the region of ‘effective compression’ (finite k), during which the energy is actually stored, is shifted to larger applied forces while keeping the same ΔF.
Following this analogy, the ionophobicity in nanopores plays a role of a ‘shifter’ that moves the region where the charging actually takes place to higher voltages, and it is because of this shift that the ionophobic pores can offer higher stored energies (but see below).
On a slightly different note, one can distinguish three elementary charging mechanisms. As a response to the applied potential, the charge accumulated in a pore can increase due to: (1) insertion of new counterions, which we call electrosorption or adsorption; (2) exchanging coions for counterions, or simply swapping; and (3) expelling coions with no counterion insertion, which we term desorption. Charging can comprise swapping and adsorption or swapping and desorption, but the equally sized adsorption and desorption simply amount to swapping.
Fig. 3 shows regions where swapping, electrosorption and desorption lead to the highest capacitance (this diagram has been calculated by using the mean-field model of ref. 17, see Methods). The region of electrosorption is surprisingly small and essentially bound to the line where only counterions are present in the pore; this line corresponds to strongly ionophobic pores, empty at no applied voltage (i.e. at zero charge). Interestingly, swapping is the second best for capacitance in the desorption region, and typically gives capacitances higher than electrosorption (see capacitance map in Fig. 3b). We can understand this result as follows. In electrosorption, counterions must overcome an entropic barrier to enter a narrow pore; and an electrostatic barrier because the counterions in a pore must pack closer to each other to accommodate the newly inserted fellows, thus increasing the overall electrostatic repulsion. Both effects are weaker (or absent) for swapping and desorption. Therefore, the thermodynamic cost of charging is high for electrosorption; this makes the system less susceptible to counterion insertion and leads27 to relatively low capacitances in this case. In some sense, this is also analogous to mechanical springs: inverse of the spring stiffness corresponds to the capacitance, and it is smaller for more rigid springs, which in turn correspond to pores with a higher thermodynamic cost of charging.
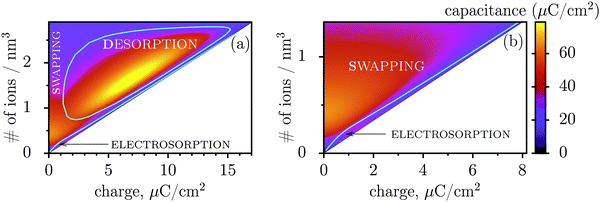 | ||
| Fig. 3 Capacitance map and the diagram of elementary charging mechanisms from a mean-field model in the plane of the total ion density and accumulated charge in a pore. (a) The diagram shows the regions denoting which of the three elementary charging mechanisms (adsorption of counterions, desorption of coions, or swapping coions for counterions) gives the highest capacitance under equal conditions. The boundaries between these regions were calculated by artificially allowing only one charging mechanism, and then comparing the capacitances obtained in this way for swapping, desorption and adsorption (see Methods for details). On the same graph we also show the values of capacitance due to the corresponding charging mechanisms in the form of a ‘heat’ map. Note that the actual capacitance can be lower as charging can comprise swapping and adsorption or swapping and desorption (see Methods). (b) A closer look at the capacitance map for smaller charges, but with only electrosorption and swapping allowed. Electrosorption gives the highest capacitance only in a small region close to the line which corresponds to the situation when only counterions are present in a pore (thin black line). This line therefore represents charging of strongly ionophobic pores, empty at zero charge. The density at zero charge is determined by the resolvation energy, which characterizes ionophobicity/philicity. Our mean-field model tends to overestimate capacitances, but gives qualitatively correct predictions, as demonstrated in ref. 18. The ion diameter is 0.7 nm and the pore width 0.75 nm. | ||
Thus, the capacitance at voltages below saturation shall typically be lower for ionophobic pores (see Fig. 2c). Indeed, the ionophobicity changes the charging mechanism from swapping-dominated for ionophilic pores to a pure electrosorption for ionophobic pores – this increases the free energy cost of charging, and hence the capacitance decreases.
Such a change in the charging mechanism has indeed been seen in recent experiments in the case of carbon nanofibers as porous electrodes and EMIMm-TFSI as ionic liquid.23 Nanofibers are fabricated by electro spinning of nafion and polyacrylonitril. They have uniformly distributed nanopores, and in operando infrared spectroelectrochemistry shows that their charging is mainly due to ion adsorption.28 Similarly, non-activated carbide-derived carbons charge mainly by adsorption too.29 When now the nanofibres are prepared in the presence of potassium hydroxide (KOH-activation), which changes the surface functionality and increases the ionophilicity, the charging mechanism changes to swapping-dominated.23 A similar swapping-dominated charging has also been observed for YP-50F activated (ionophilic) carbons and various ionic liquids,30,31 though only for positive potentials; the difference with negative potentials is likely due to asymmetry in ion sizes.
Incidentally, the change in the charging mechanism explains the double peak32 capacitance of ionophilic pores (Fig. 2c). Here, the first peak corresponds to a combination of swapping and electrosorption, while the second peak arises when the pore is nearly fully occupied by co- and counterions, and charging becomes solely determined18 by swapping. Recalling now that swapping is thermodynamically more favourable, we conclude that the second peak must be higher, as indeed observed. Similarly, it is thermodynamically cheaper to make ions enter an empty pore, than a half-filled pore, and hence there is a peak in the capacitance of ionophobic pores at low voltages, when charging commences (Fig. 2c). As the voltage increases further, the pore becomes more populated with counterions, insertion of new counterions becomes increasingly more difficult, and so the capacitance decreases.
Thus, the ionophobicity plays a dual role. On the one hand, it shifts the actual charging to higher voltages (say V0), through which the stored energy gains, roughly, CV0(V1 − V0), assuming a quasi-linear capacitance and that the charging takes place between V0 and V1 (note that in reality the capacitance is nonlinear). On the other hand, it changes the charging mechanism from swapping-dominated to electrosorption, and this lowers the capacitance and hence the energy stored in ionophobic pores. It is due to the interplay between these two competing effects that the stored energy depends on ionophobicity in a highly nontrivial way (Fig. 4). At low phobicities, the stored energy increases due to a decrease of the ion density in the pores. This makes ion electrosorption thermodynamically more profitable, and thus the capacitance of the first peak increases and so the stored energy. The energy decreases when the charging becomes adsorption dominated and the second peak in the capacitance vanishes (see solid lines in Fig. 2a–c). As the ionophobicity increases further, the charging commences only at high voltages, at which the pores are still free of ions. Thus, the thermodynamic cost of charging decreases, and the capacitance and hence the energy increase again (see dot-dash lines in Fig. 2c and d). Finally, at very high ionophobicities the pore remains (nearly) empty even at high applied voltages, and thus the stored energy starts to decrease.
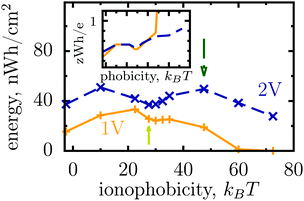 | ||
| Fig. 4 Effect of affinity of pores towards ions on the energy storage from Monte Carlo simulations. The stored energy per surface area is shown as a function of ionophobicity for two voltages. The energy increases with increasing ionophobicity but, surprisingly, shows two maxima and a minimum before vanishing at high ionophobicities. The inset shows how the storage efficiency changes with ionophobicity, and the arrows indicate the ionophobicities used in Fig. 2. The ion diameter is 0.7 nm and the pore width 1 nm. | ||
Interestingly, despite a surprisingly rich behaviour of the stored energy, the storage efficiency turns out to be a nearly monotonic function of ionophobicity (see the insets in Fig. 2d and 4). The reason is that the accumulated charge (Q) falls off as the pore becomes more ionophobic, and hence the efficiency, which is an energy per unit charge, increases; this is of course until Q vanishes at high phobicities. From a practical point of view, the stored energy is a more important quantity. Nevertheless, understanding the efficiency of charge and energy storage in nanopores may help optimize supercapacitors as well, for instance by reducing the amount of an ionic liquid used in them.
The dispersity of pore sizes does not affect qualitatively the ionophobicity dependence of energy storage (Fig. 5). However, polydisperse pores store generally less energy, as becomes apparent from comparing Fig. 2d and 4 with Fig. 5, where a two-fold decrease in the stored energy is seen. This is because at a given applied voltage some pores are saturated while some others are under-charged, as compared to a single optimal pore which maximizes the stored energy. We thus wish to emphasize de novo19 the importance of good quality porous electrodes for optimizing energy storage, where by ‘good quality’ we mean here as monodisperse as possible.
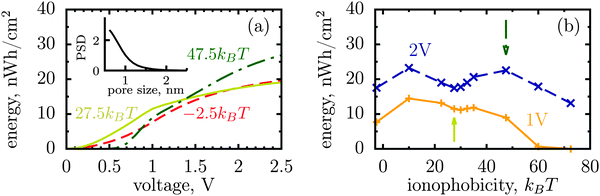 | ||
| Fig. 5 Stored energy per surface area averaged over the normalized pore size distribution (PSD) shown in the inset. The PSD was obtained from nitrogen adsorption of carbide derived carbons chlorinated at 800 °C (data taken from ref. 19). The stored energy versus voltage (a) and versus ionophobicity (b) show the same trends as for monodisperse porous electrodes (Fig. 2d and 4), but the amount of the stored energy falls in all cases due to pore size polydispersity. The arrows in (b) indicate the ionphobicities used in (a). | ||
Finally, our considerations treat pore walls as perfectly metallic surfaces, and we have silently ignored their contribution to the total capacitance of an electrode (Ctotal). Recent studies suggest33–37 that this contribution can be substantial for certain carbon materials in some range of voltages, and may even dominate Ctotal−1 ∼ CQ−1 + CIL−1, where CIL is the capacitance of an ionic liquid (calculated in this work) and CQ the so called quantum capacitance of pore walls. It is reasonable to expect, however, that CQ does not depend on the ionophobicity in an appreciable way, at least for non-functionalized carbons, and hence its qualitative effect on our results is presumably small. Nevertheless, it would be very interesting, and not less important from a practical point of view, to clarify the role of quantum capacitance, to date ignored in most studies of nanoporous supercapacitors.
To conclude, the ionophobicity of nanoporous electrodes is an important parameter, yet very little explored, in a long story of supercapacitor optimization. Ionophobic pores create obstacles in charging, prohibiting ions from entering the pores, but, surprisingly, they store energy much more efficiently and provide comparable or even higher energy capacity. Combined with a much faster charging dynamic, predicted by recent mean-field and molecular dynamics studies,38,39 the ionophobicity opens up new opportunities for optimization of nanoporous supercapacitors and, in our opinion, deserves the attention of materials scientists, experimentalists and theoreticians.
Methods
Monte Carlo simulations
Most results in this work have been obtained using grand canonical Monte Carlo simulations of a model nanopore.18 In this model, a single infinitely extended slit-shaped metallic nanopore is considered, and the external potential (voltage) is applied to the pore walls to model charging. Despite its simplicity, this or similar models have been proven to be useful in numerous studies on charging supercapacitors.17,18,32,38,40–42The ionic liquid was modeled as charged hard spheres in the superionic state.17,18 Thus, instead of the Coulomb potential, we used the exponentially screened potential for ions confined between two metal walls43
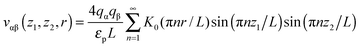 | (1) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−πr/L) decays exponentially with r. Potential (1) follows from the exact solution of the electrostatic problem of a point charge confined between metallic walls. Interestingly, recent quantum-mechanical density-functional studies for nanotubes have shown that the screened electrostatic potential in cylindrical geometry (similar to eqn (1) in a slit) is a fairly good approximation also for realistic carbons.44,45
exp(−πr/L) decays exponentially with r. Potential (1) follows from the exact solution of the electrostatic problem of a point charge confined between metallic walls. Interestingly, recent quantum-mechanical density-functional studies for nanotubes have shown that the screened electrostatic potential in cylindrical geometry (similar to eqn (1) in a slit) is a fairly good approximation also for realistic carbons.44,45
For the interaction between ions and the induced charges on the pore walls, the following exact potential was used17
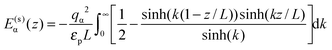 | (2) |
The ionophobicity was modelled by varying the so-called re-solvation energy, δEα, the energy of transfer of an ion from the bulk of a capacitor into the pore.17,22 This makes the electrochemical potential of ions in simulations μ± = qαV + δEα where V is applied potential. In this work we have assumed δE+ = δE− = δE for simplicity.
The resolvation energy, δE, or equivalently ionophobicity or ionophilicity determines the pore occupancy at no applied voltage. When δE + E(s)(d/2) < 0, the pore is expected to be occupied by ions at zero voltage, and we call such pores ionophilic. Here E(s)(d/2) is the self energy of an ion (see eqn (2)) at the closest distance to the pore wall, where E(s)(z) is minimal. Conversely, a large positive δE > δEtr = −E(s)(d/2) corresponds to ionophobic pores with no or small amount of an ionic liquid inside them. For a 1 nm wide pore and an ion diameter of 0.7 nm, we estimate δEtr ≈ 16.5kBT. Note, however, that even for δE = 27.5kBT the pore is not empty at zero voltage (see Fig. 2b). This is because the pore occupancy is also determined by the entropy and ion–ion interactions, which are not taken into account in δEtr.
For carbon nanotubes and neat ionic liquids, a combined quantum mechanical and molecular dynamics study22 suggests that δE can vary from −50 to about 90kBT or more, depending on the ionic liquid and pore properties (particularly pore diameter). In the case of electrolyte solutions δE shall also include a dissolvation energy of fully or partially dissolved ions. In our simulations we assumed for simplicity that δE is pore width independent. This assumption shall not alter the main conclusions of this work, since we have focused on the voltage and ionophobicity dependence at constant pore width. Energies averaged over a pore-size distribution (Fig. 5) may be affected by pore-size dependence of ionophobicity, however. Although we do not expect any drastic changes, it would nevertheless be interesting to look at this effect in future studies.
In all our simulations, we considered temperature T = 400 K and dielectric constant inside nanopores εp = 2. (For ionophilic pores, this value effectively accounts for electric polarizability of ions in a pore. For ionophobic pores, however, εp can vary between 1 and 2, depending on the ion density. We have neglected this dependence, and note that it can only influence the thermodynamic properties at low voltages where the ion density inside pores is low.) The simulations were performed for monovalent ions of diameter d = d± = 0.7 nm. The walls of a slit pore were 25 nm wide in the lateral directions. A pore was surrounded by two hard ‘gaskets’ a few angstroms thick, and the periodic boundary conditions were applied in all directions. The standard deviations are smaller than the symbols used and are not shown (see ref. 18 for an example).
Our Monte Carlo simulations consisted of the Widom insertion/deletion, translational and molecular-type swap moves. Note that it is possible to insert a single ion into a pore, as the electro-neutrality is automatically preserved via the exact solution of the electrostatic problem, eqn (1), which properly accounts for charge screening by metal walls. We performed 106 moves to equilibrate the system, and 106 to 107 moves to calculate the equilibrium densities. Other technical details can be found in ref. 18. The differential capacitance was calculated from the accumulated charge by its numerical differentiation with respect to voltage using the smooth noise-robust differentiator of Holoborodko with seven points.32,46
Electrosorption, swapping or desorption?
We pose here the following question: which of the three elementary charging mechanisms leads to the highest capacitance? To answer this question, we use the mean-field model of ref. 17, and consider a narrow pore approximately one ionic liquid (IL) layer wide; we also assume that ions position themselves on the central symmetry plane of the pore. Then, the free energy of the IL confined in such a nanopore is (in units of kBT = 1/β)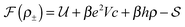 | (3) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln(2)/εpL is the self energy of an ion in the middle of the pore, i.e. at z = L/2 (see eqn (2)). The entropy is given by
ln(2)/εpL is the self energy of an ion in the middle of the pore, i.e. at z = L/2 (see eqn (2)). The entropy is given by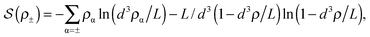 | (4) |
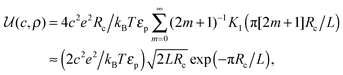 | (5) |
We look now at the free energy change due to charging a pore from V to V1 = V + ΔV by means of each elementary mechanism. For swapping of anions for cations we have 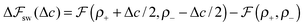 , and similarly for adsorption and desorption. Note the 1/2 in the argument of
, and similarly for adsorption and desorption. Note the 1/2 in the argument of 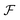 , which is because a single act of swapping brings two charges, unlike adsorption and desorption which bring one. The relation between Δc and ΔV can be obtained from a minimum of
, which is because a single act of swapping brings two charges, unlike adsorption and desorption which bring one. The relation between Δc and ΔV can be obtained from a minimum of 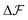 .
.
It must be emphasized that the ion densities ρ+ + Δc/2 and ρ− − Δc/2 may or may not correspond to a stable thermodynamic state at voltage V1 = V + ΔV. In the latter case it can only be realized if there is a daemon at the pore entrance allowing the exchange of coions for counterions (direct swapping), but refusing any act of electrosorption or desorption, or inverse swapping.
The capacitance per surface area due to each charging mechanism is then 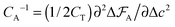 , where A = {sw,ad,de} and CT = e2/kBT [≈6.2 aF at room temperature] is thermal electric capacitance (defined as the capacitance of a capacitor in which the voltage between the plates is set to the thermal voltage, VT ≡ kBT/e, when it is charged to the elementary charge e). The diagram and capacitance map of Fig. 3 have been obtained by comparing different CA's at the same ion densities ρ±.
, where A = {sw,ad,de} and CT = e2/kBT [≈6.2 aF at room temperature] is thermal electric capacitance (defined as the capacitance of a capacitor in which the voltage between the plates is set to the thermal voltage, VT ≡ kBT/e, when it is charged to the elementary charge e). The diagram and capacitance map of Fig. 3 have been obtained by comparing different CA's at the same ion densities ρ±.
Acknowledgements
We are grateful to John Griffin, Céline Merlet, Mathieu Salanne, Paul Madden, Clarisse Péan, Alexander Forse and others for stimulating debates during the CECAM workshop in Paris (August, 2014). Fruitful discussions with Boris Dyatkin and Yury Gogotsi are appreciated. We are also thankful to John Griffin for sharing his work (ref. 31) prior to publication. S.K. acknowledges COST Action MP1004 for supporting his short-time scientific visit to Imperial College London.References
- J. R. Miller and P. Simon, Science, 2008, 321, 651 CrossRef CAS PubMed.
- P. Simon and Y. Gogotsi, Acc. Chem. Res., 2013, 46, 1094 CrossRef CAS PubMed.
- P. Simon and Y. Gogotsi, Nat. Mater., 2008, 7, 845 CrossRef CAS PubMed.
- P. Simon and Y. Gogotsi, Philos. Trans. R. Soc., A, 2010, 368, 3457 CrossRef CAS PubMed.
- C. Liu, Z. Yu, D. Neff, A. Zhamu and B. Z. Jang, Nano Lett., 2010, 12, 4863 CrossRef PubMed.
- Y. Shim and H. J. Kim, ACS Nano, 2010, 4, 2345 CrossRef CAS PubMed.
- G. Feng and P. T. Cummings, J. Phys. Chem. Lett., 2011, 2, 2859 CrossRef CAS.
- J. J. Yoo, K. Balakrishnan, J. S. Huang, V. Meunier, B. G. Sumpter, A. Srivastava, M. Conway, A. L. M. Reddy, J. Yu, R. Vajtai and P. M. Ajayan, Nano Lett., 2011, 11, 1423 CrossRef CAS PubMed.
- P. Wu, J. Huang, V. Meunier, B. G. Sumpter and R. Qiao, ACS Nano, 2011, 5, 9044 CrossRef CAS PubMed.
- C. Merlet, B. Rotenberg, P. A. Madden, P.-L. Taberna, P. Simon, Y. Gogotsi and M. Salanne, Nat. Mater., 2012, 11, 306 CrossRef CAS PubMed.
- P. Wu, J. Huang, V. Meunier, B. Sumpter and R. Qiao, J. Phys. Chem. Lett., 2012, 3, 1732 CrossRef CAS PubMed.
- J. Vatamanu, Z. Hu, D. Bedrov, C. Perez and Y. Gogotsi, J. Phys. Chem. Lett., 2013, 4, 2829 CrossRef CAS.
- J. Chmiola, C. Largeot, P.-L. Taberna, P. Simon and Y. Gogotsi, Angew. Chem., Int. Ed., 2008, 47, 3392 CrossRef CAS PubMed.
- E. Raymundo-Piñero, K. Kierczek, J. Machnikowski and F. Béguin, Carbon, 2006, 44, 2498 CrossRef PubMed.
- J. Chmiola, G. Yushin, Y. Gogotsi, C. Portet, P. Simon and P. L. Taberna, Science, 2006, 313, 1760 CrossRef CAS PubMed.
- C. Largeot, C. Portet, J. Chmiola, P.-L. Taberna, Y. Gogotsi and P. Simon, J. Am. Chem. Soc., 2008, 130, 2730 CrossRef CAS PubMed.
- S. Kondrat and A. Kornyshev, J. Phys.: Condens. Matter, 2011, 23, 022201 CrossRef CAS PubMed.
- S. Kondrat, N. Georgi, M. V. Fedorov and A. A. Kornyshev, Phys. Chem. Chem. Phys., 2011, 13, 11359 RSC.
- S. Kondrat, C. R. Pérez, V. Presser, Y. Gogotsi and A. A. Kornyshev, Energy Environ. Sci., 2012, 5, 6474 CAS.
- C. Merlet, C. Péan, B. Rotenberg, P. A. Madden, B. Daffos, P. L. Taberna, P. Simon and M. Salanne, Nat. Commun., 2013, 4, 2701 CAS.
- R. Mysyk, E. Raymundo-Piñero and F. Béguin, Electrochem. Commun., 2009, 11, 554 CrossRef CAS PubMed.
- J. F. Jover, R. Lugo, H. Toulhoat, P. Simon and T. de Bruin, J. Phys. Chem. C, 2014, 118, 864 CAS.
- F. W. Richey, C. Tran, V. Kalra and Y. A. Elabd, J. Phys. Chem. C, 2014, 118, 21846 CAS.
- K. Fic, G. Lot and E. Frackowiak, Electrochim. Acta, 2010, 55, 7484 CrossRef CAS PubMed.
- K. Fic, G. Lot and E. Frackowiak, Electrochim. Acta, 2011, 60, 206 CrossRef PubMed.
- A. Lee, S. Kondrat and A. Kornyshev, Phys. Rev. Lett., 2014, 113, 048701 CrossRef.
- D. T. Limmer, C. Merlet, M. Salanne, D. Chandler, P. A. Madden, R. van Roij and B. Rotenberg, Phys. Rev. Lett., 2013, 111, 106102 CrossRef.
- F. W. Richey, B. Dyatkin, Y. Gogotsi and Y. A. Elabd, J. Am. Chem. Soc., 2013, 135, 12818 CrossRef CAS PubMed.
- W.-Y. Tsai, P.-L. Taberna and P. Simon, J. Am. Chem. Soc., 2014, 136, 8722 CrossRef CAS PubMed.
- J. M. Griffin, A. C. Forse, H. Wang, N. M. Trease, P.-L. Taberna, P. Simon and C. P. Grey, Faraday Discuss., 2014, 176, 49–68 RSC.
- J. M. Griffin, A. C. Forse, W.-Y. Tsai, P.-L. Taberna, P. Simon and C. P. Grey, Nat. Mater., 2015, 14, 812 CrossRef CAS PubMed.
- S. Kondrat, A. Kornyshev, F. Stoeckli and T. Centeno, Electrochem. Commun., 2013, 34, 348 CrossRef CAS PubMed.
- J. Xia, F. Chen, J. Li and N. Tao, Nat. Nanotechnol., 2009, 4, 505 CrossRef CAS PubMed.
- M. D. Stoller, C. W. Magnuson, Y. Zhu, S. Murali, J. W. Suk, R. Piner and R. S. Ruoff, Energy Environ. Sci., 2011, 4, 4685 CAS.
- J. Chen, C. Li and G. Shi, J. Phys. Chem. Lett., 2013, 4, 1244 CrossRef CAS PubMed.
- A. A. Kornyshev, N. B. Luque and W. Schmickler, J. Solid State Electrochem., 2014, 18, 1345 CrossRef CAS.
- R. R. Salunkhe, Y.-H. Lee, K.-H. Chang, J.-M. Li, P. Simon, J. Tang, N. L. Torad, C.-C. Hu and Y. Yamauchi, Chem. – Eur. J., 2014, 20, 13838 CrossRef CAS PubMed.
- S. Kondrat and A. Kornyshev, J. Phys. Chem. C, 2013, 117, 12399 CAS.
- S. Kondrat, P. Wu, R. Qiao and A. Kornyshev, Nat. Mater., 2014, 13, 387 CrossRef CAS PubMed.
- K. Kiyohara and K. Asaka, J. Phys. Chem. C, 2007, 111, 15903 CAS.
- K. Kiyohara, T. Sugino and K. Asaka, J. Chem. Phys., 2010, 132, 144705 CrossRef PubMed.
- K. Kiyohara, T. Sugino and K. Asaka, J. Chem. Phys., 2011, 134, 154710 CrossRef PubMed.
- W. R. Smythe, Static and Dynamic Electricity, McGraw Hill, 1939 Search PubMed.
- A. Goduljan, F. Juarez, L. Mohammadzadeh, P. Quaino, E. Santos and W. Schmickler, Electrochem. Commun., 2014, 45, 48–51 CrossRef CAS PubMed.
- L. Mohammadzadeh, A. Goduljan, F. Juarez, P. Quaino, E. Santos and W. Schmickler, Electrochim. Acta, 2015, 162, 11–16 CrossRef CAS PubMed.
- P. Holoborodko, Smooth noise robust differentiators, http://www.holoborodko.com/pavel/numerical-methods/numerical-derivative/smooth-low-noise-differentiators/.
| This journal is © The Royal Society of Chemistry 2016 |