Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Programming the shape-shifting of flat soft matter: from self-rolling/self-twisting materials to self-folding origami†
S.
Janbaz
*,
R.
Hedayati
and
A. A.
Zadpoor
Department of Biomechanical Engineering, Faculty of Mechanical, Maritime, and Materials Engineering, Delft University of Technology (TU Delft), Mekelweg 2, 2628 CD, Delft, The Netherlands. E-mail: s.janbaz@tudelft.nl; shahram.janbaz@gmail.com
First published on 12th August 2016
Abstract
Nature uses various activation mechanisms to program complex transformations in the shape and functionality of living organisms. Inspired by such natural events, we aimed to develop initially flat (i.e. two-dimensional) programmable materials that, when triggered by a stimulus such as temperature, could self-transform their shape into a complex three-dimensional geometry. A two-dimensional starting point enables full access to the surface, e.g. for (nano-)patterning purposes, which is not available in most other manufacturing techniques including additive manufacturing techniques and molding. We used different arrangements of bi- and multi-layers of a shape memory polymer (SMP) and hyperelastic polymers to program four basic modes of shape-shifting including self-rolling, self-twisting (self-helixing), combined self-rolling and self-wrinkling, and wave-like strips. The effects of various programming variables such as the thermomechanical properties of the hyperelastic layer, dimensions of the bi- and multi-layer strips, and activation temperature on the morphology of the resulting three-dimensional objects were studied experimentally and were found to cause as much as 10-fold change in the relevant dimensions. Some of the above-mentioned modes of shape-shifting were then integrated into other two-dimensional constructs to obtain self-twisting DNA-inspired structures, programmed pattern development in cellular solids, self-folding origami, and self-organizing fibers. Furthermore, the possibility of incorporating multiple surface patterns into one single piece of shape-transforming material is demonstrated using ultraviolet-cured photopolymers.
Conceptual insightsWe present shape-shifting materials whose starting point is a two-dimensional construct and are programmed to give rise to complex three-dimensional shapes once triggered by a stimulus. Rational arrangements of rubber-like polymers and a shape-memory polymer have been used to fabricate the developed materials in an inexpensive and accessible way. A number of basic shape-shifting modes as well as a number of more complex shape transformations, which are partially based on the basic shape shifting modes, are presented. Moreover, the possibility of decorating a two-dimensional structure with arbitrarily complex surface patterns has been demonstrated. The development of materials with advanced functionalities requires combining complex three-dimensional shapes with precisely-controlled surface features including surface (nano-)patterns. The currently available approaches can either address the complex three-dimensional shape, for example, using additive manufacturing, or enable the inclusion of precisely-controlled surface features, for instance, using (nano-)lithography. When starting from a flat structure, the entire surface of the material is fully accessible and could be used to induce functionalities that stem from surface features. This has broad applications in the development of functional biomaterials where surface (nano-)patterns could be used to guide stem cell differentiation, while the three-dimensional geometry determines the mechanical and mass transport properties of the biomaterial. |
1. Introduction
Nature uses various mechanical and physical mechanisms to program events such as shriveling of the surface of fruits, fast motions in plants, solar tracking in sunflowers, growth of the skin and organs of various creatures during their metamorphosis cycle, and the folding mechanism observed in pine cones. The mechanisms include the development of cellular and extracellular layers,1,2 swelling,3 inhomogeneous contraction or expansion of underlying elements,4 different effects of dehydration on different layers,4,5 and activation of snap-through instabilities.6–8 For example, the folding mechanism observed in pine cones causing the release of the embodied seeds and the coiling (twisting) of certain seed pods are both caused by differences in the layers in terms of dehydration and orientation of reinforcing cellulose fibrils.4,5 Another example is the swelling of tissues in ice-plants that unfolds the origami-like structures that protect the seeds during the drying period.3 Finally, very fast motions of Venus flytrap leaves are the result of activation of snap-through instabilities via contraction (expansion) of their interior (exterior) layers.6–8The above-mentioned mechanisms that are exploited by nature to program the growth, movement, and morphogenesis of living creatures could be imitated to create materials with advanced functionalities and attractive properties. In particular, materials made of multiple layers and combined with activation mechanisms such as shape memory materials9–12 or swelling of gels could be used for the development of programmable materials. A number of such programmable materials have been proposed recently. Bi-layer materials are the simplest form of such constructions and could be programmed to exhibit (homogeneous) bending13,14 and a wrinkled surface.1,15,16 A number of bi- and multi-layer materials proposed by different researchers have been discussed below.
Structures equipped with bendable features are shown to exhibit shape shifting or transition in their internal structure as a response to various stimuli such as temperature, light, moisture, electric and magnetic fields, high frequency, etc.16–18 Moreover, seedpod-like hygroscopic bilayer composites reinforced in different directions using thin aluminum oxide ribbons which are aligned in a hydrogel by means of magnetic fields have been designed to demonstrate self-rolling and self-helixing in the presence of moisture.19,20 In another study, Ionov et al. fabricated a polymeric star-like self-folding bilayer which could reversibly encapsulate and release cell particles.21 Dissimilar swelling properties can also provide the bending moment needed for rolling a polymer/polymer or metal/polymer bilayer composite.22 Techniques such as ion dip-dyeing and transfer printing have also been used to program complex shape transformations in tough hydrogels from 1D to 2D, from 2D to 3D, and from 3D to more complex 3D shapes.23 Alternative approaches such as 3D printing of composite materials as well as lithography techniques have been used to produce multi-materials with various types of functionalities.24,25
In a different approach, heating over the glass transition temperature has been used to shrink pre-strained polystyrene in-plane. Dark ink printed on either sides of such transparent sheet absorbs light selectively and locally heats up the polymer leading to inhomogeneous strain relaxation in the film and, thus, folding.26,27 Surface traction can also be used to assemble the components of a 3D structure.28,29 Graphene ink printed on the surface of pre-strained polystyrene sheets can absorb microwaves and warm up the underlying sections. Exceeding the glass transition temperature of a polymer activates strain relaxation leading to selective folding.30 Graphene oxide papers can be similarly programmed using through-the-thickness gradients to reversibly deform and fold in response to slight heating or light irradiation.31
Embedding conductive elements in the structure of self-folding systems can help produce 3D electronics or active hinges applicable in automatic fabrication and robotics.32–36 Equipped with shape memory polymers, origami structures can be transformed spontaneously in response to the change in temperature.37 Intelligent elements such as Joule-heated shape memory alloys could be used to program the self-folding of origami structures to various configurations.38 Edge activation in highly thin bilayers could prescribe hinge-like folding in bilayer structures,39 while step-controlled folding of origami-like structures has been shown to enable the assembly of complex 3D structures.39,40 Sequential folding of origami structures could facilitate the actuation of locking features once folding is completed.40,41
The aim of the current study is to demonstrate the possibility of designing and programming initially flat (i.e. two-dimensional) structures that upon application of a stimulus undergo shape transformations and exhibit a complex three-dimensional geometry. This is in line with similar approaches reported in the literature recently.26,28,36–38 The fact that such complex shape-shifting could be programmed into an initially flat structure opens up many possibilities for the development of materials with advanced functionalities, because there is full access to the flat surface of the material before shape-transformation which could be used, for example, to introduce arbitrarily complex surface patterns onto the flat structure.
We used rationally-designed arrangements of simple elements for programming the desired shape-transformations based on bi- and multi-layers of active (i.e. shape memory) and passive polymers. Geometrical features, different arrangements of the passive and active polymers, and temperature fields were then used to program various types of shape transformations. Four basic modes of shape-shifting were defined including self-rolling, self-twisting (self-helixing), combined self-rolling and self-wrinkling, and shape-shifting to wave-like geometries. The basic shape-shifting modes were then combined with other two-dimensional structures to program more complex shape transformations in DNA-inspired constructs, patterned cellular solids, self-folding origami, and self-organizing fibers. To demonstrate the potential of incorporating additional functionalities, surface patterns with various designs were incorporated into some of the presented shape-shifting materials.
2. Materials and methods
The shape-shifting materials presented in the current study were, in their simplest form, made of bi-layers constituting a soft hyperelastic layer and a shape memory polymer (SMP) layer. Tri- and multi-layers were used in more complex constructions. The SMP acted as a temperature-triggered activation mechanism. The mechanical properties of the soft hyperelastic layer, the size and dimensions of the soft hyperelastic layer and the SMP, arrangement of both layers, and activation temperature were all utilized for programming the shape-shifting behavior of the developed materials.2.1. Materials and material characterization
Three types of hyperelastic polymers with different mechanical properties were used in the current study including natural rubber (NR) (RX® Luna Para, Eriks, color: beige, nominal thickness: 1–3 mm), soft polyvinyl chloride (soft PVC) (RX® Mipolam, Eriks, color: honey yellow or clear, nominal thickness: 1–3 mm), and natural rubber/styrene-butadiene rubber (NR/SBR) (RX® Noma, Eriks, color: black, nominal thickness: 1–3 mm). Hyperelastic polymers generally show rubber-like mechanical behaviors and nonlinear elastic stress–strain curves. The hyperelastic polymers were chosen to be flexible enough for bending and show different types of changes in their mechanical behavior in response to the applied high temperature. The mechanical properties and stress–strain curves of the three hyperelastic materials at different temperatures are presented in the ESI† (Fig. S1 and Table S1). A heat-triggered SMP (polyolefin, G. Apex, Taiwan Yun Lin Electronic Co. Taiwan, nominal thickness: 0.6 mm) with a 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 nominal shrinking ratio, a minimum shrinking temperature of 70 °C (nominal value), and a minimum full recovery temperature of 110 °C was used. Our experiments, however, showed that there is detectable shrinkage for temperatures as low as 55 °C. The percentage of shrinkage vs. activation temperature is presented in the ESI† (Fig. S2). Polyolefin SMPs were chosen because they are among the most commonly used SMPs that show good flexibility and fast shape recovery. Moreover, they are widely available, inexpensive, and are good representatives of temperature-triggered SMPs that can be programmed for high strain recovery applications. A layer of ethyl cyanoacrylate (LOCTITE® 401, Loctite) or methyl cyanoacrylate (LOCTITE® 496, Loctite) adhesive approximately 35 μm in thickness was used to bond the hyperelastic polymers to the SMP. In all cases, the actual thickness of the polymers was measured and used for presenting the results of the study. The mechanical and thermomechanical properties of the hyperelastic polymers were measured (see the ESI† for the details of the material characterization tests).
1 nominal shrinking ratio, a minimum shrinking temperature of 70 °C (nominal value), and a minimum full recovery temperature of 110 °C was used. Our experiments, however, showed that there is detectable shrinkage for temperatures as low as 55 °C. The percentage of shrinkage vs. activation temperature is presented in the ESI† (Fig. S2). Polyolefin SMPs were chosen because they are among the most commonly used SMPs that show good flexibility and fast shape recovery. Moreover, they are widely available, inexpensive, and are good representatives of temperature-triggered SMPs that can be programmed for high strain recovery applications. A layer of ethyl cyanoacrylate (LOCTITE® 401, Loctite) or methyl cyanoacrylate (LOCTITE® 496, Loctite) adhesive approximately 35 μm in thickness was used to bond the hyperelastic polymers to the SMP. In all cases, the actual thickness of the polymers was measured and used for presenting the results of the study. The mechanical and thermomechanical properties of the hyperelastic polymers were measured (see the ESI† for the details of the material characterization tests).
2.2. Programming basic shape-shifting modes
Four basic arrangements of the hyperelastic and SMP layers were considered (Fig. 1) each of which giving rise to one specific shape-shifting behavior. Some of these four basic types of shape-shifting behaviors were then used for programming more complex materials as described in the following sub-sections. In the first arrangement, strips made of hyperelastic polymer and SMP were adhesively bonded such that the axis of SMP activation coincided with the longitudinal axis of the bi-layer (Fig. 1a). Temperature gradients could be used to trigger self-rolling in this type of arrangement (Fig. 1a). In the second type of arrangement, the axis of SMP activation made a 45° angle with the longitudinal axis of the bi-layer (Fig. 1b). Activation of the SMP triggers self-twisting (self-helixing) in this type of arrangement (Fig. 1b). In the third arrangement, alternating types of weak and strong adhesives were used to bond the SMP and the hyperelastic polymer such that the axis of SMP activation was parallel to the longitudinal axis of the polymer (Fig. 1c). Delamination of the weakly-bonded parts of the bi-layer caused by activation of the SMP triggers wrinkling as well as rolling in this type of arrangement (Fig. 1c). Ultimately, discrete bands of the hyperelastic polymer were alternatively attached to either side of the continuous SMP strip to create a tri-layer (Fig. 1d). This flat tri-layer transforms into a curved wavy shape upon heat application (Fig. 1d).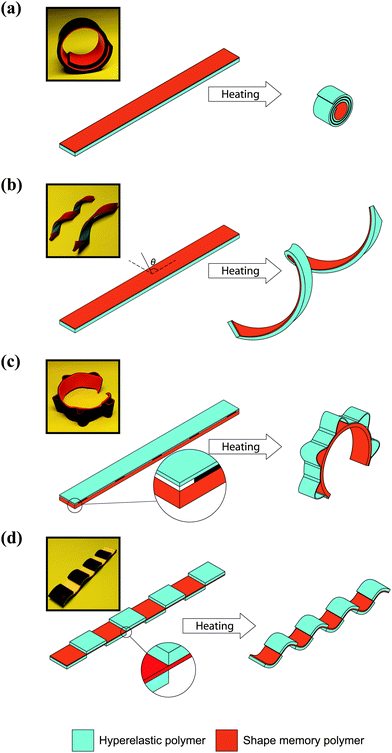 | ||
| Fig. 1 Basic modes of shape-shifting where a bi-layer of a SMP and a hyperelastic polymer transforms into a (a) rolled, (b) spiral, (c) wrinkled and rolled, or (d) wave-like structure. | ||
The effects of the thermomechanical properties of the hyperelastic polymer and the dimensions of the bi-layer strips (thickness, width) in programming the final shape of the self-rolled and self-twisted structures were studied experimentally. The shape-transformation was triggered by submerging the bi-layers in a glass hot water bath (temperature = 80 °C for self-rolling and 90 °C for self-twisting) whose temperature was controlled by a magnetic stirrer (RET CV, IKA® Werke, Germany). The dimensions of the shape-transformed shapes were measured using digital images captured under an optical microscope (Keyence VHX 5000) or using a calibrated digital camera. To measure the curvature of self-rolled structures, a circle was fitted to the points at the interface of the rolled bi-layer using a MATLAB (Mathworks, US) code. The curvature, exterior surface, and pitch size of the self-twisted (self-helixed) structures were measured using the image processing toolbox of MATLAB.
2.3. Self-twisting of DNA-inspired constructs
Two thin self-twisting bi-layer strips (width = 4 mm, thickness of the hyperelastic polymer = 2 mm) were attached to each other side-by-side using polylactic acid (PLA) rods to create some type of DNA-inspired structure. These are basically longer multi-segment versions of the basic shape-shifting mode illustrated in Fig. 1b. The shape-shifting was triggered by gradual immersion of the construct in a hot water container (temperature = 90 °C) using a protocol similar to what was described above.2.4. Programmed pattern formation in cellular solids
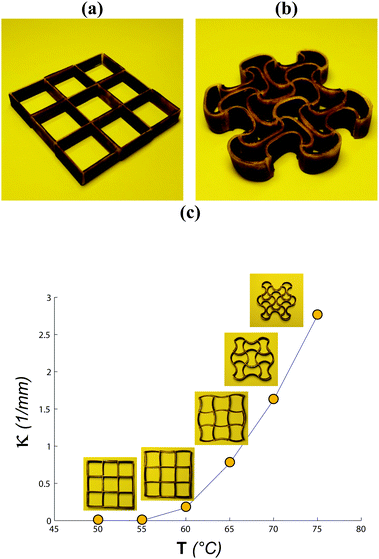
A 3D printer (Ultimaker 2 Go, Ultimaker, The Netherlands) based on the fused deposition modeling (FDM) technology was used to manufacture a 3 × 3 square array (Fig. 2a) from PLA. The dimensions of the unit cell of the resulting cellular structure were 25 mm × 25 mm with a wall thickness of 1 mm. SMP layers were then adhesively bonded to the wall of the cellular solid based on a checker-board pattern. Upon SMP activation, the thin PLA walls bend (buckle) under compressive load and the square shape of unit cells initially transforms into some type of hour-glass shape which then progresses further to generate more complex patterns. Activation temperature was used to control the programmed shape-shifting in the cellular material and the effects of temperature on the generated pattern were studied experimentally by changing the temperature between <50 °C and 90 °C. The curvature of the deformed walls was measured using a similar protocol as described above.2.5. Self-folding origami
A different 3D printer based on the direct light projection technology (Prefactory® 4, EnvisionTEC, Germany) was used to fabricate six square-shaped elements from a liquid photo-reactive acrylate resin (R5-Gray EnvisionTEC, Germany) with a glass transition temperature of 120°–150 °C. Together, these six elements create the un-folded shape of a cubic origami. The square elements (Fig. 3a) were designed such that the SMP could be integrated into their structure (Fig. 3b), attaching the elements together and providing the required activation mechanism for self-folding.2.6. Self-organizing fibers
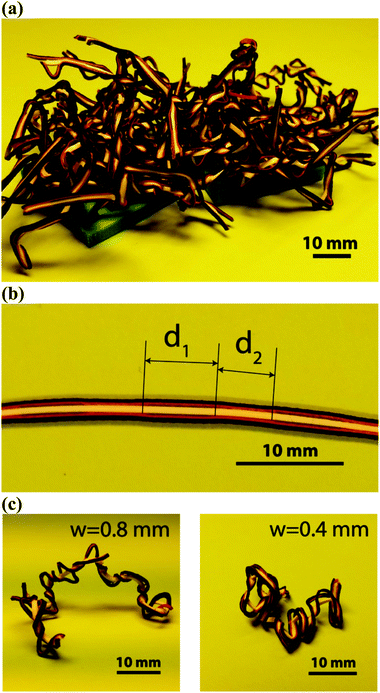
Narrow multi-layer constructs were made where the SMP strip served as the middle layer and hyperelastic polymers were attached on either side of the SMP (Fig. 4). The adhesive layer on both sides of the SMP incorporated thin layers of conventional paper tape (every 10 mm, a piece of conventional paper tape with the length of 5 mm) to facilitate delamination of the layers once the SMP was activated. The five-layer constructs had very small widths (0.4–0.8 mm) as compared to their thickness (2 mm) which further helped delamination in weakly bonded regions (i.e. the locations where thin paper tape was applied). A number of multi-layer fibers prepared according to the above-mentioned protocol were integrated into comb-like structures.2.7. Integration of surface patterns
To demonstrate the possibility of incorporating surface patterns into shape-shifting materials, self-twisting (self-helixing) materials with different types of surface patterns were developed. The hyperelastic polymer in the shape-shifting bi-layer was patterned by applying a thin layer of photosensitive polymer resin (a mixture of acrylated monomers and oligomers as well as photoinitiators) (Flexible FLGR01, Formlabs, US). Different pattern shapes including circle, square, wavy, and strip were used to demonstrate the possibility of incorporating a wide range of patterns in one single shape-shifting construct. Different pattern shapes were printed on transparent sheets using a Xerox printer to create different masks. The transparent masks were then placed on top of the hyperelastic polymer. A glass plate was compressed on top of the transparent mask to ensure uniform thickness of the liquid photosensitive polymer between the hyperelastic polymer and the mask. An ultraviolet (UV) chamber (Sun Ray 600, 150 mW cm−2, used in the half-power mode, Integrated Dispensing Solutions Inc.) was used to irradiate the masks with UV beams for ≈3 min, after which the masks were peeled from the cured photopolymer layer. The dark (printed) locations on the mask prevented the transmission of the UV beam leaving pillars on the surface, while the transparent areas allowed UV transmission and, thus, direct curing of the photosensitive polymer below them, thereby creating pits. To invert the locations of pits and pillars on the surface, a mask with negatively printed patterns was used.3. Results
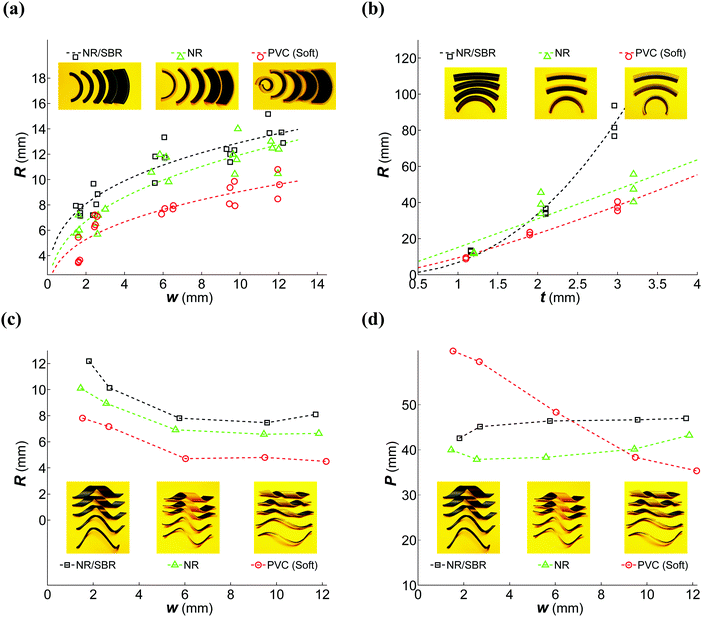
Upon activation, the structures designed to exhibit the basic shape-shifting modes behaved as expected and, respectively, exhibited self-rolling (Fig. 1a), self-twisting (Fig. 1b), combined self-wrinkling and self-rolling (Fig. 1c), and a wave-like geometry (Fig. 1d). The programming variables investigated here were found to notably influence the resulting shape (Fig. 5). For example, the radius of curvature in self-rolling could be changed with as much as ≈2 fold when the thermomechanical properties of the hyperelastic polymer were changed (e.g. compare soft PVC with NR/SBR in Fig. 5a and b). Generally speaking, NR/SBR specimens showed the highest radii of curvature as compared to two other hyperelastic polymers (Fig. 5a and b). Changing the width of the bi-layers from 2 mm to 12 mm changed the radius of curvature of the resulting structures by as much as ≈3 fold (Fig. 5a). The thickness of the hyperelastic polymer also strongly affected the radius of curvature of the self-rolled constructs (Fig. 5b): changing the thickness of the hyperelastic polymer from 1 mm to 3 mm resulted in as much as ≈10 fold increase in the radius of curvature (Fig. 5b).The helices formed in the self-twisting materials showed similar trends (Fig. 5c and d). The radius of the helix curvature and its pitch changed by as much as ≈3 fold, depending on the hyperelastic polymer used (Fig. 5c). Changing the width of the bi-layer strips between 2 mm and 10 mm strongly influenced both the radius of curvature and the pitch of the helix (Fig. 5c and d). The radius of curvature was the largest for NR/SBR (Fig. 5c). For small widths of the bi-layer strip (i.e. <6 mm), the helix pitch was the highest for the PVC specimens (Fig. 5d). The pitch size was the highest for soft NR/SBR when the width of the strip exceeded 6 mm (Fig. 5d). The sensitivity of the pitch to width was very much dependent on the type of the hyperelastic polymer (Fig. 5d). While for NR and NR/SBR specimens the changes in the pitch with width were modest, changing the width resulted in large changes in the pitch size for soft PVC (Fig. 5d).
The trailing edge of the SMP layer developed a certain curvature after self-rolling or self-twisting (Fig. 6). The curvature was clearly visible in several views of the structures with the size depending on the geometrical parameters defining the bi-layer such as the width of the bi-layer strip (Fig. 6). While the curvature was notably visible in the lateral view of self-rolling structures (Fig. 6a), it was very small in their axial view (Fig. 6b). As for the self-twisting constructs, the edge effect was similar regardless of the angle of view or location within the construct (Fig. 6c and d). No such edge effects were observed in the hyperelastic polymers, particularly the ones with larger thicknesses (Fig. 6a–d).
Gradual immersion of the DNA-inspired structure in a hot water bath resulted in gradual self-twisting and formation of a DNA-like structure (Fig. 7a). Shape-shifting started from the bottom part of the structures and propagated upward as a larger part of the structure was submerged (Fig. 7a). The time sequences of all shape-shifting events are presented in Fig. 7, while the captured movies can be found in the ESI.†
 | ||
| Fig. 7 The time sequence of the shape transformations in (a) a self-twisting DNA-inspired structure, (b) two-dimensional cellular solids, and (c) self-folding origami. | ||
Gradual immersion of the origami also resulted in self-folding into the intended cubic shape (Fig. 7c, where two sides of the cube were removed to facilitate observation of the self-folding process). At the beginning of the deformation, some hinges of the cubic structure were bent more than 90° (Fig. 7c). However, further shrinkage of the SMP strip and subsequent sliding of the 45°-sloped edges of the adjacent square elements helped the structure to finally reach its planned shape (Fig. 7c).
The activation temperature significantly influenced the pattern formed in cellular solids (Fig. 2b and c). At temperatures up to 50 °C, the geometry of the cellular solid remained unchanged after immersion in hot water. For temperatures above 50 °C, the shape of the cellular solid gradually changed with exponentially growing curvature of the unit cell walls as the temperature increased from 55 °C to 75 °C. The walls of the unit cell curved around the central point of the unit cell with alternating horizontal/vertical collapsing of the unit cells (Fig. 2c). At 75 °C, the cell walls came into contact with each other (Fig. 2c). The central part of the arced cell walls was flattened once the activation temperatures exceeded 80 °C (Fig. 2b). The patterns developed gradually as larger parts of the cellular solid were submerged in the hot water bath (Fig. 7b).
In the self-organizing fibers, delamination of the hyperelastic polymers at the locations where the bonding between layers was weak (the delamination zones) led to the buckling of the hyperelastic polymers. This was due to the fact that the length of the SMP layer was decreased after activation, while the hyperelastic polymers did not change in length. At each delamination zone, the hyperelastic polymer buckled to a different direction depending on which side had the weakest bond. The random distribution of the buckling direction resulted in the curly shape of the initially straight fibers (Fig. 4c and d). We observed that the curvature of the curly fibers was dependent on their width and generally increased as the width decreased (e.g. compare Fig. 4c with 4d). Our preliminary tests also showed that the ratio of the length of the delamination zone to that of the bonded zone (i.e. d1/d2 in Fig. 7b) must be larger than unity to ensure that the thickness of the paper tape does not prevent the SMP layer from proper bonding to the hyperelastic polymers. Arranging the fibers into two comb-like structures and activating the SMPs resulted in entanglement of the combs into each other (Fig. 4a).
The self-twisting (self-helixing) strips with surface patterns were observed under a microscope and showed the imprinted patterns with one single strip showing multiple surface patterns on the various sides of a self-twisted helical shape (Fig. 8).
4. Discussion
The most important conclusion of the current study is that by combining soft (hyperelastic) polymers with a simple SMP, it is possible to design and program shape transformations in initially flat (i.e. two-dimensional) structures so as to obtain complex three-dimensional geometries. The starting points of all cases presented here including the basic modes of shape-shifting, the DNA-inspired structures, programmed shape-shifting in cellular solids, self-folding origami, and self-organizing fibers were flat (i.e. two-dimensional) objects.The results of this study also show the importance of various variables that could be used for programming the desired shape-shifting behavior. By changing the thermomechanical properties of the passive hyperelastic polymer, the dimensions of the bi- and multi-layer strips, and the activation temperature, the shape of the resulting three-dimensional objects could be controlled. In some conditions, the dimensions describing the shape of the resulting three-dimensional structure changed by as much as ≈10 fold when the above-mentioned parameters were modified. The arrangement of the passive and active layers together with the design parameters mentioned above provide a large space within which shape-shifting of two-dimensional structures to a wide range of three-dimensional objects could be programmed. Additional parameters such as the degree of anisotropy in the contraction of the SMP could be used to further enrich the space of programmable geometries. The measured radii of curvature and pitch exhibit some deviations from the fitted curves which are, in part, caused by spatial variations in the mechanical properties and shape shifting behavior of the hyperelastic and shape memory polymers. A few other secondary effects such as thickness variations also play a role.
4.1. Mechanistic aspects
In self-rolling structures, increasing both the thickness and the width of the bi-layer strips results in increased radii of curvature after self-folding. With all other parameters being constant, increasing the thickness of the hyperelastic polymer results in increased elastic force opposing the shrinkage of the SMP, thereby increasing the radius of curvature. Increasing the width of the bi-layer strips, on the other hand, increases both the flexural stiffness and the contraction force of the SMP per unit length, which is why the width of the bi-layer influences the radius of curvature only for small widths (i.e. <≈10 mm). For smaller widths, the radius of curvature increases with increased width of the bi-layer strips probably due to secondary effects such as edge effects and the instability and lateral forces that are more important for very thin strips. The absolute values of the radii of curvature are dependent on how large the contraction force of the SMPs is as compared to the elastic force of the hyperelastic layer at the elevated temperatures required for triggering the shape shifting behavior. In the case of hyperelastic polymers that lose a significant portion of their mechanical properties at elevated temperatures, there might be some adjustments in the shape of the resulting self-rolling structures due to the increased elastic force of the hyperelastic polymer after cooling down. The shape adjustments are, however, expected to be relatively small, because after cooling down the increased elastic force of the hyperelastic polymer should overcome the elastic force (and not the contraction force) of the SMP to adjust the geometry of the self-rolled structure. The same mechanisms are at work when studying self-twisting constructs with the biggest difference being the angle of the hyperelastic polymer and the SMP that further complicates understanding the exact distribution of the stresses and strains. Finally, the relationship between activation temperature and the shrinkage of the SMP is nonlinear (see ESI†, Fig. S2). The shrinking behavior of the SMP can therefore be adjusted within a large range by properly choosing the activation temperature. Increasing the activation temperatures could, thus, amplify the effects of the deformations caused by the SMP.As for the edge effects observed both in self-rolling and in self-twisting structures, they are primarily due to the through-the-thickness difference between the surface of the SMP bonded to the hyperelastic polymer which is constrained in its deformation as compared to the free surface of the SMP that can freely deform. The width of the bi-layer strips also influences the edge effects, because the effects of such edge-related deformations are larger in strips with smaller widths, where the ratio of the perimeter of the bi-layer to the surface of the bi-layer is larger.
The shape transformations studied here are based on a number of underlying physical phenomena that need to be understood and preferably theoretically studied to enable more informed programming of the shape transformations and precise control of the dimensions of the resulting three-dimensional shapes. Increased temperature activates the SMP and results in anisotropic contraction of the SMP layer. The interaction of the SMP layer with the resisting hyperelastic polymer develops certain stress patterns that determine the course of shape transformation. Changing the activation temperature could be used to control the contraction force of the SMP layer. However, it has to be noted that the activation temperature might also change the mechanical properties of the hyperelastic material. The three hyperelastic polymers studied here were deliberately chosen to demonstrate three types of thermomechanical behavior: whereas the mechanical properties of the NR hardly change as the temperature increases from 20 °C to 100 °C, soft PVC exhibits tremendous loss of mechanical properties in the same temperature range (see ESI† for supporting Experimental data). The thermomechanical behavior of NR/SBR is somewhere between the ones exhibited by NR and soft PVC. The thickness of the hyperelastic layer could be used as an additional parameter to control the resisting elastic force in bi- and multi-layers independent of the thermomechanical properties of the hyperelastic polymer. The width of the strips influences the elastic force as well and modifies the stress distribution in bi- and multi-layer constructs. However, the width simultaneously changes the other dimensions of the resulting three-dimensional object and is, thus, a less flexible way of programming shape transformations.
Another physical mechanism used here for programming shape transformations is mechanical instability. Harnessing mechanical instability has recently received increasing attention as a technique for the development of active materials.42–45 The programmed pattern transformation observed for cellular solids (Fig. 5) is an example of how instability patterns triggered by activation of the SMP could be used to program shape-transformations. A combination of instability and buckling with rational positioning of the SMP segments in cellular materials provides additional physical pathways for programming shape transformations. Although the patterns developed in the current study remain in-plane after shape transformations, out-of-plane buckling could be harnessed in similar ways to trigger additional modes of shape transformations and provide further freedom in the design of the resulting three-dimensional object.
4.2. Surface features: wrinkling and patterns
Combining three-dimensional shapes with complex surface features such as surface wrinkles and surface (nano-)patterns is one of the most important advantages of starting from a flat structure, because full access to the surface of the material is possible. Similar access to the surface is not available in other manufacturing techniques that enable the fabrication of complex three-dimensional geometries such as 3D printing. In this study, we presented two techniques for creating surface features including delamination-assisted self-wrinkling of the surfaces (Fig. 1c) and surface patterning using UV-cured photopolymers (Fig. 8). The approach used for combining various patterns (Fig. 8) is particularly powerful, as it can be extended to any other surface-patterning technique that works on flat substrates including (nano-)lithography and all other nano-patterning techniques.If the feature sizes of the wrinkling and wavy structural elements are properly chosen, they could be used for controlling cell proliferation, migration, and alignment.46–48 These wrinkling and wavy strips can create homogeneous or hierarchical, or even more complicated patterns.46 Different studies have shown that surface features in different scales from several nanometers49 to hundreds of micrometers50 can enhance the cell response in different ways. Patterning the external surfaces of the proposed wrinkling and wavy elements could be used to combine patterns at different scales with each other, thereby obtaining hierarchical surface patterns and achieving the required biological responses. For example, it has been shown that random surface topographies affect the collective cell response, while ordered topographies influence the individual cell behavior.51 The wettability of a substrate is another critical cue in determining the cell attachment capability. The cell-to-substrate adhesion is maximized when the wettability of the surface is moderate.51–53 Architecting the surface of a substrate by tailoring the design of the larger wrinkling or wavy strips (through changing their pitch size and radius) and smaller engraved patterns (through changing the engraved pattern shape, size, and depth) could be very helpful in achieving the intended cell behavior.51
4.3. Applications
The possibility of creating complex three-dimensional shapes from flat structures could have many applications in various areas of research. An important area of potential application for the developed materials is soft robotics as well as design and manufacturing of soft actuators. Moreover, SMPs could be used in the form of biocompatible and/or biodegradable polymers for the development of medical devices.54 Stimulus-responsive elements can be used for unpacking and assembly of very big size structures, encapsulation of micro/nanoscale particles, development of medical implants, 3D electronics, sensors and smart bodies. In particular, complex three-dimensional geometries could be used for designing materials with unprecedented or rare mechanical properties within the context of mechanical meta-materials.55One of the main applications of shape-shifting bilayers can be fabrication of 3D cell culture substrates. The interaction between cells and the matrix has been found to be of great significance in many biological processes such as embryogenesis,56 tumorigenesis,57 and angiogenesis.46,58 Some of the structural elements introduced in this study have great potential in stimulating cell growth in biological systems, for example, by adjusting the curvature59 in the geometry of tissue engineering scaffolds. When concepts proposed in the current study are used for the fabrication of biomaterials, shape transformations might need to occur before bringing the biomaterial into contact with living organisms. In such an approach, the advantage of shape transformation would be the possibility to start from a flat structure whose entire surface is fully accessible for any type of surface bio-functionalization and/or bio-nanopatterning including the techniques that work only on flat surfaces. The complex 3D shape that is required for proper functioning of the biomaterial can then be obtained through programmed shape transformations.
The three-dimensional shapes of the biomaterials used for tissue regeneration are important, because parameters such as porosity, pore size, pore shape, and surface curvature could all strongly influence the rate of tissue regeneration.59 The effect of scaffold geometry on tissue regeneration occurs through multiple pathways including regulation of the mechanical stimulus for tissue regeneration60,61 as well as adjustment of mass transport properties such as permeability.62
5. Conclusions
Programming shape-transformations in initially flat soft materials was studied in the current study with the aim of obtaining complex three-dimensional structures. Bi- and multi-layers of the SMP and hyperelastic polymers were used for programming four basic modes of shape transformation including self-rolling, self-twisting (self-helixing), combined self-rolling and self-wrinkling, and generation of wave-like geometries. Some of the basic modes of shape transformation were then used for designing self-twisting DNA-inspired structures, programmed pattern formation in cellular solids, self-folding origami, and self-organizing fibers. An experimental study was performed to investigate the effects of various programming variables such as the thermomechanical properties of the hyperelastic layer, the thickness of the hyperelastic polymer, the geometrical dimensions of the bi- and multi-layers, and the activation temperature on the morphology of the obtained geometries. It was observed that the various parameters describing the resulting three-dimensional shapes could be changed by as much as 10-fold, when the above-mentioned parameters were adjusted. The possibility of incorporating multiple types of surface patterns in one single piece of shape-shifting structure was also demonstrated.References
- L. Ionov, Biomimetic 3D self-assembling biomicroconstructs by spontaneous deformation of thin polymer films, J. Mater. Chem., 2012, 22(37), 19366–19375 RSC.
- J. P. Vandenbrink, E. A. Brown, S. L. Harmer and B. K. Blackman, Turning heads: the biology of solar tracking in sunflower, Plant Sci., 2014, 224(0), 20–26 CrossRef CAS PubMed.
- M. J. Harrington, K. Razghandi, F. Ditsch, L. Guiducci, M. Rueggeberg and J. W. C. Dunlop, et al. Origami-like unfolding of hydro-actuated ice plant seed capsules, Nat. Commun., 2011, 2, 337 CrossRef PubMed.
- A. R. Studart, Biologically inspired dynamic material systems, Angew. Chem., 2015, 54(11), 3400–3416 CrossRef CAS PubMed.
- J. Dawson, J. F. V. Vincent and A. M. Rocca, How pine cones open, Nature, 1997, 390(6661), 668 CrossRef.
- C. Darwin, Insectivorous plants, Murry, London, UK, 1975 Search PubMed.
- W. H. Brown, The mechanism of movement and the duration of the effect of stimulation in the leaves of Dionaea, Am. J. Bot., 1916, 3(2), 68–90 CrossRef.
- Q. Guo, E. Dai, X. Han, S. Xie, E. Chao and Z. Chen, Fast nastic motion of plants and bioinspired structures, J. R. Soc., Interface, 2015, 12(110), 0598 CrossRef CAS PubMed.
- Q. Zhao, W. Zou, Y. Luo and T. Xie, Shape memory polymer network with thermally distinct elasticity and plasticity, Sci. Adv., 2016, 2(1), e1501297 Search PubMed.
- T. Xie, Recent advances in polymer shape memory, Polymer, 2011, 52(22), 4985–5000 CrossRef CAS.
- H. Meng and G. Li, A review of stimuli-responsive shape memory polymer composites, Polymer, 2013, 54(9), 2199–2221 CrossRef CAS.
- J. Mohd Jani, M. Leary, A. Subic and M. A. Gibson, A review of shape memory alloy research, applications and opportunities, Mater. Des., 2014, 56, 1078–1113 CrossRef CAS.
- Z. Chen, G. S. Huang, I. Trase, X. M. Han and Y. F. Mei, Mechanical Self-Assembly of a Strain-Engineered Flexible Layer: Wrinkling, Rolling, and Twisting, Phys. Rev. Appl., 2016, 5(1), 017001 CrossRef.
- L. Ionov, Soft microorigami: self-folding polymer films, Soft Matter, 2011, 7(15), 6786–6791 RSC.
- Q. Wang and X. Zhao, A three-dimensional phase diagram of growth-induced surface instabilities, Sci. Rep., 2015, 5, 8887 CrossRef CAS PubMed.
- Y. Liu, J. Genzer and M. D. Dickey, “2D or not 2D”: Shape-programming polymer sheets, Prog. Polym. Sci., 2016, 52, 79–106 CrossRef CAS.
- S. Ahmed, C. Lauff, A. Crivaro, K. McGough, R. Sheridan, M. Frecker, et al., editors. Multi-field responsive origami structures: Preliminary modeling and experiments. ASME 2013 International Design Engineering Technical Conferences and Computers and Information in Engineering Conference; 2013: American Society of Mechanical Engineers.
- Z. He, N. Satarkar, T. Xie, Y. T. Cheng and J. Z. Hilt, Remote controlled multishape polymer nanocomposites with selective radiofrequency actuations, Adv. Mater., 2011, 23(28), 3192–3196 CrossRef CAS PubMed.
- R. M. Erb, J. S. Sander, R. Grisch and A. R. Studart, Self-shaping composites with programmable bioinspired microstructures, Nat. Commun., 2013, 4, 1712 CrossRef PubMed.
- R. M. Erb, R. Libanori, N. Rothfuchs and A. R. Studart, Composites reinforced in three dimensions by using low magnetic fields, Science, 2012, 335(6065), 199–204 CrossRef CAS PubMed.
- G. Stoychev, N. Puretskiy and L. Ionov, Self-folding all-polymer thermoresponsive microcapsules, Soft Matter, 2011, 7(7), 3277–3279 RSC.
- V. Luchnikov, O. Sydorenko and M. Stamm, Self-rolled polymer and composite polymer/metal micro- and nanotubes with patterned inner walls, Adv. Mater., 2005, 17(9), 1177–1182 CrossRef CAS.
- X. Peng, Y. Li, Q. Zhang, C. Shang, Q.-W. Bai and H. Wang, Tough Hydrogels with Programmable and Complex Shape Deformations by Ion Dip-Dyeing and Transfer Printing, Adv. Funct. Mater., 2016, 26(25), 4491–5500 CrossRef CAS.
- A. Sydney Gladman, E. A. Matsumoto, R. G. Nuzzo, L. Mahadevan and J. A. Lewis, Biomimetic 4D printing, Nat. Mater., 2016, 15(4), 413–418 CrossRef CAS PubMed.
- V. Luchnikov, L. lonov and M. Stamm, Self-rolled polymer tubes: novel tools for microfluidics, microbiology, and drug-delivery systems, Macromol. Rapid Commun., 2011, 32(24), 1943–1952 CrossRef CAS PubMed.
- Y. Liu, J. K. Boyles, J. Genzer and M. D. Dickey, Self-folding of polymer sheets using local light absorption, Soft Matter, 2012, 8(6), 1764–1769 RSC.
- R. W. Mailen, Y. Liu, M. D. Dickey, M. Zikry and J. Genzer, Modelling of shape memory polymer sheets that self-fold in response to localized heating, Soft Matter, 2015, 11(39), 7827–7834 RSC.
- D. H. Gracias, V. Kavthekar, J. C. Love, K. E. Paul and G. M. Whitesides, Fabrication of micrometer-scale, patterned polyhedra by self-assembly, Adv. Mater., 2002, 14(3), 235–238 CrossRef CAS.
- K. Kuribayashi-Shigetomi, H. Onoe and S. Takeuchi, Cell Origami: Self-Folding of Three-Dimensional Cell-Laden Microstructures Driven by Cell Traction Force, PLoS One, 2012, 7(12), e51085 CAS.
- D. Davis, R. Mailen, J. Genzer and M. D. Dickey, Self-folding of polymer sheets using microwaves and graphene ink, RSC Adv., 2015, 5(108), 89254–89261 RSC.
- J. Mu, C. Hou, H. Wang, Y. Li, Q. Zhang and M. Zhu, Origami-inspired active graphene-based paper for programmable instant self-folding walking devices, Sci. Adv., 2015, 1(10), e1500533 Search PubMed.
- M. Shuhei, M. Laura, T. T. Michael, J. W. Robert and R. Daniela, Self-folding miniature elastic electric devices, Smart Mater. Struct., 2014, 23(9), 094005 CrossRef.
- S. Miyashita, C. D. Onal, D. Rus, editors. Self-pop-up cylindrical structure by global heating. 2013 IEEE/RSJ International Conference on Intelligent Robots and Systems; 2013 3–7 Nov. 2013.
- M. T. Tolley, S. M.Felton, S. Miyashita, L. Xu, B. Shin, M. Zhou, et al., editors. Self-folding shape memory laminates for automated fabrication. 2013 IEEE/RSJ International Conference on Intelligent Robots and Systems; 2013 3–7 Nov. 2013.
- S. Miyashita, S. Guitron, M. Ludersdorfer, C. R. Sung, D. Rus, editors. An untethered miniature origami robot that self-folds, walks, swims, and degrades. Robotics and Automation (ICRA), 2015 IEEE International Conference on; 2015: IEEE.
- S. Felton, M. Tolley, E. Demaine, D. Rus and R. Wood, A method for building self-folding machines, Science, 2014, 345(6197), 644–646 CrossRef CAS PubMed.
- M. T. Tolley, S. M. Felton, S. Miyashita, D. Aukes, D. Rus and R. J. Wood, Self-folding origami: Shape memory composites activated by uniform heating, Smart Mater. Struct., 2014, 23(9), 094006 CrossRef.
- E. Hawkes, B. An, N. M. Benbernou, H. Tanaka, S. Kim and E. D. Demaine, et al. Programmable matter by folding, Proc. Natl. Acad. Sci. U. S. A., 2010, 107(28), 12441–12445 CrossRef CAS PubMed.
- G. Stoychev, S. Turcaud, J. W. C Dunlop and L. Ionov, Hierarchical Multi-Step Folding of Polymer Bilayers, Adv. Funct. Mater., 2013, 23(18), 2295–2300 CrossRef CAS.
- Y. Mao, K. Yu, M. S. Isakov, J. Wu, M. L. Dunn and H. Jerry Qi, Sequential Self-Folding Structures by 3D Printed Digital Shape Memory Polymers, Sci. Rep., 2015, 5, 13616 CrossRef PubMed.
- K. Yu, A. Ritchie, Y. Mao, M. L. Dunn, H. J. Qi, editors. Controlled Sequential Shape Changing Components by 3D Printing of Shape Memory Polymer Multimaterials. IUTAM Symposium on Mechanics of Soft Active Materials, SAM 2014, 2015, Elsevier.
- S. Janbaz, H. Weinans and A. A. Zadpoor, Geometry-based control of instability patterns in cellular soft matter, RSC Adv., 2016, 6(24), 20431–20436 RSC.
- J. T. B. Overvelde, S. Shan and K. Bertoldi, Compaction through buckling in 2D periodic, soft and porous structures: effect of pore shape, Adv. Mater., 2012, 24(17), 2337–2342 CrossRef CAS PubMed.
- S. Shan, S. H. Kang, P. Wang, C. Qu, S. Shian and E. R. Chen, et al. Harnessing multiple folding mechanisms in soft periodic structures for tunable control of elastic waves, Adv. Funct. Mater., 2014, 24(31), 4935–4942 CrossRef CAS.
- J. Shim, S. Shan, A. Košmrlj, S. H. Kang, E. R. Chen and J. C. Weaver, et al. Harnessing instabilities for design of soft reconfigurable auxetic/chiral materials, Soft Matter, 2013, 9(34), 8198–8202 RSC.
- P. Yang, R. M. Baker, J. H. Henderson and P. T. Mather, In vitro wrinkle formation via shape memory dynamically aligns adherent cells, Soft Matter, 2013, 9(18), 4705–4714 RSC.
- C. C. Berry, G. Campbell, A. Spadiccino, M. Robertson and A. S. Curtis, The influence of microscale topography on fibroblast attachment and motility, Biomaterials, 2004, 25(26), 5781–5788 CrossRef CAS PubMed.
- M. J. Dalby, N. Gadegaard, R. Tare, A. Andar, M. O. Riehle and P. Herzyk, et al. The control of human mesenchymal cell differentiation using nanoscale symmetry and disorder, Nat. Mater., 2007, 6(12), 997–1003 CrossRef CAS PubMed.
- W. Loesberg, J. Te Riet, F. van Delft, P. Schön, C. Figdor and S. Speller, et al. The threshold at which substrate nanogroove dimensions may influence fibroblast alignment and adhesion, Biomaterials, 2007, 28(27), 3944–3951 CrossRef CAS PubMed.
- M. T. Eliason, E. O. Sunden, A. H. Cannon, S. Graham, A. J. Garcia and W. P. King, Polymer cell culture substrates with micropatterned carbon nanotubes, J. Biomed. Mater. Res., Part A, 2008, 86(4), 996–1001 CrossRef PubMed.
- N. M. Alves, I. Pashkuleva, R. L. Reis and J. F. Mano, Controlling cell behavior through the design of polymer surfaces, Small, 2010, 6(20), 2208–2220 CrossRef CAS PubMed.
- Y. Arima and H. Iwata, Effect of wettability and surface functional groups on protein adsorption and cell adhesion using well-defined mixed self-assembled monolayers, Biomaterials, 2007, 28(20), 3074–3082 CrossRef CAS PubMed.
- J. Y. Lim, M. C. Shaughnessy, Z. Zhou, H. Noh, E. A. Vogler and H. J. Donahue, Surface energy effects on osteoblast spatial growth and mineralization, Biomaterials, 2008, 29(12), 1776–1784 CrossRef CAS PubMed.
- A. Lendlein and S. Kelch, Shape-Memory Polymers, Angew. Chem., Int. Ed., 2002, 41(12), 2034 CrossRef CAS.
- A. A. Zadpoor, Mechanical meta-materials, Mater. Horiz., 2016 10.1039/C6MH00065G.
- M. A. Wozniak and C. S. Chen, Mechanotransduction in development: a growing role for contractility, Nat. Rev. Mol. Cell Biol., 2009, 10(1), 34–43 CrossRef CAS PubMed.
- S. Suresh, Nanomedicine: elastic clues in cancer detection, Nat. Nanotechnol., 2007, 2(12), 748–749 CrossRef CAS PubMed.
- D. E. Ingber, Mechanical signaling and the cellular response to extracellular matrix in angiogenesis and cardiovascular physiology, Circ. Res., 2002, 91(10), 877–887 CrossRef CAS PubMed.
- A. A. Zadpoor, Bone tissue regeneration: the role of scaffold geometry, Biomater. Sci., 2015, 3(2), 231–245 RSC.
- D. P. Byrne, D. Lacroix, J. A. Planell, D. J. Kelly and P. J. Prendergast, Simulation of tissue differentiation in a scaffold as a function of porosity, Young's modulus and dissolution rate: application of mechanobiological models in tissue engineering, Biomaterials, 2007, 28(36), 5544–5554 CrossRef CAS PubMed.
- J. Sanz-Herrera, J. García-Aznar and M. Doblaré, On scaffold designing for bone regeneration: a computational multiscale approach, Acta Biomater., 2009, 5(1), 219–229 CrossRef CAS PubMed.
- S. Van Bael, Y. C. Chai, S. Truscello, M. Moesen, G. Kerckhofs and H. Van Oosterwyck, et al. The effect of pore geometry on the in vitro biological behavior of human periosteum-derived cells seeded on selective laser-melted Ti6Al4V bone scaffolds, Acta Biomater., 2012, 8(7), 2824–2834 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c6mh00195e |
| This journal is © The Royal Society of Chemistry 2016 |