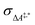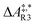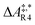Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Uncertainty quantification for quantum chemical models of complex reaction networks†
Jonny
Proppe
,
Tamara
Husch
,
Gregor N.
Simm
and
Markus
Reiher
*
Laboratory of Physical Chemistry, ETH Zürich, Zürich, Switzerland. E-mail: markus.reiher@phys.chem.ethz.ch; Fax: +41 446331594; Tel: +41 446334308
First published on 6th July 2016
Abstract
For the quantitative understanding of complex chemical reaction mechanisms, it is, in general, necessary to accurately determine the corresponding free energy surface and to solve the resulting continuous-time reaction rate equations for a continuous state space. For a general (complex) reaction network, it is computationally hard to fulfill these two requirements. However, it is possible to approximately address these challenges in a physically consistent way. On the one hand, it may be sufficient to consider approximate free energies if a reliable uncertainty measure can be provided. On the other hand, a highly resolved time evolution may not be necessary to still determine quantitative fluxes in a reaction network if one is interested in specific time scales. In this paper, we present discrete-time kinetic simulations in discrete state space taking free energy uncertainties into account. The method builds upon thermo-chemical data obtained from electronic structure calculations in a condensed-phase model. Our kinetic approach supports the analysis of general reaction networks spanning multiple time scales, which is here demonstrated for the example of the formose reaction. An important application of our approach is the detection of regions in a reaction network which require further investigation, given the uncertainties introduced by both approximate electronic structure methods and kinetic models. Such cases can then be studied in greater detail with more sophisticated first-principles calculations and kinetic simulations.
1 Introduction
Highly complex reaction networks underlie chemical reactions that involve reactive species, harsh reaction conditions, or non-innocent solvents (or a combination of all). A plethora of theoretical approaches has been developed for the description of certain aspects of such processes.1–5 All these approaches make different assumptions on the processes studied such that, from a feasibility point of view, none is generally applicable. To illustrate this point, we consider two examples. On the one hand, the dynamics on a rugged energy landscape will demand advanced sampling methods from molecular dynamics or Monte Carlo simulations rather than a standard quantum chemical approach that considers only a few selected stationary points on that surface.6,7 On the other hand, for processes on a well-structured potential energy surface with non-shallow minima, explicit dynamics may suffer from sampling problems and is often replaced by kinetic models that eventually allow one to access long time and length scales beyond the reach of explicit dynamical approaches.8Quantum chemical methods are well suited for describing energy changes due to changes in the electronic structure of reacting molecules if these electronic effects govern the overall energetics of the process. Usually, structures considered relevant as stable intermediates or transition states are optimized and their energies are compared to identify the relevant reaction paths. Clearly, this approach is limited, especially if carried out manually, to a rather small number of structures only. For predictive work on systems for which little or no experimental information is known, the exploration of potentially important structures becomes an immense task. Several approaches exist to overcome this issue. In reactive molecular dynamics simulations,9–17 for example, the nuclear equations of motion are solved to explore and sample configuration space. By contrast, heuristics-guided exploration approaches are based on rules derived from chemical concepts.18–22 By applying predefined (possibly alchemical) transformation rules to create new chemical species, explorations in configuration space are greatly accelerated. Recently, we proposed a fully automated heuristics-guided exploration protocol22 in which the heuristic rules rest on reactivity descriptors derived from quantum mechanics.
It is important to understand that to theoretically grasp the kinetics of complex reaction networks, we must be prepared to investigate an enormous number of possible intermediates (on different potential energy surfaces) not generated by simple conformational changes but by the sheer number of chemically different reactants. For truly complex chemical reaction networks, no universal protocol based on quantum chemical calculations has been established so far that would span the whole range of steps from molecular and electronic structure optimization to detailed kinetic modeling. However, significant progress in all research areas that would contribute to the establishment of such a protocol has already been made. Given the algorithmic and hardware developments accomplished in the past two decades, it should be feasible to establish such a protocol in a single, integrated implementation.
Clearly, various choices and approximations need to be made and hence the protocol to be established will not be unique. Still, we demand the development of such a protocol be subjected to constraints that will make it universally applicable. Besides, we are faced with the fact that quantum chemical raw data are affected by method-inherent errors and need to be augmented by nuclear motion and temperature corrections before they can be subjected to kinetic modeling. Hence, if we must be prepared to make certain assumptions and approximations, we expect from our protocol that the violation of an approximation can be identified within the protocol and overcome by approaches beyond the realm of the protocol's standard methods. This way, we may be able to identify possible breaches that point to more sophisticated theoretical approaches to be applied. If the number of such breaches is small, then the general basis of the protocol, which will be quantum chemical methods in our case, will remain valid. And clearly, in view of the successes of quantum chemical reaction mechanism elucidation, we have good reason to believe that this is possible. Obviously, this will only be possible if we have uncertainty measures at hand that allow us to assess the accuracy of individual simulation results. For example, Vlachos and co-workers recently applied Bayesian statistics to predict rate constants for chemical processes on surfaces.23
The ingredients of a general protocol for the generation and analysis of chemical reaction networks are: (1) the automated exploration of possibly relevant intermediates and transition states, (2) the determination of free energies for reactions in condensed phase, (3) systematic error estimation based on, for instance, Bayesian statistics, and (4) the kinetic modeling of the reaction network emerging.
In this work, we apply components (2)–(4) of the general protocol to a complex chemical reaction network in aqueous solution: the formose reaction. It is our goal to establish protocol-inherent validation measures that keep track of the validity of the assumptions made and that may point to advanced theoretical approaches to deliver more reliable data if needed. Moreover, our analysis is intended to be a general feasibility analysis of this protocol that will, as we shall show, point to interesting future developments.
2 The formose reaction
Formose reaction is the collective term for a plethora of possible autocatalytic oligomerization reactions of formaldehyde in aqueous solution.24,25 The reaction affords a highly complex (racemic) mixture of linear and branched monosaccharides (tetroses to octoses), polyols, and several degradation products. The identification of all products poses a major analytical challenge and the exact composition has not been elucidated yet, though over 50 products have already been characterized.26,27 Due to the formation of biologically important monosaccharides, such as D-ribose, the formose reaction may constitute a plausible scenario for the emergence of sugars on prebiotic earth.28–30 The first step towards the formation of sugars is the dimerization of formaldehyde, which is extremely slow and may involve catalysis31,32 or radiation-induced processes.33,34 The dimer can be regenerated autocatalytically35,36 and the reaction can therefore be easily initiated. The rapid subsequent formation of sugars is likely to proceed through an alternating series of forward and reverse aldol reactions as well as tautomerizations.35 Kua et al. investigated these key steps in the formose reaction computationally and concluded that the experimentally proposed mechanism is also plausible from a theoretical point of view.37 Rappoport et al. explored the chemical reaction network of the formose reaction automatically based on heuristic guidance and reproduced major reaction pathways as well as experimentally observed products.20 Recently, hydride shifts and associated quantum tunneling were found to play a major role in the formose reaction,38–40 which were not considered in the computational studies. The product ratios are very sensitive to the reaction conditions (e.g., solvent, temperature, and pH) and the amount and type of reactants. Catalysts significantly influence the product ratio of the formose reaction, which was discussed in the context of the origin of homochirality (L-amino acids, D-sugars).41–43 So far, the complexity of the reaction network has prevented experimental and theoretical kinetic studies of the entire process.253 Transition state theory and thermochemistry
A reaction network of all relevant intermediates and transition states of a chemical process sets the frame to study population trajectories through the network. In solution chemistry, typically trajectories of molar concentrations are studied, which depend on several conditions such as initial feed of reactants and temperature. While the correlation of these conditions with the product distribution can be determined quite straightforwardly by a suitable experimental setup, it remains a challenge to analyze why a certain product distribution was found. To resolve this issue, studying the kinetics of a chemical process is inevitable. Only then, intermediates relevant for the product distribution but not contained in it can be detected. This time-resolved picture would allow us to develop strategies to support the formation of a desired product or to suppress the formation of unintended side products.As experimental kinetics can only examine a limited number of chemical species, thorough theoretical kinetic models corresponding to complex reaction networks spanning several time scales are desired. For the construction of a general-purpose (mass-action) kinetic model, rate constants are the essential elements to be determined.
Conventional transition state theory (TST) provides a simple approach to calculate rate constants for isothermal reactions. It is assumed in conventional TST that a reaction coordinate along a Born–Oppenheimer potential energy surface is orthogonally intersected by a hyperplane in such a way that once crossed by a trajectory starting from a reactant state, that trajectory ends in the corresponding product state.44 This crossing point is approximated by the first-order saddle point of a reaction coordinate. Given a canonical ensemble of microstates, for which the number of molecules N, the temperature T, and the volume V are constant, the thermal rate constant k(T) of a reaction from a reactant to a product crossing the corresponding transition state depends on the Helmholtz free energy difference between reactant and transition state, ΔA‡,*, through an exponential function,45
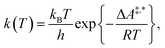 | (1) |
The only quantity we need to determine for the construction of a kinetic model based on conventional TST is the Helmholtz free energy A for all intermediates and transition states contained in a given reaction network. A is determined by the, in our case canonical, partition function Q = Q(N,V,T) through A(T,Q) = −kBT![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln
ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Q, where all energy states of the system of N molecules enter Q.
Q, where all energy states of the system of N molecules enter Q.
The direct evaluation of Q is in general not feasible. However, a well-established procedure exists50 to approximate gas-phase free energies. In the gas phase, Q may be factorized into a product of N molecular partition functions q of N isolated, indistinguishable, and non-interacting molecules, Q = qN/N!. This factorization enables the calculation of A based on an isolated-molecule quantum chemical calculation. A results from the internal energy U and the temperature-weighted entropy S,
| A(T,Q) = U(T,Q) − TS(T,Q). | (2) |
For our set-up and standard state, U can be decomposed into the sum of the temperature-independent electronic energy, Eelec, the zero-point vibrational energy, ZPE, and remaining thermal contributions to the internal energy Urest(T,Q),
| A(T,Q) = NAEelec + NAZPE + Urest(T,Q) − TS(T,Q), | (3) |
The molecular partition function q is usually approximated by a product of electronic (elec), qelec, translational (trans), qtrans, rotational (rot), qrot, and vibrational (vib), qvib, contributions – deliberately neglecting the coupling of the degrees of freedom (such as rovibrational coupling).
For the evaluation of qelec, we may assume that electronically excited states are high in energy and cannot be excited thermally at a given temperature.50 However, for intermediates with small HOMO–LUMO gaps, this may be taken as an indication for a necessary extension of this standard approach. Hence, only spin and orbital or point-group degeneracy needs to be taken into account.
To evaluate qtrans, the particle in a box model is employed to determine the energy states associated with the translation of the center of mass of the molecule in V.50qtrans depends on the mass of the molecule and V. If we neglect the existence of isotopomers, the mass is easily calculated for the most abundant isotopes. Recall that V is the volume for the chosen standard state.
To evaluate qrot, the molecule is treated as a rigid rotor.50 The molecular principal moments of inertia and the symmetry number of the molecule enter qrot. The error introduced by this assumption is severe, for instance, for microsolvated molecules, which feature not only internal rotational degrees of freedom, but also their coupling with the external rotations, i.e., the moments of inertia depend on internal rotational degrees of freedom.51
q vib is usually approximated by all energy eigenvalues of harmonic oscillators that describe the 3m − 6 normal coordinates of an m-atomic non-linear molecule.50 It is well known that the harmonic approximation will break down, if the potential energy surface deviates significantly from the quadratic harmonic potential,50,52–56 for instance, for highly anharmonic modes, which are better described as internal rotations.57 The evaluation of the contribution of these anharmonic frequencies is computationally expensive,58–63 and therefore, not feasible for the exploration of a large reaction network. If, however, reactants and products exhibit similar harmonic vibrational frequencies, error cancellation will occur (see, e.g., ref. 64).
The standard-state free reaction energy in solution, 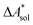 , for a reaction R → P in solution can be obtained as the sum of the standard-state free reaction energy in the gas phase,
, for a reaction R → P in solution can be obtained as the sum of the standard-state free reaction energy in the gas phase, 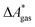 , and the difference of the free energies of solvation of the reagents,
, and the difference of the free energies of solvation of the reagents, 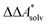 , when employing a thermodynamic cycle as illustrated in Fig. 1.
, when employing a thermodynamic cycle as illustrated in Fig. 1.
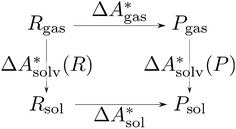 | ||
Fig. 1 Thermodynamic cycle for the calculation of the standard-state Helmholtz free reaction energy 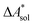 for the reaction R → P in solution (‘sol’) from gas-phase (‘gas’) and solvation (‘solv’) data. for the reaction R → P in solution (‘sol’) from gas-phase (‘gas’) and solvation (‘solv’) data. | ||
Implicit solvation models have been specifically devised to calculate 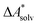 , without modeling the solvent explicitly.65–67 The solute is immersed into a cavity in the continuum leading to parameter-dependent solvent–solute interactions. Implicit solvent models vary in their description of these interactions between the solvent and the solute.66,68–70 The parameters in the implicit solvation models are determined through parametrization to experimental Gibbs free energies of solvation.66 The Gibbs free energy of solvation is taken to be equal to the Helmholtz free energy of solvation,66 which neglects volume changes. This effect was shown to be small for several test cases.71 Here, we assume that all effects associated with the transfer of the molecule from an ideal gas phase to the solution phase are absorbed in
, without modeling the solvent explicitly.65–67 The solute is immersed into a cavity in the continuum leading to parameter-dependent solvent–solute interactions. Implicit solvent models vary in their description of these interactions between the solvent and the solute.66,68–70 The parameters in the implicit solvation models are determined through parametrization to experimental Gibbs free energies of solvation.66 The Gibbs free energy of solvation is taken to be equal to the Helmholtz free energy of solvation,66 which neglects volume changes. This effect was shown to be small for several test cases.71 Here, we assume that all effects associated with the transfer of the molecule from an ideal gas phase to the solution phase are absorbed in 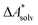 .57,72 This assumption is reasonable for small, rigid molecules, whose structures do not significantly change upon solvation. For such molecules, modern implicit solvation models (e.g., SM12)70 exhibit a mean unsigned error of about 2 kJ mol−1 in comparison to experimental data.70,72 A more pronounced error can be expected for charged species.70,72,73 The error can, however, be reduced when adding explicit solvent molecules and averaging conformationally.74–76
.57,72 This assumption is reasonable for small, rigid molecules, whose structures do not significantly change upon solvation. For such molecules, modern implicit solvation models (e.g., SM12)70 exhibit a mean unsigned error of about 2 kJ mol−1 in comparison to experimental data.70,72 A more pronounced error can be expected for charged species.70,72,73 The error can, however, be reduced when adding explicit solvent molecules and averaging conformationally.74–76
The choice of implicit solvent models limits the choice of possible temperatures, because they are usually parametrized to Gibbs free energies of solvation at ambient temperature.66 The fit to experimental data at one temperature implies that a subdivision of the 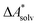 into
into 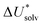 and
and 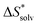 is not possible. Note, however, that Chamberlin et al. introduced a temperature-dependent implicit solvation model, which could expand the range of accessible temperatures.77
is not possible. Note, however, that Chamberlin et al. introduced a temperature-dependent implicit solvation model, which could expand the range of accessible temperatures.77
Furthermore, many popular continuum solvation models assume that thermal equilibrium between solute and solvent is reached instantaneously. This may be inadequate for reactive intermediates.67,78
In this work, a reaction or activation free energy in solution, 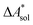 , is obtained from the difference of the electronic energies, ΔEelec, the difference of the zero-point vibrational energies, ΔZPE, the difference of the thermal contributions to the free energy in the gas phase,
, is obtained from the difference of the electronic energies, ΔEelec, the difference of the zero-point vibrational energies, ΔZPE, the difference of the thermal contributions to the free energy in the gas phase, 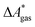 , and the difference of the free energies of solvation,
, and the difference of the free energies of solvation, 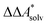 ,
,
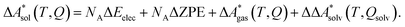 | (4) |
Here, Qsolv is a place holder for the continuum modeling of 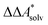 . We highlight the separation of contributions that do not depend on a partition function (ΔEelec, ΔZPE) from those that do depend on it (
. We highlight the separation of contributions that do not depend on a partition function (ΔEelec, ΔZPE) from those that do depend on it (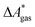 ,
, 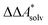 ). Recently, we have demonstrated how the error associated with ΔEelec can be assessed by applying Bayesian statistics79 (see also Section 4). This error may be considered a lower bound for the error of
). Recently, we have demonstrated how the error associated with ΔEelec can be assessed by applying Bayesian statistics79 (see also Section 4). This error may be considered a lower bound for the error of 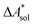 if the error of the other contributions is neglected. For the error estimation of
if the error of the other contributions is neglected. For the error estimation of 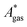 , ZPE, and
, ZPE, and 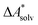 the individual contributions must be investigated.
the individual contributions must be investigated.
The model-inherent errors in Q, which is employed to calculate 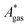 , are difficult to evaluate. We may assume that the error of qvib is dominant. As the harmonic approximation is a severe approximation for low-frequency modes,52–56 the anharmonic qvib is required to assess the effect of this approximation. The application of scaling factors for harmonic frequencies62,80 is, however, not sufficient to obtain a reference anharmonic qvib, because scaling factors neither correct the form of the quadratic harmonic potential nor the equidistance of the energy levels. Recently, procedures were outlined how the full-dimensional potential energy surface can be dissected as a sum of independent one-dimensional potentials for each vibrational mode.53–56 The one-dimensional potentials are sampled along the normal coordinates. The energy levels of the system are obtained by solving the one-dimensional nuclear Schrödinger equations for each mode.53–56 Hence, the deviation of the harmonic ZPE from the anharmonic ZPE is readily obtained. It is then possible to assess the error of the harmonic qvib by comparison with the anharmonic qvib obtained by explicit summation over all vibrational modes. This error can be considered a lower bound for the error of
, are difficult to evaluate. We may assume that the error of qvib is dominant. As the harmonic approximation is a severe approximation for low-frequency modes,52–56 the anharmonic qvib is required to assess the effect of this approximation. The application of scaling factors for harmonic frequencies62,80 is, however, not sufficient to obtain a reference anharmonic qvib, because scaling factors neither correct the form of the quadratic harmonic potential nor the equidistance of the energy levels. Recently, procedures were outlined how the full-dimensional potential energy surface can be dissected as a sum of independent one-dimensional potentials for each vibrational mode.53–56 The one-dimensional potentials are sampled along the normal coordinates. The energy levels of the system are obtained by solving the one-dimensional nuclear Schrödinger equations for each mode.53–56 Hence, the deviation of the harmonic ZPE from the anharmonic ZPE is readily obtained. It is then possible to assess the error of the harmonic qvib by comparison with the anharmonic qvib obtained by explicit summation over all vibrational modes. This error can be considered a lower bound for the error of 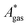 since mode–mode coupling effects and errors due to the approximations in qtrans and qrot are not taken into account.
since mode–mode coupling effects and errors due to the approximations in qtrans and qrot are not taken into account.
Accurate, theoretical reference data are difficult to obtain for 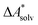 .66,81 Alternatively, the error of
.66,81 Alternatively, the error of 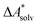 can be estimated by comparison to available experimental data for benchmark sets (e.g., the Minnesota Solvation Database82), assuming transferability.
can be estimated by comparison to available experimental data for benchmark sets (e.g., the Minnesota Solvation Database82), assuming transferability.
4 Error estimation for electronic energy differences
Despite its shortcomings with respect to accuracy and systematic improvability, density functional theory (DFT) is the first-principles approach of choice for truly extensive explorations of vast reaction networks. Results obtained from different popular density functionals may, however, significantly deviate from experimental data in a rather irregular manner.83,84 If, however, one could estimate the error of each computational result, one could assess whether conclusions drawn from the data are reliable.In general, it is difficult to predict the error of density functional calculations.83 To overcome this issue, Jacobsen, Sethna, Nørskov, and co-workers devised a scheme for systematic error estimation of DFT results based on non-hybrid density functionals.85–88 By generating an ensemble of exchange–correlation functionals, a mean and a variance could be assigned to each result (see also ref. 89 and 90).
Based on the work of Jacobsen, Sethna, Nørskov, we developed a novel approach for the construction of reliable density functionals with Bayesian error estimation capabilities.79 Our ansatz was tailored to overcome the transferability problem by relying on system-focused reference data and to exploit the better accuracy of hybrid functionals.
Instead of considering only the best-fit parameter (as commonly done with standard exchange–correlation functionals), we assign a conditional probability distribution to a linear parameter a in the exchange–correlation functional,
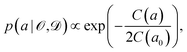 | (5) |
![[scr O, script letter O]](https://www.rsc.org/images/entities/char_e52e.gif) is some observable (typically an energy contribution),
is some observable (typically an energy contribution), ![[scr D, script letter D]](https://www.rsc.org/images/entities/char_e523.gif) is some data set containing (computational or experimental) reference results, C denotes a cost function quadratic in a, and a0 is the parameter value that minimizes C. In practice, this distribution needs to be sampled,
is some data set containing (computational or experimental) reference results, C denotes a cost function quadratic in a, and a0 is the parameter value that minimizes C. In practice, this distribution needs to be sampled,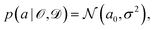 | (6) |
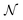 is a Gaussian distribution with mean a0 and variance σ2 = 2C(a0)/(∂2C(a)/∂a2|a0) (for a detailed derivation see ref. 79). With the set of NBEE parameters generated with eqn (6),
is a Gaussian distribution with mean a0 and variance σ2 = 2C(a0)/(∂2C(a)/∂a2|a0) (for a detailed derivation see ref. 79). With the set of NBEE parameters generated with eqn (6), ![[a with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0061_20d1.gif) = {a1,a2,…,aNBEE}, an error estimate σ for the observable
= {a1,a2,…,aNBEE}, an error estimate σ for the observable ![[scr O, script letter O]](https://www.rsc.org/images/entities/char_e52e.gif) (e.g., an activation energy) can be calculated,
(e.g., an activation energy) can be calculated,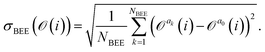 | (7) |
By a system-focused reparametrization of LC-PBE0, the long-range corrected (LC) version of the density functional PBE0,91–93 we were able to reliably estimate errors of calculated reaction energies.79 Hereinafter, we refer to such a functional as LC*-PBE0 in order to emphasize that the original parameters were modified (in this work according to data related to the formose reaction). In our previous study,79 we concluded that four parameters in this exchange–correlation functional need to be modified to achieve accurate relative energies and reliable error estimates for a specific chemical system.
For an accurate reparametrization, the reference dataset ![[scr D, script letter D]](https://www.rsc.org/images/entities/char_e523.gif) needs to be representative for the system to be studied. In this study,
needs to be representative for the system to be studied. In this study, ![[scr D, script letter D]](https://www.rsc.org/images/entities/char_e523.gif) contains structures of intermediates and transition states of the formose reaction. Specifically,
contains structures of intermediates and transition states of the formose reaction. Specifically, ![[scr D, script letter D]](https://www.rsc.org/images/entities/char_e523.gif) = {(Ai,Bi)} consists of pairs of structures on the same potential energy surface, i.e., structures with the same number and type of atomic nuclei, the same number of electrons, and the same electronic spin state. Then, the electronic energy difference ΔEelec,i = Eelec(Bi) − Eelec(Ai) between the two structures Ai and Bi of data set entry i defines the cost function C,
= {(Ai,Bi)} consists of pairs of structures on the same potential energy surface, i.e., structures with the same number and type of atomic nuclei, the same number of electrons, and the same electronic spin state. Then, the electronic energy difference ΔEelec,i = Eelec(Bi) − Eelec(Ai) between the two structures Ai and Bi of data set entry i defines the cost function C,
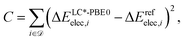 | (8) |
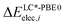 and
and 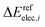 are the relative energies obtained with the LC*-PBE0 functional and the reference method, respectively. In this study, electronic energies from the DF-LCCSD(T0)-F12 method are chosen as reference. For further details, Cartesian coordinates, and the reference electronic energies in
are the relative energies obtained with the LC*-PBE0 functional and the reference method, respectively. In this study, electronic energies from the DF-LCCSD(T0)-F12 method are chosen as reference. For further details, Cartesian coordinates, and the reference electronic energies in ![[scr D, script letter D]](https://www.rsc.org/images/entities/char_e523.gif) , see the ESI.†
, see the ESI.†
To assess the transferability of the reparametrized functional, the dataset ![[scr D, script letter D]](https://www.rsc.org/images/entities/char_e523.gif) was arbitrarily split into a training set and a test set with 25 and 17 entries, respectively. By minimizing C with respect to the training set with the L-BFGS-B algorithm,94 a new set of parameter values for the LC*-PBE0 functional was obtained (see ESI†).
was arbitrarily split into a training set and a test set with 25 and 17 entries, respectively. By minimizing C with respect to the training set with the L-BFGS-B algorithm,94 a new set of parameter values for the LC*-PBE0 functional was obtained (see ESI†).
In Tables 1 and 2, the accuracy of LC*-PBE0 (in comparison to standard functionals) with respect to the training set and test set is given. It can be seen that LC*-PBE0 is significantly more accurate than most standard functionals considered here. The optimized parameters of LC*-PBE0 are close to those of PBE0 (see ESI†), which explains why the functionals are of similar accuracy. Due to its additional parameters, and therefore, higher flexibility LC-PBE0 was chosen over PBE0 for the re-parametrization. Nonetheless, with a largest absolute deviation between 8–10 kJ mol−1, it is clear that error estimation is still necessary.
| LAD | MAD | MSD | |
|---|---|---|---|
| B3LYP | 18.7 | 7.6 | 1.7 |
| B3LYP-D3 | 22.2 | 7.0 | 1.6 |
| BP86 | 28.5 | 7.3 | 1.8 |
| BP86-D3 | 32.6 | 6.5 | 1.7 |
| LC-PBE0 | 37.2 | 13.6 | 0.7 |
| M06-2X | 20.9 | 7.5 | 1.2 |
| M06-2X-D3 | 20.8 | 7.4 | 1.2 |
| M06-L | 19.4 | 9.6 | 2.1 |
| M06-L-D3 | 19.5 | 9.6 | 2.1 |
| PBE | 28.8 | 6.2 | 1.6 |
| PBE0 | 13.5 | 5.7 | 1.2 |
| PBE0-D3 | 16.3 | 5.2 | 1.2 |
| TPSS | 37.3 | 14.3 | 3.4 |
| TPSS-D3 | 33.2 | 13.9 | 3.3 |
| TPSSh | 32.3 | 13.6 | 3.0 |
| TPSSh-D3 | 29.2 | 13.1 | 2.9 |
| LC*-PBE0 | 9.8 | 3.7 | 1.0 |
| LAD | MAD | MSD | |
|---|---|---|---|
| B3LYP | 14.7 | 6.0 | −0.1 |
| B3LYP-D3 | 20.0 | 6.4 | 0.8 |
| BP86 | 19.6 | 6.7 | 0.4 |
| BP86-D3 | 25.0 | 7.8 | 1.5 |
| LC-PBE0 | 27.5 | 8.4 | −1.1 |
| M06-2X | 12.0 | 4.7 | −0.1 |
| M06-2X-D3 | 12.0 | 4.7 | −0.1 |
| M06-L | 20.0 | 7.5 | 1.5 |
| M06-L-D3 | 20.3 | 7.6 | 1.5 |
| PBE | 19.9 | 6.4 | 0.7 |
| PBE0 | 11.9 | 4.0 | −0.1 |
| PBE0-D3 | 14.7 | 4.0 | 0.5 |
| TPSS | 16.6 | 6.4 | −1.0 |
| TPSS-D3 | 17.6 | 7.4 | −0.3 |
| TPSSh | 15.0 | 5.4 | −1.2 |
| TPSSh-D3 | 15.4 | 6.2 | −0.4 |
| LC*-PBE0 | 8.0 | 2.7 | 0.1 |
In Fig. 2 and 3, LC*-PBE0 (with ±σ error bars, calculated from an ensemble of NBEE = 50 functionals as described in the ESI†) is compared to contemporary density functionals with respect to the training set and test set, respectively.
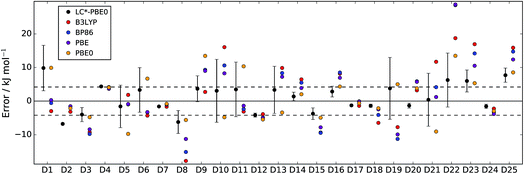 | ||
| Fig. 2 Errors of LC*-PBE0 (with error bars indicating ±σ) and several standard functionals with respect to the training set (D1–D25). The dashed lines indicate an error of ±4.2 kJ mol−1. | ||
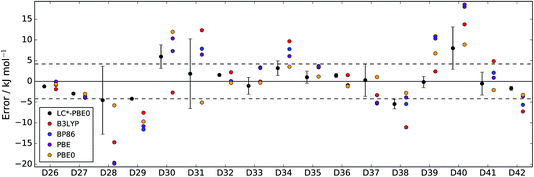 | ||
| Fig. 3 Errors of LC*-PBE0 (with error bars indicating ±σ) and several standard functionals with respect to the test set (D26–D42). The dashed lines indicate an error of ±4.2 kJ mol−1. | ||
For both data sets, we observe that the error is at least within ±4.2 kJ mol−1 (≈1 kcal mol−1), unless the error estimate reported by the functional indicates otherwise (i.e., σ > 4.2 kJ mol−1). While there are relative energies for which the errors are underestimated (D2, D4, and D25 in the training set and D30 and D38 in the test set), considering the diversity of this reference set and the error of some standard functionals (see also Tables 1 and 2), the accuracy of the error estimation is satisfactory.
5 Kinetic modeling
For the construction of an elementary kinetic model, free activation energies from first-principles calculations are required as explained above. From the rate constants calculated by eqn (1), differential equations describing the time propagation of population densities of all chemical species can be constructed. By integrating these differential equations, the underlying chemical process can be modeled.Since differential equations describing chemical processes are generally coupled, analytical integration becomes rapidly impossible. Therefore, numerical integration is the standard method of choice. However, given that reaction networks may be arbitrarily large and entangled, numerical integration may become inefficient,95 especially if the underlying process spans multiple time scales. For this purpose, a variety of approaches were designed focusing on the simplification of kinetic models.96
5.1 Network structure and properties
We describe the structure of a reaction network by a graph of n vertices and 2l edges. As we assume every chemical transformation to be reversible (we refer to such a reversible elementary process as reaction pair), the graph is strictly bidirectional, which explains the enforced even number of edges. Either of both edges corresponding to a reaction pair is assigned an arbitrary but unique direction (forward or backward). This feature is exploited for the construction of the stoichiometry matrix S. It is of dimension n × l and contains information on how many particles Sij of the i-th species are consumed or formed in the j-th elementary reaction, i.e., Sij is negative if the i-th species is consumed in the forward direction, and positive if the i-th species is formed in the forward direction.We assign time-dependent population densities yi(t) with i ∈ {1,…, n} (here: molar concentrations) to the vertices, and rate constants kforwardj and kbackwardj with j ∈ {1,…, l} to the edges. Assuming detailed balance, the rate of a reaction pair fj reads
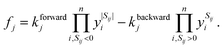 | (9) |
Note that we only consider chemical reactions with a molecularity smaller than or equal to 2. We consider this to be a good assumption for solution chemistry as long as solvent–solvent reactions are unlikely to occur (e.g., for the formose reaction in pure formaldehyde, a trimolecular reaction of formaldehyde to 1,3,5-trioxane could be feasible37).
5.2 Simplification of kinetic models
It is straightforward to deduce a kinetic model from the given network structure and properties. Given the n × l stoichiometry matrix S and the l × 1 reaction pair vector f = {fj} according to eqn (9), the n × 1 rate vector g can be constructed, which represents the first derivative of the concentration vector y with respect to time,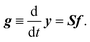 | (10) |
Our objective is to integrate this kinetic model such that concentration trajectories are obtained from the initial conditions (feed of reactants, temperature) up to thermodynamic equilibrium.
For the development of our kinetic simulation algorithm, we were inspired by two such simplification approaches, namely Markov State Models (MSMs)97,98 and Computational Singular Perturbation (CSP).99,100 MSMs were developed for molecular dynamics simulations, where the phase space is decomposed into microstates such that a formerly continuous trajectory becomes a jump process, which is no longer Markovian (memoryless). Since local information is lost in a discrete phase space, the decomposition is chosen such that transitions within a microstate are much more likely to occur than transitions between microstates. This way, rapid convergence to local equilibrium can be assumed for these microstates, which recovers Markovianity. As a consequence, a kinetic model can be constructed from these discrete microstates by counting transitions between them. The microstates may in turn form macrostates (kinetic clusters) for which transitions are much more likely to occur than transitions between them. These clusters can be determined by studying the eigenvalues λi of the n × n rate matrix K = {Kij}.101 Its elements Kij are a measure of the rate for a transition from the j-th to the i-th microstate. In the case of linear kinetic models (first-order reactions only) as studied in MSMs, the rate matrix K is time-invariant and equals the Jacobian J = {Jij},
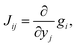 | (11) |
The time scale τi corresponding to the process described by the i-th eigenvalue is inversely related to the modulus of that eigenvalue,
| τi = |λi|−1, | (12) |
| g = gfast + gslow. | (13) |
With this decomposition at hand, it is possible to dissipate the fast processes applying a small time step τfast in the numerical integration until gfast ≈ 0. Subsequently, the slow processes can be modeled from the updated initial conditions applying a much larger time step τslow. Clearly, the larger the demanded spectral gap, the smaller the error introduced by assuming decoupling of fast and slow processes.
Since the Jacobian is time-invariant in the case of linear kinetic models, the time-scale separation is also invariant in the course of the global reaction process and needs to be examined only once. However, in non-linear kinetic models (as studied here), the Jacobian is a function of time due to the inclusion of concentrations of reaction partners.96 This poses a challenge to the time-scale separation as now a steady examination of the time gap is necessary to ensure valid decoupling of fast and slow processes.
One of the most robust approaches in this respect is CSP.102 The basis of CSP is the assumption that the concentration trajectory of a chemical process is rapidly attracted onto a slow invariant manifold Ω,99 which is an (n − m)-dimensional hypersurface in concentration space, where n denotes the number of species and m denotes the number of fast time scales. Consequently, τm and τm+1 are the time scales of the slowest of the m fast processes and of the fastest of the (n − m) slow processes, respectively. Two subspaces, the m-dimensional subspace of fast processes and the (n − m)-dimensional subspace of slow processes, are introduced, which are spanned by m n-dimensional (column) basis vectors ai (j ∈ 1,…, m) and (n − m) n-dimensional (column) basis vectors aj (j ∈ m + 1,⋯, n), respectively. Furthermore, a set of n-dimensional dual (row) basis vectors bp (p ∈1,⋯, n) is employed, which fulfill the condition bpaq = δpq, where δpq is the Kronecker delta. The decomposition ansatz for the rate vector reads
| gfast = [a1,…,am][b1,…,bm]g, | (14) |
| gslow = [am+1,…,an][bm+1,…,bn]g. | (15) |
CSP approximates the basis vectors bp and aq by an iterative refinement procedure, where each refinement introduces an accuracy increase.100 The refinement procedure requires the time derivatives of the basis vectors.99 Therefore, computational savings due to the time-scale separation may be lost by iteratively determining the basis vectors after each time step.96 However, the first refinement does not involve time derivatives and already guarantees numerical stability of the simplified model.100
5.3 Kinetic simulation algorithm
To continuously determine slow and fast processes in a rolling fashion, we study the eigenvalues of the Jacobian. Given a predefined time-gap criterion ε (0 < ε ≪ 1), we start from the second-smallest modulus of the eigenvalues, |λn−1|, and compare it to the next higher modulus, |λn−2|. If |λn−1|/|λn−2| ≥ ε, we continue by increasing each index by one. If |λi|/|λi−1| ≥ ε for all i ∈ {2,…, n − 1}, our time-gap criterion is not fulfilled and we cannot determine a spectral gap. Otherwise, the first eigenvalue pair fulfilling the condition |λi|/|λi−1| < ε sets the number of fast time scales, m = i − 1.Typically, the left and right eigenvectors of the Jacobian are chosen as an approximation for the basis vectors bp and aq, respectively, according to the CSP formalism. This approximation corresponds to the first refinement of the CSP basis vectors.95 It follows that the eigenvalues of the Jacobian can be obtained from our choice of CSP basis vectors,
| λi = biJai. | (16) |
Here, we follow an alternative approach to determine which one of the l reaction pairs contributes to the fast processes. We consider the largest modulus of eigenvalues of each of the l sub-Jacobians corresponding to the isolated reaction pairs. If a dominant modulus is larger than |λm+1|/ε (λm+1 is associated with the Jacobian of the entire reaction system), the reaction pair connected to it will contribute to the fast processes. The idea behind this approach is that an eigenvalue corresponding to the entire kinetic model is approximately the sum of the eigenvalues of sub-Jacobians with similar or smaller moduli.95 With this approach, we introduce the assumption that a reaction pair is either included in or excluded from the fast processes, which certainly is a simplification that requires careful investigation.
Next, we propagate the fast sub-network (i.e., the sub-network containing only those edges corresponding to fast reaction pairs) to local equilibrium. The stationary distribution can be determined through a non-linear optimization algorithm103 or analytically for simpler networks. Due to the time-scale separation, it is assumed that this process occurs immediately, i.e., it is not resolved in the course of the kinetic simulation.
Then, the actual simulation starts. The partially equilibrated concentration vector ypeq(t) is propagated according to the time scale τ1,slow, which corresponds to the fastest process of the Jacobian of the slow sub-network (i.e., the sub-network containing only those edges corresponding to slow reaction pairs). The update of the concentration vector reads
| y(t + τ1,slow) = ypeq(t) + g(t)τ1,slow. | (17) |
After that, the Jacobian of the entire network is decomposed again to determine the fast and slow processes for the next time step.
Our kinetic simulation algorithm can be summarized as follows:
(1) Determine the number of fast time scales m by spectral decomposition of the Jacobian corresponding to the kinetic model under consideration.
(2) Identify a reaction pair as a fast one if the largest modulus of eigenvalues of its sub-Jacobian is larger than |λm+1|/ε.
(3) Propagate the fast sub-network to local equilibrium, y(t) → ypeq(t).
(4) Determine the time step τ1,slow by decomposing the Jacobian of the slow sub-network.
(5) Update the partially equilibrated concentration vector according to eqn (17), ypeq(t) → y(t + τ1,slow).
(6) If global equilibrium is not yet reached, repeat steps 1 to 5; otherwise, stop the simulation.
6 Results and discussion
The formose reaction is an example of a large and highly entangled reaction network. The key challenge of this network is the presence of coupled reactions spanning multiple time scales. In recent work,22 we have shown how such a network can be explored in general. Since the exploration of the formose reaction is beyond the scope of this work, only a sub-network of the formose reaction is investigated here. The structure coordinates are adapted from ref. 37 (see ESI†). The heuristics-guided exploration of the whole formose network is currently being studied in our group.104This sub-network, which already features many conceptual challenges of the entire formose reaction, is shown in Fig. 4. It represents a possible mechanism for the first steps of the formose reaction as described by Kua et al.37 and comprises six chemical species and five reaction pairs (ten elementary reactions Ri). We obtained all free energies in single-point calculations as described in the ESI.† In water, formaldehyde (1) is in equilibrium with its hydrated form, methanediol (2). 1 dimerizes to glycolaldehyde (3), which is a reaction with a high free activation energy (cf.Table 3). The exact mechanism of the dimerization has not been unravelled yet.31–34 From experimental studies it is, however, well known that the dimerization proceeds very slowly. 3 can react with water to 1,1,2-ethanetriol (5). Another possible reaction of 3 is the enolization to 1,2-ethenediol (4). The addition of 1 to 4 yields glyceraldehyde (6). This bimolecular reaction introduces a significant entanglement in the model network. The model network does not capture the autocatalytic nature of the formose reaction, in which 3 can be regenerated autocatalytically from intermediates generated from 6 in subsequent reactions.
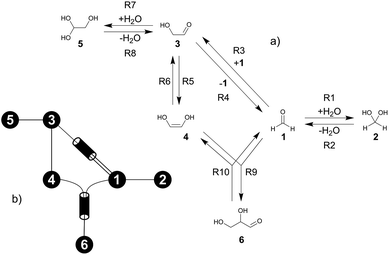 | ||
| Fig. 4 (a) Possible mechanism of the first steps in the formose reaction, (b) abstract graph representation of this reaction sub-network. | ||
| Reactant(s) | Product(s) | ΔA‡,* | k | ||
|---|---|---|---|---|---|
| R1 | 1 | 2 | 95.4 | 4.8 | 6.7 × 10−3 |
| R2 | 2 | 1 | 124.9 | 13.2 | 8.1 × 10−10 |
| R3 | 1 + 1 | 3 | 215.4 | 14.2 | 1.2 × 10−25 |
| R4 | 3 | 1 + 1 | 311.1 | 23.0 | 1.9 × 10−42 |
| R5 | 3 | 4 | 157.3 | 11.6 | 1.7 × 10−15 |
| R6 | 4 | 3 | 130.8 | 10.2 | 7.5 × 10−11 |
| R7 | 3 | 5 | 100.3 | 3.2 | 9.2 × 10−4 |
| R8 | 5 | 3 | 119.2 | 12.3 | 8.0 × 10−9 |
| R9 | 1 + 4 | 6 | 112.5 | 13.4 | 1.2 × 10−7 |
| R10 | 6 | 1 + 4 | 185.4 | 23.1 | 2.0 × 10−20 |
Table 3 presents (standard-state Helmholtz) free activation energies (in solution), ΔA‡,*, calculated according to eqn (4) and the resulting rate constants k (together with error estimates) for the reactions in the model network.
It can be seen that ΔA‡,* is high (above 100 kJ mol−1) for most reactions, and consequently, the reaction rates are small. In addition, most reactions have estimated errors of above 10 kJ mol−1, which reflects the large uncertainty of the respective reaction rates. In Section 4, we showed that the LC*-PBE0 functional provides reliable error estimates above 4.2 kJ mol−1. The estimated error for reaction R7 is below that, and therefore, most likely too small.
For the simulation we selected an absolute temperature of 298.15 K, a 1 M solution of formaldehyde in water as initial feed, and a time-gap criterion of ε = 10−3. For technical details of the kinetic modeling employed here, see the ESI.†
For every set of free activation energies, it was found that all reaction pairs but (R3, R4), the dimerization of formaldehyde (1) to glycolaldehyde (3), contribute to the fast processes. Therefore, only reaction pair (R3, R4) constitutes the slow sub-network (Fig. 5).
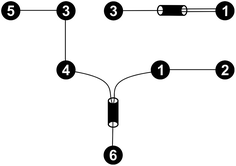 | ||
| Fig. 5 Fast (bottom left) and slow (top right) sub-networks of the reaction network shown in Fig. 4. | ||
The concentration trajectories from the kinetic simulation of the reaction network are shown in Fig. 6. The red curve corresponds to the trajectory obtained from the free activation energies listed in Table 3. The black curves correspond to the trajectories obtained from the free activation energies calculated from the ensemble of density functionals generated by our error estimation scheme according to eqn (6).
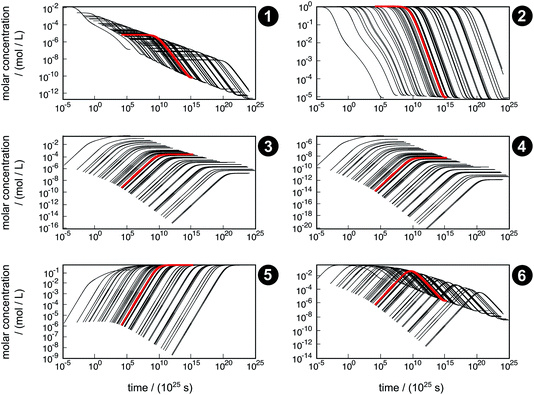 | ||
| Fig. 6 Concentration trajectories with respect to time for chemical species 1–6 according to the reaction network shown in Fig. 4. The trajectories resulting from the free activation energies listed in Table 3 are shown in red. The other trajectories (black) result from the free activation energies calculated from the ensemble of density functionals generated by the error estimation scheme. Note that the time scale of the equilibration process is extremely large, which originates from neglecting relevant intermediates and elementary reactions in our model network. For readability reasons, all plots start after the first global time step τ1,slow, which depends on the sampled free activation energies, and therefore, the onset of the trajectories is different. | ||
The simulated time scale of the global process exceeds the age of the universe in each case. This finding should not be interpreted in absolute terms, but it indicates that the uncatalyzed thermal formose reaction is very unlikely to occur if one starts from formaldehyde (1) alone, provided that the free activation energies and their estimated errors are reliable. It should be noted that glycolaldehyde (3) is autocatalytically regenerated in the formose reaction, which is not considered in our model network. This way, the dimerization of 1 to 3 (reaction R3) can be circumvented, which leads to an acceleration of the overall process not depending on the extremely slow reaction R3.
The concentration trajectories show clearly how sensitive rate constants are to variations in the free activation energies. For instance, the variation in time of the concentration trajectories of methanediol (2) spans almost 23 orders of magnitude (a factor of 8.7 × 1022 at an arbitrarily chosen concentration of y2 = 0.01 mol L−1). Since only reactions R3 and R4 contribute to the time resolution of the chemical process, uncertainties in the corresponding free activation energies need to be responsible for this significant variation. In Table 4, properties of the fastest and slowest concentration trajectories (Fig. 6, species 2, left-most and right-most curves) are compared. For reaction R3, the free activation energy spans a range of about 60 kJ mol−1, and for reaction R4, this range is about 100 kJ mol−1, leading to a deviation in rate constants of about 10 and 17 orders of magnitude, respectively. Taking the concentrations of 1 and 3 (the constituents of reactions R3 and R4) at our arbitrarily chosen concentration of y2 = 0.01 mol L−1 into account, the rates of both reactions can be calculated. For both the fastest and slowest trajectories, reaction R3 is much faster than reaction R4. Therefore, we assume only reaction R3 to be relevant for the kinetic simulation. The reaction time can be roughly estimated by the inverse of the current reaction rate. In our case, the reaction time of the slowest trajectory is higher than that of the fastest trajectory by a factor of 1.4 × 1023, which is quite close to the factor of 8.7 × 1022 determined from the concentration data of 2. Obviously, an error of this magnitude with respect to the free activation energy is far too large to quantify concentration trajectories in terms of absolute time. Moreover, it should be noted that the error introduced by choosing conventional TST to calculate rates is not considered here.
| y 1 | y 3 | r R3 = kR3(y1)2 | r R4 = kR4y3 | |
|---|---|---|---|---|
| Fastest | 1.4 × 10−4 | 2.9 × 10−2 | 9.3 × 10−28 | 6.9 × 10−35 |
| Slowest | 7.4 × 10−11 | 1.5 × 10−7 | 6.5 × 10−51 | 2.5 × 10−57 |
Even though the uncertainty in free activation energies strongly affects absolute time, it does not affect the qualitative flux of concentrations through the network in terms of non-crossing trajectories (Fig. 7). This finding can be explained by the distinct separation of the magnitude of the free activation energies. In Table 4, it can be seen that the free activation energy for reaction R3 in the slowest case is even lower than that for reaction R4 in the fastest case. Furthermore, the free activation energies and their uncertainties listed in Table 3 show that all reaction barriers are well separated from each other, which does not allow for an alternative reaction mechanism. Clearly, for small activation energy differences, such as found in enantioselective organocatalysis, large uncertainties would also lead to qualitatively different results.
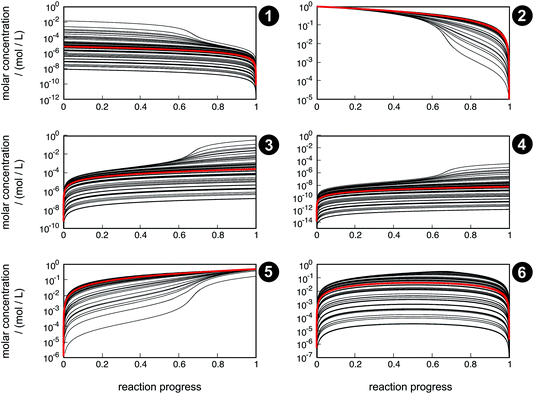 | ||
| Fig. 7 Concentration trajectories with respect to reaction progress for chemical species 1–6 according to the reaction network shown in Fig. 4. The trajectories resulting from the free activation energies listed in Table 3 are shown in red. The other trajectories (black) result from the free activation energies calculated from the ensemble of density functionals generated by the error estimation scheme. Contrary to Fig. 6, here, the trajectories are laid on top of each other. | ||
Qualitative validity of the kinetic simulation is also underlined by the fact that in all cases, 1,1,2-ethanetriol (5) is the main product at chemical equilibrium. The population dominance of 5 over 3 was also found experimentally by Kua et al.105 However, their calculated Gibbs free activation energies for the corresponding reaction pair (R7, R8)37 (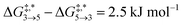 ) are very similar to each other. Their Gibbs free activation energies can be directly compared to our Helmholtz free activation energies, because volume changes are neglected. Our free activation energies for the reaction pair (R7, R8) differ significantly from each other on average (
) are very similar to each other. Their Gibbs free activation energies can be directly compared to our Helmholtz free activation energies, because volume changes are neglected. Our free activation energies for the reaction pair (R7, R8) differ significantly from each other on average (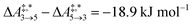 ). A reason for the observed difference is the choice of computational methods for the calculations (e.g., different density functional and solvation model). It might seem surprising that 5 is the main product in our simulation even though glyceraldehyde (6) is a thermodynamic sink. However, one should keep in mind that the concentration trajectory of 6 is temporarily significantly populated. To understand this finding, we need to discriminate between fast and slow processes (Fig. 5).
). A reason for the observed difference is the choice of computational methods for the calculations (e.g., different density functional and solvation model). It might seem surprising that 5 is the main product in our simulation even though glyceraldehyde (6) is a thermodynamic sink. However, one should keep in mind that the concentration trajectory of 6 is temporarily significantly populated. To understand this finding, we need to discriminate between fast and slow processes (Fig. 5).
Considering the fast sub-network (Fig. 5), we understand that there are two unconnected channels to form 6, i.e., (1, 2) and (3, 4, 5). This picture is equivalent to reaction A + B ⇌ C, where the initial concentration difference between A and B is conserved over the course of the reaction. It follows that
| Δ ≡ (y1 + y2) − (y3 + y4 + y5) | (18) |
Another feature of the conservation of Δ is that the kinetic model can be reduced to a single differential equation (see the ESI† for more details). This differential equation can be easily integrated by any conventional numeric solver. Here, we chose the standard fourth-order Runge–Kutta algorithm. We compared the result to that of our CSP-type method, where we employ an explicit Euler algorithm according to eqn (17), which is the simplest ansatz for numerical integration and known to be unstable due to the lack of an inherent time step selection. However, our CSP-type method provides the time step for the explicit Euler algorithm by continuously analyzing the Jacobian. We emphasize that both approaches to model the kinetics of the network (CSP/Euler vs. Runge–Kutta) yield identical results.
7 Conclusions
We established a robust protocol that combines electronic structure calculations and kinetic simulations for the accurate description of a complex kinetic network by studying stationary points across multiple potential energy surfaces. Employing a simplified model network, we highlighted and discussed the challenges of kinetic studies on complex chemical networks such as the formose reaction. We showed by employing a time-scale separation approach based on Computational Singular Perturbation99,100 how the frequently occuring stiffness (rare-event problem) in kinetic simulations can be circumvented. As a consequence, we were able to propagate uncertainties in the free activation energies through the complete kinetic simulation up to global equilibrium. Since the rate constants depend on free activation energies ΔA‡,* (in a canonical ensemble) through an exponential function, errors in ΔA‡,* strongly affect the kinetic simulation. Therefore, error estimates for ΔA‡,* are decisive for drawing meaningful conclusions from a kinetic analysis. While reliable error estimates for electronic energies can be obtained by Bayesian statistics as shown in Section 4, errors on other contributions of ΔA‡,* have not been accounted for in a systematic way yet. We proposed a strategy to also obtain error estimates for these contributions, but defer their analysis to future work. To improve the accuracy of the kinetic simulation, elementary steps with large error estimates need to be subjected to highly accurate quantum chemical calculations such as those reported in ref. 106.Then, the heuristics-guided exploration established for protonation reactions in a previous study22 needs to be extended to enable the exploration of chemical systems such as the formose reaction,104 which will facilitate a fully automated exploration and analysis of the formose reaction.
Acknowledgements
This work was supported by the Schweizerischer Nationalfonds and a TH grant of ETH Zurich (grant number: ETH-20 15-1). GNS thanks the Fonds der Chemischen Industrie for a PhD fellowship.References
- C. Masters, Homogeneous Transition-metal Catalysis, Springer Netherlands, Dordrecht, 1981 Search PubMed.
- R. Vinu and L. J. Broadbelt, Annu. Rev. Chem. Biomol. Eng., 2012, 3, 29–54 CrossRef CAS PubMed.
- J. Ross, J. Phys. Chem. A, 2008, 112, 2134–2143 CrossRef CAS PubMed.
- L. Vereecken, D. R. Glowacki and M. J. Pilling, Chem. Rev., 2015, 115, 4063–4114 CrossRef CAS PubMed.
- R. F. Ludlow and S. Otto, Chem. Soc. Rev., 2008, 37, 101–108 RSC.
- P. G. Bolhuis, D. Chandler, C. Dellago and P. L. Geissler, Annu. Rev. Phys. Chem., 2002, 53, 291–318 CrossRef CAS PubMed.
- C. Dellago and P. G. Bolhuis, Top. Curr. Chem., 2007, 268, 291–317 CrossRef CAS.
- L. J. Broadbelt and J. Pfaendtner, AIChE J., 2005, 51, 2112–2121 CrossRef CAS.
- C. Shang and Z.-P. Liu, J. Chem. Theory Comput., 2013, 9, 1838–1845 CrossRef CAS PubMed.
- A. M. Saitta and F. Saija, Proc. Natl. Acad. Sci. U. S. A., 2014, 111, 13768–13773 CrossRef CAS PubMed.
- L.-P. Wang, A. Titov, R. McGibbon, F. Liu, V. S. Pande and T. J. Martínez, Nat. Chem., 2014, 6, 1044–1048 CrossRef CAS PubMed.
- X.-J. Zhang and Z.-P. Liu, Phys. Chem. Chem. Phys., 2015, 17, 2757–2769 RSC.
- M. Döntgen, M.-D. Przybylski-Freund, L. C. Kröger, W. A. Kopp, A. E. Ismail and K. Leonhard, J. Chem. Theory Comput., 2015, 11, 2517–2524 CrossRef PubMed.
- E. Martínez-Núñez, J. Comput. Chem., 2015, 36, 222–234 CrossRef PubMed.
- E. Martínez-Núñez, Phys. Chem. Chem. Phys., 2015, 17, 14912–14921 RSC.
- S. Habershon, J. Chem. Phys., 2015, 143, 094106 CrossRef PubMed.
- S. Habershon, J. Chem. Theory Comput., 2016, 12, 1786–1798 CrossRef CAS PubMed.
- P. M. Zimmerman, J. Comput. Chem., 2013, 34, 1385–1392 CrossRef CAS PubMed.
- P. M. Zimmerman, Mol. Simul., 2015, 41, 43–54 CrossRef CAS.
- D. Rappoport, C. J. Galvin, D. Y. Zubarev and A. Aspuru-Guzik, J. Chem. Theory Comput., 2014, 10, 897–907 CrossRef CAS PubMed.
- D. Y. Zubarev, D. Rappoport and A. Aspuru-Guzik, Sci. Rep., 2015, 5, 1–7 Search PubMed.
- M. Bergeler, G. N. Simm, J. Proppe and M. Reiher, J. Chem. Theory Comput., 2015, 11, 5712–5722 CrossRef CAS PubMed.
- J. E. Sutton, W. Guo, M. A. Katsoulakis and D. G. Vlachos, Nat. Chem., 2016, 8, 331–337 CrossRef CAS PubMed.
- A. Butlerow, Justus Liebigs Ann. Chem., 1861, 120, 295–298 CrossRef.
- I. V. Delidovich, A. N. Simonov, O. P. Taran and V. N. Parmon, ChemSusChem, 2014, 7, 1833–1846 CrossRef CAS PubMed.
- T. Zweckmair, S. Böhmdorfer, A. Bogolitsyna, T. Rosenau, A. Potthast and S. Novalin, J. Chromatogr. Sci., 2014, 52, 169–175 CAS.
- P. Decker, H. Schweer and R. Pohlamnn, J. Chromatogr. A, 1982, 244, 281–291 CrossRef CAS.
- K. Ruiz-Mirazo, C. Briones and A. de la Escosura, Chem. Rev., 2014, 114, 285–366 CrossRef CAS PubMed.
- L. Orgel, Crit. Rev. Biochem. Mol. Biol., 2004, 39, 99–123 CrossRef CAS PubMed.
- A. G. Cairns-Smith and G. L. Walker, BioSystems, 1974, 5, 173–186 CrossRef CAS.
- R. F. Socha, A. H. Weiss and M. M. Sakharov, React. Kinet. Catal. Lett., 1980, 14, 119–128 CrossRef CAS.
- A. W. Schwartz and R. M. de Graaf, J. Mol. Evol., 1993, 36, 101–106 CrossRef CAS.
- E. C. C. Baly, Ind. Eng. Chem., 1924, 16, 1016–1018 CrossRef.
- C. Meinert, I. Myrgorodska, P. de Marcellus, T. Buhse, L. Nahon, S. V. Hoffmann, L. L. S. d’Hendecourt and U. J. Meierhenrich, Science, 2016, 352, 208–212 CrossRef CAS PubMed.
- R. Breslow, Tetrahedron Lett., 1959, 1, 22–26 CrossRef.
- A. J. Bissette and S. P. Fletcher, Angew. Chem., Int. Ed., 2013, 52, 12800–12826 CrossRef CAS PubMed.
- J. Kua, J. E. Avila, C. G. Lee and W. D. Smith, J. Phys. Chem. A, 2013, 117, 12658–12667 CrossRef CAS PubMed.
- A. Ricardo, F. Frye, M. A. Carrigan, J. D. Tipton, D. H. Powell and S. A. Benner, J. Org. Chem., 2006, 71, 9503–9505 CrossRef CAS PubMed.
- C. Appayee and R. Breslow, J. Am. Chem. Soc., 2014, 136, 3720–3723 CrossRef CAS PubMed.
- L. Cheng, C. Doubleday and R. Breslow, Proc. Natl. Acad. Sci. U. S. A., 2015, 112, 4218–4220 CrossRef CAS PubMed.
- R. Breslow, V. Ramalingam and C. Appayee, Origins Life Evol. Biospheres, 2013, 43, 323–329 CrossRef PubMed.
- J. E. Hein and D. G. Blackmond, Acc. Chem. Res., 2012, 45, 2045–2054 CrossRef CAS PubMed.
- J. B. Lambert, S. A. Gurusamy-Thangavelu and K. Ma, Science, 2010, 327, 984–986 CrossRef CAS PubMed.
- D. G. Truhlar, B. C. Garrett and S. J. Klippenstein, J. Phys. Chem., 1996, 100, 12771–12800 CrossRef CAS.
- E. Pollak and P. Talkner, Chaos, 2005, 15, 026116 CrossRef PubMed.
- B. C. Garrett and D. G. Truhlar, Theory and Applications of Computational Chemistry, Elsevier, Amsterdam, 2005, pp. 67–87 Search PubMed.
- W. H. Miller, Acc. Chem. Res., 1993, 26, 174–181 CrossRef CAS.
- M. H. M. Olsson, J. Mavri and A. Warshel, Philos. Trans. R. Soc. London, Ser. B, 2006, 361, 1417–1432 CrossRef CAS PubMed.
- D. R. Glowacki, J. N. Harvey and A. J. Mulholland, Nat. Chem., 2012, 4, 169–176 CrossRef CAS PubMed.
- D. A. McQuarrie, Statistical Mechanics, University Science Books, 2000 Search PubMed.
- D. R. Glowacki, C.-H. Liang, C. Morley, M. J. Pilling and S. H. Robertson, J. Phys. Chem. A, 2012, 116, 9545–9560 CrossRef CAS PubMed.
- P. Y. Ayala and H. B. Schlegel, J. Chem. Phys., 1998, 108, 2314–2325 CrossRef CAS.
- G. Piccini, M. Alessio, J. Sauer, Y. Zhi, Y. Liu, R. Kolvenbach, A. Jentys and J. A. Lercher, J. Phys. Chem. C, 2015, 119, 6128–6137 CAS.
- G. Piccini and J. Sauer, J. Chem. Theory Comput., 2014, 10, 2479–2487 CrossRef CAS PubMed.
- G. Piccini and J. Sauer, J. Chem. Theory Comput., 2013, 9, 5038–5045 CrossRef CAS PubMed.
- Y.-P. Li, A. T. Bell and M. Head-Gordon, J. Chem. Theory Comput., 2016, 12, 2861–2870 CrossRef CAS PubMed.
- R. F. Ribeiro, A. V. Marenich, C. J. Cramer and D. G. Truhlar, J. Phys. Chem. B, 2011, 115, 14556–14562 CrossRef CAS PubMed.
- N. Matsunaga, G. M. Chaban and R. B. Gerber, J. Chem. Phys., 2002, 117, 3541–3547 CrossRef CAS.
- V. Barone, J. Chem. Phys., 2005, 122, 014108 CrossRef PubMed.
- O. Christiansen, Phys. Chem. Chem. Phys., 2007, 9, 2942–2953 RSC.
- P. Daněček, J. Kapitán, V. Baumruk, L. Bednárová, V. Kopecký Jr. and P. Bouř, J. Chem. Phys., 2007, 126, 224513 CrossRef PubMed.
- J. Neugebauer and B. A. Hess, J. Chem. Phys., 2003, 118, 7215–7225 CrossRef CAS.
- P. T. Panek and C. R. Jacob, ChemPhysChem, 2014, 15, 3365–3377 CrossRef CAS PubMed.
- G. Brehm, M. Reiher and S. Schneider, J. Phys. Chem. A, 2002, 106, 12024–12034 CrossRef CAS.
- B. Mennucci, WIREs Comput. Mol. Sci., 2012, 2, 386–404 CrossRef CAS.
- J. Tomasi, B. Mennucci and R. Cammi, Chem. Rev., 2005, 105, 2999–3094 CrossRef CAS PubMed.
- C. J. Cramer and D. G. Truhlar, Chem. Rev., 1999, 99, 2161–2200 CrossRef CAS PubMed.
- S. Miertuš, E. Scrocco and J. Tomasi, Chem. Phys., 1981, 55, 117–129 CrossRef.
- A. Klamt and G. Schüürmann, J. Chem. Soc., Perkin Trans. 1, 1993, 799–805 RSC.
- A. V. Marenich, C. J. Cramer and D. G. Truhlar, J. Chem. Theory Comput., 2013, 9, 609–620 CrossRef CAS PubMed.
- A. Ben-Naim, Statistical Thermodynamics for Chemists and Biochemists, Springer Science & Business Media, 2013 Search PubMed.
- J. Ho, A. Klamt and M. L. Coote, J. Phys. Chem. A, 2010, 114, 13442–13444 CrossRef CAS PubMed.
- Y. Takano and K. N. Houk, J. Chem. Theory Comput., 2005, 1, 70–77 CrossRef PubMed.
- C. P. Kelly, C. J. Cramer and D. G. Truhlar, J. Phys. Chem. A, 2006, 110, 2493–2499 CrossRef CAS PubMed.
- A. V. Marenich, W. Ding, C. J. Cramer and D. G. Truhlar, J. Phys. Chem. Lett., 2012, 3, 1437–1442 CrossRef CAS PubMed.
- J. Ho and M. Z. Ertem, J. Phys. Chem. B, 2016, 120, 1319–1329 CrossRef CAS PubMed.
- A. C. Chamberlin, C. J. Cramer and D. G. Truhlar, J. Phys. Chem. B, 2006, 110, 5665–5675 CrossRef CAS PubMed.
- B. K. Carpenter, J. N. Harvey and A. J. Orr-Ewing, J. Am. Chem. Soc., 2016, 138, 4695–4705 CrossRef CAS PubMed.
- G. N. Simm and M. Reiher, J. Chem. Theory Comput., 2016, 12, 2762–2773 CrossRef CAS PubMed.
- I. M. Alecu, J. Zheng, Y. Zhao and D. G. Truhlar, J. Chem. Theory Comput., 2010, 6, 2872–2887 CrossRef CAS PubMed.
- B. Mennucci, J. Phys. Chem. Lett., 2010, 1, 1666–1674 CrossRef CAS.
- A. V. Marenich, C. Kelly, J. D. Thompson, G. D. Hawkins, C. C. Chambers, D. J. Giesen, P. Winget, C. J. Cramer and D. G. Truhlar, Minnesota Solvation Database, 2012 Search PubMed.
- A. J. Cohen, P. Mori-Sánchez and W. Yang, Chem. Rev., 2012, 112, 289–320 CrossRef CAS PubMed.
- T. Weymuth, E. P. A. Couzijn, P. Chen and M. Reiher, J. Chem. Theory Comput., 2014, 10, 3092–3103 CrossRef CAS PubMed.
- J. J. Mortensen, K. Kaasbjerg, S. L. Frederiksen, J. K. Nørskov, J. P. Sethna and K. W. Jacobsen, Phys. Rev. Lett., 2005, 95, 216401 CrossRef CAS PubMed.
- K. S. Brown and J. P. Sethna, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2003, 68, 021904 CrossRef PubMed.
- S. L. Frederiksen, K. W. Jacobsen, K. S. Brown and J. P. Sethna, Phys. Rev. Lett., 2004, 93, 165501 CrossRef PubMed.
- V. Petzold, T. Bligaard and K. W. Jacobsen, Top. Catal., 2012, 55, 402–417 CrossRef CAS.
- J. Wellendorff, K. T. Lundgaard, K. W. Jacobsen and T. Bligaard, J. Chem. Phys., 2014, 140, 144107 CrossRef PubMed.
- J. Wellendorff, K. T. Lundgaard, A. Møgelhøj, V. Petzold, D. D. Landis, J. K. Nørskov, T. Bligaard and K. W. Jacobsen, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 85, 235149 CrossRef.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS PubMed.
- C. Adamo and V. Barone, J. Chem. Phys., 1999, 110, 6158–6170 CrossRef CAS.
- J. P. Perdew, M. Ernzerhof and K. Burke, J. Chem. Phys., 1996, 105, 9982–9985 CrossRef CAS.
- C. Zhu, R. H. Byrd, P. Lu and J. Nocedal, ACM Transactions on Mathematical Software, 1997, 23, 550–560 CrossRef.
- M. Valorani, D. A. Goussis, F. Creta and H. N. Najm, J. Comput. Phys., 2005, 209, 754–786 CrossRef.
- T. Turányi and A. S. Tomlin, Analysis of Kinetic Reaction Mechanisms, Springer Berlin Heidelberg, 2014, pp. 183–312 Search PubMed.
- J.-H. Prinz, H. Wu, M. Sarich, B. Keller, M. Senne, M. Held, J. D. Chodera, C. Schütte and F. Noé, J. Chem. Phys., 2011, 134, 174105 CrossRef PubMed.
- G. R. Bowman, An Introduction to Markov State Models and Their Application to Long Timescale Molecular Simulation, Springer Netherlands, 2014, pp. 7–22 Search PubMed.
- S. H. Lam and D. A. Goussis, Int. J. Chem. Kinet., 1994, 26, 461–486 CrossRef CAS.
- P. D. Kourdis and D. A. Goussis, Math. Biosci., 2013, 243, 190–214 CrossRef CAS PubMed.
- N.-V. Buchete and G. Hummer, J. Phys. Chem. B, 2008, 112, 6057–6069 CrossRef CAS PubMed.
- P. Nicolini and D. Frezzato, J. Chem. Phys., 2013, 138, 234101 CrossRef PubMed.
- P. Whittle, Systems in Stochastic Equilibrium, John Wiley & Sons Ltd, Chichester, New York, 1986 Search PubMed.
- G. N. Simm, T. Husch, J. Proppe and M. Reiher, in preparation.
- J. Kua, M. M. Galloway, K. D. Millage, J. E. Avila and D. O. De Haan, J. Phys. Chem. A, 2013, 117, 2997–3008 CrossRef CAS PubMed.
- F. Claeyssens, J. N. Harvey, F. R. Manby, R. A. Mata, A. J. Mulholland, K. E. Ranaghan, M. Schütz, S. Thiel, W. Thiel and H.-J. Werner, Angew. Chem., 2006, 118, 7010–7013 CrossRef.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c6fd00144k |
| This journal is © The Royal Society of Chemistry 2016 |