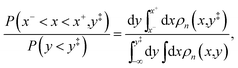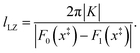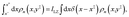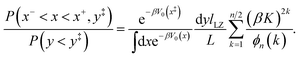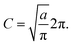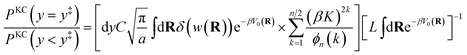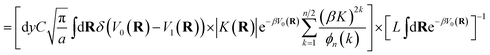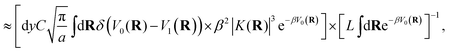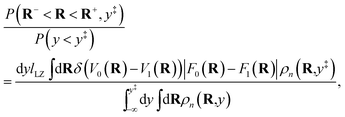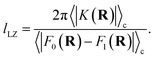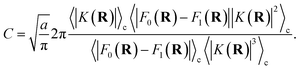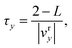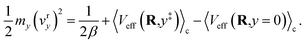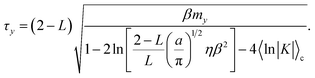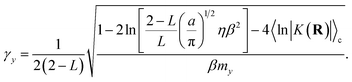DOI:
10.1039/C6FD00143B
(Paper)
Faraday Discuss., 2016,
195, 191-214
Kinetically-constrained ring-polymer molecular dynamics for non-adiabatic chemistries involving solvent and donor–acceptor dynamical effects
Received
2nd June 2016
, Accepted 23rd June 2016
First published on 23rd June 2016
Abstract
We investigate the performance of the recently developed kinetically-constrained ring polymer molecular dynamics (KC-RPMD) method for the description of model condensed-phase electron transfer (ET) reactions in which solvent and donor–acceptor dynamics play an important role. Comparison of KC-RPMD with results from Golden-Rule rate theories and numerically exact quantum dynamics calculations demonstrates that KC-RPMD accurately captures the combination of electronic- and nuclear-dynamical effects throughout the Marcus (intermediate solvent friction) and Zusman (large solvent friction) regimes of ET. It is also demonstrated that KC-RPMD accurately describes systems in which the magnitude of the diabatic coupling depends on the position of a dynamical donor–acceptor mode. In addition to these successes, however, we present an unsurprising failure of KC-RPMD to capture the enhancement of the ET rate in the low solvent friction regime associated with nuclear coherence effects. In this analysis, we re-visit several aspects of the original KC-RPMD formulation, including the form of the kinetic constraint and the choice of the mass of the auxiliary electronic variable. In particular, we introduce a Langevin bath for the auxiliary electronic variable to correct for its unphysically low coupling with the nuclear degrees of freedom. This work demonstrates that the KC-RPMD method is well suited for the direct simulation of non-adiabatic donor–acceptor chemistries associated with many complex systems, including those for which solvent dynamics plays an important role in the reaction mechanism.
1 Introduction
Non-adiabatic reactions are ubiquitous throughout chemistry and biology, including such processes as charge transfer, energy transfer and non-radiative decay. The accurate and efficient simulation of non-adiabatic dynamics in the condensed phase remains an ongoing challenge for theoretical methods.1–31 Recently we have developed an extension of the ring-polymer molecular dynamics method (RPMD),14,15 kinetically-constrained (KC) RPMD,1 which allows for the treatment of general multi-electron, non-adiabatic processes. In the current study, we explore the performance of KC-RPMD for models of condensed-phase electron transfer (ET) reactions in which the relative timescale between the electronic and nuclear degrees of freedom alters both the reaction rate and mechanism.
Like conventional RPMD in the position representation,14,15 KC-RPMD is an approximate quantum dynamics method that is based on the imaginary-time path-integral formulation of statistical mechanics.32 KC-RPMD employs a path integral discretization in the position representation for the nuclear coordinates, but in the discrete diabatic state basis for the electronic coordinates. KC-RPMD further employs (i) a coarse-graining of the discrete electronic path variables with respect to a single, continuous coordinate that reports on non-adiabatic transitions in the path variables in imaginary time and (ii) a “kinetic constraint” that prevents the formation of non-adiabatic transitions at nuclear configurations for which the diabatic states are non-degenerate. This kinetically-constrained distribution is rigorously preserved using continuous equations of motion, yielding a real-time model for the non-adiabatic dynamics of a quantum system. The KC-RPMD equations of motion preserve the useful features of conventional position-representation RPMD such as detailed balance, time-reversal symmetry, and invariance of reaction rate calculations to the choice of dividing surface. In addition, KC-RPMD allows for the simulation of electronically non-adiabatic processes beyond one-electron chemistries, which cannot be treated with conventional RPMD.25–29
Previously, KC-RPMD was successfully employed to investigate a range of model reactions, including ET reactions in the normal and inverted regimes and in the non-adiabatic and adiabatic regimes.1 In this study, we explore the performance of the method in modeling condensed-phase ET reactions in which the solvent and donor–acceptor dynamics strongly affect the ET rate and mechanism. Specifically, we investigate the ET rate as a function of the solvent friction and as a function of the frequency of a donor–acceptor mode that modulates the magnitude of the electronic coupling. In doing so, we note that the auxiliary electronic variable in KC-RPMD exhibits unphysically low coupling to the nuclear degrees of freedom, and we thus introduce a straightforward means of properly thermalizing the electronic variable via coupling to a dissipative Langevin bath. The present work demonstrates that KC-RPMD yields excellent results when used to simulate more complex systems in which dynamical effects play a strong role in determining the reaction rate and mechanism.
2 Theory
2.1 KC-RPMD
We begin by reviewing the derivation of the KC-RPMD method, following ref. 1. Particular focus is paid to the form of the kinetic constraint and mass of the auxiliary electronic variable, and small modifications are introduced to allow for more natural application to thermal reaction rates.
Consider a general, two-level system in the diabatic representation with a Hamiltonian operator of the form Ĥ = ![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) +
+ ![[V with combining circumflex]](https://www.rsc.org/images/entities/i_char_0056_0302.gif) , where
, where
| | 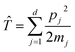 | (1) |
describes the kinetic energy of a system of
d nuclear degrees of freedom and
| | 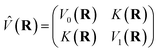 | (2) |
is the potential energy in the diabatic representation as a function of the nuclear coordinates,
R.
The canonical partition function for the two-level system is
| | 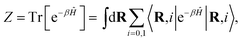 | (3) |
where
β = (
kBT)
−1 is the inverse temperature and
i denotes the diabatic electronic state. By (i) resolving the identity in the product space of the electronic state and nuclear position coordinates and (ii) employing the appropriate short-time approximation, we discretize the trace into the ring-polymer representation with
n beads and obtain the familiar result
1,33| | 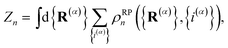 | (4) |
such that
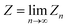
. The nuclear position and electronic state of the
αth ring-polymer bead are given by (
R(α),
i(α)) and the usual periodic constraint of the ring polymer is satisfied by (
R(n+1),
i(n+1)) = (
R(1),
i(1)). The ring polymer distribution is given by
| | 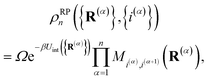 | (5) |
where
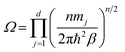
. The internal ring-polymer potential is given by
| | 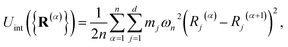 | (6) |
where
ωn = (
βnħ)
−1. The term
Mi,i′(
R) denotes the
i,
i′ element of the matrix
| | 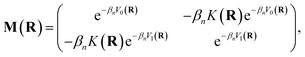 | (7) |
where
βn =
β/
n.
Eqn (4)–(7) define the usual path-integral partition function for a two-level system in the diabatic representation.
To obtain the KC-RPMD distribution and equations of motion from the usual path-integral distribution, eqn (4)–(7), we first introduce a discrete collective variable that reports on the existence of kink-pairs in the ring-polymer configuration:
| | 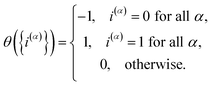 | (8) |
We then introduce a continuous dummy variable y that is tethered to θ({i(α)}) via a square-well restraining potential Vr(y,{i(α)}), such that
| | 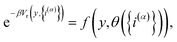 | (9) |
where
| | 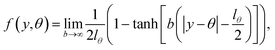 | (10) |
and
| | 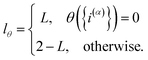 | (11) |
Eqn (10) defines a set of three square restraining potentials, one of width L, centered at y = 0, and two of width 2 − L, centered at y = ±1. Eqn (10) differs slightly from the original formulation of KC-RPMD; the functional form of eqn (10) remains the same, but now, the relative width between the square restraining potential centered at y = 0 versus centered at y = −1 or y = 1 can be varied, which is useful in the context of the Langevin bath as will be described below. It should be noted that the kinetically-constrained distribution presented below, and thus the calculation of any equilibrium properties, is invariant to the choice of L.
The kinetically-constrained distribution is obtained by reducing the ring-polymer probability distribution in eqn (5) with respect to the discrete electronic variables and by introducing a kinetic constraint that penalizes the formation of kink-pairs at ring-polymer configurations for which the diabatic surfaces are non-degenerate, such that
| | 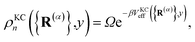 | (12) |
where
| | 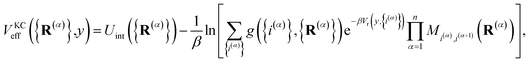 | (13) |
and
| | 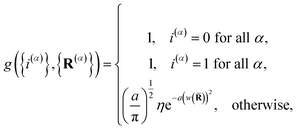 | (14) |
is the penalty function. The function
w(
![[R with combining macron]](https://www.rsc.org/images/entities/b_char_0052_0304.gif)
) = (
V0(
![[R with combining macron]](https://www.rsc.org/images/entities/b_char_0052_0304.gif)
) −
V1(
![[R with combining macron]](https://www.rsc.org/images/entities/b_char_0052_0304.gif)
))/
K(
![[R with combining macron]](https://www.rsc.org/images/entities/b_char_0052_0304.gif)
) is the scaled difference in the diabatic potential surfaces,
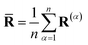
is the ring-polymer centroid coordinate, and
a is a unitless convergence parameter chosen sufficiently large to converge the free energy (FE) of kink-pair formation given by Δ
FKC =
FKC(0) −
FKC(−1), where
| | 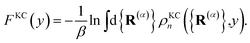 | (15) |
The prefactor η is a multiplicative factor that is chosen to avoid biasing the probability of kink-pair formation at nuclear configurations for which the diabats cross, such that
| | 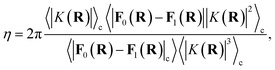 | (16) |
where
F0(
R) and
F1(
R) are the force vectors associated with electronic state 0 and 1, respectively. The brackets denote an ensemble average constrained to the intersection of the diabatic surfaces, such that
| | 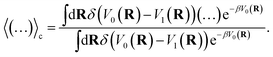 | (17) |
A detailed derivation of eqn (16) can be found in App. A.
The classical equations of motion associated with the equilibrium distribution ρKCn({R(α)},y) are
| | 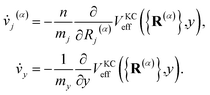 | (18) |
These equations exactly preserve the well-defined equilibrium distribution, eqn (12), and as such preserve all of the essential features of conventional RPMD including detailed balance, time-reversibility, invariance of the thermal rate constant on the choice of dividing surface, and the ability to harness the full machinery of classical molecular dynamics techniques.
The equations of motion defined in eqn (18) utilize the physical masses for the nuclear degrees of freedom mj. The mass of the auxiliary variable, my is chosen such that the KC-RPMD transition state theory (TST) rate exactly recovers the Fermi–Golden rule rate,34
| | 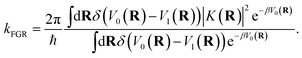 | (19) |
Though the derivation of my is analogous, the choice of the Fermi–Golden rule rate as the reference rate theory differs from the original formulation of KC-RPMD,1 in which the Landau–Zener TST rate expression for non-adiabatic transitions was utilized.35 We note that the Fermi–Golden rule and Landau–Zener TST rates differ only by a factor of two, but the Fermi–Golden rule expression is more appropriate for the calculation of thermal rate constants in the condensed phase.34 The resulting expression for the mass of the auxiliary variable is
| | 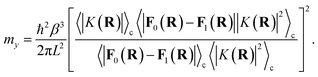 | (20) |
We note that if
L carries units of length, then
my carries units of mass.
This derivation of KC-RPMD completely follows that presented in ref. 1, although the square restraining potential, f(y,θ) in eqn (10), the multiplicative factor, η in eqn (16), and the mass of the auxiliary variable, my in eqn (20), now have slightly modified forms.
2.2 Langevin coupling for the auxiliary electronic variable
As will be shown in the Results section, the equations of motion in eqn (18) can lead to unphysically slow damping of the auxiliary electronic variable. To address this problem, we borrow insight from the T-RPMD method by effectively thermostatting the dynamics of the auxiliary electronic variable via coupling to a dissipative Langevin bath.36 The KC-RPMD equations of motion including the Langevin bath are now| | 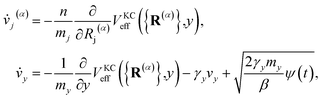 | (21) |
where γy is the friction coefficient and ψ(t) is a gaussian random force of unit width. The friction coefficient is chosen such that the timescale for thermalization of the auxiliary variable is approximately the same as the timescale for the auxiliary variable to cross the reactant basin, such that| | 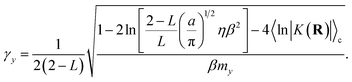 | (22) |
The detailed derivation of eqn (22) is given in App. B. Analogous to the treatment in conventional RPMD, introduction of the Langevin bath does not affect the calculation of any static equilibrium property.36
2.3 KC-RPMD rate theory
We conclude the Methods section by reviewing the KC-RPMD rate coefficient.1 The KC-RPMD rate is calculated using standard methods37–40 and is separated into a statistical and a dynamical contribution as41,42| | 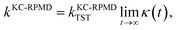 | (23) |
where kKC-RPMDTST is the TST estimate for the rate associated with the dividing surface ξ(r) = ξ‡, and κ(t) is the time-dependent transmission coefficient that corrects for dynamical recrossing at the dividing surface. Here, ξ(r) is a collective variable that distinguishes between reactant and product basins of stability, defined as a function of the position vector of the full system in the ring-polymer representation, r = {{R(α)},y}.
The KC-RPMD TST rate is calculated using15
| | 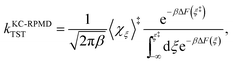 | (24) |
where
F(
ξ) is the FE along
ξ relative to a reference value
ξ°, such that
| | 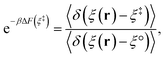 | (25) |
and
43–45| | 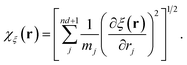 | (26) |
The sum in eqn (26) runs over all the nd + 1 degrees of freedom for the ring-polymer representation used here, and mj denotes the mass associated with each degree of freedom. The angle brackets indicate an equilibrium ensemble average
| | 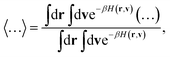 | (27) |
where
v = {{
v(α)},
vy} is the velocity vector for the full system in the ring-polymer representation and
H(
r,
v) is the ring-polymer Hamiltonian associated with the KC-RPMD effective potential. The ensemble average,
| | 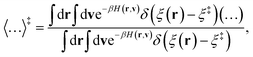 | (28) |
corresponds to the ensemble average constrained to the dividing surface. The transmission coefficient in
eqn (23) is calculated as
| | 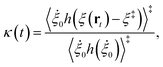 | (29) |
where
h(
x) is the Heaviside function, and the subscripts 0 and
t denote evaluation of the quantity from the trajectory at its initiation and after evolution for time
t, respectively.
3 Model systems
In this work, we consider system-bath models that describe condensed-phase ET over a wide range of regimes with respect to solvent and diabatic coupling. Atomic units are employed throughout, unless otherwise noted.
3.1 System A: solvent-controlled ET
System A models a condensed-phase ET reaction with constant coupling, for which the potential energy function takes the form46| | 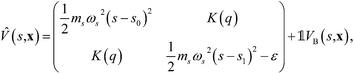 | (30) |
where s corresponds to the local solvent dipole. This solvent coordinate is linearly coupled to a set of f solvent bath modes, x, such that| | 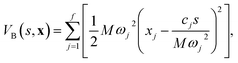 | (31) |
and M denotes the mass of the solvent bath modes. The solvent bath exhibits an ohmic spectral density with cutoff frequency ωc,| | 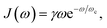 | (32) |
where γ denotes the friction coefficient of the solvent bath and controls the strength of coupling between the local solvent dipole and the dissipative solvent bath. The spectral density in eqn (32) is discretized into f oscillators with frequencies47| | 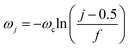 | (33) |
and coupling constants| | 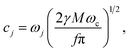 | (34) |
where j = 1 … f. Three sets of parameters (specifying system A1, system A2 and system A3) are used to model ET over a wide range of regimes. System A1 models the transition from the normal to inverted regime of ET. System A2 models the transition from the Marcus regime at intermediate values of the friction coefficient, γ, to the Zusman regime of ET at high values of the friction coefficient. System A3 models the transition from the weakly dissipative regime at low friction to the Marcus regime at intermediate values of friction. These parameters are presented in Table 1. The quantities η and my are analytically evaluated from eqn (16) and (20) and are also presented in Table 1.
Table 1 Parameters for system Aa
| Parameter |
System A1 |
System A2 |
System A3 |
|
Unless otherwise noted, values are reported in atomic units. Parameters for systems A1 and A2 are taken from ref. 1; parameters for system A3 are taken from ref. 48.
|
|
m
s
|
1836 |
1836 |
1836 |
|
ω
s
|
2.28 × 10−3 |
2.28 × 10−3 |
2.28 × 10−3 |
|
s
0
|
−2.40 |
−2.40 |
−1.198 |
|
s
1
|
2.40 |
2.40 |
1.198 |
|
ε
|
0–0.236 |
0 |
0 |
|
K
|
6.67 × 10−7 |
1 × 10−4 |
2.28 × 10−4 |
|
M
|
1836 |
1836 |
1836 |
|
ω
c
|
2.28 × 10−3 |
2.28 × 10−3 |
2.28 × 10−3 |
|
γ/Mωc |
1.0 |
0.3–300.0 |
0.013–30.0 |
|
f
|
12 |
12 |
12 |
|
T
|
300 K |
300 K |
460 K |
|
m
y
|
8.26 × 10−3 |
1.86 × 102 |
2.68 × 102 |
|
η
|
6.28 |
6.28 |
6.28 |
3.2 System B: donor–acceptor-controlled ET
System B extends system A to include an additional degree of freedom, q, which models the fluctuating distance between the electron donor and acceptor. The coupling exponentially depends on q, such that| | 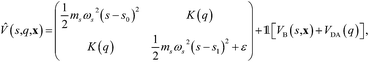 | (35) |
where| | 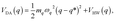 | (36) |
| | 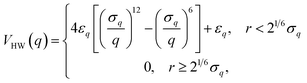 | (37) |
and| | 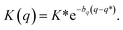 | (38) |
The parameters for system B are the same as for system A1, except for those specified in Table 2. The table also includes the additional parameters necessary to fully define system B, as well as the calculated values of my and η. The parameters are chosen to model ET between two iron atoms solvated in water.49
Table 2 Parameters for system Ba
| Parameter |
Range of values |
|
All values are reported in atomic units.
|
|
m
q
|
51![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 039 039 |
|
ω
q
|
4 × 10−4 to 3 × 10−3 |
|
q* |
12.0 |
|
ε
q
|
0.1 |
|
σ
q
|
8.0 |
|
b
q
|
3.0 |
|
K* |
6.67 × 10−7 |
|
ε
|
0 |
|
m
y
|
2.35 × 10−2 to 8.41 × 10−3 |
|
η
|
0.77–6.05 |
4 Calculation details
In all simulations, the KC-RPMD equations of motion, eqn (21), are evolved using an extension of the velocity Verlet algorithm to include the Langevin bath.50,51 The stiffness parameter for the square-well restraint, b, was found to be converged for all calculations with a value of b = 400. The width of the square restraining potential, L = 0.1, was chosen to minimize the initial degree of recrossing associated with the Langevin bath. In all cases the TST dividing surface is defined as an isosurface of the auxiliary variable, y.
4.1 KC-RPMD rate calculation in system A1
In system A1, the driving force parameter, ε, is varied to model the transition between the normal and inverted regime of ET, such that ε ∈ {0, 0.04, 0.07, 0.118, 0.18, 0.236}. For these values of ε, the calculations were found to converge with values of −log(a) ∈ {5.3, 5.3, 5.3, 5.3, 5.5}, respectively. The ring polymer is discretized using n = 32 beads for all values of ε, and both the solvent dipole coordinate, s, and the harmonic oscillator solvent bath, x, are treated classically by restricting the position of the ring-polymer beads for each nuclei to coincide.
The KC-RPMD rates are obtained from the product of the TST rates, eqn (24), and the transmission coefficients, eqn (29). The KC-RPMD TST rates are obtained from F(y), the FE profile in the continuous auxiliary variable. The FE profile is obtained by direct numerical integration.
The transmission coefficients are calculated using KC-RPMD trajectories that are released from the dividing surface associated with y‡ = 0. The values of the mass of the auxiliary variable, my, denoted in Table 1 are small in comparison to the mass of the nuclei, which in principle would necessitate an exceedingly small time step to numerically integrate the equations of motion. However, we note that any choice of the value of my that is still small in comparison to the mass of the nuclei, but allows for a larger time step, will yield the same final value for the transmission coefficient. We thus choose a value of my = 10.0 for all values of ε when integrating the KC-RPMD equations of motions for the trajectories used to calculate the transmission coefficient; it is important to note that we only use a value of my = 10.0 for the calculation of the dynamical trajectories, but use the true values of my denoted in Table 1 in the calculation of the TST rate. The value of the friction coefficient of the Langevin bath connected to y is calculated from eqn (22) using the same value of my = 10.0 as used in the dynamical KC-RPMD trajectories, such that γy = 1.49 × 10−2 for all values of ε. We have confirmed that choosing a smaller value of my yields numerically identical results as a value of my = 10.0. For each value of the driving force ε, a total of 1000 trajectories are released. Each trajectory is evolved for 200 fs using a time step of dt = 0.002 fs with initial velocities sampled from the Maxwell–Boltzmann distribution. The initial configurations for the KC-RPMD trajectories are generated from long KC-RPMD trajectories in which the auxiliary electronic variable is constrained to the dividing surface; the constrained trajectories are 200 ps in time and are thermostatted by resampling the velocities from the Maxwell–Boltzmann distribution every 100 fs.
4.2 KC-RPMD rate calculation in system A2
In system A2, the friction coefficient of the solvent bath, γ, is varied to model the transition from the Marcus to the Zusman regime of ET, such that γ/Mωc ∈ {0.3, 1, 3, 10, 30, 100, 200, 300}. For all values of γ, both the solvent dipole coordinate, s, and the harmonic oscillator solvent bath, x, are treated classically. The calculations were found to converge with a value of −log(a) = 1.5 and a value of n = 128 beads for the path-integral discretization of the electronic degrees of freedom.
The FE profile, F(y), used for the calculation of the KC-RPMD TST rate is obtained by numerical integration. The transmission coefficients are calculated using KC-RPMD trajectories that are released from the dividing surface associated with y‡ = 0. The true value of the mass of the auxiliary variable, my = 1.86 × 102, is used for the dynamical KC-RPMD trajectories and for the calculation of γy, such that γy = 1.34 × 10−3 for all values of γ. For each value of the friction coefficient γ, a total of 8000 trajectories are released. Each trajectory is evolved for 200 fs using a time step of dt = 0.005 fs with initial velocities sampled from the Maxwell–Boltzmann distribution. The initial configurations for the KC-RPMD trajectories are generated from long KC-RPMD trajectories in which the auxiliary electronic variable is constrained to the dividing surface; the constrained trajectories are 1.6 ns in time and are thermostatted by resampling the velocities from the Maxwell–Boltzmann distribution every 100 fs.
4.3 KC-RPMD rate calculation in system A3
In system A3, the friction coefficient of the solvent bath, γ, is varied to model the transition from the weakly dissipative regime to the Marcus regime of ET, such that γ/Mωc ∈ {0.013, 0.026, 0.1, 0.3, 1, 3, 10, 30}. For all values of γ, both the solvent dipole coordinate, s, and the harmonic oscillator solvent bath, x, are treated quantum mechanically. The calculations were found to converge with a value of −log(a) = 1.5 and a value of n = 128 beads for the path-integral discretization of the nuclear and electronic degrees of freedom.
For each value of γ, the FE profile, F(y), used for the calculation of the KC-RPMD TST rate is obtained by reducing the three-dimensional FE surface, F(y,![[s with combining macron]](https://www.rsc.org/images/entities/i_char_0073_0304.gif) ,ΔVeff), computed with respect to y, the ring-polymer centroid for the solvent coordinate,
,ΔVeff), computed with respect to y, the ring-polymer centroid for the solvent coordinate, ![[s with combining macron]](https://www.rsc.org/images/entities/i_char_0073_0304.gif) , and the difference between the true effective potential and the effective potential used to generate the dynamics during the sampling trajectories, ΔVeff, defined below. The FE profile F(y,
, and the difference between the true effective potential and the effective potential used to generate the dynamics during the sampling trajectories, ΔVeff, defined below. The FE profile F(y,![[s with combining macron]](https://www.rsc.org/images/entities/i_char_0073_0304.gif) ,ΔVeff) is calculated using umbrella sampling and the weighted histogram analysis method (WHAM)37,52–54 from the following umbrella sampling protocol. The KC-RPMD sampling trajectories are generated using a potential that restrains
,ΔVeff) is calculated using umbrella sampling and the weighted histogram analysis method (WHAM)37,52–54 from the following umbrella sampling protocol. The KC-RPMD sampling trajectories are generated using a potential that restrains ![[s with combining macron]](https://www.rsc.org/images/entities/i_char_0073_0304.gif) and y to s0 and y0, respectively, and has a weaker value of the steepness of the square-well restraining potential, b (eqn (10)), such that
and y to s0 and y0, respectively, and has a weaker value of the steepness of the square-well restraining potential, b (eqn (10)), such that
| | 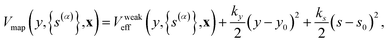 | (39) |
where
Vweakeff(
y,{
s(α)},
x) is defined as in
eqn (13), but uses a value of
b = 4.0 in comparison to the true value of
b = 400. The difference between the true effective potential and the effective potential used to generated the sampling trajectory dynamics is thus given as
| | | ΔVeff = Vweakeff(y,{s(α)},x) − VKCeff(y,{s(α)},x). | (40) |
The KC-RPMD sampling trajectories are grouped into two sets. The first set is comprised of 99 trajectories that sample the full configuration space, with s0 and y0 assuming values on a square grid. The parameter s0 assumes 11 uniformly spaced values in the region s0 = [−2.5, 2.5], and the associated force constant is ks = 0.02. For each value of s0, the parameter y0 assumes 9 uniformly spaced values in the region y0 = [−2.0, 2.0], and the associated force constant is ky = 0.01. The second set is comprised of 77 trajectories that sample mainly the barrier region along the y coordinate, with s0 and y0 assuming values on a square grid. The parameter s0 assumes 11 uniformly spaced values in the region s0 = [−2.5, 2.5], and the associated force constant is ks = 0.02. For each value of s0, the parameter y0 assumes the values of y0 = {±0.05, ±0.04, ±0.02, 0.00}, and the associated force constant is ky = 25. Each sampling trajectory is evolved for 3 ns using a time step of 0.05 fs. Thermostatting is performed by re-sampling the velocities from the Maxwell–Boltzmann (MB) distribution every 2.5 ps.
The transmission coefficients are calculated using KC-RPMD trajectories that are released from the dividing surface associated with y‡ = 0. The true value of the mass of the auxiliary variable, my = 2.68 × 102, is used for the dynamical KC-RPMD trajectories and for the calculation of γy, such that γy = 6.55 × 10−4 for all values of γ. For each value of the friction coefficient γ, a total of 8000 trajectories are released. Each trajectory is evolved for 400 fs using a time step of dt = 0.001 fs with initial velocities sampled from the Maxwell–Boltzmann distribution. The initial configurations for the KC-RPMD trajectories are generated from long KC-RPMD trajectories in which the auxiliary electronic variable is constrained to the dividing surface; the constrained trajectories are 2 ns in time and are thermostatted by resampling the velocities from the Maxwell–Boltzmann distribution every 500 fs.
4.4 KC-RPMD rate calculation in system B
In system B, the frequency of the donor–acceptor mode, ωq, that modulates the strength of the coupling, K(q), is varied such that ωq ∈ {4 × 10−4, 7 × 10−4, 1.4 × 10−3, 2.2 × 10−3, 3 × 10−3}. For these values of ωq, the calculations were found to converge with values of −log(a) ∈ {1, 3.3, 4.3, 4.3, 4.3}, respectively. For all values of ωq, the solvent dipole coordinate, s, the harmonic oscillator solvent bath, x, and the donor–acceptor mode, q, are treated classically, and the calculations were found to converge with a value of n = 128 beads for the path-integral discretization of the electronic degrees of freedom.
The KC-RPMD TST rates are obtained by numerical integration of F(y). The transmission coefficients are calculated using KC-RPMD trajectories that are released from the dividing surface associated with y‡ = 0. Due to the small values of my presented in Table 2, we utilize a value of my = 10.0 for the KC-RPMD trajectories and the calculation of γy for all values of ωq, such that γy ∈ {1.30 × 10−2, 1.36 × 10−2, 1.40 × 10−2, 1.39 × 10−2, 1.39 × 10−2}. For each value of the frequency ωq, a total of 1000 trajectories are released. Each trajectory is evolved for 100 fs using a time step of dt = 0.001 fs for ωq = 4 × 10−4 and dt = 0.002 for all other values of ωq; initial velocities were sampled from the Maxwell–Boltzmann distribution. The initial configurations for the KC-RPMD trajectories are generated from long KC-RPMD trajectories in which the auxiliary electronic variable is constrained to the dividing surface; the constrained trajectories are 200 ps in time and are thermostatted by resampling the velocities from the Maxwell–Boltzmann distribution every 100 fs.
4.5 Calculation of reference TST expressions
Reference values for the thermal reaction rates for system A are evaluated using the Marcus rate expression for non-adiabatic ET and the Zusman extension of Marcus theory to the overdamped regime of ET.
The Marcus rate expression for non-adiabatic ET with classical solvent is given by55–58
| | 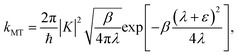 | (41) |
where
λ is the reorganization energy calculated as
λ =
V1(
s1) −
V1(
s0), and all other terms have been defined previously.
The Zusman expression of ET, which extends Marcus theory to account for frictional effects of the solvent, is given by59
| | 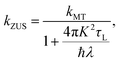 | (42) |
where
τL =
γ/(
ωs2ms) is the Debye longitudinal relaxation time.
59,60
Reference values for the thermal reaction rates for system B are evaluated using an extension of the Marcus rate expression to account for a position-dependent diabatic coupling, such that35,55
| | 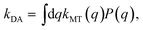 | (43) |
where
| | 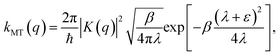 | (44) |
is the Marcus theory expression at a given value of the donor–acceptor distance
q, and
| | 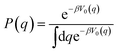 | (45) |
is the probability density at a given
q. The rate expression
eqn (43) is evaluated
via numerical integration for each value of
ωq.
5 Results
The results in this paper are presented in four parts. In the first part, we illustrate the necessity of the Langevin bath in the KC-RPMD equations of motion by investigating the transition between normal and inverted ET. In the second and third parts we explore the performance of KC-RPMD in systems in which the solvent and donor–acceptor dynamics strongly affect the ET rate.
5.1 Damping of the auxiliary electronic variable
We begin by illustrating the importance of the dissipative Langevin bath coupled to the auxiliary electronic variable by considering numerical results for system A1, which models the transition from the normal to inverted regime of condensed-phase ET. Fig. 1(a) depicts the time-dependent transmission coefficient, eqn (29), in the activationless regime, ε = 0.118, calculated with the updated form of KC-RPMD including the Langevin bath (blue) and without the Langevin bath (green). The undamped transmission coefficient (green) decreases over the entire time range of the trajectories, indicative of a large amount of recrossing of the dividing surface by the auxiliary electronic variable. The auxiliary variable and the nuclear degrees of freedom are only weakly coupled during the dynamics generated by eqn (18). Thus, the timescale for thermalization of the auxiliary variable without the Langevin bath is long in comparison to the timescale for the auxiliary variable to traverse the reactant or product basin, leaving sufficient energy for the auxiliary variable to recross the dividing surface. These recrossings in the auxiliary variable become an issue any time the solvent relaxation away from configurations from which the diabatic surfaces are degenerate is slow; in the activationless regime, the equilibrium position of the solvent coordinate in the reactant basin corresponds to a configuration for which the diabatic surfaces are degenerate, and thus the solvent coordinate never relaxes away from the crossing point. We note that these recrossings were not observed in the original KC-RPMD paper because of the short total time for the trajectories in comparison to the mass of the auxiliary electronic variable, my.1
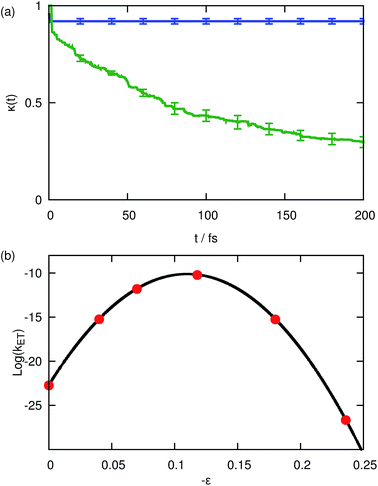 |
| | Fig. 1 (a) The time-dependent transmission coefficient, κ(t) (eqn (29)), for the activationless regime of ET calculated with KC-RPMD including the Langevin bath (blue) and without the Langevin bath (green). (b) Thermal reaction rate coefficients for system A1 as a function of the driving force, ε, obtained using KC-RPMD (red) and classical Marcus theory (eqn (41), black). | |
In comparison, Fig. 1(a) illustrates that inclusion of the Langevin bath leads to a rapid plateauing of the transmission coefficient even in the activationless regime due to proper thermalization of the auxiliary electronic variable; the initial rapid decrease in the transmission coefficient can be attributed to initial recrossing of the dividing surface due to the dissipative dynamics introduced by the Langevin bath.
Fig. 1(b) depicts the thermal reaction rates calculated using KC-RPMD with the Langevin bath (red) and classical Marcus theory using eqn (41) (black); Marcus theory constitutes the appropriate reference result since system A1 is in the weak-coupling regime (βK ≈ 7 × 10−4) and the solvent coordinate is treated classically. Comparison of the KC-RPMD results and Marcus theory demonstrates that the updated form of KC-RPMD exhibits quantitative agreement with the reference result throughout the normal, activationless and inverted regime. As shown previously,1 introduction of the kinetic constraint in KC-RPMD corrects the breakdown of instanton-based methods for describing deep tunneling through asymmetric barriers,27,61 leading to the correct description of the inverted regime for ET.
5.2 Friction-controlled electron transfer
We next present results for systems A2 and A3, which model ET as a function of the solvent friction. We consider both the transition from the Marcus (intermediate friction) regime to the Zusman (high friction) regime of ET and the transition from the weakly dissipative (low friction) regime to the Marcus regime of ET. The calculation of ET rates as a function of the solvent friction provides a stringent test of the KC-RPMD methodology and its ability to treat systems in which dynamical effects play a strong role.
Fig. 2(a) presents the thermal reactions rates for system A2 calculated using KC-RPMD (red), the Zusman expression (black, eqn (42)), and classical Marcus theory (green-dashed, eqn (41)) as a function of the friction of the solvent bath. Rates obtained using both the Zusman expression and KC-RPMD exhibit a plateau for values of log(γ/msωx) < 1.5, which corresponds to the Marcus regime of ET; in this regime, the Zusman expression reduces to the classical Marcus expression, eqn (41), and is independent of the strength of the friction coefficient. In the overdamped regime, when γ > 1.5, both the rates calculated using the Zusman expression and KC-RPMD exhibit a decrease in the ET rate associated with the diffusive dynamics of the solvent coordinate, which is not captured by classical Marcus theory.59,62–65 Comparison of the KC-RPMD results and the Zusman expression shows that KC-RPMD correctly describes the interplay between the timescale of transitions between electronic states and the timescale for motion of the nuclei.
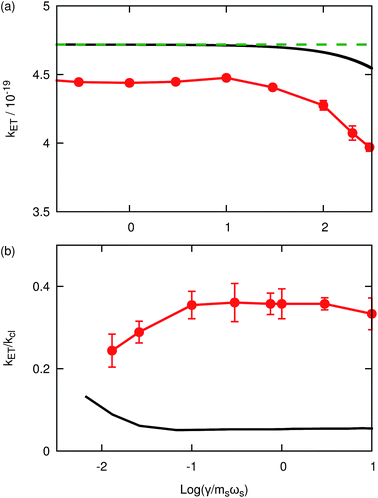 |
| | Fig. 2 (a) Thermal reaction rate coefficients for system A2 as a function of the friction of the solvent bath, γ, obtained using KC-RPMD (red), the Zusman expression (eqn (42), black) and the classical Marcus theory (eqn (41), green-dashed). (b) The dynamical recrossing factor for system A3 as a function of the friction of the solvent bath, γ, obtained using KC-RPMD (red) and numerically exact quantum dynamics calculations from ref. 48 (black). KC-RPMD is unable to capture the enhancement of the dynamical recrossing factor at low friction associated with constructive-coherence effects. | |
We now turn our attention to the transition from the weakly dissipative to Marcus regime of ET. In order to compare with the numerically exact quantum dynamics calculations from ref. 48, Fig. 2(b) presents the dynamical recrossing factor as a function of the friction of the solvent bath. The dynamical recrossing factor is defined as kET/kcl, where kET is the ET rate calculated using either KC-RPMD or exact quantum dynamics, and kcl is a classical TST rate,48
| | 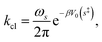 | (46) |
where
s‡ corresponds to the value of the solvent coordinate for which the diabatic states are degenerate. The dynamical recrossing factor provides a measure of the amount of recrossing of the dividing surface in the true system in comparison to the classical TST estimate.
Fig. 2(b) presents the thermal reaction rates for system A3 with quantized nuclei calculated using KC-RPMD (red) and exact quantum dynamics methods (black) as a function of the friction of the solvent bath.
48 Note that, as described in the Calculation details section, the nuclear degrees of freedom are quantized for both sets of calculations in
Fig. 2(b).
Analogous to Fig. 2(a), Fig. 2(b) shows that the dynamical recrossing factor calculated with either KC-RPMD (red) or exact quantum dynamics (black) exhibits a plateau region for intermediate values of the friction coefficient, log(γ/msωs) > −1. The value of the plateau region of the dynamical recrossing factor when calculated with KC-RPMD is in reasonable agreement with exact quantum dynamics considering the nuclei are quantized, although the error in the KC-RPMD calculation with respect to the reference result is somewhat larger than in Fig. 2(a).
As may be anticipated, Fig. 2(b) demonstrates qualitatively incorrect behavior of KC-RPMD in the weakly dissipative regime, when log(γ/msωs) < −1. The exact quantum dynamics shows an increase in the ET rate with decreasing friction, while KC-RPMD shows a decrease. In this regime, the timescale for relaxation of the solvent coordinate is long, such that the solvent coordinate passes through the crossing of the diabats numerous times, allowing for multiple transitions between the electronic states. In exact quantum dynamics simulations,48 the nuclear wavepackets constructively interfere during these crossings, leading to an enhancement of the ET rate.48,63 Like conventional RPMD,15 KC-RPMD does not capture such coherence effects, and the multiple electronic transitions lead to a decorrelation between the initial and final electronic state, causing a decrease in the ET rate. Nonetheless, the results in Fig. 2 indicate that KC-RPMD correctly describes ET in the moderate to strong solvent friction regimes that are characteristic of condensed-phase ET reactions.
5.3 Electron transfer with position-dependent coupling
We now consider results for system B, which models ET with a donor–acceptor mode that modulates the magnitude of the diabatic coupling. Fig. 3 presents the thermal reactions rates calculated using KC-RPMD (red) and the extension of classical Marcus theory to include a donor–acceptor mode (eqn (43), black). The rates calculated using KC-RPMD are in quantitative agreement with those calculated using the reference result over the entire range of the frequency of the donor–acceptor mode; the frequency provides a metric of the strength of the donor–acceptor mode. These results validate KC-RPMD for describing systems for which the diabatic coupling depends strongly on the position of the nuclei. As such, KC-RPMD is well suited to investigate complex systems in which the distance between the ET donor and acceptor is a dynamical variable.
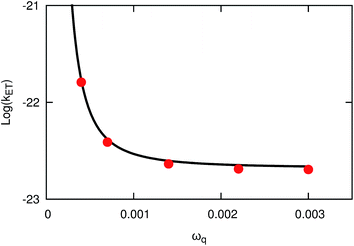 |
| | Fig. 3 Thermal reaction rate coefficients for system B as a function of frequency of the donor–acceptor mode, ωq, obtained using KC-RPMD (red) and the extension of Marcus theory to include a donor–acceptor mode (eqn (43), black). | |
6 Conclusions
In this work, we demonstrate the KC-RPMD method for applications in which solvent and donor–acceptor dynamics strongly impact the non-adiabatic reaction rate. In doing so, we revisit several aspects of the KC-RPMD derivation, including the form of the kinetic constraint and the choice of mass associated with the continuous electronic variable. In particular, we introduce a Langevin bath that is coupled to the continuous electronic variable to correct for the presence of the unphysically low coupling between the electronic variable and the nuclear degrees of freedom.
The accuracy of the KC-RPMD methodology has been verified in a variety of model systems of condensed-phase electron transfer in which nuclear dynamics plays an important role. We have illustrated that the KC-RPMD methodology correctly captures the competing timescales between solvent motion and the timescale for electronic transitions necessary to treat ET in the moderate to strong solvent-friction regimes. Furthermore, KC-RPMD correctly describes systems in which the diabatic coupling depends upon dynamical fluctuations in the donor–acceptor distance. Lastly, we present an unsurprising failure of KC-RPMD in the weakly dissipative regime of ET, due to coherence effects that lead to an enhancement of the ET rate. Taken together, the presented work demonstrates the potential applicability of KC-RPMD for describing a broad range of condensed-phase non-adiabatic chemistries.
A Derivation of the penalty function
In this appendix we derive the specific form of the multiplicative factor, η, that appears in the penalty function, g, in eqn (14). The multiplicative factor is derived such that the KC-RPMD distribution does not bias the probability of kink-pair formation at nuclear configurations for which the diabatic states are degenerate. Specifically, we consider the relative probability for kinked configurations versus configurations in the reactant basin in the constrained distribution, and we equate this ratio to the relative probability for kinked configurations at nuclear configurations within a small distance of the crossing of the diabatic surfaces versus configurations in the reactant basin in the unconstrained distribution. The unconstrained distribution, ρn({R(α)},y), is defined analogously to eqn (12), but with the penalty function g({i(α)},{R(α)}) = 1 for all {i(α)}.
For simplicity we first present the derivation for a 1D redox system with constant coupling, K, in the classical limit of the nuclear coordinates. We then outline the derivation for a general multi-dimensional system.
A.1 1D redox system with constant K and classical nuclei
For a 1D system with classical nuclei, the kinetically-constrained ring-polymer distribution (eqn (12)) has the form| | 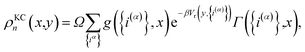 | (47) |
where 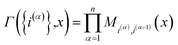 , and the penalty function in this case takes the form
, and the penalty function in this case takes the form| | 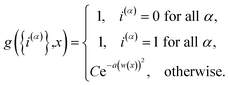 | (48) |
In the kinetically-constrained distribution the relative probability between kinked configurations and configurations in the reactant basin is given as
| | 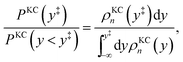 | (49) |
where the incremental length d
y is necessary to define the unitless probability,
y‡ = 0, and
| | 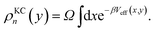 | (50) |
The relative probability in eqn (49) can be simplified by taking the limit of large a and by noting that the denominator is dominated by the statistical weight of unkinked configurations, such that1
| | 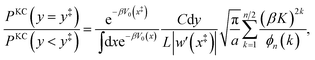 | (51) |
where
x‡ denotes the point of the intersection of the diabatic surfaces, the prime denotes differentiation with respect to the nuclear coordinate, and
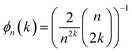
.
We equate the relative probability in eqn (51) to the relative probability between kinked configurations at nuclear configurations within a small distance of the crossing of the diabatic surfaces and configurations in the reactant basin in the unconstrained distribution,
| | 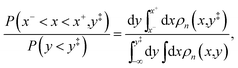 | (52) |
where the distance
x+ −
x− defines a small region around the crossing of the diabatic surfaces. We define this distance as the Landau–Zener length,
lLZ, which gives an estimate of the range of nuclear configurations for which the coupling,
K, impacts the dynamics,
34 such that
x− =
x‡ −
lLZ/2 and
x+ =
x‡ +
lLZ/2, and
| | 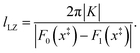 | (53) |
The definition of the numerator in eqn (52) constitutes the main difference in comparison to the original derivation.1 Noting again that the denominator in eqn (52) is dominated by the statistical weight of unkinked configurations, and making the reasonable approximation that the diabatic surfaces do not change significantly over the Landau–Zener length, such that the integral can be approximated as
| | 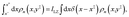 | (54) |
Eqn (52) simplifies to
| | 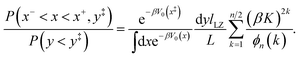 | (55) |
To obtain the final expression for the multiplicative factor in a 1D redox system with constant K and classical nuclei, we equate the two relative probabilities in eqn (51) and (55) to yield
| | 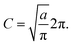 | (56) |
A.2 Multi-dimensional redox system with position-dependent K(R)
For a general multi-dimensional redox system with position-dependent K(R) and classical nuclei, the multiplicative factor η can be analogously derived. The relative probability in the constrained distribution is now given by| | 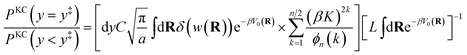 | (57) |
| | 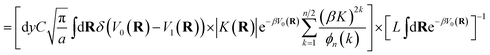 | (58) |
| | 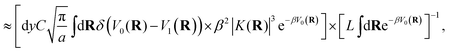 | (59) |
where in the last line we assume that terms associated with more than one kink-pair (k = 1) can be neglected.
The relative probability in the unconstrained distribution can be defined as
| | 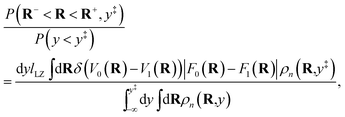 | (60) |
where in multiple dimensions we define the Landau–Zener length as
| | 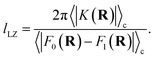 | (61) |
Here, we have again assumed that the diabatic surfaces do not change over the Landau–Zener length. Simplifying eqn (60), again assuming that terms associated with more than one kink-pair (k = 1) can be neglected, and equating the two relative probabilities yields the final form for the multiplicative constant in multiple dimensions with position-dependent coupling,
| | 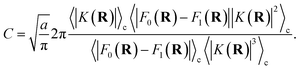 | (62) |
Eqn (62) simplifies to (56) in the limit of 1D and a position-independent diabatic coupling. For the case of a multidimensional system with quantized nuclei, the resulting expression for the multiplicative factor is unchanged if we make the approximation that the ring-polymer position is approximated by its centroid.1
B Derivation of the Langevin friction coefficient
In this appendix we derive the specific form for the Langevin friction coefficient associated with the auxiliary function that appears in the KC-RPMD equations of motion, eqn (21). The Langevin friction coefficient is chosen such that the timescale for thermalization of the auxiliary variable matches the time for the auxiliary variable to cross the reactant (or analogously the product) basin in the absence of the Langevin bath.
The timescale for relaxation, τr, is given by the exponential decay constant associated with the decay of the initial kinetic energy of the auxiliary variable when coupled to the Langevin bath, such that τr = 1/(2γy).66
The time for the auxiliary variable to cross the reactant basin in the absence of the Langevin bath is given by
| | 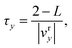 | (63) |
where 2 −
L defines the length of the reactant basin associated with the square restraining potential in
eqn (10), and
vry defines the average velocity of the auxiliary variable in the reactant basin following initialization of the auxiliary variable at the transition region
y =
y‡ with an average initial velocity given by the Maxwell–Boltzmann distribution,
| | 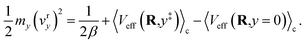 | (64) |
The first term in eqn (64) accounts for initialization of the velocity from the Maxwell–Boltzmann distribution, and the next two terms account for the average increase in the velocity associated with the auxiliary variable leaving the transition region to the reactant (or product) basin. In eqn (64) we have assumed that the motion of the nuclei is negligible on the timescale of the motion of the auxiliary variable. Simplifying eqn (64) yields the time for the auxiliary variable to cross the reactant basin,
| | 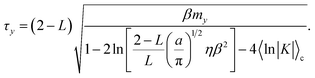 | (65) |
Equating the two timescales τt and τy yields the final form for the Langevin friction coefficient,
| | 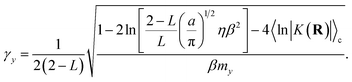 | (66) |
Acknowledgements
This work was supported by the National Science Foundation (NSF) CAREER Award under Grant CHE-1057112, and the Office of Naval Research (ONR) under Grant No. N00014-10-1-0884. Additionally, J. S. K. acknowledges support from an NSF Graduate Research Fellowship under Grant No. DGE-1144469. Computational resources were provided by the National Energy Research Scientific Computing Center, which is supported by the Office of Science of the US Department of Energy under Contract No. DE-AC02-05CH11231, and by the National Science Foundation under Grant No. CHE-1040558.
References
- A. R. Menzeleev, F. Bell and T. F. Miller III, J. Chem. Phys., 2014, 140, 064103 CrossRef PubMed.
- P. Ehrenfest, Zeitschrift für Physik, 1927, 45, 455 CrossRef.
- H. D. Meyer and W. H. Miller, J. Chem. Phys., 1979, 70, 3214 CrossRef CAS.
- D. A. Micha, J. Chem. Phys., 1983, 78, 7138 CrossRef CAS.
- J. C. Tully, Faraday Discuss., 1998, 407 RSC.
- M. D. Hack and D. G. Truhlar, J. Phys. Chem. A, 2000, 104, 7917 CrossRef CAS.
- J. C. Tully, J. Chem. Phys., 1990, 93, 1061 CrossRef CAS.
- P. J. Kuntz, J. Chem. Phys., 1991, 95, 141 CrossRef CAS.
- H. Wang, X. Sun and W. H. Miller, J. Chem. Phys., 1998, 108, 9726 CrossRef CAS.
- X. Sun, H. Wang and W. H. Miller, J. Chem. Phys., 1998, 109, 7064 CrossRef CAS.
- S. J. Cotton and W. H. Miller, J. Phys. Chem. A, 2013, 117, 7190 CrossRef CAS PubMed.
- P. Huo and D. F. Coker, J. Chem. Phys., 2010, 133, 184108 CrossRef CAS PubMed.
- P. Huo, T. F. Miller III and D. F. Coker, J. Chem. Phys., 2013, 139, 151103 CrossRef PubMed.
- I. R. Craig and D. E. Manolopoulos, J. Chem. Phys., 2004, 121, 3368 CrossRef CAS PubMed.
- S. Habershon, D. E. Manolopoulos, T. E. Markland and T. F. Miller III, Annu. Rev. Phys. Chem., 2013, 64, 387 CrossRef CAS PubMed.
- N. Ananth and T. F. Miller III, Mol. Phys., 2012, 110, 1009 CrossRef CAS.
- N. Ananth, J. Chem. Phys., 2013, 139, 124102 CrossRef PubMed.
- J. R. Duke and N. Ananth, J. Phys. Chem. Lett., 2015, 21, 4219 CrossRef PubMed.
- S. C. Althorpe, J. Chem. Phys., 2011, 134, 114104 CrossRef PubMed.
- T. J. H. Hele, M. J. Willatt, A. Muolo and S. C. Althorpe, J. Chem. Phys., 2015, 142, 191101 CrossRef PubMed.
- J. O. Richardson, J. Chem. Phys., 2015, 143, 134116 CrossRef PubMed.
- J. O. Richardson, J. Chem. Phys., 2016, 144, 114106 CrossRef PubMed.
- J. S. Cao and G. A. Voth, J. Chem. Phys., 1996, 105, 6856 CrossRef CAS.
- J. S. Cao and G. A. Voth, J. Chem. Phys., 1997, 106, 1769 CrossRef CAS.
- T. F. Miller III, J. Chem. Phys., 2008, 129, 194502 CrossRef PubMed.
- A. R. Menzeleev and T. F. Miller III, J. Chem. Phys., 2010, 132, 034106 CrossRef PubMed.
- A. R. Menzeleev, N. Ananth and T. F. Miller III, J. Chem. Phys., 2011, 135, 074106 CrossRef PubMed.
- J. S. Kretchmer and T. F. Miller III, J. Chem. Phys., 2013, 138, 134109 CrossRef PubMed.
- J. S. Kretchmer and T. F. Miller III, Inorg. Chem., 2016, 55, 1022 CrossRef CAS PubMed.
- X. Chen and V. S. Batista, J. Chem. Phys., 2006, 125, 224305 CrossRef PubMed.
- X. Kong, A. Markmann and V. S. Batista, J. Phys. Chem. A, 2016, 120, 3260 CrossRef CAS PubMed.
-
R. P. Feynman and A. R. Hibbs, Quantum Mechanics and Path Integrals, McGraw-Hill, New York, 1965, p. 14 Search PubMed.
-
D. Chandler, Introduction to Modern Statistical Mechanics, Oxford university press, 1987 Search PubMed.
-
V. May and O. Kühn, Charge and Energy Transfer Dynamics in Molecular Systems, Wiley-VCH, 2011 Search PubMed.
-
A. Nitzan, Chemical Dynamics in Condensed Phases, Oxford university press, 2006 Search PubMed.
- M. Rossi, M. Ceriotti and D. E. Manolopoulos, J. Chem. Phys., 2014, 140, 234116 CrossRef PubMed.
-
D. Frenkel and B. Smit, Understanding Molecular Simulation: from Algorithms to Applications, Academic Press, San Diego, 2002 Search PubMed.
- E. Wigner, Phys. Chem. Abt. B, 1932, 19, 203 Search PubMed.
- H. Eyring, J. Chem. Phys., 1935, 3, 107 CrossRef CAS.
- J. C. Keck, J. Chem. Phys., 1960, 32, 1035 CrossRef CAS.
- D. Chandler, J. Chem. Phys., 1978, 68, 2959 CrossRef CAS.
-
C. H. Bennet, Algorithms for Chemical Computations, American Chemical Society, Washington, DC, 1977, p. 63 Search PubMed.
- E. A. Carter, G. Ciccotti, J. T. Hynes and R. Kapral, Chem. Phys. Lett., 1989, 156, 472 CrossRef CAS.
- G. K. Schenter, B. C. Garrett and D. G. Truhlar, J. Chem. Phys., 2003, 119, 5828 CrossRef CAS.
- J. B. Watney, A. V. Soudackov, K. F. Wong and S. Hammes-Schiffer, Chem. Phys. Lett., 2006, 25, 268 CrossRef.
- M. Topaler and N. Makri, J. Chem. Phys., 1994, 101, 7500 CrossRef CAS.
- I. R. Craig and D. E. Manolopoulos, J. Chem. Phys., 2005, 122, 084106 CrossRef PubMed.
- M. Topaler and N. Makri, J. Phys. Chem., 1996, 100, 4430 CrossRef CAS.
- H. B. Gray and J. R. Winkler, Proc. Natl. Acad. Sci. U. S. A., 2005, 102, 3534 CrossRef CAS PubMed.
- L. Verlet, Phys. Rev., 1967, 159, 98 CrossRef CAS.
- E. Vanden-Eijnden and G. Ciccotti, Chem. Phys. Lett., 2006, 429, 310 CrossRef CAS.
- S. Kumar, D. Bouzida, R. H. Swendsen, P. A. Kollman and J. M. Rosenberg, J. Comput. Chem., 1992, 13, 1011 CrossRef CAS.
- S. Kumar, J. M. Rosenberg, D. Bouzida, R. H. Swendsen and P. A. Kollman, J. Comput. Chem., 1995, 16, 1339 CrossRef CAS.
- B. Roux, Comput. Phys. Commun., 1995, 91, 275 CrossRef CAS.
- R. A. Marcus and N. Sutin, Biochim. Biophys. Acta, 1985, 811, 265 CrossRef CAS.
- R. A. Marcus, J. Chem. Phys., 1965, 43, 3477 CrossRef CAS.
- R. A. Marcus, Discuss. Faraday Soc., 1960, 29, 21 RSC.
- R. A. Marcus, J. Chem. Phys., 1956, 24, 966 CrossRef CAS.
- I. Rips and J. Jortner, J. Chem. Phys., 1987, 87, 2090 CrossRef CAS.
- A. Garg, J. N. Onuchic and V. Ambegoakoar, J. Chem. Phys., 1985, 83, 4491 CrossRef CAS.
- P. Shushkov, J. Chem. Phys., 2013, 138, 224102 CrossRef PubMed.
- J. T. Hynes, J. Phys. Chem., 1986, 90, 3701 CrossRef CAS.
- J. N. Onuchic and P. G. Wolynes, J. Phys. Chem., 1988, 92, 6495 CrossRef CAS.
- D. L. Zusman, Chem. Phys., 1980, 49, 295 CrossRef.
- M. Morillo and R. I. Cukier, J. Chem. Phys., 1989, 91, 281 CrossRef.
-
M. Tuckerman, Statistical Mechanics: Theory and Molecular Simulation, Oxford University Press, 2010 Search PubMed.
|
| This journal is © The Royal Society of Chemistry 2016 |
 Open Access Article
Open Access Article![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) +
+ ![[V with combining circumflex]](https://www.rsc.org/images/entities/i_char_0056_0302.gif) , where
, where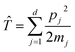
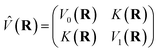
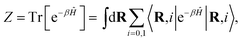
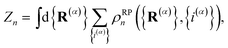
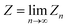 . The nuclear position and electronic state of the αth ring-polymer bead are given by (R(α),i(α)) and the usual periodic constraint of the ring polymer is satisfied by (R(n+1),i(n+1)) = (R(1),i(1)). The ring polymer distribution is given by
. The nuclear position and electronic state of the αth ring-polymer bead are given by (R(α),i(α)) and the usual periodic constraint of the ring polymer is satisfied by (R(n+1),i(n+1)) = (R(1),i(1)). The ring polymer distribution is given by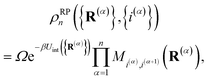
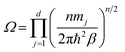 . The internal ring-polymer potential is given by
. The internal ring-polymer potential is given by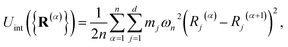
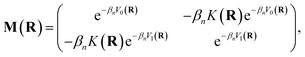
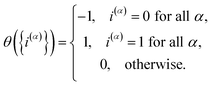
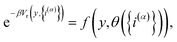
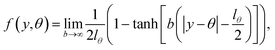
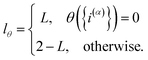
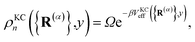
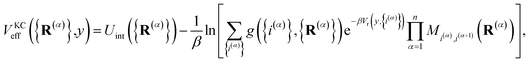
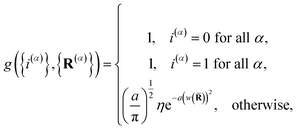
![[R with combining macron]](https://www.rsc.org/images/entities/b_char_0052_0304.gif) ) = (V0(
) = (V0(![[R with combining macron]](https://www.rsc.org/images/entities/b_char_0052_0304.gif) ) − V1(
) − V1(![[R with combining macron]](https://www.rsc.org/images/entities/b_char_0052_0304.gif) ))/K(
))/K(![[R with combining macron]](https://www.rsc.org/images/entities/b_char_0052_0304.gif) ) is the scaled difference in the diabatic potential surfaces,
) is the scaled difference in the diabatic potential surfaces, 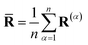 is the ring-polymer centroid coordinate, and a is a unitless convergence parameter chosen sufficiently large to converge the free energy (FE) of kink-pair formation given by ΔFKC = FKC(0) − FKC(−1), where
is the ring-polymer centroid coordinate, and a is a unitless convergence parameter chosen sufficiently large to converge the free energy (FE) of kink-pair formation given by ΔFKC = FKC(0) − FKC(−1), where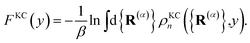
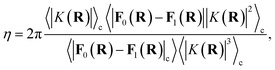
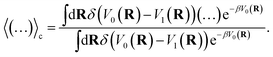
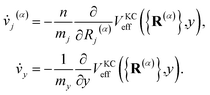
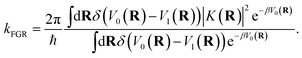
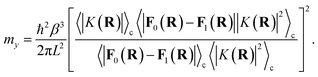
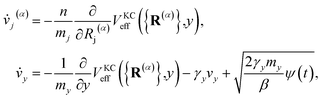
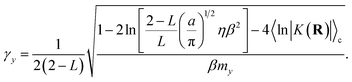
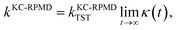
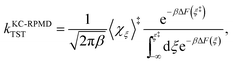
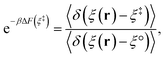
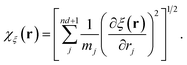
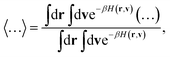
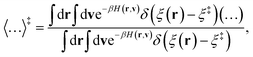
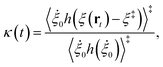
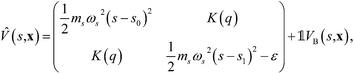
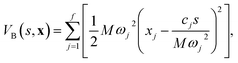
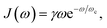
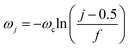
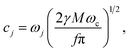
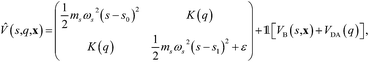
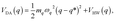
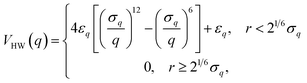
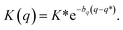
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 039
039![[s with combining macron]](https://www.rsc.org/images/entities/i_char_0073_0304.gif) ,ΔVeff), computed with respect to y, the ring-polymer centroid for the solvent coordinate,
,ΔVeff), computed with respect to y, the ring-polymer centroid for the solvent coordinate, ![[s with combining macron]](https://www.rsc.org/images/entities/i_char_0073_0304.gif) , and the difference between the true effective potential and the effective potential used to generate the dynamics during the sampling trajectories, ΔVeff, defined below. The FE profile F(y,
, and the difference between the true effective potential and the effective potential used to generate the dynamics during the sampling trajectories, ΔVeff, defined below. The FE profile F(y,![[s with combining macron]](https://www.rsc.org/images/entities/i_char_0073_0304.gif) ,ΔVeff) is calculated using umbrella sampling and the weighted histogram analysis method (WHAM)37,52–54 from the following umbrella sampling protocol. The KC-RPMD sampling trajectories are generated using a potential that restrains
,ΔVeff) is calculated using umbrella sampling and the weighted histogram analysis method (WHAM)37,52–54 from the following umbrella sampling protocol. The KC-RPMD sampling trajectories are generated using a potential that restrains ![[s with combining macron]](https://www.rsc.org/images/entities/i_char_0073_0304.gif) and y to s0 and y0, respectively, and has a weaker value of the steepness of the square-well restraining potential, b (eqn (10)), such that
and y to s0 and y0, respectively, and has a weaker value of the steepness of the square-well restraining potential, b (eqn (10)), such that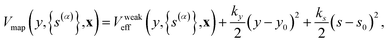
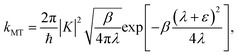
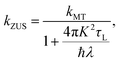
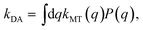
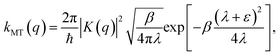
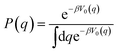


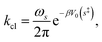

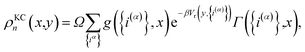
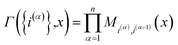 , and the penalty function in this case takes the form
, and the penalty function in this case takes the form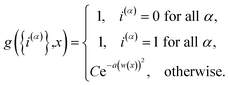
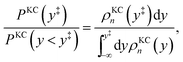
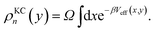
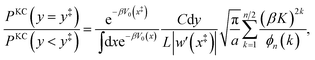
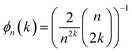 .
.