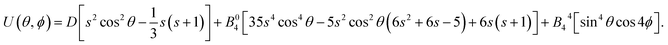Classical to quantum mechanical tunneling mechanism crossover in thermal transitions between magnetic states
Received
16th May 2016
, Accepted 21st June 2016
First published on 21st June 2016
Abstract
Transitions between states of a magnetic system can occur by jumps over an energy barrier or by quantum mechanical tunneling through the energy barrier. The rate of such transitions is an important consideration when the stability of magnetic states is assessed for example for nanoscale candidates for data storage devices. The shift in transition mechanism from jumps to tunneling as the temperature is lowered is analyzed and a general expression derived for the crossover temperature. The jump rate is evaluated using a harmonic approximation to transition state theory. First, the minimum energy path for the transition is found with the geodesic nudged elastic band method. The activation energy for the jumps is obtained from the maximum along the path, a saddle point on the energy surface, and the eigenvalues of the Hessian matrix at that point as well as at the initial state minimum used to estimate the entropic pre-exponential factor. The crossover temperature for quantum mechanical tunneling is evaluated from the second derivatives of the energy with respect to orientation of the spin vector at the saddle point. The resulting expression is applied to test problems where analytical results have previously been derived, namely uniaxial and biaxial spin systems with two-fold anisotropy. The effect of adding four-fold anisotropy on the crossover temperature is demonstrated. Calculations of the jump rate and crossover temperature for tunneling are also made for a molecular magnet containing an Mn4 group. The results are in excellent agreement with previously reported experimental measurements on this system.
1 Introduction
The assessment of the stability of magnetic states with respect to thermal fluctuations is an important problem in the theory of magnetism. The preparation of a magnetic system in a particular state can be destroyed by thermally-activated transitions to other available states.1,2 Thermal activation also needs to be taken into account when assessing the stability of a system with respect to external perturbations such as a magnetic field, contributing, for example, to the temperature dependence of hysteresis loops.3 Thermal stability is a particularly important issue in the context of novel information storage devices. As the size of such devices is reduced, the thermal stability of the magnetic states decreases. Methods for estimating the rate of magnetic transitions are, therefore, important tools when designing such systems.
Thermally-activated magnetic transitions involving a jump over an energy barrier are typically rare events on the time scale of oscillations of the magnetic moments, making direct simulations of spin dynamics an impractical way to calculate transition rates. This separation of time scales, however, makes it possible to apply statistical approaches such as transition state theory (TST)4 or Kramers theory.5 Within the harmonic approximation to TST (HTST)6 and within Kramers theory, the activation energy of a transition is given by the energy difference between the local minimum on the energy surface corresponding to the initial state and the highest energy on the minimum energy path connecting the initial and final state minima. In adaptions of these rate theories to magnetic systems,1,2,7–10 the magnitude of the magnetic vectors is either assumed to be constant as orientation changes, or it is treated as a fast variable obtained from self-consistency calculations for fixed values of the slow variables that specify orientation.11 The energy surface of a system of N magnetic moments is then a function of 2N degrees of freedom defining the orientation of the magnetic moments.
The mechanism of magnetic transitions can involve the formation of a temporary domain wall or soliton.2,9,12 This results in a flat energy barrier, i.e. the energy is practically constant along the minimum energy path in the region of high energy. An illustration of this is given below for Fe islands on a tungsten substrate. Kramers theory then overestimates the importance of recrossings and underestimates the transition rate. The transition state theory approach followed by explicit dynamical corrections is then preferable over Kramers' approach. Similar flat barrier issues arise in polymer escape problems where HTST followed by recrossing corrections has been shown to be a useful approach for estimating the transition rate.13
At low enough temperature, quantum tunneling through the energy barrier becomes the dominant transition mechanism and the rate can eventually become temperature independent. It is important to have a way to estimate the crossover temperature for tunneling when assessing the stability of a magnetic state. Quantum tunneling in spin systems has been a subject of a great deal of theoretical14–16 and experimental work17–19 over the past few decades. Molecular magnets have, in particular, been a focus of such studies. One example of a molecular magnet that has been studied extensively is the Mn4O3Cl(O2CCH3)3(dbm)3 molecule20 which has three Mn3+ ions and one Mn4+ and a total spin of s = 9/2. Experimental measurements of the rate of transitions between its magnetic states have been carried out as a function of temperature and reveal a crossover from activated transitions to nearly non-activated transitions. This experimental data is analyzed by classical and quantum mechanical calculations below.
The crossover from jumps to tunneling is in some cases abrupt, as in a first-order phase transition, but in other cases smooth, as in a second-order transition. In the latter the tunneling is thermally assisted. The shape of the energy barrier affects how sharp the transition is.21 A spin system can in some cases be mapped onto a particle system and methods developed for particles used to estimate the tunneling rate.22 Several theoretical studies of the crossover in uniaxial and biaxial spin models with two-fold anisotropy in a transverse magnetic field have been carried out using this approach.23–26 The presence of higher-order anisotropy can strongly affect the tunneling rate18,27 but is not included in this mapping approach.28 So far, systems with higher-order anisotropy have only been studied numerically by direct diagonalisation of the Hamiltonian.29,30
Here, a general approach for calculating the crossover temperature for thermally assisted tunneling involving uniform rotation of the spin vectors (the macro-spin approximation) is presented, and an equation derived in terms of the second derivatives of the energy of the system with respect to the orientation of the magnetic vector at the saddle point on the energy surface. For systems that are small enough compared to the correlation length determined by the strength of the exchange interaction between the spins, such as the molecular magnets discussed here, the uniform rotation mechanism is preferred over a mechanism where a temporary domain wall forms.2,12 By saddle point, we are referring to a first-order saddle point where the Hessian has one and only one negative eigenvalue. The formula reduces to known analytical solutions for simple spin systems with low order anisotropy, but can also be applied to more complex systems where the energy is evaluated using self-consistent field calculations.
The article is organized as follows: the methodology for estimating the jump rate based on harmonic transition state theory for magnetic systems is briefly reviewed for completeness in the following section, Section 2. Then, the crossover temperature for quantum mechanical tunneling is derived in Section 3. Applications are presented in Section 4, first to uniaxial and then biaxial systems, both with and without four-fold anisotropy, and finally to a molecular magnet which has been studied experimentally. A summary is presented in Section 5.
2 Jump rate
In order to set the stage for the discussion of the crossover temperature for tunneling, we first review briefly the methodology we use to calculate the mechanism and rate of thermally-activated jumps over the energy barrier.
The initial and final states of the system are characterized by local minima on the energy surface representing the system. The transition is characterized by the path on the energy surface for which the energy is at a minimum with respect to all orthogonal directions. Such a path is referred to as a minimum energy path (MEP). The MEP reveals the mechanism of the transition, for example whether the spins all rotate in a concerted way, a uniform rotation, or whether some rotate first and then others, the so-called temporary domain wall or soliton mechanism.2,9 Examples of the latter are shown in Fig. 1 for monolayer thick iron islands on a W(110) surface. In one case the island is elongated along the anisotropy axis, in the other case it is elongated perpendicular to the anisotropy axis. In either case, the energy barrier has small curvature at the top. The minimum energy path is calculated using the geodesic nudged elastic band (GNEB) method,31 which is an adaption of the nudged elastic band method32,33 to magnetic systems where the variables correspond to orientation of magnetic vectors and the MEP maps onto a path in a configuration space represented by a curved manifold due to the constraints on the length of the magnetic vectors. Such constraints arise when the length of the magnetic vectors is either fixed, as in a Heisenberg-type model, or is determined from self-consistent field calculations such as ab initio or semi-empirical models. Compared with the NEB method, GNEB involves an additional projection of the force vector to ensure that the magnetic constraints are satisfied and that a projection of the path tangent on the local tangent space of the configuration space properly decouples the spring force from the component of the energy gradient perpendicular to the path.
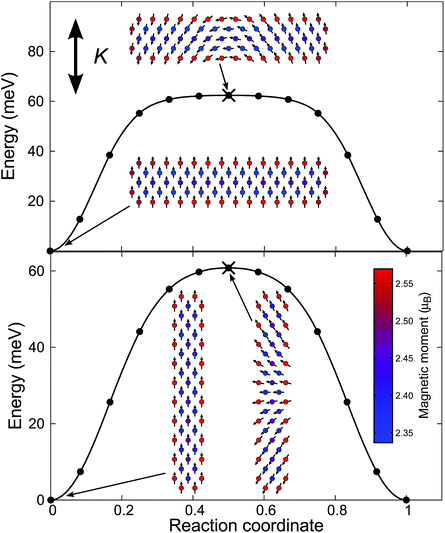 |
| | Fig. 1 Calculated minimum energy paths for magnetization reversal in Fe islands on a W(110) surface. The magnetic moments are calculated in a self-consistent way using the NCAA method.11 The direction of the anisotropy axis, K, is shown as well as a color coding for the size of the magnetic moment of each Fe atom. The island is elongated perpendicular (upper panel) or parallel (lower panel) to the anisotropy axis. In both cases, the minimum energy path is nearly flat at the maximum because the energy does not change much as the temporary domain wall propagates along the island. | |
Within HTST, the maximum energy along the MEP, E†, which corresponds to a saddle point, (θ, ϕ) = (θ†, ϕ†), on the energy surface, gives the activation energy of the transition as Ea = E† − Em, where Em is the energy of the initial state minimum. This gives the exponential dependence of the rate on temperature. The pre-exponential factor can be estimated by evaluating the Hessian and calculating its eigenvalues at the saddle point, ε†,j, and at the initial state minimum, εm,j. The HTST estimate of the rate of magnetic transitions is9,10
| | 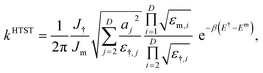 | (1) |
where
J† =
J(
θ†,
ϕ†) is a Jacobian evaluated at the saddle point, while
Jm is evaluated at the initial state minimum,
9 and
β = 1/
kBT. The lowest eigenvalue of the Hessian at the saddle point,
ε†,1, is negative and is skipped in the summation in
(1). The calculated rate of magnetization reversals using this approach for Fe islands of various size and shape on the W(110) surface
12 is in close agreement with experimentally measured rates,
34 even an observed maximum in the pre-exponential factor for islands of intermediate size that have nearly equal numbers of atoms on each side. The calculations have been carried out using both Heisenberg-type Hamiltonians as well as self-consistent field calculations based on a non-collinear extension of the Alexander–Anderson (NCAA) model
11 (see
Fig. 1).
In Kramers theory the rate estimate includes the curvature of the energy barrier at the saddle point. This results from a harmonic approximation in the estimate of the effect of recrossings due to fluctuating forces from the thermal bath.1,5 When the energy barrier is flat, as for example in magnetic transitions involving a transient domain wall, this rate estimate is too low because the harmonic approximation at the saddle point in the direction of the MEP is inaccurate. The HTST approach is more accurate in such cases, but should also be followed by calculation of the recrossing correction using short time scale dynamics simulations.35
3 Onset of quantum mechanical tunneling
The thermally-averaged transition rate is| | 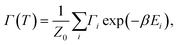 | (2) |
where Z0 is the partition function of the initial state and Γi is the quantum mechanical transition probability from state i with energy Ei. Statistical Feynman path integrals can be used to write the rate in terms of the imaginary-time (τ = it) action, S.36 A stationary phase approximation37,38 then gives an estimate of the transition rate as| | | Γ ∝ exp(−S[q(τ)]inst/ħ), | (3) |
where q(τ) is a periodic trajectory with period τ = βħ. This special trajectory, often referred to as the instanton, corresponds to a stationary point of the action, a saddle point on the action surface.36,39,40
For a spin of length s, the action is given by41–43
| | 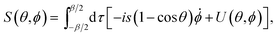 | (4) |
where
U(
θ,
ϕ) is the energy surface. From here on we use atomic units with
ħ = 1,
μB = 1/2 and the mass and charge of an electron have unit magnitude,
e = −1 and
me = 1. A scaled gyromagnetic ratio is defined as
![[g with combining tilde]](https://www.rsc.org/images/entities/i_char_0067_0303.gif)
=
g/2. The first term in
(4) is related to Berry phase
44,45| | 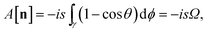 | (5) |
where
Ω is an area of a surface bounded by
γ.
To find paths for which S(θ, ϕ) is stationary, we consider the first order variation of the action
| | 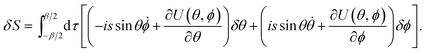 | (6) |
Setting δS = 0 gives classical equations of motion which correspond to Landau–Lifshitz equations in imaginary time:
| | 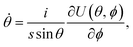 | (7) |
| | 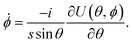 | (8) |
These equations have two types of solutions. The first one is trivial, θ = θ0 and ϕ = ϕ0, corresponding to a stationary point of the potential, U0 ≡ U(θ0, ϕ0). If the stationary point is taken to be the saddle point (θ†, ϕ†),
| | | Sjump = βU(θ†, ϕ†) = βE†, | (9) |
this trivial solution corresponds to the high-temperature jump mechanism.
The second solution is the instanton – a closed path corresponding to constant energy. In the limit of zero temperature, T → 0, i.e. β → ∞, it corresponds to quantum tunnelling from the ground state. As the temperature is increased, the amplitude of the instanton trajectory decreases until it becomes infinitesimal:
| | | θ(τ) = θ† + δθ, ϕ(τ) = ϕ† + δϕ, | (10) |
just below the crossover temperature. The instanton eventually collapses to the saddle point on the energy surface, (
θ†,
ϕ†) at
T =
Tc.
In order to find the crossover temperature, Tc, the action is expanded to second order around the saddle point on the energy surface,
| | 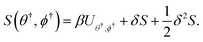 | (11) |
Since δS = 0 at the saddle point, we focus on δ2S:
| | 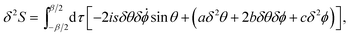 | (12) |
where
| | 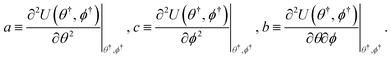 | (13) |
At the saddle point, δ2S is a quadratic form of the Hessian which has one and only one negative eigenvalue. As the temperature decreases below Tc, a second negative eigenvalue of δ2S appears, corresponding to the quantum delocalization. This signals the transition from thermally-activated jumps to quantum tunnelling.
Since the instanton is a closed trajectory, δθ and δϕ can be expanded in Fourier series:
| | 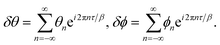 | (14) |
Here,
ϕn and
θn are complex numbers that satisfy
| | 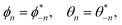 | (15) |
since
δθ and
δϕ are real.
δ2S from
(12) can now be rewritten using
(14) as
| | 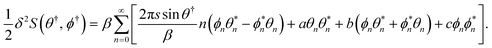 | (16) |
The matrix representing the quadratic form of the action has a block form
| |  | (17) |
where
k = 2π
s![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif)
sin
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ†
θ†/
β. To obtain the eigenvalues of this matrix we need to solve the equation
After some algebra, one obtains
| | 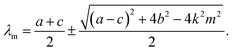 | (19) |
In order to determine the temperature at which two eigenvalues are negative, we first inspect the two eigenvalues corresponding to m = 0:
| | 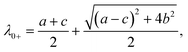 | (20) |
| | 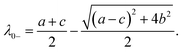 | (21) |
Clearly λ0+ > 0, but λ0− is negative if
| | 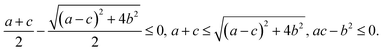 | (22) |
Since ac − b2 is the determinant of the Hessian at the saddle point, this condition is fulfilled. The second negative eigenvalue must come from m > 1. Substitution of β = 1/kBT and the expression for k into the negative branch, λm,−, in (19), gives
| | 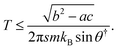 | (23) |
The highest temperature for which a second negative eigenvalue exists can be determined from the m = 1 case:
| | 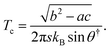 | (24) |
This equation can be rewritten as
| | 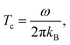 | (25) |
where
| | 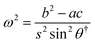 | (26) |
and
a,
b,
c are the second derivatives defined in
(13). This provides an estimate of the crossover temperature for tunneling in terms of second derivatives of the energy evaluated at the saddle point. For model Hamiltonians, the derivatives can typically be evaluated analytically. For more complicated descriptions of the magnetic system, such as self-consistent field calculations, the derivatives can be evaluated numerically from the forces, which in turn can be obtained using a force theorem.
11
This expression for the crossover temperature of spin tunneling can be compared with the corresponding equation for particle tunneling,46
| | 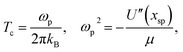 | (27) |
where now the second derivative is taken along the unstable mode at the saddle point of the energy surface and
μ is the effective mass corresponding to the unstable mode.
4 Applications
In this section, the crossover temperature for various spin models is calculated. When only a two-fold anisotropy axis is included in the model, analytical solutions are available for comparison. But when four-fold anisotropy is included, so as to better represent physical systems, only numerical solutions based on direct diagonalization of the Hamiltonian have been presented so far. Here, analytical expressions in terms of the second derivatives of the energy are obtained also for such models. Finally, the jump rate as well as the crossover temperature is evaluated for a model of the Mn4 molecular magnet and the results compared with experimental measurements.
4.1 Uniaxial systems with two- and four-fold anisotropy
A Hamiltonian which has, for example, been used to describe the Mn12 – ac molecular magnet17,19 and has been studied theoretically47 can be written as| | H = −DSz2 − BSz4 − ![[g with combining tilde]](https://www.rsc.org/images/entities/i_char_0067_0303.gif) HxSx − C(S−4 + S+4), HxSx − C(S−4 + S+4), | (28) |
where D, B and C are the anisotropy constants. The third term is the Zeeman energy associated with an applied field Hx. The last term corresponds to transverse anisotropy. The z-axis is the easy axis (the orientation for which the energy is minimal) and has four-fold symmetry, while the x- and y-axis are medium axes, and y = ±x is the hard axis (the orientation for which the energy is maximal). The corresponding energy surface is| | U(θ, ϕ) = −Ds2(cos2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ + k1s2 θ + k1s2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos4 cos4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ + 2k2s2 θ + 2k2s2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin4 sin4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ θ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos(4ϕ) + 2hx cos(4ϕ) + 2hx![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ θ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ϕ), ϕ), | (29) |
where| | k1 ≡ B/D, k2 ≡ C/D, hx ≡ ![[g with combining tilde]](https://www.rsc.org/images/entities/i_char_0067_0303.gif) Hx/2Ds. Hx/2Ds. | (30) |
The saddle point on the potential surface is located at θ† = π/2, ϕ† = 0. At a certain critical field, Hc, the energy barrier disappears. Applying the condition ∂U/∂θ|θ† = ∂2U/∂θ2|θ† = 0 gives the critical field as
The second derivatives at the saddle point are
a = 8Cs4 + ![[g with combining tilde]](https://www.rsc.org/images/entities/i_char_0067_0303.gif) sHx − 2Ds2, sHx − 2Ds2, |
c = 32Cs4 + ![[g with combining tilde]](https://www.rsc.org/images/entities/i_char_0067_0303.gif) sHx, sHx, |
After computing the coefficients of the quadratic form of the action, the formula for the crossover temperature in the presence of an applied field Hx is obtained:
| | 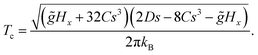 | (32) |
Fig. 2 shows the calculated crossover temperature as a function of the strength of the applied magnetic field for the following choice of parameters: D/kB = 0.548K, B/kB = 1.17 × 10−3K and C/kB = 2.19 × 10−5K. These are the same parameter values as considered by Park.47 If the four-fold anisotropy parameter, C, is set to zero and the system only contains two-fold anisotropy, the crossover temperature is zero in the absence of a magnetic field. Even a small higher-order anisotropy term has a large effect on the crossover temperature.
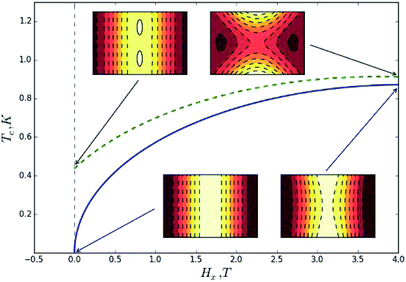 |
| | Fig. 2 Crossover temperature Tc for a uniaxial system with two-fold and four-fold anisotropy as a function of the strength of an applied magnetic field, H. The Hamiltonian is given by (28). The solid line shows results for a system with two-fold anisotropy, C = 0, while the dashed line shows results for a system with four-fold anisotropy. All parameters are taken from ref. 47. By adding higher-order anisotropy, the crossover temperature becomes finite even in the absence of a magnetic field. The insets show contour graphs of the energy surfaces (two-fold anisotropy below, four-fold above) at zero field and at a field of 4T. | |
If the model only contains two-fold anisotropy, B = C = 0, the potential surface becomes
| | U(θ, ϕ) = −Ds2(cos2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ + 2hx θ + 2hx![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ θ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ϕ). ϕ). | (33) |
The spin problem can then be mapped onto a particle in a one-dimensional potential,
| | 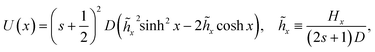 | (34) |
and an analytical expression obtained for the crossover temperature for the particle.
23 Here,
(32) simplifies to (by setting
C = 0 in
(32))
| | 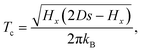 | (35) |
which is the same result as has been obtained previously using the particle mapping method by Garanin
et al. (see eqn (13) in
ref. 48).
Another spin Hamiltonian for which the crossover temperature has been estimated using the particle mapping method is49
| | | H = −DSz2 + BSy2 − HxSx. | (36) |
The corresponding particle model is unusual in that it involves coordinate-dependent mass.
The energy surface for the spin vector is
| | U(θ, ϕ) = Ds2(−cos2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ + λ θ + λ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin2 sin2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ θ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin2 sin2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ϕ − 2hx ϕ − 2hx![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ θ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ϕ), hx ≡ Hx/2Ds, λ ≡ B/D. ϕ), hx ≡ Hx/2Ds, λ ≡ B/D. | (37) |
By evaluating the second derivatives, a, b and c at the saddle point, θ† = π/2, ϕ† = 0 gives
The resulting expression for the crossover temperature is
| | 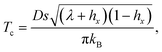 | (38) |
which coincides with the results obtained by the mapping to a particle model (see eqn (18) in
ref. 49). Again, this is an illustration that for simple systems, our method gives results that agree with those obtained previously by other methods. Our approach has the advantage that it can also be applied to more complicated models, including for example Hamiltonians with a four-fold anisotropy axis in Heisenberg-type models and self-consistent field calculations, as illustrated in
Fig. 2.
4.2 Biaxial system with two- and four-fold anisotropy
Another interesting case is the biaxial system with four-fold transverse anisotropy and a magnetic field applied along the hard direction. This has been used to describe the Fe8 molecular magnet.27 The Hamiltonian is| | H = −DSz2 + B(Sx2 − Sy2) − ![[g with combining tilde]](https://www.rsc.org/images/entities/i_char_0067_0303.gif) HxSx + C(S−4 + S+4), HxSx + C(S−4 + S+4), | (39) |
where D, B and C are anisotropy constants. In this case, the z-axis is the easy axis, the y-axis is the medium axis and the x-axis is the hard axis. The corresponding energy surface is| | U(θ, ϕ) = −Ds2(cos2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ + k1 θ + k1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin2 sin2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ θ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2ϕ + k2 2ϕ + k2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin4 sin4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ θ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 4ϕ + 2hx 4ϕ + 2hx![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ θ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ϕ), ϕ), | (40) |
where| | | k1 ≡ B/D, k2 ≡ 2Cs2/D, hx ≡ Hx/2Ds. | (41) |
The saddle point is located at (θ† = π/2 and ϕ† = ϕ0), where ϕ0 can be found as a solution of a third-order algebraic equation,
| | −16k2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos3 cos3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ϕ0 + (8k2 − 2k1)cos ϕ0 + (8k2 − 2k1)cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ϕ0 + hx = 0. ϕ0 + hx = 0. | (42) |
The second derivatives at the saddle point are
a = −2Ds2(1 − k1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2ϕ0 + 2k2 2ϕ0 + 2k2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 4ϕ0 − hx 4ϕ0 − hx![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ϕ0), ϕ0), |
c = −2Ds2(2 − k1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2ϕ0 + 8k2 2ϕ0 + 8k2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 4ϕ0 − hx 4ϕ0 − hx![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ϕ0), ϕ0), |
and the expression for the crossover temperature becomes
| | 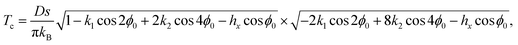 | (43) |
where
ϕ0 is the real solution of
(42).
Fig. 3 shows the dependence of Tc on the applied magnetic field for parameters that are chosen to represent an Fe8 molecular magnet, D/kB = 0.292K, B/kB = 0.046K and C/kB = −2.9 × 10−5K.50 The calculated crossover temperature is in the range between 0.4 and 0.7 K which agrees well with experimental results on the Fe8 molecular magnet.27,51,52
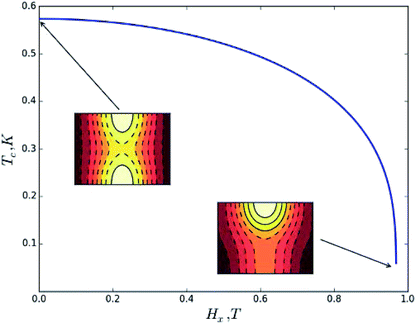 |
| | Fig. 3 Dependence of Tc on the applied field Hx for a biaxial spin model with four-fold transverse anisotropy. The parameters are chosen to represent the Fe8 molecular magnet.50 Insets show the energy surface at particular values of the applied magnetic field. | |
4.3 Molecular Mn4 magnet
The transition rate has been experimentally measured as a function of temperature for the Mn4 molecular magnet by Aubin et al.20 and a crossover observed. The full chemical formula for the molecule is Mn4O3Cl(O2CCH3)3(dbm)3. It is a trigonal pyramidal complex with one Mn4+ and three Mn3+ ions. The spins of the Mn3+ ions point in the same direction but the spin of Mn4+ points in the opposite direction (see inset in Fig. 4). The total spin is 9/2 and the transitions correspond to uniform rotation of the four spins.
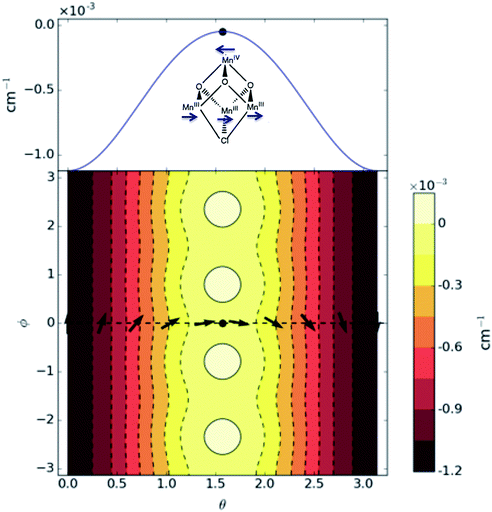 |
| | Fig. 4 Characterization of the spin Hamiltonian for the Mn4 molecular magnet (Mn4O3Cl(O2CCH3)3(dbm)3). Upper: Minimum energy path for the rotation of the total spin s = 9/2 vector. The energy along the path is given in units of 10−3 cm−1. The inset shows the structure of the Mn4 core of the molecule with the one Mn4+ and three Mn3+ ions and the orientation of the four spins at the saddle point configuration. Lower: Contour graph of the energy surface U(θ, ϕ). One of the four equivalent minimum energy paths is shown with a dashed line and the orientation of the magnetic momentum vector indicated at a few points along the path. The saddle point is indicated with a filled circle both in the upper and lower panels. | |
Various experimental measurements of this molecular magnet have established the following Hamiltonian model for the system:
| | 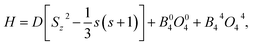 | (44) |
where
O04 = 35
Sz4 − 30
s(
s + 1)
Sz2 + 25
Sz2 + 6
s(
s + 1) and
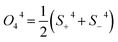
. The parameters
D and
B04 have been determined from various experiments (not rate measurements) by Aubin
et al.20 to be −0.53 cm
−1 and −7.4 × 10
−5 cm
−1, respectively. The last term in the Hamiltonian corresponds to four-fold anisotropy and the parameter
B44 can be chosen to have a similar, small value as has been determined for analogous molecular magnets.
53–56 Without it, the tunneling rate is zero because of a Kramers degeneracy.
20
Both the calculated high temperature jump rate as well as the crossover temperature can be compared with the measured rate for this molecular magnet. The energy surface corresponding to the Mn4 Hamiltonian is
| | 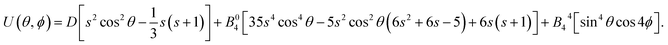 | (45) |
The system has four equivalent saddle points on the energy surface: θ† = π/2, ϕ† = 0, π/2, π, 3π/2, see Fig. 4. Here, the value of D is slightly smaller than the value estimated by Aubin et. al.,20D = −0.41 cm−1, and the value of B44 is taken to be −8.5 × 10−4 cm−1. The jump rate calculated using HTST is Γ(T) = 2.3 × 106Hzexp(−11.5K/T) and is shown in Fig. 5.
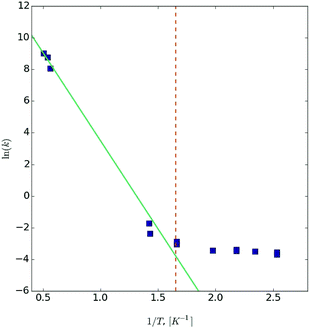 |
| | Fig. 5 The calculated jump rate using harmonic transition state theory (green line), given by (1), and the crossover temperature (dashed red line) given by (25) using the Hamiltonian in (44) and parameters chosen to represent the Mn4 molecular magnet. The experimentally measured20 transition rate is shown with filled squares. Excellent agreement is obtained between the calculated and measured results. | |
The second derivatives needed to estimate the crossover temperature are
| | | a = 2Ds2 − 60B04s3(s + 1) + 50B04s2 − 4B44s4, c = −32B44s4, b = 0. | (46) |
Inserting the values of the parameters gives a crossover temperature of
which is in close agreement with the reported experimental data
20 as shown in
Fig. 5.
Therefore, both the high-temperature jump rate obtained from HTST and the crossover temperature obtained from the formula presented here are in close agreement with the experimental measurements.
5 Summary
A method is presented for finding the crossover temperature of thermally-activated tunneling in a magnetic system that is characterized by a spin vector with orientation prescribed by continuous angular variables. Several model systems are used to verify that the general equation derived here in terms of second derivatives of the energy at the saddle point agrees with analytical results previously obtained for specific, simple Hamiltonians. More complicated Hamiltonians including four-fold anisotropy so as to better describe molecular magnets are also studied, and analytical equations for the crossover temperature presented. A more detailed study is made of the Mn4 molecular magnet where both the high-temperature jump rate and the crossover temperature for tunneling are calculated and compared with experimental data. Excellent agreement is obtained.
The crossover temperature for tunneling in molecular magnets is low partly because the energy barriers are small. For larger systems, such as metal islands on substrates, the energy barriers can be significantly larger and the onset of tunneling can be expected to occur at higher temperature. The method presented here makes it possible to estimate the crossover temperature for tunneling in a magnetic system described by a single spin vector as long as the second derivatives of the energy with respect to the angles describing the orientation of the vector can be evaluated at the saddle point on the energy surface.
The equation derived here for the crossover temperature for tunneling in a magnetic system is significantly different from the analogous equation for a particle system in that all second derivatives of the energy at the saddle point are included, while only the second derivative along the unstable mode enters the particle equation. The essential difference between the two systems is the separation of the particle Hamiltonian into a kinetic and potential energy part, which does not occur for the magnetic systems. As a result, the magnetic systems’ Hamiltonians are more difficult to deal with. The derivation of the crossover temperature for systems where the transition mechanism is not a uniform rotation as well as a method for calculating the rate of thermally-activated tunneling remain to be completed, but are being developed using an approach that is analogous to previous studies of atomic systems57,58 and will be presented at a later time.
Acknowledgements
This work was supported by the Government of Russian Federation (Grant 074-U01), RFBR (Grant 14-02-00102), the Icelandic Research Fund, the Göran Gustafsson Foundation for Research in Natural Sciences and Medicine (Grant 1303A) and the Academy of Finland FiDiPro program (grant 263294).
References
- W. F. Brown Jr, IEEE Trans. Magn., 1979, 15, 1196 CrossRef.
- H.-B. Braun, J. Appl. Phys., 1994, 76, 6310 CrossRef CAS.
- M. Moskalenko, P. F. Bessarab, V. M. Uzdin and H. Jónsson, AIP Adv., 2016, 6, 025213 CrossRef.
- H. Pelzer and E. Wigner, Z. Phys. Chem., Abt. B, 1932, 15, 445 Search PubMed; E. Wigner, Trans. Faraday Soc., 1938, 34, 29 RSC.
- H. A. Kramers, Physica, 1940, 7, 284 CrossRef CAS.
- G. H. Vineyard, J. Phys. Chem. Solids, 1957, 3, 121 CrossRef CAS.
- P. B. Visscher and R. Zhu, Phys. B, 2012, 407, 1340 CrossRef CAS.
- G. Fiedler, J. Fidler, J. Lee, T. Schrefl, R. L. Stamps, H. B. Braun and D. Suess, J. Appl. Phys., 2012, 111, 093917 CrossRef.
- P. F. Bessarab, V. M. Uzdin and H. Jónsson, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 85, 184409 CrossRef.
- P. F. Bessarab, V. M. Uzdin and H. Jónsson, Z. Phys. Chem., 2013, 227, 1543 CAS.
- P. F. Bessarab, V. M. Uzdin and H. Jónsson, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 89, 214424 CrossRef.
- P. F. Bessarab, V. M. Uzdin and H. Jónsson, Phys. Rev. Lett., 2013, 110, 020604 CrossRef PubMed.
- H. Mökkönen, T. Ikonen, T. Ala-Nissila and H. Jónsson, J. Chem. Phys., 2015, 142, 224906 CrossRef PubMed.
-
Quantum Tunneling of Magnetization – QTM'94, ed. L. Gunther and B. Barbara, Kluwer Academic, Dordrecht, 1995 Search PubMed.
-
E. M. Chudnovsky and J. Tejada, Macroscopic Quantum Tunneling of the Magnetic Moment, Cambridge University Press, New York, 1998 Search PubMed.
-
D. Gatteschi, R. Sessoli and J. Villain, Molecular Nanomagnets, Oxford University Press, New York, 2006 Search PubMed.
- L. Bokacheva, A. D. Kent and M. A. Walters, Phys. Rev. Lett., 2000, 85, 4803 CrossRef CAS PubMed.
- K. M. Mertes, Y. Zhong and M. P. Sarachik,
et al.
, Europhys. Lett., 2001, 55, 874 CrossRef CAS.
- W. Wernsdorfer, M. Murugesu and G. Christou, Phys. Rev. Lett., 2006, 96, 057208 CrossRef CAS PubMed.
- S. M. J. Aubin,
et al.
, J. Am. Chem. Soc., 1998, 120, 4991 CrossRef CAS.
- E. M. Chudnovsky, Phys. Rev. A, 1992, 46, 8011 CrossRef.
- V. V. Ulyanov and O. B. Zaslavskii, Phys. Rep., 1992, 214, 179 CrossRef.
- E. M. Chudnovsky and D. A. Garanin, Phys. Rev. Lett., 1997, 79, 4469 CrossRef.
- C.-S. Park, S.-K. Yoo and D.-H. Yoon, Phys. Rev. B: Condens. Matter Mater. Phys., 2000, 61, 11618 CrossRef CAS.
- G.-H. Kim and E. M. Chudnovsky, Europhys. Lett., 2000, 52, 681 CrossRef CAS.
- D. A. Garanin and E. M. Chudnovsky, Phys. Rev. B: Condens. Matter Mater. Phys., 2000, 63, 024418 CrossRef.
- W. Wernsdorfer and R. Sessoli, Science, 1999, 284, 133 CrossRef CAS PubMed.
- S. A. Owerre and M. B. Paranjape, Phys. Rep., 2015, 546, 1 CrossRef.
- D. H. Kang and G.-H. Kim, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 74, 184418 CrossRef.
- G. H. Kim, D. H. Kang and M. C. Shin, Eur. Phys. J. B, 2011, 83, 63 CrossRef CAS.
- P. F. Bessarab, V. M. Uzdin and H. Jónsson, Comput. Phys. Commun., 2015, 196, 335 CrossRef CAS.
- G. Mills, H. Jónsson and G. Schenter, Surf. Sci., 1995, 324, 305 CrossRef CAS.
-
H. Jónsson, G. Mills and K. W. Jacobsen, Nudged Elastic Band Method for Finding Minimum Energy Paths of Transitions, in Classical and Quantum Dynamics in Condensed Phase Simulations, ed. B. J. Berne, G. Ciccotti and D. F. Coker, World Scientific, 1998, p. 385 Search PubMed.
- S. Krause, G. Herzog, T. Stapelfeldt, L. Berbil-Bautista, M. Bode, E. Y. Vedmedenko and R. Wiesendanger, Phys. Rev. Lett., 2009, 103, 127202 CrossRef CAS PubMed.
- J. C. Keck, Adv. Chem. Phys., 1967, 13, 85 CrossRef.
- V. A. Benderskii, V. I. Goldanskii and D. E. Makarov, Phys. Rep., 1993, 233, 195 CrossRef.
- W. H. Miller, J. Chem. Phys., 1975, 62, 1899 CrossRef CAS.
- C. Callen and S. Coleman, Phys. Rev. D: Part. Fields, 1977, 16, 1762 CrossRef.
- G. Mills, G. K. Schenter, D. E. Makarov and H. Jónsson, Chem. Phys. Lett., 1997, 278, 91 CrossRef CAS.
-
G. Mills, G. K. Schenter, D. E. Makarov and H. Jónsson, RAW Quantum transition state theory, in Classical and Quantum Dynamics in Condensed Phase Simulations, ed. B. J. Berne, G. Ciccotti and D. F. Coker, World Scientific, 1998, p. 405 Search PubMed.
- J. KIauder, Phys. Rev. D: Part. Fields, 1979, 19, 2349 CrossRef.
- E. Kochetov, J. Math. Phys., 1995, 36, 4667 CrossRef.
-
E. Fradkin, Field Theories of Condensed Matter Physics, Cambridge University Press, New York, 2013, ch 7.2 Search PubMed.
- M. V. Berry, Proc. R. Soc. London, Ser. A, 1984, 392, 45 CrossRef.
- A. Garg, Am. J. Phys., 2010, 78, 661 CrossRef CAS.
- V. I. Goldanskii, Sov. Phys. Dokl., 1959, 4, 74 Search PubMed.
- C.-S. Park, J. Magn. Magn. Mater., 2003, 267, 281 CrossRef CAS.
- D. A. Garanin, X. Martinez Hidalgo and E. M. Chudnovsky, Phys. Rev. B: Condens. Matter Mater. Phys., 1998, 57, 13639 CrossRef CAS.
- G.-H. Kim, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 11847 CrossRef CAS.
- R. Caciuffo,
et al.
, Phys. Rev. Lett., 1998, 81, 4744 CrossRef CAS.
- C. Sangregorio, T. Ohm, C. Paulsen, R. Sessoli and D. Gatteschi, Phys. Rev. Lett., 1997, 78, 4645 CrossRef CAS.
- A. Caneschi,
et al.
, J. Magn. Magn. Mater., 1998, 177, 1330 CrossRef.
- A. L. Barra, D. Gatteschi and R. Sessoli, Phys. Rev. B: Condens. Matter Mater. Phys., 1997, 56, 8192 CrossRef CAS.
- I. Mirebeau, M. Hennion, H. Casalta, H. Anders, H.-U. Güdel, A. V. Irodova and A. Caneschi, Phys. Rev. Lett., 1999, 83, 628 CrossRef CAS.
- S. Hill, J. A. A. J. Perenboom, N. S. Dalal, T. Hathaway, T. Stalcup and J. S. Brooks, Phys. Rev. Lett., 1998, 80, 2453 CrossRef CAS.
- E. Del Barco, A. D. Kent, S. Hill, J. M. North, N. S. Dalal, E. M. Rumberger, D. N. Hendrikson, N. Chakov and G. Christou, J. Low Temp. Phys., 2005, 140, 119 CrossRef CAS.
- H. Jónsson, Proc. Natl. Acad. Sci. U. S. A., 2011, 108, 944 CrossRef PubMed.
- D. M. Einarsdóttir, A. Arnaldsson, F. Óskarsson and H. Jónsson, Lect. Notes. Comput. Sci., 2012, 7134, 45 Search PubMed.
|
| This journal is © The Royal Society of Chemistry 2016 |
 Open Access Article
Open Access Article
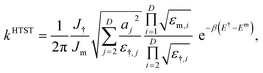
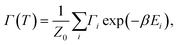
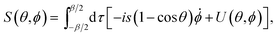
![[g with combining tilde]](https://www.rsc.org/images/entities/i_char_0067_0303.gif) = g/2. The first term in (4) is related to Berry phase44,45
= g/2. The first term in (4) is related to Berry phase44,45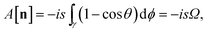
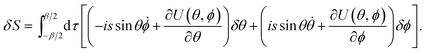
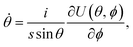
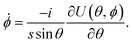
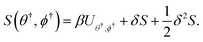
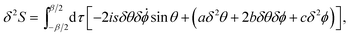
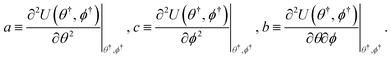
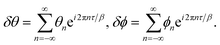
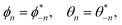
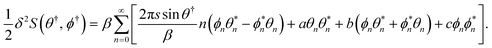

![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin
sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ†/β. To obtain the eigenvalues of this matrix we need to solve the equation
θ†/β. To obtain the eigenvalues of this matrix we need to solve the equation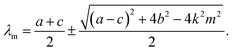
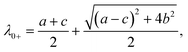
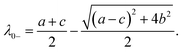
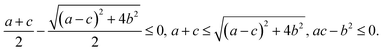
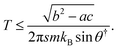
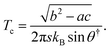
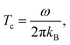
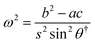
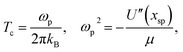
![[g with combining tilde]](https://www.rsc.org/images/entities/i_char_0067_0303.gif) HxSx − C(S−4 + S+4),
HxSx − C(S−4 + S+4),![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ + k1s2
θ + k1s2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos4
cos4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ + 2k2s2
θ + 2k2s2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin4
sin4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ
θ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos(4ϕ) + 2hx
cos(4ϕ) + 2hx![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin
sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ
θ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos
cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ϕ),
ϕ),![[g with combining tilde]](https://www.rsc.org/images/entities/i_char_0067_0303.gif) Hx/2Ds.
Hx/2Ds.![[g with combining tilde]](https://www.rsc.org/images/entities/i_char_0067_0303.gif) sHx − 2Ds2,
sHx − 2Ds2,![[g with combining tilde]](https://www.rsc.org/images/entities/i_char_0067_0303.gif) sHx,
sHx,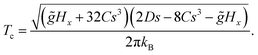

![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ + 2hx
θ + 2hx![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin
sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ
θ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos
cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ϕ).
ϕ).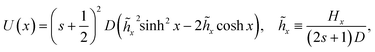
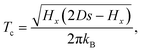
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ + λ
θ + λ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin2
sin2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ
θ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin2
sin2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ϕ − 2hx
ϕ − 2hx![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin
sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ
θ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos
cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ϕ), hx ≡ Hx/2Ds, λ ≡ B/D.
ϕ), hx ≡ Hx/2Ds, λ ≡ B/D.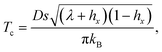
![[g with combining tilde]](https://www.rsc.org/images/entities/i_char_0067_0303.gif) HxSx + C(S−4 + S+4),
HxSx + C(S−4 + S+4),![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ + k1
θ + k1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin2
sin2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ
θ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos
cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2ϕ + k2
2ϕ + k2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin4
sin4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ
θ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos
cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 4ϕ + 2hx
4ϕ + 2hx![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin
sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ
θ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos
cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ϕ),
ϕ),![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos3
cos3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ϕ0 + (8k2 − 2k1)cos
ϕ0 + (8k2 − 2k1)cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ϕ0 + hx = 0.
ϕ0 + hx = 0.![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos
cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2ϕ0 + 2k2
2ϕ0 + 2k2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos
cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 4ϕ0 − hx
4ϕ0 − hx![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos
cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ϕ0),
ϕ0),![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos
cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2ϕ0 + 8k2
2ϕ0 + 8k2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos
cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 4ϕ0 − hx
4ϕ0 − hx![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos
cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ϕ0),
ϕ0),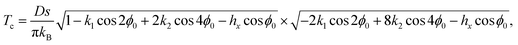

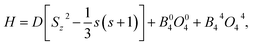
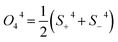 . The parameters D and B04 have been determined from various experiments (not rate measurements) by Aubin et al.20 to be −0.53 cm−1 and −7.4 × 10−5 cm−1, respectively. The last term in the Hamiltonian corresponds to four-fold anisotropy and the parameter B44 can be chosen to have a similar, small value as has been determined for analogous molecular magnets.53–56 Without it, the tunneling rate is zero because of a Kramers degeneracy.20
. The parameters D and B04 have been determined from various experiments (not rate measurements) by Aubin et al.20 to be −0.53 cm−1 and −7.4 × 10−5 cm−1, respectively. The last term in the Hamiltonian corresponds to four-fold anisotropy and the parameter B44 can be chosen to have a similar, small value as has been determined for analogous molecular magnets.53–56 Without it, the tunneling rate is zero because of a Kramers degeneracy.20