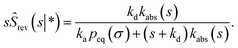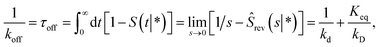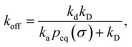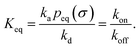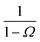DOI:
10.1039/C6FD00104A
(Paper)
Faraday Discuss., 2016,
195, 421-441
The intrinsic rate constants in diffusion-influenced reactions
Received
30th April 2016
, Accepted 30th June 2016
First published on 1st July 2016
Abstract
Intrinsic rate constants play a dominant role in the theory of diffusion-influenced reactions, but usually as abstract quantities that are implicitly assumed to be known. However, recently it has become clear that modeling complex processes requires explicit knowledge of these intrinsic rates. In this paper we provide microscopic expressions for the intrinsic rate constants for association and dissociation processes of isotropically interacting particles and illustrate how these rates can be computed efficiently using rare event simulations techniques. In addition, we address the role of the orientational dynamics, for particles interacting via anisotropic potentials.
1 Introduction
The association and dissociation of two particles are elementary steps in many processes in biology, such as receptor–ligand and enzyme–substrate binding in cell signaling, and protein–DNA binding in gene regulation. Also, in materials science association and dissociation play a central role, e.g. in the self-assembly of colloidal particles, the formation of micro-emulsions, or the phase behavior of polymer solutions. In these processes, the particles typically come into contact via diffusion, after which they bind with a rate that depends on the intrinsic association rate constant; conversely, the associated particles dissociate with an intrinsic dissociation rate, after which they move apart via diffusion.
In the past decades, theories of diffusion-influenced reactions have been developed that show how the effective rate constants depend on the diffusion constants of the particles, their cross section, their interaction potential, and the intrinsic association and dissociation rate constants.1 However, these theories assume, a priori, given intrinsic association and dissociation rate constants. Similarly, techniques to simulate networks of chemical reactions have been developed, in which the particles typically have an idealized shape, move by diffusion, and react upon contact with given intrinsic rate constants.2–7 In parallel, simulation techniques have been developed that enable the calculation of association and dissociation rate constants for pairs of particles that interact via potentially complex interaction potentials.8,9 Yet, these techniques typically compute effective rate constants, which result from the combined effects of diffusion, the interaction potential, and binding upon contact. Moreover, also in experiments typically the effective rate constants are measured. How the intrinsic rate constants depend on the interaction potential, the cross section, and the diffusion constants of the particles, has thus received little attention.
In general, an association–dissociation reaction is a complicated non-Markovian many-body problem that cannot be solved analytically. The reason is that the process of binding generates non-trivial spatio-temporal correlations between the positions of the reactants, which depend on the history of the association and dissociation events. Capturing these correlations requires knowledge of not only the diffusion constants, the interaction potential, and the cross section, but also the intrinsic rate constants.
In dilute systems, however, typically only the effective rate constants are needed to describe the system's dynamics at long times.10,11 When the concentrations are low, the time it takes for two reactants to meet each other is much longer than the time they spend in close proximity: once the reactants are near each other, they either rapidly bind or rapidly diffuse back into the bulk. Similarly, after a dissociation event, the two reactants either quickly rebind or rapidly move away from each other. Under these conditions, it is often possible to integrate-out the dynamics at the molecular scale, and describe the association–dissociation reaction as a Markovian process with effective association and dissociation rates.10,11 While these effective rates depend on the intrinsic rate constants, only the effective rate constants determine the dynamics at the relevant length and time scales.10,11
Yet, it is now clear that even in dilute systems, spatio-temporal correlations at the molecular scale can dramatically change the behavior of the system at the macroscopic scale.4,12 In the case of multi-site protein modification, enzyme–substrate rebindings can lead to the loss of ultra-sensitivity and even bi-stability, essentially because rebindings can turn a distributive mechanism into a processive one.4,12 In such a scenario, even the long-time dynamics cannot be described by effective rate constants: one needs to know the diffusion constants, the cross sections, and the intrinsic rate constants. Moreover, while spatial heterogeneity at the molecular scale can arise from these non-trivial spatio-temporal correlations, in cellular systems microscopic heterogeneity is also imposed via molecular structures. In fact, it is now becoming increasingly recognized that cells exploit the spatial heterogeneity of micro-domains, lipid rafts, clusters, and scaffolds as a computational degree of freedom for enhancing information transmission.13,14 Modeling the reactions in these spatially heterogeneous systems often requires knowledge of the intrinsic rate constants. Last but not least, for simulating association and dissociation reactions in 1D and 2D, knowledge of the intrinsic rate constants is even more pertinent, because no well-defined effective rate constant exists in the long-time limit.
In this manuscript, we provide microscopic expressions for the intrinsic rate constants, and illustrate how these expressions can be used to compute rate constants in rare-event simulation techniques such as Transition Interface Sampling (TIS)15–17 and Forward Flux Sampling (FFS).18,19 While computing both the forward and backward rate typically requires two separate simulations, we will show how, by exploiting analytical expressions for the binding and escape probability, both the association and dissociation rate constants (and hence the equilibrium constant) can be obtained in one single simulation. We discuss the relationship with the technique developed by Northrup and coworkers8 for computing effective association rates. Finally, we address the role of orientational dynamics in association and dissociation reactions.
2 Theory of diffusion-influenced reactions
We consider two particles A and B that interact via an isotropic interaction potential U(r), and move with an interparticle diffusion constant D = DA + DB, where DA and DB are the diffusion constants of A and B, respectively. Upon contact at the interparticle distance σ, the particles can associate with a rate that is determined by the intrinsic associate rate constant ka, and, when bound, the two can dissociate with an intrinsic dissociation rate kd. Following the work of Agmon and Szabo,1 we re-derive in the Appendix the following central results. The effective association rate constant is given by| | 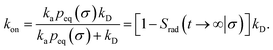 | (1) |
Here, kD is the diffusion-limited rate constant, which determines the rate at which the two particles diffuse towards each other, and peq(σ) ≃ e−βU(σ), with β = 1/(kBT), the inverse temperature, is the equilibrium probability that they are at the distance σ. The survival probability Srad(t → ∞|σ) = kD/(kapeq(σ) + kD) is the probability that the two particles, given that they are at contact, escape into the bulk before binding to each other. Hence, the effective association rate is given by the rate at which the two particles get in contact, which is determined by kD, and the probability 1 − Srad(t → ∞|σ) = kapeq(σ)/(kapeq(σ) + kD) that upon contact, they bind.
The effective dissociation rate is given by
| | 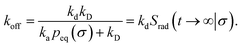 | (2) |
The effective dissociation rate is thus given by the dissociation rate kd times the probability Srad(t → ∞|σ) = kD/(kapeq(σ) + kD) that the particles upon dissociation diffuse away from each other and escape into the bulk.
It can also be verified that the equilibrium constant is given by
| | 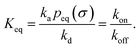 | (3) |
At this stage, a few points are worthy of note. First, these results hold for isotropic, but otherwise arbitrary interaction potentials U(r). Secondly, the contact distance σ serves to define the dividing surface that separates the bound from the unbound state. This surface is usually taken to be near the free-energy barrier that separates the bound from the unbound state. The precise location of this dividing surface is somewhat arbitrary, as the effective rate constants cannot by definition depend on the choice made for σ. This is in marked contrast to the intrinsic rate constants ka and kd and the diffusion-limited rate kD, which all sensitively depend on σ. Thirdly, the diffusion-limited rate constant depends not only on σ and D, but also on the interaction potential U(r). For arbitrary interaction potentials U(r), no analytical expression for kD is, in general, available. However, when σ is chosen to be beyond the range rc of the interaction potential, then an exact expression is well known—the Smoluchowski diffusion-limited reaction rate constant:20
Moreover, when σ > rc, then U(σ) = 0, and peq(σ) = 1. In this scenario, the effective rate constants are given by:
| | 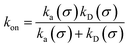 | (5) |
| | 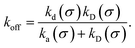 | (6) |
Here, and below, we have written
ka =
ka(
σ),
kd =
kd(
σ) and
kD =
kD(
σ) to remind ourselves that these rate constants, in contrast to the effective rate constants
kon and
koff, depend on our choice for
σ.
3 Effective positive flux expression
To obtain the intrinsic rate constants in computer simulations, we need expressions in terms of microscopic quantities that can be measured in the simulation. We will focus on the dissociation pathway, and the dissociation rate koff. To compute this rate, we use the “effective positive flux” expression of van Erp and coworkers.15–17 The progress of the dissociation reaction is quantified via a parameter λ(r), which depends on the separation r between the particles A and B. For simplicity, we use λ = r. A series of interfaces is chosen, r0, r1, …, rn−1, rn, such that r0 is deep in the bound state and rn is in the unbound state. Strictly speaking the unbound state is defined by rn → ∞, a point to which we will return in the next section. Defining the history-dependent functions indicator h![[scr B, script letter B]](https://www.rsc.org/images/entities/char_e13f.gif) and h
and h![[scr U, script letter U]](https://www.rsc.org/images/entities/char_e534.gif) such that h
such that h![[scr B, script letter B]](https://www.rsc.org/images/entities/char_e13f.gif) = 1 and h
= 1 and h![[scr U, script letter U]](https://www.rsc.org/images/entities/char_e534.gif) = 0 if the system was more recently in the bound state B (r < r0) than in the unbound state U (r > rn), and h
= 0 if the system was more recently in the bound state B (r < r0) than in the unbound state U (r > rn), and h![[scr B, script letter B]](https://www.rsc.org/images/entities/char_e13f.gif) = 0 and h
= 0 and h![[scr U, script letter U]](https://www.rsc.org/images/entities/char_e534.gif) = 1 otherwise, the rate constant koff for transitions from B to U is given by15
= 1 otherwise, the rate constant koff for transitions from B to U is given by15| | 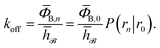 | (7) |
Here, ΦB,j is the flux of trajectories coming from the bound state B (with r < r0) that cross rj for the first time; thus, ΦB,n is the flux of trajectories from the bound state towards the unbound state, r > rn, and ΦB,0 is the flux reaching the first interface r0. The factor ![[h with combining macron]](https://www.rsc.org/images/entities/i_char_0068_0304.gif)
![[scr B, script letter B]](https://www.rsc.org/images/entities/char_e13f.gif) is the average fraction of time that the system spends in the bound state B. P(rn|r0) is the probability that a trajectory that reaches r0 subsequently arrives at interface rn instead of returning to the bound state r0. The expression thus states that the total flux of trajectories from the bound state to the unbound state is the flux of trajectories from B to r0 multiplied by the probability that such a trajectory will later reach rn before returning to r0. P(rn|r0) can be expressed as the product of the probabilities P(ri+1|ri) that a trajectory that comes from r0 and crosses ri for the first time will subsequently reach ri+1 instead of returning to r0:
is the average fraction of time that the system spends in the bound state B. P(rn|r0) is the probability that a trajectory that reaches r0 subsequently arrives at interface rn instead of returning to the bound state r0. The expression thus states that the total flux of trajectories from the bound state to the unbound state is the flux of trajectories from B to r0 multiplied by the probability that such a trajectory will later reach rn before returning to r0. P(rn|r0) can be expressed as the product of the probabilities P(ri+1|ri) that a trajectory that comes from r0 and crosses ri for the first time will subsequently reach ri+1 instead of returning to r0:| | 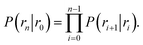 | (8) |
Combining eqn (7) and (8), the effective dissociation rate can thus be expressed as
| | 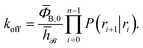 | (9) |
The individual factors P(ri+1|ri) can be determined in a Transition Interface Sampling15 (TIS) or a Forward Flux Sampling18,19 (FFS) simulation, as the fraction of trajectories crossing the interface ri that reach the interface ri+1 instead of returning to r0. FFS and TIS are both based on the effective positive flux expression, eqn (7), but differ in the way they construct the path ensembles.
4 Intrinsic dissociation rate and effective positive flux
To obtain a microscopic expression for the intrinsic dissociation rate kd, we rewrite eqn (9) as| | 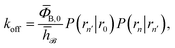 | (10) |
where 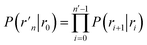 and
and 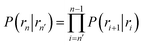 . Now, the crux is to define rn′ = σ. Comparing eqn (10) with eqn (2), we can then make the following identifications:
. Now, the crux is to define rn′ = σ. Comparing eqn (10) with eqn (2), we can then make the following identifications:| | 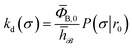 | (11) |
| | 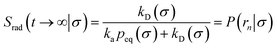 | (12) |
Eqn (11) provides a microscopic expression for the intrinsic dissociation rate, and is one of the central results of this paper. It shows that the intrinsic dissociation rate is the flux of trajectories that come from the bound state and cross the dividing surface rn′ = σ. The expression makes explicit that the intrinsic dissociation rate depends on the choice for σ. Also eqn (12) highlights the idea that not only the intrinsic rates, but also the diffusion-limited rate kD depends on this choice. We further iterate that σ need not be chosen beyond the interaction range of the potential; the expressions hold for any choice of σ.
The microscopic expressions of eqn (11) and (12) make it possible to obtain both the effective dissociation rate koff and the intrinsic dissociation rate kd from computer simulations. Again, transition interface sampling15 and forward flux sampling18,19 are particularly well suited, because they are both based on the effective positive flux expression, eqn (7).
In fact, by choosing the cross-section σ beyond the range rc of the interaction potential, it is possible to obtain from one simulation not only the intrinsic dissociation rate kd and effective dissociation rate koff, but also the intrinsic association rate ka and effective association rate kon, and hence the equilibrium constant Keq. One TIS/FFS simulation yields both kd, from eqn (11), and P(rn|σ) = Srad(t → ∞|σ), from eqn (12). Yet, when σ > rc (and U(σ) = 0), we know that the latter is also given by
| | 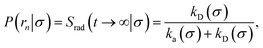 | (13) |
with
kD = 4π
σD, as discussed in Section 2. In other words, having computed
P(
rn|
σ) in the TIS/FFS simulation, we can use the above expression and the analytical solution
kD = 4π
σD, to obtain not only
kd but also
ka:
| | 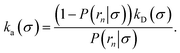 | (14) |
From kd and ka, we obtain the equilibrium constant Keq = ka/kd, from which we then find kon = Keqkoff.
As pointed out above, the effective rates are strictly defined for rn → ∞, meaning that eqn (11) and (14) are also only valid in that limit. However, to keep the simulations tractable, in practice one would like to use an interface at finite rn. In the next section we derive an expression that holds for finite interface values rn.
5 Computing the intrinsic rates for an interface at finite rn
While the intrinsic association rate constant kd does not rely on taking the position of the last interface rn → ∞, the intrinsic rate constant ka does (see eqn (14)). To obtain an expression for ka for a finite value of rn, we start by rewriting the effective association rate eqn (6) as the sum of reciprocal intrinsic rates:| | 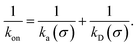 | (15) |
Since the effective association rates are independent on the choice of the dividing surface σ, we can choose to set the dividing surface at rn > σ
| | 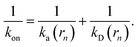 | (16) |
Combining the above two equations and rearranging yields
| | 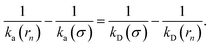 | (17) |
To make progress we need to relate the intrinsic rate constants ka(σ) and ka(rn). This relation is provided by linking the intrinsic dissociation rates, eqn (11) at the respective surfaces, yielding
| | 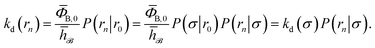 | (18) |
Since detailed balance implies Keq = ka(σ)/kd(σ) = ka(rn)/kd(rn), the desired relation for the intrinsic association rate constants is
| | | ka(rn) = ka(σ)P(rn|σ). | (19) |
Inserting eqn (19) into eqn (17) and rearranging yields
| | 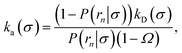 | (20) |
where
Ω ≡
kD(
σ)/
kD(
rn) which, using
kD(
b) = 4π
σb, reduces to
Ω =
σ/
rn.
Eqn (20) provides an explicit expression for the intrinsic association rate
ka for finite
rn, featuring a correction factor 1/(1 −
Ω). For
rn → ∞,
Ω vanishes and the expression reduces to
eqn (14). However, the correction factor decays slowly with
rn, and in practice it cannot be neglected. Since
Ω is known analytically,
eqn (20) turns this approach into a feasible strategy for computing both
kd and
ka in TIS and FFS, which directly give access to
P(
rn|
σ). Lastly, combining this expression with
eqn (5) and
(6), we obtain the following expressions for the effective on and off rates, respectively:
| | 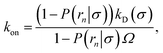 | (21) |
| | 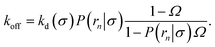 | (22) |
5.1 Illustrative example
As an illustration of the above scheme we numerically evaluated eqn (20) for a two particle system undergoing Brownian dynamics (BD).22 The interaction potential between the two particles is given by| | 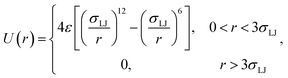 | (23) |
where σLJ sets the length-scale of the Lennard–Jones potential, ε sets the well depth, and r is the interparticle distance. In the simulations σLJ = 5 nm, ε = 10kBT. The length of the simulation box is 60σLJ. We evaluate kd(σ) and P(rn|σ) using one single FFS simulation. First, we fix the cross section σ = 3σLJ, just beyond the cut-off distance of the potential. Interfaces were set at r = {1.3, 1.5, 2.0, 2.5, 3.0, 3.2, 3.4, 3.6, 3.8, 4.0, 4.2, 4.4, 4.6, 4.8, 5.0, 5.5, 6.0, 6.5}, in units of σLJ. From each interface, 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 trajectories are started and the conditional probability as in eqn (8) is calculated.
000 trajectories are started and the conditional probability as in eqn (8) is calculated.
We test the independence of eqn (20) on the location of the final interface by varying rn, while keeping σ = 3.0σLJ fixed. As seen in Fig. 1 (left) the value of ka(σ) is independent of the position of the rn surface. Note, however, that the correction factor 1/(1 − Ω) is not negligible, even for rn = 6.5σLJ.
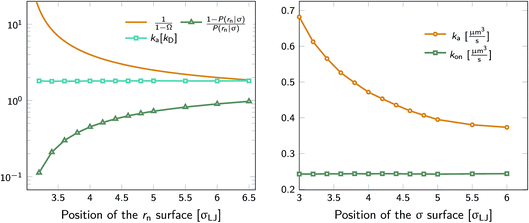 |
| | Fig. 1 The intrinsic rate constant for the isotropic Lennard–Jones potential. Left: ka(σ) as a function of the position of last interface, rn in units of kD(σ), for a fixed cross section σ = 3σLJ. The correction factor 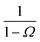 and the factor (1 − P(rn|σ))/P(rn|σ) are also shown. As expected, the value of ka(σ) remains constant as rn is varied. Right: ka(σ) and kon as a function of the cross section σ. The position of the last interface, rn, is kept constant at 6.5σLJ. It is seen that while ka varies with σ, kon does not. and the factor (1 − P(rn|σ))/P(rn|σ) are also shown. As expected, the value of ka(σ) remains constant as rn is varied. Right: ka(σ) and kon as a function of the cross section σ. The position of the last interface, rn, is kept constant at 6.5σLJ. It is seen that while ka varies with σ, kon does not. | |
Next, we plot in Fig. 1 (right) the dependence of the intrinsic association rate ka(σ) on the location of the cross section σ, keeping rn = 6.5σLJ constant. The intrinsic association rate constant decreases with σ, but the effective rate constant kon is independent of σ, as expected.
The intrinsic dissociation rate kd(σ) is evaluated viaeqn (11). From kd(σ) and ka(σ), the values of kon and koff, are evaluated using eqn (5) and (6). Keq is calculated using eqn (3). The results are summarized in Table 1.
Table 1 Comparison of the effective rate constants as determined via different approaches: FFS, using eqn (3) and (18)–(22); the autocorrelation function, eqn (25) and (26); the power spectrum, eqn (27). The Table shows good agreement between the values of kon and koff, and hence Keq, obtained via these different approaches
| |
K
eq/10−3 μm3 |
k
on/μm3 s−1 |
k
off/s−1 |
| FFS |
5.127 |
0.2417 |
47.14 |
| Time autocorrelation |
5.145 |
0.2589 |
50.33 |
| Power spectrum |
5.145 |
0.2571 |
49.99 |
5.2 Validation of the effective rate constants
To validate the values of kon and koff obtained from the FFS simulations, we calculate these values also from a brute force Brownian dynamics simulation of the same system of two particles. First, the equilibrium constant Keq is evaluated using the analytic expression| | 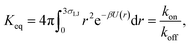 | (24) |
where U(r) is given by eqn (23), and the integral is over the bound state 0 < r < 3σLJ.
The brute force simulation generates a time trace n(t), switching from the bound state with n(t) = 1 to the unbound state with n(t) = 0. From this time trace we generate a time autocorrelation function
| | 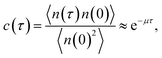 | (25) |
that relaxes exponentially with a decay constant
μ given by
Fig. 2 shows this time autocorrelation function. The simulation results are fitted to eqn (25) to obtain the value of μ and by combining with eqn (24) and (26), the effective rate constants are obtained.
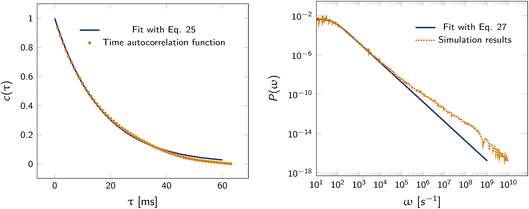 |
| | Fig. 2 Left: The autocorrelation function c(τ) obtained from simulation is fit to eqn (25), yielding μ = 59.9236 s−1. Right: Power spectrum P(ω) fitted to eqn (27) to determine the value of μ = 59.5192 s−1. In both cases the effective rate constants are calculated by solving eqn (26) and (24). | |
Alternatively, we can generate a power spectrum P(ω) from the same n(t) time trace.10 The power spectrum for a random telegraph process with switching rates kf and kb is given by
| | 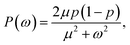 | (27) |
where
ω is the frequency,
μ =
kf +
kb is the decay rate and
p =
kf/(
kf +
kb). The low-frequency part of the power spectrum as obtained from the simulations is expected to be given by the above expression, with
kf =
kon/
V and
kb =
koff (see
ref. 10).
Table 1 compares the values of
kon and
koff as obtained
via this scheme, with those from FFS, using
eqn (3) and
(18–22), and the results from the time auto-correlation function,
eqn (25) and
(26). It is seen that the values are in very good agreement.
6 Relation to other techniques
Northrup et al.8,21 provide a method to compute the effective association rate directly from eqn (1)| | | kon = [1 − Srad(t → ∞|σ)]kD(σ) ≡ β∞kD(σ), | (28) |
where β∞ = 1 − Srad(t → ∞|σ) is defined as the probability that particles starting at a distance σ associate rather than diffuse away and escape into the bulk. This probability can be computed explicitly by generating trajectories from an isotropically distributed ensemble of configurations of particles at distance σ. To prevent needlessly long trajectories, Northrup et al. introduced an additional surface c at which they halt the trajectories. The computed association probability β ≠ β∞ is now defined as the chance to associate rather than to escape to c. They then relate β to β∞ using a branching method, adding up all probabilities of paths that leave c but return to σ rather than reach infinity,21 yielding a geometric series that can be written as| | 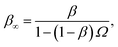 | (29) |
where Ω = kD(σ)/kD(c) = σ/c. As the association probability β∞ is related to the intrinsic rate constant through β∞ = ka(σ)/(ka(σ) + kD(σ)), it follows that| | 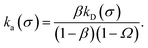 | (30) |
The link with the intrinsic rate constant expression eqn (20) can be made by realizing that the association probability β = 1 − P(c|σ), leading to
| | 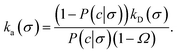 | (31) |
This expression is identical to eqn (20), with c = rn. Strikingly, while derived in a different way, the intrinsic rate expression based on the Northrup method yields the same correction factor as our analysis for finite interfaces.
7 Anisotropic interactions
The above derivations hold for particles interacting via an isotropic pair potential. However, many molecular systems, such as proteins and ligands, have anisotropic interactions that depend on the relative orientation of the particles. For such systems it is not immediately clear whether the expressions derived above are still valid. The point is that while the Boltzmann distribution of the particles' orientations is isotropic beyond the cutoff distance of the potential, the distribution in the ensemble of reactive trajectories, as harvested by TIS and FFS, is not: in these reactive trajectories, the particles tend to have their patches aligned. Naturally, one can still define and measure an effective association and dissociation rate. Yet, the simple expressions derived in the Appendix are no longer valid.
Following Northrup et al.,8,21 one can always express the effective association rate for anisotropic particles as
where the diffusion-limited rate constant is again
kD(
σ) = 4π
Dσ, and
β∞ is given by
eqn (29). Now, we define the intrinsic rate
ka(
σ)
via β∞ ≡
ka(
σ)/(
ka(
σ) +
kD(
σ)), which yields
| | 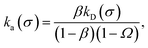 | (33) |
with
Ω, as before, given by
Ω =
kD(
σ)/
kD(
c). This yields an explicit expression for
ka(
σ) in terms of the probability
β of binding rather than reaching the surface
rn =
c, starting from an isotropic distribution at the surface
σ; this is indeed the essence of the technique of Northrup
et al.21 When the distribution, as generated in the TIS/FFS simulation, is isotropic at
σ then
eqn (20) and
(33) with
β = 1 −
P(
rn|
σ) are equivalent and both can be used. The problem arises when we want to connect
eqn (33) to the expression used in TIS/FFS to compute the dissociation rate in the case that the distribution at
σ is not isotropic. The principal idea of the scheme presented in Sections 4 and 5 is that
P(
rn|
σ), as obtained in a TIS/FFS computation of the dissociation rate, is given by the analytical result
kD(
σ)/(
ka(
σ) +
kD), for
rn → ∞. We could thus use this analytical result to obtain the intrinsic rate
ka(
σ) in
eqn (13) and
(14); the expression that relates
P(
rn|
σ) to
ka(
σ) when
rn is finite, is
eqn (20). However, in the case of anisotropic interaction potentials the distribution of reactive trajectories at the
σ interface can also become anisotropic. In that case one can no longer identify
P(
rn|
σ) as obtained in an TIS/FFS simulation with 1 −
β in
eqn (33), and
(20) or
(33) cannot be used to obtain
ka(
σ) from a TIS/FFS simulation. In summary, when the distribution at
σ as obtained in the TIS/FFS simulation is isotropic, we expect both
eqn (33) and
(20) to hold. However, if the distribution is not isotropic
eqn (20) ceases to be valid.
Nevertheless, even when the potential is anisotropic, eqn (20) still provides a route towards computing ka(σ). Indeed if, at a certain interface σ′ sufficiently far away from contact, the distribution of trajectories has become uniform the intrinsic rate for that surface is given by eqn (20)
| | 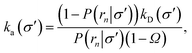 | (34) |
where
Ω =
kD(
σ′)/
kD(
rn), and
rn >
σ′. Since we know that the effective association rate is independent of the choice of the dividing surface, we can write
| | 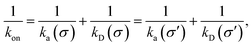 | (35) |
even if the distribution at
σ is anisotropic. Inserting
eqn (34) into this identity gives
| | 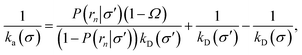 | (36) |
or, rearranging,
| | 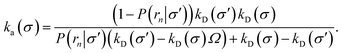 | (37) |
This expression reduces to eqn (20) when σ = σ′, as expected. For σ ≠ σ′, the expression holds even when the distribution at σ is anisotropic, provided that the distribution at σ′ is isotropic. The value of ka(σ) thus obtained via a TIS/FFS computation of the dissociation pathway, yielding an anisotropic distribution at σ, is the same as that would have been obtained from a simulation of the association pathway via the Northrup scheme starting from a uniform distribution at σ.
Inserting eqn (36) into (35) yields
| | 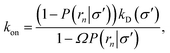 | (38) |
which is indeed identical to
eqn (21) with
σ =
σ′. Since
kon is independent of the interface
σ′, the rate given by
eqn (38) as a function of
σ′ should reach a constant value. Any deviation from this limiting value is due to a loss of isotropy. Hence, this expression provides a criterion for testing the isotropy requirement.
7.1 Illustrative example
We consider a system comprising two patchy particles interacting via a pair potential that consists of several contributions. The particles interact via a center–center potential Vcc(r) = Vcc-rep(r) + Vcc-att(r) based on the distance r between the centers of mass, that is in turn built up from a repulsive and an attractive potential. Additionally, there is an attractive patch–patch pair interaction Vpp(δ) based on the distance δ between two points (patches) located on either particle's surface. Fig. 3 illustrates this setup. The total pair interaction potential is thus| | | V(r,δ) = Vcc-rep(r) + Vcc-att(r) + Vpp(δ). | (39) |
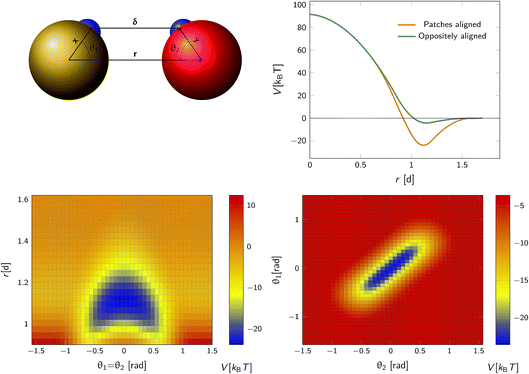 |
| | Fig. 3 The anisotropic interaction potential. Top left: The particles interact via a combination of a center–center potential Vcc(r) and a patch–patch attraction Vpp(δ) between the small patches on the surface of the particle. Top right: Total interaction potential Vcc(r) + Vpp(r − d) for two particles with perfectly aligned complementary patches (orange solid curve), and oppositely aligned patches Vcc(r) + Vpp(r + d) (dark green curve). The existence of patches introduces a strongly attractive bound state with the aligned particles in close contact. Bottom left: Heat map of the potential as a function of the distance between centres of mass r and the angle between the patch vector and inter-particle vector, θ1 and θ2 (see also top left) with θ1 = θ2. Bottom right: Heat map of potential as a function of θ1, θ2 given r = 1.1d. Note the relatively narrow range of orientations over which strong bonding occurs. | |
Note that δ implicitly depends on the location of the patch, and hence on the orientation of the particle. The potential Vcc-rep(r), Vcc-att(r) and Vpp(δ) have the simple quadratic form
| | 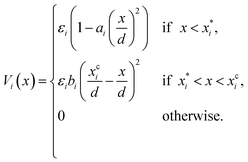 | (40) |
where the index
i refers to one of the labels {cc-rep, cc-att, pp}, and
d is the particle diameter and sets the length scale. The overall strength
εi, the stiffness
ai and the parameter
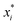
, which combined with
ai determines the range of the potential, are free parameters. Cut-offs
xci and smoothing parameters
bi are fixed by requiring continuity and differentiability at
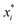
. These potentials give us a firm control over the potential shape, and allow for easy integration with potentials that are short-ranged and highly orientation-specific. For our illustrative purposes, we take the following parameters:
εcc-rep = 100
kBT,
acc-rep = 1 and
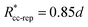
, implying
bcc-rep = 2.6036 and
Rccc-rep = 1.1764
d;
εpp = 20
kBT,
app = 20 and
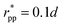
, implying
bpp = 5 and
rcpp = 0.5
d; and
εcc-att = 10
kBT,
acc-att = 1 and
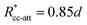
, implying
bcc-rep = 2.6036 and
Rccc-rep = 1.1764
d.
As an illustration we plot in Fig. 3 the total inter-particle potential as a function of r when the two complementary patches are aligned to face each other, so that δ = r − d. A narrow attractive well arises when the two particles are in close contact. In the same plot we also give the inter-particle potential as a function of r when the two complementary patches are oppositely aligned (with the patches facing in opposite directions) so that δ = r + d. Here, there is only a very shallow attractive interaction at contact, caused by the isotropic center–center potential Vcc(r). In Fig. 3 we also demonstrate the orientational dependence of the attractive potential, showing that the attractive interaction is highly sensitive to misalignment.
A Brownian dynamics (BD) simulation employing an anisotropic potential requires translation as well rotational dynamics. We use a first order quasi-symplectic BD integrator which works particularly well for orientational dynamics,23 and can be straightforwardly combined with FFS. We performed an FFS simulation, with interfaces based on the binding energy when the particles are within the range of the potential,23 and beyond that with interfaces based on the center-to-center distance r: r = {1.5, 1.6, 1.8, 2.0, 2.2, 2.4, 2.6, 2.8, 3.0, 3.5, 5.5, 6.5, 7.5} in units of d. From each interface, 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 trajectories are started, and the conditional probability as in eqn (8) is calculated.
000 trajectories are started, and the conditional probability as in eqn (8) is calculated.
To illustrate that eqn (20) does not hold when the distribution at σ is not isotropic, we evaluated ka(σ) using this equation for a fixed cross section σ = 1.5d, see Fig. 4. The range of the anisotropic interaction potential depends on the orientation, but even when the patches are aligned (and the range is maximal), the potential approaches zero beyond 1.5d (see Fig. 3); this is indeed why we have chosen the cross-section to be σ = 1.5d. Fig. 4 shows ka(σ) as a function of the position of the last interface, rn. It also shows the factors 1/(1 − Ω) = 1/(1 − σ′/rn) and 1 − P(rn|σ′)/P(rn|σ′), which both depend on rn. However, while for the isotropic potential, ka(σ) is independent of rn as long as σ (and rn) are beyond the range of the interaction potential (see Fig. 1), here this is not the case, because the distribution at σ is not isotropic. This shows that eqn (20) cannot be used for anisotropic interactions, if at σ the orientational distribution of the particles is still anisotropic.
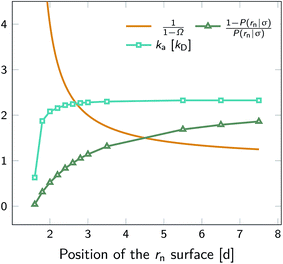 |
| | Fig. 4 The intrinsic rate constant ka(σ) from eqn (20) (in units of kD(σ)) as a function of the position of the last interface, rn, for the anisotropic interaction potential shown in Fig. 3. The cross section σ surface is kept constant at 1.5d. The correction factor 1/(1 − Ω) = 1/(1 − σ′/rn) and the factor (1 − P(rn|σ′))/P(rn|σ′) are also shown. In contrast to the behavior for the isotropic potential, Fig. 1, the value of ka(σ) depends on rn, even when rn is beyond the range of the potential r > σ = 1.5d. This is because for this anisotropic potential the distribution at σ is not uniform. As a result, eqn (20) cannot be used. | |
However, plotting the effective rate kon given by eqn (38) as a function of σ′ for rn = 7.5d in Fig. 5 (left), shows that kon becomes constant beyond σ′ = 3d, indicating that this is the distance at which the particles become isotropically distributed. This observation allows us, viaeqn (37), to determine ka(σ), even when at σ the distribution is not isotropic. This is illustrated in Fig. 5 (right), which shows ka(σ) as a function of σ from eqn (37), for several values of σ′, and for a fixed position of the last interface, rn = 7.5d. The intrinsic rate shows qualitatively similar behavior as in Fig. 1, but for σ′ < 3d, the value of ka(σ) does depend on σ′, because the distribution at σ′ is not isotropic yet. However, for σ′ > 3d, ka(σ) becomes independent of σ′, and the intrinsic rate constant ka can thus be obtained for all values of σ that are beyond the range of the interaction potential.
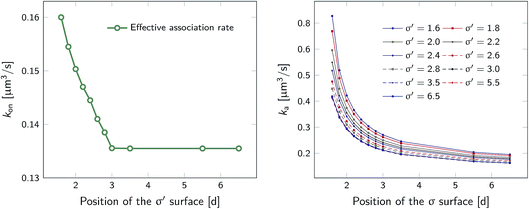 |
| | Fig. 5 The effective and intrinsic association rates for the anisotropic potential of Fig. 3. Left: Effective association rate kon, computed viaeqn (38), as a function of the position of the σ′ surface, with the position of the last surface fixed at rn = 7.5d. The value of kon is constant for σ′ ≥ 3d, indicating that at and beyond this surface the particles are isotropically distributed. Right: The intrinsic rate constant ka(σ), computed viaeqn (37), as a function of the cross section σ for different positions of the σ′ surface, with the position of the last interface fixed at rn = 7.5d. The curves for σ′ = 3.0, 3.5, 5.5, 6.5 overlap since the distribution of particles beyond this distance has become isotropic. For these values of σ′, ka(σ) as a function of σ can be obtained. | |
8 Conclusion
In this work we derived explicit microscopic expressions for the intrinsic rate constants for diffusion influenced reactions. Remarkably all intrinsic and effective rate constants, as well as the equilibrium constant can be computed from a single TIS or FFS simulation of the dissociation process. To the best of our knowledge this is a new result, and has not been reported in the literature before. We illustrated that this approach works for generic isotropic potentials and even for anisotropic potentials when the reference interface is sufficiently far from contact such that the orientational distributions are isotropic. This later condition led to a criterion for testing this isotropic behavior.
The results obtained in this paper are very general and can be used to compute accurate rate constants in complex systems using rare events techniques such as forward flux sampling or transition interface sampling. In future work we will also study how the magnitude of the intrinsic rate constant compares to that of the diffusion-limited rate constant, and how this depends on the binding affinity. This question is, for instance, important for understanding how tightly diffusion puts a fundamental upper bound on the precision of chemical sensing.11,24–26
Appendix A
The rate constants for two particles that interact via an isotropic interaction potential
It will be instructive to first revisit the derivation of the rate constants. Following Agmon and Szabo,1 we consider a single static receptor at the origin and a single ligand molecule that moves with diffusion constant D. The probability that the ligand molecule is at distance r at time t given that it was initially at a distance r0 is given by the Green's function P(r,t|r0). The evolution of the Green's function is given by the diffusion equation| | 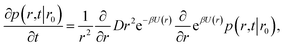 | (41) |
where β is the inverse temperature and U(r) is the interaction potential. The effective association and dissociation rate constants are obtained by solving eqn (41) with different boundary conditions. We start with the association reaction.
Association reaction
To obtain the effective association rate constant kon, we solve eqn (41) subject to the boundary condition| | 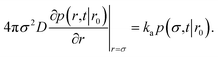 | (42) |
Here ka is the intrinsic rate constant, which determines the rate at which receptor and ligand associate given they are at the contact distance σ. If ka is finite, then the boundary condition is called a radiation boundary condition, while if ka → ∞, the boundary condition is an absorbing condition. The latter can be used to obtain the rate constant of diffusion-limited reactions, where receptor and ligand associate upon the first collision.
The survival probability Sα(t|r0) is the probability that a particle, which starts at a position r0, has not yet reacted at a later time t. It is given by
| | 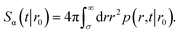 | (43) |
The subscript α is either “rad” or “abs”, corresponding to ka being finite or infinite, respectively. The propensity function Rα(t|r0) is the probability that a ligand particle, which starts at r = r0, reacts for the first time at a later time t:
| | 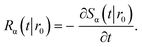 | (44) |
The time-dependent rate constant kα(t) is
| | 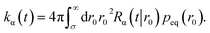 | (45) |
The distribution peq(r0) is the equilibrium radial distribution function, peq(r) = e−βU(r). If ligand and receptor only interact at contact, then U(r) = 0 for r ≥ σ and peq = 1, meaning that the equilibrium distribution corresponds to a spatially uniform distribution. The time-dependent rate constant kα(t) divided by the volume V is the probability per unit amount of time that receptor and ligand associate for the first time at a later time t, averaged over all initial positions r0 drawn from the equilibrium distribution peq(r0).
The expressions eqn (43)–(45) hold for both radiating and absorbing boundary conditions, corresponding to ka being finite and infinite, respectively. When ka is finite, Rrad(t|r0) is also given by
| | | Rrad(t|r0) = kap(σ,t|r0) | (46) |
and the time-dependent rate constant
krad(
t) is then also given by
| | 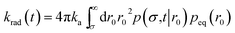 | (47) |
To relate krad(t) to kabs(t) in what follows below it will be useful to exploit the detailed-balance condition
| | | peq(r0)p(r,t|r0) = peq(r)p(r0,t|r). | (48) |
We can integrate this equation over r0 to find
| | 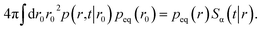 | (49) |
Combining this equation with eqn (47) we find that
| | | krad(t) = peq(σ)kaSrad(t|σ). | (50) |
The time-dependent rate constant krad(t) can be related to the time-dependent rate constant kabs(t) via
| | 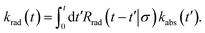 | (51) |
This can be understood by noting that kabs(t′)/V is the probability per unit amount of time that receptor and ligand come in contact for the first time at time t′, while Rrad(t − t′)|σ is the probability that receptor and ligand which start at contact r = σ at time t′ associate a time t − t′ later. In Laplace space, the above expression reads
| | ![[k with combining circumflex]](https://www.rsc.org/images/entities/i_char_006b_0302.gif) rad(s) = rad(s) = ![[R with combining circumflex]](https://www.rsc.org/images/entities/i_char_0052_0302.gif) rad(s|σ) rad(s|σ)![[k with combining circumflex]](https://www.rsc.org/images/entities/i_char_006b_0302.gif) abs(s). abs(s). | (52) |
Since Rrad(t|σ) = −∂Srad(t|σ)/∂t, ![[R with combining circumflex]](https://www.rsc.org/images/entities/i_char_0052_0302.gif) rad(s|σ) is also given by rad(s|σ) is also given by |
| | ![[R with combining circumflex]](https://www.rsc.org/images/entities/i_char_0052_0302.gif) rad(s|σ) = 1 − sŜrad(s|σ). rad(s|σ) = 1 − sŜrad(s|σ). | (53) |
Combining the Laplace transform of eqn (50) with eqn (52) and (53) yields
| | 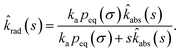 | (54) |
The effective association rate kon is given by the long-time limit of krad(t). Using eqn (54) we thus find:
| | 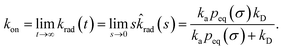 | (55) |
Here,
kD = lim
s→0s![[k with combining circumflex]](https://www.rsc.org/images/entities/i_char_006b_0302.gif) abs
abs(
s) is the diffusion-limited association rate for two particles interacting
via an interaction potential
U(
r). By combining
eqn (50) with
eqn (52) and
(53), it also follows that the probability that a particle at contact
σ does not bind but escapes, is
| | 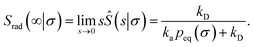 | (56) |
Hence, the effective association rate constant, eqn (55), can be interpreted as being given by the rate constant kD of arriving at the surface σ, followed by the probability 1 − Srad(∞|σ) = kapeq(σ)/(kapeq(σ) + kD) that the arrival leads to binding.
The results derived above hold for arbitrary peq(r) = e−βU(r). We now consider the case that U(r) = 0 for r ≥ σ. The time-dependent rate constant kabs(t) is then27
| | 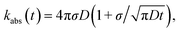 | (57) |
which in the Laplace domain becomes
| | s![[k with combining circumflex]](https://www.rsc.org/images/entities/i_char_006b_0302.gif) abs(s) = kD(1 + τ(s)), abs(s) = kD(1 + τ(s)), | (58) |
where
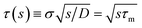
with the molecular time scale
τm =
σ2/
D and
kD ≡
kabs(
t → ∞) = 4π
σD is the diffusion-limited rate constant for two particles that do not interact except at contact. Substituting this in
eqn (54) with
U(
σ) = 0 gives
| | 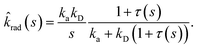 | (59) |
This expression yields for the effective association rate kon = lims→0s![[k with combining circumflex]](https://www.rsc.org/images/entities/i_char_006b_0302.gif) rad(s):
rad(s):
| | 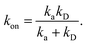 | (60) |
We note that this expression also follows from the much simpler steady state approximation of the macroscopic rate equations for association, in which the surface σ is viewed as an intermediate state. In this approximation ka is taken as the rate from the intermediate σ surface to the associated/bound state and kD is the diffusion limited rate to reach the σ surface from the unbound state. However, the above derivation is more general, and does not require the (rather strong) approximations that are made in the simple approach.
The dissociation rate constant
Following Agmon and Szabo,1 we will derive the effective dissociation rate constant koff from Srev(t|*):| | 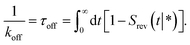 | (61) |
Here Srev(t|*) is the probability that the ligand, which is bound initially, is free at a later time t. The subscript “rev” indicates that during the time t the ligand may bind and unbind many times.
To obtain Srev(t|*), we first consider Srev(t|r0) and the following boundary condition for eqn (41):1
| | 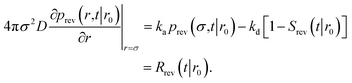 | (62) |
Using R^rev(s|r0) = 1 − sŜrev(s|r0) we can rewrite the above boundary condition as
| | 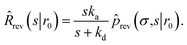 | (63) |
The rate is, analogous to eqn (45),
| | 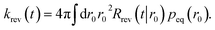 | (64) |
Using the detailed-balance relation eqn (49), this equation can be combined with eqn (63), to give
| | 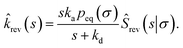 | (65) |
Combining this equation with ![[k with combining circumflex]](https://www.rsc.org/images/entities/i_char_006b_0302.gif) rev(s) =
rev(s) = ![[R with combining circumflex]](https://www.rsc.org/images/entities/i_char_0052_0302.gif) rev(s|σ)
rev(s|σ)![[k with combining circumflex]](https://www.rsc.org/images/entities/i_char_006b_0302.gif) abs(s) and
abs(s) and ![[R with combining circumflex]](https://www.rsc.org/images/entities/i_char_0052_0302.gif) rev(s|σ) = 1 − sŜrev(s|σ), we can derive that
rev(s|σ) = 1 − sŜrev(s|σ), we can derive that
| | 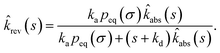 | (66) |
We now consider Srev(t|*). Since Srev(0|*) = 0, ![[R with combining circumflex]](https://www.rsc.org/images/entities/i_char_0052_0302.gif) (s|*) = −sŜrev(s|*). The boundary condition, eqn (62), then becomes
(s|*) = −sŜrev(s|*). The boundary condition, eqn (62), then becomes
| | 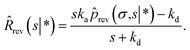 | (67) |
Exploiting the Laplace transform of the detailed balance condition kaprev(σ,t|*) = kdprev(*,t|σ) and the definition prev(*,t|σ) ≡ 1 − Srev(t|σ), the above equation yields
| | 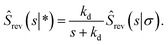 | (68) |
In the time domain, this gives
| | 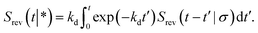 | (69) |
which can be understood by noting that
kd![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif)
exp(−
kdt′) is the probability per unit amount of time that the bound ligand dissociates at time
t′ and
Srev(
t −
t′|
σ) is the probability that the dissociated particle, which is now at contact
σ, is unbound at a later time
t −
t′ (but it could have associated and dissociated in between multiple times).
Combining eqn (68) with eqn (65) gives
| | ![[k with combining circumflex]](https://www.rsc.org/images/entities/i_char_006b_0302.gif) rev(s) = sKeqŜrev(s|*). rev(s) = sKeqŜrev(s|*). | (70) |
where
Keq ≡
kapeq(
σ)/
kd. Combining this result with
eqn (66), we find
| | 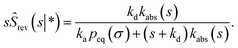 | (71) |
The off rate is then
| | 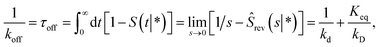 | (72) |
where, as before,
kD is the long-time limit of
kabs(
t):
kD = lim
s→0skabs(
s). This result can be rewritten as
| | 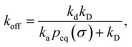 | (73) |
which, using
eqn (56), is also given by
Indeed, the effective off rate is the intrinsic dissociation rate kd times the probability Srad(∞|σ) = kD/(kapeq(σ) + kD) that the particle subsequently escapes. As written, the above results for koff hold for any U(r), when U(r) = 0 for r ≥ σ, peq(σ) = 1 and kD = 4πσD.
Finally, we note that, from eqn (55) and (73), it is clear that the equilibrium constant is also given by
| | 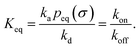 | (75) |
Acknowledgements
We thank Tom Ouldridge for stimulating discussions and help with implementing the LD integrator. This work is part of the Industrial Partnership Programme (IPP) ‘Computational Sciences for Energy Research’ of the Foundation for Fundamental Research on Matter (FOM), which is financially supported by the Netherlands Organization for Scientific Research (NWO). This research programme is co-financed by Shell Global Solutions International B. V.
References
- N. Agmon and A. Szabo, J. Chem. Phys., 1990, 92, 5270 CrossRef CAS.
- J. S. van Zon and P. R. ten Wolde, J. Chem. Phys., 2005, 123, 234910 CrossRef PubMed.
- M. J. Morelli and P. R. ten Wolde, J. Chem. Phys., 2008, 129, 054112 CrossRef PubMed.
- K. Takahashi, S. Tănase-Nicola and P. R. ten Wolde, Proc. Natl. Acad. Sci. U. S. A., 2010, 107, 2473–2478 CrossRef CAS PubMed.
- J. Lipková, K. C. Zygalakis, S. J. Chapman and R. Erban, SIAM J. Appl. Math., 2011, 71, 714–730 CrossRef.
- M. E. Johnson and G. Hummer, Phys. Rev. X, 2014, 4, 031037 Search PubMed.
- H. C. R. Klein and U. S. Schwarz, J. Chem. Phys., 2014, 140, 184112 CrossRef PubMed.
- S. H. Northrup and H. P. Erickson, Proc. Natl. Acad. Sci. U. S. A., 1992, 89, 3338–3342 CrossRef CAS.
- H.-X. Zhou, J. Chem. Phys., 1998, 108, 8139 CrossRef CAS.
- J. S. van Zon, M. J. Morelli, S. Tanase-Nicola and P. R. ten Wolde, Biophys. J., 2006, 91, 4350 CrossRef CAS PubMed.
- K. Kaizu, W. de Ronde, J. Paijmans, K. Takahashi, F. Tostevin and P. R. ten Wolde, Biophys. J., 2014, 106, 976–985 CrossRef CAS PubMed.
- I. V. Gopich and A. Szabo, Proc. Natl. Acad. Sci. U. S. A., 2013, 110, 19784–19789 CrossRef CAS PubMed.
- A. Mugler and P. R. ten Wolde, Adv. Chem. Phys., 2013, 153, 373–396 CrossRef CAS.
- A. Mugler, F. Tostevin and P. R. ten Wolde, Proc. Natl. Acad. Sci. U. S. A., 2013, 110, 5927–5932 CrossRef CAS PubMed.
- T. S. van Erp, D. Moroni and P. G. Bolhuis, J. Chem. Phys., 2003, 118, 7762 CrossRef CAS.
- T. S. van Erp and P. G. Bolhuis, J. Comput. Phys., 2005, 205, 157–181 CrossRef.
- T. S. van Erp, Adv. Chem. Phys., 2012, 151, 27–60 CrossRef CAS.
- R. J. Allen, P. B. Warren and P. R. ten Wolde, Phys. Rev. Lett., 2005, 94, 018104 CrossRef PubMed.
- R. J. Allen, C. Valeriani and P. Rein ten Wolde, J. Phys.: Condens. Matter, 2009, 21, 463102 CrossRef PubMed.
- M. Von Smoluchowski, Z. Phys. Chem., 1917, 92, 129 CAS.
- S. H. Northrup, S. A. Allison and J. A. McCammon, J. Chem. Phys., 1984, 80, 1517 CrossRef CAS.
- A. Vijaykumar, P. G. Bolhuis and P. R. ten Wolde, J. Chem. Phys., 2015, 143, 214102 CrossRef PubMed.
-
A. Vijaykumar, T. E. Ouldridge, P. R. ten Wolde and P. G. Bolhuis, 2016, to be published.
- H. C. Berg and E. M. Purcell, Biophys. J., 1977, 20, 193 CrossRef CAS PubMed.
- W. Bialek and S. Setayeshgar, Proc. Natl. Acad. Sci. U. S. A., 2005, 102, 10040–10045 CrossRef CAS PubMed.
- P. R. ten Wolde, N. B. Becker, T. E. Ouldridge and A. Mugler, J. Stat. Phys., 2016, 162, 1395–1424 CrossRef CAS.
-
S. A. Rice, Diffusion-Limited Reactions, Elsevier, Amsterdam, 1985 Search PubMed.
|
| This journal is © The Royal Society of Chemistry 2016 |
Click here to see how this site uses Cookies. View our privacy policy here.  Open Access Article
Open Access Article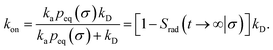
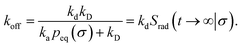
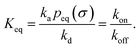
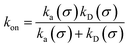
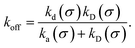
![[scr B, script letter B]](https://www.rsc.org/images/entities/char_e13f.gif) and h
and h![[scr U, script letter U]](https://www.rsc.org/images/entities/char_e534.gif) such that h
such that h![[scr B, script letter B]](https://www.rsc.org/images/entities/char_e13f.gif) = 1 and h
= 1 and h![[scr U, script letter U]](https://www.rsc.org/images/entities/char_e534.gif) = 0 if the system was more recently in the bound state B (r < r0) than in the unbound state U (r > rn), and h
= 0 if the system was more recently in the bound state B (r < r0) than in the unbound state U (r > rn), and h![[scr B, script letter B]](https://www.rsc.org/images/entities/char_e13f.gif) = 0 and h
= 0 and h![[scr U, script letter U]](https://www.rsc.org/images/entities/char_e534.gif) = 1 otherwise, the rate constant koff for transitions from B to U is given by15
= 1 otherwise, the rate constant koff for transitions from B to U is given by15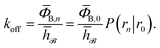
![[h with combining macron]](https://www.rsc.org/images/entities/i_char_0068_0304.gif)
![[scr B, script letter B]](https://www.rsc.org/images/entities/char_e13f.gif) is the average fraction of time that the system spends in the bound state B. P(rn|r0) is the probability that a trajectory that reaches r0 subsequently arrives at interface rn instead of returning to the bound state r0. The expression thus states that the total flux of trajectories from the bound state to the unbound state is the flux of trajectories from B to r0 multiplied by the probability that such a trajectory will later reach rn before returning to r0. P(rn|r0) can be expressed as the product of the probabilities P(ri+1|ri) that a trajectory that comes from r0 and crosses ri for the first time will subsequently reach ri+1 instead of returning to r0:
is the average fraction of time that the system spends in the bound state B. P(rn|r0) is the probability that a trajectory that reaches r0 subsequently arrives at interface rn instead of returning to the bound state r0. The expression thus states that the total flux of trajectories from the bound state to the unbound state is the flux of trajectories from B to r0 multiplied by the probability that such a trajectory will later reach rn before returning to r0. P(rn|r0) can be expressed as the product of the probabilities P(ri+1|ri) that a trajectory that comes from r0 and crosses ri for the first time will subsequently reach ri+1 instead of returning to r0: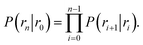
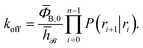
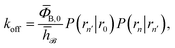
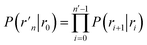 and
and 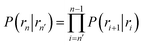 . Now, the crux is to define rn′ = σ. Comparing eqn (10) with eqn (2), we can then make the following identifications:
. Now, the crux is to define rn′ = σ. Comparing eqn (10) with eqn (2), we can then make the following identifications: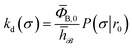
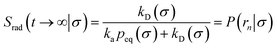
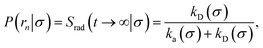
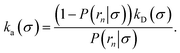
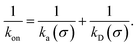
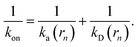
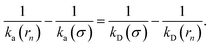
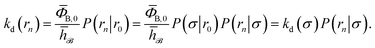
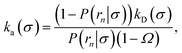
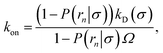
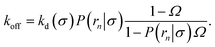
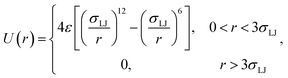
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 trajectories are started and the conditional probability as in eqn (8) is calculated.
000 trajectories are started and the conditional probability as in eqn (8) is calculated.
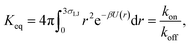
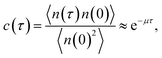

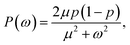
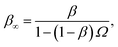
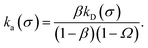
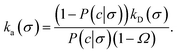
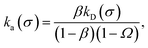
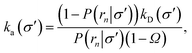
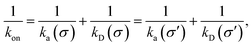
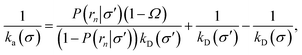
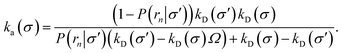
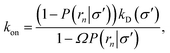
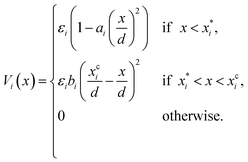
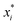 , which combined with ai determines the range of the potential, are free parameters. Cut-offs xci and smoothing parameters bi are fixed by requiring continuity and differentiability at
, which combined with ai determines the range of the potential, are free parameters. Cut-offs xci and smoothing parameters bi are fixed by requiring continuity and differentiability at 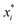 . These potentials give us a firm control over the potential shape, and allow for easy integration with potentials that are short-ranged and highly orientation-specific. For our illustrative purposes, we take the following parameters: εcc-rep = 100kBT, acc-rep = 1 and
. These potentials give us a firm control over the potential shape, and allow for easy integration with potentials that are short-ranged and highly orientation-specific. For our illustrative purposes, we take the following parameters: εcc-rep = 100kBT, acc-rep = 1 and 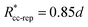 , implying bcc-rep = 2.6036 and Rccc-rep = 1.1764d; εpp = 20kBT, app = 20 and
, implying bcc-rep = 2.6036 and Rccc-rep = 1.1764d; εpp = 20kBT, app = 20 and 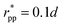 , implying bpp = 5 and rcpp = 0.5d; and εcc-att = 10kBT, acc-att = 1 and
, implying bpp = 5 and rcpp = 0.5d; and εcc-att = 10kBT, acc-att = 1 and 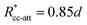 , implying bcc-rep = 2.6036 and Rccc-rep = 1.1764d.
, implying bcc-rep = 2.6036 and Rccc-rep = 1.1764d.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 trajectories are started, and the conditional probability as in eqn (8) is calculated.
000 trajectories are started, and the conditional probability as in eqn (8) is calculated.

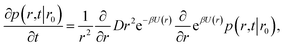
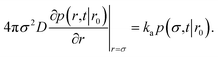
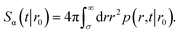
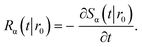
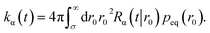
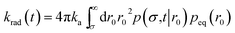
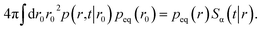
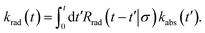
![[k with combining circumflex]](https://www.rsc.org/images/entities/i_char_006b_0302.gif) rad(s) =
rad(s) = ![[R with combining circumflex]](https://www.rsc.org/images/entities/i_char_0052_0302.gif) rad(s|σ)
rad(s|σ)![[k with combining circumflex]](https://www.rsc.org/images/entities/i_char_006b_0302.gif) abs(s).
abs(s).![[R with combining circumflex]](https://www.rsc.org/images/entities/i_char_0052_0302.gif) rad(s|σ) is also given by
rad(s|σ) is also given by![[R with combining circumflex]](https://www.rsc.org/images/entities/i_char_0052_0302.gif) rad(s|σ) = 1 − sŜrad(s|σ).
rad(s|σ) = 1 − sŜrad(s|σ).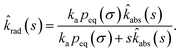
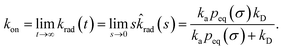
![[k with combining circumflex]](https://www.rsc.org/images/entities/i_char_006b_0302.gif) abs(s) is the diffusion-limited association rate for two particles interacting via an interaction potential U(r). By combining eqn (50) with eqn (52) and (53), it also follows that the probability that a particle at contact σ does not bind but escapes, is
abs(s) is the diffusion-limited association rate for two particles interacting via an interaction potential U(r). By combining eqn (50) with eqn (52) and (53), it also follows that the probability that a particle at contact σ does not bind but escapes, is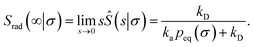
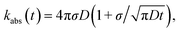
![[k with combining circumflex]](https://www.rsc.org/images/entities/i_char_006b_0302.gif) abs(s) = kD(1 + τ(s)),
abs(s) = kD(1 + τ(s)),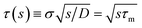 with the molecular time scale τm = σ2/D and kD ≡ kabs(t → ∞) = 4πσD is the diffusion-limited rate constant for two particles that do not interact except at contact. Substituting this in eqn (54) with U(σ) = 0 gives
with the molecular time scale τm = σ2/D and kD ≡ kabs(t → ∞) = 4πσD is the diffusion-limited rate constant for two particles that do not interact except at contact. Substituting this in eqn (54) with U(σ) = 0 gives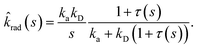
![[k with combining circumflex]](https://www.rsc.org/images/entities/i_char_006b_0302.gif) rad(s):
rad(s):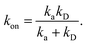
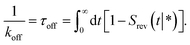
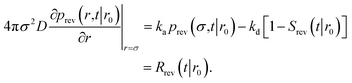
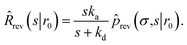
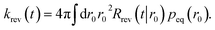
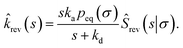
![[k with combining circumflex]](https://www.rsc.org/images/entities/i_char_006b_0302.gif) rev(s) =
rev(s) = ![[R with combining circumflex]](https://www.rsc.org/images/entities/i_char_0052_0302.gif) rev(s|σ)
rev(s|σ)![[k with combining circumflex]](https://www.rsc.org/images/entities/i_char_006b_0302.gif) abs(s) and
abs(s) and ![[R with combining circumflex]](https://www.rsc.org/images/entities/i_char_0052_0302.gif) rev(s|σ) = 1 − sŜrev(s|σ), we can derive that
rev(s|σ) = 1 − sŜrev(s|σ), we can derive that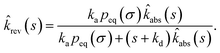
![[R with combining circumflex]](https://www.rsc.org/images/entities/i_char_0052_0302.gif) (s|*) = −sŜrev(s|*). The boundary condition, eqn (62), then becomes
(s|*) = −sŜrev(s|*). The boundary condition, eqn (62), then becomes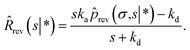
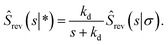
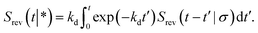
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−kdt′) is the probability per unit amount of time that the bound ligand dissociates at time t′ and Srev(t − t′|σ) is the probability that the dissociated particle, which is now at contact σ, is unbound at a later time t − t′ (but it could have associated and dissociated in between multiple times).
exp(−kdt′) is the probability per unit amount of time that the bound ligand dissociates at time t′ and Srev(t − t′|σ) is the probability that the dissociated particle, which is now at contact σ, is unbound at a later time t − t′ (but it could have associated and dissociated in between multiple times).
![[k with combining circumflex]](https://www.rsc.org/images/entities/i_char_006b_0302.gif) rev(s) = sKeqŜrev(s|*).
rev(s) = sKeqŜrev(s|*).