Open Access Article
Open Access ArticleStimulated X-ray Raman scattering – a critical assessment of the building block of nonlinear X-ray spectroscopy
Victor
Kimberg
*ab,
Alvaro
Sanchez-Gonzalez
c,
Laurent
Mercadier
a,
Clemens
Weninger
ad,
Alberto
Lutman
d,
Daniel
Ratner
d,
Ryan
Coffee
d,
Maximilian
Bucher
df,
Melanie
Mucke
e,
Marcus
Agåker
e,
Conny
Såthe
e,
Christoph
Bostedt
f,
Joseph
Nordgren
e,
Jan Erik
Rubensson
e and
Nina
Rohringer
*a
aMax Planck Institute for the Structure and Dynamics of Matter, Hamburg, Germany. E-mail: nina.rohringer@mpsd.mpg.de; kimberg@kth.se
bRoyal Institute of Technology, Stockholm, Sweden
cImperial College, Department of Physics, London, UK
dLCLS, SLAC National Accelerator Laboratory, Menlo Park, California, USA
eDepartment of Physics and Astronomy, Uppsala University, Uppsala, Sweden
fArgonne National Laboratory, Illinois, USA
First published on 14th June 2016
Abstract
With the invention of femtosecond X-ray free-electron lasers (XFELs), studies of light-induced chemical reaction dynamics and structural dynamics reach a new era, allowing for time-resolved X-ray diffraction and spectroscopy. To ultimately probe coherent electron and nuclear dynamics on their natural time and length scales, coherent nonlinear X-ray spectroscopy schemes have been proposed. In this contribution, we want to critically assess the experimental realisation of nonlinear X-ray spectroscopy at current-day XFEL sources, by presenting first experimental attempts to demonstrate stimulated resonant X-ray Raman scattering in molecular gas targets.
I. Introduction
Femtosecond stimulated Raman spectroscopy1,2 is a nonlinear optical pump probe technique that allows following vibrational structural dynamics with high spectral and temporal resolution. This relatively new all optical technique has evolved into a well-established method to study the coherent interplay between different vibrational modes and coherent vibrational wave-packet dynamics ranging from small molecules to large biomolecular complexes. Transferring this technique to the X-ray spectral domain would in principle allow following valence electronic wave packets3–5 or coupled nuclear electronic motion6 on attosecond timescales, or studying coherent long-range electronic transfer.7 The potential impact of this method could, therefore, revolutionise our understanding of electron dynamics in complex systems, light-induced catalysis, long-range electron and hole transport, etc. The conceptional generalisation of nonlinear coherent spectroscopy to electronic transitions and the X-ray domain was put forward in several papers by Shaul Mukamel and collaborators3–8 over the past decade, but present-day X-ray sources, such as X-ray free electron laser (XFEL) facilities or table-top attosecond sources, are far from achieving the required pulse characteristics. Realising the dream of coherent nonlinear electronic X-ray spectroscopy would either require a sequence of well-reproducible attosecond pulses, with well-controlled attosecond to femtosecond time separation, of different, tunable central photon energies, or, in the mixed frequency–time domain spectroscopy, the combination of a long coherent pulse (Raman probe pulse) and an attosecond pulse that can be accurately temporally shifted within the duration of the Raman probe pulse. Neither combination is available at present day sources. Moreover, the underlying basic building block of nonlinear Raman spectroscopy, that is stimulated resonant electronic X-ray Raman scattering, also referred to as stimulated resonant inelastic X-ray scattering (SRIXS), could so far only be demonstrated in isolated atoms.9,10 SRXIS is more difficult to achieve in molecules,11 due to the generally stronger competing process of inner-shell photoionisation of other atomic constituents of the molecules and an overall smaller Raman gain-cross section that is distributed over many electronic, vibrational and rotational channels.12 Here we present two experimental studies, along with theoretical predictions, that aimed at demonstrating SRIXS in CO molecules.A. Introduction to SRIXS in CO
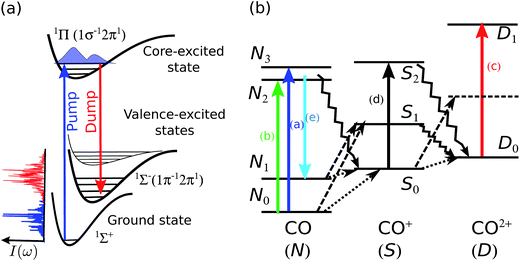
The level scheme for resonant inelastic X-ray scattering (RIXS) at the oxygen 1sO → 2π resonance in CO is shown in Fig. 1a. The X-ray “pump” pulse is tuned in resonance with the lowest unoccupied molecular orbital (LUMO) in CO populating the 1sO → 2π core-excited state at 534 eV, referred to as the π* state in the text below. The core-excited π* state predominantly decays non-radiatively with the emission of an Auger electron, the resonant Auger decay (RAD). With a small probability of 7%, the π* state can decay radiatively to several different final valence-excited states13 by the emission of an X-ray photon, the so-called RIXS process. In order to increase the radiative decay channel and the X-ray emission signal, a second X-ray pulse can be applied (the so-called “dump” pulse at Stoke-shifted lower photon energy) to stimulate the resonant scattering process. This process is referred to as stimulated resonant inelastic X-ray scattering (SRIXS). In our experiment, we aimed at stimulating the resonance scattering process to the 1Σ−(1π−12π1), which is the strongest transition in conventional RIXS measurements,13 with an energy loss of ≈9 eV and hence tuning the dump pulse to ≈526 eV. The energy of the low-frequency seed pulse is set typically 1–2 orders of magnitude lower than that of the pump pulse. In the course of the SRIXS process, the dump pulse is amplified and changes its spectral shape in the resonance region with the final electronic state.In a recent theory paper, we discussed SRIXS in a two-colour XFEL set-up,11 where both XFEL frequencies were produced from a single electron bunch by the self-amplified spontaneous emission (SASE) process. The first experimental attempt and limitations to achieve SRIXS in CO at the oxygen 1s → 2π resonance with the two-colour SASE set-up is shortly discussed in ref. 14 and a more detailed analysis of the experimental results is presented in this contribution. Despite the relatively large pulse energies (ranging from 0.07 to 0.17 mJ on target) SRIXS could not be demonstrated in this first attempt. Moreover, the relatively long pulse durations (>50 fs) and large X-ray fluxes (∼1.4 × 1011 photons per μm2) resulted in multiple ionisation of the CO molecules. These molecular ions, not necessarily in their respective ground states, were shown to have several absorption resonances, also in the 526 eV signal range. Similar absorption of transiently created molecular ions were also recently seen in water droplets.15 For the predicted small Raman amplification11 of only a few percent, the observation of the SRIXS signal in averaged spectra can, therefore, be overshadowed by spectral dips resulting from absorption. In Section III we present a second strategy to realise SRIXS, that avoids that problem: the SASE pump pulse, with quite a large pump pulse energy and bandwidth (2 eV), but only a small frequency overlap with the 1sO → 2π transition is replaced by a self-seeded FEL pulse. Our theory, adapted to the actual experimental conditions shows that we were at the onset of an observable SRIXS signal, but so far, no statistical evidence is seen to confidently report the demonstration of SXRIS in a molecular gas target. We present a critical, comprehensive experimental and theoretical case study of SRXIS in molecules and discuss challenges and the necessary experimental parameters to ultimately reach the conditions for advancing nonlinear X-ray spectroscopy.
II. Stimulated RIXS in two-colour SASE scheme
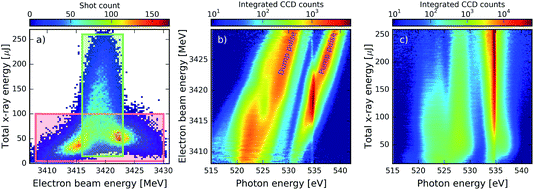
In a first experimental attempt at the AMO beam line at the LCLS in February 2014,14 a two-colour SASE scheme was applied to achieve SRIXS in CO. The undulators were set up to produce ≈100 fs duration pulses with two SASE bands, each of 2 eV width, centred at 534 and 525 eV. The experimental results for 3000 single SASE shots are reproduced in Fig. 2a. Shown are the recorded spectra (colour coded spectral intensity) as a function of the central photon energy of the pump pulse, that was determined by fitting the linear dependence of electron-beam energy to the measured spectral maximum of a reference measurement without CO. The plot clearly shows the two SASE energy bands at different intensities, separated by ∼9 eV and the absorption of the pump radiation at the π* resonance at 534.5 eV. The width of the absorption feature is defined by the broad vibrational progression excited in the π* state in agreement with the numerical simulations.11 One can observe a few weaker absorption lines at the energies below and above the π* resonance (dashed lines). The absorption features are more apparent in the total averaged spectrum, shown in Fig. 2b for two different SASE pulse combinations. Since multi-photon ionisation is a likely process at the considered pulse energies, we have to take into account some additional excitation and de-excitation channels in the neutral, singly and doubly charged CO molecule for proper assignment of these lines.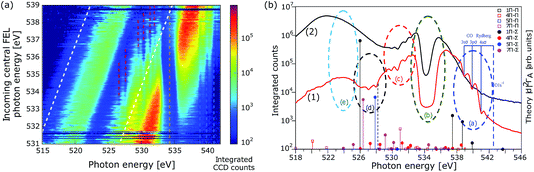 | ||
| Fig. 2 Experimental spectra (spectral intensity on a logarithmic scale) in the two-colour SASE pulse scheme. (a) Experimental single shot spectra (3000 shots) as a function of the central energy of the incoming pump pulse; colour bar gives the integrated number of counts. The pulse duration was ∼100 fs, average total pulse energy on target 0.17 mJ, and the gas pressure 225 mbar. (b) Plot (a) integrated over incoming central FEL photon energy (1); X-ray absorption near π* resonance in the presence of the strong dressing field on emission channel averaged over 2.2 × 104 SASE shots, gas pressure 85 mbar, total pulse energy on target 0.086 mJ. Vertical lines in (b) show theoretical energies and intensities (arbitrary units) of the strongest resonant X-ray absorption transitions from several 2Π states in CO+ to the Π (empty squares) and Σ (filled circles) symmetry core-excited CO+ 1s0−1 states. The absorption dips observed in areas (a)–(e) are assigned to different channels illustrated in Fig. 1(b) (see text). | ||
A level scheme of the dominant electronic states in CO, CO+ and CO++ excited by the strong X-ray light and decay processes is illustrated in Fig. 1b. Starting from the electronic ground state N0 resonant absorption of one photon can result in the occupation of the π* core-excited state N2 (transition (b) in Fig. 1b, resonant with the pump pulse of 534 eV) or one state of the ensemble of O 1s-Rydberg core-excited states N3 (transition (a) in Fig. 1b) resonant with the high frequency tails of the SASE pump pulse > 534 eV. Both absorption features, the broad π* resonance and the Rydberg absorption lines at the higher energy side of the π* feature are clearly visible in Fig. 2a and b. Resonant excitation of the π* or Rydberg resonances followed by fast Auger decay (Auger life time of ≈5 fs) results in the creation of the cationic ground state or into the occupation of low-lying valence excited states16 by resonant Auger decay (RAD), denoted by the ensemble of levels S0. The ensemble of states S0 can also be achieved by single photon valence ionisation (along with shake-up processes) of neutral CO. Reached by these different single-photon processes, the ensemble S0 will be generally quite heavily populated during the leading edge of the FEL pulse and can, in a second interaction with the photon fields of the pump or dump pulse, result in resonant O 1s excitations (depicted by the vertical arrow (d) in Fig. 1b). O 1s core excitation of the cationic ground and valence-excited states of the S0 ensemble will give rise to absorption of photons of the dump pulse (absorption lines summarised in the group (d) in Fig. 2b). A strong non-resonant absorption channel of the neutral molecule is the inner-shell ionisation of the carbon, resulting in C 1s−1 core-ionized state denoted by S1 that predominantly decays by the Auger process, resulting in the occupation of the ground state and valence excited states D0 of the doubly charged molecular ion. The ensemble of states D0 produced by single photon interaction are also quite strongly occupied, giving rise to resonant absorption lines at slightly higher photon energies as compared to absorption from S0 and are denoted with (c) in Fig. 1b and 2b.
In order to support the assignment of level groups, we made theoretical estimations for possible absorption lines in the cation: ab initio simulations of the O 1s transition energy and intensities of the absorption lines of the CO+ manifold S0 (transition group (d) for cationic states) formed in the RAS process are shown in Fig. 2b (legends explain the symmetry of the allowed X-ray absorption transitions). The intensities of the absorption lines are proportional to the partial rates of the formation of the considered ionic states in RAD17ΓA multiplied by the transition probability, proportional to the square of the transition dipole moment, to a correspondent O 1s core-excited state. The transition dipole moments calculations were performed on CASSCF theory level (including up to 7σ, 2πx and 2πy orbitals) with aug-cc-pvtz basis set using the MOLPRO package.18 The vibrational degrees of freedom were neglected and the calculations were performed for the internuclear distance 1.153 Å, corresponding to the equilibrium of the π* core-excited state of the neutral CO. The absolute energy positions of the resonances were corrected by an overall energy shift based on the assignment of the well-known CO+ O 1s → 1π transition at 526 eV observed in non-resonant emission measurements.16 The transitions from the ground 12Π (1σ−12π1) ionic state to a number of O 1s core-excited states are shown by black lines, where the target states of Π and Σ symmetries are marked with open squares and filled circles, respectively (see legends). The transitions from valence excited 4,5,72Π are shown by red, blue, and magenta lines, respectively. The large absorption probabilities were found for 5,72Π states (main electronic configuration16 1π−22π1) shown by blue and magenta circles in the region (d) of Fig. 2b.
Changing the relative intensities of the dump versus pump pulse allows for the suppression or enhancement of certain absorption features and gives supporting evidence for our assignment of different groups of transitions. Fig. 2b shows the recorded spectrum for a strong pump pulse (red line) and the case with a stronger dump pulse (black line), at albeit slightly different CO gas pressures. In the case of a strong pump pulse (0.17 mJ in the pump pulse, ∼0.013 mJ in the dump pulse), the O 1s-Rydberg absorption features are clearly visible, but are suppressed in the case for a strong dump pulse (∼0.02 mJ in the pump pulse, 0.086 mJ in the dump pulse). The reason for the difference is the ground-state depletion: in the case of a strong pump pulse, only a small fraction (20%) of the total available pulse energy depletes the ground state by the resonant O 1s–π* transition, so that ample ground-state population is available for O 1s-Rydberg transitions. In the case of a strong dump pulse, depletion of the ground state is driven by off-resonant C 1s ionisation over the whole spectral region of the dump pulse, hence, the total pulse energy that is available for ground-state depletion, so the weaker Rydberg absorption is suppressed. The changes in the relative pump and dump pulse intensity also supports the identification of the O 1s absorption group (d) of cationic valence excited states created in the resonant Auger: the absorption features (d) disappear in the case of a strong dump pulse, since the dump pulse cannot create the necessary valence-excited CO+ ions summarised as manifold S0 in Fig. 1b.
Absorption features (c) are clearly visible in a strong pump and a strong dump pulse, corroborating the hypothesis that the double ionised molecules CO2+ are predominantly produced by C 1s ionisation followed by Auger decay, a channel that is present in both experimental conditions. SRIXS and RIXS (depicted by the vertical arrow (e) pointing down, resonant with the SASE dump pulse of 525 eV) results in the occupation of one of the valence excited states in the neutral molecule, denoted by N1 and would result in amplification of the SASE seed radiation. The energy region of the expected peaks is denoted with the region (e) in Fig. 2b. No clear sign of amplification and SRIXS signal is, however, visible in the measured spectra. As it was shown in our numerical simulations,11 the SRIXS amplification is exponentially sensitive to the applied pump intensity. Our quantitative predictive theory shows that at the present experimental conditions we were at best at the onset of SRIXS. The total transmission of the beam line is unfortunately constantly decreasing at the AMO beam line at LCLS due to damage of the transport optics. Moreover, the achieved focal area of the focusing optics is not readily measurable and only estimated, so that the actually achieved intensity and pulse energy on the CO sample can only be estimated with quite a large uncertainty.
In the following, we present a second strategy for realising SRIXS in molecular CO that should result in more effective coupling to the O 1s–π* transition by replacing the SASE pump pulse with a self-seeded pulse at albeit smaller total pulse energies, which will reduce the absorption background of transiently created molecular ions in the sample.
III. SRIXS in self-seeded pump and SASE dump scheme
A. Experimental set-up and data acquisition
The experiment was performed at the AMO beamline, using the LAMP chamber. The configuration was very similar to the one described in ref. 9. The Kirkpatrick–Baez mirrors focused the XFEL beam to a spot of about 3.5 to 6 μm diameter with a Rayleigh range of ≈3 mm into a gas cell set to 3 mm length filled with CO gas at a controllable pressure of up to 700 mbar. The transmitted beam was analysed with a spectrometer consisting of a 45 mm long spherical grating with 5 m radius and a CCD camera (Andor, model Newton). The beam impinged on the 10 μm wide entrance slit of the spectrometer at a grazing incidence of 1.88° and diffracted onto the grating to enhance illumination and increase the spectral resolution. The diffracted beam was then imaged onto the CCD camera. Wavelength calibration was achieved by scanning the X-ray photon energy of regular SASE pulses to measure the π* and 1s-Rydberg absorption lines in CO. We measured a resolution power of ω/Δω ≈ 4800 at 530 eV.The data acquisition and data analysis were performed in the context of psana19 using the python interface for both online analysis and offline analysis. The main devices involved in the acquisition were standard beam diagnostics on the energy and the trajectory of the electron bunch,20 two gas monitor detectors to measure the X-ray pulse energy,21 the pressure reading in the absorption cell, and the X-ray spectrum measured by the CCD camera. Except for the pressure reading, which was only stored at 2 Hz, the information from the other devices was correlated on a shot-to-shot basis at a repetition rate limited by the CCD read-out rate. While storing the full 2048 × 512 pixel array this was limited to 1.5 Hz, by applying a hardware integration into a 2048 × 1 array a 60 Hz repetition rate was achieved. Up to 9 datasets were recorded across 12 hours. Each dataset consisted of different 10 minute runs recorded at different gas pressures, including a run at the minimum pressure (<1 mbar) to use as a no-gas reference. Different datasets were taken at different experimental conditions such as varying the position of the cell, beam focusing, and exact tuning of the pump and dump pulses.
B. Setting up of the XFEL
The required two-colour X-ray source in combination of SASE and self-seeded modus to achieve SRIXS in molecules is far from the conventional machine set-up of an XFEL source and a tight collaboration with the FEL scientists is indispensable for a successful experimental realisation. Although set-ups for two-colour SASE generation and self-seeding of the FEL have each been developed previously, the combination of both is a new development that resulted out of this collaboration. A scheme routinely used to generate two-colour pulses in X-ray FELs is the split undulator.22 There, the same electron bunch generates both X-ray pulses but in two different undulator sections. In the first section, tuned at the undulator strength K1, a photon beam at energy E1 is generated while in the second section, tuned at the undulator strength K2, a second photon beam at energy E2 is generated. The lasing process in the first section deteriorates the quality of the electron bunch used to generate the second pulse. Particularly if lasing in the first section approaches the saturation point, the electron bunch energy spread growth quickly decreases the performance in the second section, and can prevent lasing when it is too large. Therefore, balancing the colour intensities may prove difficult and is subject to shot-to-shot FEL intensity variations.The pulse duration can be controlled in several ways, ranging from a shorter electron bunch as operating in low-charge mode, or by using electron bunch collimation,23 or by using spoiling techniques.24–26 The bandwidths of each colour generated in this mode are those of a typical SASE pulse, and cannot fulfil the narrowband requirement for the pump pulse. The installation of a grating soft X-ray monochromator and of a dedicated magnetic chicane in the LCLS undulator line recently enabled self-seeding at soft X-ray wavelengths, between 500 and 1000 eV.27 In a self-seeding scheme, the photon beam generated in a first undulator section is monochromatised and serves as seed in the downstream undulator section. The magnetic chicane is used to provide the required delay to ensure temporal overlap between the monochromatic seed and the electron bunch in the downstream undulator.
The requirement of a strong pump pulse and a weak dump pulse would be easily achievable by generating the weak dump pulse upstream from the intense pump pulse, avoiding the anti-correlation due to the energy spread growth. Unfortunately, the large photon beam divergence after the monochromator mandates to generate the strong seeded pulse prior to the weak SASE pulse. Moreover, aiming for the highest power in the pump pulse prevents adopting solutions similar to the interleaved undulator.28 Typically, soft X-ray self-seeding is operated with pulses of duration between 70 and 120 fs. To shrink the pulse duration to 20 fs, slotted foil and charge collimation were experimentally tried, with charge collimation providing better performance.
An electron beam of 250 pC charge was collimated in the first bunch compressor down to 80 pC and compressed to a current of 2 kA, generating photon pulses of 25 fs of duration. Five undulator segments were used to generate a 1 μJ SASE pulse to be monochromatised in the first undulator section. The seeding monochromator was set to a photon energy of 534 eV for the pump pulse. The largest ratio between the pump and the dump pulse intensities was achieved by amplifying the monochromatised seed in an eleven undulator segments long section, reaching an average pump energy of 140 μJ, with peak values up to 350 μJ in optimal conditions. However, to match the desired colour separation, the undulator parameter K of that section had to be reduced, decreasing the efficiency, and leaving an average pump energy of 70 μJ, with peak values up to 260 μJ. The weak wideband SASE dump pulse was generated in downstream nine undulator segments at 526 eV and was measurable on the spectrometer. The balance between the intensities was tunable by decreasing the length of the undulator section amplifying the narrowband seed.
C. Data analysis
In the presented combination of self-seeded and SASE operation of the LCLS, the main challenge for data analysis is related to the strong XFEL fluctuations from shot to shot and the correlations between the different parameters. Fig. 3a shows the correlation between the electron-beam energy and the total X-ray pulse energy achieved for an ensemble of XFEL pulses. The first observation is that the high energies above 100 μJ are only reached for a specific region of the electron beam energy centred at 3419 MeV. This is due to the nature of the seeding process: in order to have a good seed, it is necessary to have some SASE emission at the right wavelength, which is only emitted efficiently for a certain electron-beam energy. Furthermore, even for the right electron-beam energy conditions, due to the stochastic nature of the SASE emission, the total X-ray pulse energy can vary between 20 and 260 μJ. As a consequence of these fluctuations, also the averaged spectrum is changing from region to region in the correlation plot. This has to be taken into consideration when trying to observe signals such as SRIXS or transient absorption in spectral averages. Fig. 3b shows the influence of the electron beam energy in the spectrum for the data contained within the red box in Fig. 3a. As expected, the SASE component of the pair of pulses shifts towards higher photon energies as the electron beam energy increases. For the pump spectral component, a much stronger pulse is emitted at the seeding condition of 534.3 eV for values of the electron-beam energy between 3415 and 3423 MeV. When seeding becomes strong the weak dump pulse shows a spectral hole. This behaviour becomes more apparent when looking at Fig. 3c, where the spectrum is shown as a function of the total X-ray energy for the narrow green region of Fig. 3a: as the total X-ray energy and seeded contribution at 534.3 eV increases and eventually saturates, the dump-pulse intensity decreases and the spectral hole in the dump becomes more pronounced, to eventually completely split the spectrum. For the highest pulse energies, the spectral intensity of the pump is more than two orders of magnitude larger than that of the dump.IV. Results and discussion
A. Theoretical simulations of SRIXS
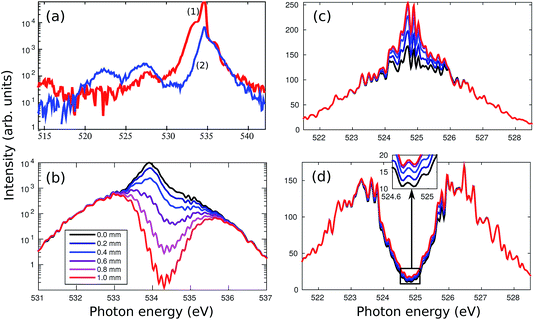
As already discussed, high spectral intensities of the pump pulse at the targeted electronic transition is of crucial importance for SRIXS.11 In the two-colour SASE scheme (Section II), supplying pulses of relatively broad spectrum (>5 eV, see Fig. 2), only a small number of photons overlap with the 1s → π* resonance (with a width <1 eV). Moreover, the photons outside of the resonance window drive off-resonant absorption, the creation of transient ionic occupations and finally are responsible for resonant absorption features in the transmitted spectrum of generally both the pump and the dump pulses. In the present section, we numerically test the advantages of using a self-seeded pump pulse in order to optimise the core-excitation and thus enhance the efficiency of SRIXS. We, however, keep SASE radiation on the dump channel, according to the experimental FEL set-up, which provides a broad-band seed pulse to stimulate various RIXS transitions.Typical averaged spectra of the self-seeded pump and SASE dump pulses measured (without gas) are shown in Fig. 4a. The profiles shown are averaged over about 100 XFEL pulses, resulting in smooth spectra. The quality of the self-seeding process varies greatly from shot to shot, as discussed in the previous sections (see Fig. 3, 7 and 8 for spectral averages and also Fig. 6, that shows examples for single-shot spectra). Spectrum (1) in Fig. 4a is an example of successful self-seeding with the high pump-pulse energy. Spectrum (2) shows a rather common example of a moderate seeding quality and low pump-pulse energy. As discussed in the previous section, the spectral shape of the dump component develops a spectral hole in case of strong self-seeding (Fig. 3b and c). The characteristics of both dump and pump spectral components are taken into consideration in our numerical simulations presented in Fig. 4b–d: the self-seeded spectrum was modelled as a narrow band (0.5 eV) Gaussian pulse on top of a weak broadband SASE pulse profile of 2.5 eV average width. For the SASE dump component, we simulate two cases: averaged Gaussian spectral profile (Fig. 4c) and a double-peak “m” profile, that corresponds to the low-frequency band SASE emission at strong self-seeding condition (Fig. 4d). All theoretical spectra in Fig. 4 are averaged over 128 simulated XFEL shots. The theory, described in detail in ref. 11, employs a coupled solution of the Liouville–von Neumann equations for the temporal evolution of the electronic-vibrational density matrix equations and Maxwell's equations in the paraxial approximation for the X-ray pulse, which allows tracing the change of the spectral shape of the X-ray fields at different lengths of the gas cell (see legends in Fig. 4b): the pump spectrum (Fig. 4b) shows formation of a strong absorption dip at the π* resonance. The vibrational structure of the π* resonance is clearly resolved, in agreement with a conventional X-ray absorption experiment,29 but difficult to observe in the XFEL experiment due to the large intensity range of about 3 orders of magnitude between the minimum of the absorption dip and the spectral wings of the pump pulse (Fig. 4b). The absorption on the π* resonance is roughly two orders of magnitude passing through 0.5 mm at the gas pressure of 500 mbar. Therefore, a strong core-inversion cannot be maintained over a longer propagation distance, so that SRIXS amplification nearly stops for long propagation distances >0.5 mm (see Fig. 4c and d).
Our numerical simulations mimicking the strongest available set of pump pulses with high seeding component (spectrum (1) in Fig. 4a) predict a SRIXS amplification of up to 50% at the spectral maximum of the emission band (see Fig. 4c). In principle, such amplification should be experimentally detectable. Since the Raman gain is independent of the dump-pulse intensity below saturation,11 the SASE (Fig. 4c) and m-shaped SASE (Fig. 4d) dump spectra show similar Raman amplification. This also becomes evident in comparing the m-shaped dump pulse in Fig. 5 for several dump intensities. Due to noise, the amplification at the local minimum of the m-shaped pulses (Fig. 4d) will be more difficult to observe experimentally than on top of the SASE spectrum (Fig. 4c). According to our simulations, the population of the core-excited state is ≈20% at the entry of the gas cell. The final state population reached by SRIXS is rather weak (≈1%), according to the small Raman gain cross section. The SRIXS amplification (see Fig. 5, that shows the relative amplification) shows a weak dependence on the number of photons in the pump pulse. A linear increase of the amplification factor is observed for an exponential increase in the number of photons of the pump pulse. In the case of a moderate pump-pulse energy – the more common scenario in our measurements (see Fig. 3b and c) – and assuming 2 × 1010 pump photons in the pump pulse on target (corresponding to a pulse energy of ∼2 μJ on target, Fig. 4a(2)), the maximal observable amplification is only 10%. In the next section, we compare these predictions to the experiment.
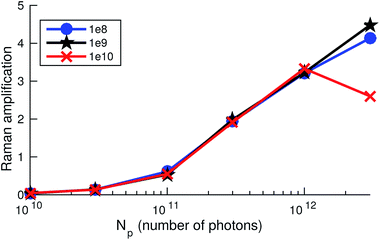 | ||
| Fig. 5 Raman amplification defined as [Id(z, ωm)eσphNz/Id(0, ωm) − 1] at the maximum of the SRIXS signal at ωm = 524.7 eV, measuring the relative increase of the spectral intensity Id(z, ωm) of the dump field, for different total numbers of photons in the dump pulse (shown in the legend) and as a function of the number of photons in the pump pulse for a propagation distance of z = 1 mm. N denotes the molecular concentration and σph is the non-resonant absorption cross section. Shown are results corresponding to Fig. 4d, giving Raman amplification of about 0.5. | ||
B. Experimental results
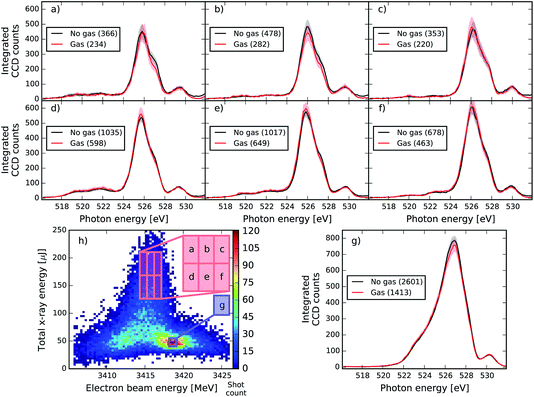
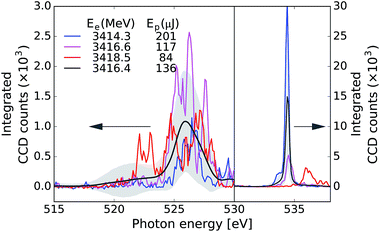
We now present results obtained in the experimental conditions described in Section III-B and in accordance with the parameters of our theoretical discussion of Section IV-A. Examples of single shot spectra without gas of a specific machine set-up (corresponding to the analysis presented in Fig. 7) are presented in Fig. 6, for different combinations of pulse energies and electron-beam energies. The spectra in the dump region show randomly spiked structures, which is a characteristic feature of the SASE process. We can clearly see the anti-correlation between the pump and dump spectral components: when the pump pulse is strong (blue curve), the dump pulse intensity is low, whereas a weaker pump (green curve) allows for a stronger dump pulse. If the electron beam energy is too high (red curve), seeding is no longer achieved and the SASE background of the pump pulse is shifted towards higher photon energies. Even for the right electron-beam energies, a large intensity fluctuation of the seeded spectral component is observed. The average spectrum is also displayed and the standard deviation reflects the highly fluctuating nature of these spectra: it is never less than 70% of the average. These spectral characteristics and fluctuations complicate the detection of a small SRIXS signal. As the signal should appear only when both the pump and dump pulse are at the right energies, we tried making a similar study to that of Fig. 3b with gas. The most promising approach is to compare the average spectra for different pressures to a no-gas reference. To avoid the systematic change of the spectrum for different electron-beam and pulse-energy settings, this average was calculated for different small regions of the correlation plot of electron-beam versus pulse energy (see Fig. 7 and 8). In the analysis, the overall absorption by 1s C and valence levels has to be corrected. By making a comparison of the integrated spectral intensity with the exception of the region near the resonant π* absorption for different pressures, it was possible to fit the Beer–Lambert law, allowing the determination of the transmission for each pressure. As this process assumes a flat transmission, and in reality there are many more resonant and non-linear absorptions, the transmission values obtained are only an approximation used mainly to make easier the qualitative comparison across different pressures. Data at each measured pressure was then compared directly to the no-gas reference corrected by the transmission factor (0.537 in Fig. 7 and 0.486 in Fig. 8 and 9) to detect changes in the shape near the 525 eV region.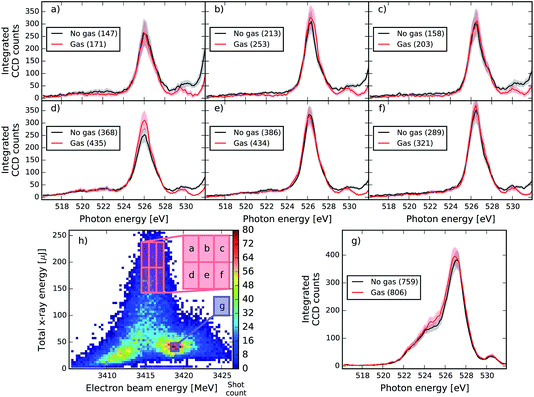 | ||
| Fig. 8 Same as Fig. 7 at different XFEL settings with a central seeded pulse energy of 534.32 eV. In this case the no-gas spectra are multiplied by a factor of 0.486 to account for 1s C and valence absorption. The average gas pressure is 107.6 mbar. | ||
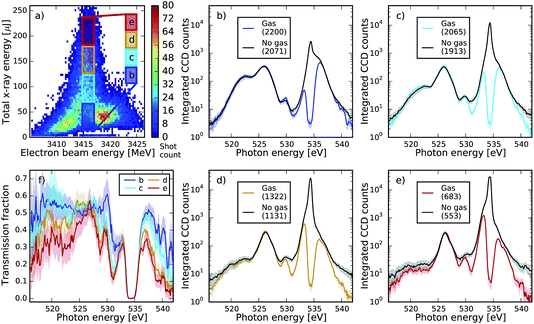 | ||
| Fig. 9 Comparison of spectra for the whole range (pump and dump, in logarithmic scale) with and without gas for the same XFEL settings as in Fig. 8. Spectra in plots (b–e) are averaged over specific regions of pulse energy and electron beam energy, which are indicated in plot (a), compared to the no gas reference adjusted by a factor of 0.486 as in Fig. 8. Plot (f) illustrates the transmission factor for each of the boxes, calculated as gas spectrum divided by the no gas reference. One can see absorption dips in the region of the Rydberg states of the neutral molecule 539–541 eV (see also Fig. 2b) in the case of small pulse energy, as well as two strong dips at ∼528 and ∼531 eV. The two dips grow with increase of the pulse energy and thus are tentatively assigned to the absorption by the double ionized molecules, consistent with the two-colour SASE experiment (Fig. 2). | ||
As can be seen, the averaged spectrum shows systematic changes for different electron beam and pulse energies. In Fig. 7 and 8, the subfigure (g) corresponds to the region with the highest number of recorded shots and with rather low pulse energies and small seeding components (see Fig. 3). In this region, no RIXS signal is expected and therefore the comparison of gas data and reference is a check for a possible drift of machine parameters between the two runs. We can see that except for the very central region of the peak at 527 eV, the overall shape of the dump spectral region is very well reproduced in Fig. 7. In the other regions of the correlation plot (Fig. 7a–f), the wings of the gas and no-gas spectra are also very well superimposed. Slight changes at the peak are observed but they are not statistically relevant: for all ensemble averages presented, we calculated the standard error and the 99% confidence interval that is given by 2.5 times the standard error and is shown as the shaded area in plots 7 and 8. If the confidence intervals of the gas and reference data split apart, it means that the spectral difference of the averages has a good chance to be real and does not reflect the finite size of the ensemble. The differences observed do not satisfy this criterion for this XFEL configuration. In Fig. 8, slight spectral changes between gas and reference data are observed already in the box (g), which can indicate a drift in the machine settings between the acquisition of the gas and no-gas datasets. An increase of the gas signal is observed at the centre of the peak of the dump in (b) and (d) but the change is not large enough to be statistically relevant. Moreover, the increase in signal does not systematically change when increasing the pulse energy, which would be expected by theory (see Fig. 4c and d). We detect, however, statistically relevant differences at energies of 528 and 531 eV in the spectra shown in Fig. 8. The loss in the spectral intensity in this region can be due to non-linear absorption of transiently created ions, but could also signal a shift in the machine parameters or even be related to not perfectly accurate background subtraction, which becomes significant in these low count regions.
To explore those features we studied the pulse energy dependence of the absorption (Fig. 9). For the same dataset shown in Fig. 4, we selected a series of boxes on increasing intensities (Fig. 9a) and plot the full spectrum for each of the boxes compared to the no-gas reference corrected by the same transmission factor (Fig. 9b–e). Additionally, we plotted the transmission factor for each box calculated as the signal divided by the no-gas reference (Fig. 9f).
We observe absorption dips at 528 and 531 eV equivalent to the absorption resonances measured in the two-colour SASE set-up (see Fig. 2b), but not as well resolved. The absorption dip at 528 eV is not visible at the lowest intensity case (box b, blue curve), but it appears as the pulse energy doubles (box c, cyan curve), and it continues to increase as the pulse energy triples and quadruples (box d and e, orange and red curves, respectively). Conversely, the absorption dip at 531 eV is already present at the lowest energies (box b), continues to increase when the energy doubles (box c), and reaches saturation when the energy triples (box d), showing almost the same absorption as in box e. This could in principle indicate different degrees of non linearity of the absorption channels. Nevertheless, these features could not be reproduced consistently at all other machine settings, in particular at settings that did not show local minima at these energy positions. This point needs further investigation, as they could be artefacts in the background subtraction at the low signal levels. In fact, we believe the observed apparent non-linear absorption in the region between 516 and 524 eV may just be a consequence of this.
In order to make small changes in the spectral averages more apparent, we also studied the absolute and relative spectral differences of gas and no-gas reference. No consistent evidence of SRIXS amplification could be observed. As our recent theoretical study suggests,11 a covariance analysis of the recorded single-shot spectra would result in a clear manifestation of the SRIXS process for small SRIXS amplification factors. This analysis is, however, complicated for pulses with systematic spectral changes. We attempted a partial covariance analysis of our data, to find correlations between the spectral pump-pulse region (absorption) and the dump pulse region (emission) as an indication of SRIXS, for low pressures where the pump pulse was not completely absorbed. However, the non-trivial negative correlations between the pump and the probe inherent to the XFEL machine set-up, induced a very strong negative background peak in the region of interest, masking any potential signs of SRIXS.
C. Critical assessment of SRIXS experimental feasibility
The experimental feasibility of SRIXS in molecules was recently addressed based on theoretical simulations of the two-colour scheme using two SASE pulses.11 The study highlighted several important issues, related to the performance of XFEL and the experimental set-up, that have to be taken into account in order to observe SRIXS signals from molecules. Let us now discuss these points in relation to the new scheme, using a self-seeded pump and SASE dump pulses: the most important requirement is the high spectral intensity of the pump pulse overlapping with the resonance region. In the case of the two-colour SASE scheme, at least 1012 photons in a spectral window of 2 eV on target (corresponding to 0.1 mJ pulse energy) in a focal spot of 3 μm diameter and pulse duration of 100 fs11 are required to obtain vibrationally resolved SRIXS spectra. These relatively high pulse energies, however, result in off-resonant ionisation and the creation of transiently occupied ionic species. This can result in absorption resonances overlapping with the SRIXS signal region. In the present experimental scheme with a self-seeded narrow-band pump pulse, our numerical simulations of Section IV-A demonstrate that much lower total pulse energies are required to efficiently stimulate RIXS. For a pump pulse containing ∼1011 photons on target in a spot of 6 μm diameter and pulse duration of 35 fs the SRIXS signal amplification should be up to be 50%. In the present experiment, these spectral intensities 2 × 108 photons per μm2 per fs per eV (for 0.5 eV self-seeded pulse of 35 fs duration), however, were on the border of attainability. One of the main limiting factors of our experiment was the detected degradation of the X-ray transport and focusing optics at the AMO beam line at LCLS, resulting in the beam-line transmission drop down to about ≈5%, as compared to the previous experimental campaign,14 when the beam-line transmission was estimated to be ≈20%. We also determined a decrease of the obtainable intensities, comparing amplified spontaneous emission of neon gas obtained in this campaign versus measurements in 2014 and 2010. Compared to 2010 the signal outcome of the neon laser was four orders of magnitude lower (with an exponential sensitivity of the signal to the incoming XFEL intensity). Our observation is in accordance with other experimental campaigns, measuring the creation of high charge states in Xe gas by nonlinear sequential photoionisation, pointing to a degradation of the focusing optics, resulting in focal spot sizes roughly twice larger, thus 4 times smaller X-ray intensity on target as compared to previous experiments. Despite the excellent operation of the XFEL and the self-seeding set-up, these deficiencies precluded the observation of SRIXS in this experiment.The main goal of the present experiment was to observe RIXS amplification as a gross feature shown in Fig. 4c, thus high spectral resolution was not the key interest. In the SASE–SASE pulse configuration, covariance analysis11 has to be applied to uncover the vibrationally resolved SRIXS maps, showing the spectrum as a function of pump and dump photon energy. To that end, the absorption features have to be properly resolved, requiring a large dynamic range of the spectrometer set-up. In the self-seeded SASE pulse configuration, the hope is that covariance is not necessary, in the case of strong seeding. The averaged spectra for a series of seed photon energies should yield high-resolution SRIXS maps. In the case of a strong superimposed SASE background of the pump spectrum, an additional partial covariance analysis might have to be applied. The partial covariance maps might, however, as seen in this experiment (results not shown in this contribution), be dominated by the XFEL-related correlations in pump and dump frequency components, such as the spectral hole at good seeding conditions. The best configuration for a successful SRIXS experiment is, therefore, to work with only the subset of best seeded pulses, and scanning the seed-energy through the resonance.
As demonstrated by the presented spectra, the averages for a given pulse-energy/e-beam energy region of the correlation plot are fairly stable over a characteristic timescale to record data sets. The detectable SRIXS signal is however limited by the standard error of a given data set. A pure analysis of the statistical error, however, does not allow for detecting drifts of the accelerator. To detect systematic changes of the machine, we monitored the stability of the distributions of all the electron beam parameters and gas detector, and benchmarked our error by comparing the shape of the spectrum for a low energy region of the map, where no SRIXS signal is expected and a good match to the reference is expected. The excellent overlap of the reference and gas spectra in Fig. 7 show that the machine was stable between the two acquisitions. This measurement protocol is applicable for studying all kinds of transient small spectral changes on the base of spectral averages, such as SRIXS and transient absorption spectroscopy at XFEL facilities.
V. Conclusions
We have presented and summarised the results of two experimental campaigns at LCLS (LAMP instrument at the AMO beam line) aimed at a proof of principle observation of the stimulated resonant X-ray Raman scattering in molecules. The high-level numerical simulations of the SRIXS in CO, taking into account vibrational excitation and nonlinear pulse propagation preceded and accompanied the experimental effort. We tested two experimental pump–dump schemes for SRIXS. In the first campaign (February 2014), two-colour SASE emission was used. The high-energy component at 534 eV pump the O 1s → π* core-excited state in CO, while the lower spectral component at 525 eV stimulates the X-ray emission to valence-excited states. In the second campaign (July 2015), we utilised a narrow band self-seeded pulse for the pump transition together with a broadband SASE pulse on the dump transition.Our theory predicts that the effect should be observable at the presently attainable parameters of XFEL, though the Raman gain is predicted to be rather moderate: ∼50% of relative amplification of the dump radiation near the RIXS resonances. In both experiments, however, we were not able to clearly identify the SRIXS spectral features. The unsuccessful SRIXS observation was explained by the deviation of the critical parameters of the XFEL machine from the optimal parameters used in the simulations. According to the theory, the SRIXS signal drops significantly with decrease of the pump intensity. Among the critical factors of XFEL and beamline performance are: pump-pulse energy (number of photons) in the spectral resonance window; limiting factors of the experiments were the quality of the focusing KB mirrors, losses through the beam transport optics and the potentially missing collinearity of the X-ray beams of pump and dump spectral components in the gas cell.
In spite of the unsuccessful SRIXS observation, our experiments show several new interesting aspects of the interaction of the strong X-rays with molecular targets. With the help of advanced spectral analysis, we were able to register the formation of molecular ions as a function of the X-ray fields intensity of Raman transitions. Moreover, we developed new methods of analysis of the XFEL-molecule interaction by using the statistical averaging of the spectral features, partial averaging by restricting the ensemble to a small region of the XFEL beam parameters (from e-beam energy–pulse energy diagrams), covariance analysis and partial covariance analysis. The methods are implemented in software that now is available for a detailed online data analysis for future experiments. The obstacles of large beam-line losses and degraded focusing mirrors can be overcome in principle, easily pushing up attainable intensities by a factor of 20. The fraction of absorbing and emitting molecules can be drastically increased by alignment of the molecules in the gas phase,12,30 that, however, requires good synchronisation and timing of an external IR laser pulse to the XFEL beam. SRIXS should, therefore, become observable by overcoming these structural and technical challenges.
Author contributions
V. Kimberg and N. Rohringer developed the theory and conceived the experiment. V. Kimberg performed the numerical simulations of SRIXS. A. Sanchez-Gonzalez performed the data analysis. L. Mercadier was responsible for the overall experimental set-up and supported the experiment. C. Weninger and A. Sanchez-Gonzalez were responsible for the data acquisition and online data analysis. A. Lutman and D. Ratner conceived the ideas and were responsible for the FEL setup in the two-colour SASE/soft X-ray self-seeding scheme. M. Mucke, M. Agåker, Conny Såthe, J.-E. Rubensson and J. Nordgren were responsible for the X-ray spectrometer setup and X-ray spectroscopy. R. Coffee, C. Bostedt and M. Bucher were responsible for the AMO instrument at LCLS and supported the experiment. N. Rohringer, V. Kimberg, A. Sanchez-Gonzalez, L. Mercadier, R. Coffee, C. Bostedt, A. Lutman and J.-E. Rubensson interpreted and discussed the data. V. Kimberg, N. Rohringer, L. Mercadier wrote the paper, with contributions from A. Lutman and A. Sanchez-Gonzalez.Acknowledgements
We acknowledge financial support from the Max Planck Society; VK also acknowledges financial support from the Knut and Alice Wallenberg Foundation (KAW-2013.0020) and Swedish Research Council (VR). AS-G also acknowledges support from the Science and Technology Facilities Council (STFC). MB and CB acknowledge support from the U.S. Department of Energy, Office of Science, Office of Basic Energy Sciences, Division of Chemical, Geological, and Biological Sciences, under Contract No. DE-AC02-06CH11357. Use of the Linac Coherent Light Source (LCLS), SLAC National Accelerator Laboratory, is supported by the U.S. Department of Energy, Office of Science, Office of Basic Energy Sciences under Contract No. DE-AC02-76SF00515. The simulations were performed on resources provided by the Swedish National Infrastructure for Computing (SNIC).References
- P. Kukura, D. W. McCamant and R. A. Mathies, Annu. Rev. Phys. Chem., 2007, 58, 461–488 CrossRef CAS PubMed.
- R. R. Frontiera and R. A. Mathies, Laser Photonics Rev., 2011, 5, 102–113 CrossRef CAS.
- S. Tanaka and S. Mukamel, Phys. Rev. Lett., 2002, 89, 043001 CrossRef PubMed.
- I. Schweigert and S. Mukamel, Phys. Rev. A, 2007, 76, 012504 CrossRef.
- U. Harbola and S. Mukamel, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 79, 085108 CrossRef.
- W. Hua, S. Oesterling, J. D. Biggs, Y. Zhang, H. Ando, R. de Vivie-Riedle, B. P. Fingerhut and S. Mukamel, Struct. Dyn., 2016, 3, 023601 CrossRef PubMed.
- Y. Zhang, W. Hua, K. Bennett and S. Mukamel, Top. Curr. Chem., 2014, 368, 273 CrossRef.
- D. Healion, H. Wang and S. Mukamel, J. Chem. Phys., 2011, 134, 124101 CrossRef PubMed.
- C. Weninger, M. Purvis, D. Ryan, R. a. London, J. D. Bozek, C. Bostedt, A. Graf, G. Brown, J. J. Rocca and N. Rohringer, Phys. Rev. Lett., 2013, 111, 233902 CrossRef PubMed.
- C. Weninger and N. Rohringer, Phys. Rev. A, 2013, 88, 053421 CrossRef.
- V. Kimberg and N. Rohringer, Struct. Dyn., 2016, 3, 034101 CrossRef PubMed.
- V. Kimberg and N. Rohringer, Phys. Rev. Lett., 2013, 110, 043901 CrossRef PubMed.
- R. C. Couto, M. Guarise, A. Nicolaou, N. Jaouen, G. S. Chiuzbăian, J. Lüning, V. Ekholm, J.-E. Rubensson, C. Såthe, F. Hennies, F. F. Guimarães, H. Ågren, F. Gel’mukhanov, L. Journel, M. Simon and V. Kimberg, Phys. Rev. A, 2016, 93, 032510 CrossRef.
- N. Rohringer, V. Kimberg, C. Weninger, A. Sanchez-Gonzalez, A. Lutman, T. Maxwell, C. Bostedt, S. C. Monterro, A. O. Lindahl, M. Ilchen, R. N. Coffee, J. D. Bozek, J. Krzywinski, T. Kierspel, T. Mullins, J. Küpper, B. Erk, D. Rolles, O. D. Mücke, R. A. London, M. Purvis, D. Ryan, J. J. Rocca, R. Feifel, R. Squibb, V. Zhaunerchyk, C. Såthe, M. Agåker, M. Mucke, J. Nordgren and J. E. Rubensson, in X-ray Lasers 2014. Proceedings of the 14th International Conference on X-Ray Lasers, ed. J. J. Rocca, C. Meloni and M. Marconi, 2016, vol. 169, p. 201 Search PubMed.
- S. Schreck, M. Beye, J. a. Sellberg, T. McQueen, H. Laksmono, B. Kennedy, S. Eckert, D. Schlesinger, D. Nordlund, H. Ogasawara, R. G. Sierra, V. H. Segtnan, K. Kubicek, W. F. Schlotter, G. L. Dakovski, S. P. Moeller, U. Bergmann, S. Techert, L. G. M. Pettersson, P. Wernet, M. J. Bogan, Y. Harada, A. Nilsson and A. Föhlisch, Phys. Rev. Lett., 2014, 113, 153002 CrossRef PubMed.
- P. Skytt, P. Glans, K. Gunnelin, J. Guo and J. Nordgren, Phys. Rev. A, 1997, 55, 146–154 CrossRef CAS.
- M. Piancastelli, M. Neeb, A. Kivimäki, B. Kempgens, H. M. Köppet, K. Maier, A. M. Bradshaw, R. F. Fink and H. M. Köppe, J. Phys. B: At., Mol. Opt. Phys., 1997, 30, 5677–5692 CrossRef CAS.
- H. J. Werner and et al., http://www.molpro.net, 2012.
- D. Damiani, M. Dubrovin, I. Gaponenko, W. Kroeger, T. J. Lane, A. Mitra, C. P. O'Grady, A. Salnikov, A. Sanchez-Gonzalez, D. Schneider and C. H. Yoon, J. Appl. Crystallogr., 2016, 49, 672–679 CrossRef CAS.
- S. Smith, S. Hoobler, R. G. Johnson, T. Straumann and A. Young, in Proceedings of PAC '09, Vancouver, British Columbia, Canada, p. TU3GRC05 Search PubMed.
- S. P. Hau–Riege, R. M. Bionta, D. D. Ryutov and J. Krzywinski, J. Appl. Phys., 2008, 103, 053306 CrossRef.
- A. Lutman, R. Coffee, Y. Ding, Z. Huang, J. Krzywinski, T. Maxwell, M. Messerschmidt and H.-D. Nuhn, Phys. Rev. Lett., 2013, 110, 134801 CrossRef CAS PubMed.
- P. Emma, R. Akre, J. Arthur, R. Bionta, C. Bostedt, J. Bozek, A. Brachmann, P. Bucksbaum, R. Coffee, F.-J. Decker, Y. Ding, D. Dowell, S. Edstrom, A. Fisher, J. Frisch, S. Gilevich, J. Hastings, G. Hays, P. Hering, Z. Huang, R. Iverson, H. Loos, M. Messerschmidt, A. Miahnahri, S. Moeller, H.-D. Nuhn, G. Pile, D. Ratner, J. Rzepiela, D. Schultz, T. Smith, P. Stefan, H. Tompkins, J. Turner, J. Welch, W. White, J. Wu, G. Yocky and J. Galayda, Nat. Photonics, 2010, 4, 641–647 CrossRef CAS.
- P. Emma, K. Bane, M. Cornacchia, Z. Huang, H. Schlarb, G. Stupakov and D. Walz, Phys. Rev. Lett., 2004, 92, 074801 CrossRef CAS PubMed.
- Y. Ding, C. Behrens, R. Coffee, F.-J. Decker, P. Emma, C. Field, W. Helml, Z. Huang, P. Krejcik, J. Krzywinski, H. Loos, A. Lutman, A. Marinelli, T. J. Maxwell and J. Turner, Appl. Phys. Lett., 2015, 107, 191104 CrossRef.
- A. Marinelli, R. Coffee, S. Vetter, P. Hering, G. N. West, S. Gilevich, A. A. Lutman, S. Li, T. Maxwell, J. Galayda, A. Fry and Z. Huang, Phys. Rev. Lett., 2016, 116, 254801 CrossRef CAS PubMed.
- D. Ratner, R. Abela, J. Amann, C. Behrens, D. Bohler, G. Bouchard, C. Bostedt, M. Boyes, K. Chow, D. Cocco, F. J. Decker, Y. Ding, C. Eckman, P. Emma, D. Fairley, Y. Feng, C. Field, U. Flechsig, G. Gassner, J. Hastings, P. Heimann, Z. Huang, N. Kelez, J. Krzywinski, H. Loos, A. Lutman, A. Marinelli, G. Marcus, T. Maxwell, P. Montanez, S. Moeller, D. Morton, H. D. Nuhn, N. Rodes, W. Schlotter, S. Serkez, T. Stevens, J. Turner, D. Walz, J. Welch and J. Wu, Phys. Rev. Lett., 2015, 114, 054801 CrossRef CAS PubMed.
- A. Marinelli, A. A. Lutman, J. Wu, Y. Ding, J. Krzywinski, H.-D. Nuhn, Y. Feng, R. N. Coffee and C. Pellegrini, Phys. Rev. Lett., 2013, 111, 134801 CrossRef CAS PubMed.
- M. Coreno, M. de Simone, K. C. Prince, R. Richter, M. Vondracek, L. Avaldi and R. Camilloni, Chem. Phys. Lett., 1999, 306, 269–274 CrossRef CAS.
- V. Kimberg, S. Zhang and N. Rohringer, J. Phys. B: At., Mol. Opt. Phys., 2013, 46, 164017 CrossRef.
| This journal is © The Royal Society of Chemistry 2016 |

![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 820 pulses and the shaded area is the associated standard deviation.
820 pulses and the shaded area is the associated standard deviation.