Emerging investigators series: using an analytical solution approach to permit high volume groundwater withdrawals†
Ivan S.
Jayawan
,
Avery H.
Demond
and
Brian R.
Ellis
 *
*
Department of Civil and Environmental Engineering, University of Michigan, Ann Arbor, MI, USA. E-mail: brellis@umich.edu; Tel: +734 763 5470
First published on 3rd October 2016
Abstract
Sustainable water management is paramount to ensuring continued access to fresh water resources. Some states have chosen to use analytical solutions to predict pumping-induced drawdowns and the reduction in groundwater baseflow to streams in an effort to predict negative impacts associated with high volume groundwater withdrawals (HVGWs). In line with this approach, the State of Michigan has developed the Water Withdrawal Assessment Tool (WWAT), which estimates streamflow depletion to evaluate whether a proposed HVGW activity will have an adverse impact on stream ecology. To assess the tool's performance, this study compared calculations for streamflow depletion estimated using the Hunt (1999) solution, as implemented in the WWAT, with those of a numerical groundwater flow model developed in MODFLOW for two different locations in Michigan where HVGW wells have been permitted. In addition, sensitivity and uncertainty analyses were conducted. The results showed that the WWAT, in general, provides a conservative estimate of stream depletion. However, to obtain a more accurate estimate, the type of aquifer (unconfined versus semi-confined) needs to be taken into account. The most critical parameters are the storativity, S, and the streambed conductance, λ. Since S has a fixed value of 0.01 in the WWAT, the role of streambed conductance becomes paramount. Given the paucity of information regarding λ, its estimation merits additional scrutiny.
Water impactTo effectively manage water resources, strategies are needed to assess proposed high-volume groundwater withdrawals (HVGWs). This study critically evaluates an on-line screening tool designed to protect ecologically important stream flows by comparing its calculations of streamflow depletion with those of a three-dimensional numerical groundwater flow model for two specific sites in the State of Michigan where HVGWs have been permitted. |
1. Introduction
The topic of water scarcity is at the forefront of national media attention as droughts in some regions of the U.S. have begun to force municipalities to reduce water consumption and pursue more sustainable water management strategies. Changing precipitation patterns associated with global climate change and increased water demand due to growth in urban populations have further exacerbated water challenges in some areas.1 As freshwater resources become scarcer, more attention is being paid to how states allocate water. New demands for large quantity withdrawals of surface or groundwater, such as those associated with hydraulic fracturing, have highlighted issues related to water allocation and to how high volume groundwater withdrawals (HVGWs) are permitted.The Great Lakes-St. Lawrence River Basin Water Resources Compact (Great Lakes Compact) was established in 2008 by the eight U.S. states that border the Great Lakes and the Canadian Provinces of Quebec and Ontario to ensure the sustainable management of waters within the Great Lakes Basin. All member states within the Great Lakes Compact are required to ban the diversion of Great Lakes water (with some limited exceptions), and to set responsible standards for water use and conservation within the watershed.2 Pursuant to this, member states have been considering the best strategies for permitting HVGWs with the goal of ensuring sustainable water management. HVGWs may be associated with a variety of end uses including municipal drinking water, agricultural irrigation, chemical or pharmaceutical manufacturing, water bottling and food processing. Recently, new demands for HVGWs have been associated with high volume hydraulic fracturing (HVHF) of unconventional oil and natural gas reservoirs.3 Hydraulic fracturing well completions in the U.S. use an average of 14![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 m3 (3.8 million gallons) of water, with several wells in Michigan reporting the use of over 75
000 m3 (3.8 million gallons) of water, with several wells in Michigan reporting the use of over 75![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 m3 (20 million gallons).4,5
000 m3 (20 million gallons).4,5
In compliance with the Great Lakes Compact, the State of Michigan developed a formal process for evaluating applications for HVGWs. Although freshwater resources in Michigan are considered to be abundant, some streams in the state are designated as “cold transitional” or “cool water” streams and are home to sensitive fish populations. As surface waters are usually hydraulically connected to groundwater, pumping-related variation in groundwater baseflow to these streams can result in fluctuations in stream temperature that may adversely impact these fish populations.6–11 Water quality may also be impaired as lower baseflow can reduce the dilution of loadings of solids or other contaminants.6,12 Thus, the objective of the process for evaluating HVGWs in Michigan is the protection of ecologically important flows, utilizing information regarding groundwater hydrogeology, river flow, and aquatic health to determine the potential adverse resource impact (ARI) due to a new HVGW well. The centerpiece of the process is the Water Withdrawal Assessment Tool (WWAT) which screens HVGW (defined as a pumping rate >378 m3 per day at any point during its use) permit applications to identify those wells that require a more thorough site-specific review based on an assessment of potential risk to the aquatic health of nearby streams.13 The State of Michigan utilizes the WWAT to determine if an ARI is likely to occur due to a given pumping activity. The criterion for an ARI occurrence is a sufficiently large reduction in streamflow that a negative impact on a stream's characteristic fish population is triggered.13
The WWAT is comprised of three different modules that are linked together through an online geospatial information system to determine the impact of potential groundwater withdrawals on stream ecology. These three modules comprise a groundwater model, a stream model and a fisheries model.13 The groundwater model is based on a modification of the analytical solution presented by Hunt14 and is used to calculate the resulting stream depletion, Qs, from a given pumping activity.15 The stream model is used to determine the index flow, Qindex, which is defined as the lowest median stream flow rate for the dry summer months. An estimate of Qindex is calculated for each stream segment through use of a regression model based on 147 streamflow gaging stations across Michigan with records of 10 or more years. This estimate is then halved to yield a more conservative value on which to base the prediction of an ARI.16 The fisheries model uses the Michigan Department of Natural Resources fisheries database, coupled with statistical modeling, to predict how fish assemblages in different types of Michigan streams would respond to decreased streamflows.17,18 An ARI is defined to occur when a HVGW causes a reduction in stream flow above a set fraction of the stream's index flow (i.e., Qs/Qindex must be above a certain threshold; see Table SI-1 in the ESI† for values of the threshold Qs/Qindex for ARIs.) If the WWAT predicts the occurrence of an ARI, the application for the new HVGW well is referred for a site-specific review.13,17
The WWAT was signed into state law in 2008.19 Since its implementation, more than 3800 applications have been submitted for permitting, with approximately 2800 approved by the WWAT and the remaining referred for site-specific review.20 There are critics who feel that the WWAT is too conservative by referring HVGW permit applications for site-specific review in areas where water is abundant and there has been no evidence of wells drying out or significant reductions in streamflow as a result of existing HVGW wells.21 Such referrals may be viewed by stakeholders as inaccuracies in the values of Qs predicted by the WWAT, when, in fact, the model may be simply providing a conservative estimate, as intended. There are also critics who feel that the WWAT is not conservative enough; for example, the values for Qindex are based on gaged streams and may be too high in the case of certain sensitive streams that are not gaged.22 Therefore, this study focuses on the groundwater component of the WWAT and seeks to evaluate its ability to characterize Qs for proposed HVGW activities, in both agricultural and HVHF settings.
Fig. 1 shows the situation considered by Hunt14 in the development of the analytical solution upon which the stream depletion component of the WWAT is based. The solution assumes a one-dimensional aquifer that is homogeneous, isotropic and of infinite extent containing a fully penetrating pumping well. Furthermore, it assumes that the ratio of vertical to horizontal velocities is small, and that the drawdown is small relative to the saturated thickness. The stream is straight and extends to negative and positive infinity in the y-direction at x = 0, has horizontal and vertical dimensions that are small relative to the aquifer and changes in its water surface elevation are small relative to changes in the water table elevation. Based on these assumptions, the streamflow depletion rate can be calculated as:14
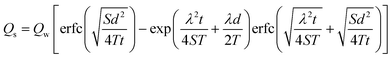 | (1) |
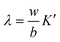 | (2) |
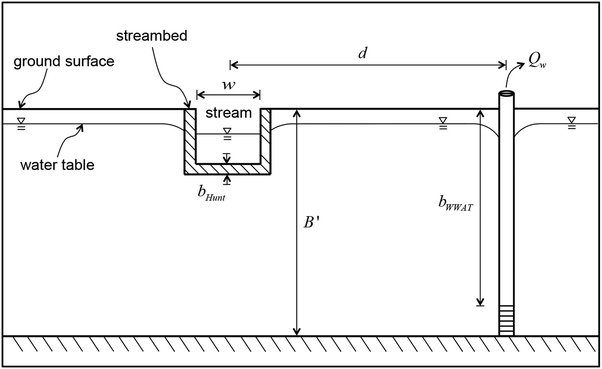 | ||
| Fig. 1 System schematic for the analytical solution of Hunt14 employed by the WWAT.15d is the distance between the stream and the pumping well, w is the width of the stream, B′ is the thickness of the surficial glacial deposits and Qw is the pumping rate of the well. bHunt and bWWAT denote the streambed thickness used by Hunt14 and in the WWAT,15 respectively. | ||
In the application of Hunt's14 solution in the context of the WWAT, the primary difference is in the calculation of the streambed conductance. The hydraulic conductivity and thickness of the streambed are actually unknown. In the WWAT, the hydraulic conductivity of the streambed is considered to be 1/10 of the hydraulic conductivity of the surficial aquifer. Furthermore, the solution by Hunt14 assumes a fully penetrating well. Yet, in reality, wells are screened at discrete depths and those screened at deeper depths will have a lower impact on surface streams. To reflect this, the vertical distance from the land surface to the top of the well screen, bWWAT, is introduced as the streambed thickness in the WWAT. Thus, the streambed conductance, λ, in the WWAT is calculated as:15
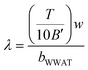 | (3) |
Given that the solution of Hunt14 is based on a number of assumptions, and, in addition, its implementation in the WWAT incorporates additional assumptions, it is important to assess how well the WWAT estimates the amount of streamflow depletion resulting from HVGWs that might be associated with water-intensive utilization activities such as HVHF or large-scale agriculture. This objective will be accomplished by comparing estimates of streamflow depletion calculated by the groundwater component of the WWAT with estimates generated by a 3-D numerical simulator at two different locations in the State of Michigan, where HVGW wells have been permitted by the Michigan Department of Environmental Quality (MDEQ). The two selected sites, one in Northern Michigan and the other in Southwestern Michigan, present two different groundwater hydrology scenarios and two sectors of water use in the State of Michigan.
2. Methods
2.1. Set-up of models
The first study location is in Bear Lake Township in Kalkaska County where HVGW wells have been approved in anticipation of HVHF activities in the vicinity (Fig. 2). The wells are located in the Manistee River watershed approximately 1000 m from Black Creek, a groundwater-fed stream classified as a “cool stream” by the WWAT. The bedrock geology is dominated by Coldwater Shale and Marshall Sandstone while the surficial geology is dominated by glacial outwash (mainly sand and gravel), with an average depth to bedrock of ±215 m.23,24 In this location, groundwater generally flows from north to south at a rate of about 0.18 m per day, following the direction of flow in the Black Creek. Almost all groundwater wells in the area are screened in shallow glacial aquifers, with depths ranging from 20–30 m.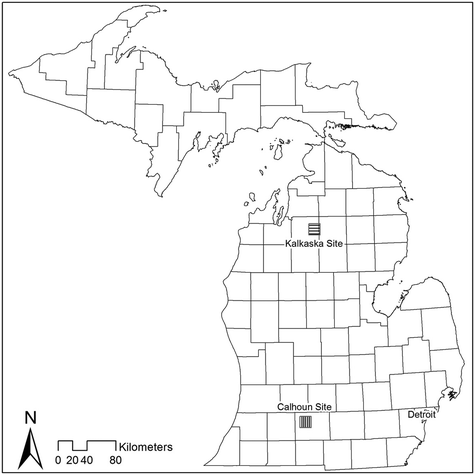 | ||
| Fig. 2 Study site locations in Kalkaska and Calhoun Counties (MI). Lines show the county boundaries in the State of Michigan. | ||
The second site is located in Emmet Charter Township in Calhoun County where a well has been approved by the MDEQ for agricultural use (Fig. 2). The well is located in the Kalamazoo River watershed, approximately 1000 m from Dickinson Creek, a groundwater-fed stream classified as “cold transitional” (the most sensitive type of stream) by the WWAT.13 Due to this stream classification, any proposed HVGW well within the Dickinson watershed would automatically require a site-specific review.13 The bedrock geology is mainly dominated by Marshall Sandstone, while the surficial geology is dominated by a combination of moraine and glacial outwash.23,24 The drift in this area is relatively thin compared to that at the study site in Kalkaska County, with an average depth to bedrock of ±25 m. The general direction of groundwater flow is from east to west, following the direction of the Kalamazoo River, at a rate of about 0.26 m per day. The streamflow direction of Dickinson Creek, however, is from northeast to southwest. Because of the thinness of the glacial deposits, only about 10% of the groundwater wells within this area are screened in the shallow glacial aquifers, with the remaining 90% terminating in bedrock.
To calculate streamflow depletion based on the algorithm used in the WWAT, the program STRMDEPL08 was used. STRMDEPL08 calculates Qs using eqn (1) and (3) in the same manner as the WWAT.25 The values for all the parameters used by the WWAT for the two study sites are given in Table 1. Both the values of T and B′ came from the Michigan Geographic Data Library which provides aquifer property estimates on a 1 km × 1 km grid across the State.26 The stream width w was estimated using a regression equation developed for the WWAT to relate stream width to drainage area in the State of Michigan:15
| w = 3.28 × (10((0.522358×log(da×1.60932))−0.18786)) | (4) |
| Description | Kalkaska site | Calhoun site | |
|---|---|---|---|
| a The values for T for the WWAT are from the Michigan Geographic Data Library,15,26 whereas those for MODFLOW are based on calibrated Kx values and aquifer thicknesses of 180 m and 100 m for the Kalkaska and Calhoun study sites, respectively. b The value of S for the WWAT is constant and consistent with reported values for leaky aquifers,15 whereas those for MODFLOW are based on typical values presented in Morris and Johnson.37 c The value of B′ is from the Michigan Geographic Data Library.15,26 d The values for recharge are from the Michigan Geographic Data Library.15,26 e The value of b for the WWAT is the vertical distance from stream to the top of the well screen,15 whereas that for MODFLOW is based on typical values of streambed thickness.27 f The value of w for the WWAT was calculated using eqn (4), whereas that for MODFLOW was set equal to 1 m based on satellite images. g The value of λ for the WWAT was calculated using eqn (3), whereas that for MODFLOW was calibrated based on a reported measured streamflow of 4 × 103 m3 per day for the Kalkaska site,30 with the same value being used for the Calhoun site in absence of additional information. h The values of Qi for WWAT are equal to Qindex,20 whereas those for MODFLOW were set as equal to Qinitial, the streamflow determined by the model in the absence of pumping. | |||
| Aquifer parameters | |||
| Transmissivity of screened aquifera, T [m2 d−1] | MODFLOW | 718 | 0.432 |
| WWAT | 521 | 435 | |
| Storage coefficientb, S [-] | MODFLOW | 0.16 | 1 × 10−3 |
| WWAT | 0.01 | 0.01 | |
| Aquifer diffusivity, T/S [m2 d−1] | MODFLOW | 4488 | 432 |
| WWAT | 52![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 100 100 |
43![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 460 460 |
|
| Aquitard (layer #2) thickness [m] | MODFLOW | 1–20 | 1–5 |
| Average glacial formation thicknessc, B′ [m] | WWAT | 180 | 25 |
| Surficial aquifer recharge rated [cm per year] | MODFLOW | 22.9 | 28.0 |
| Stream parameters | |||
| Streambed thicknesse, b [m] | MODFLOW | 1 | 1 |
| WWAT | 37 | 31 | |
| Streambed widthf, w [m] | MODFLOW | 1 | 1 |
| WWAT | 6.8 | 6.0 | |
| Streambed conductanceg, λ [m d−1] | MODFLOW | 0.026 | 0.026 |
| WWAT | 0.053 | 0.274 | |
| Streamflow rateh, Qi [m3 d−1] | MODFLOW | 4155 | 488 |
| WWAT | 15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 750 750 |
5870 | |
| Pumping well parameters | |||
| Distance between well and stream, d [m] | MODFLOW | 1000 | 1000 |
| WWAT | 1000 | 1000 | |
| Pumping rate, Qw [m3 d−1] | MODFLOW | 2530 | 6540 |
| WWAT | 2530 | 6540 | |
| Pumping schedule | MODFLOW | 3 months of pumping followed by 9 months of shutoff annually for 5 years | |
| WWAT | |||
| Well screen depth from ground level [m] | MODFLOW | 37 | 31 |
As a comparison, Visual MODFLOW 2011.1 (Schlumberger Water Services, Kitchener, ON) was used to compute stream depletion at the same two locations. The stream was assumed to be rectangular, 1 meter in width (based on satellite imagery), with a streambed thickness equal to 1 meter (based on typical values) (Table 1).27 The Stream Flow-Routing package (SFR1) was used to calculate the flow between the stream and the aquifer using the option of Manning's equation for a rectangular stream channel.28 Values of Qs were obtained by subtracting the streamflow at a particular time step from the streamflow determined in the absence of pumping, Qinitial. The domains at both locations were constructed with dimensions of 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 m in length (x-direction) and 10
000 m in length (x-direction) and 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 m in width (y-direction) (Fig. SI-1 and SI-2 in the ESI†), whereas the total thicknesses (z-direction) were 300 m and 150 m for the Kalkaska and Calhoun County sites, respectively. In both cases, the resolution of the grid varied between 25 m × 25 m in the vicinity of the pumping well and near the stream to 400 m × 400 m towards the perimeter of the domain.
000 m in width (y-direction) (Fig. SI-1 and SI-2 in the ESI†), whereas the total thicknesses (z-direction) were 300 m and 150 m for the Kalkaska and Calhoun County sites, respectively. In both cases, the resolution of the grid varied between 25 m × 25 m in the vicinity of the pumping well and near the stream to 400 m × 400 m towards the perimeter of the domain.
An analysis of hydrogeological formations of the area from well logs obtained from the MDEQ Wellogic29 database suggested that the lithology at both study sites can be simplified into three layers. The Kalkaska County site essentially consists of a glacial drift layer (layer #1), varying in thickness between 10–50 m on the northern boundary to 30–85 m on the southern boundary, a thin aquitard (layer #2) and a lower semi-confined glacial drift layer (layer #3). The Calhoun County site consists of a glacial drift layer (layer #1), varying in thickness between 10–25 m in the northeast to 5–20 m in the southwest, a thin aquitard (layer #2) and a semi-confined bedrock layer (layer #3).
The MODFLOW parameter values for the Kalkaska County site are given in Tables 1 and SI-2.† For the Kalkaska County site, constant head boundary conditions were used for all boundaries of the first layer (layer #1). For the thin aquitard and semi-confined glacial drift layers (layers #2 and #3), no-flow boundary conditions were used for the eastern and western boundaries while constant head boundary conditions were used for the northern and southern boundaries, consistent with the dominant direction of groundwater flow. The constant head values were derived from an interpolation of 51 head values measured during the summer, as reported in Wellogic.29 Calibration of the horizontal hydraulic conductivity using 17 well head observations resulted in a root-mean-squared error (RMSE) of ±15 m, and the subsequent validation using two wells resulted in a RMSE of ±12 m. The vertical hydraulic conductivities were assumed to be 1/10 of the horizontal conductivities. The recharge rate was set equal to 22.9 cm per year based on reported values in the Michigan Geographic Data Library.26 The streambed conductance was calibrated based on a reported streamflow in Black Creek of about 4000 m3 per day.30 A single well screened at 37 m below the ground surface, pumping at a rate of 2530 m3 per day, was used to represent the permitted HVHF withdrawal wells. Actual HVHF pumping may occur for only a few weeks or a month during the completion of a given well. However, in this study, the pumping pattern was set so that well was pumped for three months followed by nine months of shut-off on an annual cycle, for a total duration of five years.
The MODFLOW parameter values for the Calhoun County site are given in Tables 1 and SI-3.† For the Calhoun County site, constant head boundaries were used on all sides for the top glacial drift layer (layer #1) and the bottom bedrock layer (layer #3). For the thin aquitard (layer #2), it was assumed that the predominant flow direction was vertical; hence no-flow boundaries were used on all sides. A total of 62 head observation values from the Wellogic database were used to set the constant heads,29 with 36 values for the unconfined glacial aquifer (layer #1) and 26 values for the bedrock aquifer (layer #3). A total of 19 head observations measured during the summer were used for the calibration of the horizontal hydraulic conductivities and two were used for the validation, giving RMSEs of ±3 m and ±2 m respectively. The vertical hydraulic conductivities were assumed to be 1/10 of the horizontal conductivities. The recharge rate was set equal to 28 cm per year based on reported values in the Michigan Geographic Data Library.26 In the absence of additional information, the same value of streambed conductance calibrated for the Kalkaska study site was used for the Calhoun site (Table 1). The pumping well was screened in the bedrock layer at 31 m, as this is the depth of the permitted well at the site in Calhoun County. The assumed pumping rate was 6540 m3 per day,20 with the well being actively pumped for three months, followed by nine months of shutoff on an annual cycle, for a total duration of five years.
2.2. Types of analyses
Values of Qs calculated by STRMDEPL08 were compared with those calculated using MODFLOW. Discrepancies between the results could be attributed to two sources, as the models not only were based on different assumptions, but also used different values for the same parameters. To assess whether the difference in the output of the analytic and numerical models was based on parameter values rather than on model assumptions, additional calculations were performed using STRMDEPL08 with parameter values used in MODFLOW for the screened aquifer (Table 1) and using MODFLOW with all layers having the parameter values assigned by the WWAT for the screened aquifer (Table 1).Sensitivity and error propagation analyses were also performed to investigate which system parameters have the largest influence on estimates of streamflow depletion. In stream-aquifer interactions, the aquifer hydraulic diffusivity, defined as T/S, influences both the rate and timing of streamflow depletion.31 If the aquifer hydraulic diffusivity is large, the aquifer will be more sensitive to pumping events. The storage coefficient also represents, in a sense, the buffer capacity of an aquifer in transient or cyclical pumping events. The smaller the value of S, the less buffer capacity the aquifer has and, as a result, pumping will reduce the baseflow to a stream more rapidly. In an extreme pumping event, groundwater withdrawal could cause a gaining stream to become a losing stream.31 In addition, streambed conductance has been previously demonstrated to strongly influence the impact of HVGWs on nearby water resources.32–35 Highly conductive streambeds allow for more rapid stream-aquifer communication, which results in both a larger groundwater contribution to streamflow and a greater potential for HVGWs to cause a reduction in streamflow.
Parameters evaluated in the sensitivity analysis included the aquifer diffusivity, T/S, and the streambed conductance, λ. T/S and λ were varied independently over several orders of magnitude, while holding all other model parameters constant, and the resulting value of Qs,max/Qw was recorded. Monte Carlo analysis is often the method of choice for determining parameter uncertainty in non-linear equations;36 however, the distribution of the relevant parameters, T, S, and λ, is unknown in this situation. Therefore, Gaussian uncertainty analysis was used here, as this approach has been demonstrated to provide an adequate assessment of uncertainty for non-linear functions.36 The influence of T, S, and λ on Qs was examined by determining the uncertainty based on the partial derivatives of eqn (1) with respect to these variables (see ESI† eqn (SI-1–4)), calculated using WolframAlpha (Champaign, IL). The absolute values of ∂Qs/∂T, ∂Qs/∂S, and ∂Qs/∂λ for a unit value of Qw were then compared to determine which parameters impart the greatest uncertainty in the calculation of Qs.
3. Results and discussion
3.1. Comparison of streamflow depletion calculations
Fig. 3 shows the streamflow depletion, Qs, calculated using STRMDEPL08 and the calibrated MODFLOW model for cyclical pumping over a five-year time period for both the Kalkaska (Fig. 3a) and Calhoun (Fig. 3b) County sites. For each site, both STRMDEPL08 and MODFLOW were used with parameter values assigned by the WWAT as well with those utilized in the MODFLOW simulations (Table 1). Since the concern is whether an ARI warning would be triggered, attention was focused on the maximum streamflow depletion rate, Qs,max, over the five-year period.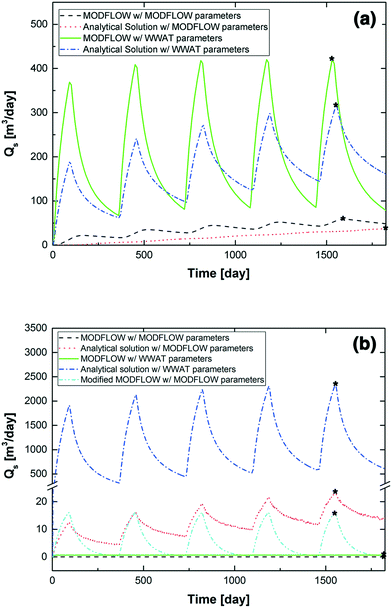 | ||
| Fig. 3 Streamflow depletion, Qs, vs. time, t, calculated by MODFLOW and STRMDEPL08 using both MODFLOW and WWAT parameter values (Table 1) for the study sites in (a) Kalkaska County and (b) Calhoun County. The asterisks denote the maximum stream depletion, Qs,max over the five-year period. In (b), note the break in the scale of the y-axis between 20 and 500. Qs,max for the MODFLOW simulations in (b) are 5 × 10−4 and 0.65 m3 d−1 when using MODFLOW and WWAT assigned parameters, respectively. Also shown are results from a simulation using a modified MODFLOW domain where the parameter values for the aquitard (layer #2) were set equal to those for layer #1. | ||
The results presented in Fig. 3a suggest that, in the case of the Kalkaska site, the large discrepancies in the estimations of Qs stem from the differences in the input parameters, as the use of the same values produced similar order of magnitude estimates (within 24–38% of one another) of the maximum streamflow depletion, Qs,max. This observation suggests that, for this study site, the assumptions employed by Hunt14 to develop his solution, such as a homogeneous lithology and a fully penetrating well, did not significantly influence the calculations. On the other hand, the selected values of the hydrogeologic parameters had a large influence on Qs,max, with those utilized by the WWAT yielding estimates of Qs,max that were an order of magnitude greater for both the analytic and numerical model simulations. An examination of the parameter values in Table 1 shows that, for example, the value of T/S used by the WWAT was over an order of magnitude larger than that in the numerical model simulations. This difference is largely due to the setting of S equal to 0.01 in the WWAT, a value typical of a leaky confined aquifer,15 whereas the aquifer storage coefficient used in the MODFLOW simulations was 0.16,37 a value more typical of an unconfined aquifer. Furthermore, the value of the streambed conductance in the WWAT for the Kalkaska site was twice that in MODFLOW (Table 1). Given the importance of this parameter noted in previous studies,33–35 the larger value of λ used in WWAT may also contribute to the six-fold greater value of Qs,max yielded by the WWAT relative to that generated by MODFLOW.
Calculations of Qs for the Calhoun County site over the cyclical five-year pumping period are shown in Fig. 3b. Of the four situations considered, the only one that predicted a value of Qs,max greater than 25 m3 per day was STRMDEPL08 using WWAT-assigned parameters, which yielded a value of Qs,max of 2354 m3 per day. The observation that using the WWAT parameter values in MODFLOW did not cause a significant difference in the calculation of Qs,max stands in contrast with the results obtained in the case of the Kalkaska County site. A major difference in the two study sites is the lithology relative to the screened depth of the pumping well. The glacial deposits are much thicker at the Kalkaska site, with an average depth to bedrock of 180 m versus only 25 m at the Calhoun site. Due to the thickness of the glacial deposits in Kalkaska County, the HVGW well was screened in this layer, while the well was screened in the bedrock aquifer at the Calhoun County site and is separated from the surficial aquifer by a 1 to 5 m thick aquitard. The presence of this lower-conductivity layer helps to confine the impact of pumping to the bedrock aquifer, reducing the impact on the stream located in the surficial glacial deposits. The discrepancy resulting from different conceptualizations of the hydrogeology is exacerbated by the use of a value of λ in the WWAT that is an order of magnitude larger than that in MODFLOW, again making the stream more responsive to the simulated pumping event than it might be in reality. Similar to that of Kalkaska site, mass balance analysis shows that greater than 95% of the withdrawn water comes from aquifer storage.
To analyze the impact of the aquitard to a greater extent, the site lithology was simplified in MODFLOW by setting the horizontal and vertical hydraulic conductivities of the aquitard (layer #2) equal to those of the surficial glacial deposits (layer #1), essentially eliminating the aquitard. The result, also shown in Fig. 3b (labelled ‘modified MODFLOW’), was that Qs,max now equaled 16.3 m3 per day, nearly 25 times larger than the value estimated using the MODFLOW model with WWAT parameters of 0.65 m3 per day, and of a similar order of magnitude to the value given by the analytic solution with MODFLOW parameters of 23.7 m3 per day. This finding underscores a key circumstance in which the analytical solution of Hunt14 may fail to reflect streamflow depletion behavior adequately. As Barlow and Leake pointed out, aquifer heterogeneity is a critical factor in determining whether an analytic solution is adequate to predict aquifer behavior.31 The findings here suggest that an essential consideration is the placement of the pumping well relative to layered heterogeneity, and even a relatively thin aquitard can have a significant impact. Although these results demonstrate the importance of the well screen location relative to the heterogeneity in the subsurface geology in predicting Qs,max, the fact that the estimate of Qs,max yielded by the analytic solution using parameter values selected by the WWAT was still two orders of magnitude higher underscores the importance of the parameters aquifer diffusivity and streambed conductance.
3.2. Sensitivity analysis
The analysis of the results presented in Fig. 3 pointed to the importance of aquifer diffusivity and streambed conductance to the determination of Qs,max. To explore the sensitivity of the estimates of streamflow depletion to aquifer diffusivity, T/S was varied over two orders of magnitude, from 103 m2 d−1 to 105 m2 d−1, with the results shown in Fig. 4(a). This figure indicates that the values of Qs,max/Qw calculated using the analytic solution in the WWAT were consistently larger than those given by the numerical model. Furthermore, the discrepancy increased with increasing T/S, with the size of the difference depending on the study site. The discrepancy between the values of Qs,max/Qw calculated using the analytical and numerical approaches was greatest at large values of T/S at the site in Calhoun County. At this site, the value of Qs,max/Qw predicted by the numerical model was close to zero regardless of the value of T/S because the pumping well is screened in the bedrock layer, overlain by an aquitard with a low hydraulic conductivity. On the other hand, the value of Qs,max/Qw predicted by the analytical solution increased with the value of T/S as this solution assumes that the system is homogeneous and the well is located in the same geologic unit as the stream. Thus, the discrepancies between the estimated streamflow depletion due to a well screened in a semi-confined bedrock aquifer versus that due to a well screened in an unconfined glacial aquifer depended on the value of T/S, with larger differences occurring at high values of T/S.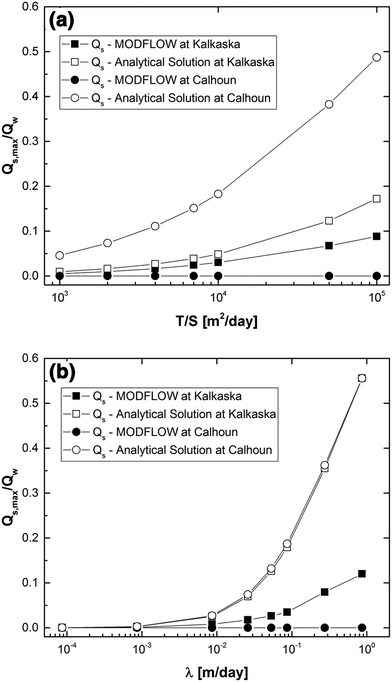 | ||
| Fig. 4 Maximum streamflow depletion, Qs,max, normalized by the well pumping rate, Qw, for both the Kalkaska and Calhoun County study sites as a function of (a) aquifer diffusivity (T/S) and (b) streambed conductance, λ, calculated using MODFLOW and STRMDEPL08 and their respective values for other parameters (Table 1). | ||
To assess the influence of streambed conductance on estimates of Qs,max/Qw, λ was varied over four orders of magnitude. The calculations of Qs,max/Qw under these circumstances, shown in Fig. 4(b), indicate that, at low values of λ, the values of Qs,max/Qw were small for all modeling scenarios, due to the impedance of stream-aquifer communication caused by low streambed conductance. At higher values of λ, the degree of stream depletion increased in all cases; however, the analytical solution yielded values of Qs,max/Qw that were approximately three to five times larger than those predicted by MODFLOW for both study sites. This difference may be attributable to the larger hydraulic diffusivities used by the WWAT, which, when coupled with high values of streambed conductance, resulted in the stream being more sensitive to pumping.
Since the value of bWWAT used by the WWAT as the streambed thickness is the vertical distance from the stream to the top of the well screen, it would be generally much greater than the true streambed thickness, with the result of reducing the value of streambed conductance (eqn (3)). In the situation here, it happened that the value of λ calculated in MODFLOW based on the measured flow in the Black Creek was smaller than those used by the WWAT (Table 1); however, if the wells had been screened at greater depths, the WWAT values of λ would have been smaller. Based on the findings presented in Fig. 4b, low values of λ would result in the calculations of Qs,max/Qw being insensitive to other system parameters. Furthermore, the value of Qs,max estimated by the WWAT would be smaller and thus, less conservative in the prediction of an ARI. Even though, generally, the WWAT calculations of Qs,max were greater than those of MODFLOW (see Fig. 3) and, as such, were more conservative, using the depth of screening as the streambed thickness may counteract the overall degree of conservatism of other assumptions used in the WWAT.
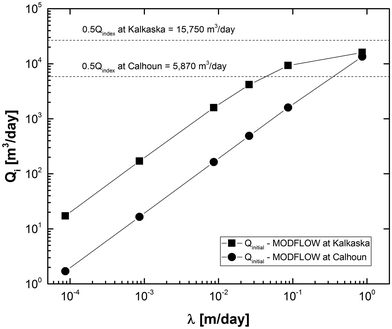
The streambed conductance also influences the quantity of the baseflow for perennial streams, as enhanced communication between the stream and the aquifer can result in a greater contribution to the stream from groundwater. However in the WWAT, streamflow is partially decoupled from groundwater in that water can flow from the stream to the aquifer but not vice versa. In the WWAT, Qi= Qindex is assumed to be constant and is based on a regression model of streamflow in gaged streams. In MODFLOW, however, Qi = Qinitial was calculated for the specific stream of interest and was dependent on the streambed conductance (Fig. 5). Fig. 4b shows that, for small values of λ, Qs is always small regardless of the modeling scenario. Yet, for small values of λ, Qi is small in MODFLOW but not in the WWAT (Fig. 5). Thus for small values of λ, the ratio of Qs,max/Qi may trigger an ARI in MODFLOW but not in the WWAT.
3.3. Uncertainty analysis
The influence of S, T, and λ on Qs was further examined by determining the partial derivative of Qs with respect to S (eqn (SI-2)†), T (eqn (SI-3)†), and λ (eqn (SI-4)†), assuming a unit value of Qw. The values for S, λ, and T determined by the WWAT for the Kalkaska site were 0.01, 0.053 m per day, and 521 m2 per day, respectively. For this set of values, |∂Qs/∂S|, |∂Qs/∂λ|, and |∂Qs/∂T| are 7.61, 4.48, and 7.14 × 10−5, respectively, suggesting that transmissivity does not have a significant influence on the calculations of Qs/Qw. S is the largest contributor to the uncertainty in the calculations when its value is less than 0.01 or larger than 0.2, whereas λ is the largest contributor when its value is between 0.01 to 0.1 m per day (Fig. 6a). At the Calhoun site, the values for S, λ, and T determined by the WWAT were 0.01, 0.274 m per day, and 435 m2 per day, respectively. For this set of values, |∂Qs/∂S|, |∂Qs/∂λ|, and |∂Qs/∂T| are 4.87, 0.603, and 3.58 × 10−3, respectively, again suggesting that the aquifer transmissivity does not have a significant influence on the value of Qs/Qw. S is the major contributor when its value is smaller than 0.005 or larger than 0.2, whereas the streambed conductance is the largest contributor when its value falls between 0.05 and 0.2 m per day (Fig. 6b). If the streambed conductance were of the same order of magnitude at both study sites, then S and λ would contribute similarly to the error in Qs/Qw. However, given that S is a fixed value in the WWAT, the uncertainty in Qs is essentially governed by the magnitude of λ.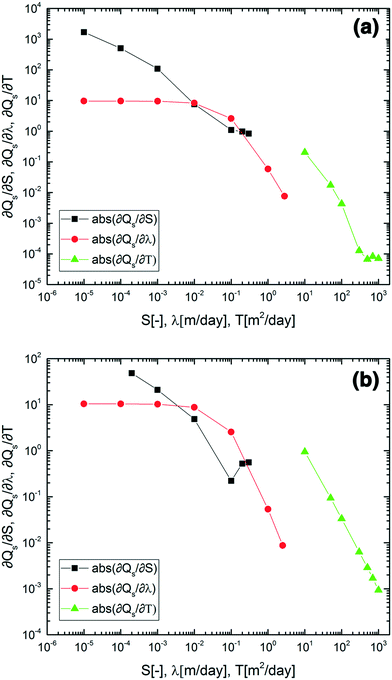 | ||
| Fig. 6 Absolute values of the partial derivatives of Qs (eqn (1)) with respect to S, T and λ (|∂Qs/∂S|, |∂Qs/∂T| and |∂Qs/∂λ|) calculated using eqn (SI-2), (SI-3) and (SI-4)† and the WWAT parameter values for the study sites in (a) Kalkaska (b) Calhoun Counties. | ||
4. Conclusions
To protect ecologically important surface waters, the State of Michigan has developed an analytic tool, the WWAT, to screen proposed HVGW wells, based on the streamflow depletion solution of Hunt.14 To evaluate the tool's performance, a case study of two sites in Michigan, one in Kalkaska County and one in Calhoun County where HVGW wells have been permitted, was undertaken. A three-dimensional numerical groundwater model was developed in MODFLOW for each of these sites and was used to estimate the depletions in streams near the wells. These estimates were then compared to those provided by the WWAT.This study suggests that this screening tool generally overestimates streamflow depletion in an effort to provide a conservative assessment of potential impact from a given HVGW well, as is its intention. Yet, the WWAT still allows the majority of proposed HVGWs to proceed without site-specific review.13,20 Thus, the level of conservatism in the screening tool does not appear to pose an undue hindrance to the permitting process. However, it is believed that the intention of the tool is to reflect the physics of the system and with that in mind, several points need to be considered based on the results of this study. An analysis of the lithology of the two sites showed that both sites could be modeled as three-layer systems. At the Kalkaska site, the layering was not of particular significance because the well was screened in the surficial glacial aquifer, whereas at the Calhoun site, the layering influenced the outcome of the estimates of streamflow depletion, since the well was screened below the aquitard in the bedrock aquifer. In such a situation where heterogeneity is important, an analytic solution, such as that presented by Ward and Lough38 which extends the solution of Hunt14 to consider pumping from a semi-confined aquifer, may give more qualitatively accurate results.
The sensitivity and uncertainty analyses suggest that storativity and streambed conductance may have a similar impact on the estimates of stream depletion. Given that the value of storativity is fixed in the WWAT, the role of streambed conductance becomes more significant. Despite its importance in determining the level of conservatism of the stream depletion estimates, it is a parameter whose value is not well defined. The streambed conductance is based on streambed thickness which, in the WWAT, is set equal to the vertical distance between the stream and the top of the well screen. Since this value is more than likely greater that the actual streambed thickness, the streambed conductance may be unrealistically low. A low value of λ may suggest that the aquifer is poorly connected to the stream, resulting in smaller estimates of stream flow depletion. As multiple studies have also suggested the importance of this parameter,33–35 its estimation in the WWAT merits additional scrutiny.
The WWAT flags a proposed HVGW for site-specific review if Qs exceeds a certain percentage of Qi. In the WWAT, the value of Qi is fixed and is based on a regression analysis of a set of river gage station data of larger rivers and streams. Thus, the role that streambed conductance has in regulating the baseflow of small streams in the absence of pumping may not be adequately represented in the analysis. If the conductance is low, then the baseflow may also be low, increasing the likelihood that a given Qs would result in the prediction of an ARI. Based on a streambed conductance of 0.026 m per day and other parameters (such as Manning's roughness coefficient), MODFLOW estimated a value of Qi of 488 m3 per day for Dickinson Creek, versus a value of 5870 m3 per day given by the WWAT. Thus, more information regarding λ is critical for determining potential ARIs due to the installation of new HVGW wells. Such information would be of use not only for the State of Michigan, but also for other states that have implemented, or are considering implementing, screening procedures based on the impact of groundwater withdrawals on surface water.
Acknowledgements
This work was supported in part by funding from the University of Michigan Water Center and from the National Science Foundation under grant number 1214416. The authors would also like to thank Howard W. Reeves for reviewing an earlier version of this manuscript and for providing access to STRMDEPL08. This publication represents the views of the authors and should not be construed to represent the views of the Michigan Department of Environmental Quality or the U.S. Geological Survey.References
- M. M. Mekonnen and A. Y. Hoekstra, Four billion people facing severe water scarcity, Sci. Adv., 2016, 2, e1500323 Search PubMed.
- Great Lakes-St. Lawrence River Basin Water Resources Council 2008, http://www.glslcompactcouncil.org/Agreements.aspx (accessed on December 2015).
- B. G. Rahm and S. J. Riha, Toward strategic management of shale gas development: Regional, collective impacts on water resources, Environ. Sci.: Processes Impacts, 2014, 16, 1400–1412 CAS.
- R. B. Jackson, A. Vengosh, J. W. Carey, R. J. Davies, T. H. Darrah, F. O'Sullivan and G. Pétron, The environmental costs and benefits of fracking, Annu. Rev. Environ. Resour., 2014, 39, 327–362 CrossRef.
- A. S. Ernstoff and B. R. Ellis, Clearing the waters of the fracking debate, Michigan Journal of Sustainability, 2013, 1, 109–129 CrossRef.
- N. G. Grannemann, R. J. Hunt, J. R. Nicholas, T. E. Reilly and T. C. Winter, The Importance of Ground Water in the Great Lakes Region, U.S. Geological Survey, Lansing, MI, 2000, Water Resources Investigation Rpt. 00-4-008 Search PubMed.
- K. E. Wehrly, M. J. Wiley and P. W. Seelbach, Influence of landscape features on summer water temperatures in lower Michigan streams, Am. Fish. Soc. Symp., 2006, 48, 113–127 Search PubMed.
- T. G. Zorn, P. W. Seelbach and M. J. Wiley, Distributions of stream fishes and their relationship to stream size and hydrology in Michigan's lower peninsula, Trans. Am. Fish. Soc., 2002, 131, 70–85 CrossRef.
- M. E. Baker, M. J. Wiley, P. W. Seelbach and M. L. Carlson, A GIS model of subsurface water potential for aquatic resource inventory, assessment, and environmental management, Environ. Manage., 2003, 32, 706–719 CrossRef PubMed.
- B. D. Richter, R. Mathews, D. L. Harrison and R. Wigington, Ecologically sustainable water management: managing river flows for ecological integrity, Ecol. Appl., 2003, 13, 206–224 CrossRef.
- P. A. Cott, P. K. Sibley, W. M. Somers, M. R. Lilly and A. M. Gordon, A review of water level fluctuations on aquatic biota with an emphasis on fishes in ice-covered lakes, J. Am. Water Resour. Assoc., 2008, 44, 343–359 CrossRef.
- M. L. Polizzotto, B. D. Kocar, S. G. Benner, M. Sampson and S. Fendorf, Near-surface wetland sediments as a source of arsenic release to ground water in Asia, Nature, 2008, 454, 505–508 CrossRef CAS PubMed.
- D. A. Hamilton and P. W. Seelbach, Michigan's Water Withdrawal Assessment Process and Internet Screening Tool, Michigan Department of Natural Resources, Lansing, MI, 2011, Fisheries Special Rpt. 55 Search PubMed.
- B. Hunt, Unsteady stream depletion from ground water pumping, Ground Water, 1999, 37, 98–102 CrossRef CAS.
- H. W. Reeves, D. A. Hamilton, P. W. Seelbach and A. J. Asher, Ground-Water-Withdrawal Component of the Michigan Water-Withdrawal Screen Tool, U.S. Geological Survey, Reston, Virginia, 2009, Scientific Investigations Rpt. 2009-5003 Search PubMed.
- D. A. Hamilton, R. C. Sorrell and D. J. Holtschlag, A Regression Model for Computing Index Flows Describing the Median Flow for the Summer Month of Lowest Flow in Michigan, U.S. Geological Survey, Reston, Virginia, 2008, Scientific Investigations Rpt. 2008-5096 Search PubMed.
- T. G. Zorn, P. W. Seelbach and E. S. Rutherford, A regional-scale habitat suitability model to assess the effects of flow reduction on fish assemblages in Michigan streams, J. Am. Water Resour. Assoc., 2012, 48, 871–895 CrossRef.
- P. W. Seelbach, M. J. Wiley, M. E. Baker and K. E. Wehrly, Initial classification of river valley segments across Michigan's lower peninsula, Am. Fish. Soc. Symp., 2006, 48, 25–48 Search PubMed.
- Michigan Legislature Public Act 185 of 2008, http://legislature.mi.gov/doc.aspx?2007-SB-0860 (accessed June 2016).
- Michigan Department of Environmental Quality, Michigan's Water Withdrawal Assessment Tool, http://www.deq.state.mi.us/wwat/ (accessed January 2016) Search PubMed.
- J. Alexander, Water, water everywhere in Michigan, but is it enough, Bridge Magazine, October 21, 2013 (accessed at http://bridgemi.com) Search PubMed.
- J. L. Jocks and C. M. Bzdok, The impact of Michigan's water withdrawal legislation on small streams and small stream riparian owners, Mich. Real Prop. Rev., 2010, 37, 28–33 Search PubMed.
- W. R. Ferrand, D. L. Bell and S. E. Wilson, Quaternary Geology of Michigan, Geological Publication QC-01, Michigan Department of Natural Resources, 1982 Search PubMed.
- Michigan Department of Natural Resources, 1987 Bedrock Geology of Michigan, http://www.michigan.gov/documents/deq/1987_Bedrock_Geology_Map_301466_7.pdf (accessed July 2015) Search PubMed.
- H. W. Reeves, STRMDEPL08—An Extended Version of STRMDEPL with Additional Analytical Solutions to Calculate Streamflow Depletion by Nearby Pumping Wells, U.S. Geological Survey, Reston, Virginia, 2008, USGS Open File Rpt. 2008-1166 Search PubMed.
- Michigan Department of Technology, Management and Budget, Michigan Geographic Data Library, https://www.mcgi.state.mi.us/mgdl/ (accessed May 2015) Search PubMed.
- L. Toran, J. E. Nyquist, A. C. Fang, R. J. Ryan and D. O. Rosenberry, Observing lingering hyporheic storage using electrical resistivity: variations around stream restoration structures, Crabby Creek, PA, Hydrol. Processes, 2013, 27, 1411–1425 CrossRef.
- D. E. Prudic, L. F. Konikow and E. R. Banta, A New Streamflow-Routing (SFR1) Package to Simulate Stream-Aquifer Interaction with MODFLOW-2000, U.S. Geological Survey, Carson City, Nevada, 2004, USGS Open File Rpt. 2004-1042 Search PubMed.
- Michigan Department of Environmental Quality, Wellogic System, https://secure1.state.mi.us/wellogic (accessed June 2015) Search PubMed.
- J. Victory, S. Biteman, B. Versical, K. Kidder and E. Kimber, Review of the Michigan State (MSU) Memorandum Entitled Preliminary Analysis of Fracking and Flows in Upper Manistee River and Assessment of Available Area Hydrogeologic Data, Interoffice Communication, Michigan Department of Environmental Quality, accessed at https://energyindepth.org/wp-content/uploads/2014/06/MDEQ-Upper-Manistee-memo.pdf.
- P. M. Barlow and S. A. Leake, Streamflow Depletion by Wells Understanding and Managing the Effects of Groundwater Pumping on Streamflow, U.S. Geological Survey, Reston, Virginia, 2012, USGS Circular 1376 Search PubMed.
- L. C. Best and C. S. Lowry, Quantifying the potential effects of high-volume water extractions on water resources during natural gas development: Marcellus Shale, NY, J. Hydrol.: Reg. Stud., 2014, 1, 1–16 CrossRef.
- G. Lackey, R. M. Neupauer and J. Pitlick, Effects of streambed conductance on stream depletion, Water, 2015, 7, 271–287 CrossRef.
- X. Chen and Y. Yin, Evaluation of streamflow depletion for vertical anisotropic aquifers, J. Environ. Syst., 1999, 27, 55–70 CrossRef.
- S. Christensen, On the estimation of stream flow depletion parameters by drawdown analysis, Groundwater, 2000, 38, 726–734 CrossRef CAS.
- J. Tellinghuisen, Statistical error propagation, J. Phys. Chem. A, 2001, 105, 3917–3921 CrossRef CAS.
- D. A. Morris and A. I. Johnson, Summary of Hydrologic and Physical Properties of Rock and Soil Materials, as Analyzed by the Hydrologic Laboratory of the U.S. Geological Survey, 1948–60, U.S. Govt. Print. Off., 1967 Search PubMed.
- N. Ward and H. Lough, Stream depletion from pumping a semiconfined aquifer in a two-layer leaky aquifer system, J. Hydrol. Eng., 2011, 16, 955–959 CrossRef.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c6ew00108d |
| This journal is © The Royal Society of Chemistry 2016 |