Critical review of mathematical approaches for quantitative microbial risk assessment (QMRA) of Legionella in engineered water systems: research gaps and a new framework
K. A.
Hamilton
* and
C. N.
Haas
Department of Civil, Architectural, and Environmental Engineering, Drexel University, 3141 Chestnut Street, Philadelphia, Pennsylvania PA 19104, USA. E-mail: kh495@drexel.edu; Fax: +1 215 895 1363; Tel: +1 215 895 2000
First published on 9th March 2016
Abstract
Legionella has been identified as the responsible agent for two-thirds of waterborne disease outbreaks in the United States from 2011–2012. The prevention of Legionella in engineered systems presents complex challenges for the drinking water industry due to its persistence, resistance to disinfection, and complex microbial ecology. Not all species of Legionella are of concern for human health, however, certain environmental conditions can cause human-virulent species such as L. pneumophila to proliferate, or modulate the distribution of virulence characteristics for relevant strains such that health risks are presented. Quantitative microbial risk assessment (QMRA) is a tool for integrating information on pathogen occurrence, infectivity, and exposure for guiding water quality management strategies. A standardized QMRA approach for Legionella has not been developed, and exposure models are highly varied based on scenario- and site-specific conditions. Detailed discussion of these varied mathematical approaches has been limited, but can aid in identifying research gaps for further QMRA development and public health risk management strategies. A summary of 18 studies that utilize Legionella exposure models for sewage treatment plants, cooling towers, drinking water distribution systems, whirlpool spas, showering, and recreational water scenarios are discussed here. Ten of these studies conducted a full QMRA, and provided human infection estimates. The summarized models utilized Gaussian dispersion, volumetric estimation, occupational hygiene, and aerosol science approaches. Parameters, implications, and limitations of each of these mathematical approaches are discussed, and a QMRA framework to address the identified limitations is proposed. This framework provides a comprehensive overview of key steps within an idealized Legionella QMRA model from exposure to risk characterization, including biofilm impacts, aerosol generation, survival and transport of bacteria within size-resolved water droplets, and interaction with a human receptor.
Water impactLegionella bacteria are responsible for numerous recent waterborne disease outbreaks, and present complex challenges for water professionals. Quantitative microbial risk assessment (QMRA) is used to navigate these challenges and prioritize management opportunities. A discussion of mathematical approaches to Legionella exposure assessment from eighteen studies highlights areas for uncertainty reduction. A framework is proposed to aid in conducting a comprehensive risk analysis. |
1. Introduction
Legionella is a genus of opportunistic bacteria with several species of significant public health importance known to occur in engineered water systems, ambient water environments and soils. Legionnaires' disease or the milder form Pontiac fever result from inhalation or aspiration of aqueous aerosols or soil dusts containing Legionella bacteria.1 The most common cause of illness is L. pneumophila, although over 50 species have been identified.2 Infections are particularly problematic for susceptible populations such as those who are immunocompromised or immunosuppressed, the elderly, smokers, and other hospitalized individuals.3,4 Although rapid diagnosis and treatment methods have improved case-fatality rates since the first recognized outbreak in 1976, prevention of Legionnaires' disease remains an important focus for water quality management.5Legionella was identified as the responsible agent for 66% of reported waterborne disease outbreaks and 26% of waterborne illnesses in the United States from 2011–2012.6The prevention of human-virulent Legionella spp. in engineered systems presents complex challenges for the drinking water industry. The presence of Legionella spp. does not necessarily dictate health risk due to variability in the occurrence of human-virulent species and virulence characteristics within individual species. Legionella is relatively resistant to disinfection compared to other waterborne bacteria, and persists in piped distribution systems due to its ability to colonize biofilms.7Legionella can also proliferate and enhance its virulence when internalized into protozoan symbionts such as Acanthamoeba within biofilms. Portions of biofilms can become detached from surfaces and enter the bulk water, becoming dispersed in mists produced by various water fixtures.8,9 Elevated temperatures (20–45 °C), increased water age, and the presence of algal deposits, sludge, or nutrients are associated with enhanced Legionella growth.10 In addition to controlling these factors, risk management challenges arise when choosing disinfectants that simultaneously mitigate multiple pathogen risks. For example, switching from free chlorine to monochloramines is more effective in preventing Legionella growth, but in some cases may favor colonization of the biofilm with Mycobacterium avium complex (MAC), another potential opportunistic pathogen of public health concern that occurs in similar ecologic niches to Legionella.11–13
Quantitative microbial risk assessment is a framework that integrates information regarding pathogen occurrence, infectivity, and exposure for determining the health implications of microbial hazards. The QMRA is conducted using a process of hazard identification, exposure assessment, dose response assessment, and risk characterization.14 Conducting a QMRA for Legionella spp. can aid in identifying opportunities for prioritizing public health risk prevention and mitigation strategies. Although guidance is available for conducting general QMRA frameworks,10 there is no standardized approach for developing a Legionella QMRA, and exposure models are highly varied based on scenario-specific conditions. These exposure models are further complicated by the need to address uncertainties in detection methodologies and identifying pathogenic subsets of Legionella bacteria, variability in environmental concentrations, viability and infectivity considerations, host immunity, and the fate and transport of bacteria in aerosols under varying environmental conditions.15 Detailed discussion of the assumptions and limitations of varied quantitative modeling approaches has been limited. This review summarizes published QMRA mathematical frameworks for Legionella (section 2) and identifies strengths, limitations, and research gaps for further QMRA model development (section 3).
2. Frameworks for Legionella risk assessment
General frameworks for microbial dispersion modeling & exposure analysis
The primary types of models for particle dispersion are simple box, Gaussian plume, Lagrangian, and Eulerian.16 Model selection typically depends on the desired spatial scale and complexity of the analysis.17 Several reviews17–19 have summarized dispersion models for bioaerosols, which have relied heavily upon modified Gaussian plume models. However, Gaussian plume models are typically valid only for downwind exposures ranging from 100 m to 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 m,19 and other techniques are necessary for short-range exposures. QMRA models for wastewater, biosolids, and spread of dusts containing pathogens between farms have used Gaussian plume models with various modifications,20–29 with several studies generating site specific, meteorological data-intensive estimates using United States Environmental Protection Agency (USEPA) AERMOD software22,29,30 or Eulerian Computational Fluid Dynamics (CFD).31–33 Additionally, Lagrangian ballistic or random walk models have been used for modeling microbial dispersion where individual aerosol behavior is accounted for, taking into account phenomena such as deposition, evaporation, and bacterial decay.34,35 Gaussian plume, empirical aerosol concentration estimates, and CFD approaches have been applied within the context of Legionella QMRA frameworks. A summary of 18 published Legionella exposure analysis and QMRA studies follows. Major study characteristics are listed in Table 1.
000 m,19 and other techniques are necessary for short-range exposures. QMRA models for wastewater, biosolids, and spread of dusts containing pathogens between farms have used Gaussian plume models with various modifications,20–29 with several studies generating site specific, meteorological data-intensive estimates using United States Environmental Protection Agency (USEPA) AERMOD software22,29,30 or Eulerian Computational Fluid Dynamics (CFD).31–33 Additionally, Lagrangian ballistic or random walk models have been used for modeling microbial dispersion where individual aerosol behavior is accounted for, taking into account phenomena such as deposition, evaporation, and bacterial decay.34,35 Gaussian plume, empirical aerosol concentration estimates, and CFD approaches have been applied within the context of Legionella QMRA frameworks. A summary of 18 published Legionella exposure analysis and QMRA studies follows. Major study characteristics are listed in Table 1.
| Reference (Number) | Model typea | Exposure source | Analytical method used to determine Legionella concentrationb | Biofilm consideration | Bacterial enrichment | Aerosol size consideration during generation or transport |
|---|---|---|---|---|---|---|
| a V = volume estimation; PC = partitioning coefficient; NFFF = near-field far field; G = Gaussian plume or puff; CFD = computational fluid dynamics; AS = aerosol science approach; NS = not specified. b Refers to the analytical method on which the concentration data is based where culture = culture-based methods, PCR = polymerase chain reaction (binary, non-quantitative); qPCR = quantitative polymerase chain reaction. c Legionella were measured using both culture and PCR based methods and were not recovered from aerosols using the culture-based method, however only a qualitative risk evaluation was provided based on these data. d Rouil et al. 2004 assumed that 1 μg m−3 aerosolized water was equivalent to 7 × 10−4Legionella per m3 air (units unspecified), computations done in terms of μg m−3. e Authors did not compute Legionella concentrations in plumes and modeled total aerosol concentrations as surrogate for potential risk. f Environmental investigation was conducted using culture and/or (q)PCR, however dispersion modeling was based on water aerosol transport only. | ||||||
| Blatny et al. (32) | AS, CFD | Biological treatment plant | Culture, qPCRf | x | ||
| Fossum et al. (33) | AS, CFD | Air scrubber | NSe | x | ||
| Nygård et al. (36) | G | Air scrubber | PCRf | x | ||
| Nguyen et al. (37) | G | Cooling tower | NSe | |||
| Rouil et al. (38) | G | Cooling tower | NSd | |||
| Storey et al. (40) | V | Drinking water distribution system | NS | x | x | |
| Ahmed et al. (44) | V | Showering, hosing | qPCR | x | ||
| Armstrong and Haas (51, 67) | PC, NFFF | Whirlpool spa, hot spring | Culture | x | x | |
| Armstrong and Haas (51, 67) | PC, NFFF | Whirlpool spa, hot spring | Culture | x | x | |
| Medema et al. (53) | PC | Sewage treatment plant | Culture, PCRc | |||
| Schoen and Ashbolt (54) | PC | Shower | Culture | x | x | |
| de Man et al. (56) | PC | Recreational splash parks that use rainwater as a source | Culture, qPCR | |||
| Sales-Ortells and Medema (57) | PC | Various urban water systems | Culture, qPCR | |||
| Sales-Ortells and Medema (63) | PC | Stormwater plaza aerosols | qPCR | |||
| Schoen et al. (64) | NS | Shower | qPCR | NS | NS | NS |
| Schoen et al. (68) | NS | Shower | qPCR | NS | NS | NS |
| Azuma et al. (74) | PC | Bathing in a residential bathroom | Culture | |||
| Bouwknegt et al. (75) | AS | Whirlpool spa | Culture | x | ||
Gaussian plume and puff models
Several studies36–38 have used Gaussian models to develop exposure estimates in conjunction with Legionnaires' disease outbreaks linked to cooling towers and are summarized elsewhere.17 Although these studies did not conduct full QMRAs, a brief discussion of the Gaussian plume model is presented here in eqn (1), as this approach can be integrated with existing exposure approaches to calculate a deposited dose for QMRA, and is useful for comparison with the other approaches discussed below.39 A Gaussian puff model further incorporates this equation with a Lagrangian trajectory model.17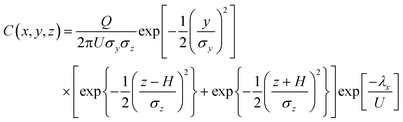 | (1) |
Nguyen et al.37 compared dispersion estimates with geographic areas in France where 86 cases resided during an outbreak using the Atmospheric Dispersion Modeling System (ADMS) model. A qualitative correlation was observed between cases and predicted concentrations. Rouil et al.38 conducted a study to assess the source of a Legionella outbreak in Lens, France hypothesized to be linked to a cooling tower using ADMS. However, the authors concluded that the model only accounted for approximately 20% of the observed variance in infection rates. Nygård et al.36 modeled a similar Norwegian outbreak with 56 cases using the Gaussian integrated puff (INPUFF) model and identified a biological treatment plant for further study.
Volumetric estimation approaches
One approach for Legionella exposure modeling assumes that a given activity produces a volume or range of volumes for aerosols in the respirable range. This volume is typically not broken down by aerosol size category, but rather aggregated by calculating the total volume of water per exposure event. Bacteria are then transferred uniformly to these aerosols and are transmitted to a receptor via inhalation as in eqn (2).| D = Cwater × Laer × IR × ET | (2) |
An early but comprehensive Legionella QMRA for drinking water distribution systems was developed by Storey et al.40 The approach considered Legionella to be ubiquitously present and uniformly distributed between biofilms and bulk water, and proportionally distributed within aerosols. However, Legionella in the bulk water was not accounted for, and only Legionella introduction into water due to biofilm sloughing was considered. A triangular distribution was used for the concentration of Legionella in biofilms with minimum, mean, and maximum of 102, 103, and 106, respectively (microbiological units not specified). Biofilm detachment and disinfection were modelled using experimental trials from stainless steel and polyvinyl chloride coupons in annular reactors.41 A shower peak concentration of 0.1–10 μm size aerosols was used to compute an average volume inhaled over the course of a 10 minute exposure of 414 ± 258 μg m−3 or 57.5 ± 35.8 μL. All Legionella inhaled were assumed to be deposited, with 365 day per year exposure. A conservative “maximum risk” curve of r = 1 was used as a dose response model for L. pneumophila was not developed until 2007.42 The maximum risk curve concept signifies that each microbial exposure will result in an infection. The simulations indicated that if 100 Legionella per cm2 biofilm is present with no disinfection during a 10% sloughing event, the probability of infection per event is 0.18 and the annual risk is 1 for inhalation of 50 μL water. It was concluded that the maximum density of Legionella in biofilms during a 10% sloughing event and inhalation of 50 μL of water that met USEPA guidelines was 0.05 Legionella per cm2. Treatment of water to 80 °C for 10 min reduced risks to below a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10
10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 benchmark.43
000 benchmark.43
Ahmed et al.44 assessed Legionella risk from inhalation of aerosols due to daily showering or twice weekly hosing with domestic roof-harvested rainwater in Southeast Queensland, Australia. The concentration of L. pneumophila was measured in 214 roof-harvested rainwater samples collected from 82 tanks using quantitative polymerase chain reaction (qPCR), assuming that one gene copy was equivalent to 1 viable, infective L. pneumophila cell as there is a single copy of the L. pneumophila mip gene per genome. The concentrations ranged from 60–170 gene copies (gc) per L (5.6% rainwater tanks positive). A survey conducted determined that 4.06% and 1.01% of households used rainwater for hosing and showering, respectively. It was assumed that all households with rainwater tanks used water for hosing, but only the percentage designated as potable would use the water for showering. To obtain the volume transmitted via aerosols for showering, the aerosol size distribution next to a shower and hose were identified45–47 and corrected for lung deposition efficiencies48 considering only aerosols in the 0.3–6.0 μm diameter range. Using an inhalation rate of 20 L min−1 for an adult undergoing “light activity” for a 7-minute hot shower, the volume inhaled was calculated to range from 0.02 μL to 0.84 μL during showering (0.84 μL worst case used), 0.008–0.04 μL during high-pressure hosing, and 0.09–0.5 μL during hosing with trigger nozzle settings (a worst case of 0.5 μL was used). Using the infection dose response model for L. pneumophila (r = 0.06),42 the number of infections per 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 exposed people per event ranged from 3.0 × 10−2–8.6 × 10−2 for showering and from 1.8 × 10−2–5.1 × 10−2 for hosing. The annual infection risk per 10
000 exposed people per event ranged from 3.0 × 10−2–8.6 × 10−2 for showering and from 1.8 × 10−2–5.1 × 10−2 for hosing. The annual infection risk per 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 Southeast Queensland residents ranged from 2.6 × 10−3–7.3 × 10−3 for showering and 2.1 × 10−3–5.8 × 10−3 for hosing.
000 Southeast Queensland residents ranged from 2.6 × 10−3–7.3 × 10−3 for showering and 2.1 × 10−3–5.8 × 10−3 for hosing.
Occupational & industrial hygiene approaches
Several concepts used in Legionella QMRA have been developed from the occupational and industrial hygiene literature for chemical exposure, including the use of near field-far field (NFFF) models and partitioning coefficients (PC).49,50 NFFF models assume well-mixed concentrations in a room, but address spatial variability in exposure by dividing the exposure zone into two areas, the near-field zone containing the source, and the far-field zone box model that exchanges air with the near-field zone. NFFF models account for ventilation (dilution), but not particle settling or viability decay.51 The partitioning coefficient (also known as an “emission factor” or “efficiency”) concept is similar to the volumetric approach, except that this is a direct measurement of the ratio between bacteria measured in water and air (eqn (3)).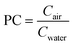 | (3) |
Partitioning coefficients are summarized in Hines et al.52 and range from 1.3 × 10−6 L m−3 (toilets) to 8.8 × 10−1 L m−3 (cool mist humidifiers) for various inhalation exposures. A general model using the partitioning coefficient or exposure factor is stated in eqn (4).52
| D = Cwater × PC × IR × ET | (4) |
Medema et al.53 conducted a Legionella risk assessment for sewage treatment workers exposed to aerosols using data gathered from five treatment plants. Seven wastewater samples were tested and although 7/7 were positive using PCR (up to 105 per mL), samples were negative using culture-based methods (detection limits <20–<200 per mL). Legionella spp. and L. pneumophila concentrations in air samples ranged from 0.56–56 gc m−3 in 3/5 treatment plants, but negative using culture-based methods. The value of the partitioning coefficient was not reported for Legionella, but was stated to be similar to the efficiency for heterotrophic plate counts of 10−10–10−4.5 presented at the same site. If computed from the PCR data, the partitioning coefficient would range from 5.6 × 10−6–5.6 × 10−4 L m−3. Using survey data on the activity patterns of sewage workers, exposure doses were estimated to be 23 Legionella per day, and 5% of the workers were exposed to 25 Legionella with a maximum exposure of 37 Legionella. The annual risk was not computed, however, the risk potential was considered low when compared to concentrations observed in the literature at other outbreak-associated sites.
Schoen and Ashbolt54 used a reverse QMRA model to identify the target concentration of Legionella in premise plumbing biofilms necessary to deliver a target dose of 1–100 CFU associated with infection in the lower respiratory tract. Exposure was considered during a 15 minute shower operating at a flow rate of 6 L min−1 and inhalation rate of 0.72–1.5 m3 h−1 using the exposure model in eqn (5). A partitioning coefficient of 1 × 10−6–1 × 10−5 CFU m−3/CFU L−1 was applied. In addition, a fraction of bacteria that partitioned proportionally into aerosols of size 1–5 μm (0.75–1), 5–6 μm (0.09–0) and 6–10 μm (0.14) diameter was considered and corrected for the proportion of aerosols in each of these ranges that deposited at the alveoli (0.2–0.54, 0.1–0.65, and 0.01–0.1, respectively).
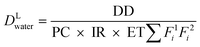 | (5) |
This approach assumed that the biofilm was the sole source of Legionella in the bulk liquid, and that exposure would occur as biofilm material was detached, released through the trophozite or cyst form of protozoa located in the biofilm, or released within vacuoles or vesicles derived from those protozoan hosts. The behavior of Legionella under these conditions was modeled in biofilms prior to a detachment event by considering the fraction and intensity at which protozoan trophozoites become infected with Legionella (0.01–1 and 10–1000 CFU per host, respectively), the total biofilm surface area (40–4000 cm2), the fraction of area sloughed off from the biofilm during a detachment event (100% and all of respirable size), and the sloughing rate (520–1560 g cm−2) (eqn (6)–(9))
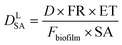 | (6) |
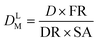 | (7) |
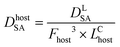 | (8) |
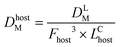 | (9) |
Predicted critical densities of Legionella ranged from 3.5 × 101–3.5 × 103 CFU m−3 in air, 3.5 × 106–3.5 × 108 in water, 7.8 × 105–7.8 × 108 CFU cm−2 (by surface area) or 5 × 102–5 × 105 CFU g−1 (by mass) in the biofilm. Within the biofilm, predicted protozoan host densities ranged from 3.1 × 104–7.8 × 107 hosts per cm2 and 2.0 × 101–5.0 × 104 hosts per g. The median target deposited dose of 10 CFU was based on the median infectious dose (ID50) of 12 CFU from the exponential dose response model for guinea pig infection with r = 0.06, but did not make use of the model function expressly.55 A sensitivity analysis demonstrated that the changes in the partitioning coefficient and target deposited dose contributed most to uncertainty in the critical density of Legionella in water.
In a risk assessment for Legionella-containing rainwater used at recreational splash parks, de Man et al.56 extracted values from the literature for the concentration of L. pneumophila with an average concentration of 1200 CFU L−1 (Gamma distribution (r = 0.045, λ = 26![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000), where CFU = colony forming units. An exposure volume of 0.394 μL min−1 (95% confidence interval 0.0446–1.27 μL min−1) for children and 0.489 μL min−1 (95% confidence interval 0.0494–1.55 μL min−1) for adults was used with a mean duration of 3.5 minutes at an interactive water fountain. The exposure volume was derived by multiplying the inhalation rate and a partitioning coefficient. Although the study specifies a “volume of inhalable water spray (VIWS)”, this is distinct from the volumetric method described previously. The VIWS (average 10.8, 95% confidence interval 1.76–36.3 μL m−3) was estimated using maximum likelihood and beta regression to ratios of measured concentrations of inhalable endotoxin in air and water near splash parks, which varied from 7.2 to 19 endotoxin units per m3 air and 9 to 2799 endotoxin units per mL water. Note that the endotoxin units cancel and partitioning coefficient units are frequently reported in both formats, for example CFU m−3/CFU L−1 or L m−3. The correlation between endotoxin units in water and air was significant (R2 = 0.645). Inhalation rates of 1.01 × 10−2–4.36 × 10−2 m3 min−1 for children and 1.03 × 10−2–7.77 × 10−2 m3 min−1 for adults were used to obtain the exposure volume [μL min−1]. The exposure duration was based on an observational study at two splash parks in urban centers, which observed 257 children and 347 adults within 2 m of a water spray. An exponential dose response model with an infection endpoint was used with r = 0.06.42 The mean risk per 3.5 min exposure duration was 9.3 × 10−5 (95% confidence interval 0–2.4 × 10−4) for children and 1.1 × 10−4 (0–82.8 × 10−4) for adults. The authors note that the duration could be much longer in a recreational water park environment, up to 0.5 h or possibly up to 2 h. Therefore, for a 2 h exposure, the risk would be 2.8 × 10−3. The results of the scenario analysis indicated that the volume of inhalable water spray was the most important input parameter for determining L. pneumophila risk.
000), where CFU = colony forming units. An exposure volume of 0.394 μL min−1 (95% confidence interval 0.0446–1.27 μL min−1) for children and 0.489 μL min−1 (95% confidence interval 0.0494–1.55 μL min−1) for adults was used with a mean duration of 3.5 minutes at an interactive water fountain. The exposure volume was derived by multiplying the inhalation rate and a partitioning coefficient. Although the study specifies a “volume of inhalable water spray (VIWS)”, this is distinct from the volumetric method described previously. The VIWS (average 10.8, 95% confidence interval 1.76–36.3 μL m−3) was estimated using maximum likelihood and beta regression to ratios of measured concentrations of inhalable endotoxin in air and water near splash parks, which varied from 7.2 to 19 endotoxin units per m3 air and 9 to 2799 endotoxin units per mL water. Note that the endotoxin units cancel and partitioning coefficient units are frequently reported in both formats, for example CFU m−3/CFU L−1 or L m−3. The correlation between endotoxin units in water and air was significant (R2 = 0.645). Inhalation rates of 1.01 × 10−2–4.36 × 10−2 m3 min−1 for children and 1.03 × 10−2–7.77 × 10−2 m3 min−1 for adults were used to obtain the exposure volume [μL min−1]. The exposure duration was based on an observational study at two splash parks in urban centers, which observed 257 children and 347 adults within 2 m of a water spray. An exponential dose response model with an infection endpoint was used with r = 0.06.42 The mean risk per 3.5 min exposure duration was 9.3 × 10−5 (95% confidence interval 0–2.4 × 10−4) for children and 1.1 × 10−4 (0–82.8 × 10−4) for adults. The authors note that the duration could be much longer in a recreational water park environment, up to 0.5 h or possibly up to 2 h. Therefore, for a 2 h exposure, the risk would be 2.8 × 10−3. The results of the scenario analysis indicated that the volume of inhalable water spray was the most important input parameter for determining L. pneumophila risk.
Sales-Ortells and Medema (2014)57 performed a screening-level microbial risk assessment of urban water locations including a river, canals, a lake, and a water playground located in the Netherlands. Twenty water bodies or features were identified by the Amsterdam water utility. Study sites were identified based on human exposure potential to contaminated waters, obtained using expert judgement. These sites were ranked, and the top 13 chosen for further study. The selected features were of categories of: 1) local storage of stormwater runoff in wide infiltration trenches (“wadi's”); 2) urban green/blue areas with temporary storage of stormwater from separated sewers in ponds and ditches; 3) urban water recreation areas such as water playgrounds, water fountains, and local surface water used for recreation; and 4) water on the street during rain events. Scenarios for which Legionella risks were calculated were aerosol exposures due to: 1) rowing on a river; 2) rowing on a river influenced by combined sewer overflow (CSO) contamination; 3) rowing on a lake; 4) rowing on a lake influenced by separate sewer overflow (SSO) contamination; 5) public water taps; 6) ornamental fountains; 7) drinking water playgrounds; and 8) fresh water playgrounds influenced by runoff from traffic roads.
The aerosolization ratio (partitioning coefficient) reported by de Man et al.58 (log transformed parameters mean ± standard deviation −8.07, 0.3) was used to estimate the concentration of L. pneumophila in air for each scenario, derived from decorative fountains. Note that these values are slightly different from those reported in de Man et al.,56 due to a different statistical fitting procedure to the original data. Due to the sparse nature of Legionella concentrations for the types of water systems identified, concentrations of L. pneumophila from the literature were pooled and fit with gamma distributions for a lake that was impacted by a wastewater discharge rich in L. pneumophila, and one scenario excluding those data.
A 1-log reduction in bacteria based on E. coli data was used to describe removal in a sedimentation pond, and a triangular distribution (0.1, 1, 2) was used to describe pathogen log reductions due to dilution and natural processes for canals in a green area and park. A 10-fold dilution for wastewater was considered for CSO-impacted waterways.
Inhalation rates were calculated for each exposure activity and age group from the USEPA 2011 Exposure Factors Handbook, but specific values were not stated.59 Inhalation rates were corrected using a lung deposition efficiency in the lower respiratory tract of 12.7%. Exposure durations and frequencies were activity specific, where rowing had the longest duration (1–4 hours per event and up to 108 events per year for river rowing). Infection (r = 0.06) and illness (r = 1.7 × 10−4) dose response models were used. The highest legionellosis risks per event were calculated from playing in pluvial floodwater impacted by a CSO (1 × 10−2), rowing on the river (1.4 × 10−5) or lake (1.4 × 10−5), and playing at a surface water playground (3.4 × 10−6). All median annual risks for L. pneumophila were below the national annual incidence of legionellosis (0.002% average 2009–2010). These risks were higher than those observed for roof-harvested rainwater systems in Australia, and the concentrations used were higher; however the authors point out variations in aerosol estimation and exposure methods that would limit direct comparisons between the two studies. According to the sensitivity analysis, the variability in legionellosis risk was higher than that for gastrointestinal pathogens; this was driven nearly entirely by the variability in L. pneumophila concentrations. The studies used to fit L. pneumophila concentration distributions were derived from culture-based,60 qPCR,61 culture and qPCR56 or unspecified methods62 from various water systems. Lesser but moderate spearman rank correlations were shown for the impact of exposure frequencies on legionellosis risk. The other inputs showed weak correlations with legionellosis risk.
Sales-Ortells and Medema (2015)63 similarly modeled microbial risks from L. pneumophila due to inhalation of stormwater aerosols in a stormwater plaza in Bellamyplein, The Netherlands. The plaza collects street runoff and diverts the first flush into a sewer system before storing the remainder in an open area. L. pneumophila was measured in the stormwater plaza using qPCR and was quantified in 2 of 10 pond samples with concentrations ranging from 1.5 × 102 to 1.1 × 103 gc L−1. A gamma distribution was fit to the concentration data, and a beta distribution to recovery efficiency measurements (average 13.2–25.8%). The recovery distribution was then used to correct the concentration data. The same aerosolization ratio approach derived from de Man et al.58 (log transformed parameters mean ± standard deviation −8.07, 0.3) was used to estimate the concentration of L. pneumophila in air. An inhalation rate for children was used (1.36 L min−1) for an exposure time of 21 ± 5 minutes and a lung deposition efficiency of 12.7%. Infection (r = 0.06) and illness (r = 1.7 × 10−4) dose response models were used. As the stormwater plaza will only fill when there is sufficient rainfall, a 10-year rainfall record was used to describe a negative binomial distribution for the frequency of exposure events. From 2004–2013, 14.6 rainfall events were equal to the fill volume and 38.3 were higher than this volume. The calculated dose was 1.1 × 10−5 gc (95% 5.21 × 10−5 gc) and the risk per person per event was 1.2 × 10−9 (95% 5.2 × 10−9). The measured pathogen concentration and aerosolization ratio had the highest impact on the risk estimates.
Schoen et al. (2014)64 modeled the annual probability of illness from inhalation of treated rainwater while showering for L. pneumophila in order to compare decentralized community water services to conventional centralized services. qPCR concentration data for rainwater was obtained from published studies.44,65 The exposure model was not specified, although based on previous work.66 An exponential dose response model for illness was used (r = 1.07 × 10−4),67 resulting in annual probabilities of illness that were generally between 10−6 to 10−9. Similarly, Schoen et al. (2015)68 conducted a review to identify treatment reduction targets for onsite water reuse. L. pneumophila was used as a reference hazard for showering in untreated rainwater, however the predicted annual probability of infection was less than 10−3 per person-year.
Armstrong and Haas (2007)51 and Armstrong and Haas (2008)67 address aspects of the same two exposure models, for a whirlpool spa and a natural hot spring thermal spa. The natural hot spring thermal spa analysis is based on data gathered from two hot spring outbreaks in the Miyazaki and Shizuoka Prefectures in Japan. A mean partitioning coefficient derived from endotoxin data from swimming pools without water features of 2.3 × 10−5 (90% range 1.6 × 10−5–3.1 × 10−5) was used to estimate occupational exposure to Legionella-containing mists. Reported concentrations from Miyazaki and Shizuoka sampling campaigns were 1.5 × 107 CFU L−1 and 7 × 105 CFU L−1, respectively, and air sampling was not conducted. Therefore, the mean estimated air concentrations using the partitioning coefficient were 360 CFU m−3 (95% CI 240–470) for Miyazaki and 17 CFU m−3 (95% CI 12–23) for Shizuoka. No decay or loss of viability for Legionella was considered in the short time between emission and inhalation for a 15 minutes exposure duration. A uniform distribution of inhalation rates ranging from 0.6–1.5 m3 h−1 was used, consistent with a light to moderate activity level. An estimated 50% of aerosols were considered to be in the respirable range and deposited at the alveoli, resulting in a calculated mean deposited dose of 47 CFU (95% confidence interval 23–78 CFU) for Miyazaki and 2.3 CFU (95% confidence interval 1.1–3.7 CFU) for Shizuoka. Using the exponential dose response model for infection (r = 0.06), the worker subclinical infection risks for Miyazaki and Shizuoka were 7.5 × 10−1–9.9 × 10−1 and 6.5 × 10−2–2.2 × 10−1, respectively. Using an exponential model (r = 8.7 × 10−5) with an animal death endpoint, the clinical severity Legionnaires' disease risk was 2.0 × 10−3–7.3 × 10−3 and 9.8 × 10−5–3.5 × 10−4 for Miyazaki and Shizuoka, respectively. The sensitivity analysis indicated that the partitioning coefficient and breathing rate contributed most to dose estimate variability.
The whirlpool spa exposure model is based on data gathered at a large outbreak that occurred at the 1999 Netherlands West Frisian Floral Show, with 133 confirmed and 55 probable cases of LD.69 A whirlpool spa injects air into spa water, forming an emission plume. A near-field far-field steady state model with estimates for aerosol generation, water composition, and building ventilation parameters was used to calculate estimates for near field (2–15 m) and far field (>15 m) occupational exposures to this plume. The equations for near field concentration, far field concentration, and air exchange rate between both zones are shown in eqn (10)–(12).
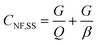 | (10) |
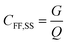 | (11) |
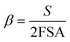 | (12) |
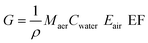 | (13) |
Enrichment, or increased concentration of an aqueous aerosol relative to the bulk water concentration of gram negative bacteria, has been reported.71,72 Therefore, two scenarios of zero enrichment and a 10-fold enrichment were derived from an estimate for surface foam in a cooling tower basin of 1000-fold enrichment.73 A value of 10 or 1% of this value was used because the mixing in a whirlpool is more likely to create a homogeneous distribution than for cooling towers. It was assumed that the Legionella in water aerosol equals the concentration in the spa's bulk water, no decay or settling of Legionella occurred within the plume, and the whirlpool bulk water would not be significantly depleted of Legionella by aerosol emissions. With no enrichment, the aerosol generation rate was 2–7 CFU min−1, and for 10-fold it was 20–70 CFU min−1.
Exposures of 30 h ± 21.8 h were used, considering the total number of hours for workers during the outbreak period at the flower show. The inhalation rate was 0.6–1.5 m3 h−1. Fifty-percent aerosol retention was assumed based on a guinea pig model,42 resulting in a deposited dose of 0.25–34.4 CFU for workers within 15 m, and 0.24–18.5 for workers greater than 15 m away from the source. Subclinical and clinical severity dose response models were with r = 0.06 and r = 1.07 × 10−4, respectively. Mean subclinical infection risks ranged from 5.8 × 10−2 (no enrichment) to 3.9 × 10−1 (enrichment) for distances less than 15 m and 4.0 × 10−2 (no enrichment) –3.2 × 10−1 (enrichment) for distances greater than 15 m. Mean clinical severity risks ranged from 8.9 × 10−5 (no enrichment) –8.9 × 10−4 (enrichment) and 6.0 × 10−5 (no enrichment) –6 × 10−4 (enrichment) for distances below and above 15 m, respectively. The results of a sensitivity analysis with rank order correlation coefficients indicated that inhalation rate, exposure time, and the microbial aerosol generation rate were the most important for determining the infection risk.
Azuma et al.74 used information from a 2007 outbreak in Adachi, Japan to determine the appropriateness of the Japanese water quality guideline for Legionella of 100 CFU L−1. Using the same approach as Armstrong and Haas51 for hot springs, a partitioning coefficient was used for assessing the risk of Legionella from bathing in residential bathrooms (Uniform distribution 2700–13![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 CFU L−1). However, a Poisson distributed exposure duration (λ = 21 min) was used. A mean of 7850 CFU L−1Legionella was measured in a hot spring water circulation system in a condo building in Adachi, Tokyo. The mean calculated concentration in air was 0.18 CFU L−1 (95% confidence interval 0.07–0.32), resulting in a mean deposited dose of 0.033 (95% confidence interval 0.010–0.069). The mean risk of infection per bath was 2.0 × 10−3 (95% confidence interval 0.6–4.1 × 10−3) while the mortality risk was 2.8 × 10−6 (95% confidence interval 0.9 × 10−6–6 × 10−6). Mean annual risks were 5.1 × 10−1 (95% confidence interval 2.0 × 10−1–7.8 × 10−1) and 1 × 10−3 (95% confidence interval 0.3 × 10−3–2.2 × 10−3) for infection and mortality dose response endpoints, respectively. The infection and mortality risks of the water quality guideline value 100 CFU L−1 were approximately 1 × 10−2 and 1 × 10−5. These findings supported a water quality guideline of 1 CFU L−1.
000 CFU L−1). However, a Poisson distributed exposure duration (λ = 21 min) was used. A mean of 7850 CFU L−1Legionella was measured in a hot spring water circulation system in a condo building in Adachi, Tokyo. The mean calculated concentration in air was 0.18 CFU L−1 (95% confidence interval 0.07–0.32), resulting in a mean deposited dose of 0.033 (95% confidence interval 0.010–0.069). The mean risk of infection per bath was 2.0 × 10−3 (95% confidence interval 0.6–4.1 × 10−3) while the mortality risk was 2.8 × 10−6 (95% confidence interval 0.9 × 10−6–6 × 10−6). Mean annual risks were 5.1 × 10−1 (95% confidence interval 2.0 × 10−1–7.8 × 10−1) and 1 × 10−3 (95% confidence interval 0.3 × 10−3–2.2 × 10−3) for infection and mortality dose response endpoints, respectively. The infection and mortality risks of the water quality guideline value 100 CFU L−1 were approximately 1 × 10−2 and 1 × 10−5. These findings supported a water quality guideline of 1 CFU L−1.
Aerosol science approaches
A more detailed treatment of processes occurring during Legionella transport are possible using aerosol science approaches that consider the physical forces acting on individual water droplets. This is useful for situations such as whirlpools and cooling towers, where dynamic aerosol behavior occurs through mechanisms of settling, evaporation, condensation, coagulation, interaction among different components of particles, and formation of secondary aerosols.36 Few studies have considered this approach, as it typically requires more data inputs and is more computationally intensive than the other approaches discussed.Risks from L. pneumophila from whirlpool use were quantified by Bouwknegt et al.75 An injected air stream produces jet bubbles that ascend rectilinearly to the water surface and intercept L. pneumophila in the bulk water at certain efficiencies. As the jet bubbles meet the water surface, they produce larger jet drops as well as small, inhalable film drops. The rise of air bubbles through a water column spanning the depth of the whirlpool was modeled. During bubble rise, the number of L. pneumophila scavenged from the bulk water was estimated using interception efficiency rates. Assuming that equal portions of jet drops and film drops are produced, half of the L. pneumophila were estimated to become entrained in film droplets and the concentration of L. pneumophila in both the whirlpool water and air above the whirlpool were assumed to be homogenous. 1 × 106 identical droplets of 0.71 cm diameter were simulated using a previously published aerosol size distribution,70 and an air concentration was computed in a cylindrical air column above the whirlpool defined by the dimensions of the pool and height of the ceiling. These factors were combined with breathing rates to achieve an inhaled dose. A combined form of the multiple exposure model equations presented in the paper is provided in eqn (14).
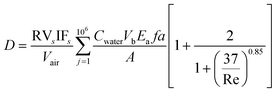 | (14) |
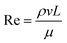 where ρ = the density of water, ν = the mean velocity of rising bubbles, L = the bubble diameter, and μ = the dynamic viscosity of water.
where ρ = the density of water, ν = the mean velocity of rising bubbles, L = the bubble diameter, and μ = the dynamic viscosity of water.
Film drops from a circular whirlpool of 3 m diameter, 70 cm depth, and water level 1 m from the ground were simulated using the air injection volume and 50% air-water mixture previously reported by Armstrong and Haas51 with airflow of 360–780 L min−1. The slowest velocity in the path of a bubble noted by Aybers and Tapucu76 of 23.7 cm s−1 was used, and assumed to be independent of water temperature. The calculated efficiency of bubbles encountering L. pneumophila in the water column was 8.4 × 10−4. The calculated generation rate was 1–2 × 106 air bubbles per min and aerosol depletion was assumed to be equivalent to L. pneumophila growth, so that the L. pneumophila in the whirlpool would not be depleted.
Various conditions for concentration (1–1 × 106 CFU L−1), inhalation rate (9 L min−1 for males and 6.7 L min−1 for females), and exposure duration (1 min, 15 min, or 2 h) were investigated. Eqn (14) resulted in approximately 0.01% of the total L. pneumophila in the whirlpool inhaled by a receptor, however this fraction was concentration-dependent. For starting water concentrations of 1000 CFU L−1, the bacterial generation rate was 4.5 × 104 CFU min−1 (95% confidence interval 4.4 × 104–4.7 × 104) and the average inhaled dose ranged from 58 CFU (males) to 43 CFU (females). Using the exponential model for infection (r = 0.06), infection risks for a 10 CFU L−1 starting water concentration ranged from 0.002 (males, 1 min exposure) to 0.24 (males, 2 h exposure). Exposure to water containing ≥1000 CFU L−1 nearly always caused infection in both males and females. A scenario analysis assessed the impacts of turbulence (changing the Reynolds number and modifying the type of motion from rectilinear to helical), the fraction of intercepted L. pneumophila that becomes airborne, and a ventilation scenario (homogeneous versus nonhomogeneous mixing in the air column). Results indicated that the fraction of intercepted L. pneumophila on film drops and turbulence of water in the whirlpool affecting the bubble path have the most influence on infection risks. The authors indicated support for a limit of 100 L. pneumophila CFU L−1 for bathing water.
With regard to other aerosol science approaches, CFD models have been applied to calculating L. pneumophila exposures but did not calculate infection risks and are summarized elsewhere.17 Three studies31–33 investigated an air scrubber at a biological treatment plant in Norway identified as a probable source of airborne Legionella in an outbreak by Gaussian modeling efforts.36 Blatny et al. (2008)32 and Fossum et al.33 used a steady state Reynolds Averaged Navier–Stokes (RANS) approach and noted that the mean plume concentration of L. pneumophila 200 m downwind was approximately 2% of the source strength. It was also observed in a related study that bacteria were principally contained by small (<4 μm) or large (>16 μm) aerosol size fractions.31
3. Limitations of current models and research needs for QMRA development
Eighteen studies are presented here that provide exposure models for Legionella in engineered water systems using Gaussian dispersion, volumetric estimation, occupational hygiene, and aerosol science approaches. Ten of these models conducted a full QMRA, and provided a full exposure model description and human infection estimates. A comparison of risk characterization parameters for studies that conducted full QMRAs is shown in Table 2. This comparison demonstrates that ranges of inhalation rates reported across studies are typically narrow (0.081–4.662 m3 h−1), and two principal dose response model functions have been used for infection and clinical severity infection or death. Beyond variability accounted for in the dose response function, variation in host susceptibility has not been considered within the risk characterization of these studies. However, differences in risk characterization parameters are small compared to the differences in parameterization across exposure models for similar exposure scenarios. Among studies that conducted sensitivity analyses, the primary factors identified as contributors to infection risk estimates are parameters from the exposure model, particularly with regards to the volume of water that becomes inhaled and/or number of bacteria that are transferred to air from the source (microbial generation rates, water volumes inhaled, and partitioning coefficient).51,54,77 However, inhalation rate and concentrations of Legionella in water sources were also identified as important factors. Note that the factors that appear in a sensitivity analysis are a function of the type of assessment; for example for the reverse QMRA conducted by Schoen and Ashbolt, the concentration of Legionella would not appear in the sensitivity analysis as this was the outcome variable, however Legionella concentration was deemed an important variable by Sales-Ortells (2015). Limitations specific to each type of exposure model are discussed in the following sections.| Reference | Exposed populationa | Inhalation rate (m3 h−1) | Exposure duration (min) | No. exposure eventsb | Dose response parameters | Parameters of importance identified by sensitivity analysis |
|---|---|---|---|---|---|---|
| a Occ = occupational; Gen = general population. b For exposure events where 1 event was indicated, risk estimates were provided on a “per event” basis; ND = not done. c Poisson parameters shown are mean, standard deviation. d Inhalation rate ranges for light activity (low end of range) to high intensity activity (high end of range). e Parameters of the normal or lognormal distribution are (μ, σ). f Not specified. g T = triangular distribution (min, mode, max); SU = step uniform, parameters (min, max); B = binomial, parameters (N, P); NB = negative binomial, parameters (μ, k). | ||||||
| Storey et al. (40) | Gen | 0.83 | 10 | 365 | Maximum risk curve r = 1 | ND |
| Ahmed et al. (44) | Gen | 1.2 | 7 | 1; annual risk with daily showering and twice weekly hosing | Infection r = 0.06 | ND |
| Armstrong and Haas (51, 67) | Occ | 0.6–1.5 | Whirlpool: 1800 ± 1260 | 1 | Subclinical infection r = 0.06; severity Legionnaires' disease or mortality r = 1.7 × 10−4 | Inhalation rate, work hours, microbial aerosol generation rate |
| Armstrong and Haas (51, 67) | Occ | 0.6–1.5 | Hot spring: 15 | 1 | Subclinical infection r = 0.06; severity Legionnaires' disease or mortality r = 1.7 × 10−4 | Breathing rate, PC |
| Schoen and Ashbolt (54) | Gen | 0.72 (best estimate) – 1.5 (high estimate) | 15 | 1 | Target deposited dose of 10 CFU based on ID50 of 12 CFU from infection dose response model (r = 0.06) | PC, target deposited dose |
| de Man et al. (56) | Gen | Children: 0.606–3.744d Adults: 0.618–4.662 | 3.5 | 1 | Infection r = 0.06 | Volume of inhalable water spray, inhalation rate |
| Sales-Ortells and Medema (57) | Gen | NSf | , Rowing: T (60, 120, 240); playing in rainwater reservoirs/street runoff: N (21, 5); playing in fresh water playground: LN (4.1, 0.80); playing in drinking water playground: LN (4.2, 0.55); walking on flooded street/car splashing: T (0.017, 0.083, 0.17); walking dog: T (15, 30, 60); public water taps: point estimate 1 | , Rowing in river: SU (1, 108); rowing in lake: NB (5.1, 12); swimming in fresh water: NB (8, 1.3); swimming in swimming pool water: NB (24, 1); wading/splashing in flooded streets: NB (8, 2); wading/splashing in water playgrounds/ornamental fountains: B (12, 0.2); walking the dog, walking close to public taps: B (12, 0.2) | Infection r = 0.06; severity Legionnaires' disease or mortality r = 1.7 × 10−4 | Concentration of L. pneumophila in water |
| Sales-Ortells and Medema (63) | Gen | Normal (0.081, 0.0036)e | 21 ± 5 | 1 | Subclinical infection r = 0.06; severity Legionnaires' disease or mortality r = 1.7 × 10−4 | Concentration of L. pneumophila in water, aerosolization ratio |
| Azuma et al. (74) | Gen | 0.6–1.5 | Poisson (21, 4.55)c | 1 per day. Risks simulated per event, per 2 months, and per year | Subclinical infection r = 0.06; severity Legionnaires' disease or mortality r = 1.7 × 10−4 | ND |
| Bouwknegt et al. (75) | Gen | 0.54 (male), 0.402 (female) | Simulated for 1, 15, 120 | 1 | Infection r = 0.06 | Fraction of intercepted bacteria on film drops; turbulence of water |
Gaussian plume and puff models
The Gaussian plume model assumes that the mean concentration of airborne particles are normally distributed about the axis downwind from a contaminant point source, and the concentration gradient diminishes as downwind distance and distance away from the plume centerline increases.19 Although the Gaussian plume is one of the most straightforward models that can be used for long-range dispersion, it is applicable generally only for downwind distances from a point source 100–10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 m, and for conditions when meteorological and source conditions are stable for periods longer than the distance of the receptor from the source divided by the mean wind speed.19 The empirical constants σy and σz represent standard deviations of the plume concentration in the horizontal and vertical directions, respectively. These constants are based on averages during experiments performed under various atmospheric stability and relatively short time duration conditions (many authors have derived methods for determining these constants, but the most widely used are those by Turner,78 based on experimental data from Pasquill79), and are therefore not universally applicable to all contaminants and environmental conditions despite their widespread use for highly varied scenarios. The impact of ground-level topography is generally not addressed by the Gaussian plume model, and more computationally intensive approaches (such as CFD) are required for these types of applications.
000 m, and for conditions when meteorological and source conditions are stable for periods longer than the distance of the receptor from the source divided by the mean wind speed.19 The empirical constants σy and σz represent standard deviations of the plume concentration in the horizontal and vertical directions, respectively. These constants are based on averages during experiments performed under various atmospheric stability and relatively short time duration conditions (many authors have derived methods for determining these constants, but the most widely used are those by Turner,78 based on experimental data from Pasquill79), and are therefore not universally applicable to all contaminants and environmental conditions despite their widespread use for highly varied scenarios. The impact of ground-level topography is generally not addressed by the Gaussian plume model, and more computationally intensive approaches (such as CFD) are required for these types of applications.
In addition to the effect of dispersion coefficients, estimates are highly sensitive to the effective stack height (H). For point sources (most Legionella sources are likely to be point sources) such as cooling towers, stack height would be higher than the actual physical stack height used for simulation in most models due to the effects of plume rise. Plume rise occurs because the plume is hotter than the surrounding air, and rises buoyantly as it exits the stack with a vertical velocity.80 In order to calculate plume rise, it is necessary to obtain specific information regarding the stack height exit velocity, stack diameter, and temperature of exiting water vapor; therefore this has not typically been included in previous generalized models of bioaerosol dispersion. However, increasing the value used for stack height will increase the downwind dispersion of a contaminant, and should be included for site-specific calculations where feasible.
Finally, the decay rates for Legionella and other microorganism transport for use in combination with the Gaussian plume model have been derived by numerous authors, typically under controlled laboratory conditions and as functions of temperature and relative humidity, but rarely taking into account the effects of light (UV) inactivation, limiting their application for realistic transport simulations.19,81–88 These factors become more important as travel time from the source to a receptor increases.19 Together, these limitations provide many challenges for comparing modeled microorganism dispersion estimates with epidemiological information on the spatial location of Legionnaires' disease cases in relation to a point source. Van Leuken et al.17 re-analyzed predicted concentrations and attack rates for qualitative data reported by Nguyen et al.37 with a linear regression function, and noted that although a correlation between Legionella dispersion during an outbreak was positive it was not significant (p ≈ 0.12).
Volumetric estimation approaches
The volumetric estimation approach assumes that systems or activities produce a given volume of water spray that can be inhaled by a human receptor. Volumetric approaches are useful, especially for screening level assessments, as they are straightforward to apply and can be performed with a low burden of data inputs. The approach is versatile in that it does not need to make assumptions about the behavior of microorganisms during transport, but can easily incorporate such data, such as the differential partitioning of bacteria into the liquid water, or into aqueous aerosols of various sizes. This can be considered a strength of the approach, especially in establishing QMRA frameworks for easy incorporation of additional data once it becomes available. However, both studies that used the volumetric approach considered a homogeneous distribution of Legionella in aerosols initially as well as during transport between the water fixture/system and receptor.Occupational & industrial hygiene approaches
Most exposure studies reviewed modeled either the transport of water droplets or of bacteria, but did not combine these approaches. The partitioning coefficient was the most common approach reported for use in QMRA (8/10 of the reviewed studies that conducted a full QMRA). The partitioning coefficient is a ratio of bacterial concentrations in air and water, and similarly to volumetric approaches, is a straightforward and relatively versatile approach for considering the airborne fraction of Legionella bacteria, especially for screening-level assessments. However, the ratio of microorganisms in water and air has been shown to change with bubble rise distance and bulk water concentration.89–91 The partitioning coefficient also does not consider the behavior of aerosol droplets. A large range of generally low partitioning coefficient values were reported across studies (ranging from 10−10–10−4.5 CFU m−3/CFU L−1). However, the partitioning coefficient typically does not specify the distance at which the ratio of bacteria in air and water were measured, making it difficult to interpret what fraction of airborne bacteria are within the respirable range at varying distances from a bacterial emission source. This makes it more difficult to combine the partitioning coefficient approach with other methods compared to the volumetric approach, where a volume associated with an initial aerosol size distribution can be used and applied in conjunction with other assumptions to develop a reasonable estimate of Legionella doses. Schoen and Ashbolt54 assumed a fractional partitioning of Legionella into aerosols of various sizes which could be used in combination with multiple exposure model approaches, however, the original submitted manuscript that was cited has not been published.The partitioning coefficient approach implicitly assumes that the ratio of bacteria in the respirable range remains constant over space and time. The use of partitioning coefficients or volumetric calculations alone does not account for aerosol size considerations in most cases. The enrichment of individual aerosol droplets is also not considered. Although partitioning coefficient values are low, indicating that only a fraction of bacteria in the bulk water become aerosolized, the increased concentration due to enrichment that occurs in small and large aerosol droplets in the initial aerosol size distribution is likely to play an important role in disease transmission, especially as smaller particles are less likely to settle during plume transport and could deliver higher doses to receptors than predicted. Blatny et al.31 emphasized the importance of considering the size distribution as Legionella were likely to be found in mostly small (<4 μm) or large (>16 μm) droplets.17
Aerosol science approaches
Determining the aerosol size distribution and downwind proportion of Legionella-containing aerosols in the respirable range remains a substantial challenge for QMRA models. Aerosol science methodology provides the most detailed and mechanistic approach for modeling Legionella dispersion from engineered water systems. However, these approaches are likely to present challenges in the form of data needs and computational requirements. It is challenging to model the evolution of aerosol size distributions over time due to co-occurring and interrelated dynamic rate physical phenomena of settling, evaporation, condensation, coalescence, and secondary aerosol formation due to bubble burst and film collapse.92,93 The fraction of aerosols in the respirable range is therefore not likely to remain constant over time. Nygård et al.,36 Bouwknegt et al.,75 and Haas and Armstrong (2007)51 made simplifying assumptions by using a single size index aerosol within the respirable range. However, bacteria are likely to survive better in an aggregated form containing biofilms and/or protozoan hosts, which are more likely to persist in larger droplet nuclei over time.34,94 These larger droplets could potentially reach a respirable size by the time they arrive at a receptor distance due to evaporation. Additional robustness conferred to Legionella bacteria during transport by biofilm elements has not been studied, and the assumption of an index aerosol droplet of small size may not be sufficient.31 Furthermore, the impact of environmental conditions on these factors remains a significant research gap. Droplets containing Legionella bacteria should be constrained to a minimum size of the diameter of Legionella (1–2 μm).51Research gaps
Due to the ubiquitous nature of Legionella in engineered water systems, continual exposure is likely. Four studies40,44,57,74 considered infection risks over more than one exposure period, and reported risks using an exposure frequency by annualizing risk estimates. However, Armstrong and Haas (2008)51 considered total individual worker exposure time over the course of several days. The authors concluded that determining human time and activity patterns can reduce uncertainty in risk estimates, especially when combined with better ventilation information for indoor exposures.The nature of most Legionella QMRA and environmental investigations have been in conjunction with outbreaks, therefore the applicability of these risk estimates to normal operating conditions may be limited.75 In addition to variability in actual Legionella concentrations under various circumstances, variability in measured Legionella concentrations is likely to be impacted by the analytical detection method used. More than half (6 of 10) of the full QMRA studies reviewed based their assessments of Legionella concentrations on determinations using culture-based data. It has been shown that molecular assays (PCR or qPCR) are more sensitive than culture-based assays as they are capable of quantifying both live and dead cells, and are not limited by non-target microorganism overgrowth and viable but non-culturable (VBNC) issues that hinder culture-based methods.95 Furthermore, cell starvation, exposure to heat or disinfectants, and passage through amoebic cells can render Legionella cells in a VBNC state, but nevertheless alive and capable of resuscitation.96–100 Accordingly, a review of culture and qPCR approaches by Whiley and Taylor101 demonstrated that 26 of 28 reviewed studies detected Legionella at a higher rate using qPCR compared to culture, and on a sample per sample basis, samples analyzed concurrently by qPCR and culture were approximately 50% more likely to return a positive result by qPCR than by culture. These findings support that the use of qPCR data has the potential to yield higher calculated risks in a QMRA than if concentration data generated using culture-based methods are used.
It is common in QMRA studies to pool concentration estimates from the literature where microbiological measurements of pathogens such as Legionella in a specific type of water source are limited. Sales-Ortells et al. (2014) and de Man et al.56,57 calculated Legionella data from studies that reported using both culture- and qPCR- methods. Although it is not clear if culture and qPCR data were pooled within a single concentration distribution, Sales-Ortells et al. (2014) noted that the Legionella concentration was the dominant factor in determining legionnellosis risks during a sensitivity analysis. It is difficult to determine the extent to which pooling sources of Legionella data generated using different microbiological methods could have an impact on risk estimates, however, it appears that this practice could potentially introduce issues in interpretation of sensitivity analyses. Reporting detailed information regarding the derivation of concentration distributions used in a QMRA would therefore be useful for interpretation, especially as sensitivity analyses are used to prioritize the collection of further data. In the case of pathogen concentration datasets, this could imply significant additional costs for collection of such data.
A correction factor parameter could be applied within the context of a QMRA to estimate the viable and/or infectious fraction for quantification of health risks in the case of using a non-culture-based dataset. However, a singular factor is not likely to be universally applicable across all conditions and therefore warrants further development and review, especially during aerosol generation and transport.
Low or highly variable recovery rates are frequently reported, especially for culture-based methods.102 One reviewed study63 corrected measured concentrations with a beta distribution for recovery efficiency. The use of uncorrected concentrations in most of the reviewed studies may underestimate risks and correcting for recovery efficiency is an important practice. However, directly correcting for recovery efficiency can also overestimate concentrations and introduce bias.103 A Bayesian framework was recommended by Schmidt et al.104 to address these issues for protozoans, and similar approaches could be applied for Legionella.103Legionella viability, infectivity, virulence state, and survival in transport as a function of environmental conditions (relative humidity, ultraviolet light, temperature, and protection by organic debris or biofilms) are additional areas for further study to improve QMRA models.
In addition to limitations associated with concentration estimates, the dose response models used in all of the reported studies were derived from culture data. Therefore, there may be some limitations in applying these models in conjunction with a qPCR dataset. This discrepancy could lead to an overestimation of qPCR risks consistent with the limitations mentioned above; i.e. as a dose–response function for culture-based data is likely to have a lower median infectious dose (ID50) than a qPCR-based dataset for the same microorganism. Therefore, a dose response model using a culture- and qPCR-method comparison is recommended as a research gap that needs to be addressed. Some limitations could presumably be overcome by recreating the laboratory conditions under which the culture-based dose response models were generated and quantifying the inoculums using both culture and qPCR methods.
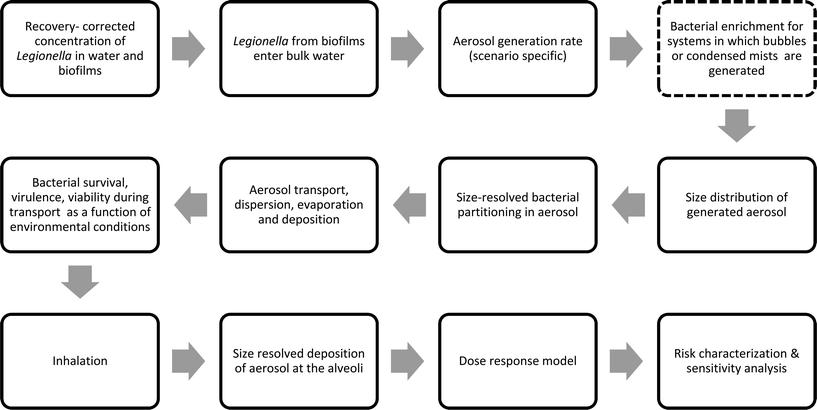
In the QMRAs reported here, the ability to directly compare risk estimates across studies is limited due to the variety of parameterizations across exposure models and varied starting concentrations of Legionella. However, the importance of the behavior of Legionella during the aerosolization process appears to be a recurrent theme across QMRAs. An ideal Legionella QMRA model would dynamically track the evolution in size distribution, and simultaneously address the fate of bacteria contained within aqueous droplets. The fate of bacteria would also be determined as a function of environmental conditions between a bacterial source and receptor. A framework for such a model that considers the limitations discussed in this review is proposed in Fig. 1. Many elements of the reviewed studies can be utilized and integrated to form the basis of this approach. Although more rigorous approaches are needed for treatment of aerosol size, these approaches are likely to require more data inputs and be more computationally intensive. However, a better integrative understanding of mathematical frameworks for Legionella modeling can lead to more rigorous risk prevention strategies and water management approaches. Furthermore, the QMRAs reviewed here highlight the importance of emerging sources of Legionella exposure that warrant further investigation, including alternative and/or decentralized water sources such as rainwater harvesting44 and stormwater management infrastructure systems.57,63,68
References
- S. P. Blatt, M. D. Parkinson, E. Pace, P. Hoffman, D. Dolan, P. Lauderdale, R. A. Zajac and G. P. Melcher, Am. J. Med., 1993, 95, 16–22 CrossRef CAS PubMed.
- B. Diederen, J. Infect., 2008, 56, 1–12 CrossRef CAS PubMed.
- F. Morio, S. Corvec, N. Caroff, F. Le Gallou, H. Drugeon and A. Reynaud, Int. J. Hyg. Environ. Health, 2008, 211, 403–411 CrossRef PubMed.
- B. J. Marston, H. B. Lipman and R. F. Breiman, Arch. Intern. Med., 1994, 154, 2417–2422 CrossRef CAS PubMed.
- A. L. Benin, R. F. Benson and R. E. Besser, Clin. Infect. Dis., 2002, 35, 1039–1046 CrossRef PubMed.
- K. D. Beer, J. W. Gargano, V. A. Roberts, V. R. Hill, L. E. Garrison, P. K. Kutty, E. D. Hilborn, T. J. Wade, K. E. Fullerton and J. S. Yoder, MMWR Morb. Mortal. Wkly. Rep., 2015, 64, 842–848 CrossRef PubMed.
- I. Cooper and G. Hanlon, J. Hosp. Infect., 2010, 74, 152–159 CrossRef CAS PubMed.
- F. Martinelli, A. Caruso, L. Moschini, A. Turano, C. Scarcella and F. Speziani, Curr. Microbiol., 2000, 41, 374–376 CrossRef CAS PubMed.
- V. Thomas, G. McDonnell, S. P. Denyer and J.-Y. Maillard, FEMS Microbiol. Rev., 2010, 34, 231–259 CrossRef CAS PubMed.
- L. Bonadonna, R. Briancesco, S. Della Libera, I. Lacchetti, R. Paradiso and M. Semproni, Cent. Eur. J. Public Health, 2009, 17, 99 Search PubMed.
- B. Flannery, L. B. Gelling, D. J. Vugia, J. M. Weintraub, J. J. Salerno, M. J. Conroy, V. A. Stevens, C. E. Rose, M. R. Moore and B. S. Fields, Emerging Infect. Dis., 2006, 12, 588–596 CrossRef CAS PubMed.
- M. R. Moore, M. Pryor, B. Fields, C. Lucas, M. Phelan and R. E. Besser, Appl. Environ. Microbiol., 2006, 72, 378–383 CrossRef CAS PubMed.
- M. Pryor, S. Springthorpe, S. Riffard, T. Brooks, Y. Huo, G. Davis and S. Sattar, Water Sci. Technol., 2004, 50, 83–90 CAS.
- C. N. Haas, J. B. Rose and C. P. Gerba, in Quantitative Microbial Risk Assessment, John Wiley & Sons, Inc, 2014, pp. i–xii, DOI:10.1002/9781118910030.fmatter.
- H. Whiley, et al., Uncertainties associated with assessing the public health risk from Legionella, Front. Microbiol., 2014, 5, 1–8 Search PubMed.
- N. S. Holmes and L. Morawska, Atmos. Environ., 2006, 40, 5902–5928 CrossRef CAS.
- J. P. G. Van Leuken, et al., Atmospheric dispersion modelling of bioaerosols that are pathogenic to humans and livestock – A review to inform risk assessment studies, Microbial Risk Analysis, 2016, 1, 19–39 CrossRef.
- R. Dungan, J. Anim. Sci., 2010, 88, 3693–3706 CrossRef CAS PubMed.
- B. Lighthart, in Atmospheric Microbial Aerosols, Springer, 1994, pp. 285–303 Search PubMed.
- J. P. Brooks, M. R. McLaughlin, C. P. Gerba and I. L. Pepper, J. Environ. Qual., 2012, 41, 2009–2023 CrossRef CAS PubMed.
- J. P. Brooks, B. D. Tanner, C. P. Gerba, C. N. Haas and I. L. Pepper, J. Appl. Microbiol., 2005, 98, 397–405 CrossRef CAS PubMed.
- M. A. Jahne, S. W. Rogers, T. M. Holsen and S. J. Grimberg, Aerobiologia, 2014, 31, 73–87 CrossRef.
- J. Teng, A. Kumar, P. L. Gurian and M. S. Olson, Open Environ. Eng. J., 2013, 6, 7–13 CrossRef CAS.
- A. Ssematimba, T. J. Hagenaars and M. C. De Jong, PLoS One, 2012, 7, e31114 CAS.
- E. Viau, K. Bibby, T. Paez-Rubio and J. Peccia, Environ. Sci. Technol., 2011, 45, 5459–5469 CrossRef CAS PubMed.
- S. E. Dowd, C. P. Gerba, I. L. Pepper and S. D. Pillai, J. Environ. Qual., 2000, 29, 343–348 CrossRef CAS.
- B. D. Tanner, J. P. Brooks, C. P. Gerba, C. N. Haas, K. L. Josephson and I. L. Pepper, J. Environ. Qual., 2008, 37, 2311–2321 CrossRef CAS PubMed.
- H. Galada, P. Gurian, A. Joe, A. Kumar, B. Olson, M. Olson, E. Richter, J. Teng, H. Zhang and I. Xagoraraki, Water Environment Research Foundation, Alexandria, VA, USA, 2012 Search PubMed.
- M. A. Jahne, et al., Emission and Dispersion of Bioaerosols from Dairy Manure Application Sites: Human Health Risk Assessment, Environ. Sci. Technol., 2015, 49(16), 9842–9849 CrossRef CAS PubMed.
- R. S. Dungan, Environ. Sci. Technol., 2014, 48, 5033–5042 CrossRef CAS PubMed.
- J. M. Blatny, J. Ho, G. Skogan, E. M. Fykse, T. Aarskaug and V. Waagen, Aerobiologia, 2011, 27, 147–162 CrossRef.
- J. M. Blatny, B. A. P. Reif, G. Skogan, O. Andreassen, E. A. Høiby, E. Ask, V. Waagen, D. Aanonsen, I. S. Aaberge and D. A. Caugant, Environ. Sci. Technol., 2008, 42, 7360–7367 CrossRef CAS PubMed.
- H. Fossum, B. P. Reif, M. Tutkun and T. Gjesdal, Boundary Layer Meteorol., 2012, 144, 21–40 CrossRef.
- B. Lighthart and J. Kim, Appl. Environ. Microbiol., 1989, 55, 2349–2355 CAS.
- B. Fattal, P. Yekutiel, Y. Wax and H. I. Shuval, Water Sci. Technol., 1986, 18, 199–209 CAS.
- K. Nygård, Ø. Werner-Johansen, S. Rønsen, D. A. Caugant, Ø. Simonsen, A. Kanestrøm, E. Ask, J. Ringstad, R. Ødegård and T. Jensen, Clin. Infect. Dis., 2008, 46, 61–69 CrossRef PubMed.
- T. M. N. Nguyen, D. Ilef, S. Jarraud, L. Rouil, C. Campese, D. Che, S. Haeghebaert, F. Ganiayre, F. Marcel and J. Etienne, J. Infect. Dis., 2006, 193, 102–111 CrossRef PubMed.
- L. Rouil, G. Gardenas and F. Marcel, Evaluation de la dispersion atmospherique d’aerosols potentiellement contamines lors de l’epidemie de legionellose de la region de Lens. Numero special consacre de la legionellose, Bull. Epidemiol. Hebd., 2004, 36–37, 182–184 Search PubMed.
- A. Bargellini, I. Marchesi, E. Righi, A. Ferrari, S. Cencetti, P. Borella and S. Rovesti, Water Res., 2011, 45, 2315–2321 CrossRef CAS PubMed.
- M. Storey, J. Ashbolt and T. Stenström, Water Sci. Technol., 2004, 50, 77 CAS.
- M. Storey and N. Ashbolt, Water Sci. Technol.: Water Supply, 2003, 3, 93–100 CAS.
- T. Armstrong and C. N. Haas, Risk Anal., 2007, 27, 1581–1596 CrossRef CAS PubMed.
- C. Clark, J. - Water Pollut. Control Fed., 1986, 58, 539–543 CAS.
- W. Ahmed, A. Vieritz, A. Goonetilleke and T. Gardner, Appl. Environ. Microbiol., 2010, 76, 7382–7391 CrossRef CAS PubMed.
- J. O'Toole, K. Leder and M. Sinclair, A series of exposure experiments–recycled water and alternative water sources. Part A. Aerosolsizing and endotoxin experiments, CRC for Water Quality and Treatment, Adelaide, Australia, 2008 Search PubMed.
- G. A. Keating and T. E. McKone, ASTM Spec. Tech. Publ., 1993, 1205, 14 Search PubMed.
- Y. Zhou, J. M. Benson, C. Irvin, H. Irshad and Y.-S. Cheng, Inhalation Toxicol., 2007, 19, 333–342 CrossRef CAS PubMed.
- R. B. Schlesinger, J. Toxicol. Environ. Health, Part A, 1985, 15, 197–214 CAS.
- O. M. Zacheus and P. J. Martikainen, Can. J. Microbiol., 1994, 40, 993–999 CrossRef CAS PubMed.
- S.-W. Huang, B.-M. Hsu, S.-F. Wu, C.-W. Fan, F.-C. Shih, Y.-C. Lin and D.-D. Ji, Water Res., 2010, 44, 4805–4811 CrossRef CAS PubMed.
- T. W. Armstrong and C. N. Haas, J. Occup. Environ. Hyg., 2007, 4, 634–646 CrossRef PubMed.
- S. A. Hines, et al., Assessment of relative potential for Legionella species or surrogates inhalation exposure from common water uses, Water Res., 2014, 56, 203–213 CrossRef CAS PubMed.
- G. Medema, B. Wullings, P. Roeleveld and D. Van Der Kooij, Water Sci. Technol.: Water Supply, 2004, 4, 125–132 Search PubMed.
- M. E. Schoen and N. J. Ashbolt, Water Res., 2011, 45, 5826–5836 CrossRef CAS PubMed.
- S. Ali, C. A. Phillips, P. S. Phillips and M. Bates, Int. J. Environ. Health Res., 2010, 20, 367–377 CrossRef CAS PubMed.
- H. de Man, M. Bouwknegt, E. van Heijnsbergen, E. J. Leenen, F. van Knapen and A. M. de Roda Husman, Water Res., 2014, 54, 254–261 CrossRef CAS PubMed.
- H. Sales-Ortells and G. Medema, Environ. Sci. Technol., 2014, 48, 9780–9789 CrossRef CAS PubMed.
- H. de Man, et al., Human exposure to endotoxins and fecal indicators originating from water features, Water Res., 2014, 51, 198–205 CrossRef CAS PubMed.
- USEPA, Exposure Factors Handbook, N. C. f. E. A. Office of Research and Development, Washington, DC, 2011 Search PubMed.
- J. S. Olsen, T. Aarskaug, I. Thrane, C. Pourcel, E. Ask, G. Johansen, V. Waagen and J. M. Blatny, Environ. Sci. Technol., 2010, 44, 8712–8717 CrossRef CAS PubMed.
- P. W. van der Wielen and D. van der Kooij, Appl. Environ. Microbiol., 2013, 79, 825–834 CrossRef CAS PubMed.
- H. Albrechtsen, Water Sci. Technol., 2002, 46, 311–316 CAS.
- H. Sales-Ortells and G. Medema, Microbial health risks associated with exposure to stormwater in a water plaza, Water Res., 2015, 74, 34–46 CrossRef CAS PubMed.
- M. E. Schoen, et. al., Comparative human health risk analysis of coastal community water and waste service options, Environ. Sci. Technol., 2014, 48(16), 9728–9736 CrossRef CAS PubMed.
- W. Ahmed, H. Brandes, P. Gyawali, J. P. S. Sidhu and S. Toze, Water Res., 2014, 53, 361–369 CrossRef CAS PubMed.
- M. E. Schoen, J. A. Soller and N. J. Ashbolt, Water Res., 2011, 45, 2670–2680 CrossRef CAS PubMed.
- T. W. Armstrong and C. N. Haas, J. Water Health, 2008, 6, 149–166 CrossRef PubMed.
- M. E. Schoen and J. Garland, Review of pathogen treatment reductions for onsite non-potable reuse of alternative source waters, Microbial Risk Analysis, 2015 DOI:10.1016/j.mran.2015.10.001.
- M. Alary and J. Joly, Appl. Environ. Microbiol., 1991, 57, 2360–2367 CAS.
- P. A. Baron and K. Willeke, Environ. Res., 1986, 39, 8–18 CrossRef CAS PubMed.
- D. C. Blanchard and L. D. Syzdek, Appl. Environ. Microbiol., 1982, 43, 1001–1005 CAS.
- M. Zhang, W. Liu, X. Nie, C. Li, J. Gu and C. Zhang, Microbes Environ., 2012, 27, 443–448 CrossRef PubMed.
- F. Codony, J. Alvarez, J. Oliva, B. Ciurana, N. Camps, J. Torres, S. Minguell, N. Jové, E. Cirera and T. Admetlla, Eur. J. Clin. Microbiol. Infect. Dis., 2002, 21, 717–721 CrossRef CAS PubMed.
- K. Azuma, I. Uchiyama and J. Okumura, Regul. Toxicol. Pharmacol., 2013, 65, 1–6 CrossRef PubMed.
- M. Bouwknegt, J. F. Schijven, J. A. Schalk, R. Husman and A. Maria, Risk Anal., 2013, 33, 1228–1236 CrossRef PubMed.
- A. Edagawa, A. Kimura, H. Tanaka, K. Tomioka, K. Sakabe, C. Nakajima and Y. Suzuki, J. Appl. Microbiol., 2008, 105, 2104–2114 CrossRef CAS PubMed.
- H. Y. Buse, M. E. Schoen and N. J. Ashbolt, Legionellae in engineered systems and use of quantitative microbial risk assessment to predict exposure, Water Res., 2012, 46(4), 921–933 CrossRef CAS PubMed.
- D. Turner, Workbook of atmospheric dispersion estimates, Report US Environmental Protection Agency Report AP-26, US Government Printing Office, Washington, DC, 1973 Search PubMed.
- F. Pasquill, Meteorol. Mag., 1961, 90, 33–49 Search PubMed.
- N. De Nevers, Air pollution control engineering, Waveland Press, 2010 Search PubMed.
- B. Lighthart, Appl. Microbiol., 1973, 25, 86–91 CAS.
- R. F. Berendt, J. Infect. Dis., 1980, 141, 689–689 CrossRef CAS PubMed.
- R. F. Berendt, Infect. Immun., 1981, 32, 690–692 CAS.
- B. Lighthart, Aerobiologia, 1989, 5, 138–144 CrossRef.
- B. Lighthart and A. Frisch, Appl. Environ. Microbiol., 1976, 31, 700–704 CAS.
- P. Dennis and J. Lee, J. Appl. Bacteriol., 1988, 65, 135–141 CrossRef CAS PubMed.
- P. Hambleton, M. Broster, P. Dennis, R. Henstridge, R. Fitzgeorge and J. Conlan, J. Hyg., 1983, 90, 451–460 CrossRef CAS PubMed.
- S. M. Katz and J. M. Hammel, Ann. Clin. Lab. Sci., 1987, 17, 150–156 CAS.
- H. Bezdek and A. Carlucci, Limnol. Oceanogr., 1972, 17, 566–569 CrossRef.
- D. C. Blanchard and L. D. Syzdek, J. Geophys. Res., 1972, 77, 5087–5099 CrossRef.
- E. Bédard, S. Fey, D. Charron, C. Lalancette, P. Cantin, P. Dolcé, C. Laferrière, E. Déziel and M. Prévost, Water Res., 2015, 71, 244–256 CrossRef PubMed.
- W. C. Hinds, Aerosol technology: properties, behavior, and measurement of airborne particles, Wiley-Interscience, New York, 2 edn, 1999 Search PubMed.
- B. Lighthart, B. Shaffer, B. Marthi and L. Ganio, Appl. Environ. Microbiol., 1991, 57, 1006–1012 CAS.
- B. Lighthart and B. T. Shaffer, Aerosol Sci. Technol., 1997, 27, 439–446 CrossRef CAS.
- S. Collins, F. Jorgensen, C. Willis and J. Walker, J. Appl. Microbiol., 2015, 119, 1158–1169 CrossRef CAS PubMed.
- H.-Y. Shih and Y. E. Lin, Appl. Environ. Microbiol., 2006, 72, 6859–6859 CrossRef CAS PubMed.
- C. W. Chang, Y. H. Hwang, W. Y. Cheng and C. P. Chang, J. Appl. Microbiol., 2007, 102, 1636–1644 CrossRef CAS PubMed.
- B. La Scola, L. Mezi, P. Weiller and D. Raoult, J. Clin. Microbiol., 2001, 39, 365–366 CrossRef CAS PubMed.
- T. J. Rowbotham, J. Clin. Pathol., 1983, 36, 978–986 CrossRef CAS PubMed.
- M. T. García, S. Jones, C. Pelaz, R. D. Millar and Y. Abu Kwaik, Environ. Microbiol., 2007, 9, 1267–1277 CrossRef PubMed.
- H. Whiley and M. Taylor, Crit. Rev. Microbiol., 2014, 1–10 CrossRef PubMed.
- M. A. Yáñez, C. Carrasco-Serrano, V. M. Barberá and V. Catalan, Appl. Environ. Microbiol., 2005, 71, 3433–3441 CrossRef PubMed.
- J. Lu, H. Buse, V. Gomez-Alvarez, I. Struewing, J. Santo Domingo and N. Ashbolt, J. Appl. Microbiol., 2014, 117, 905–918 CrossRef CAS PubMed.
- P. Schmidt, M. Emelko and M. Thompson, Water Res., 2013, 47, 2399–2408 CrossRef CAS PubMed.
| This journal is © The Royal Society of Chemistry 2016 |