Implications of observed PBDE diffusion coefficients in low density polyethylene and silicone rubber
Jhon F.
Narváez Valderrama
a,
Kine
Baek
b,
Francisco J.
Molina
a and
Ian J.
Allan
*b
aGrupo de Gestión y Modelación Ambiental – GAIA, Facultad de Ingeniería, SIU, Universidad de Antioquia UdeA, Calle 70 N° 52-21, Medellín, Colombia
bNorwegian Institute for Water Research (NIVA), Oslo Centre for Interdisciplinary Environmental and Social Research, Gaustadalléen 21, NO-0349 Oslo, Norway. E-mail: ian.allan@niva.no; Fax: +47 22 18 52 00; Tel: +47 02348
First published on 18th December 2015
Abstract
A film-stacking technique was used to estimate diffusion coefficients of polybrominated diphenyl ethers (PBDEs) in low density polyethylene (LDPE) and silicone rubber. Substantially higher PBDE diffusion coefficients were observed for silicone rubber (AlteSil™) than for LDPE. A much steeper decrease in LDPE diffusion coefficients was found with increasing PBDE molecular weight than that for silicone rubber. From a passive sampling point-of-view, this means that for equivalent polymer–water partition coefficients for these two materials, the mass transfer resistance for these substances in the LDPE will be significantly higher than that for silicone rubber. Boundary layer control of the uptake process for silicone rubber can be expected for PBDEs. With a microplastic perspective, the low diffusion coefficients of PBDEs and in particular of decabromo diphenyl ether (BDE 209) in LDPE imply that the polymer diffusion coefficients for these plastic additives used as flame retardants need to be taken into account when considering the risk posed by microplastic particle ingestion by marine organisms.
Environmental impactBoth passive sampling and marine microplastic pollution risk assessment require an understanding and calibration of the interactions between environmental contaminants and polymers. Estimates of diffusion coefficients for polybrominated diphenyl ether (PBDE) flame retardants are reported for two types of polymers, silicone rubber and low density polyethylene. The significantly higher PBDE diffusion coefficients measured in silicone rubber indicate that this polymer is the most appropriate for the passive sampling of PBDEs. PBDE diffusion coefficients measured in LDPE contribute to the assessment of the risk posed by these chemicals to marine biota when present as additives in marine plastic debris. |
Introduction
Today's consumer society is responsible for the global rise of production and usage of polymers, which in turn will result in increasing amounts of plastic litter released into the marine environment as macro or micro-plastics.1,2 Sources of micro-plastics can be pre-production pellets, particles from personal care products or from the fragmentation of macro-plastics. These micro-plastic particles can either be released into the environment loaded with contaminants such as flame retardants or plasticisers or accumulate contaminants from their surroundings once in water. Ingestion of these particles can become a pathway for contaminant transfer into marine organisms.3This capacity to sorb contaminants has made the use of polymers for other applications possible. The absorptive properties of polymers such as low density polyethylene (LDPE) or silicone rubber render them well-suited to the passive sampling of a wide range of hydrophobic organic contaminants in the environment.4–6
Assessing contaminant partitioning to these polymers is essential since (i) it can play a role in the transfer of micro-plastic-sorbed contaminants into organisms and (ii) it is needed for passive sampling data interpretation.5,7,8 Contaminant transport inside the polymer can affect the rate of exchange of contaminants between the polymer and the medium it is exposed to. Measurements of polymer diffusion coefficients (D) for polycyclic aromatic hydrocarbons (PAHs) and polychlorinated biphenyls (PCBs) have shown the significantly higher permeability of AlteSil™ and Silastic silicone rubbers when compared to LDPE.9,10 This is not surprising since silicone rubber has the lowest glass transition temperature of most polymers.11 This glass transition temperature is the temperature region at which a polymer goes from being glassy and hard to a rubbery material. Additionally, Rusina and co-workers demonstrated that D depends on the properties and structure of the molecule.9 Larger and less flexible molecules were found to diffuse more slowly and the decrease in D for LDPE with increasing molecular weight (MW) was found to be steeper than that for silicone rubbers. Values of log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) D for PAHs and PCBs in LDPE were two or more log units below those measured for silicone rubbers.
D for PAHs and PCBs in LDPE were two or more log units below those measured for silicone rubbers.
Polybrominated diphenyl ethers (PBDEs) are a class of brominated compounds widely used as flame retardants including in polymers such as LDPE.3,12 PBDEs will therefore be present in the polymer from production or will be able to accumulate from water once released into the aquatic environment. PBDEs are very hydrophobic, with log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Kow above 5.5 and molecular weights (MW) in the range 300–1000 g mol−1. As a result of their molecular size, these compounds are likely to have diffusion coefficients in LDPE and silicone rubber that are significantly lower than those previously measured for PAHs and PCBs. However, to our knowledge, no measurements of PBDE diffusion coefficients in polymers such as LDPE and silicone rubber have been conducted so far.
Kow above 5.5 and molecular weights (MW) in the range 300–1000 g mol−1. As a result of their molecular size, these compounds are likely to have diffusion coefficients in LDPE and silicone rubber that are significantly lower than those previously measured for PAHs and PCBs. However, to our knowledge, no measurements of PBDE diffusion coefficients in polymers such as LDPE and silicone rubber have been conducted so far.
In this study, we used a film stacking technique9,13 to measure and report diffusion coefficients of a range of PBDE congeners in LDPE and AlteSil™ silicone rubber at 20 °C. We then assessed the possible implications of these diffusion coefficients on (i) the fate of PBDEs present in LDPE microplastic particles and (ii) the passive sampling of these substances.
Materials and methods
Materials
All glassware and aluminium foil were either solvent rinsed or baked in a muffle furnace at 540 °C. High performance liquid chromatography-grade (or better) solvents (ethyl acetate, methanol, n-hexane and n-pentane) were from Rathburn (Scotland). Analytical-grade standards for PBDE congeners 28, 47, 99, 100, 153, 154 and 209 were purchased from LGC/Promochem (United Kingdom). Recovery standards used for PBDE analysis were BDE 119, BDE 181, and 13C-BDE 209.Polymer preparation
Polymers used in this study were LDPE and silicone rubber. The LDPE was bought from Brentwood Plastics Inc. as 2.5 cm-wide lay-flat tubing (nominal thickness of 70 μm), used for passive sampling purposes.14,15 AlteSil™ silicone rubber sheets (500 μm nominal thickness) were purchased from Altec Products Ltd. LDPE and silicone rubber were cut into sheets of 5.0 × 2.0 cm. Masses of silicone rubber and LDPE sheets were 0.68 (±0.06) g and 0.075 (±0.003) g, respectively. The LDPE was rinsed with MilliQ water, dried with a clean tissue and left to soak in hexane. The latter step was repeated twice with fresh hexane. The sheets were left to dry in a fume hood covered with a clean aluminium sheet before use. The first cleaning step for the silicone rubber sheets was Soxhlet extraction with ethyl acetate for 24 hours to remove silicone oligomers.10 Silicone rubber sheets were then left to dry in a fume hood covered with a clean aluminium sheet before further soaking in methanol (a step repeated twice with fresh solvent). Non-spiked sheets of LDPE and silicone rubber were also prepared and kept at −20 °C in air-tight containers until use. A number of these sheets were kept as blanks to assess initial PBDE concentrations. PBDE congeners 28, 47, 99, 100, 153, 154 and 209 were then spiked into sets of LDPE and silicone rubber polymer sheets with a method adapted from Booij et al.16 The spiking lasted five days. LDPE and silicone rubber sheets were introduced separately in glass bottles with 20 mL of methanol and the PBDE congeners were spiked. MilliQ water was added stepwise to the methanol for over five days to reach a final methanol![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) water volume ratio of 20
water volume ratio of 20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 80. The polymers were then removed from solution, dried with a clean tissue and kept at −20 °C until use in film-stacking experiments. For LDPE, PBDEs were also spiked onto a set of membranes using a hexane solution and with an exposure of 5 days. After exposure, sheets were retrieved from the hexane and the hexane was left to evaporate before the sheets were stored at −20 °C. Two spiked LDPE and silicone rubber sheets were kept to measure the initial PBDE concentrations from each spiking procedure (the mean calculated from replicates for each polymer).
80. The polymers were then removed from solution, dried with a clean tissue and kept at −20 °C until use in film-stacking experiments. For LDPE, PBDEs were also spiked onto a set of membranes using a hexane solution and with an exposure of 5 days. After exposure, sheets were retrieved from the hexane and the hexane was left to evaporate before the sheets were stored at −20 °C. Two spiked LDPE and silicone rubber sheets were kept to measure the initial PBDE concentrations from each spiking procedure (the mean calculated from replicates for each polymer).
Film-stacking experiment
A methodology similar to that of Reynier et al.13 and Rusina et al.9 was used to estimate PBDE diffusion coefficients in LDPE and silicone rubber. Each film-stacking test consisted of five superimposed polymer sheets with one PBDE-spiked sheet placed in between 4 non-spiked sheets. Polymer piles were wrapped in clean aluminium foil and a pressure of 0.5–1 kg cm−2 was applied. Duplicate tests were conducted for each polymer type. Experimental contact periods of 4 and 42 hours for silicone rubber and 42 and 250 hours for LDPE spiked with the methanol![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) water solution were chosen based on the work of Rusina et al. (2010).9 For LDPEs spiked with hexane, experiments were run for 250 hours. At the end of the experiment, polymer sheets were separated and placed into clean glass jars for extraction. Non-spiked and PBDE-spiked sheets were analysed at the same time as those used in the assays.
water solution were chosen based on the work of Rusina et al. (2010).9 For LDPEs spiked with hexane, experiments were run for 250 hours. At the end of the experiment, polymer sheets were separated and placed into clean glass jars for extraction. Non-spiked and PBDE-spiked sheets were analysed at the same time as those used in the assays.
PBDE extraction and analysis
Extraction and analysis were performed using methods similar to those previously reported.4 Once the experiments were completed, LDPE and silicone sheets including blanks and controls were extracted individually overnight by soaking in n-pentane (25 mL) once. Recovery standards (18 ng of BDEs 119 and 181 and 50 ng of 13C-BDE 209) were added to the extraction jar after adding the n-pentane. The following day, polymer sheets were removed from the solution using clean tweezers. Samples were then reduced to 500 μL by a gentle stream of nitrogen at room temperature. Extracts were then transferred to a chromatography vial and further reduced to 200–300 μL for analysis.PBDE congeners 28, 47, 99, 100, 153, 154 and 209 were analysed using gas chromatography coupled to a mass spectrometer (GC-MS). The GC-MS was a Hewlett Packard 6890 Plus GC linked to a Hewlett Packard 5973 MS detector, run in negative chemical ionisation and single ion monitoring (SIM) modes for analysis of PBDE congeners. SIM for ion fragments was m/z 79 and 81 for PBDEs while ions with m/z 486.2, 488.2, 492.2, and 494.2 were used for BDE 209. PBDE congener separation was carried out on a DB-5MS column (15 m long, 0.25 mm internal diameter and 0.10 μm film thickness) with a splitless injection. The oven was initially held at 120 °C for 2 min and the temperature was increased to 345 °C at the rate of 25 °C min−1 and maintained for 5 min. The gas carrier flow rate (helium) was kept at 1 mL min−1 for the first 13 min and increased to 1.4 mL min−1 at the rate of 0.1 mL min−1 (maintained for 8 min). The MS detector conditions were: ion source 250 °C, quadrupole 150 °C, and transfer line 325 °C.
Estimation of diffusion coefficients
Diffusion coefficients for PBDE congeners in the LDPE and silicone rubber were estimated using Fick's second law: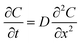 | (1) |
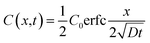 | (2) |
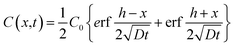 | (3) |
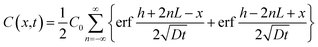 | (4) |
Complete details for these equations can be found in the book by Crank (1975).17 A Microsoft Excel spreadsheet was developed to calculate the profiles of concentrations for the diffusing compounds based on eqn (4). The time parameter t was set to the experimental durations of 4, 42 or 250 hours. In the model, LDPE and silicone rubber sheets were divided into distinct sections with thicknesses of 0.5 and 5 μm, respectively. Since the film stack has impermeable boundaries, the successive terms in eqn (4) (with n varying from −∞ to +∞) allows for successive reflection of the curve at the boundaries. For practical purposes, we used n varying between − and +100. The resulting profiles of concentrations C(X) across each polymer sheet were averaged to enable comparison of the modelled profile outputs with experimentally measured concentrations. The Solver function in Excel was used to optimise D by comparing predicted polymer profiles with those experimentally measured.
Results and discussion
PBDE diffusion coefficients in LDPE and AlteSil™ silicone rubber
Mass balances for the different replicate assays across the range of chemicals and exposure times were generally good with average recoveries of 120 (88–164), 76 (32–128) and 104 (65–126)% for experiments with silicone rubber, LDPE spiked with methanol![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) water and hexane, respectively.
water and hexane, respectively.
Diffusion coefficients in LDPE and silicone rubber were obtained for most PBDEs and are presented in Table 1 with units of m2 s−1. For the silicone rubber film-stacking experiments, all PBDE congeners had equilibrated throughout the five layers within 42 hours (equivalent to log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) D > −11). Profiles of concentration could only be observed for the 4-hour contact time, allowing the estimation of D for the silicone rubber using eqn (4) and the Excel spreadsheet. log
D > −11). Profiles of concentration could only be observed for the 4-hour contact time, allowing the estimation of D for the silicone rubber using eqn (4) and the Excel spreadsheet. log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) D obtained was in the range −10.60 to −10.80 for BDE 28 to 209, respectively. These are of a similar order of magnitude as those obtained for PCB congeners by Rusina et al.9 for the same AlteSil™ silicone rubber (see Fig. 1). The observed decrease in PBDE diffusion coefficients with increasing compound hydrophobicity (0.2 of a log unit) is low considering that over three orders of magnitude in log
D obtained was in the range −10.60 to −10.80 for BDE 28 to 209, respectively. These are of a similar order of magnitude as those obtained for PCB congeners by Rusina et al.9 for the same AlteSil™ silicone rubber (see Fig. 1). The observed decrease in PBDE diffusion coefficients with increasing compound hydrophobicity (0.2 of a log unit) is low considering that over three orders of magnitude in log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Kow separating BDE 28 from BDE 209. Rusina et al. (2010) found a decrease of 0.5 log unit across the three log
Kow separating BDE 28 from BDE 209. Rusina et al. (2010) found a decrease of 0.5 log unit across the three log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Kow unit range of the PCBs. Differences in diffusion coefficients for the various PBDE congeners in silicone rubber are relatively minor considering the range of MW of PBDEs (from 406.9 to 959.2 g mol−1 for BDE 28 to 209). For LDPE, experimental contact times of 42 and 250 hours for the LDPE sheets spiked with the methanol
Kow unit range of the PCBs. Differences in diffusion coefficients for the various PBDE congeners in silicone rubber are relatively minor considering the range of MW of PBDEs (from 406.9 to 959.2 g mol−1 for BDE 28 to 209). For LDPE, experimental contact times of 42 and 250 hours for the LDPE sheets spiked with the methanol![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) water solution both allowed the transfer of PBDEs to the adjacent LDPE layer(s). PBDE concentration profiles were used to estimate diffusion coefficients and these are reported in Table 1 and presented in Fig. 1. Diffusion coefficients varied over a much greater magnitude than those found for silicone rubber. log
water solution both allowed the transfer of PBDEs to the adjacent LDPE layer(s). PBDE concentration profiles were used to estimate diffusion coefficients and these are reported in Table 1 and presented in Fig. 1. Diffusion coefficients varied over a much greater magnitude than those found for silicone rubber. log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) D was −13.24 for BDE 28 and decreased to values around −16 for BDE congeners 153, 154 and 209. The diffusion coefficients reported in Table 1 show that the D values for meta brominated PBDEs (BDEs 99 and 153) are generally lower than those for their respective congeners with bromine in the ortho position (BDEs 100 and 154). This is consistent with the results of Rusina et al. who observed that chlorines in the meta position had the highest impact on reduction in log
D was −13.24 for BDE 28 and decreased to values around −16 for BDE congeners 153, 154 and 209. The diffusion coefficients reported in Table 1 show that the D values for meta brominated PBDEs (BDEs 99 and 153) are generally lower than those for their respective congeners with bromine in the ortho position (BDEs 100 and 154). This is consistent with the results of Rusina et al. who observed that chlorines in the meta position had the highest impact on reduction in log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) D for PCBs.9
D for PCBs.9
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) water or hexane solution for the LDPEd
water or hexane solution for the LDPEd
| PBDE congener | MW (g mol−1) | log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Kowa Kowa |
log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) D (m2 s−1) D (m2 s−1) |
||||
|---|---|---|---|---|---|---|---|
| Silicone rubber | LDPE | ||||||
Methanol![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) water water |
Methanol![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) water water |
Hexane | Generic | ||||
| 4 hours | 42 hours | 250 hours | 250 hours | ||||
a log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Kow values taken from Braekevelt et al.28
b Mean of values obtained with PBDEs spiked using methanol Kow values taken from Braekevelt et al.28
b Mean of values obtained with PBDEs spiked using methanol![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) water (42 and 250 hours) and hexane.
c log water (42 and 250 hours) and hexane.
c log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) D for BDE 209 from the linear regression of log D for BDE 209 from the linear regression of log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) D = −0.014MW − 7.30 (R2 = 0.992 and se = 0.135) obtained from generic values of log D = −0.014MW − 7.30 (R2 = 0.992 and se = 0.135) obtained from generic values of log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) D for BDEs 28, 47, 99, 100, 153 and 154.
d nd: not determined, equilibrium for BDE 28 was reached during the 250-hour long experiments. D for BDEs 28, 47, 99, 100, 153 and 154.
d nd: not determined, equilibrium for BDE 28 was reached during the 250-hour long experiments.
|
|||||||
| 28 | 406.9 | 5.94 | −10.61 | −13.24 | nd | nd | −13.24 |
| 47 | 485.8 | 6.81 | −10.60 | −14.15 | −14.10 | −14.23 | −14.19b |
| 99 | 564.7 | 7.32 | −10.71 | <−15.5 | <−15.2 | −15.56 | −15.56 |
| 100 | 564.7 | 7.24 | −10.60 | <−15.2 | <−15.0 | −15.32 | −15.32 |
| 153 | 643.3 | 7.9 | −10.77 | <−16.6 | <−16.0 | −16.70 | −16.70 |
| 154 | 643.3 | 7.82 | −10.78 | <−16.4 | <−15.9 | −16.48 | −16.48 |
| 209 | 959.2 | 9.87 | −10.80 | <−16.9 | <−16.4 | <−17.2 | −20.8c |
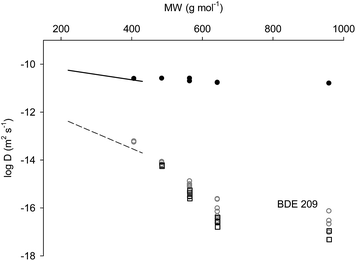 | ||
Fig. 1 Diffusion coefficients of PBDE congeners (plotted as log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) D) in AlteSil™ silicone (black-filled dots) rubber and in LDPE (empty symbols). For comparison, log D) in AlteSil™ silicone (black-filled dots) rubber and in LDPE (empty symbols). For comparison, log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) D–MW regressions for PCB diffusion coefficients in AlteSil™ silicone rubber (solid line) and in LDPE (dashed line) from Rusina et al. (2010)9 are also plotted. Grey-coloured dots and black-coloured squares are for the log D–MW regressions for PCB diffusion coefficients in AlteSil™ silicone rubber (solid line) and in LDPE (dashed line) from Rusina et al. (2010)9 are also plotted. Grey-coloured dots and black-coloured squares are for the log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) D values for LDPE sheets with PBDE spiked with a methanol D values for LDPE sheets with PBDE spiked with a methanol![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) water solution and hexane, respectively (see text for more details). water solution and hexane, respectively (see text for more details). | ||
At the first glance, these data appeared consistent and in agreement with PCB diffusion coefficients in LDPE from the same source as that used in our study.9 PBDE diffusion coefficients (excluding that of BDE 209, see Fig. 1) appeared to follow a trend with MW. Indeed, the log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) D–MW regression with a slope of −0.013 and an intercept of −8.02 has an R2 of 0.93 and a standard error (se) of 0.267. The higher variance of replicate measurements for larger PBDE congeners (Fig. 1) results from the generally low amounts of substances moving to the initially PBDE-free sheets. Apparent D for BDE 209 appears significantly higher than expected from the regression above. This can be explained by the very low BDE 209 diffusion coefficient in LDPE. The low diffusion coefficients expected for BDE 209 indicate that the congener would have travelled only a few μm across the LDPE during the initial spiking of the PBDEs into the polymer. The use of a mixture of methanol and water to spike PBDEs into LDPE is not likely to result in PBDE diffusion coefficients very different from those in the polymer on its own. Alcohols and alcohol–water mixtures have been proposed as simulants of the fatty foodstuff in the studies of chemical migration in plastics in contact with the foodstuff. The reason for this is the high solubility of the chemicals in these solvents while minimising the effect of the solvent on the diffusion coefficient in the plastic films.18 Methanol was also shown to have a minimal swelling effect on LDPE.10
D–MW regression with a slope of −0.013 and an intercept of −8.02 has an R2 of 0.93 and a standard error (se) of 0.267. The higher variance of replicate measurements for larger PBDE congeners (Fig. 1) results from the generally low amounts of substances moving to the initially PBDE-free sheets. Apparent D for BDE 209 appears significantly higher than expected from the regression above. This can be explained by the very low BDE 209 diffusion coefficient in LDPE. The low diffusion coefficients expected for BDE 209 indicate that the congener would have travelled only a few μm across the LDPE during the initial spiking of the PBDEs into the polymer. The use of a mixture of methanol and water to spike PBDEs into LDPE is not likely to result in PBDE diffusion coefficients very different from those in the polymer on its own. Alcohols and alcohol–water mixtures have been proposed as simulants of the fatty foodstuff in the studies of chemical migration in plastics in contact with the foodstuff. The reason for this is the high solubility of the chemicals in these solvents while minimising the effect of the solvent on the diffusion coefficient in the plastic films.18 Methanol was also shown to have a minimal swelling effect on LDPE.10
As we expected BDE 209 was not homogenously distributed across the polyethylene, and instead was present at high concentration at the edge of the LDPE. When such a sheet is used within a film stack, contiguous layers are exposed to a higher concentration than if the substance was homogenously distributed throughout the spiked layer, resulting in more transfer of the substance to the adjacent layers. While this issue is apparent for BDE 209 in Fig. 1, it can also be expected (from their apparent log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) D) to affect the results for penta- and hexa-brominated diphenyl ethers. This indicates that diffusion coefficients for PBDE congeners 99, 100, 153, 154 and 209 obtained with methanol
D) to affect the results for penta- and hexa-brominated diphenyl ethers. This indicates that diffusion coefficients for PBDE congeners 99, 100, 153, 154 and 209 obtained with methanol![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) water spiked LDPE given in Table 1 and plotted in Fig. 1 are (conservative) overestimates of true values. The use of hexane rather than methanol
water spiked LDPE given in Table 1 and plotted in Fig. 1 are (conservative) overestimates of true values. The use of hexane rather than methanol![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) water to spike chemicals into the LDPE was expected to result in more homogenously distributed chemicals in LDPE. Masses of PBDEs found in LDPE layers in direct contact with the central spiked sheet relative to those measured in the originally spiked layer are given in Table 2 for tests with PBDEs spiked with methanol
water to spike chemicals into the LDPE was expected to result in more homogenously distributed chemicals in LDPE. Masses of PBDEs found in LDPE layers in direct contact with the central spiked sheet relative to those measured in the originally spiked layer are given in Table 2 for tests with PBDEs spiked with methanol![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) water and hexane. For PBDEs 99, 100, 153, 154 and 209, ratios obtained with hexane-spiked LDPE are consistently lower than those for methanol
water and hexane. For PBDEs 99, 100, 153, 154 and 209, ratios obtained with hexane-spiked LDPE are consistently lower than those for methanol![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) water-spiked LDPE demonstrating that LDPE diffusion coefficients are overestimated when substances are not homogeneously distributed as a result of the spiking procedure. The use of hexane enables PBDEs to travel faster and deeper into LDPE.19 The variability between replicate measurements for hexane-spiked LDPE is consistently lower than that for methanol
water-spiked LDPE demonstrating that LDPE diffusion coefficients are overestimated when substances are not homogeneously distributed as a result of the spiking procedure. The use of hexane enables PBDEs to travel faster and deeper into LDPE.19 The variability between replicate measurements for hexane-spiked LDPE is consistently lower than that for methanol![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) water-spiked LDPE and this could be the result of the more homogeneous distribution of chemicals in the polymer. This can be explained by the much higher swelling of LDPE expected during spiking with hexane than what would be achieved with methanol
water-spiked LDPE and this could be the result of the more homogeneous distribution of chemicals in the polymer. This can be explained by the much higher swelling of LDPE expected during spiking with hexane than what would be achieved with methanol![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) water.10 log
water.10 log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) D values for hexane-based PBDE spiked LDPE sheets are reported in Table 1 and plotted in Fig. 1. The log
D values for hexane-based PBDE spiked LDPE sheets are reported in Table 1 and plotted in Fig. 1. The log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) D value for PBDE 47 differs by less than 0.2 log unit from data obtained with LDPE sheets with PBDEs spiked with methanol
D value for PBDE 47 differs by less than 0.2 log unit from data obtained with LDPE sheets with PBDEs spiked with methanol![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) water. log
water. log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) D values for PBDEs 99, 100, 153 and 154 are generally lower than those obtained with the methanol
D values for PBDEs 99, 100, 153 and 154 are generally lower than those obtained with the methanol![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) water spiking. An approximate calculation based on eqn (4) and a one LDPE layer model indicates that the methanol
water spiking. An approximate calculation based on eqn (4) and a one LDPE layer model indicates that the methanol![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) water-based spiking of LDPE sheets for 5 days would result in an approximate threshold for homogeneous distribution for a substance with log
water-based spiking of LDPE sheets for 5 days would result in an approximate threshold for homogeneous distribution for a substance with log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) D of −14.8. Since the estimated log
D of −14.8. Since the estimated log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) D values for PBDEs 99 and 100 are below the −14.8 threshold by 0.7 log unit, it is very likely that hexane-based spiking resulted in a homogeneous distribution of PBDEs 99 and 100 in spiked LDPE sheets and most accurate values of log
D values for PBDEs 99 and 100 are below the −14.8 threshold by 0.7 log unit, it is very likely that hexane-based spiking resulted in a homogeneous distribution of PBDEs 99 and 100 in spiked LDPE sheets and most accurate values of log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) D. We have then summarised the most accurate values of log
D. We have then summarised the most accurate values of log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) D from experiments with PBDEs spiked using methanol
D from experiments with PBDEs spiked using methanol![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) water and hexane spiked sheets into a set of generic log
water and hexane spiked sheets into a set of generic log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) D values (Table 1). These generic log
D values (Table 1). These generic log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) D values for BDEs 28, 47, 99, 100, 153 and 154 for LDPE are strongly correlated to compound's MW. The log
D values for BDEs 28, 47, 99, 100, 153 and 154 for LDPE are strongly correlated to compound's MW. The log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) D–MW regression (with a slope of −0.014 and an intercept of −7.30) had an R2 of 0.992 and a standard error of 0.135. Based on this regression, the log
D–MW regression (with a slope of −0.014 and an intercept of −7.30) had an R2 of 0.992 and a standard error of 0.135. Based on this regression, the log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) D for BDE 209 was expected to be close to −20.8. A strong correlation of log
D for BDE 209 was expected to be close to −20.8. A strong correlation of log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) D with MW can often be expected within classes of chemicals. Rusina et al. (2010) obtained excellent relationships of log
D with MW can often be expected within classes of chemicals. Rusina et al. (2010) obtained excellent relationships of log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) D with MW for PCBs and PAHs with LDPE.9 log
D with MW for PCBs and PAHs with LDPE.9 log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) D values obtained with hexane-based spiking of LDPE sheets with PBDEs are likely to be the closest to true log
D values obtained with hexane-based spiking of LDPE sheets with PBDEs are likely to be the closest to true log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) D values.
D values.
| PBDE congener | Ratio | |
|---|---|---|
Methanol![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) water spiking water spiking |
Hexane spiking | |
| a Relative percent difference of two replicate estimates are given in brackets. | ||
| 28 | 0.93 (26)a | 0.91 (16) |
| 47 | 0.76 (5) | 0.72 (19) |
| 99 | 0.22 (33) | 0.13 (14) |
| 100 | 0.30 (24) | 0.19 (18) |
| 153 | 0.081 (66) | 0.030 (22) |
| 154 | 0.091 (53) | 0.039 (17) |
| 209 | 0.061 (93) | 0.017 (37) |
Overall these results tend to indicate that for an accurate measurement of polymer diffusion coefficients for these slow moving substances, the film-stacking method experiment may need to be conducted over significantly longer periods of time than those tested here. Sufficient spiking time may be needed to ensure that compounds are well distributed across the entire spiked films. Alternatively, film thicknesses could be decreased.
Implications of polymer diffusion coefficients for PBDEs
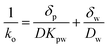 | (5) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Kpw–log
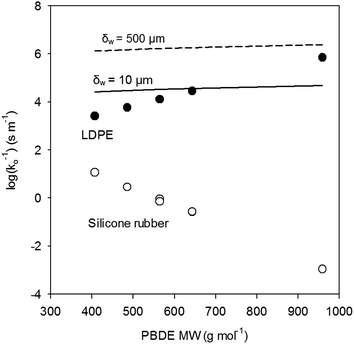
Kpw–log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Kow relationships from Lohmann for LDPE and from Smedes et al.21 (for PCBs) for AlteSil™ silicone rubber. We calculated PBDE mass transfer resistances for the polymeric membranes and compared them with the overall mass transfer resistances calculated for boundary layer-controlled uptake conditions. These are shown in Fig. 2. The resistance to mass transfer for PBDEs in the 500 μm-thick AlteSil™ silicone rubber is significantly lower than that for the 100 μm-thick LDPE. The slope of the relationship of log(1/ko) with MW is negative for the silicone rubber. This is because the assumed increase in Kpw is higher than the decrease in D for the corresponding PBDE MW increases (see eqn (5)). For LDPE, D decreases faster and this results in log(1/ko) that appears to increase with MW. Furthermore, the resistance to mass transfer for PBDEs in the LDPE is in a very similar range to those estimated for boundary-layer controlled uptake with realistic diffusive boundary layer thicknesses of 10 to 500 μm (Fig. 2). Since we expect diffusion coefficients in LDPE to be even lower than those estimated here for PBDEs with at least five bromine atoms, resistance to mass transfer in the polyethylene is likely to be higher. This can affect PBDE sampling rates for LDPE and semipermeable membrane device (SPMD) passive samplers. This could be an explanation for the lower amounts of PBDEs absorbed by LDPE than in silicone rubber in samplers of identical surface area (and exposed in a similar manner) in our study reported in 2013.4
Kow relationships from Lohmann for LDPE and from Smedes et al.21 (for PCBs) for AlteSil™ silicone rubber. We calculated PBDE mass transfer resistances for the polymeric membranes and compared them with the overall mass transfer resistances calculated for boundary layer-controlled uptake conditions. These are shown in Fig. 2. The resistance to mass transfer for PBDEs in the 500 μm-thick AlteSil™ silicone rubber is significantly lower than that for the 100 μm-thick LDPE. The slope of the relationship of log(1/ko) with MW is negative for the silicone rubber. This is because the assumed increase in Kpw is higher than the decrease in D for the corresponding PBDE MW increases (see eqn (5)). For LDPE, D decreases faster and this results in log(1/ko) that appears to increase with MW. Furthermore, the resistance to mass transfer for PBDEs in the LDPE is in a very similar range to those estimated for boundary-layer controlled uptake with realistic diffusive boundary layer thicknesses of 10 to 500 μm (Fig. 2). Since we expect diffusion coefficients in LDPE to be even lower than those estimated here for PBDEs with at least five bromine atoms, resistance to mass transfer in the polyethylene is likely to be higher. This can affect PBDE sampling rates for LDPE and semipermeable membrane device (SPMD) passive samplers. This could be an explanation for the lower amounts of PBDEs absorbed by LDPE than in silicone rubber in samplers of identical surface area (and exposed in a similar manner) in our study reported in 2013.4
Overall, these data support the use of a boundary layer-controlled model for the estimation of freely dissolved concentrations of PBDEs in water using AlteSil™ silicone rubber.9 PBDE uptake into LDPE (100 μm thickness) or SPMDs could be either boundary layer or membrane-controlled depending on the exposure conditions. Under the membrane-controlled uptake, sampling rates could be estimated from the compound's diffusion coefficients in LDPE if the influence of the temperature of these coefficients is known. At a lower sampler exposure temperature, lower PBDE diffusion coefficients in LDPE may be compensated by an expected increase in Kpw. Note that the increase and decrease in PBDE mass transfer coefficients in polymers with log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Kow shown in Fig. 2 are not necessarily real, since the values of Kpw for PBDEs or relationships with MW or log
Kow shown in Fig. 2 are not necessarily real, since the values of Kpw for PBDEs or relationships with MW or log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Kow are not accurately known. Ultimately it means that models that incorporate both membrane and boundary layer control of the uptake need to be used when working with such LDPE.
Kow are not accurately known. Ultimately it means that models that incorporate both membrane and boundary layer control of the uptake need to be used when working with such LDPE.
Knowledge of these PBDE diffusion coefficients in silicone rubber and LDPE can have further consequences for passive sampling. For example, much higher PBDE sampling rates can be expected to be achieved with silicone rubber than with LDPE when exposing samplers under high water turbulence.22,23 Equilibrium between PBDE concentration in silicone rubber samplers and that in water will be obtained much faster than with LDPE. For a 100 μm-thick LDPE membrane, 90% equilibrium (t90) can be expected to be reached after 1.25, 13.3, 141, 1480 d for PBDE congeners 28, 47, 99/100 and 153/154, respectively, under membrane-controlled uptake. These low PBDE diffusion coefficients in LDPE may also affect the time needed to obtain equilibrium in batch experiments to estimate Kpw values. Finally, another consideration is related to deuterated chrysene and benzo[a]pyrene, compounds used as PRCs in SPMDs, with log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) D values measured between −14 and −15.9 Following the injection of PRC-spiked triolein into the LDPE tubing, a lag time of over 10 days will be needed before the concentration of these substances equilibrates across the LDPE phase. This means that these compounds are not behaving as true PRCs during exposures of a month or less.
D values measured between −14 and −15.9 Following the injection of PRC-spiked triolein into the LDPE tubing, a lag time of over 10 days will be needed before the concentration of these substances equilibrates across the LDPE phase. This means that these compounds are not behaving as true PRCs during exposures of a month or less.
Implications for the risk assessment of microplastic additives in the aquatic environment
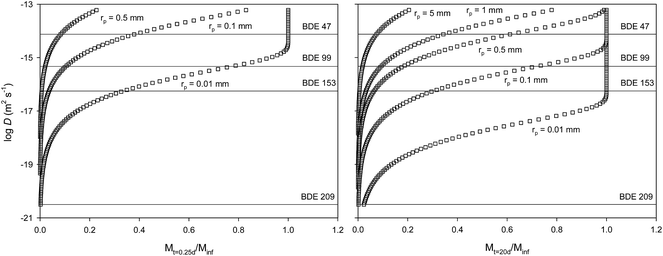
These low PBDE diffusion coefficients in LDPE may also have implications for the risk assessment of these chemicals in LDPE microplastics in the aquatic environment. PBDEs can be present in microplastic particles found in the marine environment as a result of their absorption of the particles once emitted into the environment or because these were used as additives, injected into the plastic during production, making use of their flame retardant properties. Recent studies have highlighted the presence of PBDEs in microplastics found in the environment.3,24 Concentration levels were found to be two orders of magnitude higher than those for other substances that were expected to have accumulated from the environment rather than being used as a chemical additive. One relevant question is whether LDPE microplastic-absorbed PBDEs can be transferred into the biota once the particles are ingested. Here we attempt to assess the extent to which PBDE diffusion coefficients in LDPE microparticles can affect the amount of these substances that can be transferred into an organism. For this we used a simple model of a chemical initially homogeneously distributed in a LDPE microsphere that diffuses out of the sphere based solely on diffusion within the sphere.17 In this worst-case scenario, we assume that the transfer of contaminants from the plastic into the organism is mediated by the transport in the polymer only. Koelmans et al.25 estimated that this was the case for lugworm exposed to polyethylene in sediments.The relative mass of a diffusing substance, initially homogeneously distributed throughout a polyethylene microplastic sphere, that leaves the sphere within a time t, can be estimated through eqn (6):17
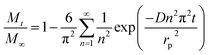 | (6) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) D for BDE 209 in a HDPE of −13. This appears unrealistic considering that we measure log
D for BDE 209 in a HDPE of −13. This appears unrealistic considering that we measure log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) D for BDE 47 below −14 for LDPE. HPDE has minimal branching of polymer chains compared to LDPE, rendering it denser, more rigid and generally less permeable than LDPE. While it is difficult to speculate the reason for these differences (unlikely effect of fish oil components on BDE 209 diffusion in HDPE, a higher experimental temperature or the more likely heterogeneous distribution in the HDPE particle), it becomes clear that the knowledge of diffusion coefficients of chemical additives such as PBDEs in polymers is important to understand the processes that control the transfer of chemicals between microplastics and their surrounding environment. While this modelling is based solely on diffusion of the PBDEs in the polymer, other processes such as particle aging and erosion or temperature and biofouling may also affect the transfer of these chemicals from microplastic particles to their surrounding environment.
D for BDE 47 below −14 for LDPE. HPDE has minimal branching of polymer chains compared to LDPE, rendering it denser, more rigid and generally less permeable than LDPE. While it is difficult to speculate the reason for these differences (unlikely effect of fish oil components on BDE 209 diffusion in HDPE, a higher experimental temperature or the more likely heterogeneous distribution in the HDPE particle), it becomes clear that the knowledge of diffusion coefficients of chemical additives such as PBDEs in polymers is important to understand the processes that control the transfer of chemicals between microplastics and their surrounding environment. While this modelling is based solely on diffusion of the PBDEs in the polymer, other processes such as particle aging and erosion or temperature and biofouling may also affect the transfer of these chemicals from microplastic particles to their surrounding environment.
Acknowledgements
The authors wish to thank the Empresas Públicas de Medellín (EPM) and Programa Enlaza Mundos for supporting JFN's doctorate studies and internship at NIVA. We also acknowledge funding from the Norwegian Research Council through NIVA's strategic Institute Initiative (SiS miljøgifter).References
- D. K. Barnes, F. Galgani, R. C. Thompson and M. Barlaz, Philos. Trans. R. Soc., B, 2009, 364, 1985–1998 CrossRef CAS PubMed.
- K. L. Law and R. C. Thompson, Science, 2014, 345, 144–145 CrossRef CAS PubMed.
- E. L. Teuten, J. M. Saquing, D. R. Knappe, M. A. Barlaz, S. Jonsson, A. Björn, S. J. Rowland, R. C. Thompson, T. S. Galloway and R. Yamashita, Philos. Trans. R. Soc., B, 2009, 364, 2027–2045 CrossRef CAS PubMed.
- I. J. Allan, C. Harman, S. B. Ranneklev, K. V. Thomas and M. Grung, Environ. Toxicol. Chem., 2013, 32, 1718–1726 CrossRef CAS PubMed.
- I. J. Allan, K. Booij, A. Paschke, B. Vrana, G. A. Mills and R. Greenwood, Environ. Sci. Technol., 2009, 43, 5383–5390 CrossRef CAS PubMed.
- B. Vrana, I. J. Allan, R. Greenwood, G. A. Mills, E. Dominiak, K. Svensson, J. Knutsson and G. Morrison, TrAC, Trends Anal. Chem., 2005, 24, 845–868 CrossRef CAS.
- T. P. Rusina, F. Smedes, M. Koblizkova and J. Klanova, Environ. Sci. Technol., 2009, 44, 362–367 CrossRef PubMed.
- E. L. Teuten, S. J. Rowland, T. S. Galloway and R. C. Thompson, Environ. Sci. Technol., 2007, 41, 7759–7764 CrossRef CAS PubMed.
- T. P. Rusina, F. Smedes and J. Klanova, J. Appl. Polym. Sci., 2010, 116, 1803–1810 CAS.
- T. P. Rusina, F. Smedes, J. Klanova, K. Booij and I. Holoubek, Chemosphere, 2007, 68, 1344–1351 CrossRef CAS PubMed.
- S. C. George and S. Thomas, Prog. Polym. Sci., 2001, 26, 985–1017 CrossRef CAS.
- F. Rahman, K. H. Langford, M. D. Scrimshaw and J. N. Lester, Sci. Total Environ., 2001, 275, 1–17 CrossRef CAS PubMed.
- A. Reynier, P. Dole, S. Humbel and A. Feigenbaum, J. Appl. Polym. Sci., 2001, 82, 2422–2433 CrossRef CAS.
- I. J. Allan, C. Harman, A. Kringstad and E. Bratsberg, Chemosphere, 2010, 79, 470–475 CrossRef CAS PubMed.
- J. N. Huckins, J. D. Petty and K. Booij, Monitors of organic chemicals in the environment: semipermeable membrane devices, Springer, 2006 Search PubMed.
- K. Booij, F. Smedes and E. M. van Weerlee, Chemosphere, 2002, 46, 1157–1161 CrossRef CAS PubMed.
- J. Crank, The mathematics of diffusion, 1975 Search PubMed.
- A. Baner, R. Franz and O. Piringer, in Food packaging and preservation, Springer, 1994, pp. 23–47 Search PubMed.
- I. Helmroth, M. Dekker and T. Hankemeier, J. Appl. Polym. Sci., 2003, 90, 1609–1617 CrossRef CAS.
- R. P. Schwarzenbach, P. M. Gschwend and D. M. Imboden, Environmental organic chemistry, John Wiley & Sons, 2005 Search PubMed.
- F. Smedes, R. W. Geertsma, T. V. D. Zande and K. Booij, Environ. Sci. Technol., 2009, 43, 7047–7054 CrossRef CAS PubMed.
- R. Lohmann, J. Klanova, P. Kukucka, S. Yonis and K. Bollinger, Environ. Sci. Technol., 2013, 47, 13967–13975 CrossRef CAS PubMed.
- I. J. Allan, H. C. Nilsson, I. Tjensvoll, C. Bradshaw and K. Næs, Environ. Pollut., 2011, 159, 2393–2397 CrossRef CAS PubMed.
- H. Hirai, H. Takada, Y. Ogata, R. Yamashita, K. Mizukawa, M. Saha, C. Kwan, C. Moore, H. Gray and D. Laursen, Mar. Pollut. Bull., 2011, 62, 1683–1692 CrossRef CAS PubMed.
- A. A. Koelmans, E. Besseling, A. Wegner and E. M. Foekema, Environ. Sci. Technol., 2013, 47, 7812–7820 CrossRef CAS PubMed.
- A. A. Koelmans, E. Besseling and E. M. Foekema, Environ. Pollut., 2014, 187, 49–54 CrossRef CAS PubMed.
- K. Tanaka, H. Takada, R. Yamashita, K. Mizukawa, M.-A. Fukuwaka and Y. Watanuki, Environ. Sci. Technol., 2015, 49, 11799–11807 CrossRef CAS PubMed.
- E. Braekevelt, S. A. Tittlemier and G. T. Tomy, Chemosphere, 2003, 51, 563–567 CrossRef CAS PubMed.
| This journal is © The Royal Society of Chemistry 2016 |