Open Access Article
Open Access ArticleThe potential for microfluidics in electrochemical energy systems†
M. A.
Modestino
*a,
D.
Fernandez Rivas
 *b,
S. M. H.
Hashemi
a,
J. G. E.
Gardeniers
b and
D.
Psaltis
a
*b,
S. M. H.
Hashemi
a,
J. G. E.
Gardeniers
b and
D.
Psaltis
a
aSchool of Engineering, École Polytechnique Fédéral de Lausanne (EPFL), Station 17, 1015, Lausanne, Switzerland. E-mail: miguel.modestino@epfl.ch; Tel: +41 21 69 33446
bMesoscale Chemical Systems Group, MESA+ Institue for Nanotechnology, University of Twente, Enschede, The Netherlands. E-mail: d.fernandezrivas@utwente.nl; Tel: +31 53 489 3531
First published on 14th September 2016
Abstract
Flow based electrochemical energy conversion devices have the potential to become a prominent energy storage technology in a world driven by renewable energy sources. The optimal design of these devices depends strongly on the tradeoffs between the losses associated with multiple transport processes: convection and diffusion of reactants and products, migration of ionic species, and electrical charge transport. In this article we provide a balanced assessment of the compromise between these losses and demonstrate that for a broad range of electrochemical reactors, the use of microfluidics can enhance the energy conversion efficiency. Moreover, we propose proven scale-up strategies of microelectrochemical reactors which could pave the way to the large scale implementation of energy microfluidic systems.
Broader contextThe transition to a world driven by clean and renewable energy sources would rely on our ability to develop and implement at large scale energy storage technologies. To this end, high efficiency electrochemical energy conversion devices will play a key role as they have the potential to buffer the fluctuation inherent to renewable energy generation from solar and wind resources. The performance of these devices depends on the balance of complex processes that range from the atomic scale all the way up to the macroscale. While molecular processes drive the electrochemical transformations that determine the energy storage potential of the devices, transport phenomena are responsible for the limitations that prevent devices to operate at the maximum possible efficiencies. Therefore, electrochemical cells and reactors need to be designed in suitable dimensions to facilitate the transport of reactants, products and charged intermediates to and from the electrochemical reaction sites. In this article, we explore a generalized flow-based electrochemical device to demonstrate that optimal performances can be achieved if cells are designed in the microscale. Then we discuss the potential to scale up these microfluidic units so that large scale energy applications can be tackled. By doing so we hope to spur discussion in the scientific community towards reactor design routes to optimize energy conversion devices. |
1. Introduction
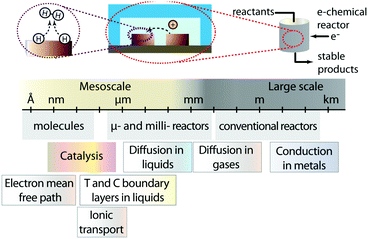
The ever-increasing drive towards the implementation of clean energy technologies and processes has propelled a strong interest towards the development of deployable energy conversion devices.1 These devices need to capture energy from renewable sources such as wind and sunlight, and convert it into usable and preferably storable forms. Historically, our society has learned that economies of scale drive energy technologies towards large dimensions: big ships for transportation and long pipelines to pump oil from reservoirs to large refineries, massive hydroelectrical dams and large nuclear power plants. In this line of thought one tends to forget that many important phenomena related to energy and mass transfer occur at very small scales. Furthermore, often the concept of scale gets confused with scalability. These considerations can result in the premature dismissal of promising energy technologies with small operating cells that may be intrinsically scalable. State-of-the-art electrochemical energy conversion devices (e.g. batteries, fuel cells, electrolyzers, flow batteries, among others) fall into this category; small operating units that can be parallelized to reach power conversion at the megawatt scale. The small size of the units encountered in these systems is inherent of the multiple mesoscale processes (from nanometers to hundreds of micrometers) that occur within them: redox reactions, transport of charge carriers to electrodes, and mass transport of ions, reactants and products to and from reaction sites (Fig. 1).2Within this opinion article, we intend to provide a fair, yet not exhaustive assessment of small technologies and their potentials to impact big energy applications. Specifically, we will focus on microfluidic electrochemical energy conversion devices, and identify the conditions under which they can be implemented in a scalable way. While scaling traditional microfluidic devices is challenging, we will point out reactor architectures that are different than lab scale microfluidic chips but can still harness the transport phenomena advantages of microfluidic regimes. Additionally, we identify opportunities where microsystems can be implemented at earlier stages for smaller and specialized energy applications.
2. Why microsystems for electrochemical energy conversion?
Our reader might ask: is there really “space” for “small” technologies in the energy challenges faced by our society? What do microsystems have to offer that large-scale technologies have not already provided? We hope that at the end of this article our answers to these questions become evident, and we inspire readers to envision new ways in which devices with microstructures can be implemented, or can be used to improve the efficiency, and the potential economic viability of energy conversion devices. For consistency, this article will refer to microsystems as devices with at least one characteristic dimension in the micrometer scale. These devices could either operate in a continuous fluid flow regime (microfluidics), such as in the case of electrolyzers, fuel cells and flow batteries, or in a static regime such as batteries or supercapacitors.The most significant consequence of going micro is the fact that by decreasing a characteristic length L (e.g. channel width, distance between electrodes, etc.), the concentration, temperature or other gradients are increased. Fluid flow in microchannels usually falls within a laminar regime that provides greater control over the flow. Additionally, short radial diffusion times result in a narrow residence-time distribution as well as an enhancement in heat and mass transfer. Moreover, microdevices have large surface-to-volume ratio (m2 m−3), which makes them particularly interesting for processes dictated by surface phenomena.3 These features allow the systems to reach thermal or surface reaction equilibrium much faster due to an increased mass and heat flux (over a given area L2). Although the enhanced heat transfer of microfluidic reactors can accelerate the transformations that occur inside the device, it can also result in larger heat losses to the external environment. This can be used to the advantage of energy conversion devices that require active cooling, but can be detrimental to other systems that require additional energy inputs to operate at elevated temperatures (e.g. solid oxide fuel cells).
Many groups have reported on the uses of microfluidic reactor technology for chemical synthesis in academic research settings, and recently it has become more prominent in industrial processes.4,5 Life-cycle analysis has hinted to significant ecological advantages of microreactors when compared to their macro-scale counterparts. The bulk of the interest in microfluidic systems has been centred on the production of high-value chemicals in the pharmaceutical and fine chemistry industry. Only until recently, researchers have started exploring the space for microfluidic technologies in the energy field because of their potential to improve the conversion efficiency of devices, to better understand energy conversion processes and be implemented in niche applications that require energy systems with small footprints.6
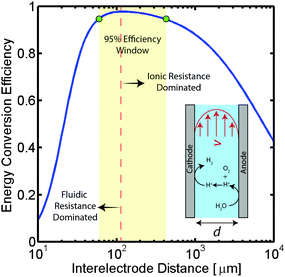
To better demonstrate the power of scalable microsystems in electrochemical energy conversion, we will introduce a simple model electrosynthetic device as an example of a prototypical electrochemical energy conversion device (Fig. 2). This model consists of a set of infinite parallel plate electrodes separated by a distance, d. In between the electrodes, a liquid electrolyte flows with a given areal flow rate, Q. An electrical potential is applied between the two infinite, parallel plates so that an electrochemical reaction can take place at the surface of the electrodes at a rate imposed by a constant current density, j. The thermodynamic equilibrium potential for the reaction is given by E0, and is imposed by the nature of the chemical transformation taking place. For simplicity, we will assume a fully developed (parabolic) flow of a Newtonian electrolytic fluid between the electrodes, a uniform electrolyte conductivity, σ, across the channel, no mass transport limitations at the surface of the electrodes, and that the volume fraction of products in the electrolyte is negligible. Within these conditions, the only two factors that depend on d and affect the energy conversion efficiency are the ionic and fluidic resistances. The power loss arising from ionic resistance, Pion, over a reactor length, L, is given by,
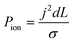 | (1) |
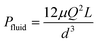 | (2) |
These losses can be compared with the chemical energy stored in the products, Pstorage,
| Pstorage = jE0 | (3) |
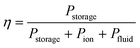 | (4) |
As demonstrated in Fig. 2 for a water splitting device, the maximum energy conversion efficiency is achieved when the separation between electrodes is in the microscale (120 μm in this example at a current density of 104 A m−2). Moreover, for this example, an algebraic expression can be obtained that defines the optimal electrode separation for maximum energy conversion efficiency,
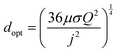 | (5) |
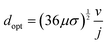 | (6) |
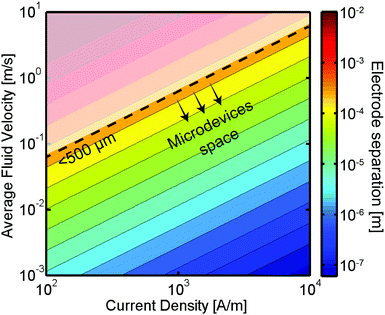
In addition to the efficiency improvements demonstrated above, microfluidic technologies offer several other benefits. Microfluidic energy conversion devices could lead to increases in power density thanks to the low amount of electrolytes required. Also, fluidic forces could be used to precisely direct species to the desired device locations, reducing losses due to mixing of reactants or products. Motivated by these performance gains, several groups have already started to exploit the multiple advantages that microsystems bring to the electrochemical energy conversion field. Below, we will briefly review the state of the art in electrochemical energy conversion microsystems and compare their performance with their large scale, conventional counterparts.
3. State-of-the-art electrochemical energy conversion microsystems
Microsystems have already found applications in a broad range of electrochemical energy conversion devices. Most notably, batteries are manufactured with an interelectrode spacing in the microscale. The small separation is desirable in order to avoid unwanted Ohmic losses in the electrolyte and achieve a high energy density while still maintaining the electrodes separated avoiding short-circuiting the device. Moreover, the miniaturization of batteries driven by the extensive use of laptops, cell phones and other portable consumer electronics has resulted in highly efficient and energy dense systems. Miniaturized flow-based electrochemical systems such as electrolyzers, fuel cells or flow batteries could also be implemented into electronic devices and potentially reach energy densities that surpass those of batteries. Furthermore, this class of energy devices could enjoy improvements in their efficiency, energy density, and materials utilization if they were designed with microscale features to facilitate the transport of reactants, products and ionic charge carriers. Additionally, the high surface area to volume ratio of microreactors is particularly useful in electrochemical systems, as the chemical transformations take place only at the surface of electrodes. In order to provide a broader context on flow-based electrochemical energy conversion microsystems the subsections below present an overview of the main advances and state of the art in the field of microfluidic fuel cells, flow batteries and electrolyzers.Fuel cells
Among the three device categories cited above, microscale fuel cells are the most studied and well-established systems. Their development has been particularly motivated by the need for high energy density power sources in portable devices. Integration of small hydrogen (H2) fuel cells can address this issue due to the large mass energy density of H2.8 Additionally, fuel cells can be charged quickly, typically by changing a hydrogen cartridge or refilling the reservoir.The two main types of fuel cells that have been implemented in the microfluidic regime are solid oxide fuel cells (SOFCs) that work at high temperatures, typically in the order of 100's °C, and proton exchange membrane fuel cells (PEMFCs) which generally operate close to room temperature. The maximal theoretical efficiency of SOFCs is a strong function of their operating temperatures. For a SOFC using CO as a fuel, the theoretical energy conversion efficiency is 63% at 900 °C and 81% at 350 °C when entropic losses are accounted.9 Unfortunately, operating at high temperatures requires long start-up and shutdown cycles, limiting their usability for portable applications. The maximal theoretical efficiency of PEMFCs accounting for entropic losses is 83% at 25 °C. However the state of the art PEMFCs operate at efficiencies in the order of 60%. It is interesting to note that in traditional, large scale PEMFCs, the dimensions of the channels in the flow plates are typically manufactured in the submillimeter scale10 to mediate mass transport limitations. Furthermore, the thickness of the polymeric electrolyte membrane tends to be in the order of tens of micrometers, since a small Ohmic drop is desirable between the two electrodes. Decreasing the thickness of flow plates is also important since these components account for more than 80% of the total weight and 30% of the total cost of fuel cells.11
The most prominent reactants in conventional PEMFCs are hydrogen and oxygen. For portable applications, hydrogen needs to be compressed to high pressures or stored in the structure of solid materials with higher volumetric energy density such as metal hydrides.12 The challenges related to the storage of H2 result in additional costs and design complexity, posing significant obstacles for the implementation of H2 in portable devices. Due to this fact, parallel research lines have evolved to develop fuel cells that operate with alternative fuels. To this end, alternative liquid fuels have been implemented including: methanol, ethanol, 2-propanol, ethylene glycol (EG), dimethoxymethane (DMM), formic acid, hydrazine, hydrogen peroxide, and dimethyl ether (DME).13 Liquid oxidants such as hydrogen peroxide and nitric acid have also been used as alternatives to oxygen in the cathodic reaction. Another interesting example of micro fuel cells are laminar flow based systems that operate without membranes. These devices take advantage of the slow diffusion-dominated mixing between fuel and oxidant streams to minimize reactant crossover. A key requirement for these systems is to keep the residence time of the fluids inside the channels small – high Péclet numbers – so that diffusion is minimal compared to convective transport. This can simplify the device design, reduce the cost of materials and fabrication, and the weight of the device. On top of that, an improved performance is possible due to higher conductivity in liquid electrolytes compared to polymer membranes. Higher power densities are achieved if the flowrates of fuel and oxidant streams are increased. Under fast flow rates, mass-transport of the fuel is enhanced but at the same time a large fractions of the fuel can exit the device without reacting at the electrode. To circumvent these fuel utilization limitations, clever device architectures can be implemented to increase the active contact area between the electrodes and the reactants,14 as well as engineered channel and electrode geometries that promote high fuel utilization, reaching levels above 90%, and deliver high power densities.15 Moreover, elimination of the polymer electrolyte relaxes the challenges of using alternative chemistries in PEMFCs such as the high permeability of methanol and other liquid fuels in Nafion.16 These types of micro fuel cells have been reviewed extensively15,17–20 and some examples achieve power densities in the same order of magnitude as in state-of-the-art macroscale PEMFCs.21,22Table 1 highlights some examples of micro fuel cell systems and provides information regarding the design characteristics, maximum power density, as well as oxidant and fuel used in each study.
| Ref. | Fuel | Oxidant | Electrolyte | Interelectrode distance [μm] | Design characteristics | Peak power density [mW cm−2] | Maximum current density [mA cm−2] | Maximum open circuit voltage [V] |
|---|---|---|---|---|---|---|---|---|
| R. C. Sekol et al.47 | H2 | O2 | Nafion 212 | 50.8 | Merging flow field and current collector functionalities by micro/nanostructuring glassy metal | 1080 at 0.25 V | 294 | 0.94 |
| S. J. Lee et al.48 | H2 | O2 | Nafion 115 | 125 | Planar stack with miniaturized fuel-cell units interconnected in series. | 42 (4 cells in series) | 210 (4 cells in series) | 3.1 (4 cells in series) |
| S. A. Mousavi Shaegh et al.49 | H2O2 | H2O2 | 0.1 M HCl | — | H2O2 working as both fuel and oxidant over selective electrocatalysts | 1.55 at 0.3 V | 10 | 0.6 |
| N. Da Mota et al.22 | 0.15 M NaBH4 in 3 M NaOH | 0.5 M H8N8CeO18 in 1 M HNO3 | 3 M NaOH and 1 M HNO3 separated by a porous barrier | 410 | Staggered-herringbone structures on the electrodes to induce oxidant/fuel mixing in cathodic/anodic reaction and alleviate mass transport limitation | 270 at 0.65 V | 480 | 2.2 |
| A. S. Hollinger et al.50 | 1 M methanol | O2 | 1 M H2SO4 | 306 | Introduction of a nanoporous separator to the interface of fuel and electrolyte in order to limit the fuel diffusion area and increase the Pmax by 45%. | 70 at 0.2 V (80 °C) | 660 (80 °C) | 0.65 (80 °C) |
| R. S. Jayashree et al.51 | 1 M HCOOH | O2 | 0.5 M H2SO4 | 1000–2000 | Hydrodynamic focusing of the fuel to a thin stream on anode and reducing is crossover to the cathode while increasing fuel utilization | 55 at 0.3 V | 320 | 0.86 |
| J. An et al.52 | H2 | Air | Yttria-stabilized zirconia (YSZ) | 0.06 | 3D nanostructuring of an ultrathin YSZ electrolyte and integration of highly active yttria doped ceria (YDC) at the cathode side to increase active area while decreasing ohmic and activation losses | 1300 at 0.32 V (450 °C) | 7200 (450 °C) | 1.08 (450 °C) |
| V. Galvan et al.26 | 5 M HCOOK | 30% H2O2 | 5 M HCOOK and 30% H2O2 | — | Capillary flow of fuel and oxidant through paper makes the fabrication cheap and easy. | 2.53 | 11.5 | 1.1 |
| L. Li et al.28 | Thin methylene blue solution | O2 | 0.5 M NaOH | 200 | Photo-oxidation of organic pollutants and generating power while treating the water. | 0.45 | 1.05 | 1.04 |
Lastly, it must be noted that new classes of micro fuel cells are emerging where the unique features of microfluidics enables their realization. Two examples will be mentioned here: paper based microfluidic fuel cells and optofluidic fuel cells.
The paper based microfluidic FCs aim at developing inexpensive and disposable power sources. They take advantage of the capillary flows in flow plates made of paper to bring in the fuel and oxidant over the surface of electrodes from dedicated reservoirs. This technique eliminates the need for peripheral equipment such as pumps and can result in significant cost reductions thanks to the simplicity of the fabrication methods and the use of inexpensive materials.23–25 Some of these devices are able to deliver energy for long periods of time and, therefore, are appropriate for low power consumer electronics.26,27
Optofluidics is a field that integrates microfluidics with optics and that has found potential applications in the energy domain.4 Recently, optofluidic approaches have been implemented to generate electricity through the photocatalytic oxidation of organic pollutants in water.28,29 The high surface to volume ratio at microscales and the possibility of fabricating transparent microfluidic devices together with controlling light/fluid interactions makes optofluidics a powerful tool for solar-based energy conversion.
Flow batteries
Flow batteries are rechargeable fuel cells which operate by placing two redox active chemical species dissolved in two liquid streams separated by an electrolyte (usually a membrane). These chemical species can be reduced or oxidized during charging or discharging cycles. Fuels and oxidant liquids are flown into the device from two separate reservoirs during discharge to generate electricity, and by reversing the process the oxidized fuel and reduced oxidant can be restored to their initial state during charge cycles. Only a few examples of micro flow batteries have been reported, and they predominantly focus on the elimination of ion-conducting membranes by implementing the aforementioned laminar flow technique. Notable approaches involve the co-laminar flow of solutions containing vanadium redox couples through porous electrodes, with demonstrated power densities as high as 330 mW cm−2.30,31 More recently, a hydrogen bromine laminar flow battery was demonstrated.32 This device achieved a remarkable power density of 795 mW cm−2, approaching the performance of state-of-the-art H2 fuel cells.Electrolyzers
Unlike fuel cells, literature reports on micro electrolyzers are limited, presumably due to the low throughput of such devices, which makes them less attractive for commercial utilization. Despite the fact that microelectrolyzers will find limited usability in large-scale hydrogen production, applications that require lower production rates are often overlooked. A relevant example is the implementation of water splitting units in solar fuel devices, where typical current densities in the light-absorber are in the order of 10 mA cm−2 whereas electrolyzers' catalyst layers can support current densities up to several A cm−2.2,33,34 This implies that a relatively large photovoltaic device can be combined with miniaturized electrolyzers for optimum cost and performance.35 Additionally, controlling transport phenomena at the microscale can bring efficiency improvements, eventually leading to benefits for large-scale electrolyzers.The first microfluidic electrolyzer was demonstrated in 2013 providing a current density of over 100 mA cm−2 at 2.5 V.36 More recently, electrolyzers that can operate under vapour-feeds37 and without membranes38 have been enabled thanks to the control of transport processes in the microscale. The vapour fed device takes advantage of small diffusion and ionic path lengths in microfluidics to split the water content of ambient air. In the membrane-less device, the gas separation task is achieved by exploiting fluidic forces to guide the product gases to independent collection ports. Furthermore, by eliminating the need of a membrane, the Ohmic resistance in the electrolyte is reduced and current densities as high as 300 mA cm−2 at 2.5 V can be achieved. Recent work in this domain also includes the analysis39 and implementation40 of a micro electrolyzer integrated with solar cells. In this system, synergistic effects can be achieved by cooling the photovoltaic components while at the same time enhancing the efficiency of the electrolysis process.33,41 A summary of the characteristics of previously reported microelectrolyzers is listed in Table 2. It is also worth noting that in addition to water electrolysis, there are several examples of microsystems that use alternative pathways for the generation of hydrogen. These include metal hydride microreactors42–44 and methanol steam reforming microreactors.45,46
| Ref. | Cathode | Anode | Electrolyte | Interelectrode distance [μm] | Design characteristics | Maximum current density [mA cm−2] |
|---|---|---|---|---|---|---|
| M. A. Modestino et al.36 | Pt | Pt | Nafion 117 and 0.5 M H2SO4 | 163.5 | In plane electrodes with Nafion membrane as the top wall of microchannels allowing for photoelectrodes integration | 175 at 2.5 V |
| S. M. H. Hashemi et al.38 | Pt or NiFe | Pt or NiFe | 1 M H2SO4 or 1 M K2CO3 or 1 M Na3PO4 buffer | 175 | Versatility in selection of electrolyte and catalysts due to the flow based gas separation mechanism | 300 at 2.5 V |
| M. A. Modestino et al.53 | Pt | Pt | Spin casted Nafion thin film | 150 | Vapor fed microelectrolyzer with double spiral microchannels for design simplicity | Less than 10 at 3 V |
| M. E. Oruc et al.34 | Pt | Pt | 0.5 M H2SO4 | — | Microelectrolyzer absorbing the heat from the attached PV and therefore increasing the overall efficiency of PVTE system | 10 at 1.82 V (80 °C) |
4. Scalability and manufacturability of energy microsystems
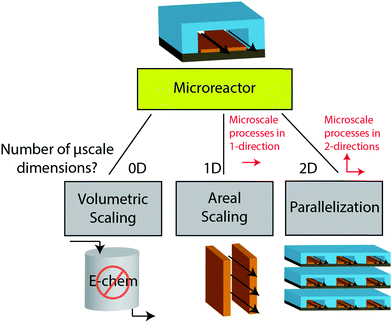
The previous sections described multiple advantages of flow-based energy microsystems, but their implementation into real-world application would ultimately depend on their scalability and our ability to manufacture them in cost-effective ways. In microsystems engineering, the most frequent way to scale the throughput is by internal numbering-up, which involves the incorporation of parallel arrangements of single microstructured units (e.g. channels, electrodes).54 In this way, the advantages achieved by microstructuring units can be maintained in higher throughput systems. It must be noted that numbering-up strategies are challenging and alternatives should be sought when possible. Parallelization of microdevices requires complex fluidic interconnections and manifolding. Also, if classical microfluidic chips are used as building blocks, the majority of the volume of the device would act as a dead volume and not participate in the chemical transformations of interest. This is in contrast with common approaches used for the scale-up of homogeneous chemical reactions that involve the volumetric scaling of reactors. In the case of electrochemical energy conversion devices, the scale-up strategy will depend on the number of processes that require transport length-scales in the micro domain. If all of the processes with a microscale dimensionality requirement occur in parallel directions, then the system can be scaled by increasing area. An areal scale-up strategy would involve the implementation of macroscopic plate electrodes separated by a micro scale distance. By doing so, classical manufacturing techniques could be implemented, simplifying the overall scale-up process. If at least two processes require transport path lengths in the microscale, and their directions are orthogonal, then the only option to scale-up the device throughput is to parallelize the units (numbering up). Fig. 4 shows a representation of the different scaling strategies described above. When determining the dimensionality of the transport process involved in energy conversion microsystems it is useful to define the characteristic path length for the species or charge carriers involved. In electrochemical devices, usually the transport processes that dominate the performance of the system are the transport of charge carriers – electrons, holes and ionic species – and the transport of neutral species – reactants and products. The characteristic length scale for transport of charged species, lion or le− for ions or electrons respectively, is determined by Ohms law,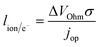 | (7) |
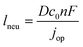 | (8) |
| Species | Characteristic conductivity (σ) | Current density (jop) | Length scale (le− or lion) |
|---|---|---|---|
| a The allowable voltage drop, ΔVOhm, is assumed to be 0.1 V. | |||
| Charged speciesa | |||
| Electrons in metallic electrodes | 105–107 S m−1 | Low (100–103 A m−2) | 10–104 m |
| High (104–105 A m−2) | 0.1–100 m | ||
| Ions in electrolytes | 0.1–10 S m−1 | Low (10–103 A m−2) | 10–104 μm |
| High (104–105 A m−2) | 0.1–100 μm | ||
| Species | Characteristic properties | Current density (jop) | Length scale (lneu) |
|---|---|---|---|
| Neutral species | |||
| Low solubility species |
c
0 ∼ 1 mol m−3
D ∼ 10−9 m2 s−1 |
Low (100–103 A m−2) | 0.1–1 μm |
| High (104–05 A m−2) | 1–10 nm | ||
| High solubility species |
c
0 ∼ 103 mol m−3
D ∼ 10−9 m2 s−1 |
Low (10–103 A m−2) | 100–103 μm |
| High (104–105 A m−2) | 1–10 μm | ||
Once a scale-up strategy has been identified, the next step is to assess the manufacturability of the scalable system. Areal scaling of electrochemical reactors is usually preferred whenever allowable. Under this strategy a large suite of common fabrication techniques can be implemented to achieve the desired structure. Classical machining can be used to manufacture parts where parallel planar electrodes are separated by 100's μm. Reactor manufacturing methods include laminate or sheet construction techniques which have been used extensively to perform gas–liquid reactions and processes with film plates,55e.g. methane steam reforming.56 This fabrication method offers flexibility in design and can accommodate multiple reactor units within a single component. Different layers of a laminate structure can be easily machined to define internal passages and channel structures. Also, as the limiting dimension in laminated reactors is defined by the thickness of the layers, interelectrode spacings in the microscale can be easily accessed. These fabrication techniques open the possibility for producing large throughput reactors at relatively low cost. Another successful scale-up example involves the redesign of a sonochemical microreactor for the controlled generation of chemically active bubbles. While the initial concept and proof-of-principle demonstrations were developed in a silicon-based device,57 large-scale reactors were redesigned using inexpensive polymeric materials in order to improve its commercialization potential.58
The use of inexpensive elastomers (e.g. PDMS) that boosted other microfluidics applications over the last decades cannot be directly used in the context of energy applications, unless new functionalized and resistant materials are integrated. Chemical compatibility and gas permeability of polymers are constraints for the long-term temperature and pressure cycling requirements of energy conversion devices. To that end, silicon and glass have suitable characteristics and have been exploited on energy related lab-on-a-chip applications where microfluidics have been proved to be powerful tools to gain important insights in the energy conversion processes present in large-scale reactors.6 Microreactors that require parallelization to achieve higher throughput face more difficult challenges for their fabrication. They also can present operational difficulties when the evolution of a different phase (e.g. solid or gas) occurs inside the microchannels (e.g. H2 and O2 evolved at the surface of electrodes). The presence of multiphase flows within reactors can cause blockage of fluidic channels, decrease in electrolyte conductivity, additional pressure drops, a reduction of the electrode active area, among other problems. Strategies to mitigate these issues will need to be incorporated in the reactor design phase. Parallelization strategies also require cost-intensive manufacturing techniques. Specifically, material costs tend to be low, yet the costs of the facilities where the fabrication takes place are high. For example, microreactors based on semiconductor technologies are processed only in cleanroom environments. Also, it is not straightforward to make arbitrary reactor shapes using classical Si processing techniques, and fabrication of early stage prototypes tend to be time-intensive. Alternatively, the recent advent of additive manufacturing (AM) technologies has resulted in a change in paradigm for the fabrication of customizable prototypes.59 The flexibility in materials used together with reduced time for developing functional prototypes, provides a powerful tool that can result in faster technical solutions not achievable with other fabrication techniques. The resolution of features achievable depends strongly on the specific material and technology used. Resolution in the order of 100's μm are commonly achieved.60 Sub-classification of 3D micro additive manufacturing has been proposed as scalable additive manufacturing, 3D direct writing, and hybrid processes; details can be found in recent literature with key processes and resolutions attainable.61–63
It is important to point out that in many flow-based electrochemical conversion devices, the capital cost of each device tends to be significantly lower than the cost of the fuel (in fuel cells) or electricity (in electrolyzers and flow batteries) required for their operation over their lifetime.35,64,65 Given this situation, the savings from efficiency improvements in microscale devices only need to outweigh the increased capital cost requirement.
5. Conclusions and perspective
Energy systems have stringent efficiency, scalability and cost-effectiveness requirements. As the world pressingly moves towards clean energy sources, the need to incorporate electrochemical energy conversion devices into the electricity grid will certainly increase, as well as the need to develop ever more efficient and cost-competitive systems that can reach large scale energy storage and production. This article aspires to provide a balanced analysis of the potential advantages of developing flow-based electrochemical energy conversion microdevices. We have explored three basic questions: (1) Can microsystems bring efficiency improvements? (2) Can they be scaled? And if so, (3) Can they be economically viable? The answer to the first question is most definitively positive. By developing electrochemical reactors in the microscale, the transport path lengths can be reduced so that ionic transport losses and mass transport limitations for reactants and products can be minimized. On the other hand, by reducing the size of channels, the fluidic resistance of devices increases, resulting in additional energy losses. Earlier in this article we demonstrated that the trade-off between these two effects points towards a maximum efficiency of devices when their interelectrode distance is between a few 10's to a few 100's of μm. These efficiency advantages have been an important motivation for the demonstration of the microfluidic energy conversion devices described in Section 3. This brings us to the second question: in order to harvest the advantages of microsystems we must be able to scale them up. Section 4 described the scale-up strategy based on the dimensionality of the limiting transport processes involved in the device. It is clear that within a large range of operating conditions of interest, both the transport of ions and reactants/products can become limiting if their transport path lengths are not restricted to the micro-domain. If the direction of these two transport processes can be accommodated in the axis normal to the plane of the electrodes, then devices could be easily scaled in a two dimensional way (i.e. large planar electrodes can be placed parallel to each other and be separated by an electrolyte flow). Under these conditions, inexpensive manufacturing processes can be implemented and have the potential to lead to cost-effective large-scale microfluidic reactors. If parallelization of microfluidic channels is required, the fabrication methods are expected to be more complex and the reactors' economic viability limited. To that end, new fabrication techniques such as high-resolution additive manufacturing have the potential to change this paradigm and lead to scalable and cost-effective energy microsystems.Microsystems will certainly continue to occupy an important space in the energy field in years to come. Energy storage and conversion devices will become more prominent as renewable energy technologies continue to penetrate the energy markets. To that end, achieving higher efficiency in energy conversion systems will become critical, and the advantages provided by microfluidic energy devices will play a significant role. At the same time, while these advantages are demonstrated at the laboratory scale, industry will be encouraged to incorporate and develop innovative manufacturing techniques to harvest the improvements that microfluidic energy technologies can bring.
Acknowledgements
M. A. M., S. M. H. H. and D. P. acknowledge the support from the Swiss National Science Foundation: Nano-Tera project 20NA21_145936 “Solar Hydrogen Integrated Nano Electrolyzer: SHINE”. D. F. R. and J. G. E. G. acknowledge the support from the Dutch national research programme on BioSolar Cells, co-financed by the Dutch Ministry of Economic Affairs.Notes and references
- S. Chu and A. Majumdar, Nature, 2012, 488, 294–303 CrossRef CAS PubMed.
- M. A. Modestino, S. M. H. Hashemi and S. Haussener, Energy Environ. Sci., 2016, 9, 1533–1551 CAS.
- O. Brand, G. K. Fedder, C. Hierold, J. G. Korvink, O. Tabata and N. Kockmann, Micro process engineering, John Wiley & Sons, 2013 Search PubMed.
- D. Erickson, D. Sinton and D. Psaltis, Nat. Photonics, 2011, 5, 583–590 CrossRef CAS.
- K. S. Elvira, X. C. i Solvas and R. C. Wootton, Nat. Chem., 2013, 5, 905–915 CrossRef CAS PubMed.
- D. Sinton, Lab Chip, 2014, 14, 3127–3134 RSC.
- J. Newman, J. Electrochem. Soc., 2013, 160, F309–F311 CrossRef CAS.
- P. P. Edwards, V. L. Kuznetsov, W. I. F. David and N. P. Brandon, Energy Policy, 2008, 36, 4356–4362 CrossRef.
- E. D. Wachsman and K. T. Lee, Science, 2011, 334, 935–939 CrossRef CAS PubMed.
- L. F. Peng, X. M. Lai, P. Y. Yi, J. M. Mai and J. Ni, J. Fuel Cell Sci. Technol., 2011, 8, 011002 CrossRef.
- X. G. Li and M. Sabir, Int. J. Hydrogen Energy, 2005, 30, 359–371 CrossRef CAS.
- M. B. Ley, L. H. Jepsen, Y.-S. Lee, Y. W. Cho, J. M. Bellosta von Colbe, M. Dornheim, M. Rokni, J. O. Jensen, M. Sloth, Y. Filinchuk, J. E. Jørgensen, F. Besenbacher and T. R. Jensen, Mater. Today, 2014, 17, 122–128 CrossRef CAS.
- W. Qian, D. P. Wilkinson, J. Shen, H. Wang and J. Zhang, J. Power Sources, 2006, 154, 202–213 CrossRef CAS.
- A. Bazylak, D. Sinton and N. Djilali, J. Power Sources, 2005, 143, 57–66 CrossRef CAS.
- E. Kjeang, N. Djilali and D. Sinton, J. Power Sources, 2009, 186, 353–369 CrossRef CAS.
- J. D. Morse, Int. J. Energy Res., 2007, 31, 576–602 CrossRef CAS.
- S. A. M. Shaegh, N. T. Nguyen and S. H. Chan, Int. J. Hydrogen Energy, 2011, 36, 5675–5694 CrossRef.
- M. N. Nasharudin, S. K. Kamarudin, U. A. Hasran and M. S. Masdar, Int. J. Hydrogen Energy, 2014, 39, 1039–1055 CrossRef CAS.
- M. A. Goulet and E. Kjeang, J. Power Sources, 2014, 260, 186–196 CrossRef CAS.
- M. Safdar, J. Janis and S. Sanchez, Lab Chip, 2016, 16, 2754–2758 RSC.
- R. S. Jayashree, M. Mitchell, D. Natarajan, L. J. Markoski and P. J. A. Kenis, Langmuir, 2007, 23, 6871–6874 CrossRef CAS PubMed.
- N. D. Mota, D. A. Finkelstein, J. D. Kirtland, C. A. Rodriguez, A. D. Stroock and H. D. Abruña, J. Am. Chem. Soc., 2012, 134, 6076–6079 CrossRef PubMed.
- J. P. Esquivel, F. J. Del Campo, J. L. G. de la Fuente, S. Rojas and N. Sabate, Energy Environ. Sci., 2014, 7, 1744–1749 CAS.
- K. H. Purohit, S. Emrani, S. Rodriguez, S. S. Liaw, L. Pham, V. Galvan, K. Domalaon, F. A. Gomez and J. L. Haan, J. Power Sources, 2016, 318, 163–169 CrossRef CAS.
- T. S. Copenhaver, K. H. Purohit, K. Domalaon, L. Pham, B. J. Burgess, N. Manorothkul, V. Galvan, S. Sotez, F. A. Gomez and J. L. Haan, Electrophoresis, 2015, 36, 1825–1829 CrossRef CAS PubMed.
- V. Galvan, K. Domalaon, C. Tang, S. Sotez, A. Mendez, M. Jalali-Heravi, K. Purohit, L. Pham, J. Haan and F. A. Gomez, Electrophoresis, 2016, 37, 504–510 CrossRef CAS PubMed.
- M. J. González-Guerrero, F. J. del Campo, J. P. Esquivel, F. Giroud, S. D. Minteer and N. Sabaté, J. Power Sources, 2016, 326, 410–416 CrossRef.
- L. Li, G. Y. Wang, R. Chen, X. Zhu, H. Wang, Q. Liao and Y. X. Yu, Lab Chip, 2014, 14, 3368–3375 RSC.
- H. Zhang, H. Z. Wang, M. K. H. Leung, H. Xu, L. Zhang and J. Xuan, Chem. Eng. J., 2016, 283, 1455–1464 CrossRef CAS.
- J. W. Lee, M. A. Goulet and E. Kjeang, Lab Chip, 2013, 13, 2504–2507 RSC.
- E. Kjeang, R. Michel, D. A. Harrington, N. Djilali and D. Sinton, J. Am. Chem. Soc., 2008, 130, 4000–4006 CrossRef CAS PubMed.
- W. A. Braff, M. Z. Bazant and C. R. Buie, Nat. Commun., 2013, 4, 2346 Search PubMed.
- M. A. Modestino and S. Haussener, Annu. Rev. Chem. Biomol. Eng., 2015, 6, 13–34 CrossRef CAS PubMed.
- M. E. Oruc, A. V. Desai, R. G. Nuzzo and P. J. Kenis, J. Power Sources, 2016, 307, 122–128 CrossRef CAS.
- C. A. Rodriguez, M. A. Modestino, D. Psaltis and C. Moser, Energy Environ. Sci., 2014, 7, 3828–3835 CAS.
- M. A. Modestino, C. A. Diaz-Botia, S. Haussener, R. Gomez-Sjoberg, J. W. Ager and R. A. Segalman, Phys. Chem. Chem. Phys., 2013, 15, 7050–7054 RSC.
- M. A. Modestino, M. Dumortier, S. M. H. Hashemi, S. Haussener, C. Moser and D. Psaltis, Lab Chip, 2015, 15, 2287–2296 RSC.
- S. M. H. Hashemi, M. A. Modestino and D. Psaltis, Energy Environ. Sci., 2015, 8, 2003–2009 Search PubMed.
- M. E. Oruc, A. V. Desai, P. J. A. Kenis and R. G. Nuzzo, Appl. Energy, 2016, 164, 294–302 CrossRef CAS.
- M. E. Oruc, A. V. Desai, R. G. Nuzzo and P. J. A. Kenis, J. Power Sources, 2016, 307, 122–128 CrossRef CAS.
- S. Tembhurne, M. Dumortier and S. Haussener, 15th International Heat Transfer Conference, Kyoto, Japan, 2014.
- D. Gervasio, S. Tasic and F. Zenhausern, J. Power Sources, 2005, 149, 15–21 CrossRef CAS.
- S. Moghaddam, E. Pengwang, R. I. Masel and M. A. Shannon, J. Power Sources, 2008, 185, 445–450 CrossRef CAS.
- L. Zhu, K. Y. Lin, R. D. Morgan, V. V. Swaminathan, H. S. Kim, B. Gurau, D. Kim, B. Bae, R. I. Masel and M. A. Shannon, J. Power Sources, 2008, 185, 1305–1310 CrossRef CAS.
- P. Reuse, A. Renken, K. Haas-Santo, O. Görke and K. Schubert, Chem. Eng. J., 2004, 101, 133–141 CrossRef CAS.
- A. V. Pattekar and M. V. Kothare, J. Microelectromech. Syst., 2004, 13, 7–18 CrossRef CAS.
- R. C. Sekol, G. Kumar, M. Carmo, F. Gittleson, N. Hardesty-Dyck, S. Mukherjee, J. Schroers and A. D. Taylor, Small, 2013, 9, 2081–2085 CrossRef CAS PubMed.
- S. J. Lee, A. Chang-Chien, S. W. Cha, R. O'Hayre, Y. I. Park, Y. Saito and F. B. Prinz, J. Power Sources, 2002, 112, 410–418 CrossRef CAS.
- S. A. M. Shaegh, N. T. Nguyen, S. M. M. Ehteshami and S. H. Chan, Energy Environ. Sci., 2012, 5, 8225–8228 Search PubMed.
- A. S. Hollinger, R. J. Maloney, R. S. Jayashree, D. Natarajan, L. J. Markoski and P. J. A. Kenis, J. Power Sources, 2010, 195, 3523–3528 CrossRef CAS.
- R. S. Jayashree, L. Gancs, E. R. Choban, A. Primak, D. Natarajan, L. J. Markoski and P. J. A. Kenis, J. Am. Chem. Soc., 2005, 127, 16758–16759 CrossRef CAS PubMed.
- J. An, Y. B. Kim, J. Park, T. M. Gur and F. B. Prinz, Nano Lett., 2013, 13, 4551–4555 CrossRef CAS PubMed.
- M. A. Modestino, M. Dumortier, M. Hashemi, S. Haussener, C. Moser and D. Psaltis, Lab Chip, 2015, 15, 2287–2296 RSC.
- T. Dietrich, Microchemical engineering in practice, John Wiley & Sons, 2011 Search PubMed.
- A. Lawal and D. Qian, US Pat., US 2008181833 A1, 2008 Search PubMed.
- W. D. Bennett, P. M. Martin, D. W. Matson, G. L. Roberts, D. C. Stewart, A. Y. Tonkovich, J. L. Zilka, S. C. Schmitt and T. M. Werner, US Pat., US6490812 B1, 2002 Search PubMed.
- D. Fernandez Rivas, A. Prosperetti, A. G. Zijlstra, D. Lohse and H. J. G. E. Gardeniers, Angew. Chem., Int. Ed., 2010, 49, 9699–9701 CrossRef CAS PubMed.
- B. Verhaagen, Y. Liu, A. G. Pérez, E. Castro-Hernandez and D. Fernandez Rivas, ChemistrySelect, 2016, 1, 136–139 CrossRef.
- G. Chisholm, P. J. Kitson, N. D. Kirkaldy, L. G. Bloor and L. Cronin, Energy Environ. Sci., 2014, 7, 3026–3032 CAS.
- M. Vaezi, H. Seitz and S. Yang, Int. J. Adv. Des. Manuf. Technol., 2013, 67, 1721–1754 CrossRef.
- A. K. Au, N. Bhattacharjee, L. F. Horowitz, T. C. Chang and A. Folch, Lab Chip, 2015, 15, 1934–1941 RSC.
- N. Bhattacharjee, A. Urrios, S. Kang and A. Folch, Lab Chip, 2016, 16, 1720–1742 RSC.
- A. K. Au, W. Huynh, L. F. Horowitz and A. Folch, Angew. Chem., Int. Ed., 2016, 55, 3862–3881 CrossRef CAS PubMed.
- Independent Review Panel, Current (2009) State-of-the-Art Hydrogen Production Cost Estimate Using Water Electrolysis, 2009.
- B. D. James and J. A. Kalinoski, Mass production cost estimation for direct H2 PEM fuel cell systems for automotive applications, 2008 Search PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: Flow diagram describing the scaling strategy for microfluidic energy systems. See DOI: 10.1039/c6ee01884j |
| This journal is © The Royal Society of Chemistry 2016 |