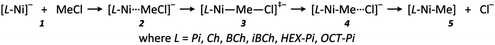Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Dehalogenation of chloroalkanes by nickel(I) porphyrin derivatives, a computational study†
L.
Szatkowski
ab and
M. B.
Hall
a
aDepartment of Chemistry, Texas A&M University, College Station, Texas 77843, USA. E-mail: hall@science.tamu.edu
bDepartment of Chemistry and Biochemistry, University of Arizona, 1306 East University Boulevard, Tucson, Arizona 85721, USA
First published on 20th September 2016
Abstract
The nickel(I) octaethylisobacteriochlorin anion ([OEiBCh-Ni(I)]−) is commonly used as a synthetic model of cofactor F430 from Methyl-Coenzyme M Reductase. In this regard, experimental studies show that [OEiBCh-Ni(I)]− can catalyze dehalogenation of aliphatic halides in DMF solution by a highly efficient SN2 reaction. To better understand this process, we constructed theoretical models of the dehalogenation of chloromethane by a simple nickel(I) isobacteriochlorin anion and compared its reactivity with that of similar Ni(I) complexes with other porphyrin-derived ligands: porphyrin, chlorin, bactreriochlorin, hexahydroporphyrin and octahydroporphyrin. Our calculations predict that all of the porphyrin derivative's model reactions proceed through low-spin complexes. Relative to the energy of the separate reactants the theoretical activation energies (free-energy barriers with solvation corrections) for the dehalogenation of chloromethane are similar for all of the porphyrin derivatives and range for the different functionals from 10–15 kcal mol−1 for B3LYP to 5–10 kcal mol−1 for M06-L and to 13–18 kcal mol−1 for ωB97X-D. The relative free energies of the products of the dehalogenation step, L-Ni–Me adducts, have a range from −5 to −40 kcal mol−1 for all functionals; generally becoming more negative with increasing saturation of the porphyrin ligand. Moreover, no significant differences in the theoretical chlorine kinetic isotope effect were discernable with change of porphyrin ligand.
Introduction
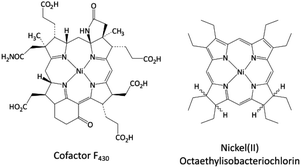
Cofactor F430![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 is a nickel(II) hydrocorphinoid prosthetic group of Methyl-Coenzyme M Reductase, one of the important enzymes in nature's methane production by Methanobacterium thermoautotrophicum.2 Over the last thirty years, pathways of methanogenesis and the role of cofactor F430 have been studied both experimentally3–6 and theoretically.7–10 Additionally, Methyl-Coenzyme M Reductase and coenzyme F430 can also catalyze the reductive dehalogenation of chlorinated α carbons.11,12 Despite differences in their spectroscopic and structural features, Stolzenberg and coworkers have shown that nickel(I) octaethylisobacteriochlorin anion ([OEiBCh-Ni(I)]−) can be used as synthetic catalyst that mimics the reactivity of cofactor F430
1 is a nickel(II) hydrocorphinoid prosthetic group of Methyl-Coenzyme M Reductase, one of the important enzymes in nature's methane production by Methanobacterium thermoautotrophicum.2 Over the last thirty years, pathways of methanogenesis and the role of cofactor F430 have been studied both experimentally3–6 and theoretically.7–10 Additionally, Methyl-Coenzyme M Reductase and coenzyme F430 can also catalyze the reductive dehalogenation of chlorinated α carbons.11,12 Despite differences in their spectroscopic and structural features, Stolzenberg and coworkers have shown that nickel(I) octaethylisobacteriochlorin anion ([OEiBCh-Ni(I)]−) can be used as synthetic catalyst that mimics the reactivity of cofactor F430![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 13–16 especially in reductive dehalogenation reactions, see Fig. 1. A similar conclusion also was reached by Helvenston and Castro.17
13–16 especially in reductive dehalogenation reactions, see Fig. 1. A similar conclusion also was reached by Helvenston and Castro.17
All these studies identified the nucleophilic attack of the [OEiBCh-Ni(I)]− anion on the haloalkane as the rate-determining step, Scheme 1, with the Ni(III)–alkyl complex as the intermediate product of this reaction.16 Further reduction and reaction (radical coupling, elimination) of this intermediate can lead to the creation of various dehalogenated alkanes and olefins.14–17 Although there are several theoretical studies about the stability of different isomers of octaethyliso-bacteriochlorin and its complexes and about other nickel porphyrin derivative complexes and their properties,18–22 we were unable to find any theoretical work describing the reactivity of [OEiBCh-Ni(I)]− with haloalkanes. Because of their high efficiency for dehalogenation of chloroalkanes, which are common, toxic organic solvents,23 it is important to better understand the reactivity of the [OEiBCh-Ni(I)]− complex and that of its derivatives.
In this work we report a theoretical study on models for the rate-determining step of dehalogenation of haloalkanes by [OEiBCh-Ni(I)]− based on density functional theory (DFT) and on a comparison of its reactivity with that of other Ni(I) anion complexes with other porphyrin derived ligands. Additionally, for each model reaction the theoretical values of the chlorine kinetic isotope effect are predicted.
Computational details
All stationary points were optimized with the Gaussian 09 RevD.01 software24 with normal convergence criteria; these geometry optimizations were done within an implicit solvation cavity by using the SMD continuum solvent model for N,N-dimethylformamide (DMF).25 Unrestricted DFT electronic structure calculations were performed for open-shell doublet (low-spin) and open-shell quartet (high-spin) systems by using three functionals: the ‘pure’ (0% exact exchange) M06-L functional,26 the hybrid B3LYP functional27–29 and the range-separated hybrid with dispersion corrections ωB97X-D functional30 with the Pople 6-311+G(d,p) basis set31–35 on Ni, N atoms in the [L-Ni] complexes, and Cl and C atoms from the MeCl molecule, while the remaining atoms were treated with the Pople 6-31+G(d,p) basis set.36–40 Despite the passage of years, the B3LYP functional gives reasonably accurate results for transition metal complexes41 and makes for useful comparisons with other work because of its popularity, while the M06-L functional has shown good ability to describe both strong and weak bonds, which may be crucial in case of porphyrin–metal complexes,42 and finally, the ωB97X-D functional with Grimme's empirical dispersion correction was chosen as it has recently shown good accuracy for organometallic complexes with transition metals.43 All energies in the text are Gibbs free energies in solution unless noted otherwise.Chlorine kinetic isotope effects (Cl-KIE) have been calculated by using the complete Bigeleisen equation44 at 298 K as implemented in the ISOEFF program.45 The calculation of Wiberg bond indices46 was made by using the NBO 3.1 module47 as implemented in Gaussian 09.
Results and discussion
Theoretical reaction model
As a simplification, the reaction model consists of the smallest chloroalkane, chloromethane, and the plain isobacteriochlorin ring rather than octaethylisobacteriochlorin (OEiBCh).Replacing the side groups of OEiBCh by hydrogen atoms reduced the computing time and avoided possibility of complicated side group (ethyl) reorientations. In addition to isobacteriochlorin (iBCh), five other porphyrin derived ligands have been examined: porphyrin (Pi), chlorin (Ch), bacteriochlorin (BCh), hexahydroporphyrin (HEX-Pi) and octahydro-porphyryn (OCT-Pi), see Fig. 2.
This investigation of the reaction mechanism concentrates on the rate-determining step of the whole process – the dehalogenation reaction; further decomposition reactions of the methyl-substituted complex [L-Ni–Me] were not investigated as they were not the main subject of this work and will be studied in the future. Scheme 2 shows the possible species that could be involved in the steps of the dehalogenation reactions. Species 1 and 5 were calculated as a separate molecules (respectively as [L-Ni]− and MeCl, and [L-Ni–Me] and Cl−), while 2 and 4 were achieved from IRC calculations,48 full geometry optimizations were performed and further fully re-optimized in SMD solvent (without use of any constrains).
Ni isobacteriochlorin complex
Experimentally, the first step involves reduction of the iBCh-Ni(II) complex to its anionic derivative [iBCh-Ni(I)]−. Although square-planar Ni(II) complexes are nearly always low-spin (LS) singlet states, high-spin (HS) triplet states are possible for other geometries, such tetrahedral, and for 5- or 6-coordinate complexes.49 Although reduction of Ni(II) to Ni(I) would produce a doublet (LS) state, reduction of the ligand in a HS Ni(II) could produce a quartet (HS) state. Since the key reaction step involves the transformation of the reduced Ni(I) complex, [iBCh-Ni(I)]−, to the 5-coordinate Ni(III) complex, iBCh-Ni(III)–Me, we have examined the steps for both LS and HS cases, in part to assure ourselves that spin crossover is not occurring. Experimentally, the reduction potential for the OEiBCh-Ni(II) complex in DMF solution is −1.46 V versus saturated calomel electrode (SCE).50 Using the reported correlation of ferrocenium/ferrocene (Cp2Fe+1/0) electrode vs. SCE electrode in DMF solvents reduction potential of iBCh-Ni(II) to the LS Ni(I)vs. Cp2Fe+1/0 electrode should be −1.92 V.51 We computed theoretical values for the reduction potential of iBCh-Ni(II) to the LS Ni(I)vs. Cp2Fe+1/0 electrode as −1.87 V, −1.53 V and −2.07 V for B3LYP, M06-L and ωB97X-D functionals, respectively. Since our theoretical model is devoid of the ethyl substituents in the iBCh ligand, this is relatively good agreement.The relative energies for the remaining steps in this reaction (Scheme 2) are shown in Fig. 3, where zero for 1 is the sum of the energies of the LS [iBCh-Ni(I)]− complex and the MeCl molecule for each functional. For all steps with all functional, the energies of species with HS configurations are well above those with LS configurations, so we should not have any spin-crossover issues in this reaction. In general, for the species leading up to the transition state (TS), 1 and 2, and the TS, 3, the HS states are further above the LS states than for the product species, 4 and 5. This difference is consistent with reactant species being Ni(I), an early Ni(I)-like TS, and product species being Ni(III), where HS states would be expected to be relatively more stable. Comparisons of these differences for the functionals show that the ωB97X-D functional predicts a noticeably larger LS–HS separation for species 1 and 2 than for the remaining species. Further results and discussion will concentrate on the LS pathway.
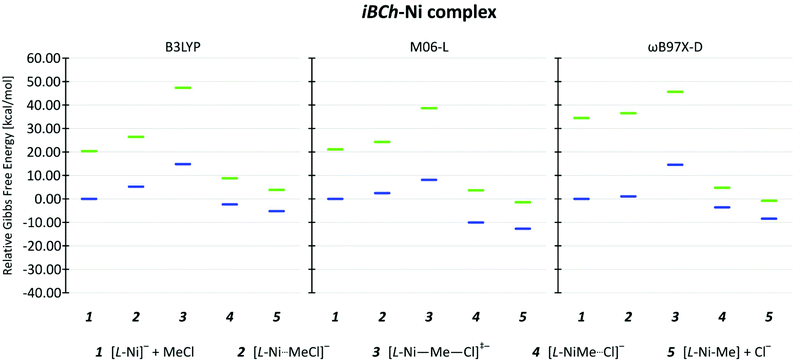 | ||
| Fig. 3 Relative energy diagram are shown for the dehalogenation of MeCl by low spin (blue) and high spin (green) [iBCh-Ni]− complexes for B3LYP, M06-L, and ωB97X-D functionals with 6-311+G(d,p)/6-31+G(d,p) basis set in SMD solvent model for DMF. For more details see Table S5 in ESI.† | ||
In the LS pathway the pre-reaction complex 2 is always higher in energy than separate reactants 1 and this energy difference decreases from B3LYP through M06-L to ωB97X-D, a trend that reflects the increasing improvement in the representation of dispersion energy in this series of functionals. The energy of the TS, 3, is almost equal for B3LYP and ωB97X-D and approximately 6 kcal mol−1 lower for M06-L. For all functionals the energies of both the product complex 4 and the separate products, [iBCh-Ni(III)–Me] complex and Cl− anion, 5 were more stable than separate reactants, 1. Detailed analyses of spin densities for all species 1 through 5 in all functionals show a very similar spin distribution pattern with one unpaired electron on Ni as expected for both Ni(I) and Ni(III) systems, see Fig. S2 in ESI.†
It is worth noting that during our research we also found another possible form of the [iBCh-Ni–Me] complex from species 5. The new structure was built from the [iBCh-Ni] neutral complex and Me˙ radical ([iBCh-Ni]⋯Me˙). Existence of this type of species was previously suggested by Helvenston and Castro.17 However, they suggested existence of nickel–methyl radical complex at the transition state stage when we only observed nickel–methyl radical complexes as another possible form of products upon relaxation from the TS. This result may suggest that the electron transfer between iBCh-Ni complex and Me substituent could happen during product formation from TS or as one of the further steps of [iBCh-Ni–Me] complex decomposition reactions. Moreover, [iBCh-Ni]⋯Me˙ species were higher in energy than [iBCh-Ni–Me] adducts by more than 8 kcal mol−1 (see discussion in S.IX in ESI†) therefore we excluded them from further analysis as energetically unfavorable products. At the same point we cannot exclude creation of Me˙ as a part of [iBCh-Ni–Me] complex decomposition reactions. However search of such a process was not the main subject of this work and will be performed in the future.
Knowledge of the experimental rate of reaction allowed us to estimate an experimental activation energy for the studied reaction.52 Helvenston and Castro reported a second-order rate constant for MeCl dehalogenation by [OEiBCh-Ni]− complex in DMF at 296.65 K of 1.1 × 104 M−1 s−1 with a 15% measurement error,17 a rate which corresponds to an free-energy barrier of 12 ± 2 kcal mol−1, based on standard transition state theory. Based on the free-energy barrier between 1 and 3 for the LS models, the calculations predict theoretical free-energy barriers of 14.8, 8.1 and 14.5 kcal mol−1 for B3LYP, M06-L and ωB97X-D functionals, respectively. Both B3LYP and ωB97X-D values are in good agreement with the experimental one, while M06-L underestimates it. Although all calculations were done for the simplified, less crowded [iBCh-Ni]− model, complex with the continuum solvent model (SMD) for DMF, the major error lies in the DFT functionals. Although the differences are larger than one might hope, such differences between functionals are to be expected when breaking and making bonds. Importantly, despite their differences all of the functionals are in qualitative agreement and the two most modern functionals bracket the experimental number. Overall our theoretical models provide a reasonably good first approximation of rate-determining step of chloroalkanes dehalogenation by the [OEiBCh-Ni] complex.
The reduction of [iBCh-Ni(III)–Me] from species 5 to [iBCh-Ni(II)–Me]− has been suggested as a contributing step in the catalytic cycle. The two most commonly suggested pathways are: by direct electron attachment15 on the [iBCh-Ni(III)–Me] complex, or by using the [iBCh-Ni(I)]− complex as an electron donor.17 However, there are no experimental data about the reduction potentials of these processes. According to our calculation, the reduction potential of direct electron attachment to [iBCh-Ni(II)–Me] complex is much more negative (−2.64 V, −2.34 V and −2.79 V respectively in B3LYP, M06-L and ωB97X-D functionals) than reduction potential for the [iBCh-Ni(II)]/[iBCh-Ni(I)]− process (−1.87 V, −1.53 V and −2.07 V respectively in B3LYP, M06-L and wB97X-D functionals). Therefore, in our opinion, reduction of the [iBCh-Ni(III)–Me] complex by electron attachment is rather unfavorable. Moreover, according to our prediction of ΔG value, we have found that the second pathway (electron transfer between [iBCh-Ni(III)–Me] and [iBCh-Ni(I)]−) is an endoenergetic process which suggest that both pathway are unfavorable (see discussion in S.X in ESI†).
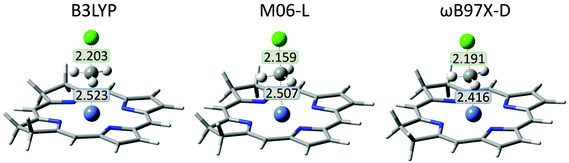
Small geometric differences between neutral and anionic complexes are present. Before its initial reduction, the iBCh moiety in the neutral [iBCh-Ni] molecule is slightly bent on the side with saturated rings, while after reduction the iBCh moiety in the anionic [iBCh-Ni]− complex is nearly planar. In the pre-reaction LS complexes, 2, for all functionals the Ni–CMeCl distances are in the range 3.1 Å to 3.7 Å, while the CMeCl–Cl bonds are about 1.8 Å, nearly equal to that in the free molecule. In the LS-TS (Fig. 4) the CMeCl–Cl bond lengthens to about 2.2 Å, while the Ni–CMeCl distance shorten to about 2.5 Å for the B3LYP and M06-L functionals and 2.4 Å for the ωB97X-D functional (see Table S1 in ESI† for the HS complexes). In the product complex, 4, the Ni–CMeCl bond shortens to about 2 Å and remains constant in 5 for all functionals.
Interesting observations can be made for the Ni–N bond length. Noticeable Ni–N bond lengths increases have been observed upon complex reduction from neutral to its anionic form by 0.10 Å to 0.12 Å for all of the functionals, see SI.VIII in ESI.† Furthermore, slightly longer Ni–N bonds have been observed in case of Ni–N interactions for N atoms within saturated pyrrole rings in isobacteriochlorin ligand, see SI.VIII in ESI.† The existence of the difference between two types of Ni–N bonds within OEiBCh-Ni complexes was observed in experimental studies (approx. 0.16 Å),53 however the experimental difference is more than ten times larger than our theoretical prediction, see SI.VIII in ESI.† Experimental data correspond better with our theoretical data for the Ni–N bond length changes from neutral to anionic forms of iBCh-Ni complex than to differences between two types of Ni–N bonds within the complex.
Isobacteriochlorin ligand vs. porphyrin derivative ligands
The impact of changing the ligand from iBCh to other porphyrin-derived ligands on the reaction parameters raises some interesting issues. The principal differences in the ligands are the number of unsaturated bonds in side rings of porphyrin moiety, which are correlated with number of π-electrons in the ring. Although iBCh and BCh ligands have the same number of π-electrons, their bonding configuration is much different; iBCh has the unsaturated side rings in a cis configuration, while BCh has them in a trans configuration, see Fig. 2. The geometric properties of all porphyrin–ligand complexes were very similar to those described earlier for the [iBCh-Ni] system.Even differences in the key geometric parameters of the LS-TS 3 were very small between all porphyrin-derived ligands, see Fig. S5 in ESI.† Thus, all of the studied ligand's transition states look nearly identical; compare Fig. 4 with Fig. S5 in ESI.† Furthermore, the geometric features were also very similar for substrate complexes 2, product complexes 4 and [L-Ni–Me] complexes 5, see Tables S2–S4 in ESI,† as well as for Ni–N bond lengths, see Tables S8–S10 in ESI.†
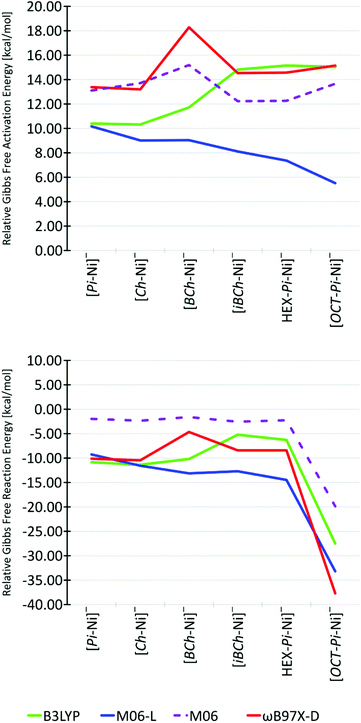
The theoretical values of the reduction potentials for all ligands from their neutral forms [L-Ni(II)] to the corresponding anionic forms [L-Ni(I)]− were very similar to those reported above for the iBCh ligand and in the range of 0.30 V, 0.29 V and 0.37 V respectively in B3LYP, M06-L and ωB97X-D functionals, see Table S14 in ESI.† Reduction potentials of methyl–nickel complexes for Pi, Ch, BCh, HEX-Pi and OCT-Pi ligands were not computed, since we believe that, like the iBCh ligand case, they should be lower than the reduction potentials of [L-Ni(II)]0/[L-Ni(I)]− system and connected with [L-Ni–Me] decomposition reactions, which will be studied in the future. The shape of the reaction-energy profiles for all ligands were also very similar to that described above for the iBCh ligand (Fig. 3). The HS steps 1 through 3 were always above LS for all ligands with all functionals, while HS product complexes 4 and 5 were closer in energy to their LS equivalents; finally falling below for the HEX-Pi-Ni and OCT-Pi-Ni complexes with nearly every functional, see Fig. S9 in ESI.† Since the LS pathway predominates for all porphyrin-derived ligands, the discussion will concentrate on LS pathway unless noted otherwise. For all functionals, the product complexes 5 were always more stable than the reactants 1 by −4.66 kcal mol−1 to −37.70 kcal mol−1, becoming much more stable only for OCT-Pi-Ni. The trends for the TS energies (Fig. 5) are less consistent between the functionals, but all predict TS's energies spanning a similar range: 10–15 kcal mol−1, 5–10 kcal mol−1 and 13–18 kcal mol−1 for B3LYP, M06-L and ωB97X-D functionals, respectively (Fig. 5). Generally, M06-L predicts lower barriers along the series from Pi-Ni to OCT-Pi-Ni, while both B3LYP and ωB97X-D predict slightly higher barriers. Most noticeable is the unexpectedly large barrier predicted by the ωB97X-D functional for the [BCh-Ni]− complex. This is not due to any difference in the geometries as the [BCh-Ni]− TS and reactant have has almost identical geometry in all functionals (Fig. S6 and S7 in ESI†). Further, this unexpected difference is not due to the dispersion correction as the addition of Grimme's empirical dispersion correction with Becke–Johnson damping (B3LYP-GD3BJ)54 on the energies from geometries achieved in pure B3LYP functionals did not show significant differences in the pattern with respect to changes in the ligands except a small stabilization for the [Ch-Ni] complex, see discussion in S.VI.1 in ESI.† Finally a “cross-energy test” calculation of the energy of 3 with the B3LYP functional in the geometry from ωB97X-D functional and vice versa, shows that the unusually high activation energy for 3 with the ωB97X-D functional is not connected with any geometric differences between structures of species 3 in B3LYP and ωB97X-D functionals, see discussion in S.VI.4 in ESI.†
Moreover, energy calculations of 3 and 5 with the M06 functional on geometries from the M06-L functional also show an unexpected higher barrier for [BCh-Ni], but not one as dramatic as ωB97X-D (dashed lines in Fig. 5). Although the Gibbs activation free energies with the M06 functional are of intermediate value, their Gibbs reaction free energies show smaller product stabilization than the other functionals. Moreover, the M06 activation energy for the iBCh-Ni complex (12.2 kcal mol−1) is very close to the estimate from the experimental rate.
The variations in the activation energies produced by the different functionals may be connected to the inclusion of true Hartree–Fock exchange energy (EHFex). Lack of any EHFex as in case of the M06-L functional may be the source of its smoothly changing TS barriers as the π-electron system changes through this series of porphyrin ligands. As was shown on Fig. 5, the energy calculation for the M06 functional (which has 27% of EHFex)55 show pattern of Gibbs activation free energies similar to that with the ωB97X-D functional. Increasing the amount of EHFex introduces additional apparently capricious fluctuations in the activation energies, see results and discussion in S.VI.2 in ESI† for the M06-2X functional56 (54% of EHFex) and the M06-HF functional56,57 (100% of EHFex). Although there is no oblivious systematic dependence between activation energies and amount of EHFex in the M06 functional family, the dramatic differences produced by the addition of Hartree–Fock exchange are manifested clearly in the spin densities (Fig. S2 in ESI†). While M06-L functional describes nearly identical spin distributions for all species of all complexes, B3LYP and ωB97X-D functionals show differences between Pi-Ni, Ch-Ni, BCh-Ni complexes and remaining complexes for species 1 and 2. While for the former group of complexes the unpaired electron is on the ligand ring, while for the latter group it is on the Ni atom, see Fig. S2 and S3 in ESI.† These differences in spin distribution are caused by changes in the energy of the molecular orbitals. With increasing saturation of side-ligand rings, the energy of the ligand's LUMOs in the neutral complex (before reduction) rises faster than that of the corresponding orbital on Ni. Therefore, for Pi-Ni, Ch-Ni, BCh-Ni complexes the LUMO is the ring orbital and accepts the reducing electron (these reduced complexes are still Ni(II)), while for iBCH-Ni, HEX-Pi-Ni, OCT-Pi-Ni complexes the LUMO orbital is on the Ni atom so it is reduced to Ni(I), see Fig. S3 and S8 in ESI.† Furthermore, there are additional differences between the OCTA-Pi-Ni complex and the less saturated complexes, where one sees increasing spin densities on N, Ni, and CMeCl atoms in the OCT-Pi-Ni complex, a result of the ground state changing to the quartet, see Fig. S2 in ESI.† Nevertheless, the spin distributions for iBCh-Ni, HEX-Pi-Ni and OCT-Pi-Ni ligands in B3LYP and ωB97X-D functionals suggest that during the reaction the unpaired electron is always on the Ni atom for both Ni(I) and Ni(III) complexes. Thus, our results from B3LYP and ωB97X-D functionals suggest that the more saturated ligands are more stable with unpaired electron on Ni atom rather than on the ligand core, while less saturated ligands (Pi, Ch, BCh) are more stable with unpaired electron on the ligand core. This may be an important clue to understand why nature has chosen more saturated system for F-430 cofactor (like the isobacteriochlorin ligand) instead the less saturated one (like for example porphyrin ligand). The iBCh ligand is the first structure, with the lowest ring saturation compared to HEX-Pi and OCT-Pi, for which we have always calculated the appearance of unpaired electron directly on the Ni atom for all stages of the reaction. To confirm this suggestion and to resolve the differences between B3LYP, ωB97X-D and M06-L functionals in electron placement for Pi, Ch, BCh ligands, further research will have to be done with other functionals. Furthermore, studies with the use of a higher level of theory (like coupled cluster methods: CCSD or CCSD(T)), with multi-electron wavefunctions, which can describe each electron in the studied system, would be a good reference tool to solve this problem and will be performed in the future. At this point we can say, that the unpaired electron should be all the time on Ni(I) atom in species 3 and Ni(III) atom in species 4 and 5. However, with current models we cannot exclude the existence of the unpaired electron on the ring for [L-Ni]− species 1 and 2 for Pi-Ni, Ch-Ni, BCh-Ni ligands.
Chlorine kinetic isotope effects (Cl-KIEs)
Chlorine kinetic isotope effects (Cl-KIE's) should be very good indicators of correctness of our theoretical models. Since in the rate-determining step chlorine anion is released it can be used as a probe. Unfortunately, to best of our knowledge, experimental values of Cl-KIE for these reactions are unknown. Therefore, we only could compare the theoretically predicted Cl-KIE values for dehalogenation of chloromethane by porphyrin derivative ligands nickel(I) anion with typical range of Cl-KIE's for SN2 reaction.Using of BEBOVIB58 calculations Paneth predicted that Cl-KIE's may have maximum values of 1.019.59 Further, theoretical research with quantum DFT methods predicted values of Cl-KIE's on SN2 reaction, when chlorine was the leaving group, in the range: 1.006–1.009.60,61 Recently higher theoretical values of Cl-KIE's were also reported by Świderek and Paneth where they showed that Cl-KIE's can be even higher than 1.025 when chlorine is the central atom passed between two other heavy atoms.62 Moreover, Szatkowski and Dybala-Defratyka predicted theoretical values of Cl-KIE's for intramolecular chlorine transfer inside chlorinated phenoxybenzenes to be in the range from 1.014 to 1.028.63 However in this process chlorine anions were not released. In case of our model we should expect Cl-KIE values to match typical values for SN2 reactions, and indeed, theoretical values of Cl-KIE for the predominant LS pathway in our models were in the range: 1.0084–1.0097, 1.0092–1.0102 and 1.0093–1.0097 for B3LYP, M06-L and ωB97X-D functionals, respectively. Further studies of SN2 dehalogenation reactions of MeCl by various nucleophiles has shown a correlation between theoretical values of the Cl-KIEs and the Wiberg bond orders for the Cα–Cl bonds in the transition states.60 In our transition state models for the dehalogenation of MeCl by [L-Ni]− complexes, the CMeCl–Cl Wiberg bond orders were in range of 0.1098–0.1136, 0.1140–0.1218 and 0.0967–0.1006 for B3LYP, M06-L and ωB97X-D functionals, respectively (see Table S7†). Since such low values of the Cα–Cl Wiberg bond order on SN2 dehalogenation reactions of chloromethane have not previously been reported, our data constitute an important extension of correlation presented by Dybala-Defratyka and coworkers to low values of the Wiberg bond order. Furthermore, our results indicated that even for such low values of the Wiberg bond order for the Cα–Cl transition states, the maximum values of Cl-KIE should be around 1.010, see Fig. 6 and Table S7 in ESI.†
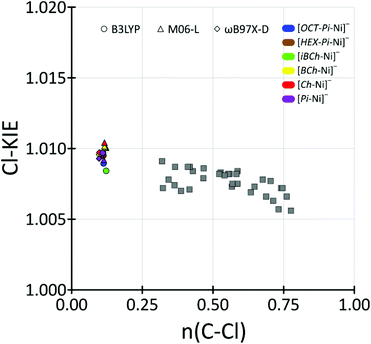 | ||
| Fig. 6 Correlation of Cl-KIEs with transition-state Wiberg Cα–Cl bond orders for dehalogenation of chloromethane by low-spin nickel(I) porphyrin-derivative anions as a extension of data presented in Table 1 from ref. 59 (grey squares).60 | ||
Summary and conclusions
For the dehalogenation of chloromethane by nickel(I) anions with the entire series of ligands: porphyrin (Pi), chlorin (Ch), bacteriochlorin (BCh), isobacteriochlorin (iBCh), hexahydroporphyrin (HEX-Pi) and octahydroporphyrin (OCT-Pi) predict that low-spin pathways have lower activation energies than high-spin pathways. Stability of the reaction products was similar for all of the ligands and for the various functionals except for OCT-Pi-Ni which had a much more stable product. The B3LYP and ωB97X-D functionals predicted Gibbs activation free energies in similar ranges for all ligands, while the M06-L functional predicted lower barriers; addition of Hatreee–Fock exchange as in M06 energies increased these barriers.Activation energy and reaction energy differences for different functional confirm that the choice of a suitable functional requires a comparison between theoretical predictions and experimental measurements. In our system comparison could only be made for the [iBCh-Ni] system, where M06//M06-L provided the most accurate values. Activation energies from B3LYP and ωB97X-D were somewhat higher, while those from M06 were significantly lower. However, no experimental data for dehalogenation of chloromethane by other nickel(I) porphyrin derivative anions complexes were available. For the transition states of all tested nickel(I) porphyrin-derived ligand anions, all the DFT methods predicted very similar geometries, which resulted in a narrow range of predicted values of the Cl-KIE's, 1.008–1.010. Additionally, the very low Cα–Cl Wiberg bond orders for these TS structures allowed us extend the previously described correlation of Cl-KIE's and Cα–Cl Wiberg bond orders in SN2 dehalogenation reactions.
Moreover B3LYP and ωB97X-D functionals predicted that for Pi-Ni, Ch-Ni, BCh-Ni anion complexes 1 and 2 the unpaired electron should be placed on the ring rather than on the Ni atom, while for iBCH-Ni, HEX-Pi-Ni, OCT-Pi-Ni complexes it was always on the Ni atom. The M06-L functional predicted the unpaired electron always on the Ni atom.
Abbreviations
| OEiBCh | (2,3,7,8-Tetrahydro-2,3,7,8,12,13,17,18-octaethyl-porphyrin dianion) octaethylisobacteriochlorin ligand |
| Pi | Porphyrin ligand |
| Ch | (2,3-Dihydroporphyrin dianion) chlorine ligand |
| BCh | (2,3,12,13-Tetrahydroporphyrin dianion) bacteriochlorin ligand |
| iBCh | (2,3,7,8-Tetrahydroporphyrin dianion) isobacteriochlorin ligand |
| HEX-Pi | (7,8,12,13,17,18-Hexahydro-21H,23H-porphine dianion) hexahydroporphyrin ligand |
| OCT-Pi | (2,3,7,8,12,13,17,18-Octahydro-21H,23H-porphine-1,4-diyl dianion) octahydroporphyrin ligand |
| LS | Low spin |
| HS | High spin |
| TS | Transition state |
| LS-TS | Low spin transition state |
| HS-TS | High spin transition state |
| SP | Single point calculation |
| Cl-KIE | Chlorine kinetic isotope effect |
Acknowledgements
The authors acknowledge the support of this work by The Welch Foundation (Grant A-0648), Texas A&M University's Super-computer Facility, and The University of Arizona's High Performance Computing Facility.References
- W. L. Ellefson, W. B. Whitman and R. S. Wolfe, Proc. Natl. Acad. Sci. U. S. A., 1982, 79, 3707–3710 CrossRef CAS.
- S. W. Ragsdale, in The Porphyrin Handbook, ed. K. M. Kadish, K. M. Smith and R. Guilard, Academic Press, New York, 2003, vol. 11, p. 205 Search PubMed.
- A. A. DiMarco, T. A. Bobik and R. S. Wolfe, Annu. Rev. Biochem., 1990, 59, 355–394 CrossRef CAS PubMed.
- P. L. Hartzell and R. S. Wolfe, Syst. Appl. Microbiol., 1986, 7, 376–382 CrossRef CAS.
- R. S. Wolfe, Annu. Rev. Microbiol., 1991, 45, 1–35 CrossRef CAS PubMed.
- R. K. Thauer, Microbiology, 1998, 144, 2377–2406 CrossRef CAS PubMed.
- T. Wondimagegn and A. J. Ghosh, Am. Chem. Soc., 2000, 122, 6375–6381 CrossRef CAS.
- V. Pelmenschikov and P. E. Siegbahn, J. Biol. Inorg. Chem., 2003, 8, 653–662 CrossRef CAS PubMed.
- L. J. Craft, Y. C. Horng, S. W. Ragsdale and T. C. Brunold, J. Am. Chem. Soc., 2004, 126, 4068–4069 CrossRef PubMed.
- L. J. Craft, Y. C. Horng, S. W. Ragsdale and T. C. Brunold, J. Biol. Inorg. Chem., 2004, 9, 77–89 CrossRef PubMed.
- U. E. Krone, K. Laufer, R. K. Thauer and H. P. Hogenkamp, Biochemistry, 1989, 28, 10061–10065 CrossRef CAS PubMed.
- T. C. Holliger, S. W. M. Kengen, G. Schraa, A. J. M. Stams and A. J. B. Zehnder, J. Bacteriol., 1992, 174, 4435–4443 Search PubMed.
- A. M. Stolzenberg and M. T. Stershic, Inorg. Chem., 1987, 26, 3082–3083 CrossRef CAS.
- A. M. Stolzenberg and M. T. Stershic, J. Am. Chem. Soc., 1988, 110, 5397–5403 CrossRef CAS.
- G. K. Lahiri, L. J. Schussel and A. M. Stolzenberg, Inorg. Chem., 1992, 31, 4991–5000 CrossRef CAS.
- G. K. Lahiri and A. M. Stolzenberg, Inorg. Chem., 1993, 32, 4409–4413 CrossRef CAS.
- M. C. Helvenston and C. E. Castro, J. Am. Chem. Soc., 1992, 114, 8490–8496 CrossRef CAS.
- A. Ghosh, J. Phys. Chem. B, 1997, 101, 3290–3297 CrossRef CAS.
- J. Jusélius and D. Sundholm, Phys. Chem. Chem. Phys., 2000, 2, 2145–2151 RSC.
- H. Ryeng, E. Gonzalez and A. Ghosh, J. Phys. Chem. B, 2008, 112, 15158–15173 CrossRef CAS PubMed.
- N. Otero, S. Fias, S. Radenković, P. Bultinck, A. M. Graña and M. Mandado, Chem. – Eur. J., 2011, 17, 3274–3286 CrossRef CAS PubMed.
- E. Kleinpeter, A. Koch, S. Schulz and P. Wacker, Tetrahedron, 2014, 70, 9230–9239 CrossRef CAS.
- F.-I. Wang, M.-L. Kuo, C.-T. Shun, Y.-C. Ma, J.-D. Wang and T.-H. Ueng, J. Toxicol. Environ. Health, Part A, 2002, 65, 279–291 CrossRef CAS PubMed.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery Jr., J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, Ö. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian 09 (Revision D.01), Gaussian, Inc., Wallingford CT, 2009 Search PubMed.
- A. Marenich, C. J. Cramer and D. G. Truhlar, J. Phys. Chem. B, 2009, 113, 6378–6396 CrossRef CAS PubMed.
- Y. Zhao and D. G. Truhlar, J. Chem. Phys., 2006, 125, 194101 CrossRef PubMed.
- A. Becke, J. Chem. Phys., 1993, 98, 5648–5652 CrossRef CAS.
- C. Lee, W. Yang and R. Parr, Phys. Rev. B: Condens. Matter, 1988, 37, 785–789 CrossRef CAS.
- P. Stephens, F. Devlin, C. Chabalowski and M. Frisch, J. Phys. Chem., 1994, 98, 11623–11627 CrossRef CAS.
- J. Chai and M. Head-Gordon, Phys. Chem. Chem. Phys., 2008, 10, 6615–6620 RSC.
- A. D. McLean and G. S. Chandler, J. Chem. Phys., 1980, 72, 5639–5648 CrossRef CAS.
- K. Raghavachari, J. S. Binkley, R. Seeger and J. A. Pople, J. Chem. Phys., 1980, 72, 650–654 CrossRef.
- A. J. H. Wachters, J. Chem. Phys., 1970, 52, 1033–1036 CrossRef CAS.
- J. P. Hay, J. Chem. Phys., 1977, 66, 4377–4384 CrossRef.
- K. Raghavachari and G. W. Trucks, J. Chem. Phys., 1989, 91, 1062–1065 CrossRef.
- P. Hariharan and J. A. Pople, Theor. Chem. Acc., 1973, 28, 213–222 CrossRef CAS.
- R. Ditchfield, W. Hehre and J. A. Pople, J. Chem. Phys., 1971, 54, 724–728 CrossRef CAS.
- M. Francl, W. Pietro, W. Hehre, J. Binkley, M. Gordon, D. DeFrees and J. A. Pople, J. Chem. Phys., 1982, 77, 3654–3665 CrossRef CAS.
- T. Clark, J. Chandrasekhar, G. Spitznagel and P. Schleyer, J. Comput. Chem., 1983, 4, 294–301 CrossRef CAS.
- M. Frisch, J. Pople and J. Binkley, J. Chem. Phys., 1984, 80, 3265–3269 CrossRef CAS.
- C. J. Cramer and D. G. Truhlar, Phys. Chem. Chem. Phys., 2009, 11, 10757–10816 RSC.
- J. Sun, B. Xiao, Y. Fang, R. Haunschild, P. Hao, A. Ruzsinszky, G. I. Csonka, G. E. Scuseria and J. P. Perdew, Phys. Rev. Lett., 2013, 111, 106401 CrossRef PubMed.
- Y. Minenkov, Å. Singstad, G. Occhipintia and V. R. Jensen, Dalton Trans., 2012, 41, 5526–5541 RSC.
- J. Bigeleisen, J. Chem. Phys., 1949, 17, 675–678 CrossRef CAS.
- V. Anisimov and P. Paneth, J. Math. Chem., 1999, 26, 75–86 CrossRef.
- K. B. Wiberg, Tetrahedron, 1968, 24, 1083–1096 CrossRef CAS.
- E. D. Glendening, J. K. Badenhoop, A. E. Reed, J. E. Carpenter and F. Weinhold, NBO Version 3.1, Theoretical Chemistry Institute, University of Wisconsin, Madison WI, 1998 Search PubMed.
- K. Fukui, Acc. Chem. Res., 1981, 14, 363–368 CrossRef CAS.
- H. Ohtsu and K. Tanaka, Inorg. Chem., 2004, 43, 3024–3030 CrossRef CAS PubMed.
- A. M. Stolzenberg and M. T. Stershic, J. Am. Chem. Soc., 1988, 110, 6391–6402 CrossRef CAS.
- N. G. Connelly and W. E. Geiger, Chem. Rev., 1996, 96, 877–910 CrossRef CAS PubMed.
- J. W. Ochterski, Thermochemistry in Gaussian, Gaussian, Inc., Wallingford CT, 2000, http://www.gaussian.com/g_whitepap/thermo.htm (accessed June 2016) Search PubMed.
- M. W. Renner, L. R. Furenlid and A. M. Stolzenberg, J. Am. Chem. Soc., 1995, 117, 293–300 CrossRef CAS.
- S. Grimme, S. Ehrlich and L. Goerigk, J. Comput. Chem., 2011, 32, 1456–1465 CrossRef CAS PubMed.
- Y. Zhao and D. G. Truhlar, Theor. Chem. Acc., 2008, 120, 215–241 CrossRef CAS.
- Y. Zhao and D. G. Truhlar, J. Phys. Chem., 2006, 110, 5121–5129 CrossRef CAS PubMed.
- Y. Zhao and D. G. Truhlar, J. Phys. Chem. A, 2006, 110, 13126–13130 CrossRef CAS PubMed.
- L. B. Sims and E. D. Lewis, in Isotopes in Organic Chemistry, ed. E. Buncel and C. C. Lee, Elsevier, Amsterdam, 1985, vol. 6, ch. 4 Search PubMed.
- P. Paneth, in Isotopes in Organic Chemistry, ed. E. Buncel and W. H. Saunders Jr., Elsevier, New York, 1992, vol. 8, ch. 2 Search PubMed.
- A. Dybala-Defratyka, M. Rostkowski, O. Matsson, K. C. Westaway and P. Paneth, J. Org. Chem., 2004, 69, 4900–4905 CrossRef CAS PubMed.
- A. Dybala-Defratyka, L. Szatkowski, R. Kaminski, M. Wujec, A. Siwek and P. Paneth, Environ. Sci. Technol., 2008, 42, 7744–7750 CrossRef CAS PubMed.
- K. Świderek and P. Paneth, J. Org. Chem., 2012, 77, 5120–5124 CrossRef PubMed.
- L. Szatkowski and A. Dybala-Defratyka, Chemosphere, 2013, 91, 258–264 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: Geometrical and energetic data and Cartesian coordinates of all porphyrin ligand complexes. See DOI: 10.1039/c6dt02632j |
| This journal is © The Royal Society of Chemistry 2016 |