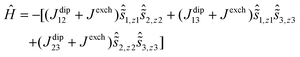Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Magnetic frustration in a hexaazatrinaphthylene-bridged trimetallic dysprosium single-molecule magnet†
Richard
Grindell
a,
Veacheslav
Vieru
b,
Thomas
Pugh
a,
Liviu F.
Chibotaru
*b and
Richard A.
Layfield
*a
aSchool of Chemistry, The University of Manchester, Oxford Road, Manchester, M13 9PL, UK. E-mail: Richard.Layfield@manchester.ac.uk
bTheory of Nanomaterials Group, Katholieke Universiteit Leuven, Celestijenlaan 200F, 3001 Heverlee, Belgium. E-mail: Liviu.Chibotaru@chem.kuleuven.be
First published on 23rd May 2016
Abstract
The synthesis, structure and magnetic properties of the HAN-bridged tri-dysprosium complex [{(thd)3Dy}3HAN] (1) are described. The complex is an SMM that shows two relaxation processes owing to the presence of two geometrically distinct Dy3+ sites in 1. Ab initio calculations reveal that the magnetic ground state of 1 is characterized by magnetic frustration.
Single-molecule magnets (SMMs) are molecular species that show magnetic bistability which, for a true SMM, results in magnetic hysteresis being observed up to a characteristic blocking temperature, TB.1 The properties of SMMs are typically rationalized in terms of correlations between the molecular and electronic structures of individual molecules,2 making such species distinct from classical atom-based inorganic magnets, in which long-range ordering is important.
Studies of SMMs have generated a significant amount of fundamental insight into the properties of highly anisotropic molecular magnets. A strong indication that the field has reached a stage of maturity is that new research areas have begun to emerge from within single-molecule magnetism. One of the most exciting recent developments has been the incorporation of some SMMs into spintronic devices.3 Most prominent amongst the applications of SMMs in molecular spintronics are sandwich-like terbium(III) complexes of phthalocyanine ligands, which have been used in, for example, molecular spin valves4 and devices that allow the coherent manipulation of individual nuclear spins using an electric field.5
An intriguing subset of SMMs that may offer an alternative approach to applications of molecular magnets in nanoscale devices are the so-called single-molecule toroics (SMTs).6 SMTs are polymetallic cage compounds possessing an overall toroidal magnetic moment, which arises from a vortex-like, non-collinear arrangement of the individual moments. To date, SMT properties have been identified in several dysprosium-containing cage compounds with nuclearities of up to Dy6,7,8 but SMT behaviour is most prominent in trimetallic compounds.9 Indeed, the first species found to display a toroidal magnetic moment was the complex cation [Dy3(μ3-OH)2(ovn)3Cl2(H2O)4]2+ (ovn = ortho-vanillin): notably, in this SMT and in all subsequent examples, the toroidal magnetism was identified through the use of ab initio calculations.10
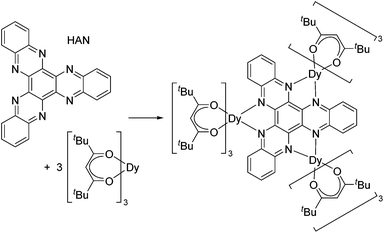
Although toroidal magnetism has been observed in several triangular Dy3 complexes, such arrangements of spin centres are no guarantee that the phenomenon will occur. Targeting SMT behaviour in a rational way is challenging but not impossible, and to achieve this aim further insight into the relationship between the molecular and electronic structure of trimetallic dysprosium complexes is required. We have developed an interest in the tritopic hexazaatrinaphthylene (HAN, Scheme 1) family of ligands,11 the three-fold symmetry of which could provide a platform on which to construct toroidal magnetism and to search for phenomena such as frustrated magnetism. Thus, we targeted a tri-dysprosium complex of HAN, which was achieved with the synthesis of [{(thd)3Dy}3HAN] (1), where thd is 2,2,6,6-tetramethylheptanedionate (Scheme 1).
Compound 1·3(toluene) was isolated as dark red crystals in a yield of 86%, and the molecular structure was determined by X-ray crystallography (Fig. 1, Table S1†). The three dysprosium centres in 1 reside in DyO6N2 environments by virtue of three bidentate [thd]− ligands and two nitrogen donors of the HAN ligand. For Dy(1), the Dy–O distances lie in the range 2.256(5)–2.342(5) Å, and for Dy(2) and Dy(3) the analogous distances are 2.251(6)–2.315(6) Å and 2.259(5)–2.318(5) Å (Table S2†). The Dy–N distances in 1 are 2.646(6)–2.760(6) Å. Although the dysprosium centres are not symmetry related, Dy(1) and Dy(2) occupy similar positions with respect to the plane of the six HAN nitrogen donor atoms. In contrast, Dy(3) is displaced out of the N6 plane by 1.044 Å. The Dy(1)⋯Dy(2), Dy(1)⋯Dy(3) and Dy(2)⋯Dy(3) separations are 8.100(10) Å, 8.147(10) Å and 8.118(9) Å, respectively.
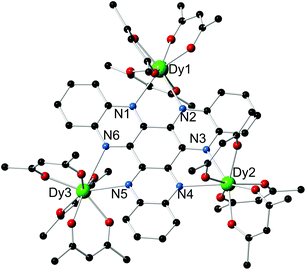 | ||
| Fig. 1 Molecular structure of 1. For clarity, the methyl groups on the [thd]− ligands and the hydrogen atoms are not shown. | ||
The metric parameters for the dysprosium centres were analysed using the SHAPE software,12 which revealed that the DyO6N2 environments can be described as distorted dodecahedra. Thus, the CShM values for Dy(1), Dy(2) and Dy(3) with respect to D2d symmetry are 0.840, 1.624 and 1.797, implying that the latter two metal centres occupy very similar geometries, both of which are more distorted from ideal dodecahedral than that of Dy(1).
Although transition metal complexes of the HAN family of ligands are well known,13 studies of their magnetic properties are uncommon. Recent examples include two-step spin-crossover in the chiral coordination polymer [Fe(HAT)(NCS)2]∞ (HAT = hexaazatriphenylene)14 and the cobalt(II) species [K(18-c-6)][(HAN){Co(N′′)2}3], which contains the radical anionic [HAN]˙− ligand.11a Compound 1 is the first tri-lanthanide complex of this type of tritopic ligand.
The molar magnetic susceptibility (χM) of 1·3(toluene) was measured in a static field of Hdc = 1 kOe in the temperature range 2–300 K (Fig. S4†). At 300 K, χMT is 41.57 cm3 K mol−1, which is consistent with the value of 42.51 cm3 K mol−1 predicted for three non-interacting Dy3+ ions with 6H15/2 ground terms and g = 4/3. As the temperature is lowered, χMT slowly decreases to reach 37.65 cm3 K mol−1 at 50 K, and at lower temperatures, χMT decreases more rapidly and reaches 16.42 cm3 K mol−1 at 2 K. The temperature dependence of χMT can, in principle, be assigned to a combination of antiferromagnetic exchange between the dysprosium centres and the depopulation of the excited Kramers doublets within the spin–orbit coupled ground term.
The field dependence of the magnetization (M) was measured at various intervals in the range 0–70 kOe and at temperatures of 1.8, 3, 5, and 8 K (Fig. S5†). For the measurement at 1.8 K, the magnetization increases sharply as the field increases to 10 kOe before levelling off and reaching a value of M = 15.54μB at 70 kOe, which agrees well with the expected value of 15.75μB for three Dy3+ ions. Using a field sweep rate of 1.9 mT s−1, the magnetic hysteresis of 1 was also investigated at 1.8 and 2.2 K, which revealed S-shaped loops that close around zero field (Fig. S12†).
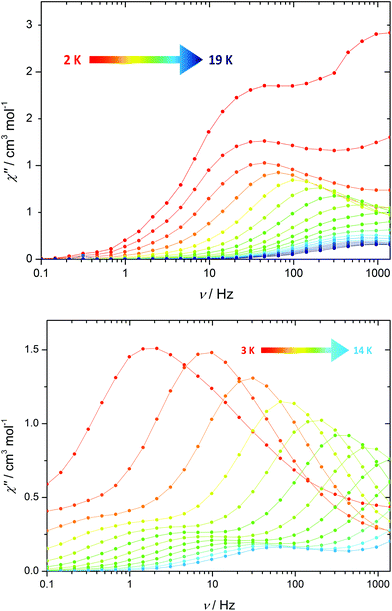
Next, we examined the magnetic properties 1·3(toluene) using an alternating current (a.c.) magnetic field of Hac = 1.55 Oe, initially with zero applied d.c. field. The in-phase (χ′) and the out-of-phase (χ′′) susceptibilities were measured as functions of the frequency of the oscillating field (ν) at 1 K intervals in the range 2–19 K (Fig. S6†). The plot of χ′′(ν) (Fig. 2) at 2 K is double-humped, which indicates SMM behaviour with two regimes of thermal relaxation. The Argand plots of χ′′ vs. χ′ (Fig. S8†) confirm the occurrence of two relaxation processes, and the fits of these data with α parameters in the range 0.09–0.59 imply a wide range of relaxation times. As the temperature is raised the maximum of the higher frequency process shifts to frequencies greater than can be achieved with our SQUID magnetometer, whereas the maximum in the lower-frequency process is discernible up to 10 K.
Conducting the χ′′(ν) measurement in an optimized d.c. field of 1 kOe allows both sets of maxima to be observed across a wider temperature range (Fig. 2 and S7†). For each relaxation process, the position of the maximum in χ′′ shifts markedly to higher frequencies as the temperature is increased, indicating that two independent thermal relaxation processes occur simultaneously. Qualitatively, this observation can be rationalised in terms of the two types of dodecahedral Dy3+ coordination environments in 1.
Further insight into the a.c. susceptibility of 1 was obtained from the relationship between the relaxation time, τ, and temperature, which yields the effective energy barrier to reversal of the magnetization, Ueff, via τ = τ0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−Ueff/kBT). The plot of ln
exp(−Ueff/kBT). The plot of ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) τ versus T−1 for the zero-field data (Fig. S11†) presents an irregular series of data points, which is a consequence of the overlapping χ′′(ν) curves. Although an anisotropy barrier of 22 cm−1 can be extracted from these data (τ0 = 8.2 × 10−6 s), the physical significance of this number is limited. In contrast, the in-field data allow two well-defined thermal relaxation processes to be characterised (Fig. 3), with modest anisotropy barriers of Ueff = 42 cm−1 and 52 cm−1 (τ0 = 3.8 × 10−6 s and 5.6 × 10−6 s), respectively. The occurrence of two relaxation processes in SMMs containing more than one type of dysprosium environment has been described previously in various polynuclear systems.15
τ versus T−1 for the zero-field data (Fig. S11†) presents an irregular series of data points, which is a consequence of the overlapping χ′′(ν) curves. Although an anisotropy barrier of 22 cm−1 can be extracted from these data (τ0 = 8.2 × 10−6 s), the physical significance of this number is limited. In contrast, the in-field data allow two well-defined thermal relaxation processes to be characterised (Fig. 3), with modest anisotropy barriers of Ueff = 42 cm−1 and 52 cm−1 (τ0 = 3.8 × 10−6 s and 5.6 × 10−6 s), respectively. The occurrence of two relaxation processes in SMMs containing more than one type of dysprosium environment has been described previously in various polynuclear systems.15
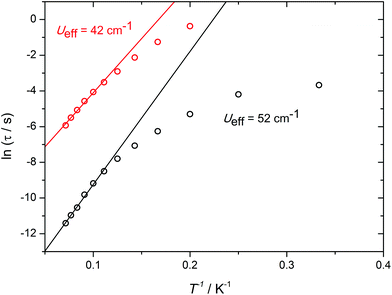 | ||
Fig. 3 Plots of ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) τ vs. 1/T for 1 in an applied field of 1 kOe. The solid lines represent fits to the high-temperature data. τ vs. 1/T for 1 in an applied field of 1 kOe. The solid lines represent fits to the high-temperature data. | ||
In order to develop a detailed picture of the electronic structure of 1, ab initio calculations of the CASSCF/RASSI type were performed using the MOLCAS software.16 Three separate [{(thd)3Dy}HAN] fragments were considered in the calculations (Fig. S13†). The energies of the eight lowest-lying Kramers doublets (KDs) for each Dy3+ centre are shown in Table 1, which reveals that the subtle differences in the coordination environments have a clear impact on the energies of the crystal field levels. The different energies for the KDs of the three Dy3+ centres reflect the fact that they are not related by crystallographic symmetry. The calculated energy gaps from ground to first-excited KD are somewhat larger than the experimentally extracted values, which might indicate that the relaxation is not of a purely activated type.
| KD | Dy(1) | Dy(2) | Dy(3) |
|---|---|---|---|
| 1 | 0 | 0 | 0 |
| 2 | 121 | 152 | 64 |
| 3 | 238 | 252 | 177 |
| 4 | 314 | 336 | 279 |
| 5 | 379 | 421 | 369 |
| 6 | 446 | 505 | 470 |
| 7 | 549 | 627 | 542 |
| 8 | 710 | 794 | 621 |
| g x | 0.016 | 0.001 | 0.009 |
| g y | 0.030 | 0.005 | 0.018 |
| g z | 19.290 | 19.950 | 19.120 |
The calculated g-tensors for the ground KD of each Dy3+ reveal strong magnetic anisotropy approach the Ising limit for dysprosium, i.e. gz = 20 and gx,y = 0 (Tables 1 and S5†). The calculations also provide a very convenient method for visualizing the orientation of the magnetic axis for the various KDs. Thus, it can be seen in Fig. 4 that the magnetic axes in the ground KDs are oriented at angles of 82°, 68° and 71° with respect to the N6 plane of the HAN ligand, suggesting that the [thd]− ligands dominate the ligand field, whereas the N-donors of the HAN ligand play a relatively minor role. The orientations of the main magnetic axes on the Dy3+ centres in 1 are consistent with that calculated for the related monometallic species [(thd)3Dy(1,10-phenanthroline)].17 Consequently, such an arrangement of magnetic moments does not meet one of the indispensible conditions for an overall toroidal moment, i.e. that the individual anisotropy axes are co-planar.
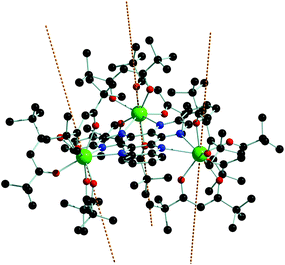 | ||
| Fig. 4 Orientation of the main magnetic axes (dashed lines) in the ground Kramers doublets of 1. Dy = green, N = blue, O = red, C = grey (hydrogen atoms omitted for clarity). | ||
The calculations also allow the total magnetic interactions in 1 to be accounted for, which was achieved using the following Hamiltonian:
The Ising exchange parameters (Jexch) were calculated from Lines parameters by taking into account the angle between the main anisotropy axes of the interacting Dy3+ sites (see ESI† for details). The Lines parameters were determined by fitting the experimental susceptibility data (Fig. S14 and S15†). The dipolar parameters were calculated straightforwardly (Table 2).
| J ex | J dip | |
|---|---|---|
| Dy(1)–Dy(2) | −2.3 | −0.29 |
| Dy(1)–Dy(3) | −2.5 | −0.29 |
| Dy(2)–Dy(3) | −2.5 | −0.28 |
Thus, the dipolar and exchange components, and hence the overall interactions between the pairs of Dy3+ ions, are antiferromagnetic in nature. Furthermore, the energies of the six lowest energy exchange states (i.e. three doublets) in 1 (Table S7†) are all approximately equal to zero, suggesting that the magnetic ground state is frustrated. This property is reminiscent of the frustration observed in the endohedral fullerene Dy3N@C80,18 and in the trimetallic dysprosium SMMs [Cp′2Dy(μ-X)]3, where X contains a soft donor atom, e.g. phosphorus, arsenic, sulphur or selenium (Cp′ = C5H4Me).19
Conclusions
In conclusion, [{(thd)3Dy}3HAN] (1), the first tri-lanthanide complex of the HAN family of ligands, has been synthesized through a rationally designed synthetic method. Dynamic magnetic susceptibility measurements in zero applied field reveal SMM behaviour and the occurrence of two overlapping relaxation processes, which can be resolved in an applied field of 1 kOe. Modest anisotropy barriers of 42 cm−1 and 52 cm−1 were determined, with the two processes being consistent with the presence of two different types of distorted dodecahedral DyO6N2 environments in 1.Ab initio calculations reveal that the main magnetic axes on the Dy3+ centres are oriented approximately perpendicular to the HAN ligand, which precludes SMT properties. However, the antiferromagnetic exchange between pairs of dysprosium ions in 1 allow this complex to be regarded as a frustrated spin system. Studies aimed at enhancing the exchange interactions between the metal centres in 1 through the use of radical derivatives of HAN are underway.
Acknowledgements
R. A. L., L. F. C. and T. P. thank the ERC for the Consolidator Grant ‘RadMag’ (646740). R. A. L. thanks UK EPSRC for Core Capability Grant EP/K039547/1. L. F. C. and V. V. acknowledge the Belgium Science Foundation (FWO) and the Concerted Action Scheme (GOA) of KU Leuven. The authors also thank Dr Fu-Sheng Guo (Manchester) for useful discussions.Notes and references
- (a) P. Zhang, L. Zhang and J. Tang, Dalton Trans., 2014, 44, 3923 RSC; (b) D. N. Woodruff, R. E. P. Winpenny and R. A. Layfield, Chem. Rev., 2013, 113, 5110 CrossRef CAS PubMed; (c) K. S. Pedersen, J. Bendix and R. Clérac, Chem. Commun., 2014, 50, 4396 RSC; (d) J. M. Frost, K. L. M. Harriman and M. Murugesu, Chem. Sci., 2016, 7, 2470 RSC; (e) R. A. Layfield, Organometallics, 2014, 33, 1084 CrossRef CAS.
- (a) J. Liu, Y.-C. Chen, J.-L. Liu, V. Vieru, L. Ungur, J.-H. Jia, L. F. Chibotaru, Y. Lan, W. Wernsdorfer, S. Gao, X.-M. Chen and M.-L. Tong, J. Am. Chem. Soc., 2016, 138, 5441 CrossRef CAS PubMed; (b) S. K. Gupta, T. R. Kumar, G. Rajaraman and R. Murugavel, Chem. Sci. 10.1039/c6sc00279j.
- L. Bogani, Struct. Bonding, 2015, 164, 331 CrossRef CAS.
- M. Urdampilleta, S. Klayatskaya, M. Ruben and W. Wernsdorfer, ACS Nano, 2015, 9, 4458 CrossRef CAS PubMed.
- S. Thiele, F. Balestro, R. Ballou, S. Klyatskaya, M. Ruben and W. Wernsdorfer, Science, 2014, 344, 1135 CrossRef CAS PubMed.
- L. Ungur, S.-Y. Lin, J. Tang and L. F. Chibotaru, Chem. Soc. Rev., 2014, 43, 6894 RSC.
- I. J. Hewitt, J. Tang, N. T. Madhu, C. E. Anson, Y. Lan, J. Luzon, M. Etienne, R. Sessoli and A. K. Powell, Angew. Chem., Int. Ed., 2010, 49, 6352 CrossRef CAS PubMed.
- L. Ungur, S. K. Langley, T. N. Hooper, B. Moubaraki, E. K. Brechin, K. S. Murray and L. F. Chibotaru, J. Am. Chem. Soc., 2012, 134, 18554 CrossRef CAS PubMed.
- J. Tang, I. Hewitt, N. T. Madhu, G. Chastanet, W. Wernsdorfer, C. E. Anson, C. Benelli, R. Sessoli and A. K. Powell, Angew. Chem., Int. Ed., 2006, 45, 1729 CrossRef CAS PubMed.
- L. F. Chibotaru, L. Ungur and A. Soncini, Angew. Chem., Int. Ed., 2008, 47, 4126 CrossRef CAS PubMed.
- (a) J. O. Moilanen, N. F. Chilton, B. M. Day, T. Pugh and R. A. Layfield, Angew. Chem., Int. Ed., 2016, 55, 5521 CrossRef CAS PubMed; (b) J. O. Moilanen, B. M. Day, T. Pugh and R. A. Layfield, Chem. Commun., 2015, 51, 11478 RSC.
- SHAPE Continuous Measures Calculation, version 2.1, Universitat de Barcelona, 2013 Search PubMed.
- S. Kitagawa and S. Masaoka, Coord. Chem. Rev., 2003, 246, 73 CrossRef CAS.
- T. Romero-Morcillo, F. J. Valverde-Muñoz, M. Carmen Muñoz, J. M. Herrera, E. Colacio and J. A. Real, RSC Adv., 2015, 5, 69782 RSC.
- (a) Y.-N. Guo, G.-F. Xu, P. Gamez, L. Zhao, S.-Y. Lin, R. Deng, J. Tang and H.-J. Zhang, J. Am. Chem. Soc., 2008, 132, 8538 CrossRef PubMed; (b) A. Venugopal, F. Tuna, T. P. Spaniol, L. Ungur, L. F. Chibotaru, J. Okuda and R. A. Layfield, Chem. Commun., 2013, 49, 901 RSC.
- (a) L. F. Chibotaru, L. Ungur, C. Aronica, H. Elmoll, G. Pilet and D. Luneau, J. Am. Chem. Soc., 2008, 130, 12445 CrossRef CAS PubMed; (b) L. F. Chibotaru and L. Ungur, J. Chem. Phys., 2012, 137, 064112 CrossRef CAS PubMed; (c) F. Aquilante, et al. , J. Comput. Chem., 2016, 37, 506 CrossRef CAS PubMed.
- (a) G.-J. Chen, C.-Y. Chao, J.-L. Tian, J. Tang, W. Gu, X. Liu, S.-P. Yan, D.-Z. Liao and P. Cheng, Dalton Trans., 2011, 40, 5579 RSC; (b) N. F. Chilton, D. Collison, E. J. L. McInnes, R. E. P. Winpenny and A. Soncini, Nat. Commun., 2013, 4, 2551 Search PubMed; (c) Y. Ma, G.-F. Xu, X. Yang, L.-C. Li, J. Tang, S.-P. Yan, P. Cheng and D.-Z. Liao, Chem. Commun., 2010, 46, 8264 RSC.
- V. Vieru, L. Ungur and L. F. Chibotaru, J. Phys. Chem. Lett., 2013, 4, 3565 CrossRef CAS.
- (a) T. Pugh, F. Tuna, L. Ungur, D. Collison, E. J. L. McInnes, L. F. Chibotaru and R. A. Layfield, Nat. Commun., 2015, 6, 7492 CrossRef PubMed; (b) T. Pugh, A. Kerridge and R. A. Layfield, Angew. Chem., Int. Ed., 2015, 54, 4255 CrossRef CAS PubMed; (c) T. Pugh, V. Vieru, L. F. Chibotaru and R. A. Layfield, Chem. Sci., 2016, 7, 2128 RSC.
Footnote |
| † Electronic supplementary information (ESI) available: Synthetic details, spectroscopic characterization, X-ray crystallography details and crystallographic information file, computational details. CCDC 1478313. For ESI and crystallographic data in CIF or other electronic format see DOI: 10.1039/c6dt01763k |
| This journal is © The Royal Society of Chemistry 2016 |