Compositional dependence of anomalous thermal expansion in perovskite-like ABX3 formates†
Abstract
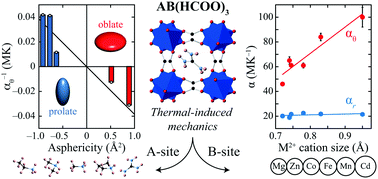
The compositional dependence of thermal expansion behaviour in 19 different perovskite-like metal–organic frameworks (MOFs) of composition [AI][MII(HCOO)3] (A = alkylammonium cation; M = octahedrally-coordinated divalent metal) is studied using variable-temperature X-ray powder diffraction measurements. While all systems show essentially the same type of thermomechanical response—irrespective of their particular structural details—the magnitude of this response is shown to be a function of AI and MII cation radii, as well as the molecular anisotropy of AI. Flexibility is maximised for large MII and small AI, while the shape of AI has implications for the direction of framework hingeing.
- This article is part of the themed collections: Celebrating the 150th anniversary of the German Chemical Society and Flexibility and Disorder in Metal-Organic Frameworks


 Please wait while we load your content...
Please wait while we load your content...