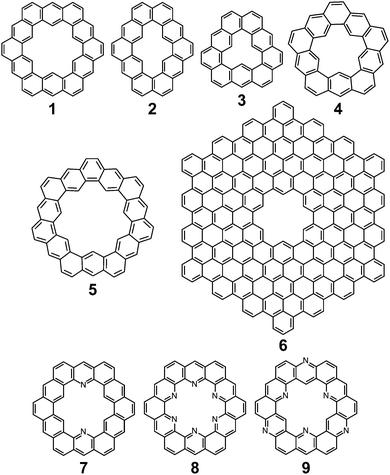
Kekulenes, cycloarenes, and heterocycloarenes: addressing electronic structure and aromaticity through experiments and calculations
Jonathan C.
Buttrick
and
Benjamin T.
King
*
Department of Chemistry, University of Nevada, Reno, 1664 North Virginia Street, Reno, NV 89557, USA. E-mail: king@chem.unr.edu
First published on 10th October 2016
Abstract
Kekulenes, cycloarenes, and heterocycloarenes have attracted much attention though the years, largely due to their electronic structure. The synthesis and characterization of these interesting molecules showed that their π electrons remained delocalized in individual benzenoid-type rings rather than globally delocalized in an annulenoid fashion. This discovery further suggested that the Clar bonding model, not the Kekulé model, is the best representation for depicting the bonding of large macrocyclic aromatic compounds. A plethora of computational studies suggest that cycloarenes gain little, if any, energetic stabilization from global delocalization, obviating the need for the concept of superaromaticity. More recently, cycloarenes have been suggested to serve as models for defects in graphene. Further study into this interesting set of compounds will continue to provide insights into fundamental questions about how aromatic compounds behave.
Key learning points1. The synthesis of cycloarenes required many key techniques that were state of the art for their time.2. Characterization of synthesized cycloarenes supports benzenoid type π electron delocalization as predicted by McWeeny. 3. The electronic structure of cycloarenes supports the use of the Clar bonding model for depicting bonding in large macrocyclic aromatic hydrocarbons. 4. Computational studies suggest that cycloarenes do not experience any superaromatic stabilization from macrocyclic electron delocalization. |
1. Introduction
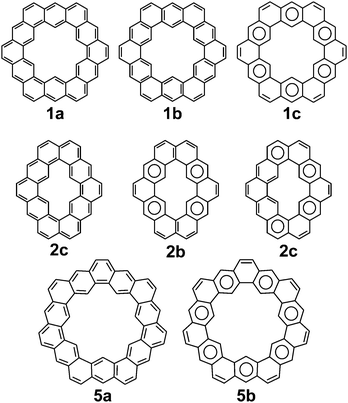
Cycloarenes are defined as, “polycyclic aromatic compounds in which, by a combination of angular and linear annelations of benzene units, fully annelated macrocyclic systems are present enclosing a cavity into which carbon–hydrogen bonds point.”1Fig. 1 shows some examples of this class of molecule, along with some heterocyclic analogues for which the synthesis has been attempted.1–9 Heterocycloarenes have one or more carbon atoms exchanged for a heteroatom and consequently do not fit the above definition of cycloarenes because they lack inward-facing protons, e.g.8. Nonetheless, heterocycloarenes are similar in structure and properties to their hydrocarbon cousins and will be reviewed all the same.1.1. History
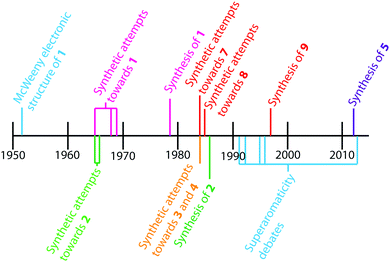
The earliest report of cycloarenes was probably in 1951 when McWeeny discussed the electronic structure of 1.10 His molecular orbital (MO) calculations suggested that despite the large conjugated structure of 1, the electrons remain delocalized only into smaller benzene type rings. These calculations contradicted calculations he made using the semi-classical approach of Pauling,10,11 which suggest the electrons in 1 are globally delocalized throughout the entire molecule. This set off many attempts to synthesize cycloarenes, in hopes that the physical data collected would answer these and future questions about their molecular and electronic structure.In 1965, at the Kekulé Centenial in Bonn, Germany, Staab reported the first attempts towards the synthesis of 1.2 It was at this time 1 was given the name Kekulene, in homage to August Kekulé, due to its planar, conjugated nature and D6h symmetry like benzene. Over the next decade the groups of both Staab12 and Jenny13,14 reported many more attempts at the synthesis of 1. It was not until 1978 that Staab and Diederich achieved the first conclusive synthesis of 1.2
Peter and Jenny first reported attempts at the synthesis of 2 in the mid 1960s (Fig. 2).15,16 More attempts were reported by Staab et al. in 1983.17 The synthesis of 2 was finally achieved by Staab and Funhoff in 1986.3 Staab and Sauer published attempts at 3 and 4 1984,4 however the synthesis of these two compounds has yet to be reported. In 2012, Kumar et al. achieved the synthesis of 5, which they named septulene.5 In 2016, Müllen and co-workers reported the synthesis of the extended cycloarene 6.6
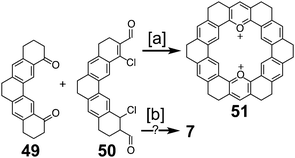
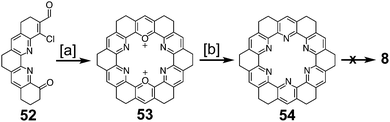
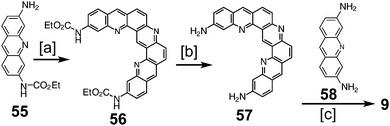
Heterocyclic analogues of kekulene have also been of interest. Katritzky and Marson reported attempts to synthesize diazakekulene 7 in 1983.7 In 1985, Ransohoff and Staab published their attempts at the synthesis of hexaazakekulene 8.8 Tatibouët et al. achieved the first conclusive synthesis of a heterocyclic cycloarene with the synthesis of 9 in 1997.9
1.2. Naming
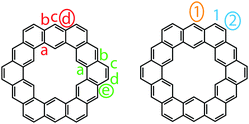
Despite the dearth of successful syntheses of cycloarenes, multiple nomenclatures have been suggested. Naming of such large compounds using IUPAC nomenclature gives long and complicated names that do not easily relate any of the structural characteristics of the compounds.1 The suggested name for 1 by Peter and Jenny, [12]coronaphene, also does not relay much about the structure or symmetry of the compound and leaves ambiguity.13 Consequently, neither of these methods caught on for naming cycloarenes.Staab and Diederich provided their own nomenclature for cycloarenes, which 1 will be used here as an example.1 First, is to indicate the number of benzene annelations present with 1 being called a cyclododecakisbenzene. Next is to indicate the annelation of these benzene units. The letters “a” and “b” are assigned to the preceding annelation, and proceeding clockwise all carbon atoms are labeled continuing with “c”. The letter of the first bond of the next annelation is used to represent that particular annelation type. This gives rise to linear annelations getting a “d” designation (Fig. 3, highlighted in red) and angular annelations receiving an “e” designation (highlighted in green). Although not specified, they tend to always start with the lower letter designation. Thus 1 would be called cyclo[d.e.d.e.d.e.d.e.d.e.d.e.]dodecakisbenzene. As a few more examples, 2 would be cyclo[d.e.d.e.e.d.e.d.e.e.]dekakisbenzene and 3 would be cyclo[d.e.e.d.e.e.d.e.e.]nonakisbenzene.
Kumar et al. suggested using the corannulene nomenclature developed by Agranat et al. to name cycloarenes.5,18 This method uses the name corannulene followed in brackets by a series of numbers each containing another superscripted number. The base number dictates the size of a specified smaller ring while the superscript number indicates the number of carbon atoms within this small ring along the outer perimeter of the overall molecule that are not shared by any other smaller rings. This leads to benzene rings getting a “6” designation with linear annelations getting a superscript “1” (Fig. 3, highlighted in orange) and angular annelations getting a superscript “2” (highlighted in blue). When determining the numbering of the smaller rings, the carbon atom designated C1 when drawn in standard orientation is chosen as the starting point. This gives 1 the name corannulene[62,61,62,61,62,61,62,61,62,61,62,61]. Kumar et al. suggested an abbreviation to this method where 1 is abbreviated as corannulene[(62,61)6] with the subscript 6 clearly indicating the six-fold symmetry of 1. 2 could then be named as corannulene[(62,61,62,61,62)2] and 3 could be named corannulene[(62,61,62)3]. For consistency, all compounds within this review will be named according to the name used most commonly for that compound in the scientific literature, and for clarity, their structures will be provided.
1.3. Bonding models
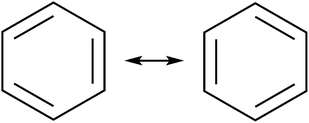
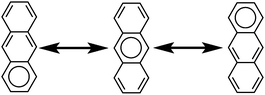
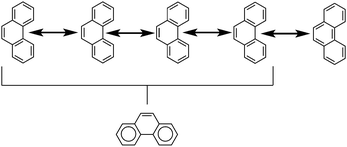
The initial motivation to prepare cycloarenes was to resolve questions concerning their π-electronic structure. We thus review the two dominant valence-bond models for π-electron distribution.Representing delocalization of electrons in aromatic systems is a difficult task of which many methods have been developed. The most widely used is using Kekulé structures.19 Benzene, for example, can be represented as a cyclic arrangement of alternating double and single bonds of which two possible Kekulé structures can be drawn (Fig. 4). Of course, the actual electronic structure of benzene is said to be neither of these structures but a combination of the two. As aromatic systems grow larger, the number of Kekulé structures increases. Naphthalene for example has three Kekulé structures, while anthracene has four and phenanthrene has five.
Another common method is that of Clar's aromatic sextets.20 In this method a circle is used to represent the delocalization of six π electrons. The most characteristic Clar structure is that which contains the maximum number of these aromatic sextets, where no two circles are drawn in adjacent rings, and all remaining electrons can be properly represented by typical Kekulé structures. Unlike with Kekulé structures, the number of Clar structures does not always increase with larger structures. For example, anthracene has three proper Clar structures (Fig. 5) while phenanthrene has only one (Fig. 6). Each Clar structure represents 2n Kekulé structures where n is the number of aromatic sextets.21 In many cases, the Kekulé structures represented by the Clar structure have been found to be more dominant representations of the electronic structure of the molecule. For example, X-ray crystal structures of phenanthrene,22 show that the middle ring has a more olefinic character than the outer two rings. Therefore the Kekulé structure not represented by the Clar structure (Fig. 6, top right) does not contribute as significantly to the real molecular and electronic structure of phenanthrene as the other four do.
These contrasting bonding models relate quite well to the contrasting ideas of Pauling11 and McWeeny.10 The Kekulé bonding model says nothing about which of the large number of possible structures should contribute most, only which ones are possible; therefore, supporting both delocalization theories equally. The use of the Kekulé model is the only way to depict the global delocalization of electrons described by Pauling. While the local delocalization of electrons described by McWeeny can also be shown using Kekulé structures, Clar structures do a better job. When used in conjunction with cycloarenes, Pauling's electron delocalization theory does not support the Clar bonding model, only the Kekulé bonding model. McWeeny's electron delocalization theory, however, supports both bonding models with the Clar model being the better one. Support for the McWeeny theory of electron delocalization goes hand in hand with support for the Clar bonding model. Meanwhile, support for the Pauling theory of electron delocalization undermines the Clar bonding model and vice versa.
1.4. Diamagnetic anisotropy
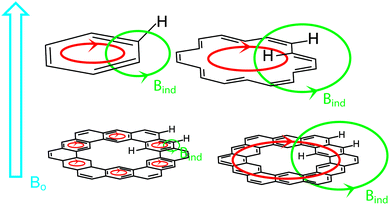
Diamagnetic anisotropy is an interesting phenomenon that is especially evident in aromatic molecules and serves as one of the most easily interpreted markers of aromatic character.23 When an aromatic molecule, such as benzene, is placed in an external magnetic field (B0, Fig. 7, highlighted in blue), the π electrons circulate (highlighted in red) creating their own magnetic field (BIND, highlighted in green) that opposes B0 inside the ring. This is commonly observed in nuclear magnetic resonance (NMR) spectroscopy. In 1H NMR, the protons of benzene exist outside the circulating ring of π electrons, and experience a BIND in the same direction as B0. These two magnetic fields have an additive effect, deshielding the protons to a lower field value (higher ppm chemical shift vs. TMS by convention).[18]Annulene, an especially important example, has protons inside and outside of the circulating flow of π electrons.24 These inner protons experience a BIND in the opposite direction as B0. These two magnetic fields have a subtractive effect, shielding the protons to a higher field value (lower ppm chemical shift vs. TMS by convention). The outer protons are still deshielded like benzene's as they still experience a BIND in the same direction as B0.
Of major interest with cycloarenes is whether the electrons remain delocalized into smaller benzenoid rings (Fig. 7, bottom left) as predicted by McWeeny10 or if they are globally delocalized across the entire molecule (Fig. 7, bottom right) as predicted by the methods of Pauling.11 The chemical shift of these inner protons makes for a very efficient spectroscopic handle for determining how the π electrons are delocalized. If they remain delocalized into benzenoid rings, the inner protons will be deshielded, supporting the electron delocalization theory of McWeeny and the Clar bonding model. If the π electrons are globally delocalized the inner protons will be shielded, supporting the electron delocalization theory of Pauling and undermining the Clar bonding model.
1.5. Superaromaticity
Another concept taught by cycloarenes is superaromaticity, the idea that macrocyclic conjugation in large, cyclic PAHs leads to an increased stabilization of the molecules.25–29 That is, delocalization about the “superring” of the cycloarenes affords additional aromatic character. While closely related to electronic structure, this idea was still debated even after the synthesis of 1 showed that electrons are delocalized mostly into only smaller benzenoid rings. The main thought behind these debates was that even though electrons in cycloarenes remain mostly delocalized into benzenoid rings, they could still have minor global delocalization that can give rise to superaromatic character.1.6. Significance of cycloarenes
The contrasting theories based on the ideas of McWeeny10 and Pauling11 brought about much debate as to how electrons are delocalized in large aromatic systems, and cycloarenes are ideal test cases of these competing hypotheses. This serves as an excellent example as to how the synthesis of complex and interesting molecules can answer fundamental scientific questions. In particular, the 1H NMRs of successfully synthesized cycloarenes all exhibited deshielding of the inner protons. This deshielding effect showed that electrons in these molecules remain delocalized in small benzenoid rings, as opposed to being globally delocalized across the entire molecule.1–3,5 This realization shows that the McWeeny electron delocalization theory is the valid one, not the Pauling theory. The Clar bonding model is therefore a more accurate representation for large macrocyclic PAHs than the Kekulé bonding model.Many computational studies have been carried out in an attempt to quantify superaromaticity in cycloarenes. Although some of these studies have shown that cycloarenes might enjoy some amount of superaromaticity,25,27 most studies agree that this is more likely caused by accumulation of errors in the computational methods26 or that any stabilization cycloarenes might experience due to superaromaticity is just too small compared to the overall energy of the molecule.26,28,29 Because these values are so small, or possibly nonexistent, computational studies of cycloarenes suggest that there is little, if any, need for the concept of superaromaticity.
A more modern application of cycloarenes is that they can serve as models for defects in graphene.30 Interest in graphene has grown astronomically in recent years due to its remarkable properties and possible applications.31 Cycloarenes can help us to better understand graphene, how it behaves, and how it can be used. Modern methods for making graphene almost always lead to imperfections of various degrees. 3, for example, is a model of a single point defect in graphene made by the removal of a single carbon atom from the graphene lattice, and 1 is a larger hole model made by removing a full benzenoid unit from the graphene lattice.
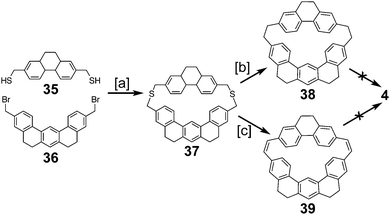
4 and 5 are interesting non-graphitic cycloarenes, in that they cannot be excised from a graphene lattice. Graphene can contain defects without six-fold symmetry.32 These defects lead to altered properties and performance of the system.33 Scott, Itami, and coworkers have recently shown how large PAHs with non-six membered rings can serve as excellent models for defects in graphene.34 While their work is a great model for fully carbon defects, cycloarenes are excellent examples for holes that exist in graphene.
2. Synthesis
The syntheses of cycloarenes are interesting in their own right. They showcase many cutting edge strategies for the synthesis of PAHs at that time. Most syntheses employ three key steps: macrocyclization, completion of the σ bond framework, and aromatization to the final product. These steps are not always carried out in the same order and in some cases multiple steps are carried out at once. Some of these then state of the art reactions included sulfur extrusion, Suzuki coupling, ring-closing metathesis (RCM), Scholl oxidation, and 2,3-dichloro-5,6-dicyano-1.4-benzoquinone (DDQ) oxidation reactions.2.1. Kekulene
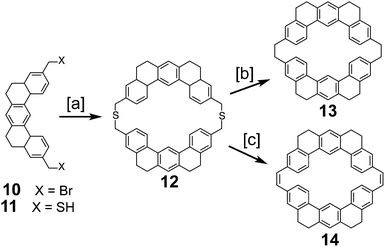
In 1978, after over a decade of attempts, Staab and Diederich reported the first successful and conclusive synthesis of 1.1,2 This approach (Scheme 1) utilized a key sulfur extrusion method in which dibromide 10 was reacted with dithiol 11 to dithiacyclophane 12. Photolysis of 12 then gave macrocycle 13 while Stevens rearrangement and sulfoxide elimination of 12 gave 14. Both 13 and 14 contain the carbon atom skeleton of 1. Although, this is not the first reported synthesis of 13,12 it is the first with a somewhat satisfactory yield.With sizable quantities of 13 and 14 in hand, many routes of oxidative C–C bond formation to 1 were explored (Scheme 2).1 Overall, two new σ bonds and either four or six new π bonds needed to be formed, with each approach selectively forming only a few of these at a time. The first approach utilized DDQ to selectively dehydrogenate the dihydrophenanthrene type bridges of 13 to give macrocycle 15; however, all attempts to further oxidize 15 to 1 were unsuccessful.
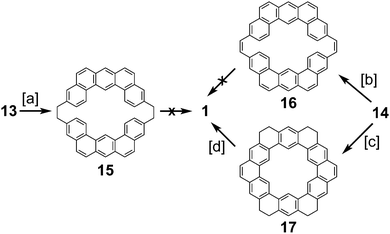 | ||
| Scheme 2 [a] DDQ, toluene, reflux, 24 h, 81%. [b] DDQ, benzene, reflux, 24 h, 66%. [c] I2, benzene, 300 W, 10 min, 70%. [d] DDQ, 1,2,4-trichlorobenzene, 100 °C, 3 d, 91%. | ||
The next approach used DDQ to dehydrogenate 14 to macrocycle 16. Photochemical cyclodehydrogenation attempts of 16 were unsuccessful. This is most likely due to the highly twisted structure of 16 brought on by the steric crowding of the inner protons attached to the carbon atoms between which the new σ bond is desired. This steric crowding does not allow 16 to adopt an appropriate geometry for photochemical cyclization. Photochemical cyclization of 14, however, proceeded well, yielding macrocycle 17. Presumably, the increased flexibility of 14 over 16 contributed to this success. 17 is the first molecule with the complete σ bond network of 1 to be conclusively synthesized. The dehydrogenation of 17 was extremely difficult due to its low volatility and low solubility, but using the uncommon solvent 1,2,4-trichlorobenzene 1 was finally obtained in measurable quantities (45 mg).
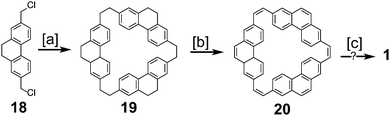
Parallel to the efforts of Staab and Diederich, Jenny and coworkers made attempts towards the synthesis of 1 (Scheme 3), which they called [12]coronaphene.13,14 Their most successful attempt utilized dichloride 18 to form macrocycle 19. Simultaneous dehydrogenation and halogenation, followed by dehalogenation gave macrocycle 20. Photochemical cyclodehydrogenation attempts of 20 gave mass spectroscopic evidence hinting at the formation of 1, however isolation or further characterization of this desired product was not reported.
2.2. Other graphitic cycloarenes
 | ||
| Scheme 4 [a] Bromobenzene, Li, ether, benzene, 60–70 °C, 30 min, 3%. [b] AlCl3, CS2. Pd/C, CO2, 320–340 °C. | ||
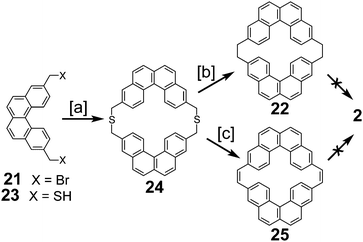
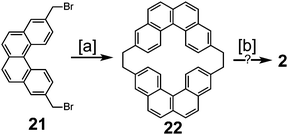
In 1983, Staab et al. reported an attempted synthesis of cycloarene 2 (Scheme 5), taking a disconnection similar to that of the synthesis of 1.17 Dibromide 21 and dithiol 23 reacted to give dithiacyclophane 24. Two different sulfur extrusion methods applied to 24 produced macrocycles 22 and 25. Scholl reaction of 22 was only successful in installing one of the two required σ bonds. Similarly, photochemical cyclodehydrogenation of 25 was also successful in installing only one of the two required σ bonds.
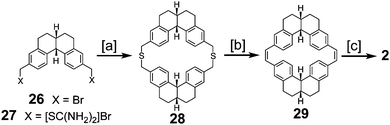
Staab and Funhoff reported the first successful approach to 2 in 1986 (Scheme 6) utilizing a similar approach to the previous one but incorporating more flexibility in the macrocycles, the same trick that was applied in the successful synthesis of 1.3 Dibromide 26 and diisothiouronium salt 27 reacted to produce dithiacyclophane 28, which then yielded macrocycle 29via sulfur extrusion. Photochemical cyclization gave a mixture of isomers that could then be dehydrogenated to give 2 for the first time in a measurable quantity.
2.3. Non-graphitic cycloarenes
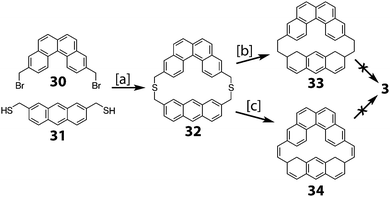
2.4. Multi-stranded cycloarenes
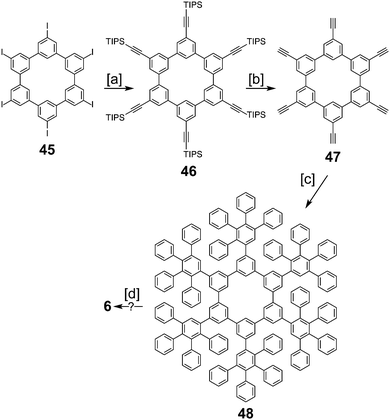
In 2016, Müllen and co-workers reported the synthesis of the extended cycloarene 6 (Scheme 11).6 Sonogashira coupling of hexa-m-phenylene 45 with TIPS-acetylene produced macrocycle 46, which was subsequently deprotected to give 47. Six-fold Diels–Alder cycloaddition with 2,3,4,5-tetraphenylcyclopenta-2,4,-dienone yielded dendrimer 48. MALDI mass spectrometry was used to identify 6 as the product of cyclodehydrogenation of 48.2.5. Heterokekulenes
3. Molecular and electronic structure
The molecular and electronic structure of cycloarenes has long been of interest. The highly conjugated nature of cycloarenes gives rise to an extraordinarily high amount of Kekulé structures. In stark contrast, there exist a low number of Clar structures with the maximum number of aromatic sextets. 1, for example, has been determined to have 200 different Kekulé structures35 while it has only one Clar structure with six aromatic sextets (Fig. 8). Of particular interest of these 200 Kekulé structures are those like 1a where the structure is composed of two concentric annulenes bridged by radial single bonds, and those like 1b where the structure is composed of six angularly annelated benzenoid rings, just like in the Clar model 1c. 2 is of interest because it can also be represented as two concentric annulenes 2a yet it has nine different Clar representations with a maximum number of aromatic sextets, two of which are shown in 2b and 2c. 5 is of interest because it cannot be represented as two concentric annulenes, instead requiring at least one radial double bond as seen in 5a. As with 1, however, 5 also has only one Clar structure with seven aromatic sextets as seen in 5b. Multiple computational studies have been performed but give contrasting results. The semi-classical approach of Pauling11 suggests structures more like 1a while MO calculations by McWeeny10 were the first to suggest structures more like 1b and 1c.3.1. 1H NMR
One way to elucidate the electronic structure of these cycloarenes would be to use nuclear magnetic resonance (NMR) spectroscopy. Structures like 1a would exhibit a different diamagnetic anisotropy than those like 1b and 1c. 1a, being comprised of two concentric [4n + 2] annulenes, allows for the delocalization of electrons across the entire molecule and would exhibit 1H NMR chemical shifts similar to [18]annulene, where the outer protons are deshielded and the inner protons are shielded due to the flow of electrons in the molecule.24 In contrast, structures like 1b and 1c would contain only localized ring currents, so both the inner and outer protons would be deshielded. All NMR chemical shifts discussed are reported in ppm vs. TMS.The acquisition of the 1H NMR of 1 in 1978 was difficult due to its extremely low solubility in all organic solvents.2 The first suitable spectrum was reported to have been taken in [d3]-1,3,5-trichlorobenzene (Table 1, column 1) at about 200 °C in an 80 MHz instrument for about 50![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 scans. Three reproducible signals were seen with an intensity ratio of 2
000 scans. Three reproducible signals were seen with an intensity ratio of 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 at 7.94, 8.37, and 10.45 ppm for the outer vinyl, outer aryl, and inner type protons respectively. No signals were seen shifted upfield. In 1983, spectra in [d2]-1,2,4,5-tetrachlorobenzene (Table 1, column 2) at 155 °C were reported with similar signals at 8.01, 8.45, and 10.47 ppm.1,36 The downfield shift of the inner protons suggests that the electronic structure is indeed more like that of 1b and 1c than 1a.
1 at 7.94, 8.37, and 10.45 ppm for the outer vinyl, outer aryl, and inner type protons respectively. No signals were seen shifted upfield. In 1983, spectra in [d2]-1,2,4,5-tetrachlorobenzene (Table 1, column 2) at 155 °C were reported with similar signals at 8.01, 8.45, and 10.47 ppm.1,36 The downfield shift of the inner protons suggests that the electronic structure is indeed more like that of 1b and 1c than 1a.
| Proton type | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
|---|---|---|---|---|---|---|---|
| Outer vinyl | 7.94 | 8.01 | 7.70 | 8.01 | 8.01 | 8.22 | 7.58 |
| Outer aryl | 8.37 | 8.45 | 8.25 | 8.78 | 8.78 | 8.71 | 8.07 |
| Inner | 10.45 | 10.47 | 10.26 | 8.67 | 9.87 | 10.42 | 9.69 |
Many calculations have predicted chemical shifts for 1 that also support an electronic structure like 1b and 1c (Table 1). Using the methods of McWeeny,10 Wilcox calculated the chemical shifts of 1 (column 3).36 In 1972, Ege and Vogler calculated the chemical shifts of 1 using a modified Hückel Molecular Orbital (HMO) theory (column 4).37 Staab et al. reported the chemical shifts of 1 calculated using a similar method to Ege and Vogler but also took into account additional van der Waals deshielding (column 5).36 In 1979, Vogler calculated chemical shifts of 1 with the coupled Hartree–Fock (HF) perturbation theory (column 6).38 In 2001, Steiner et al. predicted the chemical shifts of 1 using current-density maps (column 7).39 These last calculations also suggested that the higher deshielding seen of the inner protons over the outer protons is due to a paramagnetic rotating ring current around the inner “hub” of 1 and not from just van der Waals deshielding.
The experimental results for 2 and 5 also suggest electronic structures more like 2b, 2c, and 5b.3,5 The 1H NMR of 2 in [d2]1,2,4,5-tetrachlorobenzene exhibited chemical shifts of 8.11, 8.11, 8.29, and 8.65 ppm for the outer protons and 9.56 ppm for the inner protons. The 1H NMR of 5 in [d4]1,2-dichlorobenzene exhibited chemical shifts of 7.86 and 8.63 ppm for the outer protons and 10.19 ppm for the inner protons. Because the spectra of 1, 2, and 5 were recorded in different solvents they cannot be directly compared; however, all three show evidence of a benzenoid over an annulenoid type electronic structure.
3.2. X-Ray crystallography
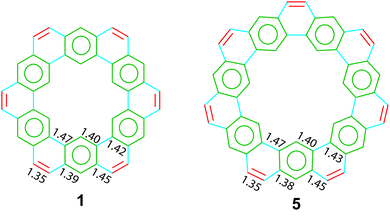
The crystal structures of two cycloarenes, 1 and 5, are known.5,36,40 The average unique C–C bond lengths (Fig. 9) tell much about the electronic structure of these compounds. These bond lengths can be grouped into three categories that fit quite well with their Clar representations. The first group (highlighted in green) agrees with typical bond lengths of benzenoid rings. The second group (highlighted in blue) is much longer and indicates a high single-bond character. The final group (highlighted in red) is very close to that of normal C–C double bonds.The crystal structures of 1 and 5 reveal just how similar these two compounds are. The C–C bond lengths of these two compounds are indeed essentially the same. Additionally, despite the planar nature of 1versus the non-planar nature of 2, the two compounds have surprisingly similar three-dimensional packings (Fig. 10). Both compounds were found to pack into slipped stacks that make up a herringbone pattern. The similarity in the molecular structure of 1 and 5 further suggests that the Clar model, which is also similar for the two compounds, is a better representation than the Kekulé model, which has some drastic differences such as total number of Kekulé structures and 5 requiring at least one radial double bond in all Kekulé structures while 1 does not.
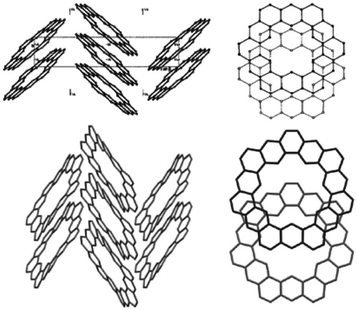 | ||
| Fig. 10 The crystal packing of 1 (top) and 2 (bottom). Figure reproduced with permission from ref. 5. | ||
3.3. Electronic spectra
The fluorescence and phosphorescence of 1 were recorded in a polycrystalline matrix of 1,2,4,5-tetrachlorobenzene at 1.3 K using the method of Shpol'skii.36,40,41 Despite being both symmetry and spin-forbidden, 0–0 bands are observed in the fluorescence and phosphorescence spectra. This has been attributed to an external heavy atom effect and a reduction in symmetry of first excited singlet and triplet states brought about by the chosen solvent. Because these 0–0 bands are observed with high intensity in the phosphorescence spectrum, it was possible to obtain optical detection magnetic resonance (ODMR) spectra, where the optical measurement is combined with electron spin resonance spectroscopy.42 With ODMR, the zero field splitting parameters |D| and |E| were determined.36,40,41 Of particular interest were the |D| values, which measure the dipolar coupling of the triplet electrons. By definition, |D| values are a function of the inverse average distance between these electrons; therefore, they should decrease with the increase in size of a π system. Anthracene, for example has a much smaller value than naphthalene, which has a much smaller value than benzene (Table 2). The |D| value of 1 was found to be surprisingly high, and in fact, is close to that of phenanthrene. This data suggests that the electrons in 1 are not coupled over long distances, and instead are localized into smaller regions, as depicted by the Clar model.| Compound | |D| (cm−1) |
|---|---|
| Benzene | 0.1581 |
| Naphthalene | 0.0994 |
| Anthracene | 0.0694 |
| Phenanthrene | 0.1053 |
| 1 | 0.1039 |
3.4. Nucleus independent chemical shifts
Nucleus independent chemical shifts (NICS) values are a standard method for calculating the aromaticity of compounds.43 Values at ring centers can be easily computed and are useful in that they are not highly dependent on the size of the system and can probe effects within individual rings of a polycyclic system. NICS-1 values differ from standard NICS values in that the probe is placed 1 Å above the ring center, and are regarded as a better measure of aromaticity. The more negative this value the more aromatic character (−9.7 ppm for benzene), the more positive this value, the more antiaromatic character (27.6 ppm for cyclobutadiene), and values close to zero show a more nonaromatic character (−2.2 ppm for cyclohexane).27 The NICS-1 values calculated for 1 and 5 validate the X-ray crystallographic data by showing more aromatic character of the benzenoid rings with higher values of −11.5 ppm for 1 and −11.3 ppm for 5 and showing less aromatic character for the olefinic rings with lower values of −6.3 ppm for 1 and −5.8 ppm for 5.5 These results also suggest the Clar model is a better representation for the electronic structure of 1 and 5 than the Kekulé model.4. Superaromaticity
Many attempts have tried to quantify the thermodynamic stabilization, if any, from macrocyclic conjugation in cycloarenes, also known as superaromaticity.25–29 These attempts are all alike in that they first calculate the overall aromaticity of the system, then determine superaromaticity by subtracting the aromaticity of a superaromaticity free reference. The methods differ in the way aromaticity is computed and how the superaromaticity free reference is defined.4.1. Additive nodal increments
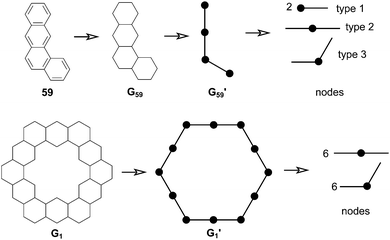
In 1991, Ciodlowski et al. attempted to use an additive nodal increment (ANI) approach to determine the superaromatic stabilization energy of 1.25 Benzenoid hydrocarbons can be represented as molecular graphs G (Fig. 11). A corresponding “dualist” G′ can be created for this graph by replacing each hexagonal ring with a dot and connecting each dot with a straight line. G′ can be broken up into its different types of vertices, called nodes. Benzo[a]anthracene 59, for example can be represented as the graph G59 and its dualist G59′. Splitting apart G59′, three types of nodes are formed: two of type 1, one of type 2, and one of type 3. Similarly 1 can be represented by the graph G1 and its dualist G1′. Splitting up G1′ gives twelve total nodes: six of type two and six of type three. Isonodal hydrocarbons have been shown to be of about the same Hückel total π-electron energy, Eπ. These energies can be approximated by eqn (1) where ni is the number of nodes of type i, and Ei is the nodal energy increment for nodes of type i. Eπ should then, in theory, be additive.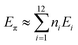 | (1) |
Ciodlowski et al. were able to approximate the energy of the desired nodes using the calculated energies of some small PAHs. The energy for node type 2 for example could be calculated by subtracting the energy of anthracene from that of tetracene, since anthracene has two type 1 nodes and one type 2 nodes while tetracene also has two type 1 nodes but has two type 2 nodes. By calculating the total HF energy, EHF, for anthracene, phenanthrene, tetracene, 59, and chrysene, they were able to approximate the energy of nodes type 1, 2, and 3 using eqn (2). From these values (Table 3) the ANI energy, EANI, of 1 could be approximated using eqn (3). Since EANI was determined from non-superaromatic PAHs, the difference between EHF and EANI should represent a molecule's superaromatic stabilization energy (SSE). Thus 1 was determined to have a SSE of 52.4 mhartree (32.9 kcal mol−1) at the STO-3G level of theory and 40.5 mhartree (25.4 kcal mol−1) at the 6-31G** level of theory (Table 4).
| EHF ≈ n1E1 + n2E2 + n3E3 | (2) |
| EANI = 6E2 + 6E3 | (3) |
| Level of theory | ||
|---|---|---|
| HF/STO-3G | HF/6-31G** | |
| Total energies | ||
| Anthracene | −529.4725 (−529.4724) | −536.0167 (−536.0167) |
| Phenanthrene | −529.4874 (−529.4875) | −536.0277 (−536.0278) |
| Tetracene | −680.2535 (−680.2564) | −688.6601 (−688.6625) |
| Benzo[a]anthracene | −680.2770 (−680.2714) | −688.6783 (−688.6736) |
| Chrysene | −680.2838 (−680.2865) | −688.6824 (−688.6847) |
| Nodal energy increments | ||
| Node type 1 | −189.3442 | −191.6854 |
| Node type 2 | −150.7840 | −152.6459 |
| Node type 3 | −150.7990 | −152.6570 |
| Error values | ||
| Rms error/ring | 0.0008 | 0.006 |
| Maximal error/ring | 0.0014 | 0.0012 |
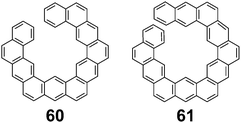
In 1992, Aihara suggested that these differences in energy are more likely due to an accumulation of errors in the energy increments that increase as the molecules get larger.26 This suggestion comes from the fact that acyclic PAHs 60 and 61 (Fig. 12), which are similar in size to 1 but cannot be superaromatic, also were found to have a difference between EHF and EANI similar to that of 1.
4.2. Conjugated circuits
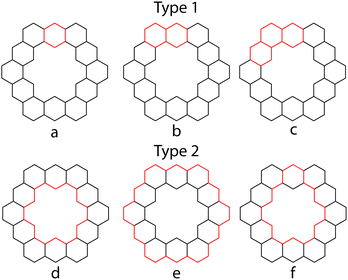
PAHs contain many cyclic paths throughout their structures. If there exists a Kekulé structure in which one of these paths is composed of alternating single and double bonds, this path is known as a conjugated circuit. In 1977, Randić demonstrated that all (4n + 2) conjugated circuits lower the energy of the system, while 4n conjugated circuits raise the energy of the system.44 Aihara applied this concept of conjugated circuits in an attempt to explain superaromaticity in 1.31 All calculations in this section are performed at the HMO level of theory.The conjugated circuits in 1 are all (4n + 2) and can be divided into two types. Type 1 circuits are those that contain one or more consecutive benzene rings while type 2 circuits are those that surround the inner cavity. 1 has been determined to contain 132 type 1 circuits and 4096 type 2 circuits.26Fig. 13 outlines a few examples of these.
Herndon45 and Randić44 have shown that the Dewar resonance energy (DRE) can be expressed in terms of conjugated circuits, and that smaller circuits, such as six and ten-membered ones, are more relevant than the larger circuits, such as eighteen or larger membered ones. Using Randić's conjugated circuit method,441 was estimated to have a DRE of 145.8 kcal mol−1,26 which is in good agreement with the calculated DRE of 141.4 kcal mol−1. The largest contribution of any type 2 conjugated circuit is only 0.02 kcal mol−1 from that of eighteen membered circuit d. Since any SSE experienced by 1 must come from type 2 conjugated circuits, and the total contribution of these circuits to the overall aromatic character of 1 is so low, Aihara concluded that using this method 1 appears to not be superaromatic.
Another approach of Aihara to explain the superaromaticity of 1 using conjugated circuits, compared the circuit resonance energies (CREs) of the conjugated circuits within 1.26 CREs have been shown to approximately measure the contribution of a conjugated circuit to the overall aromaticity of a system.46 CREs of the conjugated circuits in 1 (Table 5), show that the smaller type 1 conjugated circuits contribute much more to the aromaticity of 1 than the superaromatic type 2 conjugated circuits.26 This is in accordance with the findings using the methods of Randić.
| Circuit | CRE |
|---|---|
| a | 0.1400 |
| b | 0.0446 |
| c | 0.0327 |
| d | 0.0036 |
| e | 0.0017 |
| f | −0.0002 |
Aihara also showed how ring currents can be used to determine superaromaticity within 1.26 It has been shown that ring currents of individual conjugated circuits can be added up to give the overall ring current of the system. When 1 is placed in an external magnetic field, the overall ring current can, therefore, be said to be comprised of the ring current of all type 1 and type 2 conjugated circuits. The ring currents due to just type 2 conjugated circuits can be summed up to give the superaromatic ring currents. By definition, diamagnetic ring currents are drawn clockwise. A comparison of the calculated ring currents (Fig. 14) shows that the superaromatic ring currents in 1 are much smaller than the overall ring currents in 1, and therefore do not contribute much to the overall aromaticity of 1.
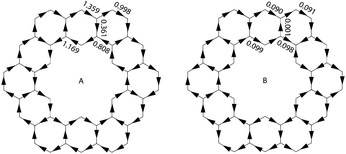 | ||
| Fig. 14 Overall (A) and superaromatic type 2 (B) ring currents within 1. Clockwise currents are diamagnetic. | ||
4.3. Polynomial references
Secular polynomials are graph theoretically defined equations that are constructed using the mathematical equivalencies of graphs, secular matrices, and characteristic polynomials.47 For chemical compounds, graphs of the compounds are broken apart into smaller subgraphs that are then compiled to construct the overall secular polynomial of the compound. A polynomial reference can then be constructed by deleting specific components of the overall secular polynomial. Secular polynomials have been shown to be useful in determining the standard aromaticity of compounds.48 By deriving the secular polynomial of a compound and deleting the cyclic components, the reference polynomial is obtained. The difference in energy between these two polynomials gives the aromatic stabilization energy of the compound.In 1995, Zhou tried to determine the superaromaticity of 1 using hardness indices.27 He claims this to be a superior method because it is much less sensitive to deviations caused by poor reference structures. This is important because the superaromaticity, if any, is so much smaller compared to traditional benzenoid aromaticity than the calculated values for superaromaticity, which are too close to the potential error of the previous methods. Superaromaticity was determined by topologically defining a secular polynomial reference structure derived from the secular polynomial of the molecule of interest. Derivation of this reference polynomial was said to be straightforward yet tedious. Superaromaticity (ηsr) could then be determined using eqn (4) where η is the hardness of the molecule of interest and ηsac is the hardness of the superaromaticity free reference. A positive ηsr indicates superaromaticity while a negative ηsr indicates superantiaromaticity. 1 was determined to have a ηsr of 0.0266 |β|, much smaller than that of 0.0744 |β| for coronene and 0.1031 |β| for corannulene tetraanion. From this relatively small value compared to the overall hardness for 1 of 0.4372, 1 was claimed to experience some slight superaromatic stabilization.
| ηsr = η − ηsac | (4) |
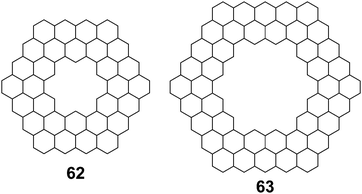
Aihara et al. also used polynomial defined references to determine superaromaticity within cycloarenes in 2013.29 Again this method has been claimed to determine SSE with a high degree of precision. Using HMO theory, they determined the total π-binding energy for many different macrocyclic PAHs, some of which are given in Table 6. Subtracting out the graph-theoretically exact polynomial reference, SSE was also determined for these compounds. The SSE for 1 and 5 was determined to be minimal, in agreement with previous methods. It is worth noting, however, that evenly stranded variants such as 62 and 63 showed much greater SSE (Fig. 15).
| Compound | Total π-binding energy (|β|) | SSE (|β|) |
|---|---|---|
| 1 | 68.610210 | 0.003483 |
| 5 | 80.041176 | 0.000002 |
| 62 | 132.513299 | 0.048368 |
| 63 | 185.085176 | 0.028038 |
4.4. Aromatic stabilization energy and diamagnetic susceptibility
In 1996, Jiao and Schleyer attempted to quantify the SSE of 1 in a method similar to the ANI approach of Ciodlowski et al. Jiao and Schleyer's approach was to calculate the aromatic stabilization energy (ASE) of 1, which measures the cyclic electron delocalization, and therefore the aromaticity, of a molecule.28 The SSE of 1 would therefore be the difference between the ASE of 1 and its smaller, non-superconjugated benzenoid hydrocarbon components. Using benzene, anthracene, phenanthrene, naphthalene, and 1,2.7,8-dibenzanthracene as reference compounds, the non-superaromatic ASE of 1 can be determined using homodesmotic eqn (5a)–(5c).| 3[anthracene + phenanthrene − 2 benzene] = kekulene | (5a) |
| 6[anthracene + phenanthrene − 2 naphthalene] = kekulene | (5b) |
| 6[1,2.7,8-dibenzanthracene − phenanthrene] = kekulene | (5c) |
The calculated ASEs (Table 7) paired with eqn (5a)–(5c) provide the SSE of 1 summarized in Table 8. These values are much smaller than those determined by Ciodlowski et al. with eqn (5c) actually giving slightly positive values. Based on these findings, it was concluded that 1 does not experience any significant extra stabilization due to superaromaticity.
| Compound | E (HF/3-21G) | E (HF/3-21G) | χ anis | Λ |
|---|---|---|---|---|
| 1 | −1821.55153 | −1821.55153 | −769.7 | −227.8 |
| Anthracene | −533.00347 | −533.00347 | −203.1 | −56.1 |
| Phenanthrene | −533.01572 | −533.01572 | −190.5 | −52.0 |
| Naphthalene | −381.21581 | −381.21581 | −135.0 | −36.5 |
| 1,2.7,8-Dibenzanthracene | −836.60869 | −836.60869 | ||
| Benzene | −229.41945 | −229.41945 | −69.8 | −16.7 |
Similarly, Jiao and Schleyer used diamagnetic susceptibility exaltation (Λ) and diamagnetic susceptibility anisotropy (χanis) to determine the superaromaticity of 1.28 The extra Λ and χanis of 1 can be determined using eqn (5a) and (5b) as done with ASE. These values (Table 8) were found to be small for the large size of 1 and therefore imply no superaromatic stabilization.
5. Conclusions
Cycloarenes have taught us much about some fundamental concepts in chemistry. Their preparation demonstrated that their electrons tend to remain delocalized into benzenoid rings as predicted by McWeeny and they are best depicted using Clar structures. Computational studies of cycloarenes have shown that they do not gain much, if any, superaromatic stabilization from macocyclic conjugation. Thus, superaromaticity is not a relevant concept, at least for cycloarenes. Their potential use as models for defects in graphene has only just been looked into. While not many examples within this interesting class of molecules have been synthesized, especially in recent years, cycloarenes still have very much to teach us and should continue to be of intense interest.Acknowledgements
We thank the R.C. Fuson endowment at the University of Nevada, Reno for support.References
- H. A. Staab and F. Diederich, Chem. Ber., 1983, 116, 3487 CrossRef CAS.
- F. Diederich and H. A. Staab, Angew. Chem., Int. Ed. Engl., 1978, 17, 372 CrossRef.
- D. J. Funhoff and H. A. Staab, Angew. Chem., Int. Ed. Engl., 1986, 25, 742 CrossRef.
- H. A. Staab and M. Sauer, Liebigs Ann. Chem., 1984, 1984, 742 CrossRef.
- B. Kumar, R. L. Viboh, M. C. Bonifacio, W. B. Thompson, J. C. Buttrick, B. C. Westlake, M. Kim, R. W. Zoellner, S. A. Varganov, P. Mörschel, J. Teteruk, M. U. Schmidt and B. T. King, Angew. Chem., Int. Ed., 2012, 51, 12795 CrossRef CAS PubMed.
- U. Beser, M. Kastler, A. Maghsoumi, M. Wagner, C. Castiglioni, M. Tommasini, A. Narita, X. Feng and K. Müllen, J. Am. Chem. Soc., 2016, 138, 4322–4325 CrossRef CAS PubMed.
- A. R. Katritzky and C. M. Marson, J. Am. Chem. Soc., 1983, 105, 3279 CrossRef CAS.
- J. E. B. Ransohoff and H. A. Staab, Tetrahedron Lett., 1985, 26, 6179 CrossRef CAS.
- A. Tatibouët, R. Hancock, M. Demeunynck and J. Lhomme, Angew. Chem., Int. Ed. Engl., 1997, 36, 1190 CrossRef.
- R. McWeeny, Proc. Phys. Soc., London, Sect. A, 1951, 64, 921 CrossRef.
- L. Pauling, J. Chem. Phys., 1936, 4, 673 CrossRef CAS.
- F. Vögtle and H. A. Staab, Chem. Ber., 1968, 101, 2709 CrossRef.
- W. Jenny and R. Paioni, Chimia, 1968, 22, 248 CAS.
- W. Jenny and R. Paioni, Chimia, 1969, 23, 41 CAS.
- W. Jenny and R. Peter, Angew. Chem., Int. Ed. Engl., 1965, 4, 979 CrossRef.
- R. Peter and W. Jenny, Helv. Chim. Acta, 1966, 49, 2123 CrossRef CAS.
- H. A. Staab, F. Diederich and V. Čaplar, Liebigs Ann. Chem., 1983, 1983, 2262 CrossRef.
- I. Agranat, B. A. Hess and L. J. Schaad, Pure Appl. Chem., 1980, 52, 1399 CrossRef CAS.
- E. V. Anslyn and D. A. Dougherty, in Modern Physical Organic Chemistry, ed. J. Murdzek, University Science Books, United States, 2006, ch. 1, pp. 20–22 Search PubMed.
- E. Clar, The Aromatic Sextet, Wiley, New York, 1972 Search PubMed.
- S. J. Cyvin, J. Brunvoll, B. N. Cyvin and E. Brendsdal, Spectrochim. Acta, Part A, 1988, 44, 975 CrossRef.
- B. S. Basak, Indian J. Phys., 1950, 24, 309 CAS.
- T. Heine, C. Corminboeuf and G. Seifert, Chem. Rev., 2005, 105, 3889 CrossRef CAS PubMed.
- J.-M. Gilles, J. F. M. Oth, F. Sondheimer and E. P. Woo, J. Chem. Soc. B, 1971, 2177 RSC.
- J. Cioslowski, P. B. O'connor and E. D. Fleischmann, J. Am. Chem. Soc., 1991, 113, 1086 CrossRef CAS.
- J. Aihara, J. Am. Chem. Soc., 1992, 114, 865 CrossRef CAS.
- Z. Zhou, J. Phys. Org. Chem., 1995, 8, 103 CrossRef CAS.
- H. Jiao and P. V. R. Schleyer, Angew. Chem., Int. Ed. Engl., 1996, 35, 2383 CrossRef.
- J. Aihara, M. Makino, T. Ishida and J. R. Dias, J. Phys. Chem. A, 2013, 117, 4688 CrossRef CAS PubMed.
- F. Banhart, J. Kotakoski and A. V. Krasheninnikov, ACS Nano, 2011, 5, 26 CrossRef CAS PubMed.
- K. S. Novoselov, V. I. Fal'ko, L. Colombo, P. R. Gellert, M. G. Schwab and K. Kim, Nature, 2012, 490, 192 CrossRef CAS PubMed.
- R. Zan, Q. M. Ramasse, U. Bandert and K. S. Novoselov, Nano Lett., 2012, 12, 3936 CrossRef CAS PubMed , as an extreme example.
- V. Kapko, D. A. Drabold and M. F. Thorpe, Phys. Status Solidi B, 2010, 247, 1197 CrossRef CAS.
- K. Kawasumi, Q. Zhang, Y. Segawa, L. T. Scott and K. Itami, Nat. Chem., 2013, 5, 739 CrossRef CAS PubMed.
- J. Aihara, Bull. Chem. Soc. Jpn., 1976, 49, 1429 CrossRef CAS.
- H. A. Staab, F. Diederich, C. Krieger and D. Schweitzer, Chem. Ber., 1983, 116, 3504 CrossRef CAS.
- G. Ege and H. Vogler, Theor. Chim. Acta, 1972, 26, 55 CrossRef CAS.
- H. Vogler, Tetrahedron Lett., 1979, 20, 229 CrossRef.
- E. Steiner, P. W. Fowler, L. W. Jenneskens and A. Acocella, Chem. Commun., 2001, 659 RSC.
- C. Krieger, F. Diederich, D. Schweitzer and H. A. Staab, Angew. Chem., Int. Ed. Engl., 1979, 18, 699 CrossRef.
- D. Schweitzer, K. H. Hausser, H. Vogler, F. Diederich and H. A. Staab, Mol. Phys., 1982, 46, 1141 CrossRef CAS.
- D. Carbonera, Photosynth. Res., 2009, 102, 403 CrossRef CAS PubMed.
- J. A. N. F. Gomes and R. B. Mallion, Chem. Rev., 2001, 101, 1349 CrossRef CAS PubMed.
- M. Randić, J. Am. Chem. Soc., 1977, 99, 444 CrossRef , and references therein.
- W. C. Herndon and M. L. Ellzey Jr., J. Am. Chem. Soc., 1974, 96, 6631 CrossRef CAS , and references therein.
- N. Mizoguchi, Bull. Chem. Soc. Jpn., 1990, 63, 765 CrossRef CAS , and references therein.
- W. C. Herndon and M. L. Ellzey Jr., J. Chem. Inf. Comput. Sci., 1979, 19, 260 CrossRef CAS.
- J. Aihara, J. Am. Chem. Soc., 1976, 98, 2750 CrossRef CAS.
| This journal is © The Royal Society of Chemistry 2017 |