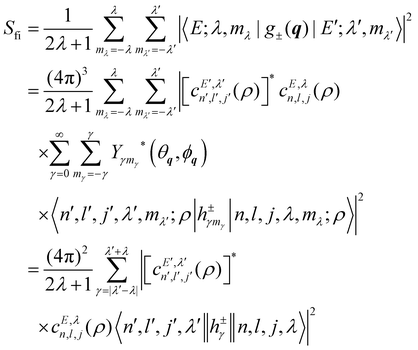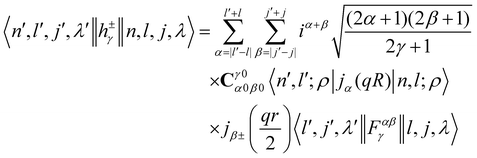Experimental, theoretical and computational investigation of the inelastic neutron scattering spectrum of a homonuclear diatomic molecule in a nearly spherical trap: H2@C60
Received
1st September 2016
, Accepted 6th October 2016
First published on 6th October 2016
Abstract
In this paper we report a methodology for calculating the inelastic neutron scattering spectrum of homonuclear diatomic molecules confined within nano-cavities of spherical symmetry. The method is based on the expansion of the confining potential into multipoles of the coupled rotational and translational angular variables. The Hamiltonian and the INS transition probabilities are evaluated analytically. The method affords a fast and computationally inexpensive way to simulate the inelastic neutron scattering spectrum of molecular hydrogen confined in fullerene cages. The potential energy surface is effectively parametrized in terms of few physical parameters comprising an harmonic term, anharmonic corrections and translation–rotation couplings. The parameters are refined by matching the simulations against the experiments and the excitation modes are identified for transfer energies up to 215 meV.
1 Introduction
The topic of confined particles lies at the foundations of quantum mechanics and textbook examples of a particle confined in a well or moving in a harmonic trap provides the starting point for a deeper understanding of many quantum systems. With the advent of “molecular surgery” techniques in organic synthesis, pioneered in the laboratories of Komatsu,1 Murata2 and more recently Whitby,3 molecular complexes have become available in which a variety of quantum rotors may be fully enclosed and confined inside a fullerene cage. These are the small molecule endofullerenes, of which H2@C60 is the primary example, representing a model system of its kind.4
With a hydrogen molecule entrapped inside C60, the endofullerene H2@C60 affords an actual realization of a quantum rotor confined in a three dimensional cage. The dynamics of H2 encapsulated within a fullerene is fundamentally quantum mechanical for several reasons. Firstly, owing to its low mass, free molecular hydrogen is characterized by a large rotational constant with sparse levels whose separation is in excess of 170 K in temperature units. Secondly once hydrogen is confined inside the C60 nano-cavity its translational degrees of freedom becomes quantised. Significantly, since the internuclear bond length in hydrogen (0.74 Å) is in the same scale as the fullerene radius, the quantised rotational and translational degrees of freedom become coupled. Thirdly, since the nuclei comprising H2 are indistinguishable fermions, the antisymmetry principle applies in determining the allowable eigenstates and there exists ortho- and para-nuclear spin isomers of H2. At low temperature these remain largely decoupled from each other and the two co-exist as independent and identifiable species in the absence of time-dependent inhomogeneous magnetic fields.
The study of the quantum dynamics of H2@C60 is relevant for understanding the interaction between carbon based materials and hydrogen. Molecular endofullerenes are ideal compounds in which the guest molecules are relatively isolated from each other within the homogenous environment provided by the cages. As a result, the spectrum of translation–rotation energy levels is sparse and when probed by various spectroscopic techniques, narrow well-separated peaks are observed.5–8 This reveals in fine detail the quantum dynamics of the entrapped translator–rotator and enables the potential energy surface (PES) experienced by the rotor to be probed meticulously along with the various interactions that characterise the Hamiltonian. With its unique ability to induce transitions between ortho- and para-spin-isomers, inelastic neutron scattering (INS) is a prime technique for studying confined hydrogen.9
Pioneering work by the group of Bačić using a rigorous computational approach to rigorously solve the Hamiltonian10–14 has been instrumental in developing an understanding of confined H2, including endofullerenes.15–17 Their methodology has been extended to determine the INS spectrum of hydrogen confined in nanocavities18,19 and in fullerenes.20,21 There, the potential energy surface is modelled using modified Lennard-Jones functions to represent the atom–atom potentials, then the Hamiltonian is solved exactly from which the spectrum may be determined.
The scope of this paper is different. Starting from the experimental spectrum, the observed low energy transitions are described in terms of excitations of a rotator angularly coupled to a harmonic oscillator. The quantum dynamics of a homonuclear diatomic molecules in a weakly perturbed isotropic harmonic trap is investigated by expanding the confining potential in symmetry adapted multipoles of the coupled angular variables. The Hamiltonian and the INS transition probabilities are represented analytically in the basis of the coupled rotor and harmonic oscillator. The INS spectrum is simulated by refining few Hamiltonian parameters, including harmonic and anharmonic terms along with translation–rotation coupling constants. In this methodology, the PES is not built from specific microscopic interactions but it is determined from a direct fit of the Hamiltonian to the experimental spectrum with the advantage that the fitted parameters represent physical attributes, such as the harmonic potential, the anharmonicity and translation–rotation coupling constants.
In the context of the spectroscopy of H2@C60, it is well-established that the quantum states of the coupled harmonic translator–rotator can be described in terms of the quantum numbers (n,l,j,λ).22 The entrapped rotor possesses both rotational and translational energy. The rotational states are characterised by j, while the translational states, defined by displacements of the centre-of-mass of the particle within the 3D-cage, are characterised by n and l. The former, n, is the principle quantum number while the latter, l, determines the translational angular momentum. Rotational and translational angular momenta couple according to the usual vector addition rules and we identify the quantum number λ to characterise the coupled translation–rotation states. A more complete account of the rotational and translational states will be discussed in Section 4. Finally, applying the antisymmetry principle, the Pauli Exclusion Principle (PEP) demands that the nuclear spin isomer para-H2 is a nuclear spin singlet with total spin IN = 0 and characterised by even j, while ortho-H2 is a nuclear spin triplet with IN = 1 and odd values of j. In this way the spatial and spin degrees of freedom are entangled. This has consequences for experiments since ortho ↔ para transitions are spin-restricted and forbidden to photon spectroscopy, whereas neutron scattering interactions couple space and spin enabling ortho ↔ para transitions to be directly observed in the INS spectrum with high intensity.
The paper is organised as follows. First the experimental INS spectrum is presented in Sections 2 and 3. The analytical approach used to represent the Hamiltonian and to determine the INS transition probabilities is discussed in Sections 4 and 5, respectively. The method is then applied to simulate the INS spectrum of H2@C60 in Section 6. The parameters characterising the cage potential and the spectral assignments are discussed in Section 7.
2 Experimental details
INS experiments were conducted using the IN1-Lagrange spectrometer at the Institut Laue-Langevin (ILL) in Grenoble.23 This instrument is supplied from the “hot source” moderator of the ILL reactor, resulting in a high-flux beam of energetic neutrons. A choice of three different single crystal monochromators is available in a primary spectrometer, where a Bragg angle defines the incident energy of the monochromatic neutron beam arriving at the sample. The monochromator crystals of Si or Cu are mounted in a double focusing geometrical arrangement, enabling selection of the Si(311), Cu(220) or Cu(331) Bragg reflections. By combining the 3 monochromators, the incident neutron energy may be scanned in the range from 5 meV to 1 eV. The scattered neutrons enter a secondary spectrometer comprising a large area array of pyrolytic graphite analyzer crystals. The Bragg scattering geometry in the secondary spectrometer ensures only neutrons of a fixed energy (4.5 meV) are detected by a 3He detector, with neutrons being collected from a wide solid angle subtended at the sample. By scanning the incident neutron energy, INS spectra were recorded in the energy transfer range 12.7 ≤ ΔE ≤ 215 meV. Over this range of energy transfer, the momentum transfer of detected neutrons scattered by the sample varies systematically in the range 2 ≤ q ≤ 12 Å. For the Si monochromator the resolution is given by the resolution of the analyser, which is 0.8 meV. For the Cu monochromators the resolution function of the instrument is a constant percentage of the incident neutron energy. Identifying singlet transitions in the INS spectrum of H2@C60, the Gaussian resolution function was measured as follows (FWHM; full-width half maximum): Cu(220) 2.3%; Cu(331) 1.5%.
The sample of H2@C60 was prepared according to published methods.1 In a final stage of purification, the presence of any intercalated solvent was substantially reduced by sublimation. The powdered sample with mass 101 mg was uniformly loaded inside a rectangular Al foil sachet, folded into a cylindrical annulus of approximate diameter 1 cm and mounted in the Lagrange spectrometer. The sample temperature was maintained at 2.5 K using a closed cycle He refrigerator. To subtract background and scattering from Al and from the C60 cage, a “blank” sample of empty C60 cages with matching mass was prepared in an identical Al foil sachet.
INS spectra of H2@C60 were recorded using the three monochromators and the corresponding energy transfer ranges were selected to provide the best available resolution as follows: Si(331) 12.7 < ΔE ≤ 27 meV; Cu(220) 27 < ΔE ≤ 63 meV and Cu(311) 63 < ΔE ≤ 215 meV. The intensities of the INS peaks recorded with the three monochromators were normalized to the same scale by comparing the integrated intensities of peaks recorded in overlapping energy transfer regions. The systematic error in energy transfer is estimated to be 0.1 meV below approximately 50 meV rising to 0.5 meV at the highest energy transfers recorded. Random errors in energy transfer were small by comparison, typically 0.02 meV for singlet peaks. Unless otherwise stated, these error bars will apply in the following discussions.
3 Experimental results
The INS spectrum of H2@C60 is presented in Fig. 1. A mass-matched “blank” has been subtracted, ensuring the spectrum arises only from scattering by H2 inside the fullerene cage. Compared with previous studies using time-of-flight spectrometers, this new spectrum substantially extends the range of energy transfer recorded from 60 meV to beyond 250 meV. Furthermore, in the range 30–60 meV the resolution function is typically two times better than the previously published IN4 spectrum (λn = 1.2 Å),24 enabling TR fine structure to be resolved for the first time in the high energy modes. The sample is at low temperature so that only the ground para-H2 and ground ortho-H2 states are occupied. At these low temperatures and in the absence of suitable time-dependent magnetic interactions, ortho–para conversion is extremely slow with no conversion being observed on the timescale of the experiments (several days). Therefore the two nuclear spin-isomers exist as distinct species and all INS transitions originate in the ground states, either (0,0,0,0) or (0,0,1,1), using the notation (n,l,j,λ) to identify the energy levels.
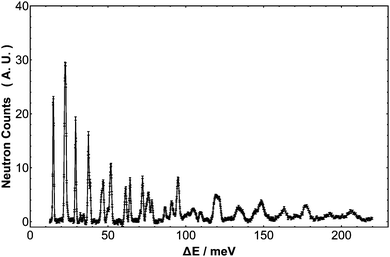 |
| | Fig. 1 The INS spectrum of H2@C60 at 2.5 K as recorded on the IN1-Lagrange spectrometer at ILL, Grenoble (France). The vertical axis represents neutron counts in arbitrary units. | |
At low temperature, and particularly in the lower energy transfer region, the spectrum is sparse with sharply resolved peaks revealing a remarkable quantity of detail. H2@C60 is clearly an extremely well-characterized and homogenous system, revealing the quantum nature of the H2 molecule and its wavelike nature in exquisite detail.
Fig. 2 shows an extract from the experimental spectrum for transfer energy up to 73 meV. The first rotational transition (0,0,0,0) → (0,0,1,1) is clearly observed as the singlet peak with energy transfer 2B = 14.7 meV, interconverting the ground states of para-H2 and ortho-H2. Another singlet peak is the second rotational transition (0,0,1,1) → (0,0,2,2) which has energy transfer approximating 4B and is centered on 29.2 meV. A third singlet with width equal to the resolution function appears at 72.2 meV. This energy approximates to 10B so the peak assigned to the ortho–ortho pure rotational transition (0,0,1,1) → (0,0,3,3). These observations indicates that barriers impeding free rotations are small in H2@C60.
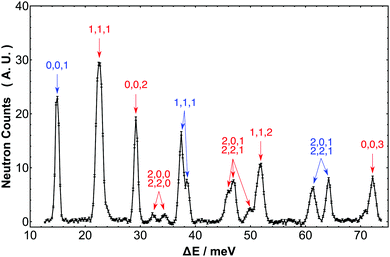 |
| | Fig. 2 Expansion of the INS spectrum of H2@C60 at 2.5 K of Fig. 1 in the range 10–75 meV. Each peak is assigned to an INS transitions for which the labels indicate the value of n, l, j in the final states. Transitions originating from the para-H2 ground state are in blue and transitions originating from the ortho-H2 ground state are in red, respectively. The vertical axis represents neutron counts in arbitrary units. | |
The prominent band centered on 22.5 meV received particular interest in our earlier papers,24 since it represents the transition from the ground state of ortho-H2 to the first excited translational state of ortho-H2, (0,0,1,1) → (1,1,1,λ). This is a ubiquitous “particle-in-a-box” mode and in the Lagrange spectrum this is observed with similar resolution to the earlier IN4 spectrum (λn = 1.6 Å). This mode is a partially resolved triplet comprising the λ = 0, 1, 2 components of the excited state. This band was significant since it represented the first observation in an INS spectrum of a splitting arising from TR coupling of rotational and translational angular momentum. Moving to higher energy transfer, a doublet is observed with energies 37.4 and 38.5 meV. Considering the energy level diagram and consistent with the assignments in our earlier papers,8,24 we infer this band is the transition (0,0,0,0) → (1,1,1,λ) involving the same final state triplet referred to in the previous paragraph, but this time originating in the ground para-H2 state. Within the resolution of the spectrometer only two components of this band can be identified while the third one is apparently missing. We shall return to this point more widely in Section 7 in the context of the discussion of the INS transition probability for diatomic molecules in spherical potentials.
The second excited translational state of ortho-H2, n = 2, j = 1, is revealed in a doublet with energy transfers 45.8 and 47.0 meV and in the small peak at 49.8 meV. These peaks were observed with the Cu(220) monochromator and have the resolution line width. The former doublet has a partner observed at 61.3 meV while the latter peak is closely related to the singlet at 64.2 meV observed with the Cu(331) monochromator, which also has the resolution line width. Allowing for systematic errors that arise from two different monochromators, these two set of peaks differ in energy transfer by 2B, so we are able to make the assignment to the same final state within the manifold n = 2, j = 1; the lower energy of the two originates in ortho-H2, while the higher energy peak originates in para-H2.
The peak in the region 51.5 meV has been observed with the Cu(220) monochromator. It is slightly broader than the resolution line width and slightly asymmetric so we can infer the feature has multiple components. As with the examples above, applying an offset equal to a multiple of 2B provides an energy that coincides with a known splitting in the spectrum. In this case subtracting 4B coincides with the translational splitting so we can infer these two peaks correspond to the ortho–para transition from (0,0,1,1) → (1,1,2,λ).
Finally, two low intensity peaks occur at 32.3 and 34.3 meV. These identify the states n = 2, j = 0, corresponding to the transitions (0,0,1,1) → (2,0,0,0) and (0,0,1,1) → (2,2,0,2).
As the above few examples show, with good instrument resolution and a spectrum which is sufficiently sparse, substantial progress can be made in the assignment of n, l, j quantum numbers based solely on the experimental data. This enables the energy level diagram to be determined for all low lying states up to approximately 73 meV. As both para to ortho and ortho to ortho transitions are allowed, and the same final states are represented by multiple peaks, the assignments may be confirmed by correlating transition energies. However, with increasing energy transfer, the number of transitions significantly increases while anharmonicities lead to non-integer relationships between peak energies. It becomes clear that a definitive assignment of the INS peaks, including the TR multiplet components, increasingly demands the assistance of a more sophisticated theoretical framework. Therefore we shall return to consider more detailed assignments in the spectrum in Section 7 after describing the computational simulation of the H2@C60 spectrum.
4 Quantum dynamics
In this section we discuss the quantum dynamics of a H2 molecule confined in a C60 cage. The C60 cage is assumed to be rigid, fixed and non-rotating. The laboratory reference frame is taken with origin in the centre of the cage. The geometric configuration of the cage is completely identified by the orientation of a frame fixed with the cage C with respect to the laboratory frame L. Mathematically the orientation of the cage frame with respect to the laboratory frame is described by the set of three Euler angles ΩLC. For example, in the case of C60, the cage fixed frame can be chosen so that the Z axis is directed along a C5 axis with the X axis along one of the 5 orthogonal C2 axes and the Y axis determined by the right-handed condition. The configuration of the diatomic molecule is determined by the centre of mass vector R and the internuclear vector r.
The molecule–cage interaction is described by the potential V(R,r;ΩLC). The function V can be thought as the PES of an H2 molecule confined inside the fullerene cage. It is worth noting that any symmetry operation Ô of the icosahedral point group Ih acting on all the position coordinates leave the potential unaffected:
| | | V(R,r;ΩLC) = V(ÔR,Ôr;Ô[ΩLC]) = V(ÔR,Ôr;ΩLC) | (1) |
and the last equality follows from the fact that the Euler angles are unchanged under
Ô. As a consequence the potential is invariant under operation of the symmetry group acting only on the variables
R and
r, see also
ref. 25 and 26. In the following the dependence of
V on
ΩLC will be understood. To discuss the effect of symmetry on the potential at fixed cage orientation, it is convenient to expand out the angular dependence in multipoles
| | 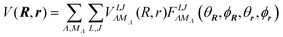 | (2) |
where the bipolar spherical harmonics are a complete set of functions for the angular variables defined by
27| | 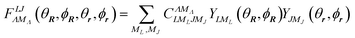 | (3) |
and where
C is a Clebsch–Gordan coefficient and {
θR,
ϕR} and {
θr,
ϕr} are polar angles of the centre of mass and internuclear vector, respectively.
Λ is the rank and
MΛ is the projection of the bipolar harmonic. For sake of simplicity, the dependence on the ordered set of angular variables will be understood henceforth.
The symmetry of the confinement is reflected in the number and types of multipoles present in the potential expansion, eqn (2). In icosahedral symmetry it is possible to prove that the rank of the multipoles that form invariant functions is restricted to Λ = 0, 6, 10, 12, 16.28 Since the centre of the potential is a point of inversion symmetry, only multipoles with L + J = even are allowed. For multipoles with rank Λ = 0, only terms with Λ = 0, MΛ = 0 and L = J are allowed. The next lowest non-zero rank terms for an icosahedral potential is:29
| | 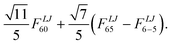 | (4) |
In treating the quantum dynamics of H
2@C
60, the effect of multipoles with
Λ > 0 can be neglected in first instance and eventually reconsidered perturbatively.
25 Retaining only terms with
Λ = 0 is equivalent to treating C
60 as spherical. The internal symmetry of the homonuclear molecule determines the invariance of the potential under the exchange of
r in −
r which in turn implies that only even-
J bipolar harmonics are present in
eqn (2).
The vibrationally averaged effective five-dimensional Hamiltonian for a diatomic molecules moving in a spherical potential can be written as
| | 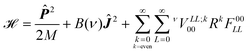 | (5) |
where
![[P with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_0050_0302.gif)
is the linear momentum operator associated with the centre of mass vector,
Ĵ is the angular momentum operator associated with end to end rotations,
B(
ν) is the effective rotational constant in the vibrational state
ν and
νVLL;k00 are coefficients of the expansion of the averaged molecule–cage interaction potential in bipolar harmonics of the angular variables. For a homonuclear molecule, only even
k terms enter in the expansion of the potential in
eqn (5) because of the symmetry of the potential under inversion. In this work the attention is restricted to H
2@C
60 in the ground vibrational state
ν = 0 and the label
ν will be dropped henceforth.
It is a general statement of quantum mechanics that the total angular momentum of a system with spherical symmetry commutes with the Hamiltonian, so providing “good” quantum numbers for labelling the energy levels. For a diatomic molecule in a spherical trap, the total angular momentum ![[capital Lambda, Greek, circumflex]](https://www.rsc.org/images/entities/b_i_char_e0a8.gif) =
= ![[L with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_004c_0302.gif) + Ĵ is given by the sum of the orbital angular momentum of the centre of mass
+ Ĵ is given by the sum of the orbital angular momentum of the centre of mass ![[L with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_004c_0302.gif) and of the end to end rotational angular momentum Ĵ. The bipolar spherical harmonics
and of the end to end rotational angular momentum Ĵ. The bipolar spherical harmonics 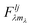 are eigenfunctions of the angular momentum operators
are eigenfunctions of the angular momentum operators ![[capital Lambda, Greek, circumflex]](https://www.rsc.org/images/entities/b_i_char_e0a8.gif) 2 and
2 and ![[capital Lambda, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0a8.gif) z with eigenvalues λ(λ + 1) and mλ, respectively. They provide a complete basis set for the coupled angular motion.
z with eigenvalues λ(λ + 1) and mλ, respectively. They provide a complete basis set for the coupled angular motion.
A complete basis set for the radial motion is provided by the set of radial eigenfunctions for the Schrödinger equation of a particle in a central potential. Early ab initio determinations of the potential energy surface of H2@C60 suggest to use the eigenfunctions of a three-dimensional isotropic harmonic trap. These are discussed in the appendix, Section A.1. The coupled harmonic translation–rotation wave-function is written in ket notation as
| | 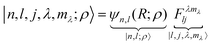 | (6) |
using the notation of Section A.1 and the definition of bipolar harmonic of
eqn (3). Here
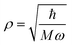
is the scale length associated to the harmonic oscillator with mass
M and frequency
ω. The ket in
eqn (6) is an eigenstate of the spherical three-dimensional oscillator represented by the Hamiltonian in
eqn (5) when terms with
L = 0 and up to
k = 2 are considered. In this case
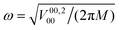
. The zero-order energy of the undecoupled translator and rotator is
| | | E0n,j = ħω(n + 3/2) + Bj(j + 1) | (7) |
Anharmonic terms with
L = 0,
k > 2 mix states with different
n while translation–rotation couplings are characterized by
L =
J > 0 and mix states with different
n,
l,
j. In presence of anharmonicities and translation–rotation couplings the eigenfunctions of the Hamiltonian given in
eqn (5) are characterized by definite angular momentum quantum number
λ and
mλ and can be written as
| | 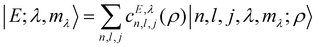 | (8) |
where the coefficients
c do not depend on
mλ. In the following we will use the notation
Eλ to denote the energy level comprising the set of 2
λ + 1 degenerate states of
eqn (8). The symmetry under inversion implies that parity is a good quantum number. Since the parity under inversion for the bipolar harmonics states is (−1)
l+j, it follows that either even- or odd-sum
l,
j pairs appear in the expansion
(8).
5 INS transition probability
In a typical neutron scattering “spectrum” the intensity of a transition between an initial energy level i and a final energy level f is determined by the double differential cross section:30| | 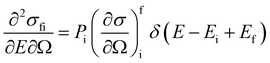 | (9) |
where Pi is the population of the energy level i, 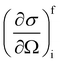 represents the transition probability for the scattering of neutrons and the delta function δ enforces the energy conservation in the scattering process. As shown with greater detail in Section A.4, the INS transition probability for homonuclear molecules in unpolarised experiments can be written as a product of a spin sfi and a space part Sfi:
represents the transition probability for the scattering of neutrons and the delta function δ enforces the energy conservation in the scattering process. As shown with greater detail in Section A.4, the INS transition probability for homonuclear molecules in unpolarised experiments can be written as a product of a spin sfi and a space part Sfi:| | 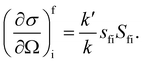 | (10) |
Specifically in the case of molecular hydrogen, I = 1/2 and IN = 0 for para-hydrogen and IN = 1 for ortho-hydrogen, so that the spin dependent part of the INS cross section becomes| |  | (11) |
where o and p stands for ortho and para, respectively and where bc and bi are the bound coherent and incoherent scattering lengths of bound 1H, respectively. The space dependent part Sfi for transitions between an initial energy level i = Eλ and a final energy level  is obtained by tilting the reduced matrix element of the INS transition probability from the spherical basis to the appropriate eigen system basis:
is obtained by tilting the reduced matrix element of the INS transition probability from the spherical basis to the appropriate eigen system basis:| | 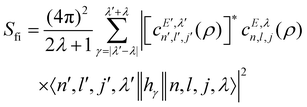 | (12) |
where the INS reduced matrix element is given by:| | 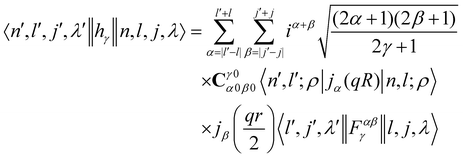 | (13) |
Interestingly, the derivation of the transition probability via the Wigner–Eckart theorem, as discussed in Section A.4, allows us to recover the selection rule for INS transitions in diatomic molecules confined in potentials of spherical symmetry, originally found by Xu et al.20,31 and later extended and explained by Poirier in the context of group theory.26 Indeed in the evaluation of the reduced matrix element of eqn (13) the terms with
| | 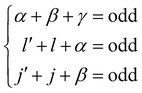 | (14) |
are exactly 0 since both the Clebsch–Gordan term
Cγ0α0β0 and the reduced matrix elements of bipolar harmonics involve 3-j symbols with 0 projections, see
eqn (29) and (30). These 3-j symbols are zero if the sum of the arguments are odd, see
eqn (20). When the initial level is characterized by
λ = 0 total angular momentum,
l =
j and
γ =
λ′ because of the triangular condition for the rows and column of the 9-j symbols implied by the reduced matrix element of the bipolar harmonic,
eqn (29). By subtracting the last two identities out of the first one in 14, it follows that the reduced matrix element 〈
n′,
l′,
j′,
λ′‖
h±γ‖
n,
l,
j,
λ〉 is zero when the initial level has
λ = 0 and the final level angular numbers satisfy
λ′ −
l′ −
j′ = odd. The selection rule for the transition probability follows from the observation that
l′ +
j′ is either even or odd for all the coefficients in
eqn (12) as a consequence of the inversion symmetry for diatomic molecules in a spherical trap, see Section 4. The equivalent selection rule for final states with
λ′ = 0 follows exchanging the role of primed and non-primed labels in the discussion above.
6 Calculations
The methodology described in Sections 4 and 5 can be applied to determine the INS spectrum of H2@C60 according to the following prescription. Firstly a finite coupled basis set is chosen by fixing the maximum number of translational and rotational excitations to nmax and jmax, respectively. The para (even j) and the ortho (odd j) coupled states |n,l,j,λ,mλ〉 are gathered separately in blocks with the same angular momentum λ. For each spin isomer and each λ-block, the finite matrix basis representation of the Hamiltonian (5) is built in the basis |n,j,l,λ,mλ = 0〉 using eqn (7), (22) and (23). The rotational constant in the ground vibrational state is written as B = B0 − D0j(j + 1) where the coefficient D0 accounts for centrifugal corrections to the rotational energy.32 The potential expansion is truncated to include the harmonic term V00;200, two anharmonic terms, V00;400 and V00;600 and one translational–rotational coupling term V22;200. The blocks with different angular momentum λ are diagonalized separately. The eigenvalues are used to determine the thermal populations, the levels and the transition energies that fall within the observation range. Assuming no spin-isomer interconversion, the ortho to para ratio can be fixed to 3 and the thermal equilibrium populations can be determined for the two spin isomer independently. The eigenvector coefficients, eqn (8), are used to calculate the total intensity of the INS transitions as a function of q, by evaluating the double differential cross section, eqn (9), viaeqn (11) and (12). For numerical simulation the values bc = −3.74 × 10−15 m and bi = 25.27 × 10−15 m have been used as scattering lengths for the coherent and incoherent scattering length of bound 1H, respectively.33
To achieve a more direct visual comparison between experiments and simulations, the transition probability, eqn (10), is integrated over the q-range appropriate to the instrumental apparatus at energy ΔEfi = Ef − Ei. In an inverse geometry neutron spectrometer the final energy of the scattered neutron is fixed to En, while the incident neutron energy is scanned through. A detector at angle θ with respect the direction of the incident neutron beam records scattered neutrons at transferred momentum
| | 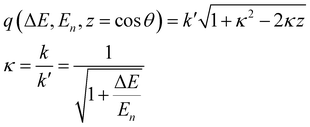 | (15) |
so that integrating over
q across the polar angular opening of the instrument
| | 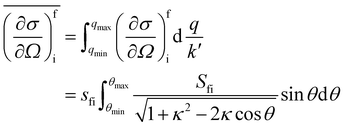 | (16) |
The integration can be effectively performed averaging over an appropriate angular distribution describing the geometry of the apparatus. This procedure gives rise to a stick peak
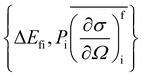
for each possible transition. To emulate finite width transitions the peaks are finally convoluted with the instrumental resolution, assuming negligible intrinsic line-width in H
2@C
60.
In the simulation of the IN1-Lagrange spectrum of H2@C60 the number of scattered neutrons was determined by averaging over a uniform distribution of 20 polar angles in the nominal angular ranges 34° ≤ θ ≤ 70° at fixed En = 4.5 meV and using the instrumental resolution discussed in Section 2.
7 Discussion
The INS spectrum of H2@C60 was simulated using a set of purpose-built packages in Mathematica.34 In the actual calculations, the basis was defined by nmax = 11 and jmax = 7, giving rise to 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 192 para states and 13
192 para states and 13![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 104 ortho states, of which only 800 distinct reduced para states and 972 reduced ortho states were necessary for the evaluation of the Hamiltonian and of the INS transition probability. The initial rotational parameters were fixed to the values of free H2: B0 = 7.357 meV and D0 = 0.0056 meV.35,36 Starting from the uncoupled oscillator with translational excitation ħω = 22 meV, the potential parameters
104 ortho states, of which only 800 distinct reduced para states and 972 reduced ortho states were necessary for the evaluation of the Hamiltonian and of the INS transition probability. The initial rotational parameters were fixed to the values of free H2: B0 = 7.357 meV and D0 = 0.0056 meV.35,36 Starting from the uncoupled oscillator with translational excitation ħω = 22 meV, the potential parameters 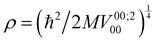 , Ṽ00;400 = ρ4V00;400, Ṽ00;600 = ρ6V00;600 and Ṽ22;200 = ρ2V22;200 were varied until satisfactory agreement with the experimental spectrum was found. The optimized values are reported in Table 1.
, Ṽ00;400 = ρ4V00;400, Ṽ00;600 = ρ6V00;600 and Ṽ22;200 = ρ2V22;200 were varied until satisfactory agreement with the experimental spectrum was found. The optimized values are reported in Table 1.
Table 1 Summary of the optimized values of the Hamiltonian parameters used for calculating the INS spectrum of H2@C60 in Fig. 3
| Hamiltonian parameter |
Optimized value |
|
B
0/meV |
7.375 |
|
D
0/meV |
0.012 |
|
ρ/Å |
0.311 |
|
Ṽ
00;400/meV |
−3.90 |
|
Ṽ
00;600/meV |
1.52 |
|
Ṽ
22;200/meV |
8.9 |
Fig. 3 shows the comparison between the experimental and calculated spectrum of H2@C60 at 2.5 K.
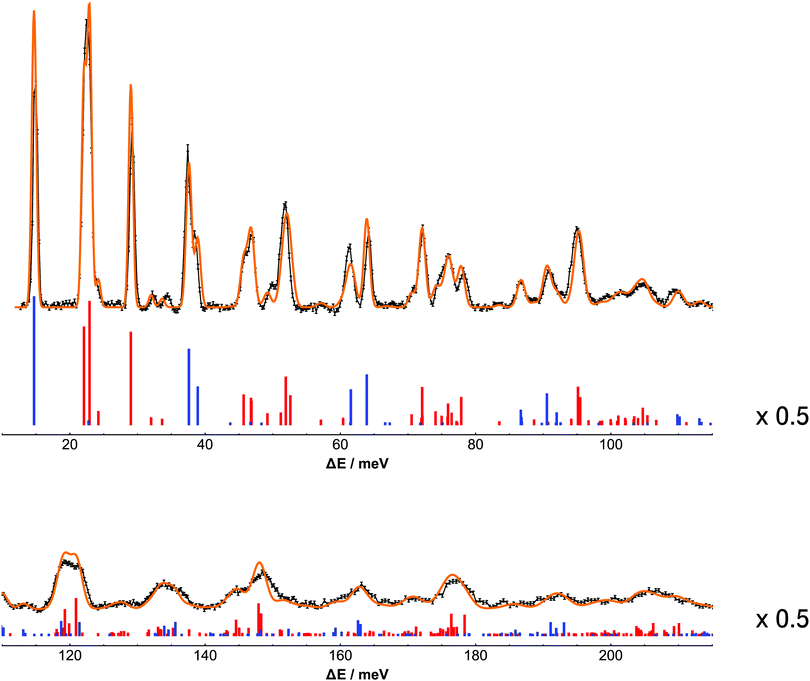 |
| | Fig. 3 Comparison between the experimental and calculated spectrum of H2@C60. For clarity the plot is split into two equally wide panels spanning the transfer energy ranges from 10 meV to 215 meV. The black line with error bars represent the spectrum of H2@C60 recorded at 2.5 K on IN1-Lagrange at ILL. The bars represent the calculated stick spectrum of H2@C60 at 2.5 K, where the colors blue and red are used to distinguish transitions originating in the para and ortho ground states, respectively. The orange line overlayed to the experimental spectrum represent the calculated spectrum obtained by convolving the stick spectrum with the instrumental resolution of IN1-Lagrange. For clarity the peaks in the stick spectrum are scaled by a factor 0.5 with respect to the numerical values and vertically shifted. | |
The calculated spectra confirm the peak assignment up to 73 meV given in Section 3, that were mainly based on the approximation of uncoupled rotation and translation, see eqn (7). However even at low energy the presence of couplings has a major impact on the appearance of the spectrum. By providing intensities and transition energies as well, the calculations establish a firm framework for the analysis of the spectrum.
The experimental peaks at 14.7, 29.2 and 72.2 meV are singlet rotational peaks, corresponding to the para–ortho (0,0,0,0) → (0,0,1,1) and ortho–para (0,0,1,1) → (0,0,2,2) transitions, respectively. The presence of anharmonic and translation–rotation coupling has a minor impact on pure rotational transition between states with n = 0, l = 0. However other rotational transitions are more difficult to identify because of the reduced intensity and their use as milestones for spectral assignment is less poignant.
The structure underlying multi-component peaks is clearly resolved in the stick spectrum. The experimental peak at 22 meV is resolved into three main components corresponding to the intra-ortho translational transitions (0,0,1,1) → (1,1,1,λ) with λ = 1, 2, 0 in order of increasing energy. As shown in ref. 37 using group theoretical methods and successively in ref. 25 by using perturbation theory, the order of the λ levels in the (1,1,1,λ) multiplet is dictated by the positive sign of the translational–rotational coupling term Ṽ22;200. As observed previously the λ = 0 component is much weaker in intensity than the other two and, importantly, these observations are in agreement with the simulation of the H2@C60 spectrum by Xu et al.15,20 In a similar manner, the experimental peaks at 37.4 and 38.5 meV are assigned to the λ = 2 and λ = 0 components of the para–ortho translational transition (0,0,0,0) → (1,1,1,λ), respectively. There is no evidence of the λ = 1 component of the triplet. This highlights a striking prediction from the earlier papers,20,21 namely the existence of a selection rule for INS transitions in diatomic molecules in a spherical confinement.26,31
Transitions towards levels with two quanta of translational excitations have been identified in the experimental discussion. The peaks at 32.3 and 34.3 meV are assigned to the transitions (0,0,1,1) → (2,2,0,2) and (0,0,1,1) → (2,0,0,0), respectively. Transitions towards states with n = 2 and j = 1 reveal a larger degree of mixing between different translational–rotational states. The calculations identifies the transitions towards (2,2,1,2) and (2,2,1,3) with the peaks at 45.8 and 47.0 meV, respectively. Concealed under the latter peak, there is a transition to an energy level comprising a superposition of the (2,0,1,1) and (2,2,1,1) states with a ratio close to 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2. Similarly the peak at 49.8 meV corresponds to a transition to an energy level comprising a superposition of the (2,0,1,1) and (2,2,1,1) states in a ratio close to 2
2. Similarly the peak at 49.8 meV corresponds to a transition to an energy level comprising a superposition of the (2,0,1,1) and (2,2,1,1) states in a ratio close to 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1. The partner transitions to these superposition states originating from the para ground state are found at 61.3 and 64.2 meV, respectively, while the para transition towards (2,2,1,2) is forbidden and the para transition towards (2,2,1,3) has negligible intensity.
1. The partner transitions to these superposition states originating from the para ground state are found at 61.3 and 64.2 meV, respectively, while the para transition towards (2,2,1,2) is forbidden and the para transition towards (2,2,1,3) has negligible intensity.
The peak centered at 51.5 meV is resolved in three transitions starting from the ortho ground state towards (1,2,1,λ) state with λ = 2, 3, 1 in order of increasing energy.
The stick spectrum demonstrates the existence of para–para transitions that are easily overlooked in the experimental spectrum. Owing to the small ratio between the coherent and incoherent cross section for 1H, para–para peaks generate a very low scattered neutron count and are difficult to observe. For example the fundamental translational transition in the para manifold (0,0,0,0) → (1,1,0,1) is shadowed by the ortho transitions (0,0,1,1) → (1,1,1,λ).
At higher energy transfer the absolute resolution becomes worse, the number of accessible transitions increases and the peaks become relatively less sparse and less intense. This is particularly evident in the region above 96 meV. The calculations identify 162 transitions originating from the ground para state and 191 transitions originating ground ortho state in the energy range between 96 and 215 meV. In contrast to the low energy case, where most of the levels are represented by the nominal (n,l,j,λ) state with at least 95% probability except where noted, states with different n, l, j become more and more mixed at high energies, so hampering their use as labels for the energy levels. A semi-empirical approach that tries to fit more prominent features to a minimal number of Gaussian lines may still work where few high intensity transitions are clustered.8 However in other regions where transitions are more spread in energy and there is no dominant component, it is practically impossible to produce any meaningful assignment of this type. Simulations remains the only method to make sense of the complexity of the spectrum at high energy transfer. Indeed the simulated spectrum provide a realistic representation of the experimental observations over all the accessed energy range. The simulated transitions follow closely but not exactly the experimental ones. Higher order spherical terms may improve the match at the expense of increasing the parameter space. However improved accuracy appears to be not worthwhile with the current experimental resolution also considering that shifts and splittings of the mλ components in the energy levels of order of fractions of meV are introduced by terms of icosahedral symmetry38 as well as intermolecular effects.39
8 Conclusions
In this paper the low-temperature INS spectrum of H2@C60 covering excitations up to 215 meV was presented. The assignment of the experimental peaks was aided by developing a model which makes use of the nearly spherical symmetry of the confinement. The guest–host interaction was expanded in terms of coupled angular spherical bipolar harmonic functions. The effective potential was then described by few physical parameters comprising a harmonic term and terms describing anharmonic corrections and translational–rotational couplings. This approach affords a good flexibility in representing the overall non-bonding interaction between the hydrogen molecule and the fullerene cage when compared with other interaction models based on interactions between atomic units. The effective potential then represents a benchmark for any ab initio determination of the PES in H2@C60. The model does not involve any numerical integration: matrix elements and transition probabilities are shown to integrate into closed algebraic expressions in the coupled rotational translational oscillator basis. The analytical expressions may be useful in the analysis of the q-dependence of the INS transitions probability in similar systems. More importantly, the numerical evaluation of these expressions comes at a relatively inexpensive computational cost. Starting from the uncoupled harmonic system, the effect of each term on the spectrum can be varied independently until the spectrum is reproduced correctly. The agreement between experiments and calculations is overall very good. The INS transitions are well reproduced indicating that the icosahedral non spherical terms give rise to minor splittings and shifts within the instrumental resolution.
The theoretical and computational model developed in this paper may be useful for investigating the quantum dynamics and the INS spectrum of confined molecular hydrogen in systems such as clathrates hydrates,40,41 zeolites42,43 and MOFs.9,44,45 We anticipate its extension to treat heteronuclear diatomic molecules as well as water molecules confined in C60. In systems with high symmetry or when the effect of non spherical multipoles are small, such as H2@C60, realistic INS spectra can be generated promptly. For systems with lower symmetry the method can be used to provide a starting approximate description useful to identify the main features of the INS spectrum and it can be eventually augmented to include non-spherical terms perturbatively.
Appendix A: mathematical appendix
In this section we provide an extended presentation of the mathematical aspects that lie at the basis of the algebraic and numeric treatment developed for the analysis of the INS spectroscopy of H2@C60. The solution of the Schrödinger equation for the spherical oscillator provides the radial wave-functions for the coupled translational–rotational states. The matrix elements for local operators appearing in the Hamiltonian and in the INS probability are separated into a radial and an angular part. The radial matrix elements are integrated into closed algebraic forms. The angular matrix elements are evaluated using the Wigner–Eckart theorem. Finally the INS transition probability for diatomic molecules in spherically symmetric confinement is derived.
A.1 The isotropic three-dimensional harmonic oscillator
Following the treatment presented in ref. 46 and the relations between the hypergeometric confluent function 1F1 and Laguerre polynomials,47 the normalized eigenfunctions of the Schrödinger equation for the three-dimensional spherical oscillator with mass M and angular frequency ω are written as the product of a radial and an angular term:| | 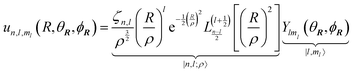 | (17) |
in which 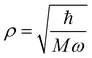 is the scale length associated to the harmonic oscillator, L(α)n is a generalized Laguerre polynomial47 and
is the scale length associated to the harmonic oscillator, L(α)n is a generalized Laguerre polynomial47 and| | 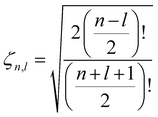 | (18) |
is a normalization constant. The principal quantum number n is a non-negative integer that determines the energy, En = ħω(n + 3/2), of the eigenfunction in eqn (17). The orbital angular momentum quantum number l is a non-negative integer. For a given n the angular momentum quantum number is limited to the range l = n, n − 2,…, 3, 1 for odd n and l = n, n − 2,…, 2, 0 for even n. The degeneracy of the level with energy En is gn = n(n + 1)/2.
A.2 Clebsch–Gordan coefficients and 3-j symbols
Clebsch–Gordan coefficients appear naturally in quantum mechanics when adding the angular momentum of two subsystems as in formula (3). 3-j symbols are a more symmetrized version of the Clebsch–Gordan coefficients. The two symbols are related by| | 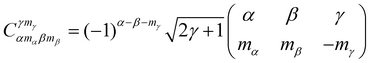 | (19) |
The 3-j symbols are invariant under even transpositions of the columns and take the sign (−1)α+β+γ under odd transposition. 3-j symbols are 0 if mγ ≠ mα + mβ and if the triangular condition α − β ≤ γ ≤ α + β is not satisfied. It is worth to note the following parity property of the 3-j symbol| | 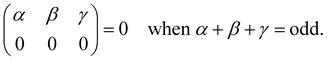 | (20) |
Similarly 6-j symbols and 9-j symbols appear when combining the angular momentum for three subsystems and four subsystems. 9-j symbols appear in the evaluation of the reduced matrix element of two coupled subsystem as well, see eqn (29). They are defined in terms of 6-j symbols as:
| | 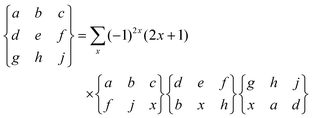 | (21) |
where max(|
a −
j, |
b −
f|, |
d −
h|) ≤
x ≤ min(
a +
j,
b +
f,
d +
h). 9-j symbols are zero if the triangular conditions is not satisfied by any of the rows or of the columns.
3-j symbols and 6-j symbols can be calculated from generating formulae27 and are available as built-in objects in computational softwares such as Mathematica.34
A.3 Evaluation of matrix elements
The evaluation of matrix elements for a function which is a direct product of a radial and a coupled angular part, such as the potential term in eqn (2) and the INS cross section in eqn (10), are evaluated as direct product of a radial and an angular part:| | 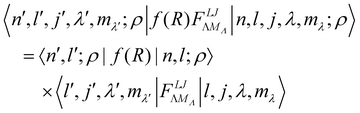 | (22) |
A.3.1 Radial matrix elements.
The evaluation of radial matrix elements for non-negative power of local operator f(R) = Rk over the radial translational wave-functions, |n,l;ρ〉 of eqn (17), is found by integration| | 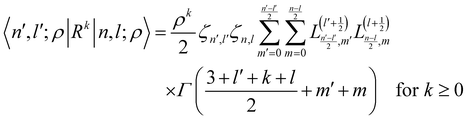 | (23) |
where Γ is the gamma function47 and| | 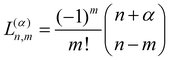 | (24) |
are the coefficients for the Laguerre expansion of L(α)n(x) in power of xm.
Similarly the radial matrix elements of the spherical Bessel function47jβ(qR) for integer β ≥ 0, which enter in the space part of the INS transition matrix, can be integrated in a closed form
| | 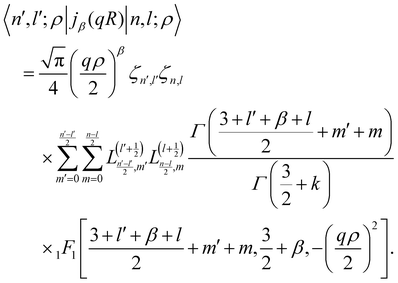 | (25) |
For sake of completeness, we note that only matrix elements of spherical Bessel functions
jβ with |
l′ −
l| ≤
β ≤
l′ +
l and
l′ +
l +
β = even needs to be evaluated. In such case the confluent hypergeometric function
1F1 reduces to:
47| | 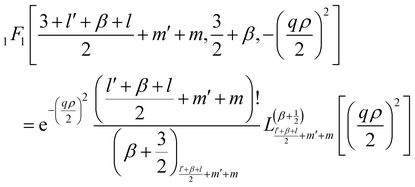 | (26) |
where
| | | (a)n = a(a + 1)(a + 2)…(a + n − 1), (a)0 = a | (27) |
is the Pochammer symbol.
47
A.4 INS transition probability
In neutron scattering experiments involving transitions between two energy levels in a homonuclear diatomic molecule, labelled here as i and f respectively, the main quantity of interest is the differential cross section in Born approximation30| | 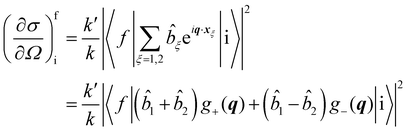 | (32) |
where the sum is over the nuclear species ξ in the system at position xξ = R + (−1)ξ(r/2), k and k′ are the wave-vectors labelling the incident and scattered neutron wave-function, q = k − k′ is the transferred momentum, ![[b with combining circumflex]](https://www.rsc.org/images/entities/i_char_0062_0302.gif) is the scattering length operator and
is the scattering length operator and| | 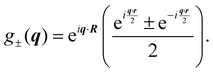 | (33) |
For nuclei with non zero spin I, the scattering length operator is defined by33| | 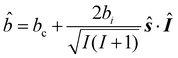 | (34) |
where ŝ and Î are the neutron and nuclear spin operators, respectively and bc and bi are the bound coherent and incoherent scattering length.
When evaluating the neutron cross-section for homonuclear diatomic molecules, only the symmetric combination intervenes in transitions where the total molecular nuclear spin does not change, ΔIN = 0, while the antisymmetric combination intervenes in transitions where the total molecular nuclear spin changes of one unit, |ΔIN| = 1. In experiments with non polarised neutrons and non polarised molecular system, the cross section can be written as product of a spin dependent part sfi and space dependent part Sfi:
| | 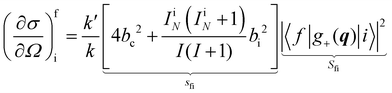 | (35) |
when
IfN ←
IiN and
| | 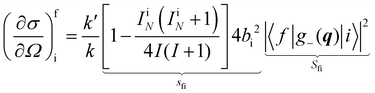 | (36) |
when
IfN ± 1 ←
IiN.
The spatial dependent part of the INS cross section involves the evaluation of the matrix elements of the local operator g±(q) where q = k − k′ is the transferred momentum. The plus and minus sign are alternatively required for direct (ortho–ortho and para–para) and cross spin transitions (ortho–para and para–ortho), respectively. For our scopes, this operator can be conveniently written as
| | 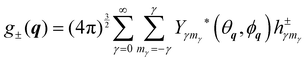 | (37) |
where * stands for complex conjugate and
| | 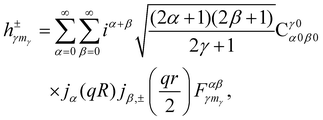 | (38) |
having used the expansion of a plane wave into spherical harmonics and spherical Bessel functions
jα27| | 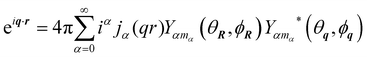 | (39) |
and the expansion of the product of two spherical harmonics into a single spherical harmonic (Clebsch–Gordan series)
27| | 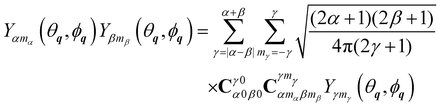 | (40) |
together with the definition of bipolar harmonics,
eqn (3). The shorthand notation
jβ,±(
x) = [
jβ(
x) ±
jβ(−
x)]/2 has been introduced in
eqn (38).
In systems with spherical symmetry, the space dependent part of the INS cross section for transitions between an initial energy level i = Eλ and a final energy level 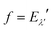 is given by the transition probability of the operator g±(q) summed over the final states mλ′ and averaged over the 2λ + 1 initial states mλ:
is given by the transition probability of the operator g±(q) summed over the final states mλ′ and averaged over the 2λ + 1 initial states mλ:
| | 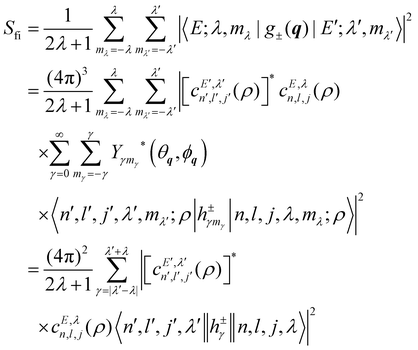 | (41) |
where
| | 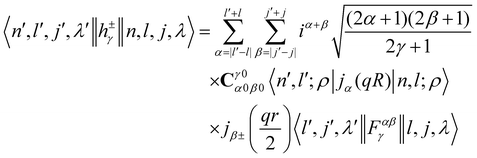 | (42) |
having used the Wigner–Eckart theorem,
48 see
eqn (28) together with the orthogonality properties of the 3j symbols
27| | 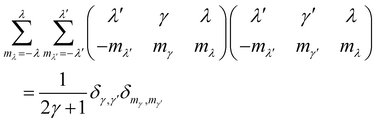 | (43) |
and of the spherical harmonics
27| | 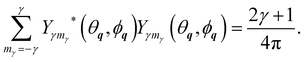 | (44) |
The condition 20 together with the identity
jβ,±(
x) = [1 ± (−1)
β]
jβ(
x)/2 valid for integer
β values allows to drop the ± sign from
eqn (43) and (44).
Acknowledgements
This work was funded by the UK Engineering and Physical Sciences Research Council (EPSRC), grant number EP/M001970/1. The authors are indebted to Nicholas J. Turro for providing the original samples and Mark Denning for purifying it.
References
- K. Komatsu, M. Murata and Y. Murata, Science, 2005, 307, 238–240 CrossRef CAS PubMed.
- K. Kurotobi and Y. Murata, Science, 2011, 333, 613–616 CrossRef CAS PubMed.
- A. Krachmalnicoff, R. Bounds, S. Mamone, S. Alom, M. Concistrè, B. Meier, K. Kouřil, M. E. Light, M. R. Johnson, S. Rols, A. J. Horsewill, A. Shugai, U. Nagel, T. Rõõm, M. Carravetta, M. H. Levitt and R. J. Whitby, Nat. Chem., 2016, 1–5 Search PubMed.
- M. H. Levitt, Philos. Trans. R. Soc., A, 2013, 371, 20120429 CrossRef PubMed.
- S. Mamone, M. Ge, D. Hüvonen, U. Nagel, A. Danquigny, F. Cuda, M. C. Grossel, Y. Murata, K. Komatsu, M. H. Levitt, T. Rõõm and M. Carravetta, J. Chem. Phys., 2009, 130, 081103 CrossRef CAS PubMed.
- M. Ge, U. Nagel, D. Hüvonen, T. Rõõm, S. Mamone, M. H. Levitt, M. Carravetta, Y. Murata, K. Komatsu, J. Y.-C. Chen and N. J. Turro, J. Chem. Phys., 2011, 134, 054507 CrossRef PubMed.
- A. J. Horsewill, S. Rols, M. R. Johnson, Y. Murata, M. Murata, K. Komatsu, M. Carravetta, S. Mamone, M. H. Levitt, J. Y.-C. Chen, J. A. Johnson, X. Lei and N. J. Turro, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 82, 081410 CrossRef.
- A. J. Horsewill, K. Goh, S. Rols, J. Ollivier, M. R. Johnson, M. H. Levitt, M. Carravetta, S. Mamone, Y. Murata, J. Y.-C. Chen, J. A. Johnson, X. Lei and N. J. Turro, Philos. Trans. R. Soc., A, 2013, 371, 20110627 CrossRef CAS PubMed.
- T. Pham, K. A. Forrest, B. Space and J. Eckert, Phys. Chem. Chem. Phys., 2016, 18, 17141–17158 RSC.
- Z. Bačić and J. C. Light, Annu. Rev. Phys. Chem., 1989, 40, 469–498 CrossRef.
- M. Xu, Y. S. Elmatad, F. Sebastianelli, J. W. Moskowitz and Z. Bačić, J. Phys. Chem. B, 2006, 110, 24806–24811 CrossRef CAS PubMed.
- F. Sebastianelli, M. Xu, Y. S. Elmatad, J. W. Moskowitz and Z. Bačić, J. Phys. Chem. C, 2007, 111, 2497–2504 CAS.
- F. Sebastianelli, M. Xu, D. K. Kanan and Z. Bačić, J. Phys. Chem. A, 2007, 111, 6115–6121 CrossRef CAS PubMed.
- M. Xu, F. Sebastianelli and Z. Bačić, J. Phys. Chem. A, 2007, 111, 12763–12771 CrossRef CAS PubMed.
- M. Xu, F. Sebastianelli, Z. Bačić, R. Lawler and N. J. Turro, J. Chem. Phys., 2008, 129, 064313 CrossRef PubMed.
- M. Xu, F. Sebastianelli, B. R. Gibbons, Z. Bačić, R. Lawler and N. J. Turro, J. Chem. Phys., 2009, 130, 224306 CrossRef PubMed.
- S. Ye, M. Xu, Z. Bačić, R. Lawler and N. J. Turro, J. Phys. Chem. A, 2010, 114, 9936–9947 CrossRef CAS PubMed.
- M. Xu, L. Ulivi, M. Celli, D. Colognesi and Z. Bačić, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 83, 241403 CrossRef.
- M. Xu and Z. Bačić, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 84, 1–10 Search PubMed.
- M. Xu, S. Ye, A. Powers, R. Lawler, N. J. Turro and Z. Bačić, J. Chem. Phys., 2013, 139, 064309 CrossRef PubMed.
- M. Xu, M. Jiménez-Ruiz, M. R. Johnson, S. Rols, S. Ye, M. Carravetta, M. S. Denning, X. Lei, Z. Bačić and A. J. Horsewill, Phys. Rev. Lett., 2014, 113, 123001 CrossRef PubMed.
- S. Mamone, J. Y.-C. Chen, R. Bhattacharyya, M. H. Levitt, R. G. Lawler, A. J. Horsewill, T. Rõõm, Z. Bačić and N. J. Turro, Coord. Chem. Rev., 2011, 255, 938–948 CrossRef CAS.
- A. Ivanov, M. Jimenéz-Ruiz and J. Kulda, J. Phys.: Conf. Ser., 2014, 554, 012001 CrossRef.
- A. J. Horsewill, K. S. Panesar, S. Rols, J. Ollivier, M. R. Johnson, M. Carravetta, S. Mamone, M. H. Levitt, Y. Murata, K. Komatsu, J. Y.-C. Chen, J. A. Johnson, X. Lei and N. J. Turro, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 85, 205440 CrossRef.
-
S. Mamone, PhD thesis, University of Southampton, UK, 2011.
- B. Poirier, J. Chem. Phys., 2015, 143, 101104 CrossRef PubMed.
-
D. A. Varshalovich, A. Moskalev and V. Khersonskii, Quantum Theory of Angular Momentum, World Scientific, Singapore, 1988, p. 514 Search PubMed.
- S. Mamone, G. Pileio and M. H. Levitt, Symmetry, 2010, 2, 1423–1449 CrossRef.
- W. G. Harter and D. E. Weeks, J. Chem. Phys., 1989, 90, 4727 CrossRef CAS.
-
S. W. Lovesay, Theory of Neutron scattering from Condensed Matter, Oxford University Press, 1984, vol. 1, p. 329 Search PubMed.
- M. Xu, S. Ye and Z. Bačić, J. Phys. Lett., 2015, 6, 3721–3725 CAS.
-
G. Herzberg, Molecular Spectra and Molecular Structure – I. Spectra of Diatomic Molecules, Van Nostrand, 1950 Search PubMed.
- V. F. Sears, Neutron News, 1992, 3, 26–37 CrossRef.
-
Mathematica, Wolfram Research Inc., 2015 Search PubMed.
- G. Herzberg and L. L. Howe, Can. J. Phys., 1959, 37, 636–659 CrossRef CAS.
- U. Fink, T. Wiggins and D. Rank, J. Mol. Spectrosc., 1965, 18, 384–395 CrossRef.
- T. Yildirim and A. B. Harris, Phys. Rev. B: Condens. Matter Mater. Phys., 2002, 66, 214301 CrossRef.
- P. M. Felker and Z. Bačić, J. Chem. Phys., 2016, 145, 084310 CrossRef PubMed.
- S. Mamone, M. R. Johnson, J. Ollivier, S. Rols, M. H. Levitt and A. J. Horsewill, Phys. Chem. Chem. Phys., 2016, 18, 1998–2005 RSC.
- L. Ulivi, M. Celli, A. Giannasi, A. J. Ramirez-Cuesta, D. J. Bull and M. Zoppi, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 76, 161401 CrossRef.
- K. T. Tait, F. Trouw, Y. Zhao, C. M. Brown and R. T. Downs, J. Chem. Phys., 2007, 127, 134505 CrossRef PubMed.
- J. M. Nicol, J. Eckert and J. Howard, J. Phys. Chem., 1988, 92, 7117–7121 CrossRef CAS.
- J. Eckert, J. M. Nicol, J. Howard and F. R. Trouw, J. Phys. Chem., 1996, 100, 10646–10651 CrossRef CAS.
- M. H. Rosnes, M. Opitz, M. Frontzek, W. Lohstroh, J. P. Embs, P. A. Georgiev and P. D. C. Dietzel, J. Mater. Chem. A, 2015, 3, 4827–4839 CAS.
- T. Pham, K. A. Forrest, E. H. L. Falcão, J. Eckert and B. Space, Phys. Chem. Chem. Phys., 2016, 18, 1786–1796 RSC.
-
S. Flügge, Practical Quantum Mechanics, Springer, Berlin, Heidelberg, 1971, p. 620 Search PubMed.
-
Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, Issue 55, ed. M. Abramowitz and I. A. Stegun, U.S. Government Printing Office, 10th edn, 1964, p. 1046 Search PubMed.
-
R. N. Zare, Angular Momentum: Understanding Spatial Aspects in Chemistry and Physics, John Wiley & Sons, 1988, p. 368 Search PubMed.
|
| This journal is © the Owner Societies 2016 |
Click here to see how this site uses Cookies. View our privacy policy here.  Open Access Article
Open Access Article

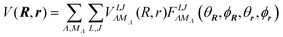
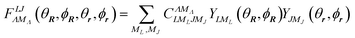
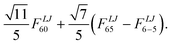
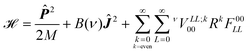
![[P with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_0050_0302.gif) is the linear momentum operator associated with the centre of mass vector, Ĵ is the angular momentum operator associated with end to end rotations, B(ν) is the effective rotational constant in the vibrational state ν and νVLL;k00 are coefficients of the expansion of the averaged molecule–cage interaction potential in bipolar harmonics of the angular variables. For a homonuclear molecule, only even k terms enter in the expansion of the potential in eqn (5) because of the symmetry of the potential under inversion. In this work the attention is restricted to H2@C60 in the ground vibrational state ν = 0 and the label ν will be dropped henceforth.
is the linear momentum operator associated with the centre of mass vector, Ĵ is the angular momentum operator associated with end to end rotations, B(ν) is the effective rotational constant in the vibrational state ν and νVLL;k00 are coefficients of the expansion of the averaged molecule–cage interaction potential in bipolar harmonics of the angular variables. For a homonuclear molecule, only even k terms enter in the expansion of the potential in eqn (5) because of the symmetry of the potential under inversion. In this work the attention is restricted to H2@C60 in the ground vibrational state ν = 0 and the label ν will be dropped henceforth.
![[capital Lambda, Greek, circumflex]](https://www.rsc.org/images/entities/b_i_char_e0a8.gif) =
= ![[L with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_004c_0302.gif) + Ĵ is given by the sum of the orbital angular momentum of the centre of mass
+ Ĵ is given by the sum of the orbital angular momentum of the centre of mass ![[L with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_004c_0302.gif) and of the end to end rotational angular momentum Ĵ. The bipolar spherical harmonics
and of the end to end rotational angular momentum Ĵ. The bipolar spherical harmonics 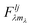 are eigenfunctions of the angular momentum operators
are eigenfunctions of the angular momentum operators ![[capital Lambda, Greek, circumflex]](https://www.rsc.org/images/entities/b_i_char_e0a8.gif) 2 and
2 and ![[capital Lambda, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0a8.gif) z with eigenvalues λ(λ + 1) and mλ, respectively. They provide a complete basis set for the coupled angular motion.
z with eigenvalues λ(λ + 1) and mλ, respectively. They provide a complete basis set for the coupled angular motion.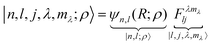
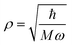 is the scale length associated to the harmonic oscillator with mass M and frequency ω. The ket in eqn (6) is an eigenstate of the spherical three-dimensional oscillator represented by the Hamiltonian in eqn (5) when terms with L = 0 and up to k = 2 are considered. In this case
is the scale length associated to the harmonic oscillator with mass M and frequency ω. The ket in eqn (6) is an eigenstate of the spherical three-dimensional oscillator represented by the Hamiltonian in eqn (5) when terms with L = 0 and up to k = 2 are considered. In this case 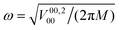 . The zero-order energy of the undecoupled translator and rotator is
. The zero-order energy of the undecoupled translator and rotator is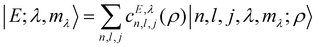
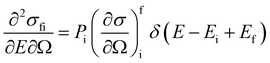
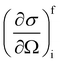 represents the transition probability for the scattering of neutrons and the delta function δ enforces the energy conservation in the scattering process. As shown with greater detail in Section A.4, the INS transition probability for homonuclear molecules in unpolarised experiments can be written as a product of a spin sfi and a space part Sfi:
represents the transition probability for the scattering of neutrons and the delta function δ enforces the energy conservation in the scattering process. As shown with greater detail in Section A.4, the INS transition probability for homonuclear molecules in unpolarised experiments can be written as a product of a spin sfi and a space part Sfi: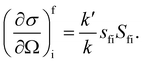

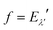 is obtained by tilting the reduced matrix element of the INS transition probability from the spherical basis to the appropriate eigen system basis:
is obtained by tilting the reduced matrix element of the INS transition probability from the spherical basis to the appropriate eigen system basis: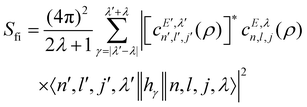
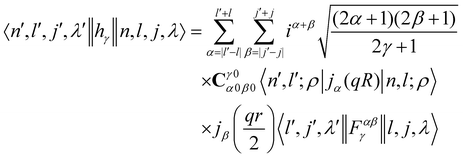
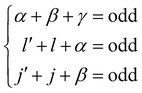
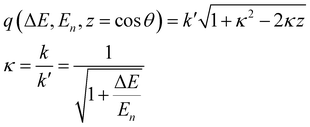
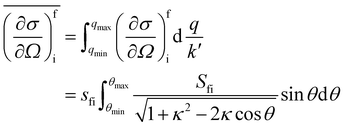
 for each possible transition. To emulate finite width transitions the peaks are finally convoluted with the instrumental resolution, assuming negligible intrinsic line-width in H2@C60.
for each possible transition. To emulate finite width transitions the peaks are finally convoluted with the instrumental resolution, assuming negligible intrinsic line-width in H2@C60.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 192 para states and 13
192 para states and 13![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 104 ortho states, of which only 800 distinct reduced para states and 972 reduced ortho states were necessary for the evaluation of the Hamiltonian and of the INS transition probability. The initial rotational parameters were fixed to the values of free H2: B0 = 7.357 meV and D0 = 0.0056 meV.35,36 Starting from the uncoupled oscillator with translational excitation ħω = 22 meV, the potential parameters
104 ortho states, of which only 800 distinct reduced para states and 972 reduced ortho states were necessary for the evaluation of the Hamiltonian and of the INS transition probability. The initial rotational parameters were fixed to the values of free H2: B0 = 7.357 meV and D0 = 0.0056 meV.35,36 Starting from the uncoupled oscillator with translational excitation ħω = 22 meV, the potential parameters 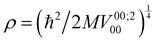 , Ṽ00;400 = ρ4V00;400, Ṽ00;600 = ρ6V00;600 and Ṽ22;200 = ρ2V22;200 were varied until satisfactory agreement with the experimental spectrum was found. The optimized values are reported in Table 1.
, Ṽ00;400 = ρ4V00;400, Ṽ00;600 = ρ6V00;600 and Ṽ22;200 = ρ2V22;200 were varied until satisfactory agreement with the experimental spectrum was found. The optimized values are reported in Table 1.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2. Similarly the peak at 49.8 meV corresponds to a transition to an energy level comprising a superposition of the (2,0,1,1) and (2,2,1,1) states in a ratio close to 2
2. Similarly the peak at 49.8 meV corresponds to a transition to an energy level comprising a superposition of the (2,0,1,1) and (2,2,1,1) states in a ratio close to 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1. The partner transitions to these superposition states originating from the para ground state are found at 61.3 and 64.2 meV, respectively, while the para transition towards (2,2,1,2) is forbidden and the para transition towards (2,2,1,3) has negligible intensity.
1. The partner transitions to these superposition states originating from the para ground state are found at 61.3 and 64.2 meV, respectively, while the para transition towards (2,2,1,2) is forbidden and the para transition towards (2,2,1,3) has negligible intensity.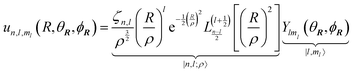
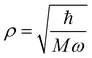 is the scale length associated to the harmonic oscillator, L(α)n is a generalized Laguerre polynomial47 and
is the scale length associated to the harmonic oscillator, L(α)n is a generalized Laguerre polynomial47 and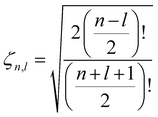
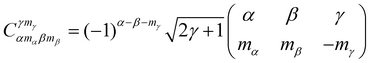
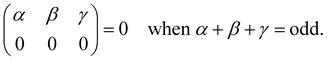
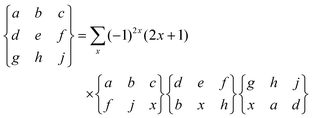
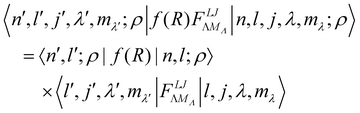
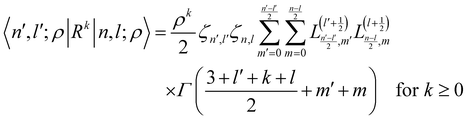
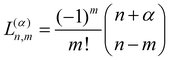
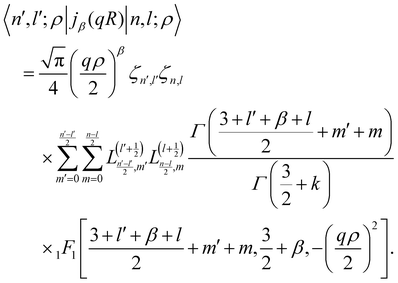
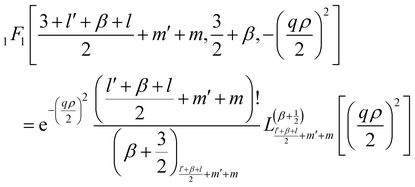
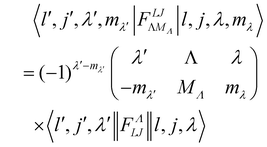
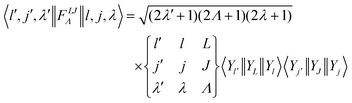
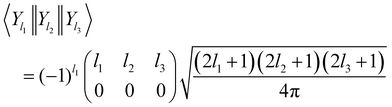
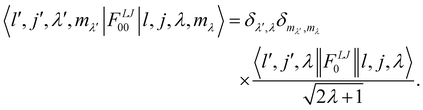
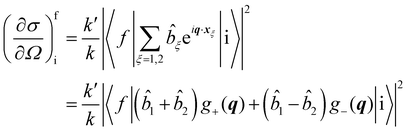
![[b with combining circumflex]](https://www.rsc.org/images/entities/i_char_0062_0302.gif) is the scattering length operator and
is the scattering length operator and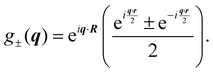
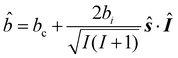
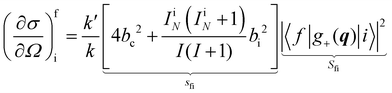
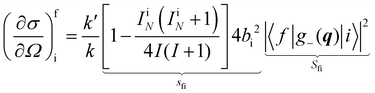
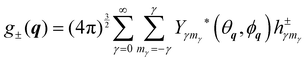
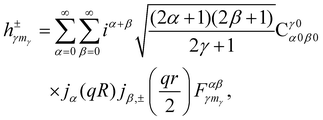
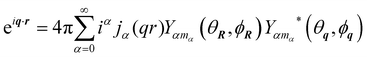
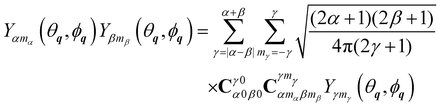
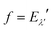 is given by the transition probability of the operator g±(q) summed over the final states mλ′ and averaged over the 2λ + 1 initial states mλ:
is given by the transition probability of the operator g±(q) summed over the final states mλ′ and averaged over the 2λ + 1 initial states mλ: