Open Access Article
Open Access ArticleRevisiting the F + HCl → HF + Cl reaction using a multireference coupled-cluster method†
Yuri Alexandre
Aoto
* and
Andreas
Köhn
Institut für Theoretische Chemie, Universität Stuttgart, Pfaffenwaldring 55, D-70569 Stuttgart, Germany. E-mail: yuri.aoto@theochem.uni-stuttgart.de; koehn@theochem.uni-stuttgart.de
First published on 21st September 2016
Abstract
We have constructed a new potential energy surface for the title reaction, based on the internally contracted multireference coupled-cluster method. The calculated barrier height is 1.59 ± 0.08 kcal mol−1. This value is much lower than that obtained in previous ab initio calculations and it is close to the experimentally suggested value. Other features of the [F,H,Cl] system are also analysed, such as van der Waals minima and conical intersections. The rate constant and the vibrational and rotational distributions of the products were calculated using a fully converged time independent quantum mechanical approach. The calculated rate constant agrees well with the experimental values. Qualitative agreement for the vibrational distribution is obtained and it is shown that it is strongly influenced by the initial rotational state distribution.
1 Introduction
The dynamics of the chemical reaction F + HCl → HF + Cl has been explored in great detail,1–17 but calculations from first principles have not been able to fully reproduce and rationalise the experimental results.11,14–17 This chemical reaction is highly exothermic and proceeds through a small barrier, a transition state with a bent geometry whose ab initio description has been proven to be very challenging. It has multireference character and is affected by two conical intersection seams at collinear geometries.12 Several ab initio theories predict very different values for the barrier height, ranging from 6.22 kcal mol−1, at the UMP2 level of theory (unrestricted Møller–Plesset second-order perturbation theory),7 to the ROHF-UCCSD(T) result of 2.38 kcal mol−1 (unrestricted coupled-cluster theory with singly and doubly excited clusters and non-iterative triply excited clusters with a restricted open-shell reference).15 All of them are, however, well above the experimentally suggested value of 1.2 kcal mol−1.1Deskevich et al. employed the multireference configuration interaction method with Davidson correction (MRCI + Q) and extrapolation to the complete basis set (CBS) limit to construct the currently most accurate potential energy surface for this reaction.12 This potential energy surface, denoted as DHTSN PES in the following, was fitted using 3230 points calculated at the MRCISD + Q/CBS level of theory, with the correlation energy scaled to reproduce the experimental exothermicity of −33.06 kcal mol−1 (the MRCISD + Q/CBS value is −30.88 kcal mol−1). The MRCISD + Q/CBS estimate for the barrier height is 4.2 kcal mol−1 and the scaled PES has a transition state energy of 3.8 kcal mol−1 (still largely overestimating the experimental suggestion). As this value is similar to the barrier height calculated at the partially spin restricted CCSD(T) level using a restricted open-shell reference function and a basis set of triple-ζ quality, Deskevich et al. argue that the value of 3.8 kcal mol−1 should be accurate. However, calculations using the DHTSN PES strongly underestimate the experimental reaction rate constant,5,6 suggesting that its transition state energy is too high. Using an accurate time-dependent quantum mechanical approach, Bulut et al.16 obtained a value of 2 × 10−13 cm−3 s−1 at 300 K, while the experimental result is (7.2 ± 0.3) × 10−12 cm−3 s−1.5 This disagreement increases at lower temperatures, reaching a difference of more than two orders of magnitude.
Calculations using the DHTSN PES have also been unable to predict more detailed information on the dynamics of this reaction. The state-to-state process can be described by:
| F + HCl(vi,ji) → HF(vf,jf) + Cl |
Interestingly, studies using semi-empirical global potential energy surfaces, or based on less accurate ab initio calculations, show very good agreement with the experimental rate constant and vibrational distribution of the products.7–10 Sayós et al. constructed a global PES for this system based on spin projected MP2 (PUMP2) ab initio calculations with the 6-311G(3d2f,3p2d) basis set, but scaled the PES to fit the experimental rate constant.7 The final barrier height of the scaled PES is 1.12 kcal mol−1. A study based on quasi-classical trajectory calculations was made using this potential energy surface,8 with good agreement with the experimental rate constant and vibrational distribution of the products. Quantum wave packet calculations using this PES were also able to give good agreement with the experimental rate constant.9 A semi-empirical LEPS (London-Eyring-Polanyi-Sato) PES was determined by Kornweits and Persky, also constructed to reproduce the experimental results.10 The good agreement with the experimental rate constant obtained with these PESs is not surprising, since they were constructed to reproduce such quantity. It is interesting, however, that Sayós et al. were able to reproduce the experimental vibrational distribution.8
The rotational distribution was also investigated experimentally, but with fundamental differences among reported results. The most recent study, conducted by Zolot and Nesbitt,13 shows a bimodal rotational distribution, with a large probability of HF formation at high values of jf, but also with non-vanishing probability for lower rotational quantum numbers. This bimodal distribution is not observed in older experiments,2,3 showing only the rotationally hot HF. Zolot and Nesbitt have also performed calculations of quasi-classical trajectories using the DHTSN PES. The results obtained from calculations involving only the exit channel indicate that the bimodal distribution is associated with the reactants being trapped in the HF–Cl van der Waals well. The quantum mechanical calculations carried out by Li et al., however, do not show the bimodal distribution,15 but are very close to the previous experimental results reported by Ding et al., for vf = 2, the (experimentally) most populated state. The rotational distribution calculated by Sayós et al., using quasi-classical trajectories and their PUMP2-based PES, also does not present the bimodal distribution.8
In this article, we report our study on the F + HCl → HF + Cl reaction employing the internally contracted multireference coupled-cluster (icMRCC) theory.19–21 The icMRCC method with single and double excitations and perturbative treatment of triples, icMRCCSD(T),22 is here for the first time applied to the computation of a global potential energy surface. This method promises to merge the accurate description of dynamical correlation by a cluster expansion with the ability to properly describe spin-coupled open-shell fragments. The present implementation of the icMRCC theory is size-consistent, size-extensive and is invariant under rotations of the orbitals within the closed, active and virtual orbitals.20,21,23 As we will show, the icMRCCSD(T) method is able to give an accurate value for the barrier height of this reaction, very close to the experimentally suggested value. An analytic PES based on the many-body expansion was fitted to a set of about 5000 ab initio points. This PES is further used to investigate the reaction dynamics with the coupled-channel hyperspherical coordinate method.24–26 Although the present PES does not describe multisurface, non-adiabatic and full spin–orbit coupling effects, the results agree very well with experiments, showing that this is the first ab initio PES for this reaction able to reproduce the details of the dynamics.
2 Ab initio calculations
The construction of accurate analytic representations of global potential energy surfaces has been mainly restricted to MRCI + Q calculations. This is because a multireference treatment is usually required when scanning different regions of the PES, possibly containing electronic degeneracies. A well-known deficiency of the MRCI method, however, is its lack of extensivity due to the linear ansatz for the wavefunction. The use of an exponential ansatz in the icMRCC theory recovers a much larger portion of the dynamical correlation and offers a more systematic hierarchy of methods, in particular by perturbative estimates of three-body correlation. Therefore, rather small active spaces can be used in multireference coupled-cluster theories with good results.22,27 Only the orbitals that are really relevant to the chemical phenomena need to be included in the active space. This is in contrast to the MRCI method, that usually needs all the valence orbitals and electrons in the active space to obtain accurate results. The active space used in our calculations consists of three electrons distributed in three orbitals. This allows one to describe the three separated atoms (each one in the doublet state, with one electron in the singly occupied orbital of each atom) and the three possible dissociation channels, namely, F + HCl (the entrance channel), HF + Cl (the exit channel) and H + FCl (the second, highly energetic, exit channel). In each one of these dissociation channels the lowest energy active orbital (doubly occupied in the dominant configuration) is the σ-bonding orbital of the diatomic fragment, followed by the singly occupied orbital of the atom. The σ-anti-bonding orbital of the diatomic is the most energetic active orbital. The three active orbitals belong to the a′ irreducible representation in the Cs point group. Although this active space breaks the symmetry of the three atomic P states, this does not pose a problem. The degenerate component that is not described by this active space is antisymmetric with respect to the molecular plane and it does not mix with the A′ states.The reference space generated by a complete active space self-consistent field (CASSCF) procedure was used as zeroth order space for the subsequent icMRCCSD(T) calculations. In most of the calculations the electrons of the core (1s of fluorine and 1s, 2s, and 2p of chlorine) were not correlated. Core–valence correlation effects for the diatomic molecules (and thus for the two-body contributions to the global PES) were obtained by an additive scheme. Two sets of calculations were carried out at the icMRCCSD(T)/aug-cc-pwCVTZ level, one correlating and one freezing the external core (1s of fluorine and 2s and 2p of chlorine). The core-correlation contribution is estimated as the difference of these two energies. The results with this correction are denoted by icMRCCSD(T)-cc.
The basis sets aug-cc-pVXZ (X = T, Q, 5)28 were used for the hydrogen and fluorine atoms and the basis sets aug-cc-pV(X+d)Z for chlorine.29 Core-correlation effects were estimated using the aug-cc-pwCVTZ basis set. They are collectively denoted by aVXZ in this article. Complete basis set (CBS) extrapolation for the correlation energy (i.e. the icMRCCSD(T) energy minus the CASSCF energy) was done for the diatomic molecules, using the aVQZ and aV5Z results and the formula30,31
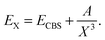 | (1) |
The icMRCC calculations were carried out with the General Contraction Code (GeCCo), as described in ref. 21. The CASSCF33,34 reference wave functions and required integrals were calculated with Dalton35 and Molpro36 packages.
3 Details on the chemical system
3.1 The diatomic fragments
The potential energy curves for the dissociation channels were calculated at several levels of theory, and their dissociation energies and spectroscopic properties are shown in Table 1. These were obtained from analytic fits of about 55 ab initio points along the potential energy curve, using the analytic representation discussed below (eqn (3) in Section 4) at each level of theory. The dissociation energies and spectroscopic properties calculated with the aV5Z basis set are already well converged and do not differ significantly from the aVQZ values. Table 1 also shows the values obtained using the DHTSN PES, described in ref. 12, and the experimental reference values. The dissociation energies obtained with the highest level of theory, icMRCCSD(T)-cc/CBS, show close agreement with the experimental results, as well as with the values described by Deskevich et al. We recall, however, that the good agreement with experiments for the dissociation energies of the DHTSN PES is a result of a scaling procedure, to match the experimental exothermicity. Pure MRCI + Q/CBS results show a somewhat worse agreement to the experimental dissociation energies. The icMRCCSD(T)-cc/CBS predictions of the spectroscopic parameters are also in good agreement with the experimental values.| Method/basis | D e | r e | ω e | ω e x e | B e | α e |
|---|---|---|---|---|---|---|
| HF | ||||||
| icMRCCSD/aVTZ | 138.53 | 1.739 | 4129.0 | 87.5 | 20.7933 | 0.770 |
| icMRCCSD(T)/aVTZ | 139.28 | 1.741 | 4116.2 | 87.4 | 20.7452 | 0.768 |
| icMRCCSD(T)/aVQZ | 140.91 | 1.735 | 4133.0 | 89.9 | 20.8925 | 0.791 |
| icMRCCSD(T)/aV5Z | 141.20 | 1.734 | 4133.2 | 89.9 | 20.9098 | 0.793 |
| icMRCCSD(T)-cc/CBS | 141.68 | 1.733 | 4133.0 | 88.1 | 20.9421 | 0.797 |
| Experimental | 141.63 | 1.733 | 4138.3 | 89.9 | 20.9557 | 0.798 |
| DHTSN PES | 141.58 | 1.732 | 4143.0 | 76.4 | 21.0586 | 0.701 |
| MRCI + Q/CBS | 140.50 | 1.732 | 4143.2 | 77.1 | 21.0599 | 0.705 |
| HCl | ||||||
| icMRCCSD/aVTZ | 104.88 | 2.413 | 2991.1 | 53.0 | 10.5583 | 0.303 |
| icMRCCSD(T)/aVTZ | 105.29 | 2.414 | 2986.7 | 52.8 | 10.5429 | 0.303 |
| icMRCCSD(T)/aVQZ | 106.51 | 2.414 | 2985.3 | 52.0 | 10.5432 | 0.302 |
| icMRCCSD(T)/aV5Z | 106.93 | 2.413 | 2988.2 | 53.1 | 10.5501 | 0.303 |
| icMRCCSD(T)-cc/CBS | 107.62 | 2.410 | 2991.3 | 51.0 | 10.5790 | 0.301 |
| Experimental | 107.36 | 2.409 | 2990.9 | 52.8 | 10.5934 | 0.307 |
| DHTSN PES | 107.35 | 2.412 | 2980.2 | 45.4 | 10.6433 | 0.294 |
| MRCI + Q/CBS | 106.67 | 2.413 | 2978.2 | 45.6 | 10.6388 | 0.295 |
| ClF | ||||||
| icMRCCSD/aVTZ | 57.89 | 3.100 | 769.7 | 5.1 | 0.5090 | 0.004 |
| icMRCCSD(T)/aVTZ | 59.28 | 3.104 | 767.7 | 5.0 | 0.5075 | 0.004 |
| icMRCCSD(T)/aVQZ | 61.45 | 3.091 | 778.3 | 4.9 | 0.5119 | 0.004 |
| icMRCCSD(T)/aV5Z | 62.14 | 3.085 | 781.5 | 4.9 | 0.5137 | 0.004 |
| icMRCCSD(T)-cc/CBS | 63.02 | 3.077 | 786.3 | 4.9 | 0.5164 | 0.004 |
| Experimental | 61.50 | 3.077 | 786.2 | 6.2 | 0.5165 | 0.004 |
| DHTSN PES | 61.73 | 3.081 | 816.3 | 5.8 | 0.5155 | 0.004 |
| MRCI + Q/CBS | 60.54 | 3.083 | 811.7 | 5.8 | 0.5148 | 0.004 |
3.2 Transition state
The transition state geometry was optimised at the icMRCCSD and icMRCCSD(T) levels, using the aVTZ and aVQZ basis sets. The results are presented in Table 2 and one can see a large decrease of the barrier height, when compared to standard methods like MRCI and single reference coupled-cluster theory. Without considering the effects of connected triples, i.e., at the icMRCCSD/aVTZ level, a result of 3.66 kcal mol−1 is obtained, comparable to the RCCSD(T) value and to the value of the DHTSN PES. The result obtained at the icMRCCSD(T)/aVTZ level of theory is 1.35 kcal mol−1, very close to the experimentally suggested value of 1.2 kcal mol−1.1 This shows the importance of the triples correction, not included in the MRCI calculations, to describe the transition state, lowering the barrier height by more than 2 kcal mol−1. Note that in the case of MRCI calculations the only way to improve the results is to extend the active space. Since a full valence active space was employed by Deskevich et al., a double shell approach would be needed. In the case of the Cl atom, this would imply to also include the 3d orbitals, leading to an intractably large active space.| Method/basis | E TS | R HF | R HCl | θ FHCl | ω 1 | ω 2 | ω 3 |
|---|---|---|---|---|---|---|---|
| a Ref. 12. b Ref. 15. | |||||||
| icMRCCSD/aVTZ | 3.66 | 2.830 | 2.485 | 123.8 | 1317.8i | 2240.1 | 188.0 |
| icMRCCSD/aVQZ | 3.57 | 2.829 | 2.486 | 123.1 | 1319.6i | 2253.0 | 187.1 |
| icMRCCSD(T)/aVTZ | 1.35 | 2.898 | 2.489 | 112.2 | 1117.5i | 2415.8 | 195.8 |
| icMRCCSD(T)/aVQZ | 1.07 | 2.901 | 2.489 | 110.9 | 1090.5i | 2429.7 | 197.8 |
| Initial PES | 1.34 | 2.949 | 2.482 | 111.1 | 1150.7i | 2475.3 | 190.8 |
| Final PES | 1.59 | 2.920 | 2.485 | 111.2 | 1191.5i | 2435.3 | 199.2 |
| DHTSNb | 3.8 | 2.69 | 2.51 | 123.5 | 1117.2i | 2205.1 | 293.4 |
| MRCI + Q/aVTZa | 4.2 | 2.52 | 2.72 | 123.2 | — | — | — |
| RCCSD(T)/aVTZa | 3.7 | 2.65 | 2.53 | 119.3 | — | — | — |
| UCCSD/aVTZ-DZb | 5.46 | 2.74 | 2.54 | 124.6 | — | — | — |
| UCCSD(T)/aVTZ-DZb | 2.38 | 2.74 | 2.52 | 115.9 | 1057.2i | 2320.5 | 219.9 |
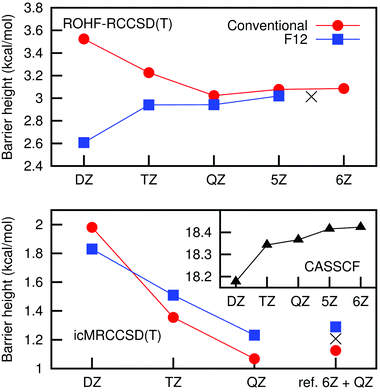
The convergence of the barrier height with the basis set was investigated running icMRCCSD(F12*) + (T) single point calculations at the icMRCCSD(T)/aVQZ geometry. As one can see in Fig. 1, although the barrier height calculated with conventional icMRCCSD(T) theory decreases with the basis set, the value obtained with F12 theory is higher. icMRCC calculations using a basis set larger than aVQZ are prohibitively expensive, but calculations with single reference coupled-cluster theory show a non-monotonic convergence of the barrier height. For these reasons, an aVTZ/aVQZ CBS extrapolation for the barrier height would probably give an inaccurate result. We hence argue that a more reliable estimate is obtained from the CASSCF energy calculated with the aV6Z basis (that is well converged, see the inset graph) and the correlation energy obtained with the aVQZ basis set. The values obtained in this way with conventional and F12 theories are 1.13 and 1.29 kcal mol−1, respectively. These can be seen as lower and upper bounds and we will use the average, 1.21 kcal mol−1, as an estimate for the icMRCCSD(T)/CBS barrier height. The barrier height obtained in a similar way for the ROHF-RCCSD(T) case is also shown in Fig. 1.
In the absence of spin–orbit effects, the electronic ground state in the entrance channel, F(2P) + HCl(1Σ), is threefold degenerate. As the two reactants approach each other, these states correlate with two 2A′ and one 2A′′ states. In the non-relativistic description, these three states are degenerate. However, if the spin–orbit coupling is considered, two of these states have their energy lowered by 0.39 kcal mol−1 and one increased by 0.77 kcal mol−1 (associated with the states 3P3/2 and 3P1/2 of fluorine, respectively, and using the experimental splitting of 1.16 kcal mol−1).37 Only one of the lower states is reactive; see the ESI,† and Section 5.2 for a deeper discussion. In the transition state region, the other two states have much higher energies and the spin–orbit coupling has no influence on the ground state energy. This effectively increases the barrier height by an amount of 0.39 kcal mol−1, not considered in the icMRCC calculations. If this correction is added to the icMRCCSD(T)/CBS barrier height estimated above, the value of 1.59 ± 0.08 kcal mol−1 is obtained, which is our final estimate for the barrier height.
The geometry of the transition state also changes considerably compared to the DHTSN PES (see Table 2), becoming even more bent and with a larger FH distance, resulting in an even earlier transition state in comparison to the DHTSN PES. The geometry almost does not change when the aVQZ basis set is used. As a general trend, the barrier height decreases and the transition state becomes more bent as the level of theory increases. The vibrational frequencies in the transition state are also given in Table 2. The icMRCCSD(T) imaginary frequency (ω1, antisymmetric stretch) is very close to the DHTSN one. The symmetric stretch (ω2) and the bending frequency (ω3), on the other hand, differ substantially from the DHTSN values.
4 PES fitting
With our present implementation, icMRCCSD(T) calculations are computationally very expensive, even with the small active space used in most of our calculations. For instance, an icMRCCSD(T) calculation on this system with the aVTZ basis set takes about 3 hours of CPU time on an Intel® Xeon® processor (E5-2680 v2 2.80 GHz) and uses 10 Gb of RAM. These values increase to about 20 hours and 24 Gb with the aVQZ basis set. Currently our code is not parallelised and each calculation runs on a single core. To construct a reliable global PES based on this method we have to perform about 5000 ab initio calculations, which restricts the basis set to a moderate size. We were able to perform such number of calculations with the aVTZ basis set. The barrier height at this level of theory is already much lower than in the DHTSN PES and close to our estimate of 1.21 kcal mol−1. The transition state geometry and frequencies also do not change considerably from the triple to the quadruple-ζ basis set, see Table 2. This indicates that the topology of the icMRCCSD(T)/aVTZ PES is already good. The dissociation energies and the spectroscopic parameters of the fragments, however, can be much improved with the CBS extrapolation and core–valence correlation effects.We aim at an analytic representation of the PES that takes into account our best estimate of each feature of the PES: the global topology of the PES to be described at the icMRCCSD(T)/aVTZ level of theory, the barrier height as described in Section 3.2 and the diatomic fragments with the quality of the icMRCCSD(T)-cc/CBS calculations. This was done using the many-body expansion:
| V(R) = V(1) + V(2)FH(RFH) + V(2)HCl(RHCl) + V(2)ClF(RClF) + αV(3)(R), | (2) |
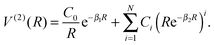 | (3) |
| Method/basis | RMSD, in kcal mol−1 |
|---|---|
| V (2)FH – icMRCCSD(T)/aVTZ | 0.0011 |
| V (2)HCl – icMRCCSD(T)/aVTZ | 0.0055 |
| V (2)ClF – icMRCCSD(T)/aVTZ | 0.0143 |
| V (2)FH – icMRCCSD(T)-cc/CBS | 0.0083 |
| V (2)HCl – icMRCCSD(T)-cc/CBS | 0.0066 |
| V (2)ClF – icMRCCSD(T)-cc/CBS | 0.0116 |
| V (3) – icMRCCSD(T)/aVTZ (all) | 0.1737 |
| V (3) – icMRCCSD(T)/aVTZ (valley) | 0.1591 |
The functional form employed for the three-body term is:
V(3)(R) = x(R)![[scr V, script letter V]](https://www.rsc.org/images/entities/char_e149.gif) (3)TS(R) + (1 − x(R)) (3)TS(R) + (1 − x(R))![[scr V, script letter V]](https://www.rsc.org/images/entities/char_e149.gif) (3)LR(R), (3)LR(R), | (4) |
![[scr V, script letter V]](https://www.rsc.org/images/entities/char_e149.gif) (3)TS, to the long range region, described by
(3)TS, to the long range region, described by ![[scr V, script letter V]](https://www.rsc.org/images/entities/char_e149.gif) (3)LR. These two functions have the same form, as suggested in ref. 41:
(3)LR. These two functions have the same form, as suggested in ref. 41: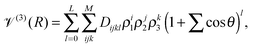 | (5) |
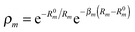 . R0m are the diatomic internuclear distances and
. R0m are the diatomic internuclear distances and 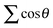 is the sum of the cosines of the three internal angles. The indices are restricted to the following conditions:42
is the sum of the cosines of the three internal angles. The indices are restricted to the following conditions:42| i + j + k ≠ i ≠ j ≠ k, | (6) |
| i + j + k ≤ M. | (7) |
This function was fit to 5207 points, chosen to cover the most important regions of the potential energy surface. The main set of points, 2984 in total, was placed in the valley of the potential energy surface where the reaction takes place. Higher weights were given to the points closer to the transition state. 164 extra points around the transition state were added to guarantee the correct description of the curvature of the potential energy surface and the vibrational frequencies. In the dissociation limits and in the H + FCl reaction channel, 1456 more sparse points were calculated. Extra 434 points in the repulsive wall and 169 points in the atomic fragmentation region (F + H + Cl) were calculated to avoid a non-physical behaviour of the potential energy surface in these regions. Low weights were given to these points. These points were chosen based on the already known topology of the DHTSN PES and on the optimised icMRCCSD(T) transition state. A detailed description of the points and the weights is given in the ESI.†
The three-body term was fitted to ab initio points calculated at the icMRCCSD(T)/aVTZ level, after removing the corresponding one-body and two-body contributions. The root mean square deviation (RMSD) of this fit is very good, and it amounts to only 0.17 kcal mol−1. The RMSD considering only the valley of the reaction is slightly smaller. To get a deeper insight into the quality of this fit, the transition state properties for the PES obtained with this three-body term and the corresponding two-body terms, obtained at the icMRCCSD(T)/aVTZ level, are given in Table 2 (“initial PES”). These are to be compared with the values at the line “icMRCCSD(T)/aVTZ”, obtained directly from the ab initio calculations. The transition state energy and geometry are very similar and the vibrational frequencies differ in less than 2.5%.
To ensure that the potential energy surface describes the fragments as accurately as possible, the two-body terms used in the final expansion were the ones obtained at the icMRCCSD(T)-cc/CBS level of theory. This is possible since the three-body term vanishes in the fragment region. Finally, the three-body term is scaled by a constant factor α = 1.02403 such that the final barrier height has the value of 1.59 kcal mol−1, our best estimate as described in Section 3.2. The transition state properties of this potential energy surface are described in Table 2, as “final PES”. One can see that the geometric parameters and the vibrational frequencies of the transition state do not substantially change from the “initial PES”.
5 The global topology of the PES
A good understanding of the global topology of the potential energy surface can be obtained from the level surfaces in perimetric coordinates.38–40 They are defined by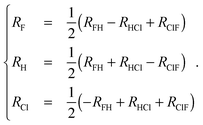 | (8) |
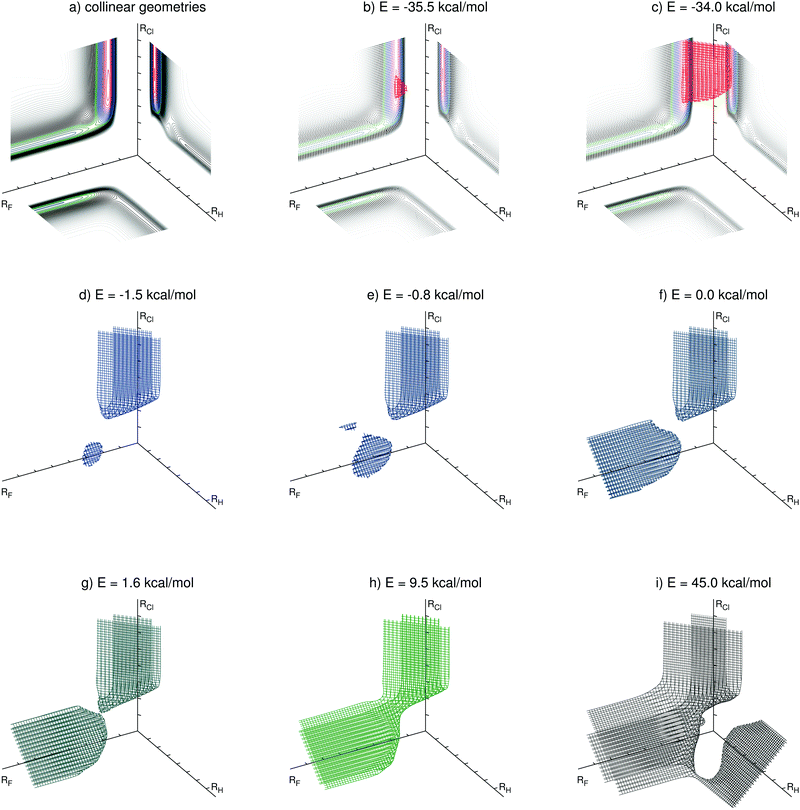 | ||
| Fig. 2 Level surfaces for selected energies (relative to the entrance channel) in perimetric coordinates. | ||
The overall potential energy surface has three van der Waals minima along the reaction F + HCl → HF + Cl, discussed in Section 5.1. The position of the deepest one, with linear geometry at the exit channel, can be seen in the level surface for the energy E = −35.5 kcal mol−1 (Fig. 2b). The level surface shown in Fig. 2c encloses the exit channel of the potential energy surface. For the energies E = −1.5 kcal mol−1 (Fig. 2d) and E = −0.8 kcal mol−1 (Fig. 2e) two van der Waals minima in the entrance channel can be identified. The bent van der Waals minimum is clearly visible in both Fig. 2d and e, whereas the linear one displays a tiny additional surface in Fig. 2e. For E = 0.0 kcal mol−1 the level surface has also a branch covering the entrance channel. For energies higher than the transition state energy (ETS = 1.59 kcal mol−1) the two branches are joined, as for the case depicted in Fig. 2g. In this level surface one can clearly see the position of the transition state, being the point that connects its two parts. Higher energy level surfaces have a broader connection between the entrance and exit channels, as shown in Fig. 2h for the level surface at the energy E = 9.5 kcal mol−1. This energy is close to the total energy of the average initial condition (Ec = 4.3 kcal mol−1, vi = 0, ji = 5) of the most recent experiment for this reaction.13 A classical trajectory of this reaction with such total energy is contained in the region inside this level surface. The level surface for E = 45.0 kcal mol−1 is shown in Fig. 2i. The H + FCl channel (the branch towards the right side) and the F–Cl–H linear transition state (its connecting point to the rest of the level surface) are visible. We recall, however, that the present PES was constructed focusing the F + HCl → HF + Cl reaction and this high energy channel is probably not so accurately described as the other two.
Fig. 3 shows a cut of the PES along the geometries with the angle θFHCl fixed at the value of the transition state. One can see that this PES has an early transition state, the reason why products with high vibrational energy are formed.
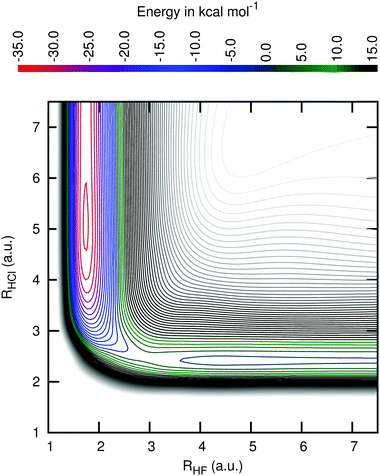 | ||
| Fig. 3 Level curves for the region of the potential energy surface with the angle F–H–Cl fixed at the transition state value of 111.2 degree. The energies of the contour lines are spaced by 2.5 kcal mol−1. The top panel shows the correspondence between the energy levels and their colours. The same correspondence is used in Fig. 2. | ||
5.1 Van der Waals minima
The properties of the three van der Waals minima are given in Table 4. All of them are deeper than in the DHTSN PES, but the geometries do not change considerably, except for the RHF distance of the bent minima at the entrance channel. The van der Waals complex at the exit channel, in particular, deserves a brief analysis. It was experimentally described by Merritt et al.43 and the infrared spectrum of the Cl–HF complex in helium nanodroplets shows a peak at 3887.54 cm−1. To take into account the effects of anharmonicity and from the helium nanodroplets on the frequencies, a scaling factor is suggested by the authors, obtained from the HF vibrational frequency, see Table 1 of ref. 43. With this correction, this value is scaled to 4046.5 cm−1. The harmonic frequency calculated with our PES is 4110.7 cm−1, not far from the scaled experimental value. Based on calculations with the DHTSN PES, Zolot and Nesbitt suggested that this van der Waals minimum can play an important role in the dynamics of the title reaction to explain the experimentally observed rotational distribution.13 According to these authors it might behave as a trap for the nascent HF product, allowing for a rotational cooling and leading to a modified rotational distribution, where the probability for lower rotational levels is increased. If this is indeed the case, our proposed PES should be able to reproduce the same effect because the van der Waals minimum is deeper, as compared with the DHTSN PES, but has similar geometric and vibrational parameters.| Method/basis | Depth | R HF | R HCl | θ FHCl | ω 1 | ω 2 | ω 3 |
|---|---|---|---|---|---|---|---|
| Linear, at the entrance channel | |||||||
| Present PES | 0.94 | 4.64 | 2.41 | 180.0 | 3047.8 | 79.7 | 70.4 |
| DHTSN PES | 0.67 | 4.44 | 2.42 | 180.0 | 2925.2 | 122.9 | 65.3 |
| Bent, at the entrance channel | |||||||
| Present PES | 2.45 | 4.86 | 2.41 | 62.2 | 3044.7 | 412.7 | 183.9 |
| DHTSN PES | 0.94 | 5.67 | 2.41 | 75.1 | 3034.0 | 177.7 | 42.8 |
| Linear, at the exit channel | |||||||
| Present PES | 2.60 | 1.74 | 4.54 | 180.0 | 4110.7 | 250.7 | 146.9 |
| DHTSN PES | 1.95 | 1.75 | 4.73 | 180.0 | 4035.2 | 321.4 | 93.4 |
5.2 Conical intersections
Any arbitrary geometry of the FHCl system belongs to the Cs point group and the ground state PES is of A′ symmetry. At linear geometries, with the hydrogen atom in the centre, the system belongs to the C∞v point group and the three states that dissociate into the ground state of the entrance channel are a 2Σ state and the two components of a 2Π state. At the entrance and exit channels the state of the lowest energy is the 2Π state, but in the region where the three atoms are close to each other the 2Σ state has the lowest energy. At the geometries where these two states intersect, two conical intersection seams arise.Extra icMRCCSD(T) calculations for these states were carried out for the minimum energy path of the fitted PES. They were performed with an extended active space with seven electrons distributed in five orbitals. In this active space three σ orbitals and the highest occupied πx and πy orbitals are included. These curves are depicted in Fig. 4. Note that the Π and Σ states cross each other at two points, one slightly before and the other slightly after the transition state.
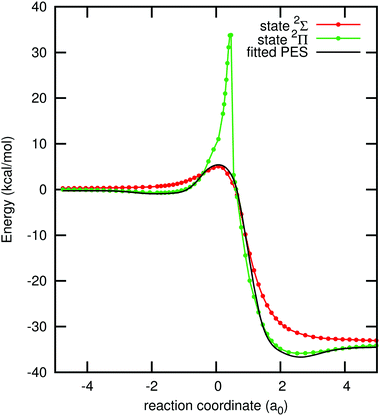 | ||
| Fig. 4 Minimum energy path of the fitted PES along the collinear geometries F–H–Cl and the 2Σ and the 2Π states along these geometries, calculated with icMRCCSD(T)/aVTZ and an (7,5) active space. | ||
At the MRCI + Q level of theory, the energies of the conical intersections are lower than the transition state energy.12 Although the transition state has a bent geometry and the conical intersections are at the collinear geometries, the reactants that are energetically able to cross the classical barrier will also be able to reach the conical intersection and possibly be affected by it. At the icMRCCSD(T) level, the conical intersection energies are 3.4 kcal mol−1 (at the entrance channel) and −1.4 kcal mol−1 (at the exit channel), without considering the spin–orbit coupling. Since the barrier height is 1.21 kcal mol−1 (or 1.59 kcal mol−1 including spin–orbit effects), the conical intersection at the entrance channel has a higher energy than the barrier and its role in the dynamics might not have the large extent expected by the same analysis at the MRCI + Q level. Moreover, it would decrease the rate constant, since a wave packet hopping across it to the above state is affected by a higher barrier. The effects of these conical intersection seams on the dynamics are, however, not clear. A multistate potential energy surface and rigorous treatment of the dynamics including non-adiabatic effects are needed to know the full extent of the effects of these conical intersections on this chemical reaction.
Our new PES also describes the conical intersection regions with a smooth transition between both states. The active space used in our calculations includes only one of the three p orbitals of the fluorine atom. The orbital perpendicular to the molecular plane does not contribute to the described A′ state and its absence in the active space is not a problem. Close to the conical intersection, the p orbital in the active space has to switch from a perpendicular one (describing one component of the Π state) to a collinear one to form a Σ state. For non-linear geometries the orbitals in the active space can adapt continuously. At linear geometries, on the other hand, this gives rise to small discontinuities in the MRCC PES at the regions close to the conical intersections. We have overcome this in the fitting procedure by giving lower weights to these points. One can see that the final PES is smooth and fits well the state of the lowest energy, whether it is the Σ or the Π state. This approach can be justified by the fact that indeed the conical intersection is replaced by an avoided crossing if spin–orbit effects are included, see the ESI.† We recall that, with a proper active space, the icMRCC theory is able to accurately describe avoided crossings.44
The small differences between the fitted PES and the lowest energy 2Σ/2Π state curves in Fig. 4 come from the fact that we used CAS(3,3) points in the fitting, that we are employing a scaling in the three-body term and that the two-body term is from a higher level of theory; see Section 4.
6 Chemical dynamics
The dynamics of the F + HCl → HF + Cl chemical reaction was studied with the full quantum mechanical approach implemented in the ABC program of Skouteris et al.26 It solves the time independent nuclear Schrödinger equation for the reactive scattering process by the coupled-channel hyperspherical coordinate method,24–26 for each value of total angular momentum J and total energy E. Calculations for all values of J up to 99 were carried out, without the J-shifting approximation. The S-matrix elements for each state-to-state transition are obtained and used to calculate the various quantities of interest. Since the PES has a barrier height corrected for the spin–orbit splitting of the fluorine atom, the main effect of the spin–orbit coupling is automatically considered in the calculations. An a posteriori multisurface statistical factor is included in the rate constant calculations to take into account the fraction of the reactants that collide through the non-reactive surfaces. See ref. 9, 16 and 26 for a detailed description of the necessary equations. We note that there is a typo in eqn (7) of ref. 16: the multisurface factor (G(T) in the notation of ref. 9) was mistakenly denoted as Qv,j(T). It should not be confused with the rovibrational partition function used in the denominator of their eqn (6).The parameters used in the calculations were the same as those employed in ref. 15. Test calculations were carried out varying these parameters for selected values of J and the results did not change appreciably. See the ESI† for a detailed comparison.
6.1 Rate constant
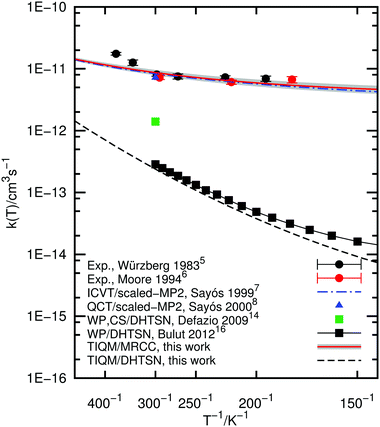
The rate constant of the title chemical reaction was calculated within the temperature range 100–500 K. To provide an unbiased comparison between the DHTSN and our current PES, we also computed the rate constant using the DHTSN PES and the coupled-channel method as outlined in the previous section. The results are depicted in Fig. 5, along with previous results from the literature. The rate constant obtained with the new PES is very close to the experimental values, in contrast to the results obtained using the DHTSN PES. The present rate constant practically matches the theoretical results from Sayós et al.,7,8 obtained with a PES whose barrier height was scaled to reproduce the experimental values. This shows, as suggested by some authors,16,17 that the DHTSN PES has a very large barrier height. The present MRCC PES is the first potential energy surface obtained from first principles that yields for the title reaction a rate constant in close agreement with experiment.The error in the barrier height, estimated in Section 3.2, was used to obtain an estimate of the error in the rate constant. Two other PESs were generated by scaling the three-body term to match the upper and lower bounds for the barrier height (1.67 and 1.51 kcal mol−1). Using these PESs, reaction probabilities were calculated for selected values of angular momentum and rate constants were obtained using the J-shifting interpolation. These are interpreted as lower and upper bounds for the calculated rate constant. The shaded area in Fig. 5 corresponds to the region between these two estimates. The variation in the rate constant associated with the uncertainty in the barrier height is small and the close agreement with experimental results is preserved.
We note, however, that the experimental rate constant shows a strong non-Arrhenius behaviour, not exactly reproduced in our calculations. For temperatures below room temperature, the experimental rate constant does not change appreciably with temperature. Our calculations match the experimental data and the flat rate constant at low temperatures is probably a consequence of tunnelling through the small barrier. At room temperature, however, the slope of the Arrhenius plot changes and the reaction rate rapidly increases with the temperature. This does not happen with the calculated rate constant. According to the analysis carried out by Würzberg and Houston,5 this behaviour is related to the deepest van der Waals complex at the entrance channel. It would act as an intermediate for this reaction, trapping the reactants at low collision energies. For higher collision energies, on the other hand, the van der Waals well should not affect the scattering process, and the Arrhenius behaviour is expected. Were this model correct, our calculations should reproduce the strong non-Arrhenius behaviour. The present PES describes the van der Waals minimum at the entrance channel and the scattering calculations are essentially exact, for a single surface model.
Multisurface effects can be an explanation for the large rate constant at higher temperatures. Possible pathways through excited potential energy surfaces, not accessible at lower temperatures, might come into play and increase the rate constant. Experimental data at higher temperatures and non-adiabatic dynamics over multiple PESs are further steps to understand the origin of the non-Arrhenius behaviour of this reaction.
6.2 Rovibrational energy distribution
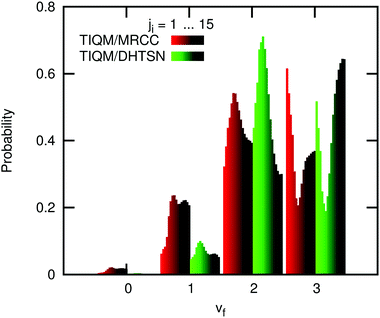
The energy distribution among the vibrational and rotational states of the product HF has been calculated and compared with previous experimental and theoretical values. Fig. 6 shows the vibrational distribution. The experimental results agree very well among themselves, showing a maximum probability at vf = 2. The third excited vibrational level has low population and higher vibrational levels are essentially not populated, since they are not energetically accessible at the collision energies of these experiments. Previous theoretical calculations using the DHTSN PES predict that the third excited vibrational state is formed with the highest probability, which is not observed in the experiments.11,15 These calculations were performed under single energy conditions, i.e. with fixed collision energy and with reactants at a single rovibrational state. Li et al. have considered only the ground rovibrational state of HCl, arguing that this should be sufficient since the most recent experiments were carried out at very low temperature. Moreover, they have fixed the collision energy to Ec = 4.3 kcal mol−1, although a collision energy distribution was reported.13 Older theoretical studies were performed considering room or higher temperatures, but using lower level PESs.8,10 For the DHTSN PES, studies considering the effect of the initial state were only focused on the total reactivity, showing that it increases with the initial rotational state.11,14,16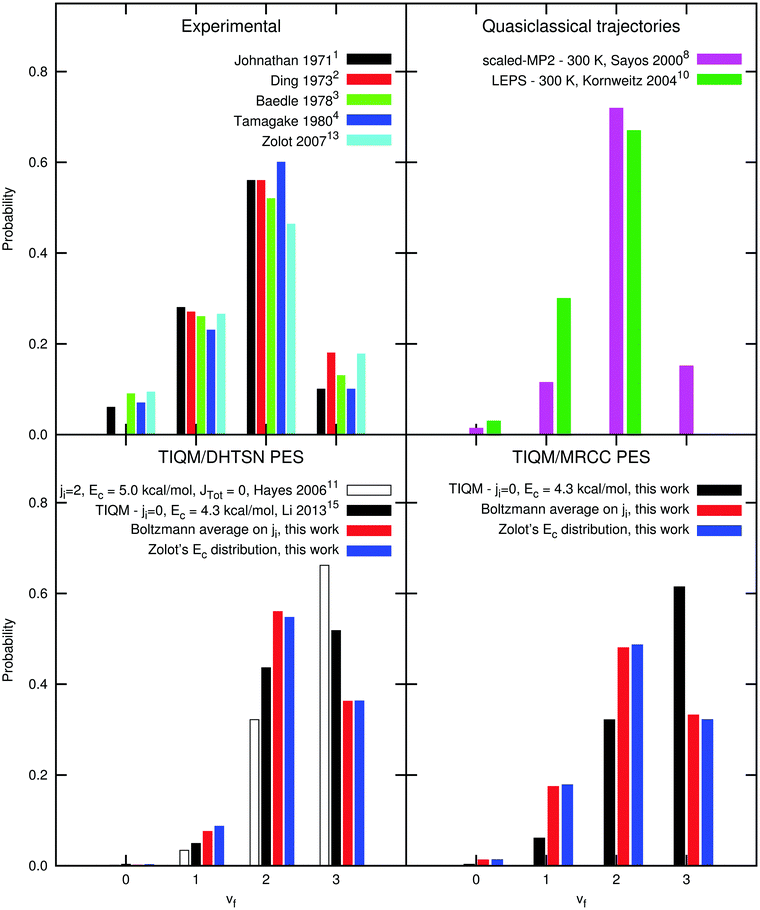 | ||
| Fig. 6 Normalised vibrational distribution of the product HF. Values indicated by “Zolot's Ec distribution” were obtained with a Boltzmann distribution over rotational states at 300 K but with the experimental distribution used by Zolot and Nesbitt13 for collision energies. | ||
Initially, we used our potential energy surface to obtain the vibrational distribution considering only the ground rovibrational state and collision energy of Ec = 4.3 kcal mol−1, as in the work of Li et al.15 The result is shown in the last panel of Fig. 6 and it does not significantly differ from the one obtained using the DHTSN PES. The vibrational state vf = 3 is again the most populated one. However, experiments were not carried out under perfect single energy conditions. To obtain a more realistic comparison with the experiments, an initial energetic distribution must be considered. We will first analyse how the final vibrational probabilities are affected by the initial rotational distribution, for a single collision energy. Fig. 7 shows how the normalised vibrational distribution depends on the HCl initial rotational state, for a fixed collision energy of 4.3 kcal mol−1 (the average collision energy in the experimental setup of Zolot and Nesbitt13). The vf = 3 state is the most populated one when the reactant is on the ground rovibrational level, but its probability decreases, compared to the HF(vf = 2) formed from the same HCl(vi = 0, ji) state. When ji = 3–7, close to the maximum of the Boltzmann distribution at 300 K, the second excited vibrational level is the one with the highest probability of being formed. This observation is independent of the choice of the PES. The vibrational distribution considering a Boltzmann distribution at 300 K over the initial rotational states is shown in Fig. 6, for both PESs. These distributions have the correct behaviour, and the most populated vibrational state is vf = 2, although the probability for vf = 3 still overestimates the experimental one.
The effect of the spread of the collision energy on the final vibrational probabilities was studied considering the energy distribution of the experimental setup of Zolot and Nesbitt.13 It is given in the inset of their Fig. 1 and we will denote it by fZN(Ec), being further described in the ESI.† The final vibrational distribution is thus proportional to the rate constant of the process
| F + HCl → HF(vf, all) + Cl, |
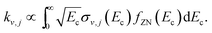 | (9) |
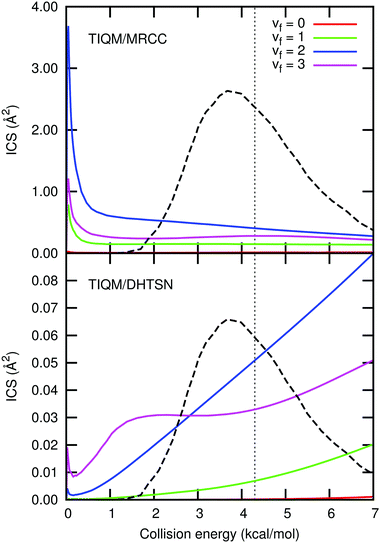 | ||
| Fig. 8 Integral cross section resolved into the final vibrational states and averaged over the initial rotational states with a Boltzmann distribution at 300 K. The black dashed line shows Zolot's13 collision energy distribution and the vertical dotted line its average energy. The larger integral cross section for the MRCC PES is a consequence of the smaller barrier height, resulting in a larger rate constant. | ||
We also considered the effect of the energetic distribution among the initial rotational states and collision energies on the rotational distribution. Experimental and theoretical results are shown in Fig. 9, for the vibrational manifolds vf = 1 and vf = 2. The bimodal distribution experimentally obtained by Zolot and Nesbitt13 is not reproduced in the calculations, irrespective of the PES or the initial state distribution. The rotational distribution obtained with our new PES has a maximum and a shape similar to the experimental results of Ding et al.,2 who reports the formation of HF in excited rotational states only. The distributions calculated with the DHTSN PES are narrower than those for the new icMRCC PES and shifted to higher values of jf.
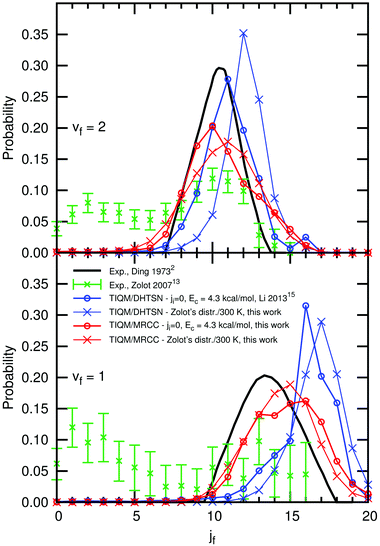 | ||
| Fig. 9 Normalised rotational distribution of the product HF, for the vibrational states vf = 1 and vf = 2. | ||
Neither of the PESs is able to reproduce the contribution from low rotational states obtained by Zolot and Nesbitt, hence its origin is still unclear. Based on the present results, we can disregard the spread in collision energy and initial rotational states as possible origins of this behaviour. If the van der Waals minimum in the exit channel acts as a rotational cooler,13 this effect should also be captured by our (and previous) calculations on the dynamics of this reaction. Non-adiabatic processes were not considered in this calculation and their effects remain to be studied. However, given the similarities between our present results and the experimental rotational distribution of Ding et al., the possibility of rotational relaxation in the experimental study carried out by Zolot and Nesbitt should be carefully reviewed.
7 Conclusions
In this work we report a multireference coupled-cluster study of the reaction F + HCl → HF + Cl. It involves the construction of a global potential energy surface and the study of the reaction dynamics by quantum mechanical methods. Contrary to standard ab initio methods like MRCI and single reference coupled-cluster theory, the icMRCCSD(T) value for the barrier height is very close to the experimentally suggested value. As a direct result of the lower barrier height, the computed rate constant is in good agreement with the experimental value and greatly differs from the previous most accurate calculations. We can conclude that the lowering of the barrier height is caused by the triples correction in the icMRCCSD(T) method. PESs with barrier heights near the experimentally suggested value, whether empirically adjusted7,10 or obtained from ab initio calculations as in the present work, give rate constants with close agreement to experiments.The vibrational distribution of the products is studied and it is shown that it is strongly influenced by the initial rotational state. Such an influence is not considered in previous calculations using the DHTSN PES, but is taken into account in older works,8,10 where thermal distribution over the initial states is used and a good agreement with experiments is reported.
Our calculated rotational distribution shows close agreement with the experimental results obtained by Ding et al.2 and does not present the bimodal behaviour obtained in recent experiments.13 Although Zolot and Nesbitt claim that their rotational distribution is completely from nascent HF and that rotational relaxation does not play a role, such a possibility should be reviewed in light of the present work.
We hope that the new PES motivates further work on the F + HCl → HF + Cl reaction and improves the understanding of its dynamics. Moreover, several chemical reactions have transition states that are difficult to describe with ab initio methods. For instance, MRCI calculations also seem to overestimate the barrier height of the F + H2O → HF + OH reaction, when compared to single reference coupled-cluster results.45,46 This suggests that internally contracted multireference coupled-cluster theory may become a useful tool for obtaining accurate global PESs for this and other elementary chemical reactions.
Acknowledgements
Y. A. A. is grateful to the Alexander von Humboldt Foundation and to the Coordenação de Aperfeiçoamento de Pessoal de Nível Superior (CAPES) of Brazil for a post-doctoral fellowship. A. K. acknowledges the generous start up funding by the University of Stuttgart. The authors acknowledge support by the state of Baden-Württemberg through bwHPC and the German Research Foundation (DFG) through grant no. INST 40/467-1 FUGG. The authors thank Prof. Hans-Joachim Werner for inspiring discussions on the topic.References
- N. Jonathan, C. M. Melliar-Smith and D. H. Slater, Chem. Phys. Lett., 1970, 7, 257–259 CrossRef CAS
.
- A. M. G. Ding, L. J. Kirsch, D. S. Perry and J. C. Polanyi, Faraday Discuss. Chem. Soc., 1973, 55, 252–276 RSC
.
- P. Baedle, M. R. Dunn, N. B. H. Jonathan, J. P. Liddy and J. C. Naylor, J. Chem. Soc., Faraday Trans. 2, 1978, 74, 2170–2181 RSC
.
- K. Tamagake, D. W. Setser and J. P. Sung, J. Chem. Phys., 1980, 73, 2203–2217 CrossRef CAS
.
- E. Würzberg and P. L. Houston, J. Chem. Phys., 1980, 72, 5915–5923 CrossRef
.
- C. M. Moore, I. W. M. Smith and D. W. A. Stewart, Int. J. Chem. Kinet., 1994, 26, 813–825 CrossRef CAS
.
- R. Sayós, J. Hernando, J. Hijazo and M. González, Phys. Chem. Chem. Phys., 1999, 1, 947–956 RSC
.
- R. Sayós, J. Hernando, R. Francia and M. González, Phys. Chem. Chem. Phys., 2000, 2, 523–533 RSC
.
- B.-Y. Tang, B.-H. Yang, K.-L. Han, R.-Q. Zhang and J. Z. H. Zhang, J. Chem. Phys., 2000, 113, 10105–10113 CrossRef CAS
.
- H. Kornweitz and A. Persky, J. Phys. Chem. A, 2004, 108, 140–145 CrossRef CAS
.
- M. Y. Hayes, M. P. Deskevich, D. J. Nesbitt, K. Takahashi and R. T. Skodje, J. Phys. Chem. A, 2006, 110, 436–444 CrossRef CAS PubMed
.
- M. P. Deskevich, M. Y. Hayes, K. Takahashi, R. T. Skodje and D. J. Nesbitt, J. Chem. Phys., 2006, 124, 224303 CrossRef PubMed
.
- A. M. Zolot and D. J. Nesbitt, J. Chem. Phys., 2007, 127, 114319 CrossRef CAS PubMed
.
- P. Defazio and C. Petrongolo, J. Phys. Chem. A, 2009, 113, 4208–4212 CrossRef CAS PubMed
.
- A. Li, H. Guo, Z. Sun, J. Kłos and M. H. Alexander, Phys. Chem. Chem. Phys., 2013, 15, 15347–15355 RSC
; J. Kłos, private communication.
- N. Bulut, J. Kłos and M. H. Alexander, J. Chem. Phys., 2012, 136, 104304 CrossRef PubMed
.
- M. Bai, D. Lu, Y. Li and J. Li, Phys. Chem. Chem. Phys., 2016 10.1039/c6cp03306g
.
- N. Jonathan, C. M. Melliar-Smith, S. Okuda, D. H. Slater and D. Timlin, Mol. Phys., 1971, 22, 561–574 CrossRef CAS
.
- A. Banerjee and J. Simons, Int. J. Quantum Chem., 1981, 19, 207–216 CrossRef CAS
.
- F. Evangelista and J. Gauss, J. Chem. Phys., 2011, 134, 114102 CrossRef PubMed
.
- M. Hanauer and A. Köhn, J. Chem. Phys., 2011, 134, 204111 CrossRef PubMed
.
- M. Hanauer and A. Köhn, J. Chem. Phys., 2012, 136, 204107 CrossRef PubMed
.
- M. Hanauer and A. Köhn, J. Chem. Phys., 2012, 137, 131103 CrossRef PubMed
.
- D. E. Manolopoulos, J. Chem. Phys., 1986, 85, 6425–6429 CrossRef CAS
.
- G. C. Schatz, Chem. Phys. Lett., 1988, 150, 92–98 CrossRef CAS
.
- D. Skouteris, J. F. Castillo and D. E. Manolopoulos, Comput. Phys. Commun., 2000, 133, 128–135 CrossRef CAS
.
- W. Liu, M. Hanauer and A. Köhn, Chem. Phys. Lett., 2013, 565, 122–127 CrossRef CAS
.
- R. A. Kendal, T. H. Dunning and R. J. Harrison, J. Chem. Phys., 1992, 96, 6796 CrossRef
.
- T. H. Dunning Jr., K. A. Peterson and A. K. Wilson, J. Chem. Phys., 2001, 114, 9244–9253 CrossRef
.
- A. Halkier, T. Helgaker, P. Jørgensen, W. Klopper, H. Koch, J. Olsen and A. K. Wilson, Chem. Phys. Lett., 1998, 286, 243–252 CrossRef CAS
.
- T. Helgaker, W. Klopper, H. Koch and J. Noga, J. Chem. Phys., 1997, 106, 9639–9646 CrossRef CAS
.
- F. Weigend, Phys. Chem. Chem. Phys., 2002, 4, 4285–4291 RSC
.
- H.-J. Werner and P. J. Knowles, J. Chem. Phys., 1985, 62, 5053–5063 CrossRef
.
- P. J. Knowles and H.-J. Werner, Chem. Phys. Lett., 1985, 115, 259–267 CrossRef CAS
.
- DALTON, a molecular electronic structure program, see http://daltonprogram.org/.
- MOLPRO, version 2012.1 a package of ab initio programs. H.-J. Werner, P. J. Knowles, G. Knizia, F. R. Manby, M. Schütz, and others, see http://www.molpro.net.
- G. A. Laguna and W. H. Beattie, Chem. Phys. Lett., 1982, 88, 439–440 CrossRef CAS
.
- C. L. Pekeris, Phys. Rev., 1958, 112, 1649–1658 CrossRef CAS
.
- E. R. Davidson, J. Am. Chem. Soc., 1977, 99, 397–402 CrossRef CAS
.
- Y. A. Aoto and F. R. Ornellas, Theor. Chem. Acc., 2014, 133, 1547 CrossRef
.
- K. A. Peterson, S. Skokov and J. Bowman, J. Chem. Phys., 1999, 111, 7446–7456 CrossRef CAS
.
- A. Aguado and M. Paniagua, J. Chem. Phys., 1992, 96, 1265–1275 CrossRef CAS
.
- J. M. Merritt, J. Küpper and R. E. Miller, Phys. Chem. Chem. Phys., 2005, 7, 67–78 RSC
.
- Y. A. Aoto and A. Köhn, J. Chem. Phys., 2016, 144, 074103 CrossRef PubMed
.
- T. L. Nguyen, J. Li, R. Dawes, J. F. Stanton and H. Guo, J. Phys. Chem. A, 2013, 117, 8864–8872 CrossRef CAS PubMed
.
- J. Li, R. Dawes and H. Guo, J. Chem. Phys., 2012, 137, 094304 CrossRef PubMed
.
Footnote |
| † Electronic supplementary information (ESI) available: Ab initio points, PES subroutines and extra information. See DOI: 10.1039/c6cp05782a |
| This journal is © the Owner Societies 2016 |