Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Columnar shifts as symmetry-breaking degrees of freedom in molecular perovskites
Hanna L. B.
Boström
,
Joshua A.
Hill
and
Andrew L.
Goodwin
*
Inorganic Chemistry Laboratory, Department of Chemistry, University of Oxford, South Parks Road, Oxford OX1 3QR, UK. E-mail: andrew.goodwin@chem.ox.ac.uk; Tel: +44 (0)1865 272137
First published on 20th October 2016
Abstract
We introduce columnar shifts—collective rigid-body translations—as a structural degree of freedom relevant to the phase behaviour of molecular perovskites ABX3 (X = molecular anion). Like the well-known octahedral tilts of conventional perovskites, shifts also preserve the octahedral coordination geometry of the B-site cation in molecular perovskites, and so are predisposed to influencing the low-energy dynamics and displacive phase transitions of these topical systems. We present a qualitative overview of the interplay between shift activation and crystal symmetry breaking, and introduce a generalised terminology to allow characterisation of simple shift distortions, drawing analogy to the “Glazer notation” for octahedral tilts. We apply our approach to the interpretation of a representative selection of azide and formate perovskite structures, and discuss the implications for functional exploitation of shift degrees of freedom in negative thermal expansion materials and hybrid ferroelectrics.
1 Introduction
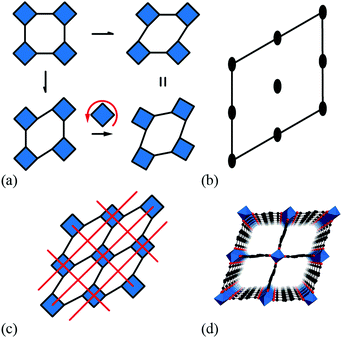
A large variety of important physical properties of perovskite oxides are the result of symmetry-breaking processes that involve ordering of structural, electronic, or magnetic degrees of freedom. From a materials design viewpoint, the role of octahedral tilts is especially important because so-called “tilt engineering” approaches now allow control over macroscopic polarisation1 and magnetisation.2,3 Moreover, because tilt degrees of freedom often dominate the vibrational behaviour of perovskites, the same approaches can allow control over dynamical phenomena such as negative thermal expansion (NTE).4 Central to these design approaches is an understanding of the ways in which activation of specific tilt systems can affect space group symmetry.5–7 Formally, this relationship is given by the irreducible representation of a given tilt distortion, which can be used either to account for static symmetry breaking (e.g. emergence of long-range polarisation) if tilts are frozen in or to label the corresponding phonon branch, if tilts remain dynamic. The soft-mode description of displacive phase transitions links these two pictures, with the symmetry of the soft phonon dictating the descent in space-group symmetry as the tilt distortions become static.8In addition to conventional inorganic perovskites, there are several molecular perovskite analogues, including organic halide perovskites,9,10 dicyanamides,11–14 azides,15,16 Prussian blue analogues,17,18 dicyanometallates,19,20 thiocyanates,21–23 and formates.24–26 These are systems of strong scientific currency in which at least one component of the ABX3 perovskite structure is molecular: typically the A-site cation and/or the anionic linker X. An important consequence of the incorporation of molecular components is the emergence of new structural degrees of freedom for which there is no analogue in conventional perovskites. Examples include (i) the so-called “forbidden” tilts found in some azides, Prussian blue analogues, and dicyanometallates, in which neighbouring octahedra (no longer corner-sharing) rotate in the same sense as one another,20,27–29 and (ii) multipolar order associated with orientational degrees of freedom of molecular A-site cations.30,31 Coupling of these exotic degrees of freedom to the lattice then allows for entirely new symmetry-breaking mechanisms,32 and hence new crystal engineering strategies for targeting e.g. multiferroic or NTE responses.1,2,4,33
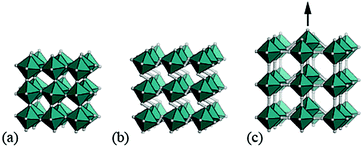
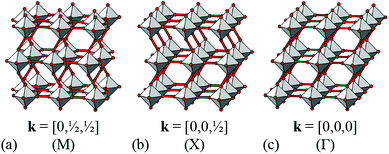
It is natural then to ask: are there any other degrees of freedom of general relevance to the structural chemistry of molecular perovskites? Here, a key consideration is the energy scale associated with different deformations, since those with high energies (e.g. bond stretches or distortion of coordination geometries) are unlikely to behave as soft modes. Fortunately, simple geometric tools34 can be used to identify distortion modes that preserve bond lengths and coordination geometries and hence are predisposed to play a key role in the low-energy dynamics of materials; these are termed the rigid unit modes (RUMs) of a given topology. So, for example, it was shown in ref. 34 that the only RUMs supported by the conventional perovskite structure are the well-known octahedral tilts discussed above [Fig. 1(a)]. A similar analysis of the ABX3 lattice with molecular X components, however, revealed the existence of two types of rotational degrees of freedom (these are the conventional and forbidden tilts) together with a translational degree of freedom involving correlated displacements of columns of connected BX6 octahedra [Fig. 1(b) and (c)].35
We refer to these columnar translations as shifts and argue here that they can indeed play an important role in the structural chemistry of certain families of molecular perovskites. Our paper begins by establishing the conceptual framework for interpreting and characterising columnar shifts. By focusing initially on a two-dimensional simplification of the perovskite framework, we explore the interplay between shift activation and symmetry breaking, the relationship to shear modes, and the potential for coupling with tilt degrees of freedom. We proceed to extrapolate this analysis to the interpretation of static symmetry-breaking distortions in three-dimensional molecular perovskites, drawing on topical case studies from the recent crystal engineering literature. The link to dynamical properties is then made via a simple lattice-dynamical model, which we then use to demonstrate that dynamic shift distortions have a distinctive NTE character. A simple density functional theory (DFT) phonon calculation for CdPd(CN)6 supports the relevance of shift modes in the low-energy phonon spectrum of this specific Prussian blue analogue. Our paper concludes with a discussion regarding the possibility of developing shift engineering approaches as an alternative mechanism for accessing polar states in molecular perovskites.
2 Theory
Rigid unit modes in molecular perovskites
Our starting point is a brief recap of the key results in the RUM analysis of ref. 35; our aim is to clarify the particular periodicities at which shift distortions can occur in molecular perovskites and their 2D analogues. This analysis makes use of a dynamical matrix approach in which a simplified lattice-dynamical model is used to assign energies to distortion patterns.34,36 While the absolute energies are not themselves meaningful, the model is set up such that those modes—and only those modes—which do not result in changes to individual bond lengths or coordination environments correspond to solutions with energies exactly equal to zero. Formally, this is achieved using a molecular rigid unit translation/rotation basis for the dynamical matrix with the lattice enthalpy determined by the variation in separation between neighbouring rigid units: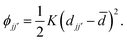 | (1) |
![[d with combining macron]](https://www.rsc.org/images/entities/i_char_0064_0304.gif) the equilibrium separation, and K ≠ 0 the (fictitious) force constant. Having set up the dynamical matrix D(k) as in ref. 34 and 35, the RUMs are identified by the eigenstates of D(k) for which the corresponding eigenvalue is zero. By varying the distortion periodicity k, the entire set of RUM-type degrees of freedom can be determined comprehensively.
the equilibrium separation, and K ≠ 0 the (fictitious) force constant. Having set up the dynamical matrix D(k) as in ref. 34 and 35, the RUMs are identified by the eigenstates of D(k) for which the corresponding eigenvalue is zero. By varying the distortion periodicity k, the entire set of RUM-type degrees of freedom can be determined comprehensively.
In practice, the form of D(k) is simple for molecular perovskites. Even so, we consider first the (even simpler) 2D analogue of connected squares, for which
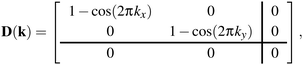 | (2) |
These results translate directly to the three-dimensional case of molecular perovskites. The dynamical matrix now assumes the form
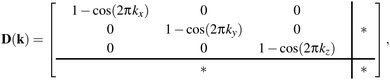 | (3) |
Shifts in 2D: enumeration and symmetry breaking
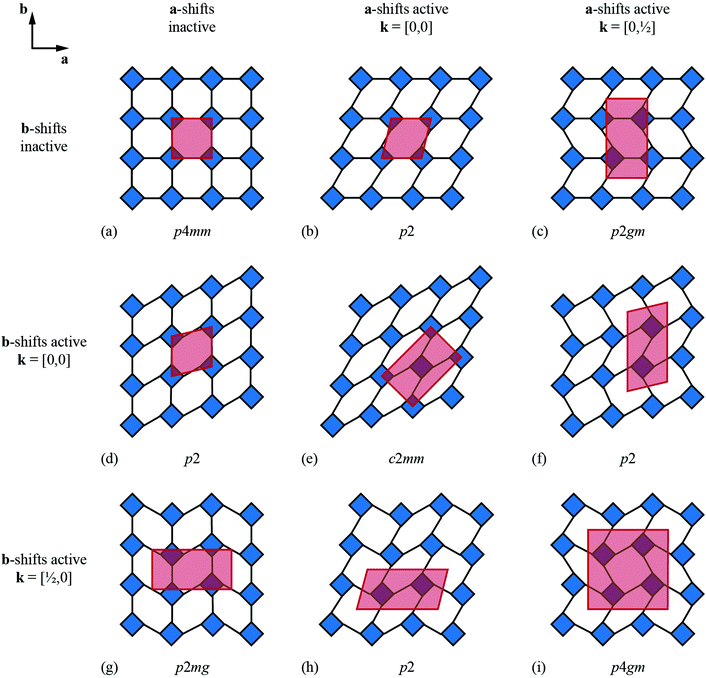
We now consider the explicit form of the various possible shift modes for the 2D molecular perovskite analogue of connected squares. The analysis given above indicates that this system supports two types of shifts: one involving collective translations of rows of connected squares along a direction parallel to a and modulated with periodicity k = [0, ky]; the other involving collective translations of columns of connected squares parallel to b, where the modulation is now characterised by k = [kx, 0]. By analogy to the common displacive instabilities in conventional perovskites, we anticipate that the physically most relevant cases are those for which k lies either at the zone centre or at the zone boundary—i.e., kx, ky ∈ {0, ½}. We limit our analysis to the corresponding set of wave-vectors, such that for each of the two orthogonal shift systems there are three possibilities: (i) the shifts are inactive, (ii) the shifts are active with k = [0, 0], or (iii) the shifts are active with k ∈ 〈0, ½〉. Since the two sets of shifts are orthogonal this gives us a total of nine cases to consider; we now take these in turn, summarising our discussion in Fig. 3.What at face value might appear to be the simplest case—namely, activation of a single shift system with periodicity k = [0, 0]—turns out to give rise to a relatively complex situation. These shifts describe a shear of the perovskite lattice polarised along one of the lattice vectors a or b; the corresponding distortions are illustrated in Fig. 3(b) and (d). In both cases the vast majority of the symmetry elements present in the p4mm plane-group symmetry of the parent lattice are lost and the crystal symmetry is now reduced to p2. This symmetry lowering is so severe that activation of these shifts allows coupling to an entirely different type of rigid-body distortion—namely, the “forbidden” (in-phase) tilts also at k = [0, 0] [Fig. 4(a) and (b)]. In fact, these tilts provide a continuous pathway between k = [0, 0] shifts polarised along a, on the one hand, and those polarised along b, on the other hand, such that the former type of shift cannot be distinguished from a combination of the latter shift type together with an in-phase tilt (or vice versa). This confusing situation arises because k = [0, 0] shifts polarised along either a or b are characterised by the same irreducible representation; in other words, the two shift systems break the parent symmetry in identical ways.
 | ||
| Fig. 4 Some symmetry relationships in 2D shift systems. (a) Activation of zone-centre shifts leads to structures that are related to one another via in-phase tilts of the rigid units. (b) This transformation is continuous because the plane group symmetry elements of the shifted structures (2-fold rotation axes distributed as illustrated here) are compatible with the activation of in-phase tilts. (c) For some shift systems, such as the c2mm distortion shown here, the persistence of mirror symmetry elements (red lines) forbids mixing of shifts and tilts. (d) This particular shift system is related to the compliant structure of the MIL-53 family,37,38 shown here in polyhedral representation. | ||
Coupling to tilts is by no means a universal feature of shift distortions, and a counter-example is given by the case in which the two k = [0, 0] shifts are active to precisely the same extent. This situation corresponds to a shear polarised along the cell diagonal, which results in a much less severe symmetry-lowering process: the resulting plane group is now c2mm [Fig. 3(e)]. Importantly, the persistence of mirror symmetry elements bisecting the rigid units means that coupling to tilts can only occur by further symmetry lowering [Fig. 4(c)]. So in this case, the particular shift modes can be uniquely identified from the lattice symmetry. Of course, the transition from p4mm to c2mm structures—couched here in terms of activation of k = [0, 0] shifts—corresponds to a ferroelastic distortion of the lattice.39,40 The ferroelastic state is well known to be mechanically compliant,41,42 and as such is often associated with phenomena such as uniaxial NTE and negative linear compressibility (NLC).43–45 Indeed, the 2D model we consider here may be interpreted as a projection of the 3D “wine-rack” structure of well-known compliant framework materials such as the MIL-53 family, which is certainly known to exhibit both NTE and NLC [Fig. 4(d)].37,38
Whereas zone-centre shift modes describe ferroelastic distortions, those at the zone boundary give rise to antiferroelastic states. In the case of shifts polarised along a, the relevant zone-boundary periodicity is k = [0, ½]. Consequently, activation of this shift mode results in a doubling of the cell in the b direction with the corresponding plane-group symmetry now p2gm [Fig. 3(c)]. Once again, the persistence of mirror symmetry elements bisecting the rigid units forbids coupling to tilts. The equivalent shift mode polarised along b gives rise to an analogous distortion: the cell now doubles along a and the plane-group symmetry is p2mg [Fig. 3(g)]. In contrast to the situation for the corresponding zone-centre shift modes, in this case there is clearly no continuous pathway between the two states. Simultaneous activation of both zone-boundary shift modes to identical extents results in the appealing antiferroelastic distortion shown in Fig. 3(i). This distortion requires doubling along both cell axes and is described by the plane group p4gm. Once again, the point symmetry at the rigid unit site includes a mirror plane (at 45° to the cell axes) and so this particular shift system is symmetry forbidden from coupling with tilt modes. For completeness, we consider the final possibility in which a zone-centre shift mode polarised along one axis is combined with a zone-boundary shift polarised along the remaining axis. The corresponding distortions for the two possible axis choices are illustrated in Fig. 3(f) and (h). In both cases the cell doubles and in both cases the resulting plane-group symmetry is p2. Yet, while each shift distortion now has sufficiently low symmetry to couple with tilt modes (as above), there is no continuous path between the two: they are distinguishable by virtue of the particular axis along which the cell has doubled. Our key point in covering all these different possibilities is to demonstrate that activation of different shift modes results in different symmetry-breaking processes that can be fundamentally distinct from those accessible via tilt degrees of freedom—whether conventional46 or forbidden.20,27–29
Notation
Given the complexity of shift distortions and their combinations—even in 2D—it is clearly desirable to develop a concise notation to represent the particular set of shift modes active in a given structure. In the case of tilt distortions, the most widely-used notation is that of Glazer;5 we first review this notation with the view of subsequently extending the approach to shifts.Like shifts, independent tilt systems can be associated with each of the three crystal axes. In conventional perovskites, rotations around the a axis (by way of example) can propagate with periodicity k = [kx, ½, ½]. Hence, the particular tilt distortion associated with a single axis α is described by two terms: the tilt magnitude uα and the relevant wave-vector component kα, which—as discussed above—is usually either 0 (in-phase tilts) or ½ (out-of-phase tilts). Glazer condenses this information for each axis into a compound symbol λμ. The index μ ∈ {0, +, −} denotes whether a tilt is inactive (μ = 0; uα = 0), in-phase (μ = +; kα = 0) or out-of-phase (μ = −; kα = ½); the primary symbol λ reflects the magnitude of an active tilt in order to show the existence or absence of symmetry relationships between tilts along different axes of the parent perovskite lattice. The untilted aristotype has Glazer symbol a0a0a0; the term a−a−a− denotes equal-magnitude out-of-phase tilts around each of the three crystal axes; and the term a+b−b− denotes in-phase tilts around a with distinct equal-magnitude out-of-phase tilts around b and c. Howard and Stokes established a link between these labels and the corresponding space-group symmetries.6 We note that the index μ is equal to the value of uα![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp[2πikα] if (i) the symbol + can be associated with 1 and − with −1, and (ii) uα is taken to equal 1 for active tilt modes and 0 for inactive tilt modes.
exp[2πikα] if (i) the symbol + can be associated with 1 and − with −1, and (ii) uα is taken to equal 1 for active tilt modes and 0 for inactive tilt modes.
The various shift distortions of the 2D molecular perovskite structure discussed above are also describable in terms of the magnitude and periodicity of collective translations along each crystal axis. This immediately suggests an analogous notation to that of Glazer's for tilts, with only one subtle conceptual modification: the periodicity implied by the index μ must now refer to the component of k perpendicular to the corresponding crystal axis. So, for example, the diagonal ferroelastic distortion discussed in terms of k = [0, 0] shifts along both a and b might be summarised by the Glazer symbol a+a+: here the + index would indicate ky = 0 for shifts parallel to a and kx = 0 for shifts parallel to b; likewise the use of the same primary symbol a would indicate that the shifts have identical magnitude along these two crystal axes. The corresponding symbols for each of the distortions originally presented in Fig. 3 are given in Table 1.
| a-shifts | b-shifts | Glazer symbol | Matrix symbol | Plane group |
|---|---|---|---|---|
| a As described in the main text, there is no unique assignment of shifts for this system since a+b0, a+b+ and a0b+ states are continuously interchangeable via activation of in-phase tilts. | ||||
| Inactive | Inactive | a 0 a 0 |

|
p4mm |
| In-phase | Inactivea | a + b 0 (≡ a+b+) |
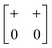
|
p2 |
| In-phase | In-phase | a + a + |
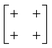
|
c2mm |
| Out-of-phase | Inactive | a − b 0 |
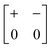
|
p2gm |
| Out-of-phase | In-phase | a − b + |
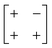
|
p2 |
| Out-of-phase | Out-of-phase | a − a − |
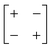
|
p4gm |
We will come to show that an unambiguous extrapolation of this notation to 3D molecular perovskites is not straightforward, and so we present an alternative—albeit perhaps more cumbersome—approach similar to that developed in ref. 20 to describe “forbidden” tilts. Here the idea is to exploit the equivalence μ ≡ u![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp[2πik] noted above. We assemble the matrix
exp[2πik] noted above. We assemble the matrix
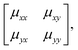 | (4) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp[2πikβ] describes both the magnitude uα of shift displacements parallel to axis α and also the component kβ of the corresponding periodicity k parallel to axis β. We note that if β = α then kβ = 0; this is the result of the RUM analysis given above. For consistency we use the Glazer 0, +, − symbols for μ rather than the numerical values of uα
exp[2πikβ] describes both the magnitude uα of shift displacements parallel to axis α and also the component kβ of the corresponding periodicity k parallel to axis β. We note that if β = α then kβ = 0; this is the result of the RUM analysis given above. For consistency we use the Glazer 0, +, − symbols for μ rather than the numerical values of uα![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp[2πikβ]. So, for the diagonal ferroelastic distortion (assigned Glazer symbol a+a+ above) we now have the matrix representation
exp[2πikβ]. So, for the diagonal ferroelastic distortion (assigned Glazer symbol a+a+ above) we now have the matrix representation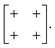 | (5) |
Extension to 3D
The key result of our RUM analysis was to show that the shift degrees of freedom in 3D molecular perovskites involve collective displacements of columns of octahedra along a direction parallel to the column axis α. Shifts may occur along any combination of the three crystal axes; the only constraint on the periodicity k of these displacements is that component kα must equal zero for shifts polarised along axis α. Consequently, the shifts associated with each axis now require three terms if they are to be described completely: a magnitude uα together with the two wave-vector components kβ, kγ corresponding to the two axes perpendicular to α. It is this additional complexity that renders ambiguous the direct extrapolation of the Glazer notation to 3D shifts.By contrast, the more cumbersome matrix notation is straightforwardly extended to 3D shifts: we use the representation
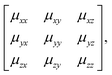 | (6) |
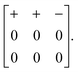 | (7) |
![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m aristotype to Pmma.
m aristotype to Pmma.
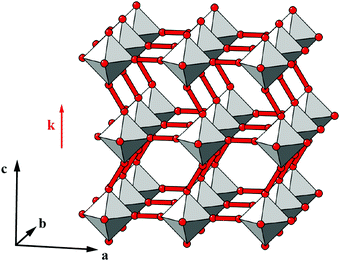 | ||
| Fig. 5 An antiferroelastic planar shift system characterised by displacements parallel to a, correlated with modulation wave-vector k = [0, 0, ½]. | ||
One possible approach to modifying the Glazer-type notation for these 3D shifts might be to exploit the Bradley–Cracknell abbreviations for high-symmetry points in the Brillouin zone.47 In some cases, the use of this abbreviation as the Glazer index μ would allow unambiguous identification of the two required wave-vector components. For example, the Pmma shift system discussed immediately above might be assigned the Glazer symbol aXb0c0. Here, the index X of the first term signifies that shifts polarised along a are active and are modulated with a periodicity k ∈ 〈½, 0, 0〉. Since kx must equal zero, we know that k = [0, ½, 0] or [0, 0, ½]; in the absence of active shifts along b or c these two periodicities give rise to symmetry-equivalent distortions. Despite the success of the nomenclature in this one example, it is straightforward to envisage scenarios in which unambiguous identification is not possible. Nevertheless, for each of the case studies below, we try to give both Glazer and matrix notations, with the understanding that future usage will likely determine limitations of the two approaches and identify of which of these is the more useful in practice.
3 Case studies
Having established a theoretical basis with which to identify and categorise shift distortions in molecular perovskites, we proceed to interpret the structures of three experimental systems in this context. Our goals are to demonstrate that a variety of different shift systems is observed experimentally, and to highlight the potential for interplay with tilt and A-site orientational degrees of freedom.Tetramethylammonium calcium azide
Our first example is the azide-containing perovskite framework [NMe4]Ca[N3]3 (Me = CH3), the structure of which was reported in ref. 48. At room temperature, this system adopts a tetragonal structure (space group P4/nmm) with cell parameters related to that of the cubic aristotype (a0) by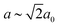 and c ∼ a0 [Fig. 6(a)]. It can be shown that this symmetry is entirely accounted for by the presence of an active shift system along the tetragonal axis.49 In this particular example, columns of CaN6 octahedra aligned parallel to c are shifted along c relative to their immediate neighbours. The shift pattern alternates along a and b such that the distortion is clearly associated with the modulation wave-vector k = [½, ½, 0] (given relative to the parent cell). There are no shifts along either a or b. So, using the approaches described above, we identify this distortion with the Glazer symbol a0a0cM and the matrix representation
and c ∼ a0 [Fig. 6(a)]. It can be shown that this symmetry is entirely accounted for by the presence of an active shift system along the tetragonal axis.49 In this particular example, columns of CaN6 octahedra aligned parallel to c are shifted along c relative to their immediate neighbours. The shift pattern alternates along a and b such that the distortion is clearly associated with the modulation wave-vector k = [½, ½, 0] (given relative to the parent cell). There are no shifts along either a or b. So, using the approaches described above, we identify this distortion with the Glazer symbol a0a0cM and the matrix representation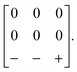 | (8) |
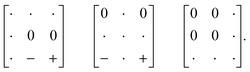 | (9) |
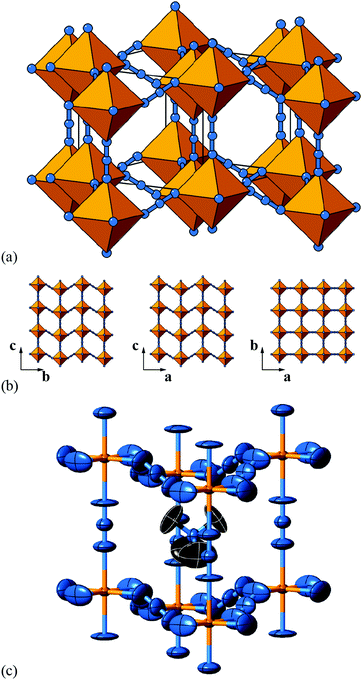 | ||
| Fig. 6 Static shift distortions in [NMe4]Ca[N3]3. (a) A polyhedral/ball-and-stick representation of the crystal structure of [NMe4]Ca[N3]3, as reported in ref. 48. Ca atoms are shown in yellow and N atoms in blue. The [NMe4]+ cations have been omitted for clarity. Shifts are polarised along c (the vertical axis in this representation) and are related to those illustrated originally in Fig. 2(a). (b) 2D sections of the crystal structure using the same representations as in (a). These sections lie perpendicular to the a, b, and c axes (left–right) and relate the 2D shift systems enumerated in Fig. 3 with the matrix representation of the full 3D shift system active in this material. (c) A representation of the local environment of the [NMe4]+ cation in this material; colours are as for (a) and (b), with C atoms shown in black and H atoms omitted for clarity. Thermal ellipsoids are given at 50% probability. There is a close match in A-site cation geometry and the framework distortion effected by shift activation. The relatively large thermal ellipsoids suggest substantial dynamic disorder in this system. | ||
As in a number of the simple 2D cases studied above, the particular shift distortion mode we observe in [NMe4]Ca[N3]3 retains a number of the mirror symmetry elements of the aristotype, which has the effect of preventing mixing between shifts and octahedral tilts. Indeed, there are no static active tilts in the reported structure. What is clear, however, is that there is likely a large degree of dynamic distortion, given the magnitude of the thermal ellipsoids. Consequently, it is possible that this system will exhibit displacive phase transitions on cooling; a re-examination using variable temperature methods may be rewarding in this case.
But what drives the presence of static shifts in this system? We offer two suggestions. The first concerns the coordination preference of the azide anion as a bridging linker. It has long been known that the preferred end-to-end bridging geometry involves substantially bent M–N–N angles; together with the trans-EE coordination of the N−3 ion this is presumably what allows such large (≃1.3 Å) displacements between neighbouring Ca2+ ions [Fig. 6(a)]. Indeed this propensity of azide to allow activation of shifts is likely a general phenomenon, even if this point does not explain why it is this particular a0a0cM shift system that is adopted here. So our second observation concerns the relationship between the geometry of the [NMe4]+ cation and the structural distortions to the A-site cavity that occur as a result of columnar shifts. In the aristotype structure, the point symmetry at the A site is m![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m (Oh), which is a supergroup of the
m (Oh), which is a supergroup of the ![[4 with combining macron]](https://www.rsc.org/images/entities/char_0034_0304.gif) 3m (Td) symmetry of tetramethylammonium; consequently the cation must exhibit orientational disorder in this parent structure. On activation of the a0a0cM shifts, the A-site point symmetry is reduced to
3m (Td) symmetry of tetramethylammonium; consequently the cation must exhibit orientational disorder in this parent structure. On activation of the a0a0cM shifts, the A-site point symmetry is reduced to ![[4 with combining macron]](https://www.rsc.org/images/entities/char_0034_0304.gif) 2m (D2d), a subgroup of
2m (D2d), a subgroup of ![[4 with combining macron]](https://www.rsc.org/images/entities/char_0034_0304.gif) 3m. This allows orientational order of the cation. Indeed, there is a close match between the geometry of the (ordered) cation and the shape of the A-site cavity that suggests the distortions is driven largely by packing and cation-framework interactions [Fig. 6(c)].
3m. This allows orientational order of the cation. Indeed, there is a close match between the geometry of the (ordered) cation and the shape of the A-site cavity that suggests the distortions is driven largely by packing and cation-framework interactions [Fig. 6(c)].
Dimethylammonium manganese azide
A closely-related system that supports two orthogonal shift systems at once is the ambient phase of [NMe2H2]Mn[N3]3.50 The reported crystal structure has orthorhombic Cmce symmetry with a ∼ 2a0, b ∼ 2a0, c ∼ 2a0 [Fig. 7(a)]. The two shift systems present involve displacements along c and b. The former is of precisely the same form as in [NMe4]Ca[N3]3; the latter involves concerted alternating displacements of sheets of octahedra and is associated with the modulation wave-vector k = [0, 0, ½]. Once again, it can be shown that these two distortions acting together account entirely for the observed space-group symmetry;49 in other words, their combined effect acts as the primary order parameter. Using the approach of Section 2 we assign to this distortion the Glazer label a0bXcM and the shift matrix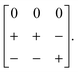 | (10) |
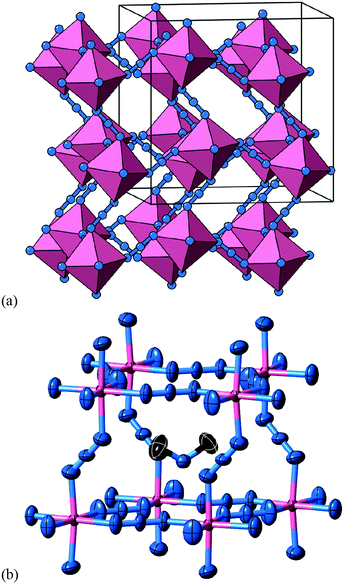 | ||
| Fig. 7 Static shift distortions in [NMe2H2]Mn[N3]3. (a) A representation of the crystal structure as reported in ref. 50. Mn atoms are shown as pink polyhedra; N atoms as blue spheres; [NMe2H2]+ cations have been omitted for clarity. There are two orthogonal shift distortions active in this system. One is precisely the same as that shown in Fig. 6(a) and gives rise to alternating columnar displacements polarised along c (the vertical axis in our representation here). At the same time there is an antiferroelastic planar shift system polarised along the b direction (the horizontal axis in this representation) that by itself gives rise to the type of distortion shown in Fig. 5 (albeit with axes relabelled). (b) Thermal ellipsoid representation of the local environment of [NMe2H2]+ cations within the distorted perovskite framework. C atoms are shown in black and H atoms have been omitted for clarity. | ||
The arguments presented to explain the activation of a0a0cM shifts in [NMe4]Ca[N3]3 appear to hold again for the a0bXcM shifts we find in [NMe2H2]Mn[N3]3. Clearly the azide linker is common to both, but we find also that the point symmetry at the A site is reduced in order to allow orientational order of the [NMe2H2]+ cation [Fig. 7(b)]. The crystallographic point symmetry of this site is 2 (C2) in the Cmce structure, which is a subgroup of the idealised 222 (C2v) molecular point symmetry.
One effect of the activation of multiple shift systems is that the crystal symmetry is now sufficiently low that a set of octahedral tilts couples to the shift-induced distortions. This tilt system is characterised by the (conventional) Glazer label a−b0b0 and cannot by itself account for the Cmce symmetry. In other words, octahedral tilts do not act as the primary order parameter in this system.
Dimethylammonium manganese formate
In our final case study, we consider a system for which shift distortions are present but clearly not the primary order parameter: [NMe2H2]Mn[HCOO]3. In the high-temperature phase of this compound, the crystal symmetry is R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) c with
c with 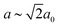 and
and 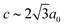 [Fig. 8].25 The existence of a rhombohedral distortion itself implies activation of a shear strain polarised along the body diagonal of the ABX3 cube. Consequently the shift distortion is given by the straightforward labels aΓaΓaΓ and
[Fig. 8].25 The existence of a rhombohedral distortion itself implies activation of a shear strain polarised along the body diagonal of the ABX3 cube. Consequently the shift distortion is given by the straightforward labels aΓaΓaΓ and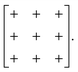 | (11) |
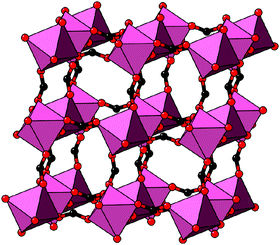 | ||
| Fig. 8 Representation of the crystal structure of [NMe2H2]Mn[HCOO]3, as reported in ref. 25. Mn coordination polyhedra are shown in pink, O atoms as red spheres, and C atoms as black spheres. [NMe2H2]+ cations and H atoms have been omitted for clarity. Here the shift distortions are associated with macroscopic shear of the lattice. | ||
This distortion reduces the Pm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m aristotype symmetry to R
m aristotype symmetry to R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m (
m (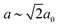 and
and 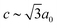 ), which is a minimal supergroup of the observed space group R
), which is a minimal supergroup of the observed space group R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) c (
c (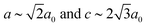 ) and so cannot act as a primary order parameter. Instead, it is the conventional octahedral tilt distortion (Glazer notation a−a−a−) that is responsible for breaking the aristotypic symmetry; so, in this case, the shifts couple to the tilts.
) and so cannot act as a primary order parameter. Instead, it is the conventional octahedral tilt distortion (Glazer notation a−a−a−) that is responsible for breaking the aristotypic symmetry; so, in this case, the shifts couple to the tilts.
Trends, shift identification, and some complications
Having identified the relevance of shift distortions in the structural chemistry of molecular perovskites, one of the key challenges now to be faced is that of selectively controlling the activation of specific shift systems through chemical modification. This is of course a related problem to that of controlling tilt activation in perovskite analogues, for which some significant progress has recently been made.51,52 While at this stage we make no claim of identifying design approaches for activating specific shifts, our analysis above would suggest that at least two considerations will become key: the molecular shape of the A-site cation, on the one hand, and the bonding preferences of molecular X anions, on the other hand. In order to facilitate the elucidation of trends, we summarise in Table 2 the active shift systems for those examples given above, together with two other relevant systems reported in the literature. We include in this summary a measure of the corresponding magnitude of shift distortion, which we report in terms of relative displacement (i.e. normalised with respect to B⋯B separation of the aristotypic lattice). In this way our metric corresponds directly to shear strains for shifts associated with k → Γ.In selecting the various case studies included here we have intentionally focussed on systems for which the active shift distortions are relatively straightforward. A more general approach for identifying shifts would be to employ group-theoretical analysis of the corresponding distortion modes, as implemented in e.g. ISODISTORT.49,54 Irrespective of how shifts are identified, there is absolutely no difficulty in anticipating complicating factors in other systems that would make the kind of analysis we present much trickier. We briefly highlight some of these factors here, noting that many of these are complications also in the characterisation of octahedral tilts in conventional perovskites.
First, there will be systems for which the difference in magnitude of shifts for different directions will meaningfully affect the symmetry of the distorted state. Glazer notation allows this distinction to be made through the use of different primary symbols λ; however, the matrix notation as presented would need to be modified to reflect this variation—perhaps through the use of variables or constants ∉ {0, ±1} in the matrix itself. Second, we have focused on shifts characterised by periodicities at the zone centre or zone boundary. More complex periodicities are allowed: an example occurs in the material [NPr4]Ni[N(CN)2]3 (Pr = C3H7), for which a-shifts are active and modulated by the wave-vector k = [0, ¼, ¼].13 One might anticipate the use of the Bradley–Cracknell symbol Σ in the corresponding Glazer notation; likewise there is in principle no reason why complex (or in this case, imaginary) values of exp[2πikα] might not be used in the matrix notation. Nevertheless, in both cases there are issues of distortion phase that are probably too difficult to be unambiguously resolved by a terse symbolic representation. And, third, it is perfectly feasible for a system to support more than one shift distortion along a given axis. Indeed, this may not be particularly rare, given that zone-centre shifts correspond to shear modes.50 This situation is akin to the well-known case of compound tilts found in the study of some inorganic perovskites.55
4 Dynamic shifts
So far, our focus has been on the characterisation and understanding of static shift distortions in molecular perovskites. For a structural degree of freedom—such as shifts—to influence the phase behaviour of a broad family, its effect on the lattice dynamics is an equally important consideration. The field would surely benefit from experimental studies of the lattice dynamics in molecular framework analogues (noting, for example, the transformative role played by inelastic neutron scattering in developing the soft-mode theory of phase transitions in conventional perovskites).56–58 Our approach here, however, is to develop an extremely simple computational lattice-dynamical model, from which we calculate the corresponding phonon dispersion curves. Through interrogation of the corresponding eigenvectors, we are able to explore the role of shift modes in the phonon spectrum for this representative model. We proceed to calculate the corresponding Grüneisen parameters—a measure of the role of individual modes in the thermal expansion behaviour of a material59—and demonstrate that dynamic shifts may play an as-yet under-appreciated role in the NTE properties of some molecular perovskites. Our analysis concludes with a simple DFT study of phonon instabilities in the Prussian blue analogue CdPd(CN)6.60 We show explicitly that shift modes are amongst the set of unstable distortions for this system (together with the conventional octahedral tilts), and hence would be expected to play a key role in the finite-temperature dynamics and phase behaviour of this molecular perovskite analogue.Lattice-dynamical model
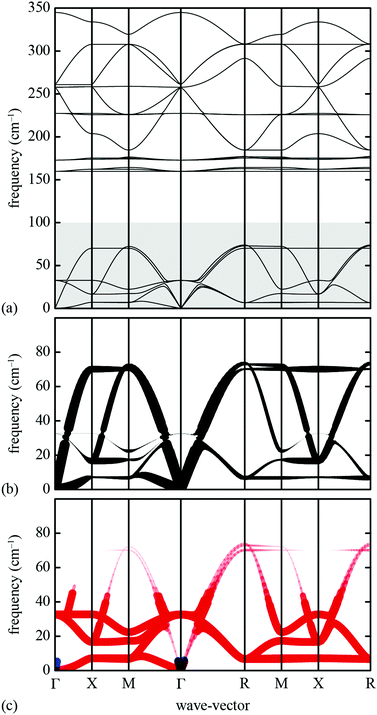
The essential features of the simple lattice-dynamical model we develop to study shift distortions are: (i) a perovskite topology, (ii) molecular linkers within the perovskite framework, (iii) rigid metal–linker and intra-linker bonds, (iv) rigid linker–metal–linker bond angles, and (v) flexible metal–linker–metal bond angles. We satisfy these criteria with a simple cubic cell (symmetry Pm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m) containing a single atom (B) at the cell origin, and a linker atom (X) at the 6e site (x, 0, 0) with x = 0.4. This model has nominal composition B[X2]3. Because we are primarily concerned with deformations of the framework lattice, and because we want to keep our model as simple as possible, we do not include an A-site cation and we treat both B and X atoms as charge neutral. Our model is made elastically stable through the introduction of harmonic bond-length and bond-angle interactions, as represented in Fig. 9. Consequently, the lattice enthalpy of our model is given by
m) containing a single atom (B) at the cell origin, and a linker atom (X) at the 6e site (x, 0, 0) with x = 0.4. This model has nominal composition B[X2]3. Because we are primarily concerned with deformations of the framework lattice, and because we want to keep our model as simple as possible, we do not include an A-site cation and we treat both B and X atoms as charge neutral. Our model is made elastically stable through the introduction of harmonic bond-length and bond-angle interactions, as represented in Fig. 9. Consequently, the lattice enthalpy of our model is given by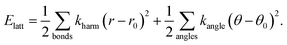 | (12) |
| Parameter | Value |
|---|---|
| Space group |
Pm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m m |
| a (Å) | 5.0 |
| m(B) (a.m.u.) | 54.94 |
| m(X) (a.m.u.) | 16.00 |
| k harm(B–X) (eV Å−2) | 1.0 |
| r 0(B–X) (Å) | 2.0 |
| k harm(X–X) (eV Å−2) | 1.0 |
| r 0(X–X) (Å) | 1.0 |
| k harm(X⋯X) (eV Å−2) | 1.0 |
| r 0(X⋯X) (Å) | 2.828 |
| k angle(X–B–X) (eV rad−2) | 1.0 |
| θ 0(X–B–X) (°) | 90.0 |
| k angle(X–X–X) (eV rad−2) | 0.01 |
| θ 0(X–B–X) (°) | 135.0 |
We proceeded to calculate the harmonic phonon dispersion relation for this simple lattice-dynamical model, making use of a k-grid of roughly 0.025 reciprocal lattice units. The corresponding phonon dispersion curves along specific high-symmetry directions are shown in Fig. 10(a). We do not attach any significance to the absolute energy scale of these excitations, since we have not aimed to replicate experimental values in our choice of harmonic spring constants. What is significant is the partitioning of the spectrum into a low-energy regime (which we will come to show dominates NTE behaviour) and a higher-energy regime. With respect to the low-energy component, we note the anomalous slope of the transverse acoustic branch along the Γ–X direction that is diagnostic of a shear instability, the existence of multiple dispersionless bands (evidence of localised degrees of freedom), and also the presence of zone-boundary soft modes.
 | ||
| Fig. 10 Phonon dispersion curves for our lattice-dynamical model and their interpretation in terms of shift degrees of freedom. (a) The entire phonon dispersion across selected high-symmetry directions in reciprocal space, as determined using GULP.61 The shaded region at frequencies below 100 cm−1 contains the modes responsible for NTE behaviour. (b) The low-frequency region of the phonon dispersion (as shown in (a)) where the branches have been broadened according to the corresponding value of ρ(k, ν). Consequently, those branches that appear bold in this representation correspond to modes with significant translational components. (c) The same low-frequency region of the phonon spectrum now coloured and broadened according to the value of the mode Grüneisen parameter: blue values correspond to γ > 0 and red to γ < 0. The branches that appear bold and red are the most important for NTE; our key result is that these include the shift modes as discussed in the text. | ||
In order to better understand the distribution of shift modes throughout this phonon dispersion, we exploited the observation that shifts are associated with eigenvectors e(k, ν) uniformly polarised along a single Cartesian axis. Consequently, the projections
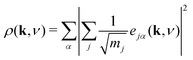 | (13) |
What is immediately clear is that shifts play an active role in the low-energy dynamics for those branches along which they are allowed. For the Γ–X direction, by way of example, the soft acoustic branch is almost entirely accounted for in terms of shift distortions. This branch is doubly degenerate; its low energy reflects the ease with which planar shifts can be accommodated in this simple model. As k → X, this branch anti-crosses with a rotational RUM branch, such that at the X point itself the shifts correspond to the set of modes with the second lowest phonon frequencies. Note that the longitudinal acoustic branch has increased significantly in energy at this point, such that translations polarised along the same direction as k have very much higher energies. Across the X–M direction, one of the two shift degrees of freedom accessible at X becomes increasingly stiff. As k → M there is only one shift degree of freedom remaining at the lowest energies; this degree of freedom couples strongly with the rotational RUMs such that it contributes to all three lowest-energy phonon branches. These observations are entirely consistent with the RUM analysis of Section 2.
Negative thermal expansion
The phonon spectrum is directly linked to NTE behaviour via the Grüneisen parameters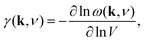 | (14) |
The combination of large negative Grüneisen parameters and low phonon frequencies also suggests shift-type vibrational modes are likely to show strongly anharmonic behaviour. Hence, the soft mode instabilities normally associated with octahedral tilts and/or ferroelectric displacements may also involve correlated shifts in perovskite analogues. The equilibrium geometry of the B–X–X angle and the presence and charge distribution of A-site cations will help shape the phonon dispersion and—by virtue of the close match in A-site geometry and perovskite deformation noted in the various case studies above—might also be expected to drive phonon softening in suitable cases. Molecular dynamics studies, such as those used to interrogate negative thermal expansion in Zn(CN)2,68,69 would provide valuable insight into the possible existence and phenomenology of displacive transitions involving shift degrees of freedom.
Displacive instabilities in CdPd(CN)6
The simple lattice-dynamical model we have presented is intentionally general, and we conclude our discussion here with a brief study of dynamic instabilities in a specific physical realisation of this model. For this purpose we have chosen the Prussian blue analogue CdPd(CN)6.60 The cyanide anion is the simplest molecular linker, but its asymmetry means that we are forced to study a system with two types of B-site cation in order to avoid the computationally difficult problem of CN− head-to-tail disorder. Because mass plays a key role in determining phonon localisation in ω-space, we chose a system in which these two B-site cations were as similar in mass as possible: hence CdPd(CN)6, which is a 4d analogue of the NTE material CdPt(CN)6.64,65 This particular system has the additional advantage that both transition-metal cations adopt S = 0 states (Cd2+d10, Pd4+ low-spin d6), allowing standard DFT approaches to be employed to determine the ab initio 0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) K phonon spectrum.
K phonon spectrum.
Using the CASTEP code,70 we optimised the Fm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m geometry of the CdPd(CN)6 crystal structure60 and calculated its phonon spectrum. For these calculations, we used plane-wave basis sets, with the GGA-PBE functional and CASTEP's on-the-fly norm-conserving pseudopotentials for Cd, Pd, C, and N.71,72 We did not include any empirical dispersion corrections, and treated the system explicitly as non-metallic. We used a plane wave cutoff of 750
m geometry of the CdPd(CN)6 crystal structure60 and calculated its phonon spectrum. For these calculations, we used plane-wave basis sets, with the GGA-PBE functional and CASTEP's on-the-fly norm-conserving pseudopotentials for Cd, Pd, C, and N.71,72 We did not include any empirical dispersion corrections, and treated the system explicitly as non-metallic. We used a plane wave cutoff of 750![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) eV, a single wave-vector for integration of electronic states across the Brillouin zone, and standard convergence tests for convergence (energy shift per atom of 2
eV, a single wave-vector for integration of electronic states across the Brillouin zone, and standard convergence tests for convergence (energy shift per atom of 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) μeV). The CASTEP phonon calculations makes use of density-functional perturbation theory;73 we used a 2 × 2 × 2 Monkhorst–Pack grid74 with a phonon convergence tolerance of 10−5
μeV). The CASTEP phonon calculations makes use of density-functional perturbation theory;73 we used a 2 × 2 × 2 Monkhorst–Pack grid74 with a phonon convergence tolerance of 10−5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) eV Å−2 and explicitly accounted for LO/TO splitting and enforcement of the acoustic sum rule. Phonons were calculated at evenly-spaced intervals across the Brillouin zone path Γ–X–M–Γ–R–M–X–R.
eV Å−2 and explicitly accounted for LO/TO splitting and enforcement of the acoustic sum rule. Phonons were calculated at evenly-spaced intervals across the Brillouin zone path Γ–X–M–Γ–R–M–X–R.
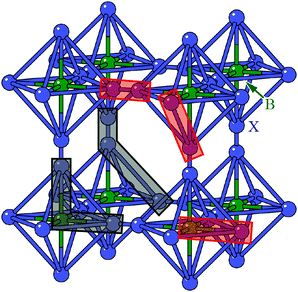
We found the system to be unstable with respect to a number of distortions characterised by phonon wave-vectors k distributed throughout the Brillouin zone. The most significant of these distortion modes actually occurs at the zone centre; these modes—which may be interpreted as low-energy modes of the finite-temperature parent structure—are illustrated in Fig. 11. An important point is that the double-perovskite structure of CdPd(CN)6 means that k = 0 distortions for this system include all those characterised by periodicities Γ, X, M, and R of the parent perovskite lattice. So we should expect to find zone-boundary (X-type and M-type) shifts amongst these distortions if they are indeed relevant to the dynamical behaviour of CdPd(CN)6. There are in fact 21 unstable modes for CdPd(CN)6 at k = 0 (we show the 15 most significant), which fall into three categories. Those corresponding to the largest imaginary frequencies (98i cm−1) are conventional tilt distortions: the six such modes correspond to in-phase and out-of-phase tilt combinations for rotations around each of the three Cartesian axes. The second category corresponds to columnar shift distortions, with nine modes in total: two X-type (95i cm−1) and one M-type (80i cm−1) shift combination for displacements parallel to each of three Cartesian axes. The third and final set of unstable modes are distortive tilts, which are much less significant (50i cm−1). In Fig. 11(b) we highlight the atomic displacement pattern associated with one of the M-type instabilities, which we note is of precisely the same form as the static distortion observed in [NMe4]Ca[N3]3 [Fig. 6].
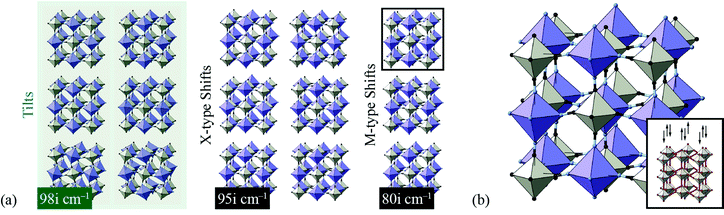 | ||
| Fig. 11 Key zone-centre displacive instabilities in CdPd(CN)6 as determined using DFT calculations. (a) Conventional tilts (highlighted in green) are the least stable modes, followed by X-type and M-type shifts. (b) A representation of the phonon eigenvector associated with one of the M-type shift instabilities (highlighted in panel (a)), together with a schematic relating the collective displacements to the cartoon shown in Fig. 2(a). | ||
Our key result in this simple DFT study is that all possible octahedral shifts are amongst the set of phonon instabilities for this molecular perovskite analogue. This reinforces our point that shifts play a role in the low-energy dynamics of these systems and, in suitable cases, may be responsible for displacive phase transitions and/or NTE behaviour (including e.g. in the MPt(CN)6 family65). There is clearly scope for a more detailed DFT investigation of this—and related—systems, including determination of mode Grüneisen parameters as carried out in ref. 67.
5 Concluding remarks
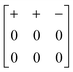
Our study has demonstrated that shift distortions are bona fide structural degrees of freedom in molecular perovskite analogues: they influence the crystal structures of a number of known compounds, and they are likely to play a key role in the low-energy dynamics of these systems, including anomalous thermal responses such as NTE. We have shown the potential for interplay between shift and tilt degrees of freedom, and again between shift and A-site orientational (multipolar) degrees of freedom; consequently, variation in cation size and geometry might be expected to allow control over the selective activation of specific shift distortions.A crucial result of our study has been to show that shift distortions can give rise to symmetry-lowering processes inaccessible through e.g. octahedral tilt mechanisms. The importance of this result lies in the emerging interest in exploiting compound distortions as indirect mechanisms of driving polarisation:33,75,76 this is the strategy of so-called “tilt engineering”, which is allowing access to entirely new families of multiferroic materials.2 The new symmetry-breaking mechanisms we identify here allow, in principle, for analogous “shift engineering” approaches, where combinations of various correlated shifts—perhaps coupled with tilt or cation order—might be used to break inversion symmetry. For instance, we find that the combination of aXb0c0 shifts characterised by the matrix
 | (15) |
Finally, we emphasise the point made in ref. 35 that the incorporation of defects—and in particular B-site vacancies—can influence the number of shift-type instabilities in perovskite systems. The key geometric effect of vacancies is to relax the constraint kα = 0 for shift displacements along the direction α ∈ {a, b, c}: chains on opposite sides of a B-site vacancy are in principle free to displace in different directions via compression of the vacancy. Since defects increasingly appear to be ubiquitous amongst perovskite analogues—and not least so for the Prussian blue analogues, which can support extremely high defect concentrations17—the use of defect structures to influence the importance and nature of shift-type distortions may indeed prove a fruitful avenue for future research.78
Acknowledgements
We thank M. S. Senn (Oxford) for assistance with our DFT calculations, and J. M. Bermúdez-García (A Coruña) for useful discussions. J. A. H. and A. L. G. gratefully acknowledge funding through the European Research Council (Grant 279705) and the E.P.S.R.C.References
- N. A. Benedek and C. J. Fennie, Phys. Rev. Lett., 2011, 106, 107204 CrossRef PubMed.
- M. J. Pitcher, P. Mandal, M. S. Dyer, J. Alaria, P. Borisov, H. Niu, J. B. Claridge and M. J. Rosseinsky, Science, 2015, 347, 420–424 CrossRef CAS PubMed.
- N. A. Benedek, J. M. Rondinelli, H. Djani, P. Ghosez and P. Lightfoot, Dalton Trans., 2015, 44, 10543–10558 RSC.
- M. S. Senn, C. A. Murray, X. Luo, L. Wang, F.-T. Huang, S.-W. Cheong, A. Bombardi, C. Ablitt, A. A. Mostofi and N. C. Bristowe, J. Am. Chem. Soc., 2016, 138, 5479–5482 CrossRef CAS PubMed.
- A. M. Glazer, Acta Crystallogr., Sect. B: Struct. Crystallogr. Cryst. Chem., 1972, 28, 3384–3392 CrossRef CAS.
- C. J. Howard and H. T. Stokes, Acta Crystallogr., Sect. B: Struct. Sci., 1998, 54, 782–789 CrossRef.
- C. J. Howard, B. J. Kennedy and P. M. Woodward, Acta Crystallogr., Sect. B: Struct. Sci., 2003, 59, 463–471 CrossRef.
- M. T. Dove, Introduction to Lattice Dynamics, Cambridge University Press, Cambridge, 1993 Search PubMed.
- H. J. Snaith, J. Phys. Chem. Lett., 2013, 4, 3623–3630 CrossRef CAS.
- D. B. Mitzi, J. Chem. Soc., Dalton Trans., 2001, 1–12 RSC.
- M.-L. Tong, J. Ru, Y.-M. Wu, X.-M. Chen, H.-C. Chang, K. Mochizuki and S. Kitagawa, New J. Chem., 2003, 27, 779–782 RSC.
- J. A. Schlueter, J. L. Manson, K. A. Hyzer and U. Geiser, Inorg. Chem., 2004, 43, 4100–4102 CrossRef CAS PubMed.
- J. A. Schlueter, J. L. Manson and U. Geiser, Inorg. Chem., 2005, 44, 3194–3202 CrossRef CAS PubMed.
- J. M. Bermúdez-García, M. Sánchez-Andújar, S. Yáñez-Vilar, S. Castro-García, R. Artiaga, J. López-Beceiro, L. Botana, A. Alegría and M. A. Señarís-Rodríguez, J. Mater. Chem. C, 2016, 4, 4889–4898 RSC.
- Z.-Y. Du, T.-T. Xu, B. Huang, Y.-J. Su, W. Xue, C.-T. He, W.-X. Zhang and X.-M. Chen, Angew. Chem., Int. Ed., 2015, 54, 914–918 CrossRef CAS PubMed.
- L. C. Gómez-Aguirre, B. Pato-Doldán, A. Stroppa, L.-M. Yang, T. Frauenheim, J. Mira, S. Yáñez-Vilar, R. Artiaga, S. Castro-García, M. Sánchez-Andújar and M. A. Señarís-Rodríguez, Chem. – Eur. J., 2016, 22, 7863–7870 CrossRef PubMed.
- H. J. Buser, D. Schwarzenbach, W. Petter and A. Ludi, Inorg. Chem., 1977, 16, 2704–2710 CrossRef CAS.
- D. Aguilà, Y. Prado, E. S. Koumousi, C. Mathonière and R. Clérac, Chem. Soc. Rev., 2016, 45, 203–224 RSC.
- J. Lefebvre, D. Chartrand and D. B. Leznoff, Polyhedron, 2007, 26, 2189–2199 CrossRef CAS.
- J. A. Hill, A. L. Thompson and A. L. Goodwin, J. Am. Chem. Soc., 2016, 138, 5886–5896 CrossRef CAS PubMed.
- Q. Jiang, D. Rebollar, J. Gong, E. L. Piacentino, C. Zheng and T. Xu, Angew. Chem., Int. Ed., 2015, 54, 7617–7620 CrossRef CAS PubMed.
- D. Thiele and D. Messer, Z. Anorg. Allg. Chem., 1980, 464, 255–267 CrossRef.
- K.-P. Xie, W.-J. Xu, C.-T. He, B. Huang, Z.-Y. Du, Y.-J. Su, W.-X. Zhang and X.-M. Chen, CrystEngComm, 2016, 18, 4495–4498 RSC.
- E. Sletten and L. H. Jensen, Acta Crystallogr., Sect. B: Struct. Crystallogr. Cryst. Chem., 1973, 29, 1752–1756 CrossRef CAS.
- Z. Wang, B. Zhang, T. Otsuka, K. Inoue, H. Kobayashi and M. Kurmoo, Dalton Trans., 2004, 2209–2216 RSC.
- X.-Y. Wang, L. Gan, S.-W. Zhang and S. Gao, Inorg. Chem., 2004, 43, 4615–4625 CrossRef CAS PubMed.
- Z.-Y. Du, Y.-P. Zhao, C.-T. He, B.-Y. Wang, W. Xue, H.-L. Zhou, J. Bai, B. Huang, W.-X. Zhang and X.-M. Chen, Cryst. Growth Des., 2014, 14, 3903–3909 CAS.
- S. G. Duyker, J. A. Hill, C. J. Howard and A. L. Goodwin, J. Am. Chem. Soc., 2016, 138, 11121–11123 CrossRef CAS PubMed.
- C. M. Kareis, S. H. Lapidus, J.-H. Her, P. W. Stephens and J. S. Miller, J. Am. Chem. Soc., 2012, 134, 2246–2254 CrossRef CAS PubMed.
- N. L. Evans, P. M. M. Thygesen, H. L. B. Boström, E. M. Reynolds, I. E. Collings, A. E. Phillips and A. L. Goodwin, J. Am. Chem. Soc., 2016, 138, 9393–9396 CrossRef PubMed.
- X. Zhang, X.-D. Shao, S.-C. Li, Y. Cai, Y.-F. Yao, R.-G. Xiong and W. Zhang, Chem. Commun., 2015, 51, 4568–4571 RSC.
- W.-J. Xu, Z.-Y. Du, W.-X. Zhang and X.-M. Chen, CrystEngComm, 2016, 18, 7915–7928 RSC.
- A. Stroppa, P. Barone, P. Jain, J. M. Perez-Mato and S. Picozzi, Adv. Mater., 2013, 25, 2284–2290 CrossRef CAS PubMed.
- A. P. Giddy, M. T. Dove, G. S. Pawley and V. Heine, Acta Crystallogr., Sect. A: Found. Crystallogr., 1993, 49, 697–703 CrossRef.
- A. L. Goodwin, Phys. Rev. B, 2006, 74, 134302 CrossRef.
- G. S. Pawley, Phys. Status Solidi B, 1972, 49, 475–488 CrossRef CAS.
- C. Nanthamathee, S. Ling, B. Slater and M. P. Attfield, Chem. Mater., 2015, 27, 85–95 CrossRef CAS.
- P. Serra-Crespo, A. Dikhtiarenko, E. Stavitski, J. Juan-Alcañiz, F. Kapteijn, F.-X. Coudert and J. Gascon, CrystEngComm, 2015, 17, 276–280 RSC.
- K. Aizu, J. Phys. Soc. Jpn., 1969, 27, 1171–1178 CrossRef CAS.
- E. K. H. Salje, Annu. Rev. Mater. Res., 2012, 42, 265–283 CrossRef CAS.
- A. U. Ortiz, A. Boutin, A. H. Fuchs and F.-X. Coudert, Phys. Rev. Lett., 2012, 109, 195502 CrossRef PubMed.
- F.-X. Coudert, Chem. Mater., 2015, 27, 1905–1916 CrossRef CAS.
- S. J. Hunt, M. J. Cliffe, J. A. Hill, A. B. Cairns, N. P. Funnell and A. L. Goodwin, CrystEngComm, 2015, 17, 361–369 RSC.
- A. B. Cairns and A. L. Goodwin, Phys. Chem. Chem. Phys., 2015, 17, 20449–20465 RSC.
- S. A. T. Redfern and E. Salje, J. Phys. C: Solid State Phys., 1988, 21, 277–285 CrossRef CAS.
- B. J. Kennedy, C. J. Howard and B. C. Chakoumakos, J. Phys.: Condens. Matter, 1999, 11, 1479–1488 CrossRef CAS.
- G. J. Bradley and A. P. Cracknell, The Mathematical Theory of Symmetry in Solids, Clarendon Press, Oxford, 1972 Search PubMed.
- F. A. Mautner, H. Krischner and C. Kratky, Monatsh. Chem., 1988, 119, 1245–1249 CrossRef CAS.
- B. J. Campbell, H. T. Stokes, D. E. Tanner and D. M. Hatch, J. Appl. Crystallogr., 2006, 39, 607–614 CrossRef CAS.
- X.-H. Zhao, X.-C. Huang, S.-L. Zhang, D. Shao, H.-Y. Wei and X.-Y. Wang, J. Am. Chem. Soc., 2013, 135, 16006–16009 CrossRef CAS PubMed.
- J. Young and J. M. Rondinelli, J. Phys. Chem. Lett., 2016, 7, 918–922 CrossRef CAS PubMed.
- J.-H. Lee, N. C. Bristowe, J. H. Lee, S.-H. Lee, P. D. Bristowe, A. K. Cheetham and H. M. Jang, Chem. Mater., 2016, 28, 4259–4266 CrossRef CAS.
- J. M. Bermúdez-García, M. Sánchez-Andújar, S. Yáñez-Vilar, S. Castro-García, R. Artiaga, J. López-Beceiro, L. Botana, Á. Alegría and M. A. Señarís-Rodríguez, Inorg. Chem., 2015, 54, 11680–11687 CrossRef PubMed.
- ISOTROPY Software Suite, iso.byu.edu.
- M. D. Peel, S. P. Thompson, A. Daoud-Aladine, S. E. Ashbrook and P. Lightfoot, Inorg. Chem., 2012, 51, 6876–6889 CrossRef CAS PubMed.
- R. A. Cowley, Phys. Rev., 1964, 134, 981–997 CrossRef CAS.
- G. Shirane, Rev. Mod. Phys., 1974, 46, 437–449 CrossRef CAS.
- M. T. Dove, Eur. J. Mineral., 2002, 14, 203–224 CrossRef CAS.
- F. Grüneisen, Ann. Phys., 1912, 344, 257–306 CrossRef.
- H.-J. Buser, G. Ron, A. Ludi and P. Engel, J. Chem. Soc., Dalton Trans., 1974, 2473–2474 RSC.
- J. D. Gale, J. Chem. Soc., Faraday Trans., 1997, 93, 629–637 RSC.
- E. Grüneisen, in Thermische Eigenschaften der Stoffe, ed. H. Geiger and K. Scheel, Springer, Berlin, 1926, vol. X, pp. 1–59.
- J. S. O. Evans, J. Chem. Soc., Dalton Trans., 1999, 3317–3326 RSC.
- A. L. Goodwin, K. W. Chapman and C. J. Kepert, J. Am. Chem. Soc., 2005, 127, 17980–17981 CrossRef CAS PubMed.
- K. W. Chapman, P. J. Chupas and C. J. Kepert, J. Am. Chem. Soc., 2006, 128, 7009–7014 CrossRef CAS PubMed.
- S. Adak, L. L. Daemen, M. Hartl, D. Williams, J. Summerhill and H. Nakotte, J. Solid State Chem., 2011, 184, 2854–2861 CrossRef CAS.
- L. H. N. Rimmer, M. T. Dove, A. L. Goodwin and D. C. Palmer, Phys. Chem. Chem. Phys., 2014, 16, 21144–21152 RSC.
- F. Trousselet, A. Boutin and F.-X. Coudert, Chem. Mater., 2015, 27, 4422–4430 CrossRef CAS.
- Q.-L. Fang, J.-M. Zhang and K.-W. Xu, Phys. B, 2013, 424, 79–83 CrossRef CAS.
- S. J. Clark, M. D. Segall, C. J. Pickard, P. J. Hasnip, M. I. J. Probert, K. Refson and M. C. Payne, Z. Kristallogr., 2005, 220, 567–570 CAS.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS PubMed.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1997, 78, 1396 CrossRef CAS.
- K. Refson, P. R. Tulip and S. J. Clark, Phys. Rev. B, 2006, 73, 155114 CrossRef.
- H. J. Monkhorst and J. D. Pack, Phys. Rev. B, 1976, 13, 5188–5192 CrossRef.
- Y. S. Oh, X. Luo, F.-T. Huang, Y. Wang and S.-W. Cheong, Nat. Mater., 2015, 14, 407–413 CrossRef CAS PubMed.
- A. Stroppa, P. Jain, P. Barone, M. Marsman, J. M. Perez-Mato, A. K. Cheetham, H. W. Kroto and S. Picozzi, Angew. Chem., Int. Ed., 2011, 50, 5847–5850 CrossRef CAS PubMed.
- J. M. Rondinelli and C. J. Fennie, Adv. Mater., 2012, 24, 1961–1968 CrossRef CAS PubMed.
- A. K. Cheetham, T. D. Bennett, F.-X. Coudert and A. L. Goodwin, Dalton Trans., 2016, 45, 4113–4126 RSC.
| This journal is © the Owner Societies 2016 |