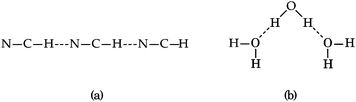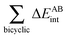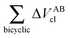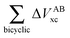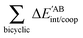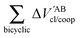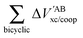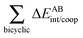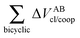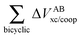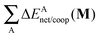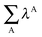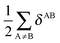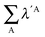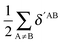Cooperative and anticooperative effects in resonance assisted hydrogen bonds in merged structures of malondialdehyde†
Received
13th July 2016
, Accepted 30th August 2016
First published on 1st September 2016
Abstract
We analyzed non-additive effects in resonance assisted hydrogen bonds (RAHBs) in different β-enolones, which are archetypal compounds of these types of interactions. For this purpose, we used (i) potential energy curves to compute the formation energy, ΔERAHBform, of the RAHBs of interest in different circumstances along with (ii) tools offered by quantum chemical topology, namely, the Quantum Theory of Atoms In Molecules (QTAIM) and the Interacting Quantum Atoms (IQA) electronic energy partition. We established the effect that a given H-bond exerts over ΔERAHBform associated with another RAHB, determining in this way the cooperativity or the anticooperativity of these interactions. The mesomeric structures and the QTAIM delocalisation indices are consistent with the determined cooperative or anticooperative character of two given RAHBs. The HB cooperativity and anticooperativity studied herein are directly reflected in the IQA interaction energy EO⋯Hint, but they are modulated by the surrounding hydrocarbon chain. The IQA decomposition of ΔEcoop, a measure of the cooperativity between a pair of interacting RAHBs, indicates that the analyzed H-bond cooperative/anticooperative effects are associated with greater/smaller (i) strengthening of the pseudo-bicyclic structure of the compounds of interest and (ii) electron localisations with its corresponding changes in the intra and intermolecular exchange–correlation contributions to ΔERAHBform. Overall, we expect that this investigation will provide valuable insights into the interplay among hydrogen bonded atoms and the π system in RAHBs contributing in this way to the understanding of the general features of H-bonds.
1 Introduction
Since its discovery in the 1920s1 many different experimental and theoretical investigations have been dedicated to the hydrogen bond (HB). The importance of this interaction resides not only on its effects on diverse systems in chemistry and biology but also on its complexity. For instance, the energetics of an O–H⋯O H-bond might lie in the range of 1–30 kcal mol−1.2 Further problems in the characterization of HBs arise from the dissimilar proportions of their covalent, electrostatic and dispersion contributions.3 This situation has led to the coinage of the term “H-bond puzzle” to indicate the lack of an overall H-bond model to predict the structure and energetics from the chemical formulae of the interacting fragments, as opposed to, for example, Lewis' electron pair theory. Indeed, the intricate character of the HB makes it very versatile and ubiquitous in many processes: from giving water its extraordinary features4 to the HB involvement in complicated biochemical reactions5 among other phenomena.
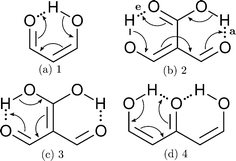
Part of the difficulty in the understanding of the HB originates in its non-additivity. Apart from the electrostatic component in non-covalent interactions, the distinct contributions to the HB formation energy are non-additive,6i.e., the value of the component of the interaction energy of two species is affected by the presence of a third electronic system, which leads to cooperative and anticooperative effects of the HB. The former occurs when hydrogen bonds strengthen each other whereas the latter involves a mutual weakening of the interactions. For example, the HBs in a linear structure of the type BH⋯BH⋯BH, like that shown in Fig. 1(a), display cooperative effects7 as opposed to those present in a double hydrogen bond donor (Fig. 1(b)), which exhibit HB anticooperativity. The charge transfer leading to the referred non-additive effects takes place through σ bonds and hence it is called “σ-bond” cooperativity or anticooperativity.3
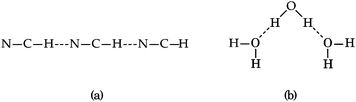 |
| | Fig. 1 (a) Hydrogen bond cooperative effects in the linear HCN trimer: both H-bonds strengthen each other. (b) Water molecule acting as a double hydrogen bond donor: the H-bonds are reciprocally weakened. | |
In addition to these σ-bond non-additive effects, conjugated systems might also influence HBs, for example in β-diketones8 shown in Fig. 2. These H-bonds are called Resonance Assisted Hydrogen Bonds (RAHBs) and they were introduced as “the interplay between hydrogen bond and heterodienes (or more generally heteroconjugated systems) leading to a strengthening of the hydrogen bond itself”.8Fig. 2(a) shows this interaction between the hydrogen bond and the π system within malondialdehyde, CHO–CH![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) CH–OH. Resonance assisted hydrogen bonds have been of considerable interest in physical chemistry, a situation which has led to numerous theoretical9–11 and experimental12,13 reports concerned with the nature of these HBs. In addition, the RAHB concept has been used to better understand intermolecular interactions in relevant systems in chemistry and biology, like those present in DNA14–16 and proteins.3
CH–OH. Resonance assisted hydrogen bonds have been of considerable interest in physical chemistry, a situation which has led to numerous theoretical9–11 and experimental12,13 reports concerned with the nature of these HBs. In addition, the RAHB concept has been used to better understand intermolecular interactions in relevant systems in chemistry and biology, like those present in DNA14–16 and proteins.3
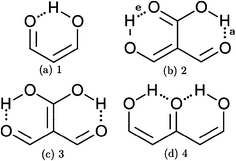 |
| | Fig. 2 Systems addressed in this study. X-ray crystallography results suggest that the H-bonds within compound 2 strengthen each other as opposed to systems 3 and 4 which exhibit H-bond anticooperativity.17 | |
The HB cooperative and anticooperative effects that might occur due to an adjacent π system, as in Fig. 2(b)–(d), have been however relatively unexplored.17–20 We chose these systems to study π-bond HB cooperativity and anticooperativity, because it has been suggested that compound 2 presents HB cooperative effects whereas it occurs the opposite for systems 3 and 4, i.e. the H-bonds within these systems weaken each other.17 Thus, this work deals with the examination of the hydrogen bond π non-additive effects in RAHBs along with the reciprocal action between these HBs and the accompanying conjugated system by considering molecules 1–4 in Fig. 2 as archetypal models. For this aim, we calculated potential energy curves to determine the RAHB formation energy, ΔERAHBform, of the intramolecular H-bonds in Fig. 2 in distinct circumstances which enabled us to assess the nature of the π non-additive effects in these systems. In addition, we used tools offered by quantum chemical topology to gain further insights into the studied RAHBs. More specifically, we employed the Interacting Quantum Atoms (IQA) energy partition as well as the Quantum Theory of Atoms in Molecules (QTAIM) to analyze the interplay between a given RAHB and its surrounding π bonds as well as the resultant HB cooperative or anticooperative effects. We have chosen these methods of wavefunction analyses for this investigation due to their successful use in the study of different non-additive interactions such as those in the H-bond within small water clusters,21,22 back-bonding in transition metal carbonyl complexes,23,24 or in n → π* transitions in electronic excited states.25 Altogether, our results provide an assessment of the interaction of an RAHB and its neighboring conjugated system on top of HB π cooperative and anticooperative effects. We expect that the results presented in this investigation will prove useful in a further understanding of the important non-additive effects within resonance assisted hydrogen bonds.
2 Methods
The wavefunction analyses presented in this work are based on a partition of the real space into disjoint basins in accordance with the QTAIM,26 an approach founded on the topology of the charge distribution ρ1(r), which is invariant under orbital rotations because it is the expectation value of a Dirac observable, i.e., 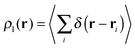 .27 The QTAIM basins, denoted generally as Ω, are proper open subsystems for which one can compute the expectation values of quantum mechanical operators such as the Hamiltonian, the kinetic energy, and the number operators.26 The QTAIM also defines localisation and delocalisation indices (LI and DI respectively) in terms of the integration of the Fermi and Coulomb correlation holes over the QTAIM atoms.28 The LI and DI descriptors are useful to examine electron sharing, i.e. covalency, in different chemical bonding scenarios. The sum of the atomic properties, 〈O〉Ω, throughout the whole of the system, yields the expectation value of the corresponding observable for the complete molecule or molecular cluster under consideration. Since the QTAIM is completely built on ρ1(r), it can be used to address on equal footing a wide variety of chemical compounds and processes, such as metal–ligand bonding,23 interactions within a molecular cluster,29 π-electron delocalised30 and H-bonded systems,11,31 being the two last-mentioned examples of particular interest for this work.
.27 The QTAIM basins, denoted generally as Ω, are proper open subsystems for which one can compute the expectation values of quantum mechanical operators such as the Hamiltonian, the kinetic energy, and the number operators.26 The QTAIM also defines localisation and delocalisation indices (LI and DI respectively) in terms of the integration of the Fermi and Coulomb correlation holes over the QTAIM atoms.28 The LI and DI descriptors are useful to examine electron sharing, i.e. covalency, in different chemical bonding scenarios. The sum of the atomic properties, 〈O〉Ω, throughout the whole of the system, yields the expectation value of the corresponding observable for the complete molecule or molecular cluster under consideration. Since the QTAIM is completely built on ρ1(r), it can be used to address on equal footing a wide variety of chemical compounds and processes, such as metal–ligand bonding,23 interactions within a molecular cluster,29 π-electron delocalised30 and H-bonded systems,11,31 being the two last-mentioned examples of particular interest for this work.
In a similar fashion to QTAIM, the IQA energy partition is based on scalar fields derived from the wavefunction, more specifically, the first order reduced density matrix ρ1(r1,r1′), and the pair density, ρ2(r1,r2). The availability of ρ1(r1,r1′) and ρ2(r1,r2), along with a sectioning of the real space, e.g., the one defined by QTAIM, allows us to dissect the electronic energy of a system as
| | 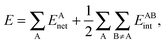 | (1) |
wherein
EAnet denotes the net energy of basin A whereas
EABint indicates the interaction energy between atoms A and B. The pairwise nature of the potential energy operator in the electron Hamiltonian allows us to further divide the IQA net and interaction energies as
| | | EAnet = TA + VAAne + VAAne, | (2) |
| | | EABint = VABnn + VABee + VABne + VBAne, | (3) |
wherein
EAnet and
EABint are, respectively, the IQA net energy of atom A and the interaction energy between atoms A and B. In further detail,
TA in
eqn (2) represents the kinetic energy of basin A and by letting σ and τ denote either nuclei or electrons, then
VABστ designates the contribution to the potential energy from the interaction of σ contained in atom A with τ within basin B. The detailed expressions of every summand in the RHS of
eqn (2) and (3) in terms of the first and second order reduced density matrices can be found in
ref. 32 and 33. Additionally, the LHS of
eqn (1) can be expressed in terms of IQA additive energies,
| | 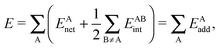 | (4) |
whose sum yields the total electronic energy in a similar fashion to the QTAIM atomic energies.
26
The separation of ρ2(r1,r2) in its coulombic (J) and exchange–correlation (xc) contributions
| | | ρ2(r1,r2) = ρJ2(r1,r2) + ρxc2(r1,r2), | (5) |
may be utilized to define a classical, that is, electrostatic,
| | | VABcl = VABJ + VABne + VBAne + VABnn, | (6) |
component of
EABint, along with a quantum,
i.e., exchange–correlation contribution which fulfil the relation
| | | EABint = VABcl + VABxc. | (7) |
The division of EABint in eqn (7) allows us to assess the covalent or ionic character of a given interaction A–B, which makes the IQA energy partition a powerful tool for the analysis of distinct chemical interactions.
3 Computational details
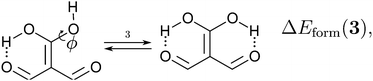
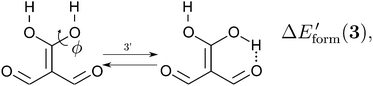
Because the examined RAHBs are intramolecular, it is not possible to take apart the fragments linked by a H-bond in order to analyse the changes in the system after the dissociation of the HB. Therefore, we computed potential energy curves as a function of the rotation of the C–OH bond, as illustrated in| | 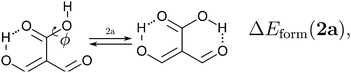 | (8) |
| |  | (9) |
| |  | (10) |
| |  | (11) |
and| | 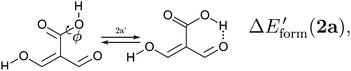 | (12) |
| |  | (13) |
| |  | (14) |
| |  | (15) |
in order to determine the formation energy of each RAHB in the presence and absence of the accompanying H-bond in the molecule. The potential energy curves were computed using the MP234 method in its efficient RIJCOSX variant35 together with the aug-cc-pVTZ basis functions36 as implemented in the Orca program package.37 We chose to use the MP2/aug-cc-pVTZ approximation, since O–H⋯O hydrogen-bonded systems are well accounted by second order Møller–Plesset perturbation theory and augmented Dunning basis sets.38
Afterwards, we carried out the IQA and QTAIM wavefunction analysis based on HF density functions which were computed using the GAMESS-US39 software. The use of HF wavefunctions is justified, because this approach was recently used to successfully study the H-bond cooperative effects within small water clusters21 and the nature of the resonance assisted hydrogen bonds.40 Furthermore, the RAHB formation energies examined in this work are considerably larger in magnitude than those within these H2O systems and therefore more easily describable using electronic structure methods. Besides, HF and MP2 approximations give a similar description of the potential energy curves for determining the RAHB formation energy of 1 and those in eqn (8)–(11) as shown in Fig. S1 and S2 in the ESI.† Finally, the use of IQA in a way that it fully recovers the correlated energy of the systems addressed in this investigation, for example by either CC41 or MP2, is beyond the current capabilities of the available software to carry out this energy partition due to the large size of the two-particle density matrices involved.
The QTAIM and IQA analyses were carried out using the AIMALL42 and PROMOLDEN43 programs respectively. In addition, we used the software packages GNUPLOT44 and AVOGADRO45,46 to visualize data and chemical structures.
4 Results and discussion
4.1 Potential energy curves
We assessed RAHB cooperative and anticooperative effects of the systems addressed in this work by comparing the formation energy of the hydrogen bonds under consideration, with (eqn (8)–(11)) and without (expressions (12)–(15)) the accompanying RAHB in the molecule. That is to say, we contrast the quantities ΔEform(2a), ΔEform′(2a); ΔEform(2e), ΔEform′(2e); etc.
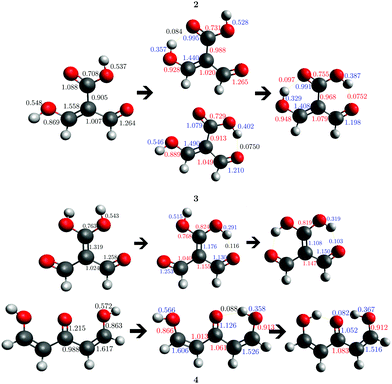
Fig. 3 shows the corresponding potential energy curves for the processes (8)–(15). The zero of every potential energy curve corresponds to the minimum in which ϕ is close to 180°, that is, where the RAHB is dissociated. This allows us to read directly ΔERAHBform at ϕ = 0. We note that generally, the magnitude of the RAHB formation energies is considerably larger than in other uncharged O–H⋯O systems, e.g. water clusters, which allows us to establish the strong effect of the π system over the H-bond energetics. We point out that the scanning of the dihedral angle for system 3 computed with the RIJCOSX-MP2/aug-cc-pVTZ approximation is accompanied by the intramolecular proton transfer shown in Fig. 4. This process entails the transformation of compound 3 into 2. For this reason, we built the corresponding potential energy curve in Fig. S2 in the ESI† by constraining the bond length of the dissociated O–H bond to 1.02 Å, i.e., its distance in the local minimum at ϕ = 0. The referred intramolecular Brønsted–Lowry reaction might be related to the fact that so far it has not been possible to synthesize crystals with moiety 3 in their structure.17
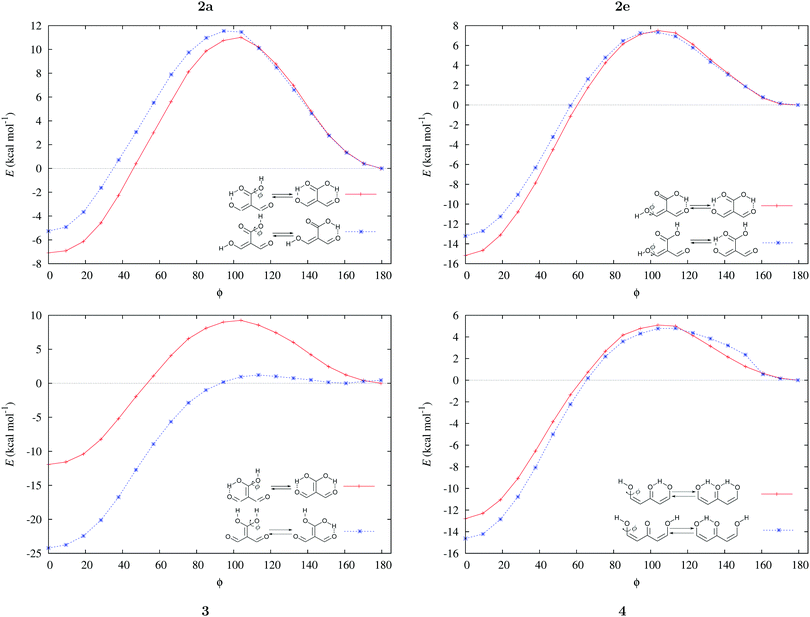 |
| | Fig. 3 Potential energy curves for the formation of the resonance assisted hydrogen bonds of interest for this work: 2aeqn (8) and (12); 2e processes (9) and (13); 3 reactions (10) and (14); 4 expressions (11) and (15). The approximation RIJCOSX-MP2 was used throughout. | |
 |
| | Fig. 4 Proton transfer occurred in the scanning of the dihedral angle of system 3 using the approximation RIJCOSX-MP2/aug-cc-pVTZ. | |
We find that the formation energy of H-bond 2a is larger in the presence of HB 2e (Fig. 3 – 2a) and vice versa (Fig. 3 – 2e). This means that these H-bonds strengthen each other and present cooperative effects throughout the π system. The opposite situation is observed in the H-bonds within systems 3 and 4: these interactions weaken one another and present π anticooperative effects. These results are in concordance with the experimental evidence17 and the mesomeric structures of Fig. 5. The resonance structure of compound 2 suggests that the RAHBs 2a and 2e strengthen each other, whereas in systems 3 and 4 both RAHBs compete for the π electrons within the system. Besides, the central carbonyl in 4 is a double H-bond acceptor which may also induce HB anticooperative effects.3,22
 |
| | Fig. 5 Resonance structures of the systems under investigation consistent with the H-bond cooperativity in system 2 and the anticooperative effects in compounds 3 and 4. We also show the mesomeric structures corresponding to 1 as a reference. | |
In order to analyse more thoroughly these non-additive effects, we can consider the differences between the formation energies of the RAHBs within a molecule in the presence of the other HB and in its absence as a measure of cooperativity in these systems:
| | | ΔEcoop(2a) = ΔEform(2a) − ΔE′form(2a) | (16) |
| | | ΔEcoop(2e) = ΔEform(2e) − ΔE′form(2e) | (17) |
| | | ΔEcoop(3) = ΔEform(3) − ΔE′form(3) | (18) |
| | | ΔEcoop(4) = ΔEform(4) − ΔE′form(4) | (19) |
The more negative the value of Δ
Ecoop(
N), wherein
N denotes either of the H-bonds
2a,
2e,
3 and
4, the larger the π cooperative effects for this interaction. The converse holds for positive values of Δ
Ecoop(
N) and π anticooperativity in the system. It is not difficult to show that Δ
Ecoop(
2a) = Δ
Ecoop(
2e).
Table 1 reports the values of Δ
Eform(
N), Δ
E′form(
N) and Δ
Ecoop(
N) from which we indeed observe that the hydrogen bonds of molecule
2 present π cooperative hydrogen bonds whereas molecules
3 and
4 exhibit HB π anticooperativity. We highlight the positive value of Δ
Ecoop(
3) = 12.29 kcal mol
−1 which is mainly due to the very large formation of one hydrogen bond of
3 in the absence of the other HB in the molecule and also consistent with the proton transfer described in
Fig. 4.
Table 1 Assessment of π-non additive effects using the values of ΔEcoop(N) with N = 2a, 2e, 3 and 4 as defined in eqn (16)–(19). The values are reported in kcal mol−1
| HB |
ΔEcoop(N) |
ΔEform(N) |
ΔEform′(N) |
|
2a
|
−1.82 |
−7.09 |
−5.27 |
|
2e
|
−1.97 |
−15.18 |
−13.21 |
|
3
|
12.29 |
−11.93 |
−24.22 |
|
4
|
1.84 |
−12.79 |
−14.63 |
The energy barriers for the dissociation in the plots of Fig. 3 provide another way to characterize the π non-additive effects of the systems examined in this work. As Fig. 6 shows, the activation energies for the dissociation of the H-bonds of molecule 2 are larger in the presence of the second HB, whereas the contrary is true for compounds 3 and 4. This means that the HBs in system 2 impair the dissociation of one another while the hydrogen bonds in 3 and 4 facilitate the breaking of any of the two interactions. This is consistent with the previous assignation of π anticooperative effects in the molecules 3 and 4 along with π cooperative effects in system 2.
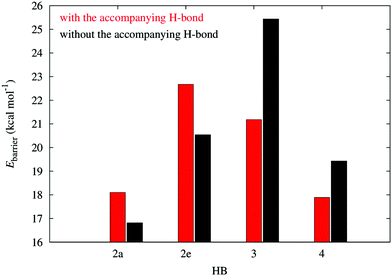 |
| | Fig. 6 Potential energy barriers in systems 2–4 in the dissociation of the resonance assisted hydrogen bonds in Fig. 2. | |
4.2 Quantum chemical topological analyses
Regarding the QTAIM and IQA analyses, first, we estimate the hydrogen bond formation energy by means of the topological properties of ρ(r), i.e.,47| | 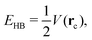 | (20) |
wherein V(rc) is the potential energy density at the bond critical point related to the H-bond. Table 2 reports the values of EHB together with those of the delocalisation index for the atoms directly involved in the hydrogen bond and the IQA interaction energy for the O⋯H bonds in addition to their classical and exchange–correlation components. Despite the correspondence between the data in Table 2 (|EHB| and |EO⋯Hint| increase with δ(O⋯H) and diminish with δ(O−H)), the indications of RAHB cooperativity or anticooperativity based on eqn (20) are not fully consistent with the results of the electronic structure calculations reported in Fig. 3. More specifically, Table 2 predicts that the enolic hydrogen bond exerts a slightly anticooperative effect on the carboxylic acid H-bond within compound 2.
Table 2 Formation energies for the resonance assisted H-bonds shown in Fig. 2 estimated through expression (20). The delocalisation indices δ(O⋯H) and δ(O–H) together with the IQA interaction energies EO⋯Hint, VO⋯Hcl and VO⋯Hx. EHB is reported in kcal mol−1 whereas the rest of the quantities are given in atomic units
| RAHB |
E
HB
|
δ(O⋯H) |
δ(O–H) |
E
O⋯Hint
|
V
O⋯Hcl
|
V
O⋯Hx
|
|
1
|
−19.888 |
0.090 |
0.353 |
−0.329 |
−0.306 |
−0.023 |
|
2a (2e present) |
−13.881 |
0.075 |
0.387 |
−0.301 |
−0.283 |
−0.018 |
|
2a (2e absent) |
−14.235 |
0.075 |
0.402 |
−0.296 |
−0.278 |
−0.018 |
|
2e (2a present) |
−22.375 |
0.097 |
0.329 |
−0.354 |
−0.328 |
−0.026 |
|
2e (2a absent) |
−18.267 |
0.084 |
0.357 |
−0.332 |
−0.311 |
−0.021 |
|
3 (accompanying HB present) |
−24.005 |
0.103 |
0.319 |
−0.356 |
−0.329 |
−0.027 |
|
3 (accompanying HB absent) |
−30.751 |
0.116 |
0.291 |
−0.383 |
−0.351 |
−0.032 |
|
4 (accompanying HB present) |
−17.296 |
0.082 |
0.367 |
−0.324 |
−0.304 |
−0.020 |
|
4 (accompanying HB absent) |
−18.556 |
0.088 |
0.358 |
−0.326 |
−0.304 |
−0.022 |
We stress, however, that the topological values of Table 2 refer only to the atoms directly involved in the H-bond. Table 2 of ref. 21 shows that the IQA interaction energies of the atoms that do not participate directly in the HB are also important in evaluating the formation energy of hydrogen bonding in contrast to the consideration of solely the properties in the O⋯H–O region as done in expression (20). In the case of intermolecular interactions, say between two monomers ![[capital G, script]](https://www.rsc.org/images/entities/char_e112.gif) and
and ![[script letter H]](https://www.rsc.org/images/entities/char_e142.gif) , we can consider directly all pairwise values of EA⋯Bint wherein atom A belongs to monomer
, we can consider directly all pairwise values of EA⋯Bint wherein atom A belongs to monomer ![[capital G, script]](https://www.rsc.org/images/entities/char_e112.gif) and B to
and B to ![[script letter H]](https://www.rsc.org/images/entities/char_e142.gif) . This division is not straightforward in intramolecular interactions, but such an issue is elegantly addressed by IQA additive energies (expression (4)), to consider the effect of the hydrocarbon chain in the RAHBs under examination as reported in Table 3. The data show that the formation of the RAHB involves a stabilization of the atoms participating directly in the H-bond, but in addition, the energy of the rest of the system is substantially increased. This indicates that the hydrocarbon chain has an important effect in the RAHB formation energy and its different components. Indeed, the energetic change of the π system modulates the magnitude of ΔERAHBform. This complicates the quantitative establishment of the magnitudes of H-bond formation energies in these molecules by the consideration of only the O⋯H–O moiety as done in formula (20). Conversely, the hydrocarbon chain suffers important modifications on account of the RAHB in agreement with the notion that a HB may substantially affect the energy of a π-system.48 More specifically to the non-additive effects previously described, the presence of either of RAHBs 2a or 2e is accompanied by larger magnitudes for ΔEO–H⋯Oadd and ΔE⋯CH
. This division is not straightforward in intramolecular interactions, but such an issue is elegantly addressed by IQA additive energies (expression (4)), to consider the effect of the hydrocarbon chain in the RAHBs under examination as reported in Table 3. The data show that the formation of the RAHB involves a stabilization of the atoms participating directly in the H-bond, but in addition, the energy of the rest of the system is substantially increased. This indicates that the hydrocarbon chain has an important effect in the RAHB formation energy and its different components. Indeed, the energetic change of the π system modulates the magnitude of ΔERAHBform. This complicates the quantitative establishment of the magnitudes of H-bond formation energies in these molecules by the consideration of only the O⋯H–O moiety as done in formula (20). Conversely, the hydrocarbon chain suffers important modifications on account of the RAHB in agreement with the notion that a HB may substantially affect the energy of a π-system.48 More specifically to the non-additive effects previously described, the presence of either of RAHBs 2a or 2e is accompanied by larger magnitudes for ΔEO–H⋯Oadd and ΔE⋯CH![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) CH–C⋯add for the formation of the other H-bond. The effect of the former being dominant leading thereby to the hydrogen bond π cooperativity observed in molecule 2. A similar analysis of molecules 3 and 4 shows that the presence of a previous hydrogen bond reduces the stability of the O–H⋯O system in consistency with the RAHB π anticooperativity previously described for these molecules.
CH–C⋯add for the formation of the other H-bond. The effect of the former being dominant leading thereby to the hydrogen bond π cooperativity observed in molecule 2. A similar analysis of molecules 3 and 4 shows that the presence of a previous hydrogen bond reduces the stability of the O–H⋯O system in consistency with the RAHB π anticooperativity previously described for these molecules.
Table 3 Change in the IQA additive energies after the formation of the hydrogen bonds under examination in the presence and absence of the accompanying hydrogen bond within the molecule. The data are reported in kcal mol−1
| HB |
ΔEO–H⋯Oadd |
ΔE⋯CH![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) CH–C⋯add CH–C⋯add |
ΔE |
|
1
|
−22.27 |
12.99 |
−9.28 |
|
2a (2e present) |
−20.33 |
16.38 |
−3.96 |
|
2a (2e absent) |
−15.48 |
13.29 |
−2.19 |
|
2e (2a present) |
−24.25 |
11.10 |
−13.15 |
|
2e (2a absent) |
−20.64 |
9.25 |
−11.38 |
|
3 (accompanying HB present) |
−21.86 |
12.91 |
−8.96 |
|
3 (accompanying HB absent) |
−28.43 |
7.62 |
−20.80 |
|
4 (accompanying HB present) |
−18.21 |
6.74 |
−11.47 |
|
4 (accompanying HB absent) |
−20.93 |
9.27 |
−11.66 |
Table 4 Interaction energy components of ΔEABint (eqn (8)–(11)) and 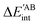 (expressions (12)–(15)) across the pseudo-bicyclic structure of the analyzed compounds in the formation of the H-bonds 2a, 2e, 3 and 4. The data are reported in kcal mol−1
(expressions (12)–(15)) across the pseudo-bicyclic structure of the analyzed compounds in the formation of the H-bonds 2a, 2e, 3 and 4. The data are reported in kcal mol−1
| H-bond |
ΔEform |
ΔE′form |
|
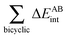
|
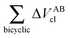
|
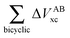
|
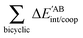
|
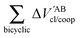
|
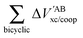
|
|
2a
|
−79.05 |
−103.75 |
24.71 |
−65.62 |
−102.07 |
36.45 |
|
2e
|
−67.71 |
−103.48 |
35.78 |
−66.50 |
−94.66 |
28.16 |
|
3
|
−98.44 |
−126.67 |
28.23 |
−150.62 |
−203.25 |
52.62 |
|
4
|
−26.84 |
−60.99 |
34.15 |
−45.32 |
−82.22 |
36.90 |
The quantities (16)–(19) can also be dissected in IQA net and interatomic contributions,
| |  | (21) |
wherein
M =
2,
3 or
4.
‡ A negative component of either Δ
EAnet/coop(
M) or Δ
EABint/coop(
M) is indicative of cooperativity of the H-bonds in species
M and conversely for positive values of these quantities and anticooperativity.
Fig. 7 plots the values of Δ
EABint/coop(
M) for the O⋯H bonds and the covalent interactions throughout the pseudo-bicyclic structure of the compounds examined in this investigation. We observe that the value of Δ
EO⋯Hint/coop(
M) corresponds to the cooperative (Δ
EO⋯Hint/coop(
2) < 0) or anticooperative (Δ
EO⋯Hnet/coop(
3) > 0 and Δ
EO⋯Hcoop/int(
4) > 0) effects discussed above. In correspondence with previous descriptions of other RAHBs
40 in which
VABcl has a preponderant role in this interaction, the classical contribution is the dominant component of Δ
Eint/coop(
M). Apart from compound
4, whose graph in
Fig. 7 strongly indicates anticooperativity of the H-bonds in this system (most of the shown bars are above zero), there is an alternating pattern of the data in
Fig. 7 concerning systems
2 and
3. Nonetheless, most of the bonds in the pseudo-bicyclic moiety of system
2 indicates cooperativity as shown in
Fig. 8-
2. The opposite occurs in systems
3 and
4 (
Fig. 8-
3 and
8-
4). In other words, the π cooperative effects of the HB analyzed in this work are reflected in a more noticeable strengthening
§ of the conjugated system governed by the classical interaction as shown in
Table 5. A less fortified structure is related to the anticooperativity of RAHBs in systems
3 and
4, with larger anticooperative effects for the former molecule as mentioned above. As might be expected, the other contributions to Δ
Ecoop(
M),
i.e.,
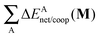
and

, modulate these cooperative (molecule
2) and anticooperative (systems
3 and
4) effects described above (
Table 6).
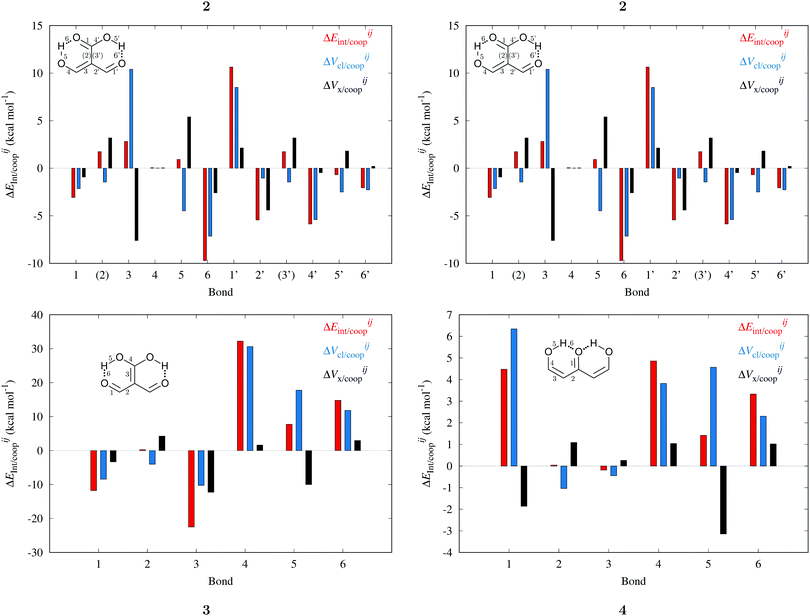 |
| | Fig. 7 Values of ΔEint/coop for the bonds comprising the pseudobicyclic systems of molecules 2, 3 and 4. Note the considerably larger scale for compound 3. | |
 |
| | Fig. 8 Cooperative (red) and anticooperative (blue) components of ΔEA–Bint/coop for contiguous atoms between the pseudo-bicyclic moieties for systems 2, 3 and 4. | |
Table 5 Interaction energy components of ΔEABint/coop (eqn (21)) across the hydrogen and covalent bonds forming the pseudo-bicyclic moiety of compounds 2, 3 and 4. The data are reported in kcal mol−1
| System |
|
|
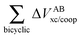
|
|
2
|
−10.70 |
−7.48 |
−3.22 |
|
3
|
64.66 |
85.98 |
−21.31 |
|
4
|
26.39 |
27.77 |
−1.38 |
Table 6 Partition of ΔEcoop(M) (M = 2, 3, 4) as established in eqn (21) in its interacting quantum atoms contributions, 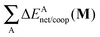 and
and 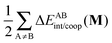 . The data are reported in kcal mol−1
. The data are reported in kcal mol−1
| System |
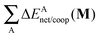
|

|
ΔEcoop(M) |
|
2
|
−13.84 |
12.10 |
−1.75 |
|
3
|
−58.47 |
63.47 |
5.00 |
|
4
|
−8.68 |
8.96 |
0.29 |
The non-additive effects of the RAHBs considered in this study can also be analysed in terms of the sum of the intra and intermolecular exchange–correlation contributions to the total energy of the system,
| | 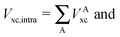 | (22) |
| | 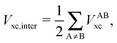 | (23) |
with a similar contribution to RAHB cooperativity or anticooperativity as in
eqn (21),
| | | ΔVxc,X/coop(N) = ΔVxc,X(N) − ΔV′xc,X(N), | (24) |
wherein X = intra or inter;
N =
2,
3, or
4 and the unprimed values refer to
processes (8)–(11) and the primed quantities to
eqn (12)–(15). We examine Δ
Vxc,intra/coop and Δ
Vxc,inter/coop because the formation of an RAHB is accompanied by a reduction of the magnitude of
Vxc,inter, at the expense of an increase of |
Vxc,intra|.
40Table 8 shows that the components of
Vxc,intra and
Vxc,inter to Δ
Ecoop(
N) have a similar role in the previous description of RAHBs,
i.e., the H-bonds in
2 rise the magnitude of
Vxc,intra and diminish that of
Vxc,inter. The opposite occurs in molecules
3 and
4.
The changes in the quantities Vxc,intra and Vxc,inter in the formation of an RAHB are mirrored by those of the localised and delocalised electrons. Table 7 shows that the formation of each of the examined RAHBs conduces to a localisation of the electrons in the system. We can also compare the diminution of the delocalisation in a similar way to eqn (21) and (24),
| | 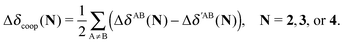 | (25) |
in which the primed and unprimed quantities have the same meaning as that in
eqn (24). We observe in
Table 8 that the second H-bond in
2 leads to a larger diminution of delocalisation (Δ
δcoop(
2) < 0) in contrast to
3 and
4 (Δ
δcoop(
3) > 0 and Δ
δcoop(
4) > 0). In other words, the results of
Table 8 indicate that the cooperative/anticooperative RAHB effects studied herein reinforce/debilitate the electron localisation associated with this type of interaction.
40 These changes in the LIs and DIs correspond to those of the intra and interatomic changes in the components of the exchange–correlation to Δ
Eform of a given resonance assisted hydrogen bond. In other words, the RAHB cooperative and anticooperative effects considered in this investigation can be inferred from the mesomeric structures of
Fig. 5. RAHB non-additivity follows from deviations of electron localisation in the investigated systems as compared with an isolated resonance assisted hydrogen bond, which in turn modify the values of
Vxc,intra,
Vxc,inter and above all
Vcl which ultimately affects the strengthening of the pseudo-bicyclic structure associated with these interactions.
Table 7 Changes in the sum of the localisation and delocalisation indices after the formation of the resonance assisted hydrogen bond under investigation. The unprimed quantities refer to processes(8)–(11) and the primed values to eqn (12)–(15)
| H-bond |
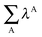
|
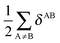
|
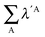
|
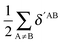
|
|
2a
|
0.0575 |
−0.0592 |
0.0314 |
−0.0319 |
|
2e
|
0.1049 |
−0.1046 |
0.0788 |
−0.0773 |
|
3
|
0.0453 |
−0.0448 |
0.1440 |
−0.1424 |
|
4
|
0.0902 |
−0.0895 |
0.0996 |
−0.1000 |
Table 8 Contributions of the intra and interatomic exchange components (in kcal mol−1) to ΔEcoop(N) with N = 2, 3, or 4 (eqn (24)). The values of Δδcoop (expression (25)) are reported as well
| System |
ΔVxc,intra/coop |
ΔVxc,inter/coop |
Δδcoop |
|
2
|
−1.51 |
0.91 |
−0.03 |
|
3
|
34.89 |
−30.00 |
0.10 |
|
4
|
1.26 |
−1.70 |
0.01 |
Finally, we discuss the changes in the electron delocalisation throughout the pseudo-bicyclic structure of compounds 2, 3 and 4. The changes in the delocalisation indices in the conjugated system 1 due to the formation of the RAHB indicate that the double bonds involving one or two carbon atoms reduce their number of shared electrons, whereas the single bonds increase their associated DIs.40 In other words, the delocalised electrons become more evenly distributed across the conjugated π system. This occurs despite the fact that this increase in the uniformity in the number of delocalised electrons is accompanied by an increment of the IQA additive energy forming the hydrocarbon chain as revealed in Table 3. It is noteworthy that the δ(O–H) index is substantially diminished due to the generation of the RAHB. We considered the effect of the generation of one and two hydrogen bonds on the delocalisation indices throughout the conjugated system of molecules 2–4 (Fig. 11). Overall, the delocalisation indices computed when only one RAHB is formed are intermediate between (i) the values calculated if the two hydrogen bonds are present in the molecule and (ii) the corresponding data observed when the two RAHBs are dissociated. Again, the formation of RAHBs, regardless of their cooperative or anticooperative nature, makes the number of delocalised electrons across the system more uniform.
Fig. 9 and 10 leads to similar conclusions to those based on delocalisation indices. When the RAHBs are formed, double bonds A![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) B diminish their corresponding magnitude of |EA
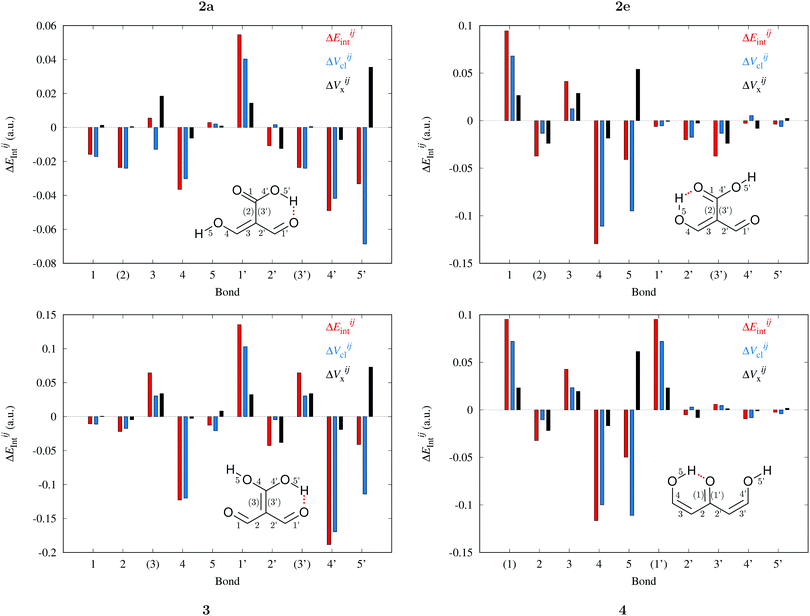
B diminish their corresponding magnitude of |EA![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) Bint|, whereas single bonds exhibit the opposite behaviour as revealed in the alternating patterns of the plots in Fig. 9 and 10. Generally, the changes in |EABint| for bonds which involve an oxygen atom are principally driven by VABcl while VABxc becomes more important for the bonds entailing only carbon atoms. The changes in the classical component are more important than those in the exchange component in accordance with a previous description of RAHBs based on quantum chemical topology.40
Bint|, whereas single bonds exhibit the opposite behaviour as revealed in the alternating patterns of the plots in Fig. 9 and 10. Generally, the changes in |EABint| for bonds which involve an oxygen atom are principally driven by VABcl while VABxc becomes more important for the bonds entailing only carbon atoms. The changes in the classical component are more important than those in the exchange component in accordance with a previous description of RAHBs based on quantum chemical topology.40
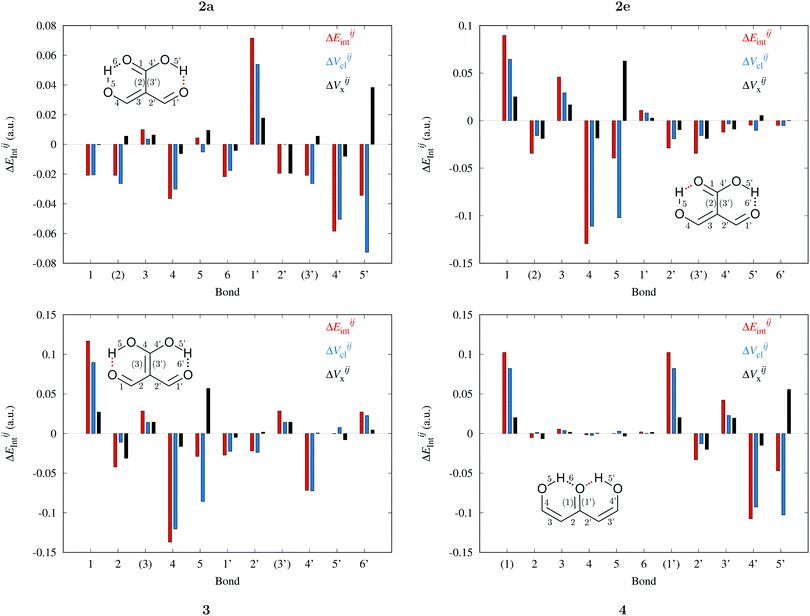 |
| | Fig. 9 Components of the interaction energies throughout the bicyclic system of the systems of interest in accordance with the expression 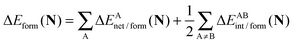 in eqn (8)–(11) in the body of the manuscript. The classical and exchange contributions are shown as well. in eqn (8)–(11) in the body of the manuscript. The classical and exchange contributions are shown as well. | |
 |
| | Fig. 10 Contributions of the interaction energies across the bicyclic system of the molecules of interest in accordance with the expression 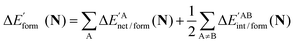 in expressions (12)–(15) in the body of the manuscript. The classical and exchange contributions are displayed as well. in expressions (12)–(15) in the body of the manuscript. The classical and exchange contributions are displayed as well. | |
 |
| | Fig. 11 Delocalisation indices throughout the conjugated π system in the open structure and after the formation of one and two hydrogen bonds in systems 2, 3 and 4 of Fig. 2. We present in red the values of δ(i,j) that increase with the formation of the RAHB while those that are diminished in the same process are reported in blue. Atomic units are used throughout. | |
5 Concluding remarks
We have presented an analysis of resonance assisted hydrogen bond cooperative and anticooperative effects in β-enolones which result from the condensation of two molecules of malondialdehyde. This investigation includes a comparison of the RAHB formation energies in the absence and presence of the accompanying H-bond in the examined molecules. We suggest a measure of H-bond cooperativity or anticooperativity as the difference between these formation energies. The mesomeric structures and the IQA EO⋯Hint interaction energies are in agreement with the observed RAHB cooperative or anticooperative effects. Concerning the interplay between the examined H-bonds and the surrounding π system, the formation of an RAHB is accompanied by important energetic changes in the encircling hydrocarbon chain. Consistently, the established cooperative/anticooperative effects herein are related to a greater/lesser strengthening of the bicyclic structure of the analyzed compounds. This effect is mainly governed by the IQA classical contribution, although the RAHB cooperativity and anticooperativity are also reflected in the QTAIM delocalisation indices and the intra and intermolecular contributions of the exchange–correlation component of the corresponding formation energies. We hope that the results presented herein provide useful insights into the relatively unexplored cooperative and anticooperative effects in resonance assisted hydrogen bonds.
Acknowledgements
The authors acknowledge financial support from DGAPA/UNAM (project PAPIIT IN209715), CONACyT/México (grant 253776, and scholarships 308773 and 381482) and the Spanish government (grant CTQ-2015-65790-P) as well as computer time from DGTIC/UNAM (project SC16-1-IG-99). T. R.-R. is also grateful to David Vázquez Cuevas, Gladys Cortés Romero and Magdalena Aguilar Araiza for technical support.
References
- W. M. Latimer and W. H. Rodebush, J. Am. Chem. Soc., 1920, 42, 1419–1433 CrossRef CAS.
-
G. Gilli and P. Gilli, The Nature of the Hydrogen Bond: Outline of a Comprehensive Hydrogen Bond Theory, Oxford University Press, USA, 2009 Search PubMed.
- T. Steiner, Angew. Chem., Int. Ed., 2002, 41, 48–76 CrossRef CAS.
- C. Seife,
et al.
, Science, 2005, 309, 78–102 CrossRef CAS PubMed.
- J. Trylska, P. Grochowski and J. McCammon, Protein Sci., 2004, 13, 513–528 CrossRef CAS PubMed.
-
A. J. Stone, The Theory of intermolecular forces, Oxford University Press, New York, 1997 Search PubMed.
-
S. Scheiner, Hydrogen Bonding: A Theoretical Perspective, Oxford University Press, USA, 1997 Search PubMed.
- G. Gilli, F. Bellucci, V. Ferretti and V. Bertolasi, J. Am. Chem. Soc., 1989, 111, 1023–1028 CrossRef CAS.
- I. Alkorta, J. Elguero, O. Mó, M. Yañez and J. E. Del Bene, Chem. Phys. Lett., 2005, 411, 411–415 CrossRef CAS.
- F. Fuster and S. J. Grabowski, J. Phys. Chem. A, 2011, 115, 10078–10086 CrossRef CAS PubMed.
- T. Cristina, G. Sánchez-Sanz, I. Alkorta, J. Elguero, O. Mó and M. Yáñez, J. Mol. Struct., 2013, 1048, 138–151 CrossRef.
- J. Chin, C. K. Dong, H. J. Kim, F. B. Panosyan and M. K. Kwan, Org. Lett., 2004, 6, 2591–2593 CrossRef CAS PubMed.
- M. Rospenk, P. Majewska, B. Czarnik-Matusewicz and L. Sobczyk, Chem. Phys., 2006, 326, 458–464 CrossRef CAS.
- C. Fonseca Guerra, F. M. Bickelhaupt, J. G. Snijders and E. J. Baerends, Chem. – Eur. J., 1999, 5, 3581–3594 CrossRef.
- C. F. Guerra, F. M. Bickelhaupt, J. G. Snijders and E. J. Baerends, J. Am. Chem. Soc., 2000, 122, 4117–4128 CrossRef CAS.
- Y. Mo, J. Mol. Model., 2006, 12, 665–672 CrossRef CAS PubMed.
- V. Bertolasi, L. Pretto, G. Gilli and P. Gilli, Acta Crystallogr., Sect. B: Struct. Sci., 2006, 62, 850–862 Search PubMed.
- V. Bertolasi, P. Gilli, V. Ferretti and G. Gilli, J. Am. Chem. Soc., 1991, 113, 4917–4925 CrossRef CAS.
- P. Gilli, V. Bertolasi, L. Pretto, A. Lycka and G. Gilli, J. Am. Chem. Soc., 2002, 124, 13554–13567 CrossRef CAS PubMed.
- R. Otero, M. Schöck, L. M. Molina, E. Lœgsgaard, I. Stensgaard, B. Hammer and F. Besenbacher, Angew. Chem., Int. Ed., 2005, 44, 2270–2275 CrossRef CAS PubMed.
- J. M. Guevara-Vela, R. Chávez-Calvillo, M. García-Revilla, J. Hernández-Trujillo, O. Christiansen, E. Francisco, A. Martín Pendás and T. Rocha-Rinza, Chem. – Eur. J., 2013, 19, 14304–14315 CrossRef CAS PubMed.
- J. M. Guevara-Vela, E. Romero-Montalvo, V. A. Mora Gomez, R. Chavez-Calvillo, M. Garcia-Revilla, E. Francisco, A. Martín Pendás and T. Rocha-Rinza, Phys. Chem. Chem. Phys., 2016, 19557–19566 RSC.
- D. Tiana, E. Francisco, M. A. Blanco, P. Macchi, A. Sironi and A. Martn Pendás, Phys. Chem. Chem. Phys., 2011, 13, 5068–5077 RSC.
- D. Ferro-Costas, E. Francisco, A. Martín Pendás and R. A. Mosquera, Phys. Chem. Chem. Phys., 2015, 17, 26059–26071 RSC.
- D. Ferro-Costas, A. Martín Pendás, L. González, R. A. Mosquera and L. González, Phys. Chem. Chem. Phys., 2014, 16, 9249–9258 RSC.
-
R. F. W. Bader, Atoms in molecules: A Quantum Theory, Oxford University Press, 1990 Search PubMed.
-
T. Helgaker, P. Jørgensen and J. Olsen, Molecular Electronic Structure theory, John Wiley & Sons, Sussex, England, 2004 Search PubMed.
- X. Fradera, M. A. Austen and R. F. W. Bader, J. Phys. Chem. A, 1999, 103, 304–314 CrossRef CAS.
- L. Albrecht, R. J. Boyd, O. Mó and M. Yáñez, Phys. Chem. Chem. Phys., 2012, 14, 14540 RSC.
- S. J. Grabowski, J. Phys. Org. Chem., 2003, 16, 797–802 CrossRef CAS.
- R. W. Gora, S. J. Grabowski and J. Leszczynski, J. Phys. Chem. A, 2005, 109, 6397–6405 CrossRef CAS PubMed.
- M. A. Blanco, A. Martn Pendás and E. Francisco, J. Chem. Theory Comput., 2005, 1, 1096–1109 CrossRef CAS PubMed.
- E. Francisco, A. Martín Pendás and M. Blanco, J. Chem. Theory Comput., 2006, 2, 90–102 CrossRef CAS PubMed.
- C. Møller and M. S. Plesset, Phys. Rev., 1934, 46, 618–622 CrossRef.
- S. Kossmann and F. Neese, J. Chem. Theory Comput., 2010, 6, 2325–2338 CrossRef CAS PubMed.
- T. H. Dunning, Jr., J. Chem. Phys., 1989, 90, 1007 CrossRef.
- F. Neese, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2012, 2, 73–78 CrossRef CAS.
- C. Pérez, M. T. Muckle, D. P. Zaleski, N. A. Seifert, B. Temelso, G. C. Shields, Z. Kisiel and B. H. Pate, Science, 2012, 336, 897–901 CrossRef PubMed.
- M. W. Schmidt, K. K. Baldridge, J. A. Boatz, S. T. Elbert, M. S. Gordon, J. H. Jensen, S. Koseki, N. Matsunaga, K. A. Nguyen, S. Su, T. L. Windus, M. Dupuis and J. A. Montgomery, J. Comput. Chem., 1993, 14, 1347–1363 CrossRef CAS.
- J. M. Guevara-Vela, E. Romero-Montalvo, A. Costales, A. Martín Pendás and T. Rocha-Rinza, Phys. Chem. Chem. Phys. 10.1039/C6CP04386K.
- F. J. Holguín-Gallego, R. Chávez-Calvillo, M. García-Revilla, E. Francisco, A. Martín Pendás and T. Rocha-Rinza, J. Comput. Chem., 2016, 37, 1753–1765 CrossRef PubMed.
-
T. A. Keith, AIMAll (Version 14.11.23), TK Gristmill Software, Overland Park KS, USA, 2012, aim.tkgristmill.com Search PubMed.
-
A. Martn Pendás and E. Francisco, Promolden. A QTAIM/IQA code, unpublished.
-
T. Williams and C. Kelley, Gnuplot 4.6: An Interactive Plotting Program, 2010, http://gnuplot.sourceforge.net/ Search PubMed.
- Avogadro: an open-source molecular builder and visualization tool. Version 1.XX. http://avogadro.openmolecules.net/.
- M. D. Hanwell, D. E. Curtis, D. C. Lonie, T. Vandermeersch, E. Zurek and G. R. Hutchison, J. Cheminf., 2012, 4, 17 CAS.
- E. Espinosa, E. Molins and C. Lecomte, Chem. Phys. Lett., 1998, 285, 170–173 CrossRef CAS.
- L. Gutierrez-Arzaluz, F. Cortes-Guzman, T. Rocha-Rinza and J. Peon, Phys. Chem. Chem. Phys., 2015, 17, 31608–31612 RSC.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c6cp04877c |
‡ We recall at this point that 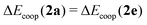 as defined in eqn (16) and (17). as defined in eqn (16) and (17). |
| § The formation of one or two HBs in molecules 2, 3 and 4 fortifies the bicyclic structures of these systems with respect to the system with no H-bonds as shown in Fig. 9, 10 and Table 4. Such strengthening is modified by the presence of one or two HBs in accordance with the hydrogen bond π cooperative or anticooperative effects discussed in the paper. |
|
| This journal is © the Owner Societies 2017 |
Click here to see how this site uses Cookies. View our privacy policy here.  *a
*a
![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) CH–OH. Resonance assisted hydrogen bonds have been of considerable interest in physical chemistry, a situation which has led to numerous theoretical9–11 and experimental12,13 reports concerned with the nature of these HBs. In addition, the RAHB concept has been used to better understand intermolecular interactions in relevant systems in chemistry and biology, like those present in DNA14–16 and proteins.3
CH–OH. Resonance assisted hydrogen bonds have been of considerable interest in physical chemistry, a situation which has led to numerous theoretical9–11 and experimental12,13 reports concerned with the nature of these HBs. In addition, the RAHB concept has been used to better understand intermolecular interactions in relevant systems in chemistry and biology, like those present in DNA14–16 and proteins.3
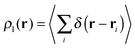 .27 The QTAIM basins, denoted generally as Ω, are proper open subsystems for which one can compute the expectation values of quantum mechanical operators such as the Hamiltonian, the kinetic energy, and the number operators.26 The QTAIM also defines localisation and delocalisation indices (LI and DI respectively) in terms of the integration of the Fermi and Coulomb correlation holes over the QTAIM atoms.28 The LI and DI descriptors are useful to examine electron sharing, i.e. covalency, in different chemical bonding scenarios. The sum of the atomic properties, 〈O〉Ω, throughout the whole of the system, yields the expectation value of the corresponding observable for the complete molecule or molecular cluster under consideration. Since the QTAIM is completely built on ρ1(r), it can be used to address on equal footing a wide variety of chemical compounds and processes, such as metal–ligand bonding,23 interactions within a molecular cluster,29 π-electron delocalised30 and H-bonded systems,11,31 being the two last-mentioned examples of particular interest for this work.
.27 The QTAIM basins, denoted generally as Ω, are proper open subsystems for which one can compute the expectation values of quantum mechanical operators such as the Hamiltonian, the kinetic energy, and the number operators.26 The QTAIM also defines localisation and delocalisation indices (LI and DI respectively) in terms of the integration of the Fermi and Coulomb correlation holes over the QTAIM atoms.28 The LI and DI descriptors are useful to examine electron sharing, i.e. covalency, in different chemical bonding scenarios. The sum of the atomic properties, 〈O〉Ω, throughout the whole of the system, yields the expectation value of the corresponding observable for the complete molecule or molecular cluster under consideration. Since the QTAIM is completely built on ρ1(r), it can be used to address on equal footing a wide variety of chemical compounds and processes, such as metal–ligand bonding,23 interactions within a molecular cluster,29 π-electron delocalised30 and H-bonded systems,11,31 being the two last-mentioned examples of particular interest for this work.
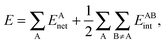
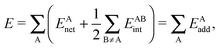











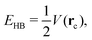
![[capital G, script]](https://www.rsc.org/images/entities/char_e112.gif) and
and ![[script letter H]](https://www.rsc.org/images/entities/char_e142.gif) , we can consider directly all pairwise values of EA⋯Bint wherein atom A belongs to monomer
, we can consider directly all pairwise values of EA⋯Bint wherein atom A belongs to monomer ![[capital G, script]](https://www.rsc.org/images/entities/char_e112.gif) and B to
and B to ![[script letter H]](https://www.rsc.org/images/entities/char_e142.gif) . This division is not straightforward in intramolecular interactions, but such an issue is elegantly addressed by IQA additive energies (expression (4)), to consider the effect of the hydrocarbon chain in the RAHBs under examination as reported in Table 3. The data show that the formation of the RAHB involves a stabilization of the atoms participating directly in the H-bond, but in addition, the energy of the rest of the system is substantially increased. This indicates that the hydrocarbon chain has an important effect in the RAHB formation energy and its different components. Indeed, the energetic change of the π system modulates the magnitude of ΔERAHBform. This complicates the quantitative establishment of the magnitudes of H-bond formation energies in these molecules by the consideration of only the O⋯H–O moiety as done in formula (20). Conversely, the hydrocarbon chain suffers important modifications on account of the RAHB in agreement with the notion that a HB may substantially affect the energy of a π-system.48 More specifically to the non-additive effects previously described, the presence of either of RAHBs 2a or 2e is accompanied by larger magnitudes for ΔEO–H⋯Oadd and ΔE⋯CH
. This division is not straightforward in intramolecular interactions, but such an issue is elegantly addressed by IQA additive energies (expression (4)), to consider the effect of the hydrocarbon chain in the RAHBs under examination as reported in Table 3. The data show that the formation of the RAHB involves a stabilization of the atoms participating directly in the H-bond, but in addition, the energy of the rest of the system is substantially increased. This indicates that the hydrocarbon chain has an important effect in the RAHB formation energy and its different components. Indeed, the energetic change of the π system modulates the magnitude of ΔERAHBform. This complicates the quantitative establishment of the magnitudes of H-bond formation energies in these molecules by the consideration of only the O⋯H–O moiety as done in formula (20). Conversely, the hydrocarbon chain suffers important modifications on account of the RAHB in agreement with the notion that a HB may substantially affect the energy of a π-system.48 More specifically to the non-additive effects previously described, the presence of either of RAHBs 2a or 2e is accompanied by larger magnitudes for ΔEO–H⋯Oadd and ΔE⋯CH![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) CH–C⋯add for the formation of the other H-bond. The effect of the former being dominant leading thereby to the hydrogen bond π cooperativity observed in molecule 2. A similar analysis of molecules 3 and 4 shows that the presence of a previous hydrogen bond reduces the stability of the O–H⋯O system in consistency with the RAHB π anticooperativity previously described for these molecules.
CH–C⋯add for the formation of the other H-bond. The effect of the former being dominant leading thereby to the hydrogen bond π cooperativity observed in molecule 2. A similar analysis of molecules 3 and 4 shows that the presence of a previous hydrogen bond reduces the stability of the O–H⋯O system in consistency with the RAHB π anticooperativity previously described for these molecules.![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) CH–C⋯add
CH–C⋯add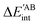 (expressions (12)–(15)) across the pseudo-bicyclic structure of the analyzed compounds in the formation of the H-bonds 2a, 2e, 3 and 4. The data are reported in kcal mol−1
(expressions (12)–(15)) across the pseudo-bicyclic structure of the analyzed compounds in the formation of the H-bonds 2a, 2e, 3 and 4. The data are reported in kcal mol−1

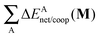 and
and  , modulate these cooperative (molecule 2) and anticooperative (systems 3 and 4) effects described above (Table 6).
, modulate these cooperative (molecule 2) and anticooperative (systems 3 and 4) effects described above (Table 6).


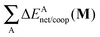 and
and 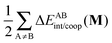 . The data are reported in kcal mol−1
. The data are reported in kcal mol−1
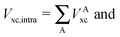
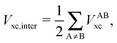
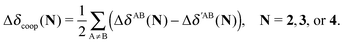
![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) B diminish their corresponding magnitude of |EA
B diminish their corresponding magnitude of |EA![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) Bint|, whereas single bonds exhibit the opposite behaviour as revealed in the alternating patterns of the plots in Fig. 9 and 10. Generally, the changes in |EABint| for bonds which involve an oxygen atom are principally driven by VABcl while VABxc becomes more important for the bonds entailing only carbon atoms. The changes in the classical component are more important than those in the exchange component in accordance with a previous description of RAHBs based on quantum chemical topology.40
Bint|, whereas single bonds exhibit the opposite behaviour as revealed in the alternating patterns of the plots in Fig. 9 and 10. Generally, the changes in |EABint| for bonds which involve an oxygen atom are principally driven by VABcl while VABxc becomes more important for the bonds entailing only carbon atoms. The changes in the classical component are more important than those in the exchange component in accordance with a previous description of RAHBs based on quantum chemical topology.40
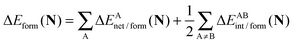 in eqn (8)–(11) in the body of the manuscript. The classical and exchange contributions are shown as well.
in eqn (8)–(11) in the body of the manuscript. The classical and exchange contributions are shown as well.
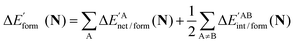 in expressions (12)–(15) in the body of the manuscript. The classical and exchange contributions are displayed as well.
in expressions (12)–(15) in the body of the manuscript. The classical and exchange contributions are displayed as well.
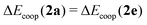 as defined in eqn (16) and (17).
as defined in eqn (16) and (17).