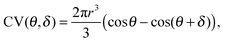An atomistic view on carbocyanine photophysics in the realm of RNA†
Received
18th June 2016
, Accepted 25th August 2016
First published on 26th August 2016
Abstract
Carbocyanine dyes have a long-standing tradition in fluorescence imaging and spectroscopy, due to their photostability and large spectral separation between individual dye species. Herein, we explore the versatility of cyanine dyes to probe the dynamics of nucleic acids and we report on the interrelation of fluorophores, RNA, and metal ions, namely K+ and Mg2+. Photophysical parameters including the fluorescence lifetime, quantum yield and dynamic anisotropy are monitored as a function of the nucleic acid composition, conformation, and metal ion abundance. Occasional excursions to a non-fluorescent cis-state hint at the remarkable sensitivity of carbocyanines to their local environment. Comparison of time-correlated single photon experiments with all-atom molecular dynamics simulations demonstrate that the propensity of photoisomerization is dictated by sterical constraints imposed on the fluorophore. Structural features in the vicinity of the dye play a crucial role in RNA recognition and have far-reaching implications on the mobility of the fluorescent probe. An atomic level description of the mutual interactions will ultimately benefit the quantitative interpretation of single-molecule FRET measurements on large RNA systems.
Introduction
Fluorescence microscopy and single-molecule detection have revolutionized our understanding of the structure and dynamics of biomacromolecules.1–7 At the heart of all fluorescence technologies are molecules whose chemical properties allow the absorption and subsequent reemission of photons on a timescale from a few hundred picoseconds to several dozens of nanoseconds. Nowadays, a variety of organic dyes are employed as probes for super-resolution imaging and single-molecule spectroscopy in combination with Förster resonance energy transfer (FRET).8,9 Amongst the most thoroughly investigated families of fluorescent dyes are carbocyanines.10–12 Their molecular fingerprint is a polymethine chain linking two heteroaromatic moieties. In their sulfonated form (denoted as sCy), two negative charges, one on each ring, compensate for the inherent hydrophobic nature of the chromogenic scaffold. The long-lasting popularity of cyanine dyes is not only due to their photophysical properties but also because of their availability in various spectral and functional forms.13 Carbocyanines indeed combine many characteristics of an ideal fluorophore for smFRET, including a relatively high extinction coefficient, comparable quantum yields of donor (sCy3) and acceptor (sCy5) dye as well as a high photostability when used in combination with an oxygen scavenger system (OSS) and protective agents such as 1,3,5,7-cyclooctatetraene (COT), 4-nitrobenzylalcohol (NBA) or Trolox.13–15 The large spectral separation between different dye species (∼100 nm) reduces cross-talk and direct laser excitation, while the donor emission and acceptor absorption profile still overlap sufficiently to allow for efficient energy transfer. A key feature of most carbocyanines is their propensity to photoisomerize from an all-trans to a dark cis-state depending on the local environment.12,16,17 In spite of the modest quantum efficiency, carbocyanines are well suited to study the dynamics of nucleic acids on the single-molecule level by total internal reflection fluorescence (TIRF) microscopy since they are, in contrast to many rhodamine derivatives, hardly quenched by any of the nucleobases.18
Cyanine dyes offer a wide range of labeling strategies depending on the nature of the biomolecule.19–21 Terminal labeling of nucleic acids is commonly achieved via an amino-linker and an N-hydroxysuccimidyl (NHS) functionality on the fluorophore (Fig. 1). The former governs the distance between the dye and the molecule of interest and therefore makes the accessible volume (AV) of the fluorescent probe expand or contract. The AV defines the conformational space explored by the fluorophore when linked to a macromolecule.22,23 Choosing a reasonably sized linker (C6) between the dye and the molecule of interest is the prerequisite to assume an isotropic rotation of the fluorescent probe. Mutual interactions between dyes and biomolecules on the other hand inevitably alter the steric and electronic properties of the fluorophore.12 Changes are reflected in the fluorescence lifetime, the quantum yield or the fluorescence anisotropy. All these parameters are readily accessible by time-resolved or steady-state measurements and report on the physicochemical characteristics of the fluorophore within its anisotropic, macromolecular environment.24 The photophysics of carbocyanines in the context of DNA are well established,12,25–28 however, our knowledge about the interaction propensity with RNA on an atomic level remains elusive. Recent work has demonstrated the applicability of protein induced fluorescence enhancement (PIFE) as a spectroscopic ruler to close the gap between the distance regimes covered by photoinduced electron transfer (PET, <2 nm) and FRET (3–10 nm).29–31 The diversity of secondary and tertiary structure adopted by single-stranded RNA suggests that a similar framework may be devised for nucleic acids and RNA in particular. In analogy to PIFE we will refer to the effects described thereafter as NAIFE (short for nucleic acid-induced fluorescence enhancement) and RIFE (RNA-induced fluorescence enhancement) as a special case thereof.
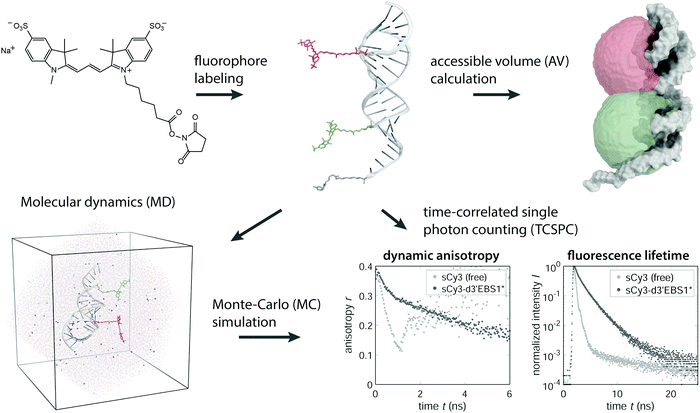 |
| | Fig. 1 Conceptual overview of the methods used to study carbocyanine dyes in an RNA microenvironment. NHS functionalized cyanine fluorophores are covalently coupled to an RNA to form a FRET pair. The accessible volume of the dyes is modeled by a geometrical search algorithm.22,23 The motion of the fluorophores can be monitored by molecular dynamics (MD) after solvating the construct in a triclinic water box. By tracking the dipole moment oriented along the polymethine chain, one can simulate the dynamic anisotropy, which is experimentally accessible via TCSPC. | |
Herein, we examine various ribonucleic frameworks, beginning with the building blocks of RNA and ending with a large regulatory RNA of over 275 nucleotides. Moreover, we elaborate on how the abundance of mono- and divalent metal ions affects the photophysics of the labeled nucleic acids. Impacts on the fluorescence lifetime and rotational diffusion are discussed in terms of the isomerization potential of carbocyanines, which has been recognized as the major cause for the short-lived excited state and low quantum efficiency of the free Cy3 species.12,32 Experimental data from time-correlated single photon counting (TCSPC) experiments are complemented by molecular dynamics (MD) simulations casting an atomistic view on specific RNA–dye interactions (Fig. 1).
Material and methods
Sample preparation
All chemicals for buffer preparation and transcription solutions were puriss p. a. (Merck KGaA). Oligonucleotides fluorescently labeled with sulfonated carbocyanines dyes (sCy3 and sCy5) were obtained in HPLC-grade in both RNA and DNA form (IBA lifescience). The btuB riboswitch was transcribed in vitro as described previously,33 purified by 10% (w/v) denaturing PAGE and recovered via electroelution. The RNA was thermally denatured (70 °C, 5 min) in the presence of fluorescently labeled DNA oligonucleotides and refolded under 50 mM KCl and 3 mM MgCl2 with incubation at 37 °C and room temperature for 30 min each. Unless stated otherwise, all samples including nucleoside 5′-triphosphates, oligonucleotides, and transcribed RNA were buffered in 34 mM Tris-HCl and 66 mM HEPES (pH 7.5) with an ionic background of 50 mM KCl and 3 mM MgCl2.
Lifetime, quantum yields, and dynamic anisotropy
TCSPC experiments employed a picosecond laser source (DD-510L & DD-635L, Horiba Jobin Yvon GmbH) at a repetition rate of 20 MHz in combination with a double-grating emission monochromator and a PPD-900 detection module (Fluorolog3 FL3-222, Horiba). Samples were kept at 25 °C by means of a Varian Cary PCB-150 Peltier water bath (Agilent). Lifetimes were collected under magic angle conditions with a channel width of 27 ps and retrieved from a series of weighted exponentials by iterative reconvolution with the instrument response function (IRF) using a custom-written MATLAB routine (R2015b)| | | I(t) = IRF * ∑aiτi with ∑ai = 1. | (1) |
Quantum yields were determined relative to aqueous solutions of rhodamine 6G (0.95 at 25 °C34) or Alexa 647 (0.32 at 22 °C35). The time-resolved anisotropy was computed by sequentially recording the parallel IVV and perpendicular IVH polarization components with respect to the field vector of the exciting light pulse| | 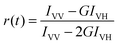 | (2) |
where the G-factor is defined as G = IHV/IHH.33
The dynamic anisotropy of the free fluorophores is modeled in terms of a single exponential decay, whereas the dye-labeled RNA and DNA molecules are best described by two components, a hindered, local rotation
| | | rlocal(t) = (r0 − r∞)e−t/τr,local + r∞ | (3) |
and a global tumbling of the dye along with the biomolecule, yielding
| | | rglobal(t) = rlocale−t/τr,global | (4) |
where
r0 is the fundamental anisotropy,
r∞ represents the value to which the local anisotropy decays and
τr is the correlation time of the local or global component.
36,37
Molecular dynamics and Monte Carlo simulations
The structures of d3′EBS1*˙IBS1* (RNA/RNA) and d3′EBS1*˙dIBS1* (RNA/DNA) were previously solved by NMR38,39 while the other RNAs (19/44 nt) were constructed using RNAComposer40 on the basis of a secondary structure prediction with Mfold.38 Sulfonated carbocyanine fluorophores (sCy3/sCy5) were attached terminally via a C6 amino linker using PyMOL (Schrödinger LLC). On the d3′EBS1* hairpin we introduced a canonical 3′-tetraU overhang, which has been used for immobilization purposes in single-molecule TIRF experiments.41,42 The nucleic acids were solvated in explicit water (TIP3P and TIP4P/200543) and neutralized with K+ ions. Force field parameters for RNA and DNA were taken from amber99sb44 while dye parameters originate from the AMBER-DYE package.45 The Antechamber46 interface acpype47 was used to generate topologies for the nucleotide 5′-triphosphates. All constructs were energy-minimized in GROMACS 5.148 by a steepest descent algorithm. RNA and solvent molecules (including K+ ions) were separately coupled to an external heating bath at 298 K by harnessing the V-rescaling algorithm with a relaxation time of 0.1 ps. The system was further connected to a Parinello–Rahman barostat at 1 bar with a time constant of 2 ps. Bonds were constrained by applying the LINCS algorithm,49 while non-bonded pair forces were calculated using the Verlet scheme50 with a cut-off of 1 nm for both van der Waals and Coulomb interactions. Long-range electrostatic forces were treated with the smooth particle-mesh Ewald method51 (SPME) by setting a Fourier grid spacing of 0.16 nm with cubic interpolation. After equilibration (NVT and NPT ensemble, 2 × 5 ns) the position restraints were released and the system was propagated for 50 ns using a leap from integration scheme with a time step of 2 fs. In all runs atom coordinates were printed out every picosecond. Individual MD trajectories were concatenated and served as a framework for the rotational diffusion of the fluorophore. In a Monte Carlo (MC) approach we sampled time points of laser pulses and photon arrival times by using the experimentally determined lifetime histograms as a probability distribution for photon detection. The angle θ(t − t0) between the excitation and emission dipole moment at time points t0 and t respectively represents as a direct measure for the polarization of the incoming photon (ESI,† Methods). Independent binning of the photon arrival times for both polarization directions allowed the calculation of the dynamic anisotropy according to eqn (1). A prefactor of 2/5 accounted for the discrepancy between a single fluorophore oriented along the z-axis and an ensemble population as in the experiment (=photoselection).
Results and discussion
Stacking interaction between NTPs and carbocyanines
Nucleoside 5′-triphosphates (NTPs) were titrated individually against at diluted solution of freely diffusing sulfonated Cy3 or Cy5 fluorophores (100 nM). Fluorescence lifetime histograms of sCy3 decay monoexponentially and only at nucleoside concentrations above 50 μM a second, minor component emerges. The weighted average lifetime ![[small tau, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d4.gif) with respect to τ0 (0 mM NTP), accounting for the second lifetime component at higher NTP concentrations, increases linearly as a function of the NTP concentration (Fig. 2a for sCy3 and ESI,† Fig. S1d for sCy5). The photophysical response is more pronounced for the purines (A/G) than for the pyrimidines (C/U). Similar findings have been reported for deoxynucleoside 5′-monophosphates, where a longer lifetime and higher quantum yield is accompanied by a bathochromic shift of about 4 nm in the emission spectrum.52 It is commonly argued that stacking interactions hamper the transition to the dark cis-state, thereby reducing the flux through the photoisomerization pathway (Fig. 4c), which effectively competes with fluorescence.9,12,52,53 In order to discriminate specific intermolecular contacts from a bulk viscosity effect, we have recorded dynamic fluorescence anisotropy decays. A highly viscous environment restricts the mobility of the fluorophore and is thus expected to increase the rotational correlation time τr, assuming the simplest decay model of a single rotor.54 In fact, the tumbling time of free sCy3 rises from 0.17 ± 0.01 ns in aqueous media to 60 ± 5 ns in pure glycerol (η (25 °C) = 934 mPa s,55 ESI,† Fig. S1a). The NTPs on the other hand do not affect the correlation time τr. Instead, they widen the time window of fluorescence depolarization as a consequence of the increased lifetime (ESI,† Fig. S1b). The absence of a mere viscosity effect portends to specific interactions of the nucleobases with the fluorophore. Molecular dynamics simulations of sCy3 with either ATP or CTP in explicit water indeed show several stacking geometries (Fig. 2b). In order to minimize their solvent-exposed surface area nucleotides associate with the electron-rich dye scaffold. Both NTPs preferentially adopt a slightly off-centered parallel arrangement to maximize complementary electrostatics while avoiding sterical clashes with the methyl group on the heterocycle. However, the residence time of ATP in the MD simulations is more than double that of CTP. In light of the larger surface of purines, the hydrophobic effect appears to be the predominant energetic contribution that drives the association of nucleotide and fluorophore. In fact, the stabilization effect of the NTPs on the fluorescence lifetime is dependent on the polarity of the solvent. In a solution of 60% 1,4-dioxane (ε at 25 °C = 2.2156) ATP barely influences the lifetime of sCy3, suggesting that the tendency of the two partners to interact is decreasing (ESI,† Fig. S1c). The entropic gain upon desolvation is likely lower since fewer water molecules are expelled from both the nucleotide and the dye surface. We conclude that all NTPs, albeit to a different extent, act as a scaffold to which the dyes may associate and thereby get restricted along the dihedral reaction coordinate. In this way, non-radiative relaxation through the twisted intermediate to the dim cis-state is attenuated and the survival of the trans-isomer, in return, is enhanced. In short, these observations provide evidence for RIFE to occur even on the single nucleotide level.
with respect to τ0 (0 mM NTP), accounting for the second lifetime component at higher NTP concentrations, increases linearly as a function of the NTP concentration (Fig. 2a for sCy3 and ESI,† Fig. S1d for sCy5). The photophysical response is more pronounced for the purines (A/G) than for the pyrimidines (C/U). Similar findings have been reported for deoxynucleoside 5′-monophosphates, where a longer lifetime and higher quantum yield is accompanied by a bathochromic shift of about 4 nm in the emission spectrum.52 It is commonly argued that stacking interactions hamper the transition to the dark cis-state, thereby reducing the flux through the photoisomerization pathway (Fig. 4c), which effectively competes with fluorescence.9,12,52,53 In order to discriminate specific intermolecular contacts from a bulk viscosity effect, we have recorded dynamic fluorescence anisotropy decays. A highly viscous environment restricts the mobility of the fluorophore and is thus expected to increase the rotational correlation time τr, assuming the simplest decay model of a single rotor.54 In fact, the tumbling time of free sCy3 rises from 0.17 ± 0.01 ns in aqueous media to 60 ± 5 ns in pure glycerol (η (25 °C) = 934 mPa s,55 ESI,† Fig. S1a). The NTPs on the other hand do not affect the correlation time τr. Instead, they widen the time window of fluorescence depolarization as a consequence of the increased lifetime (ESI,† Fig. S1b). The absence of a mere viscosity effect portends to specific interactions of the nucleobases with the fluorophore. Molecular dynamics simulations of sCy3 with either ATP or CTP in explicit water indeed show several stacking geometries (Fig. 2b). In order to minimize their solvent-exposed surface area nucleotides associate with the electron-rich dye scaffold. Both NTPs preferentially adopt a slightly off-centered parallel arrangement to maximize complementary electrostatics while avoiding sterical clashes with the methyl group on the heterocycle. However, the residence time of ATP in the MD simulations is more than double that of CTP. In light of the larger surface of purines, the hydrophobic effect appears to be the predominant energetic contribution that drives the association of nucleotide and fluorophore. In fact, the stabilization effect of the NTPs on the fluorescence lifetime is dependent on the polarity of the solvent. In a solution of 60% 1,4-dioxane (ε at 25 °C = 2.2156) ATP barely influences the lifetime of sCy3, suggesting that the tendency of the two partners to interact is decreasing (ESI,† Fig. S1c). The entropic gain upon desolvation is likely lower since fewer water molecules are expelled from both the nucleotide and the dye surface. We conclude that all NTPs, albeit to a different extent, act as a scaffold to which the dyes may associate and thereby get restricted along the dihedral reaction coordinate. In this way, non-radiative relaxation through the twisted intermediate to the dim cis-state is attenuated and the survival of the trans-isomer, in return, is enhanced. In short, these observations provide evidence for RIFE to occur even on the single nucleotide level.
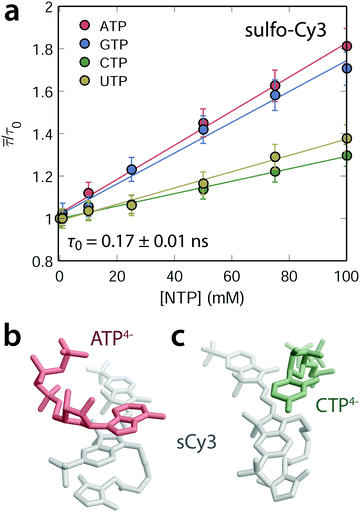 |
| | Fig. 2 NTP dependent stabilization of the carbocyanine fluorescence lifetime. (a) The average lifetime of sCy3 increases linearly as a function of the NTP concentration (with a background of 50 mM K+ and 3 mM Mg2+). Error bars are estimated from the standard error of τ0 (absence of any NTP). (b and c) Representative snapshots of the stacking interactions between non-hydrolyzed, sulfonated sCy3 (gray) and ATP4− (red, b) or CTP4− (green, c) extracted from a 50 ns MD trajectory. | |
Magnesium(II) mediates RNA–dye interactions
The polyanionic nature of nucleotides 5′-triphosphates and nucleic acids in general calls for counter ions to neutralize the large number of negative charges accumulating on the sugar–phosphate backbone.57 The question arises to what extent metal cations may modulate non-covalent interactions between two anionic molecules like carbocyanines and RNA. We address this issue by monitoring the lifetime and anisotropy change upon addition of potassium(I) or magnesium(II). For this purpose, sCy3 and sCy5 are conjugated to DNA and RNA oligonucleotides that differ in length, composition and secondary structure content (ESI,† Fig. S2). Out of a total of four sequences, two are derived from the group IIB intron Sc.ai5γ and have been previously investigated by NMR38,39 and smFRET41,42 (d3′EBS1*˙IBS1*, PDB entries 2m23 and 2m24; d3′EBS1*˙dIBS1*, PDB entry 2m1v). The other set of cyanine labeled oligonucleotides (hereafter termed sCy3/sCy5–DNA or sCy3/sCy5–RNA respectively) has been designed to hybridize to a regulatory RNA located in the 5′-untranslated region of the btuB gene from E. coli.21,58 In order to disentangle the influence of the mono- and divalent cations, the latter were chelated by 100 μM EDTA. TCSPC readings were taken prior to and after addition of 100 mM K+. Even high concentrations of monovalent salt hardly affect the lifetime of the carbocyanine constructs (ESI,† Table S1). Conversely, a titration series of Mg2+ with a constant background of K+ reveals rising fluorescence lifetimes for all sCy3-labeled nucleic acids (Fig. 3a). The data are modeled according to a classical single-site binding isotherm| | 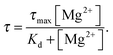 | (5) |
Seeing that the effect of the metal ion on the dye alone is negligible, the equilibrium constant indeed describes the interaction between Mg2+ and the nucleic acid, with sCy3 as a reporter. The model yields a Kd of 9 ± 2 mM for Mg2+ binding to the 3′-sCy3 DNA and 10 ± 3 mM in the case of the corresponding RNA oligo. d3′EBS1* shows indeed a single Mg2+ binding site within the range of sCy3, yielding a Kd of 2 ± 3 mM, which is ill-defined due to the error but compatible with the value determined by NMR chemical shift perturbations (2.19 ± 0.05 mM).42
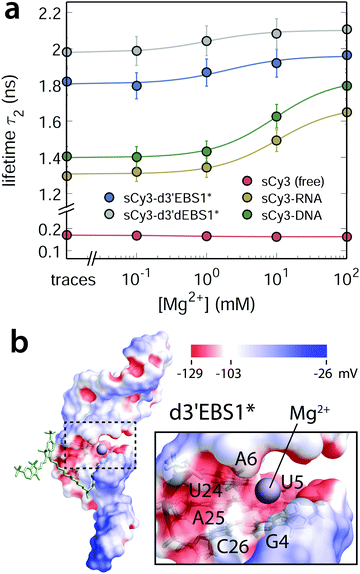 |
| | Fig. 3 Magnesium(II) dependence of the fluorescence lifetime in different microenvironments: sCy3 free in solution or bound to nucleic acids with different secondary structure content. (a) The second lifetime component τ2 of sCy3-coupled nucleic acids scales hyperbolically with the concentration of Mg2+ ions in solution. Error bars are estimated from triplicates of the sCy3–DNA titration (b) van der Waals surface of d3′EBS1* (PDB: 2m24) including the tetraU overhang color coded with the electrostatic surface potential (ESP, calculated with APBS62,63). The putative location of the Mg2+ ion is indicated by a violet sphere and is based on the ESP and previously recorded NMR chemical shifts38,42 between G4·C26 and A6·U24 (nucleotide labeling according to ESI,† Fig. S2).39,42 | |
Compared to potassium(I), magnesium(II) is more likely to occupy discrete binding sites within the major groove of nucleic acids (Fig. 3b).59 One reason is the lower entropic penalty for constraining ion mobility, since only half of the ions are required to neutralize the electrostatic surface potential.60 Charge compensation by K+ is commonly attributed to an ion atmosphere, a sheath of fluctuating ions encompassing the polyelectrolyte.61 Considering the marginal influence of the monovalent ion on the photophysics of the two cyanine dyes, we expect the titration curves of Mg2+ to reflect a specific binding event and not only diffuse screening. Such a localized shielding of negative charges promotes interactions of the fluorophore with the nucleic acid, in particular at the 3′-dangling end of d3′EBS1*. The extent to which the dye stacks to the biomolecule can be inferred from the amplitude of the global anisotropy rglobal (ESI,† Fig. S3a–c). The latter increases linearly over the range of the Mg2+ titration suggesting that the cations sequester locally some negative charges of phosphate backbone to favor interactions between the fluorophore and the nucleic acid.
Bioconjugation interferes with photoisomerization
Levitus and coworkers have previously shown that cyanine dyes interact with DNA in a sequence-dependent manner that is based on strand flexibility and relative purine content.26,53 Accordingly, biopolymers like DNA or RNA need to be flexible enough in order to interact with a fluorophore. Variations in the lifetime of the Cy-labeled DNAs and RNAs (Fig. 3a) are therefore likely due to subtle differences in the stiffness of the nucleic acids. Slightly lower lifetimes for sCy3–RNA oligonucleotides are in line with the longer persistence length reported for a toy model of ssRNA versus ssDNA, that is rU40 and dT40.64 On the other hand, a pure analysis of the purine content within the first few nucleotides of the dye would predict very similar lifetimes for the unstructured sCy3–RNA and the d3′EBS1* hairpin but the experiment does not. Thus, the physicochemical properties of the building blocks alone do not capture the full picture of the delicate interplay of fluorophore, biomolecule, and metal ions. Beyond strand composition, secondary and tertiary structure contacts are expected to affect dye stacking significantly and thus alter the photophysics of carbocyanines. NAIFE and RIFE are governed by the nature of the excited states. So, why does the coupling of carbocyanines to nucleic acids give rise to a second lifetime component? Fig. 4a contrasts the fluorescence lifetime decays of sCy3 with the conformationally locked variant Cy3B (Fig. 4a).65 With cis–trans isomerization precluded in Cy3B, the two dyes span a lifetime interval populated by different carbocyanine labeled nucleic acid constructs that may undergo photoisomerization, yet to a varying extent. The free fluorophores represent the lower and upper rate limits for the torsion along the polymethine chain. While their lifetimes decay monoexponentially, a second component appears for all dyes that are conjugated to nucleic acids. The relative weight of the second component increases in the order: sCy3–RNA oligo < sCy3–DNA oligo < sCy3–DNA–btuB < sCy3–d3′EBS1* < sCy3–d3′dEBS1* (Fig. 4a and ESI,† Fig. S3e for sCy5; all values are provided in ESI,† Table S2). From experiments with the NTPs we know that dye and bases are present in a dynamic equilibrium of association and dissociation in which stacking stabilizes the fluorescence lifetime. Therefore, it is conceivable that the first lifetime reports on the dye tumbling about the linker (wobbling-in-cone), while the second component is associated with the dye sticking to the nucleic acid. The relative weighting of the second lifetime constituent is thus indicative for the tendency of the dye to interact with the biomolecule. In case of a completely stacked fluorophore, the effective, weighted lifetime is expected to converge ultimately to the single lifetime that is observed for the rigidified Cy3B.
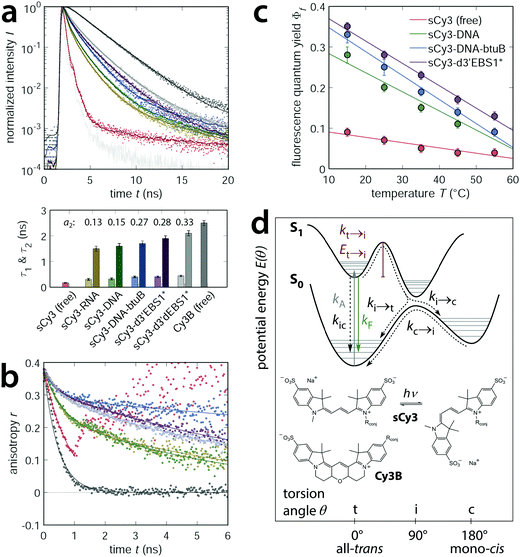 |
| | Fig. 4 RNA dependent photoisomerization propensity of carbocyanine dyes. (a) The freely diffusing fluorophores sCy3 and Cy3B span a lifetime interval populated by sCy3 species that are covalently coupled to nucleic acids of different size and complexity (background of 50 mM K+ and 10 mM Mg2+). Lifetime histograms are normalized and described by one (free dyes) or two exponentials (conjugated dyes). An additional long lifetime component accounts for the tail of the histogram but its contribution is very low (<1%). (b) The dynamic anisotropy decay describes the tumbling of the fluorophore along with the biomolecule and is composed of a local and global correlation time with different relative amplitudes (r0 ≡ 0.38). (c) Decrease of the relative quantum yield as a function of the temperature. Errors are estimated from the variability in the absorption spectra. (d) Potential energy diagram (adapted from Levitus and Ranjit, 2011) illustrating the concept of cis–trans isomerization of carbocyanines in terms of the different rate constants.12 | |
The degree of motional restriction on the fluorophores by macromolecular environment can be deduced from dynamic anisotropy measurements (Fig. 4b for sCy3 and ESI,† Fig. S3f for sCy5). Differences between the less structured oligonucleotides and the d3′EBS1* stem loop are manifested in the amplitude of the local hindered rotation given by the prefactor r0 − rglobal (ESI,† Table S2). The fast motion represented by the initial decay is far more pronounced in the RNA oligo than in d3′EBS1* (Fig. 4b). Hence, the dye is less constrained by the single stranded RNA molecule than by the hairpin, which is in agreement with the lifetime predictions above. Since interactions with the biomolecular surface decouple the global correlation time τr,global from the local wobbling-in-cone, the stacked dye population can provide valuable information on the rotational diffusion of the host molecule. Comparison of the hydrodynamic radii calculated from the global correlation time and measured by dynamic light scattering (DLS) in the absence of fluorophores suggests the anisotropy decay model to be appropriate (ESI,† Fig. S4 and Table S2).
In order to correlate the extent of motional constraints to the propensity of photoisomerization we recorded quantum yields as a function of temperature. Upon increasing the kinetic energy of the system the quantum efficiency gradually diminishes (Fig. 4c for sCy3 and ESI,† Fig. S3d for sCy5). Photoisomerization of Cy–dyes is commonly depicted in terms of a potential energy diagram where an excited molecule has to overcome an energy barrier before passing via a twisted intermediate to the non-fluorescent cis-state (Fig. 4d).12,25,32 Relating the quantum yield of sCy3 to the rigidified Cy3B (Fig. 4e), using the Arrhenius equation kN→t = A![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−EN→t/RT), affords
exp(−EN→t/RT), affords
| | | ln[Φf−1(sCy3) − Φf−1(Cy3B)] = ln(A/kf) − EN→t/RT | (6) |
whereupon the activation energy
EN→t can be inferred from the slope (
Fig. 4d).
25 We find the barrier increasing in the order sCy3–NHS (19 ± 3 kJ mol
−1) ≪ sCy3–DNA oligo (27 ± 2 kJ mol
−1) ≈ sCy3–d3′EBS1* (27 ± 1 kJ mol
−1) < sCy3–DNA–
btuB (32 ± 2 kJ mol
−1). Hence, structural complexity around the fluorophores is intimately linked to the extent of photo-induced
cis–trans isomerization which is assumed by the lifetime and dynamic anisotropy experiments. The presence of a biomolecule – be it a protein or a strand of DNA/RNA – in close proximity of a dye, no matter whether it is covalently linked (
e.g. sCy3–d3′EBS1*) or non-covalently associated (
e.g. sCy3 with NTPs, or PIFE
29), intrinsically reduces the conformational space accessible to the fluorescent probe. Our and previous
30 work suggests that the bigger the excluded volume the less likely it is for the fluorophore to wobble freely around its linker. Hence, the fraction of unstacked fluorophore, which is susceptible to isomerization, could be estimated from a calculation of the dye's accessible volume and be used to predict the brightness of photoswitchable cyanine dyes in a specific microenvironment.
Contact interface in accessible volume simulations
Following up on the discussion above, quantum yields, lifetime, and anisotropy measurements indicate that structural characteristics in the vicinity of the fluorophore play a key role in RNA recognition. A computationally inexpensive way to sample the conformational space explored by a dye in a biomolecular environment are so-called accessible volume (AV) simulations.22,23 Herein, a coarse-grained model of a fluorophore is attached to a macromolecule in order to sample all dye positions within a given linker length that do not cause steric clashes with the surface (ESI,† Fig. S5). Even though the algorithm itself treats all locations as equiprobable, and hence disregards dye stacking per se, the amount of volume exclusion can be taken as a measure for steric hindrance as reported previously.30 We quantified the accessible volume of sCy3 and sCy5 both free in solution (i.e. AVmax) and attached to the nucleic acids. The resulting AV fraction correlates inversely with the proportion of stacked dye as given by the prefactor a2 = 1 − a in the lifetime fitting model (eqn (1) and Fig. 5a). This strategy considers the restriction in dye mobility, i.e. translational and rotational diffusion degrees of freedom, as the cause for the reduced cis–trans isomerization. Here, we propose a different approach which targets the dihedral reaction coordinate directly. The rationale is the following: when stacked to the biomolecule, the fluorophore occupies a narrow rim of the accessible volume defined by the dimensions of a triaxial ellipsoid that represents the probe. The ratio of this volume segment over the AV is expected to correlate directly with the stacked dye population. The rim volume is modeled by two spherical sectors with half cone angles θ and θ + δ where δ is the minimum angle for accommodating the fluorophore on the biomolecular surface (compare Fig. 5d):| | 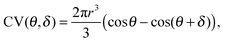 | (7) |
where δ = sin−1(Rdye(3)/Llink) with Rdye(3) as the smallest dye parameter and Llink as the linker length. In practice, we first extract coordinates of the AV cloud that are in contact with the nucleic acid surface and then calculate a sheath with a thickness of the Rdye(3) = 3 Å (see ESI,† Fig. S5). The such obtained volume segment, as part of the AV, constitutes the space occupied by a fluorophore when stacked onto the biomolecular surface (Fig. 5c). By dividing this contact volume (CV) by the total AV we can define a stacking parameter ζ that scales between 0 and 1 and therefore reflects the lifetime weighting factor a2 = 1 − a (Fig. 5b). In case of the dye pair sCy3/Cy3B, where the limiting lifetimes are known, this parameter can be used to predict the effective, weighted lifetime of any dye–RNA construct, provided that a tertiary structure is available.
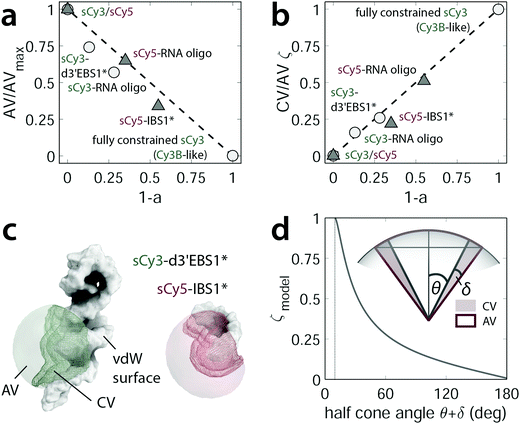 |
| | Fig. 5 The contact volume (CV) as a measure for the stacking probability of carbocyanines within an RNA environment. (a) Normalized AV plotted as a function of the stacking propensity as given by the prefactor a2 = 1 − a in the lifetime fitting model. The free fluorophores sCy3/sCy5 and Cy3B represent the theoretical lower and upper boundaries. Cy3B in fact mimics a completely constrained fluorophore that is not amenable to photoisomerization. (b) Linear correlation of the stacking parameter ζ = CV/AV and the lifetime weighting factor. (c) Mesh representation of the CV within the AV cloud that surrounds the van der Waals (vdW) surface near the fluorophore attachment position. (d) Theoretical model of the stacking parameter ζ and its dependence on the half cone angle θ + δ. | |
Fluorophore tracking by molecular dynamics
The picture cast by AV simulations is of static nature and lacks atomic resolution. Both of these aspects are overcome by MD simulations at the expense of computation time. To get an idea of the fluorophore dynamics, we propagated the dye–RNA constructs with different initial velocities (200–400 ns in total) in two different water models and computed the anisotropy decay in a MC approach (Fig. 6a and ESI,† Methods). With TIP3P water the simulated decays are consistently faster than those recorded by TCSPC. We attribute the high mobility of the dyes to an overestimated solvent self-diffusion, that is the spontaneous mixing of water molecules in the absence of a concentration gradient. The self-diffusion coefficient Dsim is computed from the mean square displacement and exceeds the experimental value Dexp by a factor of about 2.4 (simulation at 298 K: 5.54 ± 0.03 × 10−9 m2 s−1, experiment at 298 K:66 2.299 ± 0.005 × 10−9 m2 s−1).67–69 We therefore corrected the photon arrival times by a factor cdiff = Dsim/Dexp (Fig. 6a). After calibration the calculated decays of the free sCy5 and the short sCy5–IBS1* conform nicely to the experiment (upper and middle panel in Fig. 6b). The TIP4P/2005 water models the self-diffusion more accurately and reproduces the experiment (free, hydrolyzed sCy3) perfectly without any correction factor. On the other hand, the water solvates the dye to such an extent that within the studied time regime no interactions with IBS1* are observed. As a result, the anisotropy decays slightly faster than in the corrected TIP3P simulation.
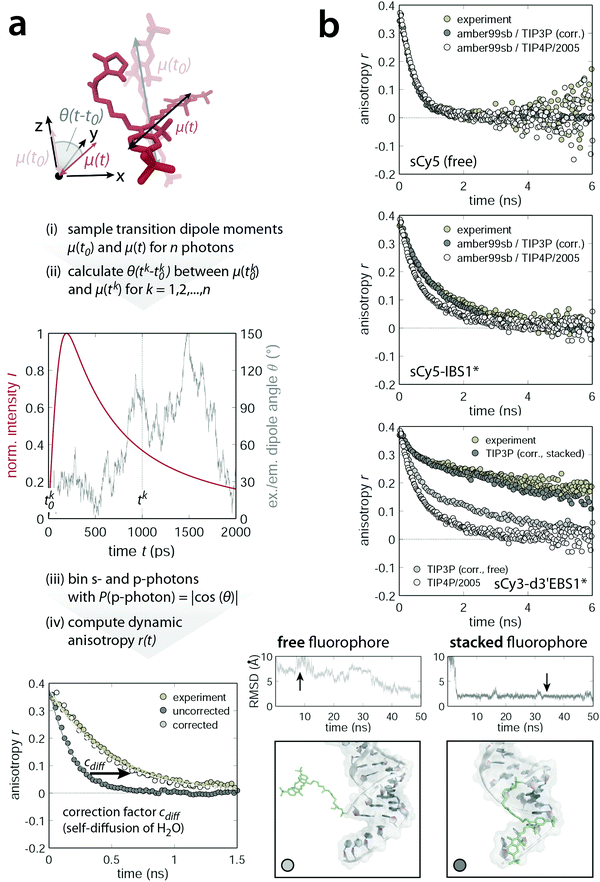 |
| | Fig. 6 Dynamic anisotropy calculation using a hybrid molecular dynamics/Monte Carlo algorithm. (a) Scheme of the workflow for computing anisotropy decays from MD trajectories. Absorption and emission dipole moment vectors are sampled for n photons (upper panel). The coordinate system is defined such that the absorption dipole points along the z-direction. Time stamps for the excitation dipole vector (tk0) are drawn uniformly while those of the emission dipole (tk) are weighted by the experimental fluorescence lifetime decay convoluted with a Gaussian-shaped IRF (middle panel). The angle θ(t − t0) formed by the absorption dipole at time t0 and the emission dipole at time t (assuming the molecular absorption and emission dipoles to be parallel at time t0) is a direct measure for the probability of detecting a parallel (p) photon. Upon binning all s- and p-photons independently (bin width: 25 ps) the dynamic anisotropy is calculated and corrected by cdiff which accounts for the overestimated self-diffusion of the water molecules in the TIP3P solvation model (lower panel). (b) Comparison of experimental and simulated dynamic anisotropy decays. The simulations are based on MD trajectories with two different water models (cdiff corrected TIP3P or TIP4P/2005) and are superimposed for the free sCy5 (top), sCy5 coupled to IBS1* (middle) and sCy3 attached to d3′EBS1* (bottom). Snapshots are taken within regions of different dye mobility (black arrow on the RMSD trace of the fluorophore and the 3′-tetraU overhang), providing an atomistic picture of the specific dye–RNA interactions. | |
In case of the d3′EBS1* hairpin with TIP3P water, the simulated anisotropy decays are quite heterogeneous (lower panel in Fig. 6b). Examination of the root mean square deviation (RMSD) of the dye and the 3′-tetraU overhang reveals intervals of high mobility and others where almost no fluctuation is observed. Snapshots within low RMSD regions unveil a stable conformation, in which sCy3 is stacked longwise on the dangling end of d3′EBS1* (Fig. 6b, bottom right). This interaction mode extends the depolarization and may have far-reaching consequences on measurements where an isotropic rotation of the fluorophore is generally assumed. Comparison with the experimental decay suggests that the fluorophore indeed spends a non-negligible amount of time attached to the single-stranded overhang. The contribution of the fast initial decay, arising from either completely free or end-stacked dye populations (Fig. 6b, bottom left), is comparatively small. Trajectories from TIP4P/2005 show virtually no interactions of dye and RNA, thereby ensuring a rapid decay to zero (lower panel in Fig. 6b, white data points). The simulations demonstrate that the choice of the water model (TIP4P or TIP3P) is key to an accurate description of the dynamic fluorescence anisotropy. Intriguingly, both water models prove appropriate in different respects. The TIP4P has been designed to accurately render the thermodynamic properties of liquid water over a wide range of the phase diagram.41 However, it overestimates the free cone-wobbling component relative to stacked dye conformations, which are observed extensively with TIP3P. The extent to which metal ions of both mono- and divalent nature may modulate the stacking propensity in the simulation is subject to further research.
Conclusion
In order to draw a comprehensive picture of carbocyanine fluorescence in the context of nucleic acids and RNA in particular, we have addressed the major photophysical parameters governing brightness, observation time frame and rotational diffusion for the popular FRET pair sCy3 and sCy5. Following the terminology previously used for proteins, we propose the notion of RNA-induced fluorescence enhancement (RIFE) to describe a series of photophysical effects caused by structural motifs of RNA in vicinity of an isomerizable cyanine fluorophore. Our study sheds light on the relative variations of lifetime, quantum yield, and dynamic anisotropy in response to changes in the microenvironment of the dye. On the ribonucleotide level, we have identified base-specific stacking interactions, which increase the excited state lifetime of the fluorophores. The divalent metal ion Mg2+ mediates the interaction of fluorophore and RNA by locally attenuating electrostatic repulsion. Conversely, the fluorescence lifetime reports on the binding affinity of Mg2+ towards nucleic acids with varying secondary structure content. Dynamic anisotropy measurements mirror the flexibility of the dyes in their local environment. We postulate that the first lifetime component of cyanine labeled RNAs and DNAs is associated with the local correlation time describing the rotational diffusion of the fluorophore within the dye-accessible volume. The second lifetime reflects various interaction modes with the host molecule. As long as the dyes stack to a macromolecular surface, the polymethine chain is not amenable to cis–trans isomerization and relaxation from the excited state occurs mostly via fluorescence emission. Apart from strand composition, structural features of the biomolecule play a fundamental role in RNA–dye recognition. In this respect, the wealth of secondary structure motifs and its intrinsic flexibility sets RNA well apart from DNA and justifies the introduction of RIFE as a phenomenon akin to PIFE. RNA samples a vast conformational space which makes it even more prone to interact with fluorophores than known so far for DNA. With the help of molecular dynamic simulations, we could exemplify that the dangling end of an RNA hairpin has a great impact on fluorophore mobility. Such interactions should be taken into account when interpreting spectroscopic data in general. Careful calibration measurements are needed especially when using absolute single-molecule FRET with photoswitchable Cy–dyes for studying dynamic RNAs. As demonstrated herein, the wobbling of the fluorophores might deviate quite dramatically from the special case of isotropic rotation. As such, the enhanced photophysical properties of carbocyanines in an RNA environment, notably longer lifetimes and higher quantum yields, ultimately come at the expense of spatial restraints. On the positive side, an increased brightness of the fluorescent probe allows for longer observation times and a better signal-to-noise ratio particularly when imaging single molecules. Specific interactions of the fluorophore with certain RNA regions can be harnessed to investigate domain motion and introduce orientational constraints for intramolecular stem-loop modeling. Moreover, the dependence of the dye–RNA interplay on the abundance of metal ions, provides an additional spectroscopic handle for ion-mediated RNA folding studies.
Our dual approach combining picosecond photon counting techniques and molecular dynamics simulations bridges the gap between a time-resolved ensemble parameter, the dynamic anisotropy, and an atomistic view on the biological system. All-atom simulations provide detailed information on the mutual interactions of fluorophores and nucleic acids. Not only do they support the interpretation of experimental data but they also improve our understanding of the underlying photophysical processes on a structural level. We have shown how theory and experiment complement each other in predicting and assessing preferred orientations of nucleic acid bound fluorophores. The same methodology can be applied to evaluate Förster-type transfer efficiencies and calculate accurate distances within RNA systems of various sizes and complexity. After all, a rigorous analysis of the photophysics of carbocyanine dyes in the context of RNA and metal ions is key to understanding structural heterogeneity on the single-molecule level.
Author contributions
R. B. designed the research. F. D. S. prepared the RNA, measured the photophysics, performed the simulations and analyzed the data. R. K. O. S. and R. B. supervised the project. All authors wrote the manuscript.
Competing financial interests
The authors declare no competing financial interests.
Acknowledgements
The authors thank Hauke Paulsen and Christian G. Hübner (University of Lübeck) for access to their computational infrastructure, Ben Schuler (University of Zurich) for valuable discussions and Michelle Schaffer for providing the btuB plasmid. Financial support from the European Research Council (MIRNA No. 259092 to R. K. O. S.), SystemsX.ch (to R. K. O. S), the Swiss National Science Foundation (SNSF, to R. K. O. S.), and the Forschungskredit Grant of the University of Zurich (FK-14-096 and FK-15-095 to R. B.) are gratefully acknowledged.
References
- S. Weiss, Nat. Struct. Biol., 2000, 7, 724–729 CrossRef CAS PubMed.
- W. E. Moerner and D. P. Fromm, Rev. Sci. Instrum., 2003, 74, 3597 CrossRef CAS.
- C. Joo, H. Balci, Y. Ishitsuka, C. Buranachai and T. Ha, Annu. Rev. Biochem., 2008, 77, 51–76 CrossRef CAS PubMed.
- R. Zhao and D. Rueda, Methods, 2009, 49, 112–117 CrossRef CAS PubMed.
- J. Hohlbein, K. Gryte, M. Heilemann and A. N. Kapanidis, Phys. Biol., 2010, 7, 031001 CrossRef PubMed.
- B. Schuler and H. Hofmann, Curr. Opin. Struct. Biol., 2013, 23, 36–47 CrossRef CAS PubMed.
- R. Börner, D. Kowerko, H. Guiset Miserachs, M. F. Schaffer and R. K. O. Sigel, Coord. Chem. Rev., 2016 DOI:10.1016/j.ccr.2016.06.002.
- T. Ha and P. Tinnefeld, Annu. Rev. Phys. Chem., 2012, 63, 595–617 CrossRef CAS PubMed.
- E. M. S. Stennett, M. A. Ciuba and M. Levitus, Chem. Soc. Rev., 2014, 43, 1057–1075 RSC.
- R. B. Altman, D. S. Terry, Z. Zhou, Q. Zheng, P. Geggier, R. A. Kolster, Y. Zhao, J. A. Javitch, J. D. Warren and S. C. Blanchard, Nat. Methods, 2012, 9, 68–71 CrossRef CAS PubMed.
- R. B. Mujumdar, L. A. Ernst, S. R. Mujumdar, C. J. Lewis and A. S. Waggoner, Bioconjugate Chem., 1993, 4, 105–111 CrossRef CAS PubMed.
- M. Levitus and S. Ranjit, Q. Rev. Biophys., 2011, 44, 123–151 CrossRef CAS PubMed.
- Q. Zheng, M. F. Juette, S. Jockusch, M. R. Wasserman, Z. Zhou, R. B. Altman and S. C. Blanchard, Chem. Soc. Rev., 2014, 43, 1044–1056 RSC.
- I. Rasnik, S. A. McKinney and T. Ha, Nat. Methods, 2006, 3, 891–893 CrossRef CAS PubMed.
- R. Roy, S. Hohng and T. Ha, Nat. Methods, 2008, 5, 507–516 CrossRef CAS PubMed.
- J. Widengren and P. Schwille, J. Phys. Chem. A, 2000, 104, 6416–6428 CrossRef CAS.
- A.-Y. Jee, S. Park and M. Lee, Phys. Chem. Chem. Phys., 2011, 13, 15227–15232 RSC.
- M. Torimura, S. Kurata, K. Yamada, T. Yokomaku, Y. Kamagata, T. Kanagawa and R. Kurane, Anal. Sci., 2001, 17, 155–160 CrossRef CAS PubMed.
- G. J. Smith, T. R. Sosnick, N. F. Scherer and T. Pan, RNA, 2005, 11, 234–239 CrossRef CAS PubMed.
- H. Sahoo, RSC Adv., 2012, 2, 7017 RSC.
- D. Egloff, I. A. Oleinich, M. Zhao, S. L. B. König, R. K. O. Sigel and E. Freisinger, ACS Chem. Biol., 2016 DOI:10.1021/acschembio.6b00343.
- S. Sindbert, S. Kalinin, H. Nguyen, A. Kienzler, L. Clima, W. Bannwarth, B. Appel, S. Müller and C. A. Seidel, J. Am. Chem. Soc., 2011, 133, 2463–2480 CrossRef CAS PubMed.
- S. Kalinin, T. Peulen, S. Sindbert, P. J. Rothwell, S. Berger, T. Restle, R. S. Goody, H. Gohlke and C. A. Seidel, Nat. Methods, 2012, 9, 1218–1225 CrossRef CAS PubMed.
- R. Börner, N. Ehrlich, J. Hohlbein and C. G. Hübner, J. Fluoresc., 2016, 26, 963–975, DOI:10.1007/s10895-016-1784-5.
- M. E. Sanborn, B. K. Connolly, K. Gurunathan and M. Levitus, J. Phys. Chem. B, 2007, 111, 11064–11074 CrossRef CAS PubMed.
- B. J. Harvey, C. Perez and M. Levitus, Photochem. Photobiol. Sci., 2009, 8, 1105–1110 CAS.
- E. M. S. Stennett, N. Ma, A. van der Vaart and M. Levitus, J. Phys. Chem. B, 2014, 118, 152–163 CrossRef CAS PubMed.
- B. G. Moreira, Y. You and R. Owczarzy, Biophys. Chem., 2015, 198, 36–44 CrossRef CAS PubMed.
- H. Hwang and S. Myong, Chem. Soc. Rev., 2014, 43, 1221–1229 RSC.
- E. Lerner, E. Ploetz, J. Hohlbein, T. Cordes and S. Weiss, J. Phys. Chem. B, 2016, 120, 6401–6410 CrossRef CAS PubMed.
- E. M. S. Stennett, M. A. Ciuba, S. Lin and M. Levitus, J. Phys. Chem. Lett., 2015, 6, 1819–1823 CrossRef CAS PubMed.
- C. Rullière, Chem. Phys. Lett., 1976, 43, 303–308 CrossRef.
- S. Gallo, M. Furler and R. K. O. Sigel, Chimia, 2005, 59, 812–816 CrossRef CAS.
- K. H. Drexhage, J. Res. Natl. Bur. Stand., Sect. A, 1976, 80, 421–428 CrossRef.
- N. K. Lee, A. N. Kapanidis, Y. Wang, X. Michalet, J. Mukhopadhyay, R. H. Ebright and S. Weiss, Biophys. J., 2005, 88, 2939–2953 CrossRef CAS PubMed.
- G. Lipari and A. Szabo, Biophys. J., 1980, 30, 489–506 CrossRef CAS PubMed.
-
J. R. Lakowicz, Principles of fluorescence spectroscopy, Springer, New York, 3rd edn, 2006 Search PubMed.
- D. Kruschel, M. Skilandat and R. K. O. Sigel, RNA, 2014, 20, 295–307 CrossRef CAS PubMed.
- M. Skilandat and R. K. O. Sigel, J. Biol. Chem., 2014, 289, 20650–20663 CrossRef CAS PubMed.
- M. Popenda, M. Szachniuk, M. Antczak, K. J. Purzycka, P. Lukasiak, N. Bartol, J. Blazewicz and R. W. Adamiak, Nucleic Acids Res., 2012, 40, e112 CrossRef CAS PubMed.
- S. L. König, D. Kowerko and R. K. O. Sigel, Chimia, 2013, 67, 240–243 CrossRef.
- D. Kowerko, S. L. König, M. Skilandat, D. Kruschel, M. C. A. S. Hadzic, L. Cardo and R. K. O. Sigel, Proc. Natl. Acad. Sci. U. S. A., 2015, 112, 3403–3408 CrossRef CAS PubMed.
- J. L. F. Abascal and C. Vega, J. Chem. Phys., 2005, 123, 234505 CrossRef CAS PubMed.
- V. Hornak, R. Abel, A. Okur, B. Strockbine, A. Roitberg and C. Simmerling, Proteins: Struct., Funct., Bioinf., 2006, 65, 712–725 CrossRef CAS PubMed.
- T. Graen, M. Hoefling and H. Grubmüller, J. Chem. Theory Comput., 2014, 10, 5505–5512 CrossRef CAS PubMed.
- J. Wang, W. Wang, P. A. Kollman and D. A. Case, J. Mol. Graphics Modell., 2006, 25, 247–260 CrossRef CAS PubMed.
- A. W. Sousa da Silva and W. F. Vranken, BMC Res. Notes, 2012, 5, 367 CrossRef PubMed.
- M. J. Abraham, T. Murtola, R. Schulz, S. Páll, J. C. Smith, B. Hess and E. Lindahl, SoftwareX, 2015, 1–2, 19–25 CrossRef.
- B. Hess, H. Bekker, H. J. C. Berendsen and J. G. E. M. Fraaije, J. Comput. Chem., 1997, 18, 1463–1472 CrossRef CAS.
- S. Páll and B. Hess, Comput. Phys. Commun., 2013, 184, 2641–2650 CrossRef.
- U. Essmann, L. Perera, M. L. Berkowitz, T. Darden, H. Lee and L. G. Pedersen, J. Chem. Phys., 1995, 103, 8577 CrossRef CAS.
- B. J. Harvey and M. Levitus, J. Fluoresc., 2008, 19, 443–448 CrossRef PubMed.
- J. Spiriti, J. K. Binder, M. Levitus and A. van der Vaart, Biophys. J., 2011, 100, 1049–1057 CrossRef CAS PubMed.
-
B. Valeur, Molecular fluorescence. Principles and applications, Wiley-VCH, Weinheim, New York, 2002 Search PubMed.
-
W. M. Haynes, CRC handbook of chemistry and physics. A ready-reference book of chemical and physical data, Taylor & Francis, 96th edn, 2015 Search PubMed.
- C. Reichardt, Angew. Chem., Int. Ed. Engl., 1979, 18, 98–110 CrossRef.
-
R. K. O. Sigel and H. Sigel, Comprehensive Inorganic Chemistry II, Elsevier, 2013, pp. 623–660 Search PubMed.
- A. Nahvi, J. E. Barrick and R. R. Breaker, Nucleic Acids Res., 2004, 32, 143–150 CrossRef CAS PubMed.
- D. E. Draper, RNA, 2004, 10, 335–343 CrossRef CAS PubMed.
- D. E. Draper, D. Grilley and A. M. Soto, Annu. Rev. Biophys. Biomol. Struct., 2005, 34, 221–243 CrossRef CAS PubMed.
- J. Lipfert, S. Doniach, R. Das and D. Herschlag, Annu. Rev. Biochem., 2014, 83, 813–841 CrossRef CAS PubMed.
- N. A. Baker, D. Sept, S. Joseph, M. J. Holst and J. A. McCammon, Proc. Natl. Acad. Sci. U. S. A., 2001, 98, 10037–10041 CrossRef CAS.
- T. J. Dolinsky, P. Czodrowski, H. Li, J. E. Nielsen, J. H. Jensen, G. Klebe and N. A. Baker, Nucleic Acids Res., 2007, 35, W522–W525 CrossRef PubMed.
- H. Chen, S. P. Meisburger, S. A. Pabit, J. L. Sutton, W. W. Webb and L. Pollack, Proc. Natl. Acad. Sci. U. S. A., 2012, 109, 799–804 CrossRef CAS PubMed.
- M. Cooper, A. Ebner, M. Briggs, M. Burrows, N. Gardner, R. Richardson and R. West, J. Fluoresc., 2004, 14, 145–150 CrossRef CAS PubMed.
- M. Holz, S. R. Heil and A. Sacco, Phys. Chem. Chem. Phys., 2000, 2, 4740–4742 RSC.
- D. van der Spoel, P. J. van Maaren and H. J. C. Berendsen, J. Chem. Phys., 1998, 108, 10220 CrossRef CAS.
- G. F. Schröder, U. Alexiev and H. Grubmüller, Biophys. J., 2005, 89, 3757–3770 CrossRef PubMed.
- R. B. Best, H. Hofmann, D. Nettels and B. Schuler, Biophys. J., 2015, 108, 2721–2731 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: Photophysical data for sCy5 along with further methodological and experimental details. See DOI: 10.1039/c6cp04277e |
|
| This journal is © the Owner Societies 2016 |
Click here to see how this site uses Cookies. View our privacy policy here.  Open Access Article
Open Access Article
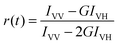
![[small tau, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d4.gif) with respect to τ0 (0 mM NTP), accounting for the second lifetime component at higher NTP concentrations, increases linearly as a function of the NTP concentration (Fig. 2a for sCy3 and ESI,† Fig. S1d for sCy5). The photophysical response is more pronounced for the purines (A/G) than for the pyrimidines (C/U). Similar findings have been reported for deoxynucleoside 5′-monophosphates, where a longer lifetime and higher quantum yield is accompanied by a bathochromic shift of about 4 nm in the emission spectrum.52 It is commonly argued that stacking interactions hamper the transition to the dark cis-state, thereby reducing the flux through the photoisomerization pathway (Fig. 4c), which effectively competes with fluorescence.9,12,52,53 In order to discriminate specific intermolecular contacts from a bulk viscosity effect, we have recorded dynamic fluorescence anisotropy decays. A highly viscous environment restricts the mobility of the fluorophore and is thus expected to increase the rotational correlation time τr, assuming the simplest decay model of a single rotor.54 In fact, the tumbling time of free sCy3 rises from 0.17 ± 0.01 ns in aqueous media to 60 ± 5 ns in pure glycerol (η (25 °C) = 934 mPa s,55 ESI,† Fig. S1a). The NTPs on the other hand do not affect the correlation time τr. Instead, they widen the time window of fluorescence depolarization as a consequence of the increased lifetime (ESI,† Fig. S1b). The absence of a mere viscosity effect portends to specific interactions of the nucleobases with the fluorophore. Molecular dynamics simulations of sCy3 with either ATP or CTP in explicit water indeed show several stacking geometries (Fig. 2b). In order to minimize their solvent-exposed surface area nucleotides associate with the electron-rich dye scaffold. Both NTPs preferentially adopt a slightly off-centered parallel arrangement to maximize complementary electrostatics while avoiding sterical clashes with the methyl group on the heterocycle. However, the residence time of ATP in the MD simulations is more than double that of CTP. In light of the larger surface of purines, the hydrophobic effect appears to be the predominant energetic contribution that drives the association of nucleotide and fluorophore. In fact, the stabilization effect of the NTPs on the fluorescence lifetime is dependent on the polarity of the solvent. In a solution of 60% 1,4-dioxane (ε at 25 °C = 2.2156) ATP barely influences the lifetime of sCy3, suggesting that the tendency of the two partners to interact is decreasing (ESI,† Fig. S1c). The entropic gain upon desolvation is likely lower since fewer water molecules are expelled from both the nucleotide and the dye surface. We conclude that all NTPs, albeit to a different extent, act as a scaffold to which the dyes may associate and thereby get restricted along the dihedral reaction coordinate. In this way, non-radiative relaxation through the twisted intermediate to the dim cis-state is attenuated and the survival of the trans-isomer, in return, is enhanced. In short, these observations provide evidence for RIFE to occur even on the single nucleotide level.
with respect to τ0 (0 mM NTP), accounting for the second lifetime component at higher NTP concentrations, increases linearly as a function of the NTP concentration (Fig. 2a for sCy3 and ESI,† Fig. S1d for sCy5). The photophysical response is more pronounced for the purines (A/G) than for the pyrimidines (C/U). Similar findings have been reported for deoxynucleoside 5′-monophosphates, where a longer lifetime and higher quantum yield is accompanied by a bathochromic shift of about 4 nm in the emission spectrum.52 It is commonly argued that stacking interactions hamper the transition to the dark cis-state, thereby reducing the flux through the photoisomerization pathway (Fig. 4c), which effectively competes with fluorescence.9,12,52,53 In order to discriminate specific intermolecular contacts from a bulk viscosity effect, we have recorded dynamic fluorescence anisotropy decays. A highly viscous environment restricts the mobility of the fluorophore and is thus expected to increase the rotational correlation time τr, assuming the simplest decay model of a single rotor.54 In fact, the tumbling time of free sCy3 rises from 0.17 ± 0.01 ns in aqueous media to 60 ± 5 ns in pure glycerol (η (25 °C) = 934 mPa s,55 ESI,† Fig. S1a). The NTPs on the other hand do not affect the correlation time τr. Instead, they widen the time window of fluorescence depolarization as a consequence of the increased lifetime (ESI,† Fig. S1b). The absence of a mere viscosity effect portends to specific interactions of the nucleobases with the fluorophore. Molecular dynamics simulations of sCy3 with either ATP or CTP in explicit water indeed show several stacking geometries (Fig. 2b). In order to minimize their solvent-exposed surface area nucleotides associate with the electron-rich dye scaffold. Both NTPs preferentially adopt a slightly off-centered parallel arrangement to maximize complementary electrostatics while avoiding sterical clashes with the methyl group on the heterocycle. However, the residence time of ATP in the MD simulations is more than double that of CTP. In light of the larger surface of purines, the hydrophobic effect appears to be the predominant energetic contribution that drives the association of nucleotide and fluorophore. In fact, the stabilization effect of the NTPs on the fluorescence lifetime is dependent on the polarity of the solvent. In a solution of 60% 1,4-dioxane (ε at 25 °C = 2.2156) ATP barely influences the lifetime of sCy3, suggesting that the tendency of the two partners to interact is decreasing (ESI,† Fig. S1c). The entropic gain upon desolvation is likely lower since fewer water molecules are expelled from both the nucleotide and the dye surface. We conclude that all NTPs, albeit to a different extent, act as a scaffold to which the dyes may associate and thereby get restricted along the dihedral reaction coordinate. In this way, non-radiative relaxation through the twisted intermediate to the dim cis-state is attenuated and the survival of the trans-isomer, in return, is enhanced. In short, these observations provide evidence for RIFE to occur even on the single nucleotide level.
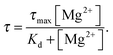


![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−EN→t/RT), affords
exp(−EN→t/RT), affords