Open Access Article
Open Access ArticleFluorescence quantum yield rationalized by the magnitude of the charge transfer in π-conjugated terpyridine derivatives†
Marie
Humbert-Droz
*a,
Claude
Piguet
b and
Tomasz A.
Wesolowski
c
aUniversity of Geneva, Geneva, Switzerland. E-mail: Marie.Humbert-Droz@unige.ch
bSciences II, Department of Inorganic Analytical Chemistry, University of Geneva, Geneva 4, Switzerland
cUniversity of Geneva, Physical Chemistry, 30, quai Ernest-Ansermet, Geneve, Switzerland. E-mail: Tomasz.Wesolowski@unige.ch
First published on 16th September 2016
Abstract
Terpyridine derivatives are of great interest due to their unique photophysical properties when used as antennas in metallic complexes. Several experimental and theoretical studies indicate strong charge-transfer character of the lowest electronic excited state, which could be exploited for predicting fluorescence quantum yields from the magnitude of the charge separation induced by electronic transitions. Focusing on substituted 4′-phenyl-2,2′:6′2′′-terpyridyl, we report on two measures of the charge separation obtained from high-level calculations in ground and excited states (length of the change of the dipole moment and the electron–hole distance). Our refined model confirms that the fluorescence quantum yield shows a global S-shape dependence on the magnitude of the charge separation, which can be quantified either by the change in dipole moments between the ground and excited states or by the associated charge–hole distances. This approach provides a remarkable tool for the molecular design of a fluorescent polyaromatic antenna.
Introduction
The design and synthesis of organic chromophores with predetermined fluorescence quantum yields could be greatly simplified if the latter property could be related to some simple molecular descriptors. In this context, Yamaguchi et al. investigated the photo-physical properties of conjugated (1–7, P0–P3) and fused (C1–C4) aromatic hydrocarbons (Fig. 1 and Table S1, ESI†).1 These authors suggest that a π conjugation length Aπ, characteristic of a polyaromatic chromophore, can be interpreted as the charge separation produced by the electronic excitation (Fig. 2b).1 Inspired by this idea, one can take advantage of modern quantum chemistry methods, which – in principle – can be used to obtain the charge densities for the considered electronic states. The charge separation between the ground- and excited state wavefunctions could be estimated with the help of two scalar quantities (1) the length of the change of the dipole moment |Δ![[small mu, Greek, vector]](https://www.rsc.org/images/entities/i_char_e0e9.gif) | between the ground and excited state and (2) the charge–hole distance dhe, which are both theoretically accessible.2 However, correlations of these electronic probes with the conjugation length Aπ defined in Fig. 2 are not straightforward because both |Δ
| between the ground and excited state and (2) the charge–hole distance dhe, which are both theoretically accessible.2 However, correlations of these electronic probes with the conjugation length Aπ defined in Fig. 2 are not straightforward because both |Δ![[small mu, Greek, vector]](https://www.rsc.org/images/entities/i_char_e0e9.gif) | and dhe vanish for the centrosymmetrical molecules considered in Fig. 1.
| and dhe vanish for the centrosymmetrical molecules considered in Fig. 1.
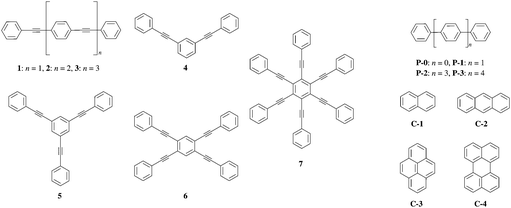 | ||
| Fig. 1 Structures of π-conjugated hydrocarbons used in ref. 1. | ||
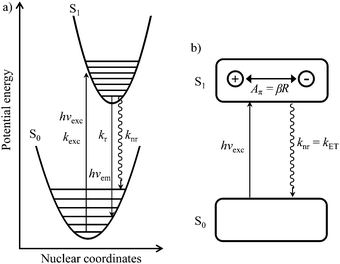 | ||
| Fig. 2 (a) Potential energy diagram showing light absorption (hνexc,kexc), fluorescence emission (hνem,kr) and radiationless (knr) processes for the excitation of conjugated aromatic molecules. (b) Simple electron-transfer model proposed by Yamaguchi et al.1 illustrating the π-conjugation length (Aπ) in the S1 state of a π conjugated molecule. | ||
In order to model the fluorescence quantum yield ΦF = kr/(kr + knr), both radiative kr and non-radiative de-excitation processes should be at hand (left part of Fig. 2). Obviously, the S0 → S1 transition is expected, and indeed does, modify the electronic structure of the aromatic molecule,2 a process assigned by Yamaguchi et al. to the formation of a permanent dipole in the S1 state represented by the so-called π conjugation length (see Fig. 2).1
With this hypothesis in mind, the radiative emission rate constant kr is given by Einstein's equation where A1,0 is the Einstein transition rate constant for spontaneous emission (in s−1).3–5
| kr = A1,0 | (1) |
Since the energy gap between the S1 and S0 levels in polyaromatic molecules is usually larger than 20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cm−1 (Table S1 in the ESI†), any deactivation due to coupling with high-energy phonons can be neglected.6 The non-radiative rate constant (knr, the sum of intersystem crossing and internal conversion)7–9 was thus assigned by Yamaguchi et al.1,10 to the relaxation of the induced dipole resulting from the intramolecular electron transfer. The constant knr can then be modelled by means of the Hush equation:
000 cm−1 (Table S1 in the ESI†), any deactivation due to coupling with high-energy phonons can be neglected.6 The non-radiative rate constant (knr, the sum of intersystem crossing and internal conversion)7–9 was thus assigned by Yamaguchi et al.1,10 to the relaxation of the induced dipole resulting from the intramolecular electron transfer. The constant knr can then be modelled by means of the Hush equation:
| knr ≡ kET = k0e−βR | (2) |
Taking βR = Aπ as a measure of the π conjugation length of the aromatic system in the S1 state, its limiting values k0 for Aπ = 0 were assigned to Einstein transition probability for stimulated emission B1,0 (in [m3 J−1 s−2]) induced by the spectral energy density ρ(ν) (in [J s m−3]) produced by an isotropic radiation field at the frequency ν of the emission band (h is Planck's constant, kB is Boltzmann's constant, c is the vacuum speed of light and T is the absolute temperature).1,3–5 Let us stress here that the original derivation1 neglects the contribution of the spectral energy density. This approximation can be lifted in a straightforward manner with the introduction of the Boltzmann factor exp(hν/kBT) measuring the effect of the energy band gap on the non-radiative relaxation process:
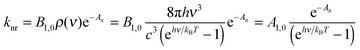 | (3) |
From eqn (1) and (3) it follows that:
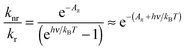 | (4) |
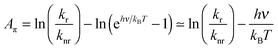 | (5) |
Note the similarity of eqn (5) to eqn (10) from ref. 1, which can be cast in the form:
| Aπ − Arefπ = ln(kr/knr) | (6) |
Eqn (6) mirrors eqn (5) of the present work if all members of the family of aromatic hydrocarbons under investigation possess the same energy gap hνref separating the S1 and S0 states (then Arefπ = −hνref/kBT).
Since the fluorescence quantum yield ΦF is defined as:
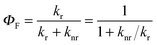 | (7) |
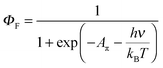 | (8) |
A π can thus be easily computed for a family of compounds as soon as their quantum yields and emission energy frequencies are available (Table S1, column 10 in the ESI†). The plot of Aπ computed for compounds 1–3, P0–P3 and C1–C4 against their longest molecular axis (Fig. 3) indeed suggests the existence of an intriguing correlation between the experimental spectroscopic Aπ parameter and some molecular dimensions attributed to the π-conjugation length.1
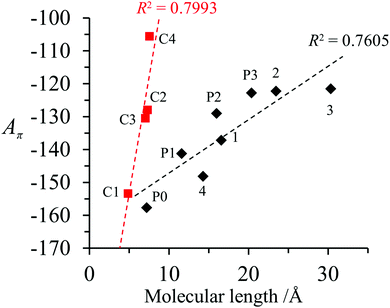 | ||
| Fig. 3 Plot of Aπ against longest molecular lengths taken from ref. 1 in the ground state for conjugated (black diamonds) and fused (red squares) aromatic hydrocarbons (built using the data reported in Table S1, ESI†).1 Assuming a 10% uncertainty for the measured ΦF, the size of the resulting error bars on Aπ is smaller than the size of the symbols. The error bars are thus not shown. | ||
Pushing further this strategy, the next step consists in the identification of one or several physically-relevant electronic properties which could be used as reliable estimations of Aπ parameters. The obvious choice suggested by Fig. 2b1 is the length of the difference between the dipole moments (|Δ![[small mu, Greek, vector]](https://www.rsc.org/images/entities/i_char_e0e9.gif) |) in states S1 and S0. If |Δ
|) in states S1 and S0. If |Δ![[small mu, Greek, vector]](https://www.rsc.org/images/entities/i_char_e0e9.gif) | is expressed in [e Å], its numerical value corresponds to the charge separation in Å. Moreover, the vector Δ
| is expressed in [e Å], its numerical value corresponds to the charge separation in Å. Moreover, the vector Δ![[small mu, Greek, vector]](https://www.rsc.org/images/entities/i_char_e0e9.gif) provides the information about the direction of the charge transfer. Unfortunately, this simple measure of charge separation is not applicable for centrosymmetric molecules 1–3, P0–P3 and C1–C4 gathered in Fig. 1.1 In such a case, the first non-vanishing change in the electric moment has a quadrupole character, and the interpretation of the change in the quadrupole moment as the displacement of electric charge is not unique.
provides the information about the direction of the charge transfer. Unfortunately, this simple measure of charge separation is not applicable for centrosymmetric molecules 1–3, P0–P3 and C1–C4 gathered in Fig. 1.1 In such a case, the first non-vanishing change in the electric moment has a quadrupole character, and the interpretation of the change in the quadrupole moment as the displacement of electric charge is not unique.
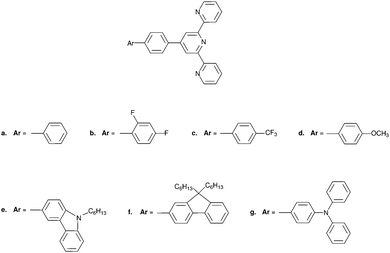
The alternative charge–hole separation distance (dhe), evaluated for the one-particle transition density matrix,2 may independently support the change in dipole moments, but it also vanishes for centrosymmetrical molecules. In order to remove symmetry limitations in the interpretation of Aπ, we decide to compute |Δ![[small mu, Greek, vector]](https://www.rsc.org/images/entities/i_char_e0e9.gif) | and dhe for a series of non-centrosymmetric 4′-phenly-2,2′:6′,2′′-terpyridyl compounds 1a–1g (Fig. 4), the photo-physical properties of which were recently reported which allow us to determine the experimental Aπ parameter using eqn (5) (see Table 1).12 It is worth reminding here that terpyridine derivatives are of great interest due to their unique photo-physical properties if used as sensitizers for transition metals. Several experimental and theoretical studies indicate strong charge-transfer character of the lowest electronic excited state12–14 and the presence of nitrogen atoms in the aromatic molecules 1a–1g (compared with the pure hydrocarbons gathered in Fig. 1) is known to reinforce the spin–orbit coupling constant. Intersystem crossing (ISC) processes then become the dominant contributions to the non-radiative deexcitation rate constants of the S1 states, which optimizes light downshifting in luminescent metallic complexes.7–9,15
| and dhe for a series of non-centrosymmetric 4′-phenly-2,2′:6′,2′′-terpyridyl compounds 1a–1g (Fig. 4), the photo-physical properties of which were recently reported which allow us to determine the experimental Aπ parameter using eqn (5) (see Table 1).12 It is worth reminding here that terpyridine derivatives are of great interest due to their unique photo-physical properties if used as sensitizers for transition metals. Several experimental and theoretical studies indicate strong charge-transfer character of the lowest electronic excited state12–14 and the presence of nitrogen atoms in the aromatic molecules 1a–1g (compared with the pure hydrocarbons gathered in Fig. 1) is known to reinforce the spin–orbit coupling constant. Intersystem crossing (ISC) processes then become the dominant contributions to the non-radiative deexcitation rate constants of the S1 states, which optimizes light downshifting in luminescent metallic complexes.7–9,15
| Cmpd | Φ F | λ em (nm) | ν em (s−1) | log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) εa εa |
λ abs (nm) | τ (ns) | k r (s−1) | k nr (s−1) | A π eqn (5) | hν/kBT | |Δ![[small mu, Greek, vector]](https://www.rsc.org/images/entities/i_char_e0e9.gif) | (e Å) | (e Å) |
d ch (Å) |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| a Data taken from ref. 12. | ||||||||||||
| 1a | 0.18 | 360 | 8.33 × 1014 | 4.89 | 291 | 2.14 | 8.41 × 107 | 3.83 × 108 | −135.7 | 134.2 | 1.51 | 5.05 |
| 1b | 0.16 | 358 | 8.37 × 1014 | 4.86 | 287 | 1.77 | 9.04 × 107 | 4.75 × 108 | −136.6 | 134.9 | 1.12 | 4.64 |
| 1c | 0.17 | 359 | 8.35 × 1014 | 4.87 | 289 | 1.48 | 1.15 × 108 | 5.61 × 108 | −136.1 | 134.5 | 0.43 | 4.12 |
| 1d | 0.50 | 403 | 7.44 × 1014 | 4.71 | 298 | 2.15 | 2.33 × 108 | 2.33 × 108 | −119.8 | 119.8 | 2.58 | 5.43 |
| 1e | 0.73 | 447 | 6.71 × 1014 | 4.52 | 296 | 1.51 | 4.83 × 108 | 1.79 × 108 | −107.1 | 108.0 | 4.05 | 6.38 |
| 1f | 0.92 | 409 | 7.33 × 1014 | 4.56 | 327 | 0.77 | 1.19 × 109 | 1.04 × 108 | −115.6 | 118.1 | 1.50 | 5.32 |
| 1g | 0.60 | 489 | 6.13 × 1014 | 4.60 | 284 | 2.68 | 8.41 × 108 | 1.79 × 108 | −98.4 | 98.8 | 3.67 | 6.30 |
For each considered compound, the charge-separation magnitudes (|Δ![[small mu, Greek, vector]](https://www.rsc.org/images/entities/i_char_e0e9.gif) | and dhe) were evaluated in the following procedure. (A) The geometry of the isolated species was optimized at the ground state. (B) Electronic excited states were obtained. The lowest state with a high oscillator strength (the one corresponding to the lowest maxima of the absorption band) was identified. It was usually the lowest excitation. The calculated vertical excitation energy was compared to the experimental absorption band maximum in order to validate the used methodology. (C) The charge-separation magnitudes |Δ
| and dhe) were evaluated in the following procedure. (A) The geometry of the isolated species was optimized at the ground state. (B) Electronic excited states were obtained. The lowest state with a high oscillator strength (the one corresponding to the lowest maxima of the absorption band) was identified. It was usually the lowest excitation. The calculated vertical excitation energy was compared to the experimental absorption band maximum in order to validate the used methodology. (C) The charge-separation magnitudes |Δ![[small mu, Greek, vector]](https://www.rsc.org/images/entities/i_char_e0e9.gif) | and dhe, which were used as the first-principles counterparts of the empirical parameter Aπ in subsequent analyses, were evaluated at the ground-state geometry for the state identified in step B. This simple procedure providing numerical values of the charge-separation magnitudes is obviously not general. It neglects the fact that fluorescence occurs at excited state geometry, the solvent effects on both the geometry and the electronic structure, and the fact that if the state with the highest oscillator strength appears not to be the lowest excitation (three out of seven investigated compounds) violating thus Kasha's rule. Last but not least, the procedure is not applicable if both ground and excited state geometries remain centrosymmetric. The compounds chosen for the present analysis are not centrosymmetric and are rigid. Their geometry is not expected to be significantly affected by either the solvent or the excitation. The effect of the solvent and the relaxation of geometry upon excitation might change the order of states nevertheless. Without explicitly modelling these effects, we have chosen to evaluate the charge separation magnitudes for the same state assigned to the lowest maximum of the absorption band assuming that it becomes the emitting state in the excited state geometry and in the presence of the solvent. We underline that the primary objective of the present work is to verify if there exists a relation at all between the empirical parameter Aπ and the quantum mechanical observable measuring the charge-separation magnitude.
| and dhe, which were used as the first-principles counterparts of the empirical parameter Aπ in subsequent analyses, were evaluated at the ground-state geometry for the state identified in step B. This simple procedure providing numerical values of the charge-separation magnitudes is obviously not general. It neglects the fact that fluorescence occurs at excited state geometry, the solvent effects on both the geometry and the electronic structure, and the fact that if the state with the highest oscillator strength appears not to be the lowest excitation (three out of seven investigated compounds) violating thus Kasha's rule. Last but not least, the procedure is not applicable if both ground and excited state geometries remain centrosymmetric. The compounds chosen for the present analysis are not centrosymmetric and are rigid. Their geometry is not expected to be significantly affected by either the solvent or the excitation. The effect of the solvent and the relaxation of geometry upon excitation might change the order of states nevertheless. Without explicitly modelling these effects, we have chosen to evaluate the charge separation magnitudes for the same state assigned to the lowest maximum of the absorption band assuming that it becomes the emitting state in the excited state geometry and in the presence of the solvent. We underline that the primary objective of the present work is to verify if there exists a relation at all between the empirical parameter Aπ and the quantum mechanical observable measuring the charge-separation magnitude.
Computational details
The ground-state geometries of all compounds were obtained from DFT/CAM-B3LYP/cc-pVTZ calculations and are provided in the ESI.† For all ab initio calculations (ADC(2) and CC2), the cc-pVTZ basis set with frozen core orbitals was used as well as the resolution-of-identity approximation. The ground-state geometries, and LR-TDDFT calculations were performed using the GAUSSIAN09 software,16 whereas the TURBOMOLE v. 6.6 program package17 was used for ADC(2) and CC2. The analysis of the transition in terms of the exciton size and the generation of electron and hole densities was performed using the TheoDORE 1.2 program.18Results and discussion
The key issue of the present work is the relation between the computed |Δ![[small mu, Greek, vector]](https://www.rsc.org/images/entities/i_char_e0e9.gif) | (or deh) and the measured fluorescence quantum yield. The discussion of this relation hinges on the quality of the calculated |Δ
| (or deh) and the measured fluorescence quantum yield. The discussion of this relation hinges on the quality of the calculated |Δ![[small mu, Greek, vector]](https://www.rsc.org/images/entities/i_char_e0e9.gif) |. Unfortunately, the relevant chromophores, considered in the present study, are rather large as far as the feasibility of benchmark-quality quantum-chemistry methods is concerned. The evaluation of |Δ
|. Unfortunately, the relevant chromophores, considered in the present study, are rather large as far as the feasibility of benchmark-quality quantum-chemistry methods is concerned. The evaluation of |Δ![[small mu, Greek, vector]](https://www.rsc.org/images/entities/i_char_e0e9.gif) | is, therefore, limited to medium-quality quantum chemistry methods. In the absence of dedicated studies concerning the reliability of |Δ
| is, therefore, limited to medium-quality quantum chemistry methods. In the absence of dedicated studies concerning the reliability of |Δ![[small mu, Greek, vector]](https://www.rsc.org/images/entities/i_char_e0e9.gif) | and dhe obtained using different quantum-chemistry methods, we used an ad hoc criterion for selecting the molecules for which the theoretical calculations yield |Δ
| and dhe obtained using different quantum-chemistry methods, we used an ad hoc criterion for selecting the molecules for which the theoretical calculations yield |Δ![[small mu, Greek, vector]](https://www.rsc.org/images/entities/i_char_e0e9.gif) | and dhe suitable for further analysis. Any method failing to yield accurate excitation energy is expected to provide unreliable numerical value of |Δ
| and dhe suitable for further analysis. Any method failing to yield accurate excitation energy is expected to provide unreliable numerical value of |Δ![[small mu, Greek, vector]](https://www.rsc.org/images/entities/i_char_e0e9.gif) | and dhe. The excitation energies calculated by means of a given method were directly compared to the maxima of the experimental absorption spectra12 in order to select the method yielding the excited state wavefunctions admissible for the validation of eqn (5). Three methods were considered: (a) Linear-Response Time-Dependent Density Functional Theory (LR-TDDFT)19 with CAM-B3LYP approximation20 for the exchange–correlation energy functional, (b) second-order approximate Coupled Cluster (CC2),21 and (c) second-order Algebraic-Diagrammatic-Construction (ADC(2)).22 The high-level wavefunction based methods (ADC(2) and CC2) are expected to be the most reliable ones. The strategy to construct correlated excited state wavefunction is different in both cases, but either method can describe reliably both local and charge-transfer excitations. Among LR-TDDFT methods, the range-separated approximations to the exchange–correlation energy, such as the chosen one (CAM-B3LYP), are known to handle charge-transfer in electronic excitations in the most reliable way. Other approximations for the exchange–correlation energy such as B3LYP, originally used for the study of terpyridyl compounds 1a–1g,12,13 are not considered in the present work due to their known unreliable performance in describing the excited states of charge-transfer character.23,24 The computational costs of CAM-B3LYP calculations are significantly lower than either ADC(2) or CC2. The CAM-B3LYP method was, therefore, also considered in the present work in view of possible future applications for larger molecules.
| and dhe. The excitation energies calculated by means of a given method were directly compared to the maxima of the experimental absorption spectra12 in order to select the method yielding the excited state wavefunctions admissible for the validation of eqn (5). Three methods were considered: (a) Linear-Response Time-Dependent Density Functional Theory (LR-TDDFT)19 with CAM-B3LYP approximation20 for the exchange–correlation energy functional, (b) second-order approximate Coupled Cluster (CC2),21 and (c) second-order Algebraic-Diagrammatic-Construction (ADC(2)).22 The high-level wavefunction based methods (ADC(2) and CC2) are expected to be the most reliable ones. The strategy to construct correlated excited state wavefunction is different in both cases, but either method can describe reliably both local and charge-transfer excitations. Among LR-TDDFT methods, the range-separated approximations to the exchange–correlation energy, such as the chosen one (CAM-B3LYP), are known to handle charge-transfer in electronic excitations in the most reliable way. Other approximations for the exchange–correlation energy such as B3LYP, originally used for the study of terpyridyl compounds 1a–1g,12,13 are not considered in the present work due to their known unreliable performance in describing the excited states of charge-transfer character.23,24 The computational costs of CAM-B3LYP calculations are significantly lower than either ADC(2) or CC2. The CAM-B3LYP method was, therefore, also considered in the present work in view of possible future applications for larger molecules.
Assignment of excited states and validation of the calculated excited states
All compounds show a very intense absorption band assigned to the spin-allowed π–π* transition.12 This is consistent with our calculations, the details of which are given below. In addition to this very intense transition, the measured spectra of the larger compounds show a shoulder at long wavelength that is attributed to the intra-molecular charge transfer (ICT) transition.12Interpreting the character of the transition looking at the orbitals (Fig. S15–S21 in the ESI†), our CC2 or ADC(2) calculations give transitions of ICT characters for compounds 1c, 1e, and 1g (strong) and a weak ICT character for compound 1f. In contrast, compounds 1a, 1b and 1d show an excitation delocalized on the π system. Analyzing the transition in terms of electron–hole densities, using the one particle transition density matrix,2,25 gives a more precise picture on the nature of the excitation. Fig. 5 shows the electron and hole densities of the considered transition for all compounds. The interpretation remains mostly the same as given by orbital analysis, except for compound 1c that shows a highly local π–π* excitation on the central ring of the terpyridyl unit.
 | ||
| Fig. 5 The electron (green) and hole densities of the excitation of interest deduced from the one-particle transition density matrix. | ||
The first step in the analysis of charge separation upon electronic excitation is the identification of the state from which the fluorescence occurs. According to Liu et al.,12 the emitting state which controls the experimental quantum yield can be assigned to the specific π–π*/ICT state (Fig. 6). We consequently assume the π–π* state for compounds 1a, 1b, 1c and 1d and the ICT state for compounds 1e, 1f, and 1g. All the incriminated transitions display large computed oscillator strengths (f > 1), except for compound 1c, for which a very intense transition lies 0.4 eV above the considered state. For compounds 1a and 1b, LR-TDDFT overestimates the charge transfer excitation energy, giving rise to an ordering of the states different to that found using CC2 and ADC(2). For the other compounds, the ordering of the states is the same as the one obtained from CC2 and ADC(2) calculations. The excitation energies are, however, mostly overestimated (by more than 0.2 eV). Fig. 6 shows the orbitals participating in those transitions for compound 1a. Pictures of orbitals for all remaining compounds are provided in the ESI† (Fig. S15–S21).
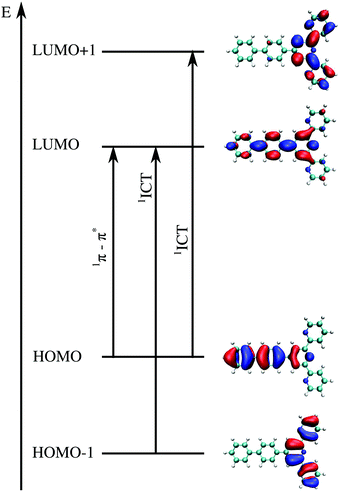 | ||
| Fig. 6 Illustrative example of molecular orbitals involved in the two transitions of interest for compound 1a. The intense π–π* transition involves orbitals of the type of HOMO → LUMO whereas the intramolecular charge transfer has usually two main components, involving MO HOMO−1 → LUMO and from HOMO → LUMO+1. The details of all excitations of interest including orbitals can be found in the ESI† (Tables S31–S44 and Fig. S15–S21). | ||
The calculated energies are compared with energies corresponding to the maxima of the absorption bands  in Fig. 7 and collected in Table 2. The observed differences can be attributed not only to the accuracy of the used computational method, but also to other factors. Firstly, the vertical excitation energies and the maxima of the absorption bands are not the same quantity. Secondly, the calculations are made in a vacuum at ground-state DFT geometries without taking into account the vibronic structure of the solvated chromophore. Large discrepancies between the vertical excitation energies calculated in the gas phase and the maxima of the absorption bands in non-polar solvents can be attributed to the flaws of the used quantum mechanical method. In the case of LR-TDDFT, the differences between the experimental and calculated energies are widely scattered (red crosses in Fig. 7 represent the correlation coefficient: 0.79), and this despite the use of the CAM-B3LYP functional, which is known to describe reasonably well the charge transfer excitations. Unfortunately, this method does not satisfy the necessary conditions to be used for the evaluation of the charge separation magnitudes.
in Fig. 7 and collected in Table 2. The observed differences can be attributed not only to the accuracy of the used computational method, but also to other factors. Firstly, the vertical excitation energies and the maxima of the absorption bands are not the same quantity. Secondly, the calculations are made in a vacuum at ground-state DFT geometries without taking into account the vibronic structure of the solvated chromophore. Large discrepancies between the vertical excitation energies calculated in the gas phase and the maxima of the absorption bands in non-polar solvents can be attributed to the flaws of the used quantum mechanical method. In the case of LR-TDDFT, the differences between the experimental and calculated energies are widely scattered (red crosses in Fig. 7 represent the correlation coefficient: 0.79), and this despite the use of the CAM-B3LYP functional, which is known to describe reasonably well the charge transfer excitations. Unfortunately, this method does not satisfy the necessary conditions to be used for the evaluation of the charge separation magnitudes.
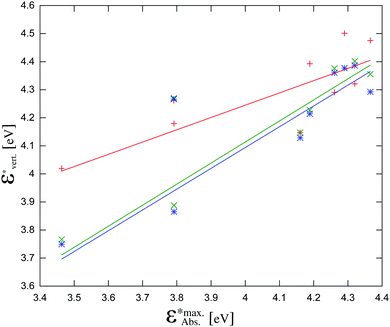 | ||
Fig. 7 The calculated vertical excitation energies (π–π* for all compounds and ICT for 1c, 1e, 1f, 1g) calculated using the three considered methods vs. experimental maxima of the absorption bands (taken from ref. 12): red crosses: LR-TDDFT, green crosses: CC2, blue stars: ADC(2). The data points at 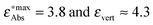 correspond to compound 1f. correspond to compound 1f. | ||
| Compound | Character | CAM-B3LYPa | CC2a | ADC(2)a | Exp.b |
|---|---|---|---|---|---|
| a This work. b Y. Liu et al., J. Lumin., 2015, 157, 249. | |||||
| 1a | π–π* | 4.2903 | 4.3759 | 4.3607 | 4.2606 |
| 1b | π–π* | 4.3207 | 4.4018 | 4.3864 | 4.3200 |
| 1c | π–π* | 4.5011 | 4.3770 | 4.3771 | 4.2901 |
| 1d | π–π* | 4.1471 | 4.1472 | 4.1285 | 4.1605 |
| 1e | π–π* | 4.1793 | 3.8877 | 3.8649 | 3.7916 |
| 1e | ICT | 4.3927 | 4.2275 | 4.2141 | 4.1887 |
| 1f | π–π* | 4.2619 | 4.2691 | 4.2664 | 3.7916 |
| 1g | ICT | 4.0193 | 3.7662 | 3.7494 | 3.4633 |
| 1g | π–π* | 4.4753 | 4.3552 | 4.2923 | 4.3656 |
The vertical excitation energies calculated with CC2 and ADC(2) show a remarkable agreement with each other within 0.02 eV for most excitation energies (Fig. 7 and Table S2, ESI†). The agreement with the energies corresponding to the experimental maxima of the absorption bands is not perfect, but of much better quality than that obtained with LR-TDDFT/CAM-B3LYP (green and blue crosses in Fig. 7 represent correlation coefficients: 0.87 and 0.85 respectively). For one molecule – compound 1f – neither CC2 nor ADC(2) yield satisfactory excitation energies. Without taking into account compound 1f, the slopes of the linear regression lines in Fig. 7 are 0.75 for CC2 and 0.74 for ADC(2), respectively. The corresponding correlation coefficients are 0.97 and 0.96, respectively. The exceptional failure of both ADC(2) and CC2 to yield reliable excitation energy for compound 1f indicates that other excited state properties can be expected to be less accurately described using these methods. For this reason, although we report the obtained values of |Δ![[small mu, Greek, vector]](https://www.rsc.org/images/entities/i_char_e0e9.gif) | for compound 1f, we do not use it in the discussion of the phenomenological model linking |Δ
| for compound 1f, we do not use it in the discussion of the phenomenological model linking |Δ![[small mu, Greek, vector]](https://www.rsc.org/images/entities/i_char_e0e9.gif) | with ΦF.
| with ΦF.
The case of compound 1f
The calculated values of the excitation energy for the considered state show clearly that the used quantum mechanical method does not yield a reliable description of the electronic excited state of compound 1f. The ADC(2) vertical excitation energy for the lowest excitation (which is also the brightest one) overestimates the experimental value significantly (4.26 eV vs. 3.79 eV). This discrepancy is about one order of magnitude larger than that in the case of the remaining molecules used for the analysis (see Table 2). |Δ![[small mu, Greek, vector]](https://www.rsc.org/images/entities/i_char_e0e9.gif) | evaluated using the wave function yielding such large error in energy cannot, therefore, be considered as reliable. Unfortunately, using a more accurate method from the arsenal of Quantum Chemistry methods (ADC(3) or higher order coupled cluster methods than CC2 for instance) is not practical for a molecule of this size.
| evaluated using the wave function yielding such large error in energy cannot, therefore, be considered as reliable. Unfortunately, using a more accurate method from the arsenal of Quantum Chemistry methods (ADC(3) or higher order coupled cluster methods than CC2 for instance) is not practical for a molecule of this size.
This exception calls for a further attention as it can be the result of (a) experimental measurement of ΦF, (b) unbalanced errors in wavefunction at ground- and excited states obtained by the selected method, (c) inadequate description of the system (thermal motions of the system, the effect of the solvent), (d) evaluation of |Δ![[small mu, Greek, vector]](https://www.rsc.org/images/entities/i_char_e0e9.gif) | for the wrong excited state (not the one which is involved in fluorescence), and last but not least (d) approximations underlying eqn (8). Since it is relatively straightforward to estimate in a rough way the effect of the solvent in which the measurements are made (CH2Cl2), a polarizable continuum model (PCM) with the corresponding dielectric constant ε = 8.93 combined with LR-TDDFT was used for this purpose. Neither the indirect effect of the solvent on the geometry nor the direct effect of the solvent on the excitation energy affect the excitation energy significantly enough (at most 0.1 eV and 0.12 eV, respectively) to explain the discrepancy between the experimental and calculated excitation energy in the case of compound 1f. Another factor which might explain the observed discrepancy could be the used geometry at which the excitation energy is calculated. The planarization of the molecule lowers the excitation energy from 4.26 eV to 4.02 eV, thus reducing the overestimation by half. The value of the vertical excitation energy nevertheless remains out of the correlation. Note that a perpendicular arrangement of the aromatic rings drastically increases the excitation energies (Tables S76–S79 and Fig. S30 and S31, ESI†).
| for the wrong excited state (not the one which is involved in fluorescence), and last but not least (d) approximations underlying eqn (8). Since it is relatively straightforward to estimate in a rough way the effect of the solvent in which the measurements are made (CH2Cl2), a polarizable continuum model (PCM) with the corresponding dielectric constant ε = 8.93 combined with LR-TDDFT was used for this purpose. Neither the indirect effect of the solvent on the geometry nor the direct effect of the solvent on the excitation energy affect the excitation energy significantly enough (at most 0.1 eV and 0.12 eV, respectively) to explain the discrepancy between the experimental and calculated excitation energy in the case of compound 1f. Another factor which might explain the observed discrepancy could be the used geometry at which the excitation energy is calculated. The planarization of the molecule lowers the excitation energy from 4.26 eV to 4.02 eV, thus reducing the overestimation by half. The value of the vertical excitation energy nevertheless remains out of the correlation. Note that a perpendicular arrangement of the aromatic rings drastically increases the excitation energies (Tables S76–S79 and Fig. S30 and S31, ESI†).
The charge separation upon electronic excitation
The dipole moments for compounds 1a–1g were thus computed using the ADC(2) method and reported in units of [e Å] in order to relate the change in the dipole moment with a displacement of charge per unit of distance (as proposed for Aπ in Fig. 2b). One immediately notes that, the S0 and S1 states for compounds 1a, 1b, 1c and 1d correspond to π–π* excitations whereas for compounds 1e, 1f and 1g they have ICT character. The computed values of |Δ![[small mu, Greek, vector]](https://www.rsc.org/images/entities/i_char_e0e9.gif) | do not show specific correlations with the nature of the reorganization of the electronic structure (Fig. 8) upon excitation. It is worthwhile to note that the orientation of the vectors Δ
| do not show specific correlations with the nature of the reorganization of the electronic structure (Fig. 8) upon excitation. It is worthwhile to note that the orientation of the vectors Δ![[small mu, Greek, vector]](https://www.rsc.org/images/entities/i_char_e0e9.gif) shown in Fig. 8, which is a well-defined quantum-mechanical observable, not always coincides with the intuitive line defined by the chain of conjugated π systems (the case of compound 1e). In agreement with Neuman's principle,26 the change in dipole moment is aligned with the two-fold axis in the C2-symmetrical terpyridines 1a, 1c and 1g. Only minimal deviations can be detected for 1b, 1d, 1e and 1f which possess only a pseudo-C2 axis (Fig. 8). We also notice that Δ
shown in Fig. 8, which is a well-defined quantum-mechanical observable, not always coincides with the intuitive line defined by the chain of conjugated π systems (the case of compound 1e). In agreement with Neuman's principle,26 the change in dipole moment is aligned with the two-fold axis in the C2-symmetrical terpyridines 1a, 1c and 1g. Only minimal deviations can be detected for 1b, 1d, 1e and 1f which possess only a pseudo-C2 axis (Fig. 8). We also notice that Δ![[small mu, Greek, vector]](https://www.rsc.org/images/entities/i_char_e0e9.gif) systematically points from the central pyridine ring towards the substituent, except for compound 1c, in which a strongly electron-withdrawing –CF3 group is attached. A careful look at the frontier orbitals, and whatever the exact rotational position of the CF3 group with respect to the aromatic phenyl ring to which it is connected (see Tables S59–S66 and Fig. S22–S25 in the ESI†), shows that compound 1c is the only one for which the HOMO is entirely localized onto the terpyridine unit.
systematically points from the central pyridine ring towards the substituent, except for compound 1c, in which a strongly electron-withdrawing –CF3 group is attached. A careful look at the frontier orbitals, and whatever the exact rotational position of the CF3 group with respect to the aromatic phenyl ring to which it is connected (see Tables S59–S66 and Fig. S22–S25 in the ESI†), shows that compound 1c is the only one for which the HOMO is entirely localized onto the terpyridine unit.
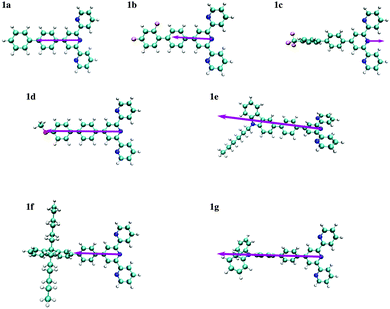 | ||
Fig. 8 Schematic representation of vector of the changes in dipole moments Δ![[small mu, Greek, vector]](https://www.rsc.org/images/entities/i_char_e0e9.gif) computed for substituted 4′-phenyl-2,2′:6′2′′-terpyridines 1a–1g. The length of the arrows representing Δ computed for substituted 4′-phenyl-2,2′:6′2′′-terpyridines 1a–1g. The length of the arrows representing Δ![[small mu, Greek, vector]](https://www.rsc.org/images/entities/i_char_e0e9.gif) is proportional to the change in the dipole moment given in Table 2. Δ is proportional to the change in the dipole moment given in Table 2. Δ![[small mu, Greek, vector]](https://www.rsc.org/images/entities/i_char_e0e9.gif) is oriented along the pseudo two-fold molecular axis. is oriented along the pseudo two-fold molecular axis. | ||
We are now in a position to plot the experimental values of the spectroscopic π-conjugation length Aπ calculated using eqn (5) (Table 1, column 10) as a function of the computed change in dipole moments. Fig. 9, blue dataset, shows that there is roughly a linear correlation between |Δ![[small mu, Greek, vector]](https://www.rsc.org/images/entities/i_char_e0e9.gif) | and Aπ. As a second measure of the charge separation upon excitation, the exciton sizes dhe have also been plotted against Aπ in Fig. 9 (green diamonds), which indeed confirms the existence of a linear correlation.
| and Aπ. As a second measure of the charge separation upon excitation, the exciton sizes dhe have also been plotted against Aπ in Fig. 9 (green diamonds), which indeed confirms the existence of a linear correlation.
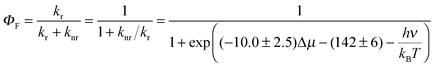 | (9a) |
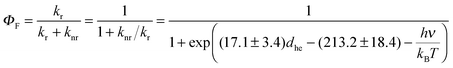 | (9b) |
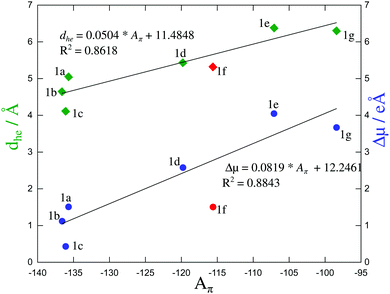 | ||
| Fig. 9 Computed change in the dipole moment (in [e Å−1]) and exciton size (in [Å]) as a function of the π-conjugation length Aπ calculated from eqn (5). Assuming a 10% uncertainty for the measured ΦF, the size of the resulting error bars on Aπ is smaller than the size of the symbols. The error bars are thus not shown. The linear regression lines used data for all compounds except for 1f (data shown in red). | ||
The estimations of Aπ with the help of either |Δ![[small mu, Greek, vector]](https://www.rsc.org/images/entities/i_char_e0e9.gif) | (eqn (9a)) or dhe (eqn (9b)) finally show satisfying sigmoidal correlation with the quantum yields (Fig. 10) for all terpyridyl compounds – except 1f. Clearly, |Δ
| (eqn (9a)) or dhe (eqn (9b)) finally show satisfying sigmoidal correlation with the quantum yields (Fig. 10) for all terpyridyl compounds – except 1f. Clearly, |Δ![[small mu, Greek, vector]](https://www.rsc.org/images/entities/i_char_e0e9.gif) | computed for 1f lies far from the sigmoidal curve. The reported value of |Δ
| computed for 1f lies far from the sigmoidal curve. The reported value of |Δ![[small mu, Greek, vector]](https://www.rsc.org/images/entities/i_char_e0e9.gif) | was evaluated for the first (and also the brightest) excited state of compound 1f. For higher excited states, |Δ
| was evaluated for the first (and also the brightest) excited state of compound 1f. For higher excited states, |Δ![[small mu, Greek, vector]](https://www.rsc.org/images/entities/i_char_e0e9.gif) | is even smaller (between 3.24 and 4.7 for S2–S4, ESI†), which results in even larger deviation. Finally, the rough estimation of the solvent effects using the PCM model on top of LR-TDDFT(CAM-B3LYP) calculations shows a negligible solvent effect on |Δ
| is even smaller (between 3.24 and 4.7 for S2–S4, ESI†), which results in even larger deviation. Finally, the rough estimation of the solvent effects using the PCM model on top of LR-TDDFT(CAM-B3LYP) calculations shows a negligible solvent effect on |Δ![[small mu, Greek, vector]](https://www.rsc.org/images/entities/i_char_e0e9.gif) | (Tables S17–S30 and Fig. S8–S14 in the ESI†). Due to the fact that neither ADC(2) nor CC2 predict correctly excitation energies for this compound, we attribute this deviation to the quantum mechanical method used to evaluate |Δ
| (Tables S17–S30 and Fig. S8–S14 in the ESI†). Due to the fact that neither ADC(2) nor CC2 predict correctly excitation energies for this compound, we attribute this deviation to the quantum mechanical method used to evaluate |Δ![[small mu, Greek, vector]](https://www.rsc.org/images/entities/i_char_e0e9.gif) | more than to assumptions underlying eqn (8).
| more than to assumptions underlying eqn (8).
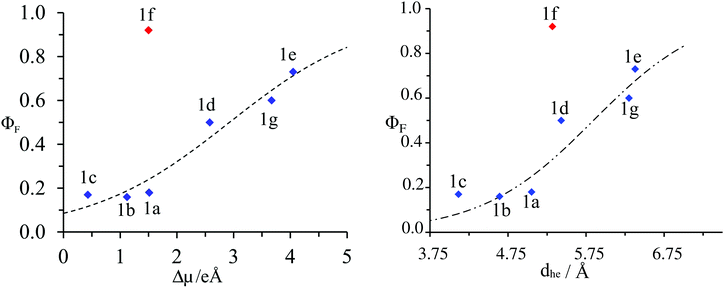 | ||
Fig. 10 Plot of the experimental fluorescence quantum yield (ΦF) as a function of: left computed changes in dipole moments |Δ![[small mu, Greek, vector]](https://www.rsc.org/images/entities/i_char_e0e9.gif) | right charge–hole separation distance for substituted 4′-phenyl-2,2′:6′2′′-terpyridines 1a–1g. The dotted trace corresponds to the best fit obtained with eqn (9a) and (9b) respectively. | right charge–hole separation distance for substituted 4′-phenyl-2,2′:6′2′′-terpyridines 1a–1g. The dotted trace corresponds to the best fit obtained with eqn (9a) and (9b) respectively. | ||
Conclusions
The present work explores the idea and some rationalizations behind a model which puts into relation two apparently unrelated quantities: the experimental fluorescence quantum yield (ΦF) and a parameter measuring the charge separation upon excitation (conjugation length Aπ).1 The relation between ΦF and Aπ was refined by including the spectral density missing in the original derivation to give a new relation (eqn (8)). At first sight (Fig. 2b), the parameter Aπ can be intuitively attributed to the length of the dipole moment change |Δ![[small mu, Greek, vector]](https://www.rsc.org/images/entities/i_char_e0e9.gif) | following the electronic excitation. Owing to this interpretation, Aπ can be evaluated by means of high-level quantum chemistry calculations. To this end, we propose to use either |Δ
| following the electronic excitation. Owing to this interpretation, Aπ can be evaluated by means of high-level quantum chemistry calculations. To this end, we propose to use either |Δ![[small mu, Greek, vector]](https://www.rsc.org/images/entities/i_char_e0e9.gif) | or the charge–hole separation distance dhe as a measure of the charge transfer magnitude. The parameters |Δ
| or the charge–hole separation distance dhe as a measure of the charge transfer magnitude. The parameters |Δ![[small mu, Greek, vector]](https://www.rsc.org/images/entities/i_char_e0e9.gif) | or dhe, although evaluated in a very simple manner (the first ground-state gas phase geometry of the chromophore obtained using the ADC(2) or CC methods), show a remarkable correlation with experimental Aπ for six out seven investigated compounds. Compound 1f appears as an exception, which we attribute to the insufficient accuracy of the electronic structure obtained with the considered method and probably not to the validated model relating Δ
| or dhe, although evaluated in a very simple manner (the first ground-state gas phase geometry of the chromophore obtained using the ADC(2) or CC methods), show a remarkable correlation with experimental Aπ for six out seven investigated compounds. Compound 1f appears as an exception, which we attribute to the insufficient accuracy of the electronic structure obtained with the considered method and probably not to the validated model relating Δ![[small mu, Greek, vector]](https://www.rsc.org/images/entities/i_char_e0e9.gif) to ΦF. The error in the ADC(2) excitation energy for this compound is exceptionally large compared to other compounds, which suggests that the other observables associated with the excited state such as the charge-separation parameters are also less reliable. According to our estimation of the solvent effects on the wavefunction or on geometry, as well as our estimations of the solvent effects, these factors cannot explain this particular exception.
to ΦF. The error in the ADC(2) excitation energy for this compound is exceptionally large compared to other compounds, which suggests that the other observables associated with the excited state such as the charge-separation parameters are also less reliable. According to our estimation of the solvent effects on the wavefunction or on geometry, as well as our estimations of the solvent effects, these factors cannot explain this particular exception.
The results obtained in the present work indicate that the use of the charge separation parameters derived from ab initio calculations as a criterion for designing ligands of desired fluorescence properties is a promising strategy for improving light-downshifting. Although the present work provides a clear physical interpretation of the experimental parameter Aπ, and a strategy to quantify it using ab initio calculations in the case of non-centrosymmetric rigid chromophores, the applied computational protocol requires refinements in more general cases. For centrosymmetric molecules, such as the ones considered in ref. 1, or molecules where a geometry change upon excitation is expected to be large, most likely the protocol should involve the optimisation of the lowest excited state geometry. This might brake the symmetry of centrosymmetric molecules and/or allow reordering the states to satisfy Kasha's rule. Taking into account the solvent, especially if it results in reordering of states is also unavoidable. The results of the present work suggest that such refinements are worthwhile trying.
Finally, we would like to point out that the use of low-costs methods such as the ones based on Linear-Response Time-Dependent DFT, using even approximations for the exchange–correlation energy designed to handle charge-transfer excitations (CAM-B3LYP in our case), proved not to be sufficiently accurate as far as excitation energies are concerned. They were, therefore, not considered for the further analysis of the magnitude of the charge separation.
Acknowledgements
We thank Mr A. Castillo for assistance in the evaluation of the solvent effect of excitation energies and the Swiss National Science Foundation (grant number 200021_152779) for financial support.References
- Y. Yamaguchi, Y. Matsubara, T. Ochi, T. Wakamiya and Z.-I. Yoshida, J. Am. Chem. Soc., 2008, 130, 13867–13869 CrossRef CAS PubMed.
- F. Plasser, B. Thomitzni, S. A. Bäppler, J. Wenzel, D. R. Rehn, M. Wormit and A. Dreuw, J. Comput. Chem., 2015, 36, 1609–1620 CrossRef CAS PubMed.
- A. Einstein, Phys. Z., 1917, 18, 121–128 CAS.
- S. Strickler and S. J. Berg, J. Chem. Phys., 1962, 37, 814–822 CrossRef CAS.
- J. B. Berks and D. J. Dyson, R. London Soc. Ser. A, 1963, 275, 135–148 CrossRef.
- V. L. Ermolaev and E. B. Sveshnikova, Opt. Spectrosc., 2015, 119, 627–641 CrossRef.
- P. Avouris, W. M. Gelbart and M. A. El-Sayed, Chem. Rev., 1977, 77, 793–833 CrossRef CAS.
- D. Beljonne, Z. Shuai, G. Pourtois and J. L. Bredas, J. Phys. Chem. A, 2001, 105, 3899–3907 CrossRef CAS.
- K. Schmidt, S. Brovelli, V. Coropceanu, D. Meljonne, J. Cornil, C. Bazzini, T. Caronna, R. Tubino, F. Meinardi, Z. Shuai and J.-L. Brédas, J. Phys. Chem. A, 2007, 111, 10490–10499 CrossRef CAS PubMed.
- Y. Yamaguchi, T. Ochi, Y. Matsubara and Z.-I. Yoshida, J. Phys. Chem. A, 2015, 119, 8630–8642 CrossRef CAS PubMed.
- N. S. Hush, Coord. Chem. Rev., 1985, 64, 135–157 CrossRef CAS.
- Y. Liu, J. Guo, R. Liu, Q. Wang, X. Jin, L. Ma, W. Lv, S. Liu, S. Yuan and H. Zhu, J. Lumin., 2015, 157, 249–256 CrossRef CAS.
- X. Bi and Y. Pang, J. Phys. Chem. B, 2016, 120, 3311–3317 CrossRef CAS PubMed.
- A. Wild, A. Winter, F. Schlütter and U. S. Schubert, Chem. Soc. Rev., 2011, 40, 1459–1511 RSC.
- J.-F. Lemonnier, L. Babel, L. Guénée, P. Mukherjee, D. H. Waldeck, S. V. Eliseeva, S. Petoud and C. Piguet, Angew. Chem., Int. Ed., 2012, 51, 11302–11305 CrossRef CAS PubMed.
- M. J. Frisch, et al., Gaussian09 Revision D.01, Gaussian Inc., Wallingford, CT, 2009 Search PubMed.
- TURBOMOLE V6.6 2014, a development of University of Karlsruhe and Forschungszentrum Karlsruhe GmbH, 1989–2007, TURBOMOLE GmbH, since 2007, available from http://www.turbomole.com.
- F. Plasser, TheoDORE: A Package for Theoretical Density, Orbital Relaxation, and Exciton Analysis, available at http://theodore-qc.sourceforge.net/.
- M. E. Casida, in Recent Advances in Computational Chemistry, ed. D. P. Chong, World Scientific, Singapore, 1995, part 1, vol. 1, p. 155 Search PubMed.
- T. Yanai, D. Tew and N. Handy, Chem. Phys. Lett., 2004, 393, 51–57 CrossRef CAS.
- C. Hättig and F. Weigend, J. Chem. Phys., 2000, 113, 5154 CrossRef.
- C. Hättig, Adv. Quantum Chem., 2005, 50, 37–60 CrossRef.
- A. Dreuw, J. L. Weisman and M. Head-Gordon, J. Chem. Phys., 2003, 119, 2943–2946 CrossRef CAS.
- A. Dreuw and M. Head-Gordon, J. Am. Chem. Soc., 2004, 126, 4007–4016 CrossRef CAS PubMed.
- F. Plasser and H. Lischka, J. Chem. Theory Comput., 2012, 8, 2777–2789 CrossRef CAS PubMed.
- J. F. Nye, Physical Properties of Crystals, Clarendon Press, 1985, p. 20 Search PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c6cp04252j |
| This journal is © the Owner Societies 2016 |