Shock wave and modeling study of the reaction CF4 (+M) ⇔ CF3 + F (+M)
Abstract
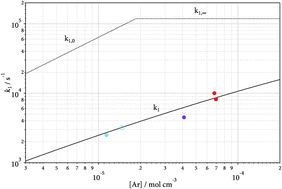
The thermal decomposition of CF4 (+Ar) → CF3 + F (+Ar) was studied in shock waves over the temperature range 2000–3000 K varying the bath gas concentration [Ar] between 4 × 10−6 and 9 × 10−5 mol cm−3. It is shown that the reaction corresponds to the intermediate range of the falloff curve. By combination with room temperature data for the reverse reaction CF3 + F (+He) → CF4 (+He) and applying unimolecular rate theory, falloff curves over the temperature range 300–6000 K are modeled. A comparison with the reaction system CH4 (+M) ⇔ CH3 + H (+M) is made.
- This article is part of the themed collection: Celebrating the 150th anniversary of the German Chemical Society

 Please wait while we load your content...
Please wait while we load your content...