Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Bayesian inference of protein ensembles from SAXS data
L. D.
Antonov
 *a,
S.
Olsson
*a,
S.
Olsson
 bc,
W.
Boomsma
bc,
W.
Boomsma
 d and
T.
Hamelryck
d and
T.
Hamelryck
 *a
*a
aBioinformatics Centre, Department of Biology, University of Copenhagen, Ole Maaloes Vej 5, DK-2200 Copenhagen N, Denmark. E-mail: lubo.antonov@gmail.com; thamelry@binf.ku.dk
bLaboratory of Physical Chemistry, Swiss Federal Institute of Technology, ETH-Hönggerberg, Vladimir-Prelog-Weg 2, CH-8093 Zürich, Switzerland
cInstitute for Research in Biomedicine, Università della Svizzera Italiana, Via Vincenzo Vela 6, CH-6500 Bellinzona, Switzerland
dStructural Biology and NMR Laboratory, Department of Biology, University of Copenhagen, Ole Maaloes Vej 5, DK-2200 Copenhagen N, Denmark
First published on 28th October 2015
Abstract
The inherent flexibility of intrinsically disordered proteins (IDPs) and multi-domain proteins with intrinsically disordered regions (IDRs) presents challenges to structural analysis. These macromolecules need to be represented by an ensemble of conformations, rather than a single structure. Small-angle X-ray scattering (SAXS) experiments capture ensemble-averaged data for the set of conformations. We present a Bayesian approach to ensemble inference from SAXS data, called Bayesian ensemble SAXS (BE-SAXS). We address two issues with existing methods: the use of a finite ensemble of structures to represent the underlying distribution, and the selection of that ensemble as a subset of an initial pool of structures. This is achieved through the formulation of a Bayesian posterior of the conformational space. BE-SAXS modifies a structural prior distribution in accordance with the experimental data. It uses multi-step expectation maximization, with alternating rounds of Markov-chain Monte Carlo simulation and empirical Bayes optimization. We demonstrate the method by employing it to obtain a conformational ensemble of the antitoxin PaaA2 and comparing the results to a published ensemble.
Introduction
Recent years have witnessed increased recognition of the ubiquity and importance of intrinsically disordered proteins (IDPs) and multi-domain proteins with disordered intra-domain linker regions (IDRs).1–5 Long unstructured regions can be found in more than half of eukaryotic proteins and at least 25% are completely disordered.6 It is becoming evident that structural plasticity plays an important role in the function of biological macromolecules, e.g. in areas such as transcription regulation, cell signaling, and the function of chaperones.1,7,8 Misfolding and aggregation of IDPs are associated with many human diseases, such as Alzheimer's and Parkinson's.9,10 These flexible proteins comprise dynamic systems that explore a conformational space that cannot be adequately described by a single state, but requires an ensemble of conformations.Small-angle X-ray scattering (SAXS) and nuclear magnetic resonance (NMR), as solution structure methods, are well-suited to characterize structural ensembles. SAXS, in particular, is a powerful technique, yielding averaged, low-resolution structural information across multiple spatial orders of magnitude. Combined with appropriate ensemble-based computational methodology, it could allow for the characterization of IDP and IDR flexibility not accessible through NMR spectroscopy or X-ray crystallography alone.11,12
Current computational methods aim to recover a representative ensemble as a subset of conformations from a large pool of candidate structures, based on experimental SAXS data.11–14 The initial pool of structures is generated from either knowledge- or physics-based models. A common assumption in these approaches is that the structural ensemble can be represented accurately by a weighted average of discrete conformations. Small sets of conformers are typically used as an approximation,15 in order to avoid overfitting and to reduce the computational load. The Ensemble Optimization Method (EOM) uses a genetic algorithm with a predefined number of structures of equal weight for ensemble selection,16 while the improved EOM 2.0 optimizes individual weights together with an ensemble size within a customizable range.12 Minimal Ensemble Search (MES) uses a genetic algorithm on a population of ensembles of sizes between 2 and 5 structures.17 In the Basis-Set Supported SAXS (BSS-SAXS) approach, conformations are assigned to a small number of clusters, first by RMSD and then by scattering pattern similarity, after which a Bayesian MC algorithm is used to determine the cluster weights.18 The Ensemble Refinement of SAXS (EROS) method similarly uses RMSD clustering followed by maximum entropy19 cluster weight optimization.20 In the program ENSEMBLE, a predetermined number of conformations is employed, with either equal or varied weights, and the ensemble is optimized using axial descent or simulated annealing algorithms.21–24 The Sparse Ensemble Selection (SES) method reformulates the ensemble selection problem as a linear least-squares problem that optimizes the weights of all structures in the initial pool, yielding a sparse ensemble of conformations.25 Many of these approaches limit the ensemble size explicitly while others, e.g. BSS-SAXS and SES, use sparsity-inducing algorithms. However, in flexible systems, such as IDPs and IDRs, a small number of conformations may not adequately explain the data.25
In contrast, a number of methodologies that have been applied to NMR data eschew reweighing of structures in favor of probabilistic sampling according to the maximum entropy principle.15,26–32 In this manner, an ensemble-based description is obtained that balances the experimental data with prior information, typically encoded in a force field.
Here, we approach SAXS data in a similar manner, resulting in a new method for inference of structural ensembles, called Bayesian Ensemble SAXS (BE-SAXS). BE-SAXS combines a generative, fine-grained (i.e. atomic-level) model of protein structure with experimental SAXS data. Through an iterative expectation maximization (EM) algorithm the method adapts a prior distribution concerning protein structure in atomic detail to match the SAXS ensemble average, within the experimental uncertainty. The resulting posterior distribution takes the ensemble nature of the data into account and correctly balances information present in both the force field and the experimental data. The number of model parameters depends only on the number of experimental observables and representative structures can be sampled a posteriori. Furthermore, since conformations are not restricted to a subset of an initial pool of structures, bias attributable to the initial selection process and limited sampling is avoided.
We apply the BE-SAXS method to SAXS data for the flexible antitoxin PaaA2 and show substantial agreement between the recovered distribution of conformations and the published structural ensemble of the protein. These results illustrate the utility of the method in elucidating the flexibility of partially- or fully-disordered proteins.
Theory and methods
Inferential structural ensemble determination
In probabilistic inferential structure determination (ISD) the goal is to establish a posterior distribution p(x|d,σ2) of protein conformations x, given some experimental data d with experimental errors σ2.33 The classic ISD approach assumes that the experimental data represent a single conformation. Consequently, application of the method to disordered systems, which are characterized by highly heterogeneous ensembles, may give misleading results.27 Such flexible systems require an ensemble-based inference method.SAXS experiments measure the temporal (i.e. over the measurement duration) and ensemble average of the X-ray scattering from all orientations and conformations of the proteins in a solution. Therefore, d is a noisy observation of the true ensemble average e of the scattering f for each individual conformation of a protein. f is a lower-dimensional projection, or coarse-grained representation, of the fine-grained variable x, through a deterministic function, f ≡ h(x). A model for such ensemble-averaged data was previously expressed as a Bayesian network and applied in the context of NMR data.27,28 It gives rise to the following posterior distribution over the coarse-grained variables:
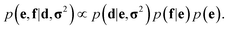 | (1) |
This coarse-grained probabilistic model is then combined with the prior distribution of the fine-grained variable x, according to an appropriate probabilistic prior model M, using the reference ratio method (RRM).34 The RRM is based on the principles of probability kinematics, a variant of Bayesian updating that can be used to modify a given probability distribution in the light of new evidence regarding partitions of the distribution's sample space.35 The updated posterior is:
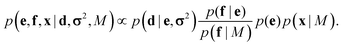 | (2) |
This combined posterior is the distribution with minimum Kullback–Leibler divergence from the fine-grained prior p(x|M), under the requirement that the marginal distribution of the coarse-grained variables follows eqn (1).36
SAXS ensembles
In the case of SAXS, the experimental data d and the ensemble average e constitute vectors of scattering intensities, while the structures x are represented as vectors of atomic coordinates. A force field or a fragment library could be used to sample from the prior distribution p(x|M); here, we use the PROFASI force field.37 A coarse-grained vector f is generated through a forward model by approximating the scattering function h(x) with the Debye formula, which holds for spherical scatterers:38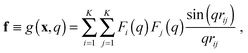 | (3) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin
sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ)/λ is the momentum transfer, with scattering angle 2θ and wavelength of the X-ray beam λ. Fi(q) is the atomic form factor for atom i, rij is the distance between atoms i and j, and K is the number of atoms in the structure. The X-ray scattering factors are calculated using a linear combination of Gaussians fit to empirical data.39
θ)/λ is the momentum transfer, with scattering angle 2θ and wavelength of the X-ray beam λ. Fi(q) is the atomic form factor for atom i, rij is the distance between atoms i and j, and K is the number of atoms in the structure. The X-ray scattering factors are calculated using a linear combination of Gaussians fit to empirical data.39
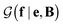 with a link function l(B,e) = Be−1,40
with a link function l(B,e) = Be−1,40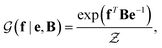 | (4) |
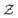 is a normalization constant. The matrix B serves to match the first moment, 〈f〉, of the coarse-grained prior represented by the PROFASI force field to the ensemble average e. This model is scale-invariant when f and e are scaled together, i.e.
is a normalization constant. The matrix B serves to match the first moment, 〈f〉, of the coarse-grained prior represented by the PROFASI force field to the ensemble average e. This model is scale-invariant when f and e are scaled together, i.e.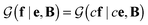 for any constant c. This is required due to the arbitrary scale of SAXS data.
for any constant c. This is required due to the arbitrary scale of SAXS data.
Assuming a uniform prior for e, the joint posterior distribution from eqn (2) for SAXS ensembles becomes:
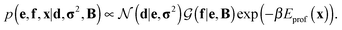 | (5) |
In the last term, Eprof is the energy of the PROFASI force field and β ≡ 1/kT, where T is the temperature and k is the Boltzmann constant.
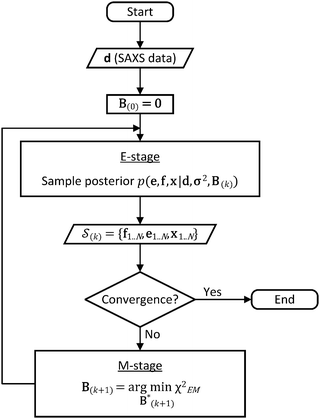
In the E-stage of iteration k of the algorithm, a Markov chain Monte Carlo (MCMC) simulation, as implemented in the PHAISTOS framework,41 produces N samples 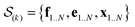 from the posterior p(e,f,x|d,σ2,B(k)). The result is a conformational ensemble of structures together with their forward-computed SAXS profiles, whose average optimally matches the experimental data. The iterative algorithm is initialized with the zero matrix, B(0)= 0, resulting in an unrestrained simulation with the structural prior, exp(−βEprof(x)).
from the posterior p(e,f,x|d,σ2,B(k)). The result is a conformational ensemble of structures together with their forward-computed SAXS profiles, whose average optimally matches the experimental data. The iterative algorithm is initialized with the zero matrix, B(0)= 0, resulting in an unrestrained simulation with the structural prior, exp(−βEprof(x)).
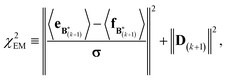
A new scaling matrix B(k+1) is estimated in the M-stage, by minimizing a χ2EM objective function:
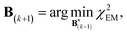 | (6) |
 | (7) |
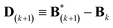 .
.
Conceptually, the M-stage aims to ensure that a given ensemble average e and the matching coarse-grained average of the sampled structures 〈f〉 coincide. It is necessary to normalize by the experimental errors in eqn (7), since SAXS data ranges over several orders of magnitude across the scattering profile. The role of the second term is to use Tikhonov regularization to avoid overfitting.42 Here, it is utilized specifically to avoid excessive changes to the matrix B due to finite sampling issues, allowing for monotonous convergence of the parameters.
The expectation of the coarse-grained variable, 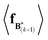 , is estimated from the N samples using importance sampling:43
, is estimated from the N samples using importance sampling:43
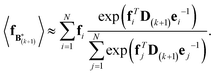 | (8) |
It is notable that the importance weights in eqn (8) do not change when f and e are scaled together. In practice, both the coarse-grained vector f and the ensemble average e are brought to scale with the experimental data d – the former through a scaling coefficient determined at initialization, and the latter through the Gaussian ensemble likelihood. Therefore, the matrix B(k+1) and the associated structural ensemble produced by the algorithm remain invariant, regardless of the absolute magnitude of d.
The expectation of the ensemble average is approximated by the sample average:
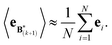 | (9) |
For further details see the work of Olsson et al.28
We use the basin hopping stochastic global optimization algorithm44 for the minimization of the objective function in eqn (6); however, other optimization techniques such as genetic algorithms or parallel tempering may be utilized. In principle, because the function is convex, gradient descent algorithms are also applicable but we found that they can be unstable due to finite statistical sampling. Convergence can be considered achieved once the objective function falls below 0.5, indicating incremental improvements within the experimental uncertainty of the data.
Simulations
The published structural ensemble of PaaA2 consists of 50 conformations and is available from the PDB database under the code 3ZBE. The structures were selected by the application of a jackknife procedure to EOM-derived SAXS ensembles from a pool of NMR-restrained conformers.45 Following the Reference Ensemble Method,47 in order to validate the BE-SAXS algorithm we used a SAXS forward model to create a synthetic data set from the reference ensemble of 50 conformations. This allows controlling for all sources of uncertainty in the evaluation. We constructed the SAXS ensemble average data d for the protein by generating SAXS profiles di for each conformation, using the FoXS program,48 and averaging the individual profiles:
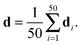 | (10) |
Experimental errors σ2 were assigned as the population variance of the data.
 were saved every 103 steps to be used in the M-stage, after a 40% burn-in. The global optimization algorithm of the M-stage was run for up to 20 independent iterations, or until a stable solution was found. The algorithm reached convergence at iteration 10, as judged from the change in fit between EM steps, χ2EM, from the ensemble SAXS profile fit, χ2SAXS, and from the magnitude of the changes in the scaling matrix B. The measure of fit to the experimental data was defined as:
were saved every 103 steps to be used in the M-stage, after a 40% burn-in. The global optimization algorithm of the M-stage was run for up to 20 independent iterations, or until a stable solution was found. The algorithm reached convergence at iteration 10, as judged from the change in fit between EM steps, χ2EM, from the ensemble SAXS profile fit, χ2SAXS, and from the magnitude of the changes in the scaling matrix B. The measure of fit to the experimental data was defined as: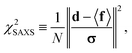 | (11) |
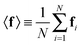 | (12) |
The generative probabilistic models TorusDBN and BASILISK were used as proposal distributions during the MCMC simulation for main chain and side chain moves, respectively.49,50 The introduced bias was subsequently removed. The PROFASI force field at T = 300 K was used as the prior distribution of the structures x.37
To accelerate the M-stage, we implemented an OpenCL kernel that calculates eqn (8) on the GPU.53 The efficiency of this approach depends on the number of samples used; for this simulation, the GPU acceleration reduced the stage time by a factor of 3.
Results and discussion
Algorithm convergence for PaaA2
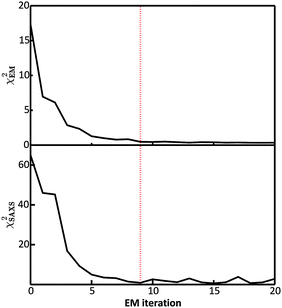
In the E-stage of the first iteration of the BE-SAXS algorithm, the conformational ensemble EM0 of the protein PaaA2 was effectively sampled from an unrestrained PROFASI force field. The resulting ensemble average does not fit the SAXS scattering profile well, as evidenced by the high value of the χ2SAXS measure (Fig. 2). This suggests that PROFASI alone, as a minimalistic force field, does not accurately capture the details of the flexibility of PaaA2 represented in the calculated ensemble-averaged SAXS data. In subsequent iterations, however, the fit improves rapidly and reaches a stable region. The objective function, χ2EM, also reaches a low value quickly and falls below 0.5 in iteration 9 (Fig. 2). At this level, by the nature of χ2EM, modifications to the matrix B produce changes in the importance sampling approximating distribution that are within the experimental uncertainty of the data. The individual coefficients of B also stabilize at iteration 9, further indicating convergence. The equilibrium reached thereby is dynamic, due to the stochastic nature of the basin hopping global optimization algorithm used in the M-stage, combined with the underdetermined optimization problem in eqn (6).Convergence in the BE-SAXS algorithm has to be evaluated comprehensively, by examination of both χ2EM and χ2SAXS, since a low χ2EM does not guarantee that the conformational ensemble provides a good fit to the data. If there is an insufficient number of steps in the E-stage to allow for the MCMC to reach equilibrium, then the Boltzmann distribution will not be sampled successfully. Thus, a low χ2EM could be achieved at a specific iteration and still result in a B matrix that does not produce an ensemble average matching the experimental data. Furthermore, it is necessary to examine the behavior of the χ2 statistics and the B coefficients over a range of EM iterations, to determine if an equilibrium has in fact been reached. Because the optimization problem in eqn (6) is underdetermined, fluctuations in both the matrix B and χ2SAXS are expected. However, in order to assume convergence, these fluctuations should be confined to a stable and relatively narrow region.
BE-SAXS restrains the PaaA2 ensemble
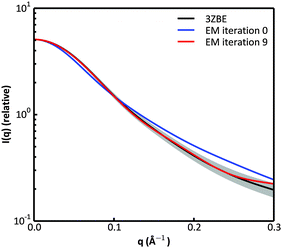
We examined and compared the EM0 and EM9 structural ensembles of the protein PaaA2, in order to evaluate the performance of the BE-SAXS method. The scattering average for the initial, unrestrained ensemble EM0 exhibits a poor fit to the SAXS profile, d, (χ2SAXS = 65.0) while the average for the restrained ensemble EM9 shows good agreement with the data (χ2SAXS = 0.9), within the margins of error (Fig. 3). The high q range of the SAXS profile contains atomic-level data and the larger deviation observed there could be due to the stronger influence of the PROFASI force field on the local structure of the simulated IDP protein than on the overall shape. While the deviation is within the error bounds, it may be desirable to further penalize discrepancies within this range during the M-stage optimization. Alternatively, better sampling of the local structure could be achieved by a longer simulation that emphasizes local and side chain moves. This may allow for a more accurate assessment of the agreement between the ensemble averages of the target and approximating distributions in the M-stage.To further characterize the EM0 and EM9 ensembles, we compared their radius of gyration (Rg) distributions to the Rg distribution of the published PaaA2 reference ensemble (Fig. 4). The 50-structure 3ZBE ensemble is relatively compact, while the unrestrained PROFASI-driven EM0 exhibits a wider variation of Rg with two prominent modes. On the other hand, the SAXS-restrained EM9 closely matches the original ensemble in both its mean and sample error, suggesting that BE-SAXS is able to extract ensemble-level Rg information from the SAXS profile.
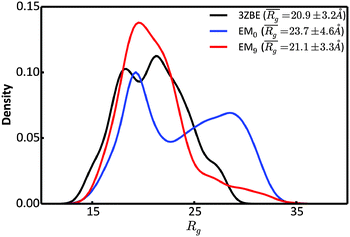 | ||
| Fig. 4 Comparison of the distributions of the radius of gyration, Rg, for the 3ZBE ensemble reported by Sterckx et al.45 (black) and the ensembles at EM iterations 0 (blue) and 9 (red). The distribution for 3ZBE was derived through kernel density estimation, due to the limited number of conformations. | ||
Due to the low information content of SAXS data, it is not possible to summarize the ensemble using only a few representative conformations, despite the presence of a force field. However, the scattering profile can inform about the general shape of the protein. Taking advantage of the stable α-helical regions in PaaA2, we defined a shape descriptor, Ksh, as a proxy to the 3-dimentional shape. The Ksh measure is calculated as the ratio of the distances between the distal and proximal ends of the two helices (the Cα atoms of residue pairs (16, 57) and (28, 42), respectively); thus Ksh is an indicator of the “openness” of the overall structure. We compared the distributions of the descriptor for the EM0, EM9, and reference ensembles (Fig. 5). The unrestrained EM0 gives rise to a bimodal distribution for Ksh and favors open structures. The shape descriptor distributions for the reference ensemble and the SAXS-restrained EM9 show substantial similarity to each other, and share a propensity for more compact structures.
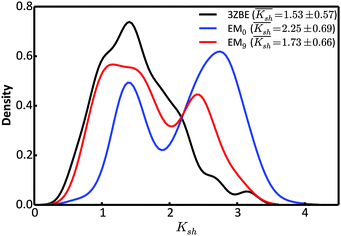 | ||
| Fig. 5 Comparison of the distributions of the shape descriptor, Ksh, for the 3ZBE ensemble reported by Sterckx et al.45 (black) and the ensembles at EM iterations 0 (blue) and 9 (red). The distribution for 3ZBE was derived through kernel density estimation, due to the limited number of conformations. | ||
The ability of the BE-SAXS method to restrict the solution space to areas consistent with the experimental data is further evident in the visualized ensembles (Fig. 6). EM9 exhibits characteristics similar to the reference ensemble – it favors conformations in which the two α-helices are packed closely together, while maintaining significant overall flexibility. At the same time, the unrestrained EM0 comprises structures that are consistent with uniform rotation around the disordered linker. The linker flexibility is greater in EM9 than in EM0, with more diversity in the relative orientations of the two helices, as in the original ensemble.
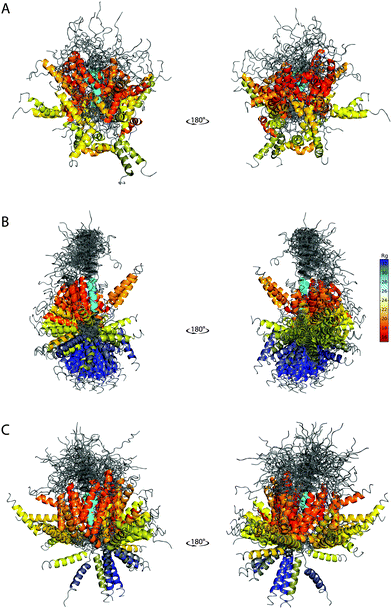 | ||
| Fig. 6 SAXS-derived conformational ensembles of PaaA2. (A) The published 50-member ensemble of PaaA2 (PDB 3ZBE), derived from NMR and SAXS data. (B) Subsample of 128 conformations from EM0, the unrestrained ensemble at iteration 0 of BE-SAXS. (C) Subsample of 128 conformations from EM9, the SAXS-restrained ensemble at iteration 9 of BE-SAXS. All structures are aligned on the first helix (colored in cyan). The color of the second helix corresponds to the Rg of the structure in Å (indicated in the color bar). | ||
The peripheral disordered regions in both EM0 and EM9 exhibit much more helical structure than the 3ZBE ensemble. This is likely the effect of the PROFASI force field on local structure and it helps explain the larger deviation of the scattering profile at high q values. The main advantage of PROFASI is efficiency, but a more sophisticated force field would presumably produce a better fit with the data.
Conclusions
A novel method for inference of protein ensembles from SAXS data, which we call Bayesian Ensemble SAXS, was described and demonstrated here as a proof of principle. BE-SAXS proceeds through successive expectation maximization steps and uses a Bayesian probabilistic model for ensemble-averaged SAXS data to modify a probabilistic model of protein structure, in agreement with an experimental scattering profile. This results in a generative model that can be used directly to characterize a protein's conformational ensemble, or that can be further restrained with other types of experimental data, such as NMR. The generative approach offers a particular advantage for flexible systems, such as intrinsically disordered proteins and proteins with long disordered regions, since it does not impose restrictions on the ensemble size and allows sampling of the full conformational space allowed by the data. The number of parameters of the generative probabilistic model only depends on the number of experimental observables, and not on the size of the ensemble. This stands in contrast to many existing SAXS ensemble methods that fit a set of structures to the data and where each replica results in a linear increase in the number of parameters.To illustrate the BE-SAXS method, we applied it to the ensemble-averaged SAXS data for the published conformational ensemble of the highly flexible antitoxin PaaA2. We showed that our approach restrains the conformational space accessible to the protein simulation and yields ensembles with characteristics consistent with the original set of structures. The ability of the method to model protein flexibility suggests its utility in characterizing other IDPs and multi-domain proteins. The Bayesian probabilistic formulation used here can be complemented by other probabilistic models based on experimental observables. In particular, NMR residual dipolar couplings (RDCs) and chemical shifts are commonly utilized in the context of disordered proteins.29,54 We expect that employing BE-SAXS in concert with methods that make use of other experimental data, can greatly help elucidate the native state ensembles of flexible macromolecular systems.
Acknowledgements
S. O. is funded by an Independent Postdoc grant from The Danish Council for Independent Research for Natural Sciences (ID: DFF-4002-00151). T.H. acknowledges support from the University of Copenhagen 2016 Excellence Programme for Interdisciplinary Research (UCPH2016-DSIN). W. B. is supported by the Villum Foundation.Notes and references
- P. E. Wright and H. J. Dyson, J. Mol. Biol., 1999, 293, 321–331 CrossRef CAS PubMed.
- P. Tompa, Curr. Opin. Struct. Biol., 2011, 21, 419–425 CrossRef CAS PubMed.
- P. Tompa, Nat. Chem. Biol., 2012, 8, 597–600 CrossRef CAS PubMed.
- A. Mittal, N. Lyle, T. S. Harmon and R. V Pappu, J. Chem. Theory Comput., 2014, 10, 3550–3562 CrossRef CAS PubMed.
- V. N. Uversky, Front. Aging Neurosci., 2015, 7, 18 Search PubMed.
- V. N. Uversky and A. K. Dunker, Biochim. Biophys. Acta, 2010, 1804, 1231–1264 CrossRef CAS PubMed.
- L. M. Iakoucheva, C. J. Brown, J. D. Lawson, Z. Obradović and A. K. Dunker, J. Mol. Biol., 2002, 323, 573–584 CrossRef CAS PubMed.
- P. Tompa, P. Buzder-Lantos, A. Tantos, A. Farkas, A. Szilágyi, Z. Bánóczi, F. Hudecz and P. Friedrich, J. Biol. Chem., 2004, 279, 20775–20785 CrossRef CAS PubMed.
- K. Uéda, H. Fukushima, E. Masliah, Y. Xia, A. Iwai, M. Yoshimoto, D. A. Otero, J. Kondo, Y. Ihara and T. Saitoh, Proc. Natl. Acad. Sci. U. S. A., 1993, 90, 11282–11286 CrossRef.
- K. K. Dev, K. Hofele, S. Barbieri, V. L. Buchman and H. Van Der Putten, Neuropharmacology, 2003, 45, 14–44 CrossRef CAS PubMed.
- D. Schneidman-Duhovny, S. J. Kim and A. Sali, BMC Struct. Biol., 2012, 12, 17 CrossRef CAS PubMed.
- G. Tria, H. D. T. Mertens, M. Kachala and D. I. Svergun, IUCrJ, 2015, 2, 207–217 CAS.
- M. Hammel, Eur. Biophys. J., 2012, 41, 789–799 CrossRef CAS PubMed.
- S. Yang, Adv. Mater., 2014, 26, 7902–7910 CrossRef CAS PubMed.
- A. Cavalli, C. Camilloni and M. Vendruscolo, J. Chem. Phys., 2013, 138, 094112 CrossRef PubMed.
- P. Bernadó and D. I. Svergun, Mol. BioSyst., 2012, 8, 151–167 RSC.
- M. Pelikan, G. L. Hura and M. Hammel, Gen. Physiol. Biophys., 2009, 28, 174–189 CrossRef CAS PubMed.
- S. Yang, L. Blachowicz, L. Makowski and B. Roux, Proc. Natl. Acad. Sci. U. S. A., 2010, 107, 15757–15762 CrossRef CAS PubMed.
- E. T. Jaynes, Phys. Rev., 1957, 106, 620–630 CrossRef.
- B. Różycki, Y. C. Kim and G. Hummer, Structure, 2011, 19, 109–116 CrossRef PubMed.
- W. Y. Choy and J. D. Forman-Kay, J. Mol. Biol., 2001, 308, 1011–1032 CrossRef CAS PubMed.
- J. A. Marsh, C. Neale, F. E. Jack, W.-Y. Choy, A. Y. Lee, K. A. Crowhurst and J. D. Forman-Kay, J. Mol. Biol., 2007, 367, 1494–1510 CrossRef CAS PubMed.
- J. A. Marsh and J. D. Forman-Kay, Proteins, 2012, 80, 556–572 CrossRef CAS PubMed.
- M. Krzeminski, J. A. Marsh, C. Neale, W.-Y. Choy and J. D. Forman-Kay, Bioinformatics, 2013, 29, 398–399 CrossRef CAS PubMed.
- K. Berlin, C. A. Castañeda, D. Schneidman-Duhovny, A. Sali, A. Nava-Tudela and D. Fushman, J. Am. Chem. Soc., 2013, 135, 16595–16609 CrossRef CAS PubMed.
- W. Boomsma, J. Ferkinghoff-Borg and K. Lindorff-Larsen, PLoS Comput. Biol., 2014, 10, e1003406 Search PubMed.
- S. Olsson, J. Frellsen, W. Boomsma, K. V. Mardia and T. Hamelryck, PLoS One, 2013, 8, e79439 CAS.
- S. Olsson, B. R. Vögeli, A. Cavalli, W. Boomsma, J. Ferkinghoff-Borg, K. Lindorff-Larsen and T. Hamelryck, J. Chem. Theory Comput., 2014, 10, 3484–3491 CrossRef CAS PubMed.
- S. Olsson, D. Ekonomiuk, J. Sgrignani and A. Cavalli, J. Am. Chem. Soc., 2015, 137, 6270–6278 CrossRef CAS PubMed.
- J. W. Pitera and J. D. Chodera, J. Chem. Theory Comput., 2012, 8, 3445–3451 CrossRef CAS PubMed.
- B. Roux and J. Weare, J. Chem. Phys., 2013, 138, 084107 CrossRef PubMed.
- S. Olsson and A. Cavalli, J. Chem. Theory Comput., 2015, 11, 3973–3977 CrossRef CAS PubMed.
- W. Rieping, M. Habeck and M. Nilges, Science, 2005, 309, 303–306 CrossRef CAS PubMed.
- T. Hamelryck, M. Borg, M. Paluszewski, J. Paulsen, J. Frellsen, C. Andreetta, W. Boomsma, S. Bottaro and J. Ferkinghoff-Borg, PLoS One, 2010, 5, e13714 Search PubMed.
- P. Diaconis and S. L. Zabell, J. Am. Stat. Assoc., 1982, 77, 822–830 CrossRef.
- Bayesian Methods in Structural Bioinformatics, ed. T. Hamelryck, K. Mardia and J. Ferkinghoff-Borg, Springer, 2012 Search PubMed.
- A. Irbäck, S. Mitternacht and S. Mohanty, PMC Biophys., 2009, 2, 2 Search PubMed.
- P. Debye, Ann. Phys., 1915, 351, 809–823 CrossRef.
- D. Waasmaier and A. Kirfel, Acta Crystallogr., Sect. A: Found. Crystallogr., 1995, 51, 416–431 CrossRef.
- P. McCullagh and J. A. Nelder, Generalized Linear Models, 2nd edn, Chapman & Hall, 1989 Search PubMed.
- W. Boomsma, J. Frellsen, T. Harder, S. Bottaro, K. E. Johansson, P. Tian, K. Stovgaard, C. Andreetta, S. Olsson, J. B. Valentin, L. D. Antonov, A. S. Christensen, M. Borg, J. H. Jensen, K. Lindorff-Larsen, J. Ferkinghoff-Borg and T. Hamelryck, J. Comput. Chem., 2013, 34, 1697–1705 CrossRef CAS PubMed.
- A. N. Tikhonov, Dokl. Akad. Nauk SSSR, 1943, 39, 195–198 Search PubMed.
- C. M. Bishop, Pattern Recognition and Machine Learning, 2006 Search PubMed.
- D. J. Wales and J. P. K. Doye, J. Phys. Chem. A, 1997, 101, 5111–5116 CrossRef CAS.
- Y. G. J. Sterckx, A. N. Volkov, W. F. Vranken, J. Kragelj, M. R. Jensen, L. Buts, A. Garcia-Pino, T. Jové, L. Van Melderen, M. Blackledge, N. A. J. van Nuland and R. Loris, Structure, 2014, 22, 854–865 CrossRef CAS PubMed.
- Y. G. J. Sterckx, A. Garcia-Pino, S. Haesaerts, T. Jové, L. Geerts, V. Sakellaris, L. Van Melderen and R. Loris, Acta Crystallogr., Sect. F: Struct. Biol. Cryst. Commun., 2012, 68, 724–729 CrossRef CAS PubMed.
- C. K. Fisher and C. M. Stultz, Curr. Opin. Struct. Biol., 2011, 21, 426–431 CrossRef CAS PubMed.
- D. Schneidman-Duhovny, M. Hammel and A. Sali, Nucleic Acids Res., 2010, 38, W540–W544 CrossRef CAS PubMed.
- W. Boomsma, K. V Mardia, C. C. Taylor, J. Ferkinghoff-Borg, A. Krogh and T. Hamelryck, Proc. Natl. Acad. Sci. U. S. A., 2008, 105, 8932–8937 CrossRef CAS PubMed.
- T. Harder, W. Boomsma, M. Paluszewski, J. Frellsen, K. E. Johansson and T. Hamelryck, BMC Bioinf., 2010, 11, 306 CrossRef PubMed.
- L. Antonov, C. Andreetta and T. Hamelryck, Proceedings of the International Conference on Bioinformatics Models, Methods and Algorithms (BIOINFORMATICS 2012), 2012, pp. 102–108.
- L. D. Antonov, C. Andreetta and T. Hamelryck, in Biomedical Engineering Systems and Technologies SE – 15, ed. J. Gabriel, J. Schier, S. Huffel, E. Conchon, C. Correia, A. Fred and H. Gamboa, Springer, Berlin, Heidelberg, 2013, vol. 357, pp. 222–235 Search PubMed.
- J. E. Stone, D. Gohara and G. Shi, Comput. Sci. Eng., 2010, 12, 66–72 CrossRef PubMed.
- J. M. Krieger, G. Fusco, M. Lewitzky, P. C. Simister, J. Marchant, C. Camilloni, S. M. Feller and A. De Simone, Biophys. J., 2014, 106, 1771–1779 CrossRef CAS PubMed.
| This journal is © the Owner Societies 2016 |