Requirements of first-principles calculations of X-ray absorption spectra of liquid water†
Thomas
Fransson
 a,
Iurii
Zhovtobriukh
b,
Sonia
Coriani
cd,
Kjartan T.
Wikfeldt
be,
Patrick
Norman
a and
Lars G. M.
Pettersson
*b
a,
Iurii
Zhovtobriukh
b,
Sonia
Coriani
cd,
Kjartan T.
Wikfeldt
be,
Patrick
Norman
a and
Lars G. M.
Pettersson
*b
aDepartment of Physics, Chemistry and Biology, Linköping University, SE-581 83 Linköping, Sweden
bFysikum, Stockholm University, Albanova, SE-106 91 Stockholm, Sweden. E-mail: lgm@fysik.su.se; Tel: +46 (8)5537 8712
cDipartimento di Scienze Chimiche e Farmaceutiche, Università degli Studi di Trieste, I-34127 Trieste, Italy
dAarhus Institute of Advanced Studies, Aarhus University, DK-8000 Aarhus, Denmark
eScience Institute, University of Iceland, VR-III, 107 Reykjavik, Iceland
First published on 19th November 2015
Abstract
A computational benchmark study on X-ray absorption spectra of water has been performed by means of transition-potential density functional theory (TP-DFT), damped time-dependent density functional theory (TDDFT), and damped coupled cluster (CC) linear response theory. For liquid water, using TDDFT with a tailored CAM-B3LYP functional and a polarizable embedding, we find that an embedding with over 2000 water molecules is required to fully converge spectral features for individual molecules, but a substantially smaller embedding can be used within averaging schemes. TP-DFT and TDDFT calculations on 100 MD structures demonstrate that TDDFT produces a spectrum with spectral features in good agreement with experiment, while it is more difficult to fully resolve the spectral features in the TP-DFT spectrum. Similar trends were also observed for calculations of bulk ice. In order to further establish the performance of these methods, small water clusters have been considered also at the CC2 and CCSD levels of theory. Issues regarding the basis set requirements for spectrum simulations of liquid water and the determination of gas-phase ionization potentials are also discussed.
I. Introduction
Of all compounds necessary for the existence of life on Earth, water is the most important and most common—it is involved in almost all physical, biological, and geological processes of relevance. As a result, water, especially in the liquid phase, has been studied in great detail, and a number of anomalous properties have been identified: the density increase upon melting, the decrease in viscosity under pressure, the high surface tension and many more.1 These anomalies are typically more pronounced in the supercooled region, but they appear already under ambient conditions. A fundamental understanding of the origin of these anomalous properties is yet to be attained, but it is expected to be found in the minute details of the structure and dynamics of the hydrogen bonding (H-bonding) network, for which the development of new experimental and theoretical tools is essential. The most prevalent view of water, which dominates textbooks today, is that of a homogeneous distribution of near-tetrahedral H-bonded structures, similar to that of ice but more dynamical. Following the publication of the article by Wernet et al. in 2004,2 this view has been challenged by a heterogeneous model of liquid water in which the thermal fluctuations are instead centered around two separate underlying structural motifs. This hypothesis was initially based on the results from X-ray absorption spectroscopy (XAS) and X-ray Raman scattering (XRS) measurements, as these techniques are especially suitable for the determination of a local molecular structure—the time-scale of a core-excitation is of the order of attoseconds, while the H-bond dynamics occur on a time-scale of hundreds of femtoseconds. With these spectroscopic techniques we thus obtain a measure of the instantaneous structure of the sample and can utilize this in order to understand the details of the H-bonding network. However, the execution and interpretation of such a study is challenging, due to many difficulties associated with conducting high-quality experimental measurements and spectrum calculations of core-excitation processes.From an experimental point of view, the advent of third-generation synchrotron radiation sources has been pivotal for the measurement of high-quality X-ray absorption spectra, offering tunable X-ray radiation of unprecedented brilliance. The continuing development of fourth-generation synchrotron facilities, e.g. free-electron lasers, will provide even more opportunities for novel experimental studies on the interaction of matter and X-ray radiation, such as the recent investigation of the liquid water structure at temperatures below that of homogeneous ice nucleation.3 In terms of experimental difficulties, XAS measurements of liquid water are challenging due to difficulties in, e.g., fulfilling the ultra-high vacuum requirements and avoiding saturation effects.4 Alternatively, X-ray absorption spectra can be measured by the use of XRS, if the momentum transfer q is low (using small scattering angles) and nondipolar contributions to the spectrum are thus avoided. For the purpose of this article, we will refer to data obtained using either technique by the designation of XAS. The basic principles of pure XAS measurements can be found in ref. 5, and a recent review on XAS and XRS measurements of liquid water can be found in ref. 4.
In terms of spectral features, the X-ray absorption spectrum of liquid water is dominated by three distinct features: a weak but sharp pre-edge feature centered at 535 eV, an intense main-edge feature centered at 537 eV, and an intense but smeared out post-edge feature centered at approximately 541 eV. While the fine details of the interpretation of these features remain intensely debated, it is generally agreed that the pre-edge feature is associated with weakened or broken H-bonds, while the post-edge feature is associated with more delocalized excited states and ice-like, tetrahedral coordination.2,6–11 The main-edge feature is sensitive to the local structure similarly to the pre-edge, but it also responds more to the order in the second solvation shell.12 These conclusions are drawn from, e.g., comparisons to ice spectra,2,13–18 or by investigating the delocalization rates using resonant Auger spectroscopy.19 The sensitivity of the pre-edge feature to the local disorder in the H-bonding network can be understood by comparison to gas-phase water, for which the highest occupied states are polarized mainly towards the oxygen. As the unoccupied valence states (4a1 and 2b2) are orthogonal to these states, they are polarized towards the hydrogen atoms and thus sensitive primarily to H-bond donation. For O 1s core-excitations, the local unoccupied states of p-character are probed, and by symmetric H-bond donation the excited states are given more of an s-character.4,6 We can hence expect the pre-edge feature to diminish as the fraction of donated symmetric H-bonds is increased. By subjecting water to conditions that affect the H-bond disorder, it is thus possible to correlate the X-ray absorption spectrum to the degree of such disorder. By increasing the temperature of the sample, the pre- and main-edge features are found to be red-shifted with an increase in intensity, while the post-edge feature is weakened.2,4,18,20 However, the pre-edge feature does not broaden with increasing temperature, indicating that the electronic states associated with the pre-edge are rather localized and thus insensitive to further distortions in the near environment. By introduction of solutes it is possible to either increase or decrease the local order, affecting the features in a manner similar to using different temperatures but without additional thermal energy.21–29 The effects of the local order can also be studied systematically by adsorption to metal surfaces, where different coverages yield structures ranging from gas-like to ice-like.16,17 The spectral changes for variations in pH have also been investigated,30–32 as well as that of supercritical water33 and water contained in reverse micelles.34 Further, isotope substitution has been utilized in order to obtain additional information on the dynamics of the H-bonding network.23,35 Consequently, the behavior of the X-ray absorption spectrum is well investigated experimentally, and what is needed in order to reach a fundamental understanding of the structure and dynamics of the H-bonding network is mainly theoretical considerations.
From a theoretical point of view, the calculation of the X-ray absorption spectra of liquid water is challenging, partially due to the difficulties in performing accurate molecular dynamics simulations and partially due to the challenges of modeling core-excitation processes. The former difficulty will not be discussed further in this work, but we note that high-quality ab initio molecular dynamics simulations with van der Waals interactions reliably accounted for are necessary, as a classical force field cannot properly account for cooperativity effects and tends to yield overstructured MD snapshots.36 It is also important to note that it is not clear if the inability to, as of yet, obtain good theoretical X-ray absorption spectra of liquid water is due to deficiencies in the molecular dynamics simulations or in the spectrum calculations. With high-quality molecular dynamics structures available, several challenges remain for the spectrum calculations: the excitations are embedded in a manifold of valence excitations, such that these must either be calculated or avoided by some means. Due to the significant reduction in the screening of the nucleus following core-excitation, relaxation effects are highly influential and thus need to be accounted for in a reliable manner. These relaxation effects affect the molecular system in two distinct ways: (i) the ‘direct’ relaxation contracting mainly the valence electron density, thus acting as an attractive effect, and (ii) the interaction between the excited electron and the valence electrons, this giving rise to repulsive screening/polarization effects. Further, a sufficiently large structural model is required in order to appropriately incorporate long-range interactions and delocalized excited states, and this can be achieved using either a large cluster in a finite cluster approach or a large unit cell in a periodic scheme. Additional issues that must be considered include, e.g., the employed basis sets and spectrum broadening schemes.
Although there is agreement on the qualitative interpretation of the spectral features, the quantitative interpretation in terms of degree of H-bond distortion and the amount of broken H-bonds is contested. The two most prominent interpretations of the X-ray absorption spectrum rationalize the observed behavior either in terms of fluctuations around an underlying homogeneous tetrahedral structure,7,8,11,15,37–41 or as arising from fluctuations around two separate structural motifs.2,4,10,18,28,42–45
In the two-structure model, it is hypothesized that liquid water under ambient conditions is dominated by disordered high-density liquid (HDL) water exhibiting more weakened or broken H-bonds with local fluctuations into patches of tetrahedrally coordinated water, designated low-density liquid (LDL), of spatial extent and persistence time that increase upon cooling.45,46 The instantaneous LDL patches are deemed at ambient temperature to be of a size of 1 nm47 and driven by directional and strong H-bonds and favored by enthalpy, while the HDL water is driven by more isotropic van der Waals interactions together with less directional, bifurcated H-bonds48 and favored by entropy, as quantized low-frequency modes are available for excitations in this case. This hypothesis is formalized in thermodynamic two-state models49,50 that have been reinvigorated largely as a result of the two-state interpretation of X-ray spectroscopic measurements; in order to reach a fundamental understanding of this issue, very reliable theoretical simulations are needed, but this goal has so far remained elusive. It is to be noted that it may not be necessary to reproduce the exact spectral features under different conditions, but reliably capturing the correct trends is a priority.
In order to investigate the validity of different hypotheses, what is needed is to correlate the spectral features to local geometries using some reliable and unambiguous categorization. Several schemes to determine whether an H-bond is present or not have been suggested, but the purely geometrical definitions have thus far proven to be insufficiently sensitive.7 A scheme that provides a bimodal distribution of LDL/HDL local structures,51,52 when considering the inherent structure53 of simulated water, is the local structure index54 (LSI). This order parameter accounts for the structure and coordination of the first and second solvation shells. Other schemes of categorizing the MD snapshots include, e.g., topological definitions55 and theoretical energy decomposition approaches.56
In terms of spectrum calculations, improvements are needed to meet the above mentioned challenges since the theoretical studies conducted to date experience a number of discrepancies when compared to experimental data, e.g., too narrow absorption band,8,9,36,43,56–58 insufficient pre-edge intensity,7,39,43,59 and insufficient post-edge intensity.41,58 Pinpointing the sources of these discrepancies for any specific study is not trivial, since they could be the result of inaccurate core-excitation methods, improper structures, too small cluster or unit cell for core-excitation calculations, or other effects. Due to the large-size models that are necessary to suitably describe the disorder and long-range interactions, only relatively inexpensive theoretical methods can be used for spectrum calculations. Particularly interesting in this respect are methods based on density functional theory (DFT), amongst which especially the transition-potential DFT (TP-DFT) method60 has been used extensively for calculations of water X-ray absorption spectra.2,7–10,21,26,30,43,44,57,59,61–63 What is needed is to establish whether TP-DFT, and in particular the workhorse of optical DFT-based spectrum calculations, i.e. time-dependent DFT64 (TDDFT), can produce results of sufficiently good quality to correlate the spectral features to molecular structures. In terms of TDDFT, only a single study addressing the X-ray absorption spectrum of liquid water can be found in the present literature.58 An alternative method that has been utilized for the consideration of liquid water is the many-body perturbative Bethe–Salpeter equation (BSE) approach,65 as used in conjunction with the GW approximation of the self-energy41 or solved within the static Coulomb-hole and screened exchange (COHSEX) approximation.36,39
In order to evaluate the ability of these methods to properly reproduce X-ray absorption spectra, comparisons are to be made to experiments as well as more demanding ab initio methods. For such a comparison, the coupled cluster (CC) method offers a physically sound scheme in which the correct electronic wave function and excited states can be approached in a hierarchical manner, and implementations for calculating X-ray absorption spectra have been developed using damped linear response theory,66–69 equation-of-motion CC,70 as well as multi-reference CC.71 Similar electronic structure methods have also been extended for the calculation of X-ray absorption spectra, such as the algebraic-diagrammatic construction (ADC) approach,72–74 and the symmetry-adapted cluster configuration interaction (SAC-CI) approach.75,76
II. Methodology
Here we will briefly present the methods used in the present work. For a more detailed description of the theory and application of TP-DFT on water we refer to a previous extensive review,10 and for a general description of (linear) response theory to ref. 77 and 78.A. Transition-potential density functional theory
The transition-potential DFT (TP-DFT) approach60 is an approximation of the Slater transition-state DFT method,79,80 in which relaxation of the core-hole state is included through a fully relaxed, half-occupied core-hole state, with oscillator strength determined from transition dipole moments using the same orbitals to describe both initial and final states. Within Slater transition-state DFT the core-hole is prepared with half an electron and explicit excited states are formed by adding the excited half electron in various states. This can be shown to give relaxation effects correct to second order, but as this involves explicit treatment of each and every excited state, the TP-DFT method has been developed,10,60 in which the excited half electron is neglected and the excited states are obtained from a single matrix diagonalization. However, as a result of this approximation, the degree by which the core-hole should be filled cannot any longer be rigorously decided. For water, this issue has been discussed,8–10,57,62 and it has been concluded that exciting half an electron, i.e. using the half-core-hole (HCH) approach, provides the best balance between initial and final state effects.9,10 In the (Z + 1) approximation, this can be understood in terms of oxygen being replaced by the more electronegative fluorine—using a full core-hole (FCH) yields excitation energies in good agreement with experiment, but the transition intensities are erroneously computed with respect to the empty states of the p-character of the fluorine atom rather than the oxygen atom.10,62 For other molecular systems and other edges, e.g., the carbon K-edge in biomolecules or in fullerenes,81 this balance may shift as the influence of changes in electronegativity is smaller.As the TP-DFT approach neglects the relaxation of the remaining molecular ion core in the presence of the excited electron, additional energy corrections must be introduced to obtain a correct absolute energy scale. Contributions from the DFT functional deficiencies, relativistic effects, and basis set incompleteness are also to be accounted for.82 Relaxation effects for the lowest valence-excitations can be included using the ΔKohn–Sham (ΔKS) correction, i.e. as the total energy difference between the ground state and the variationally computed fully relaxed core-excited state.10,83 For the remaining states, the same shift should be applied as for the last fully relaxed core-excited state. Other types of energy discrepancies are mainly associated with the core-level and can be evaluated as the difference between calculated and experimental core-electron binding energies (CEBE) and added as a constant shift to the previously shifted TP-DFT spectrum.10 It is also possible to improve the TP-DFT results by explicitly using exact Slater transition states for the first few core-excitations. In this calculation scheme, Slater transition states are calculated using the ΔKS procedure with one-half electron excited from the core orbital.79,80 After this is done, the corresponding transition energies in the TP-DFT spectrum are replaced by the orbital energy differences between the excited orbital of the Slater transition states and the half-occupied 1s oxygen core orbital. The final absolute energy scale is obtained by shifting the overall spectrum according to the fully relaxed lowest core-excited state in addition to the CEBE correction.
B. Linear response theory
Within the framework of response theory, molecular properties are determined as the response of the electronic wave function (or electron density), subjected to some internal or external perturbation. Here, the cross section for linear absorption of radiation can be written in the electric-dipole approximation as84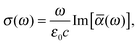 | (1) |
![[small alpha, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0c2.gif) denotes the isotropic average of the complex electric-dipole polarizability. Alternatively, the different tensor components can be used to treat polarization dependences of the sample, relevant for, e.g., the treatment of self-assembled monolayers on metal surfaces.85 For the calculation of the polarizability, standard linear response theory suffers from divergences at resonance energies, related to the lack of decay from the excited states. By introducing a damping term γn for each excited state |n〉, spontaneous and collision-induced relaxation/de-excitation effects can be included in a phenomenological manner. The damping factor then corresponds to the inverse of the lifetime of the excited state, and the molecular polarizability can be written as the resonant-convergent complex polarization propagator (CPP),86,87
denotes the isotropic average of the complex electric-dipole polarizability. Alternatively, the different tensor components can be used to treat polarization dependences of the sample, relevant for, e.g., the treatment of self-assembled monolayers on metal surfaces.85 For the calculation of the polarizability, standard linear response theory suffers from divergences at resonance energies, related to the lack of decay from the excited states. By introducing a damping term γn for each excited state |n〉, spontaneous and collision-induced relaxation/de-excitation effects can be included in a phenomenological manner. The damping factor then corresponds to the inverse of the lifetime of the excited state, and the molecular polarizability can be written as the resonant-convergent complex polarization propagator (CPP),86,87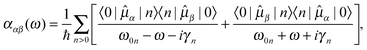 | (2) |
![[small mu, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cd.gif) α denoting the electric-dipole operator along axis α and ℏω0n being the transition energy between the ground state |0〉 and the excited state |n〉. In approximate state response theory, this complex polarization propagator will turn into different forms of matrix equations, for which relaxation effects are included on par with the inclusion of electronic correlation effects. In this framework, no explicit treatment of the excited states is necessary, as the electronic Hessian does not need to be diagonalized, and any arbitrary energy interval can be considered directly without need of restricting excitation channels or any other manipulations. However, as the present study is associated with correlating spectral features to local structures, as well as a comparison to the core-state-specific TP-DFT method, we will only consider excitations from a single (central) water molecule at a time. From the damped response theory point of view we could equally well include a larger core-cluster of water molecules with full account of core-valence excitations. By simply removing the damping parameter in eqn (2) the expression for standard linear response theory is retrieved.
α denoting the electric-dipole operator along axis α and ℏω0n being the transition energy between the ground state |0〉 and the excited state |n〉. In approximate state response theory, this complex polarization propagator will turn into different forms of matrix equations, for which relaxation effects are included on par with the inclusion of electronic correlation effects. In this framework, no explicit treatment of the excited states is necessary, as the electronic Hessian does not need to be diagonalized, and any arbitrary energy interval can be considered directly without need of restricting excitation channels or any other manipulations. However, as the present study is associated with correlating spectral features to local structures, as well as a comparison to the core-state-specific TP-DFT method, we will only consider excitations from a single (central) water molecule at a time. From the damped response theory point of view we could equally well include a larger core-cluster of water molecules with full account of core-valence excitations. By simply removing the damping parameter in eqn (2) the expression for standard linear response theory is retrieved.
For the inclusion of electron correlation effects at a low computational cost, Kohn–Sham DFT is a convenient electronic structure method. The CPP then yields a different manner of calculating time-dependent DFT (TDDFT) spectra. By comparison, standard considerations of TDDFT typically consist of computing the eigenvalues in the Casida equation64 using some implementation of the Davidson algorithm,88 from which transition energies, transition moments and information on the nature of the excited states are obtained. As restriction of the excitation channels typically yields negligible discrepancies, we utilize this approach for the small molecular systems considered here. However, when the density of states becomes large, e.g., when considering large molecular systems, resolving the full spectral region of interest becomes an issue and, for liquid water and ice, we thus utilize the CPP approach as implemented for KS-DFT.89–92 Alternatively, it is possible to treat TDDFT by other means, such as using real-time approaches.93 For the application of core-excitations TDDFT suffers from a large functional dependency, originating from the self-interaction error (SIE). As a result of this the absolute energetics can be incorrect by up to 20 eV for second-row elements, with the magnitude of the discrepancy depending on the element and functional. Nevertheless, TDDFT provides spectral profiles in good agreement with experiment, and functionals tailored for core-excitation processes are being developed.94–96 Additionally, the SIE can be accounted for by use of the self-interaction correction (SIC), both for ionization potentials97 and excitation energies.98 In the present study we will refrain from using either the specially tailored functionals or the SIC, as we argue that the absolute energetics are of less interest than the relative energetics—the SIC has been observed to vary by, at most, 0.2 and 0.4 eV for oxygen and carbon K-edge ionization potentials, considering 14 different molecular systems.97 For the functional utilized in the present study, the discrepancy in relative energetics of fluorine-substituted ethenes has been shown to amount to less than 0.1 eV, even as the absolute energetics differ by almost 5 eV due to strong environmental effects.99 With the ground state 1s orbital being relatively insensitive to the molecular environment, we argue that the SIE is very similar for different MD structures of liquid water and we thus correct the energetics by a common overall shift to align theoretical spectra with experimental counterparts. Potentially more damaging is the issue concerning the ability or inability of TDDFT to reliably include relaxation effects, as well as criticism on the predictive power of TDDFT.100–102 Nonetheless, TDDFT has proven to yield accurate results, and we refer to the work of Besley and Asmuruf for a review on its use for core-excitation processes.95 The functional chosen here is a tailored version of CAM-B3LYP,89,90 for which we have previously reported excellent spectral profiles for fluorine-substituted ethenes.99
In order to get a more strict inclusion of the electron correlation effects than what is achieved by the plethora of exchange–correlation functionals in DFT, one is well advised to turn to an ab initio wave function theory such as the coupled cluster (CC) method. In this approach the dynamic correlation effects are addressed by an expansion of the wave function, such that a truncation of this expansion operator yields a systematic hierarchy of models. The complex polarization propagator has been implemented in this electronic structure method, enabling the calculation of X-ray absorption spectra utilizing the CC models CC2,103 CCSD,104 and CCSDR(3),105 in which approximate double, full double, and full double and approximate triple excitations in the CC manifold are included, respectively. The CPP has been implemented utilizing both a direct complex solver by which the molecular response at arbitrary photon energies can be considered,68 and an asymmetric Lanczos-chain driven algorithm in which the full spectrum is constructed iteratively.66,67 In the latter approach an approximate tri-diagonal representation of the CC Jacobian is constructed, with an accuracy that depends on the dimension (also designated as the Lanczos chain-length) of this matrix.
If heterogeneous environmental effects are important for the spectrum calculations, the use of a polarizable embedding enables the inclusion of thousands of molecules described by charges and an electronic dipole–dipole polarizability tensor. Most significantly, this scheme enables the self-consistent inclusion of mutual polarization effects both for ground and excited states and thus enables the use of a very small QM region. The approach has been implemented in standard TDDFT106 as well as TDDFT with the complex polarization propagator,107 and recent developments in CC theory have included this approach also in standard linear response108 and CPP coupled cluster theory.69
III. Computational details
All TP-DFT calculations have been performed using the deMon2k109 and StoBe110 codes. For the water dimers, trimers, and summed up cluster calculations, respectively, the first three, six, and nine excited states were computed using Slater transition states, while the remaining transitions were treated in the potential of a half-core-hole (HCH). The absolute energy scale was obtained by applying ΔKS and CEBE corrections. A double-basis set technique was used with the diffuse sets of basis functions as defined below,10,111 and the spectrum calculations utilized the standard PBE112 gradient-corrected functional. All TDDFT and CC calculations have been performed using the DALTON program.113,114 For the TDDFT calculations of the water monomer, dimers, and trimers the Davidson algorithm was utilized to obtain the transition energies and intensities in a bottom-up manner, including only excitations from the solute O 1s, i.e. the central, core-excited molecule in the model cluster. The cluster calculations were performed using the CPP algorithm described in ref. 92. Appropriate long-range Coulomb interaction between initial and final electronic states has been ensured by the use of the Coulomb-attenuated B3LYP (CAM-B3LYP) functional,115 with parameters modified according to ref. 89 and 90 (α = 0.19, β = 0.81, and μ = 0.33). A complex CC solver68 was adopted for all CC2 calculations and the CCSD monomer calculations. For the dimer and the acceptor–acceptor trimer, a Lanczos-chain-driven algorithm67 was utilized at the CCSD level of theory, with excitation space dimension truncated to J = 8000 (dimers) or J = 3000 (trimers) for each symmetry-unique component of the dipole operator. All excitation channels have been active in the CC and damped linear response TDDFT calculations. A common lifetime broadening (half-width at half maximum) of γ = 1000 cm−1 (or 0.124 eV) has been used for all calculations, yielding spectral features with a resolution exceeding that of experimental measurements. In the case of TP-DFT and restricted channel TDDFT, this broadening was imposed using a Lorentzian line-shape convolution function on the obtained excitation energies and oscillator strengths.The basis sets for the water solute molecule were chosen as IGLO-III for oxygen (7s6p2d) and IGLO-II for hydrogen (3s1p).116 In order to improve the description of the excited states these basis sets were further augmented with additional diffuse functions centered at the oxygen atom, these being either Rydberg functions as suggested by Kaufmann et al.117 (6s6p6d basis functions, with principal quantum numbers of n = 1.5, 2.0, 2.5, 3.0, 3.5, 4.0) or a tailored 19s19p19d basis set (even-tempered basis set with the first two exponents amounting to 1.238 and 0.884). For the solvent molecules (i.e. the surrounding molecules), a MWB effective core potential118 was used for the oxygen atoms in order to ensure that only core excitations from the solute oxygen are accounted for, as well as to decrease the computational cost. For the solvent molecules a double-ζ basis set was used for hydrogen (2s)119 and the MWB double-ζ basis set was used for oxygen (2s2p, the last p-function has been removed).118 A triple-ζ basis set was constructed by the use of IGLO-II for hydrogen (3s1p)116 and the MWB double-ζ basis set converted to a triple-ζ level for oxygen (3s3p1d, uncontracting the third PGTO in the first CGTO and adding a d-function with an exponent of 0.7). Unless otherwise specified, the liquid water and ice cluster calculations have utilized a triple-ζ basis set for the solute molecules and six innermost solvent molecules, and a basis set of double-ζ quality for all remaining molecules. Due to differences in code implementations, the 100 structures for the summed up spectrum utilized a slightly different ECP120 with corresponding basis set for TP-DFT, but tests show that the difference in spectral features is minimal. For the QM/MM calculations a polarizable embedding with the Ahlström force field121 was utilized.
The geometries used for gas phase monomers, dimers and trimers are given in the ESI.† For the present study the key is to use the same structures for all methods and that these represent different H-bond situations. Thus, the O–O distances were set to 2.8 Å to match the first peak in the O–O radial distribution function,122 and for the trimers the angle to the two solute oxygens was set to close to tetrahedral or to 180° to yield H-bond situations corresponding to double-acceptor, single-donor/single-acceptor and double-donor.
In previous work, the sensitivity of TP-DFT spectrum calculations to nuclear quantum effects and the interaction model used for generating liquid water structures has been demonstrated.123 Here, liquid water model structures were generated by performing DFT path integral molecular dynamics (PIMD) simulations using the VASP124 code with projector-augmented wave potentials,125 a plane-wave cutoff energy of 400 eV and a k-space sampling limited to the gamma-point. Since long-ranged dispersion forces are missing in standard functionals based on the generalized gradient approximation, we used the optPBE-vdW functional which explicitly contains a non-local energy functional.126 To generate model structures, we first performed optPBE-vdW classical MD simulations for 20 ps in the NVT ensemble using the Andersen thermostat127 for a cubic box with 64 water molecules. The final snapshot from the MD trajectory was then used as a starting structure for PIMD, which was run for 5 ps using 32 ring-polymer beads and the normal-mode transformation. For XAS calculations, the cluster structures were extracted by randomly sampling both central molecules and ring-polymer replicas from the final 2 ps of the PIMD trajectory.
The ice structure was generated from an ice 3 × 2 × 2 unit cell containing 96 molecules. The cell oxygen positions were generated using the basic elementary orthorhombic unit cell with eight oxygens by translation nx, ny, nz times along the x, y, and z directions, respectively (labeled as nx × ny × nz in the unit cell name). In order to get a zero dipole moment of the whole cell, additional constraints were applied to the hydrogen positions in such a way that equal numbers of each of the 24 available hydrogen orientations were included. A more detailed description of the cell building process can be found in the paper by Hayward and Reimers (the generation of such a model structure is therein designated 3 × 2 × 2-C2).128
IV. Results and discussion
Before investigating the performance and requirements of TP-DFT and TDDFT calculations of liquid water, we evaluate these methods for smaller molecular complexes, with reference made to damped CC linear response theory and experiment; in this way structural issues that otherwise plague spectrum simulations on water are avoided. We consider the water monomers, dimers, and trimers in connection to a discussion on the effects of H-bond donation and H-bond acceptance in terms of spectral features, as well as the estimation of ionization potentials. Following this, the requirements of spectrum calculations of liquid water are investigated regarding the choice of basis set, cluster size, and effects when averaging over 100 random structures from PIMD snapshots. Finally, bulk ice is treated as an example of a more ordered system.A. Water monomers
In Fig. 1, the theoretical X-ray absorption spectra of gas-phase water are reported and compared with experiment.73 A comparison of the small (6s6p6d) and large (19s19p19d) sets of diffuse functions shows similar spectral features for both augmentations, save the high-energy fine structure details of the CC2 results. This is somewhat surprising, as CCSD would be expected to be most sensitive to the quality of the basis set, but is here observed to be least sensitive in terms of both relative energies and intensities. For absolute energetics, however, the CCSD results are influenced the most by the change of basis sets. The agreement in terms of relative features is likely only fortuitous, as the improved description of electron correlation in CCSD will in general require a more flexible basis set as compared to CC2 or DFT-based methods. The energies and oscillator strengths of the first three transitions are given in Table 1, where we also present earlier results at the CCSDR(3) level of theory.66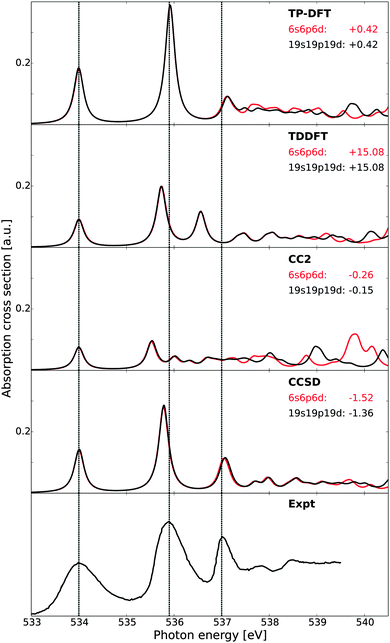 | ||
| Fig. 1 X-ray absorption spectra of gas-phase water as obtained using transition-potential DFT, time-dependent DFT, and damped CC linear response theory at the CC2 and CCSD levels of theory, compared against experiment.73 All theoretical spectra have been aligned to the first experimental excitation energy by values reported beneath each model label, expressed in eV. Vertical dashed lines indicate experimental transition energies of the first three features. Basis sets augmented with a 6s6p6d or 19s19p19d set of diffuse functions centered at the oxygen atom. | ||
| Method | 4a1 | 2b2 | First Rydberg state (2b1) | |||
|---|---|---|---|---|---|---|
| ω | f | ω | f | ω | f | |
| a From ref. 66, including scalar relativistic effects. b From ref. 73. | ||||||
| TP-DFT | 533.57 | 1.81(1.0) | 535.49 | 3.84(2.1) | 536.67/536.71 | 0.44/0.30(0.4) |
| TDDFT | 518.92 | 0.90(1.0) | 520.65 | 1.94(2.2) | 521.48/521.48 | 0.49/0.62(1.2) |
| CC2 | 534.15 | 0.74(1.0) | 535.68 | 0.92(1.2) | 536.19/536.16 | 0.16/0.25(0.6) |
| CCSD | 535.36 | 1.41(1.0) | 537.14 | 2.81(2.0) | 538.40/538.52 | 0.76/0.52(0.9) |
| CCSDR(3)a | 534.87 | 1.29(1.0) | 536.70 | 2.62(2.0) | 537.8 | 1.26(1.0) |
| Expt.b | 534.0 | (1.0) | 535.9 | (1.3) | 537.0 | (0.7) |
Of the methods utilized in Fig. 1, it is clear that the CCSD spectrum is in best agreement with experiment, followed closely by TP-DFT and then by TDDFT. CC2 reproduces the relative excitation energies and oscillator strengths of the 4a1 and 2b2 features well, but has difficulties in emulating the fine structure details and yields a compressed spectrum—the latter hinting on the lack of sufficient polarization effects. The intensities of the CC2 peaks are observed to be substantially smaller than those of the other methods, consistent with the earlier results.66,67,99 However, for excited states of π*-character the intensities obtained using CC2 have been shown to be similar to those obtained using CCSD.66,99 The reason for this behavior in terms of absolute intensities is currently unknown. We note that the relaxation effects are less accounted for in the CC2 method, as compared to the CCSD scheme, due to restrictions for double excitations in the CC Jacobian in the former approach. This can explain the underestimation of the polarization effects in the CC2 results, but it is unclear how this could affect the transition moments in the described manner. In terms of absolute energetics, TDDFT possesses the largest discrepancy compared with experiment due to the self-interaction error. For TP-DFT, we report good absolute energetics, after computed ΔKS and CEBE shifts amounting to −3.62/+1.36 and −3.64/+1.37 eV using a 6s6p6d set of diffuse functions or a 19s19p19d set of diffuse functions for the calculation of the excited state, respectively—in the latter case the augmentation is only introduced for the spectrum calculation and no such diffuse functions are used for determining the electron density or the ΔKS and CEBE corrections.
At the CC level of theory, we report a discrepancy in absolute energy which is larger for the CCSD results than for the more approximate CC2 results. This increase is caused by a cancellation of errors.67 For the relative energetics, the TP-DFT, TDDFT, and CCSD results are in good agreement with experiment, with a discrepancy of at most 0.17 eV for the relative energies of the antibonding 4a1 and 2b2 states, at the TDDFT level of theory. For the first Rydberg feature, the agreement of the TDDFT results is reduced, with a discrepancy of 0.44 eV compared to experiment.
It is to be noted that this comparison is made only to study the relative performance of the different theoretical approaches, and not to reproduce experimental data. As such, we have only considered excitations from the equilibrium geometry and thus lack vibrational effects. For a more thorough comparison to the experimental results, see, e.g., ref. 10, where spectra computed for 8000 vibrationally distorted geometries were summed and correct broadening thus achieved. It is to be noted that the 2b2 transition of that study was shown to have too large oscillator strength for calculations using only the equilibrium geometry, consistent with the present study, and that this was improved when also a sampling of the vibrational probability distribution was included.
The ionization potential (IP) of molecular systems can be estimated using a number of theoretical methods, e.g., by Koopmans' theorem, ΔSCF, and EOM-CC, but it would be desirable to obtain this at the same level of theory as the spectrum calculations for any study combining these results. For TP-DFT, the IP is already accounted for, while, for damped CC linear response theory, it can be estimated by introducing minor changes in the basis set exponents. With a small increase or decrease in the exponents, the physical features below the IP should be left unaffected, provided that the basis set is sufficiently saturated. However, for the discrete representation of the continuum states above the IP, relative energies and intensities are expected to shift significantly (provided the basis set is incomplete), thus enabling determining the IP. This has been demonstrated at the TDDFT level of theory in an earlier study,90 and we repeat this calculation here for TDDFT and CCSD. For this reason, we have uncontracted the basis sets with the more extended set of diffuse functions and rescaled the exponents by 0.98 and 0.98−1, with the resulting spectra reported in Fig. 2. While it is difficult to pin-point the position of the IP exactly, both electronic structure methods give term values (i.e. energy separation between the 4a1 transition and the IP) correct to within a few tenths of an eV, with CCSD showing superior results as compared to TDDFT. Using Koopmans' theorem on the KS-DFT orbital energies, the IP is estimated to be 524.30 eV, or 539.38 eV with the absolute shift used here, included as a blue line. This estimate coincides with the initiation of the fluctuations due to different exponents, as neither approach properly accounts for the relaxation of the valence electrons and can thus be expected to yield IPs of similar quality. A third manner of estimating the IP, using very diffuse basis functions or basis functions centered far away from the molecular system and investigating excitations to these states, yields similar IP estimate for TDDFT. It is to be noted that the estimate at the CCSD level of theory using the smaller set of diffuse functions was more ambiguous as this original basis set is not sufficiently well saturated, further strengthening the argument that the surprising agreement between the CCSD results for the different basis sets is largely fortuitous. Note that, in the condensed phase, a clear onset of the ionization continuum is lacking, as excited electrons can adapt a free-electron nature only upon escaping the solid, and we have thus not attempted a similar analysis in this case.
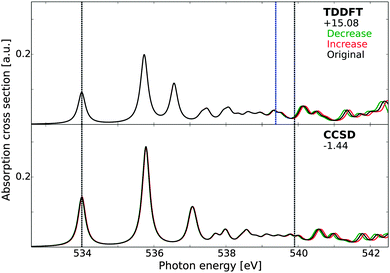 | ||
| Fig. 2 X-ray absorption spectra of gas-phase water as obtained using time-dependent DFT and damped CCSD linear response theory. The spectra have been aligned to the first experimental excitation energy73 by values reported beneath each model label, expressed in eV. Grey vertical lines indicate the positions of the experimental excitation energy of the first transition (534.0 eV) and the experimental ionization potential (539.9 eV). The blue vertical line in the TDDFT panel indicates the KS-DFT ionization potential as estimated using Koopmans' theorem. The results have been obtained using an uncontracted basis set of triple-ζ quality augmented with 19s19p19d functions, with original exponents (black) and exponents rescaled by factors of 0.98 (green) and 0.98−1 (red). | ||
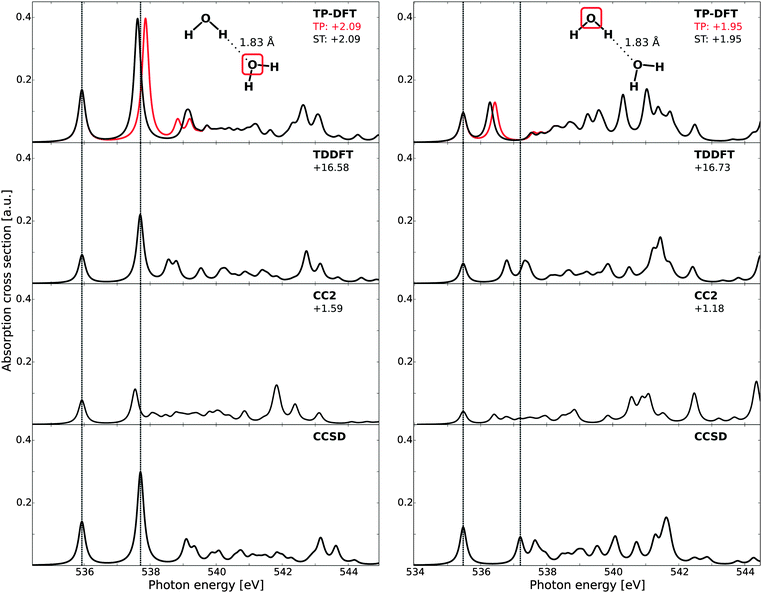
B. Water dimers
Theoretical spectra of each of the two molecules in the water dimer are reported in Fig. 3, where the results have been aligned to the first CCSD peak. Due to slow convergence of the CCSD spectra when using a complex solver, the CCSD results have been obtained using a Lanczos-chain driven algorithm.67 As a result of the high computational costs of CC calculations, we also utilize the smaller set of diffuse functions (6s6p6d) for the dimers and trimers. At the TP-DFT level of theory, a common potential (TP) has been utilized, as well as using explicitly relaxed Slater transition states for the first three excited states (ST).For the H-bond accepting molecule (left panels), the resulting spectral features are similar to those of the monomer, as the excited states are polarized towards the hydrogens and the hybridization of these states thus remains relatively unchanged by accepting an H-bond. For TP-DFT, the first two features are in good agreement with CCSD, both in terms of relative energetics and oscillator strengths, while the fine structure details have an earlier onset than what is found in the CCSD spectrum. This situation is changed somewhat when explicitly relaxing the first few states, for which the third and fourth features are combined into a single feature with a later onset. At the TDDFT level of theory a similar behavior is observed, with a slightly improved agreement for the splitting between the third and fourth features and an underestimation of the intensity of the first two peaks. For CC2, we note a smaller absolute intensity and spectral features similar to those of the monomer—the first two transitions are well reproduced but there are pronounced discrepancies in the fine structure details. Also note that all methods give a moderately intense band at high energy, with relative energetics similar in all cases. For the H-bond donating molecule (right panels), the spectral features are substantially changed as compared to the monomer due to a change in hybridization of the excited states, where the lowest core-excited state localizes on the free OH through 4a1–2b2 mixing, while the other state of antibonding valence character localizes along the H-bond and gets pushed up in energy and contributes in the post-edge region.6 We also note a general decrease in the onset energy of the spectra when comparing to the H-bond acceptor, amounting to 0.61, 0.61, 0.67, and 0.46 eV for TP-DFT, TDDFT, CC2, and CCSD, respectively. These results are consistent with earlier studies of small water complexes at the TP-DFT level of theory.6 The TDDFT and CCSD results are observed to have second and third spectral features of significantly higher relative energies than TP-DFT, for which a single feature is observed of similar total absorption cross section. A compression of the spectral features is also observed for the TDDFT and CC2 results, but to a smaller extent.
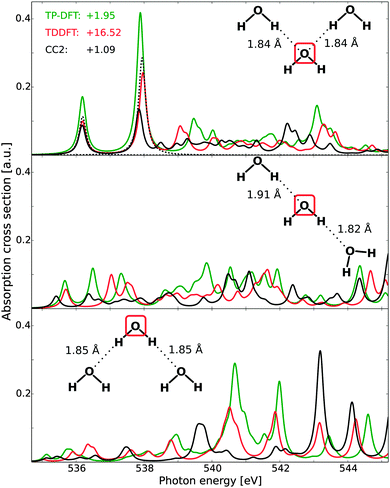
C. Water trimers
For the water trimers, the CCSD complex solver was, in the present case, unable to fully converge all spectral features in the adopted energy region, and the Lanczos-chain driven implementation was unable to utilize sufficiently large chain lengths to ensure sufficiently converged fine-structure details. It is to be noted that this issue is not related to the performance of damped CCSD linear response theory per se, but rather to difficulties in the present implementations (either for spanning a sufficiently large tri-diagonal representation or pre-conditioning new trial vectors). For this reason, Fig. 4 reports the full spectra of TP-DFT, TDDFT, and CC2, with CCSD being included only for the first two features of the acceptor–acceptor trimer.The effects of H-bond donation are consistent with those of the water dimer. For the acceptor–acceptor molecule (top panel), the spectra are similar to those of the monomer and the acceptor dimer, with excellent TP-DFT and TDDFT relative energies and intensities as compared to the CCSD level of theory. For the high-energy features, TDDFT yields a somewhat more compressed spectral region than TP-DFT, but with similar trends: an intense feature with a shoulder followed by a smeared-out region, which in turn is followed by a final intense feature with several shoulders. At the CC2 level of theory, the general features are the same, but the spectral region is again observed to be compressed and we note that the third spectral feature is not resolved. For the donor–acceptor trimer (mid panel), the agreement between the theoretical spectra is somewhat reduced, but the trends remain the same, with spectral features similar to that of the donating dimer molecule. The discrepancy between the spectra is partially increased for the donor–donor trimer (bottom panel), but we again observe similar trends for especially TP-DFT and TDDFT. Further, it is to be noted that TP-DFT generally yields a higher absorption cross section, and this is especially the case for the high-energy regions of the donor–acceptor and donor–donor trimers. As the local structure of liquid water will be dominated by single- and double-donors, this means that TP-DFT could be expected to give more pronounced post-edge features.
D. Liquid water
In order to investigate the requirements of reliable calculations of liquid water, we first focus on the treatment of excitations from a single molecule in a single MD structure using different basis sets and cluster sizes. Previous studies of similar computational parameters have focused on the effects on summed spectra from a number of MD structures,9,10,61 but here we focus on the convergence with cluster size of a single spectrum where all states, bound as well as unbound, are represented using localized Gaussian basis sets. The post-edge might be considered a special case since it is a resonance above the IP and as such could be handled, e.g., through Stieltjes imaging and continuum wave functions.129 Stieltjes imaging is a well-defined, moment-based approach to convert a discretely represented continuous cross section into a continuous spectrum. However, it has the drawback that the spectrum depends on the value of the IP and also tends to produce spectra that have lost fine-structure; the dependence on the IP becomes problematic when studying ionic solutions where an added ion or ion-pair changes the IP but not necessarily the distribution of oscillator strengths, while the smoothing has been problematic for instance when studying excitons at oxide surfaces130 and also spectra computed for various polymers.131 On the other hand, it has been demonstrated in, e.g., ref. 10 that an expansion of the continuum states in the near-edge region using a large set of diffuse Gaussian basis functions results in a computed cross section that closely reproduces experiment. The case investigated was gas phase water and the largest basis set comprised of close to 1500 extra functions distributed on 9 fictitious centers in addition to the oxygen of the molecule, which resulted in a very dense sampling and faithful representation of the cross section up to ≈20 eV beyond the edge. A further demonstration of the viability of this approach is also found in ref. 10, where near-perfect agreement was found for the post-edge computed for an ice model either as a sum of spectra from 174 clusters with 39 molecules each using the Gaussian basis set approach or as spectra computed directly from the unit cell under fully periodic boundary conditions and using a plane-wave representation of the wave functions. This approach is furthermore very inexpensive and was used throughout the present work.The sensitivity of TP-DFT spectrum calculations to nuclear quantum effects and interaction models used for generating liquid water structures has been demonstrated in previous work.10 Here, we generate model structures by performing DFT path integral molecular dynamics (PIMD) simulations for a box of 64 water molecules. The resulting oxygen–oxygen radial distribution function (RDF) is compared to the most accurate currently available experimental RDF122 in Fig. 5. It is clear that the optPBE-vdW PIMD simulation accurately reproduces the first peak of the experimental measurements, while the second peak is shifted to somewhat too short distance. Importantly, the explicit description of nuclear quantum effects through PIMD simulations should lead to an accurate description of intramolecular geometries and local H-bonding structures, and thus to realistic structure models for the XAS calculations.
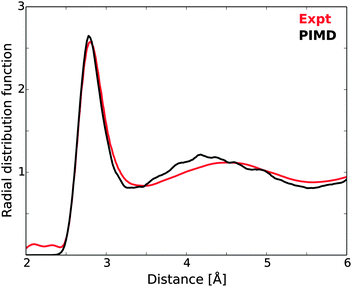 | ||
| Fig. 5 Oxygen–oxygen radial distribution function of the PIMD simulations, compared against experimental measurements.122 | ||
The single PIMD structure investigated in this section represents a rather disordered local H-bond environment as measured using the local structure index (LSI),54 which for this structure was 0.005 while the average of the 100 randomly selected model structures was 0.030. We thus expect the selected structure to exhibit a strong pre-edge. It is to be noted that the underlying PIMD simulation employs a box with 64 water molecules, such that the larger clusters in this study are pseudo-periodic due to this limitation (generated by extending the cluster into neighboring unit cells from the periodic simulation). This does not affect our study per se, but it is a limiting factor in comparison with experiment.
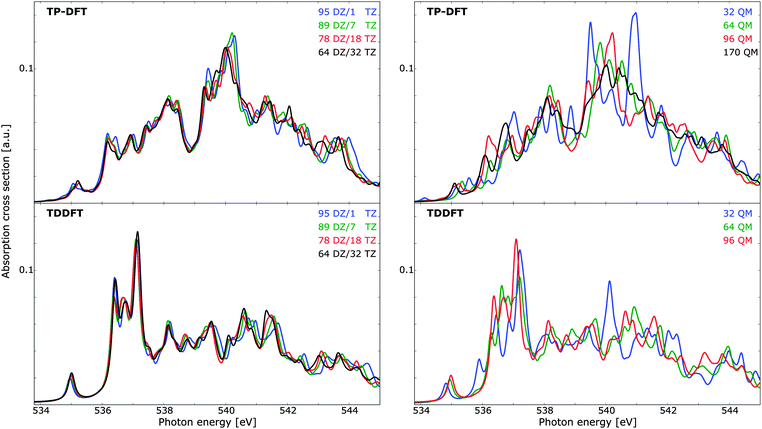
In Fig. 6 (left panels), the effects of utilizing a triple-ζ basis set for the innermost (solvent) molecule and a double-ζ basis set for the outermost molecules are illustrated. Both the TP-DFT and TDDFT results are shown to be relatively insensitive to this parameter, with minor discrepancies in mainly the high-energy/post-edge region. The scale of the theoretical spectra is such that a variational calculation yields a total integrated cross section equal to the number of electrons, in accordance with the Thomas–Kuhn–Reiche sum rule. It is clear that TP-DFT yields a higher intensity in the spectral region considered, with an integrated absorption cross section amounting to 0.50–0.52 a.u. for the energy window of the figure, compared to 0.41 a.u. for TDDFT. For the remaining calculations we have chosen to utilize a triple-ζ basis set for the six innermost solvent molecules, in order to ensure that the first solvation shell is well described. In terms of spectral features, both theoretical methods give a pre-edge feature of approximately the same magnitude, but the remaining features are significantly dissimilar. The TDDFT results exhibit a pronounced main-edge feature, while TP-DFT yields more intensity in the post-edge region and higher integrated absorption cross section. This is consistent with the results for the small water clusters, for which TP-DFT demonstrated a tendency towards more intense high-energy features.
Due to the high level of disorder in liquid water, it is necessary to utilize relatively large cluster sizes in order to ensure a suitable account of long-range interactions and delocalized excited states. With a too small cluster size, the spectra tend to be overstructured and the post-edge is typically underestimated, as this region is associated with delocalized excited states. Cluster size effects have been studied before,9,10,61 and for ice relatively small clusters are qualitatively well converged. However, if a quantitative analysis of, e.g., temperature effects is sought, care must be taken to ensure that the noise level (i.e. fine-structure induced by long-range interactions) is not of the same order of magnitude as the physical effects. The spectrum dependence on cluster size can be found in Fig. 6 (right panels), where TP-DFT is benchmarked up to a cluster of 170 molecules, and TDDFT has been used to treat clusters of maximum 96 QM molecules. The trends are similar for the TP-DFT and TDDFT results, with large fluctuations in spectral features that converge towards the results of the largest cluster size, and a smoothing of the features as more water layers are added. For TP-DFT the differences are found to be most significant in the post-edge region, while for TDDFT the primary difference is found in the main-edge region. TDDFT calculations of a cluster with 64 molecules but with the basis set of 96 molecules indicate that the effects on the spectra for clusters of these sizes are mainly due to long-range interactions, rather than the additional flexibility of the basis set. In terms of cluster radius, 32, 64, 96, and 170 molecules yield radii of circa 6.0, 7.4, 9.0, and 10.5 Å, respectively. The integrated cross section is found to be conserved for all cluster sizes treated, and it amounts to 0.50–0.51 a.u. for TP-DFT and 0.41 a.u. for TDDFT for the energy interval displayed in the figure.
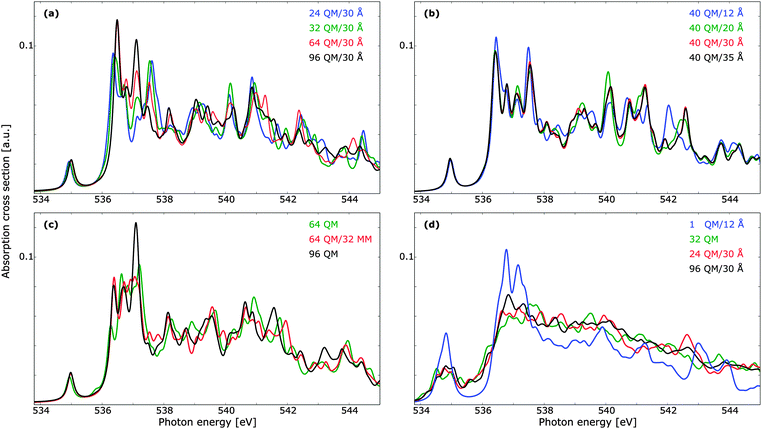
Provided that the excited states do not significantly overlap with the MM region in such a manner that the lack of Pauli repulsion becomes an issue, the use of a polarizable embedding is well suited for the description of disordered materials. As such, we have considered the cluster size dependence of TDDFT with a polarizable embedding, with the results reported in Fig. 7. The dependence on the size of the QM region is reported in panel (a), and we note that a smaller number of QM waters can be used while retaining the correct spectral features, as compared to pure QM calculations. Discrepancies are present mainly in the main-edge feature. It is further to be noted that the benchmark result here is markedly different from that of Fig. 6 (right panels), with peaks in the main- and post-edge regions shifting visibly in intensity. A QM cluster of 96 molecules is thus not sufficient to obtain spectrum convergence. Note, however, that when computing the summed TP-DFT spectrum of molecules in a 192 molecule unit cell of ice using either clusters with 39 molecules or the fully periodic simulation box virtually no differences were found.10 The radii designations used here indicate the total radius of the cluster, such that the total number of water molecules is the same for all the results reported in panel (a). In Fig. 7b, the convergence with respect to total cluster size is investigated using a QM cluster of 40 water molecules. A cluster radius of upwards to 30 Å is necessary for a converged individual spectrum, especially in terms of the post-edge region as these features are associated with more delocalized states.19 Calculations with a cluster size of 25 Å yield results very similar to 30 Å, but as the additional computational cost is small, we consider a total cluster size of 30 Å to be suitable for the treatment of liquid water. The total number of molecules of this cluster is 3702, while the cluster of 25 Å contains 2133 molecules and the cluster of 20 Å contains 1103 molecules. It is thus clear that a very large number of water molecules is needed in order to ensure convergence with respect to cluster size for single core-excitation calculations. One could consider embedding the QM/MM cluster in a continuum solvent model to reduce the size of the MM region,132,133 but the computational savings are expected to be marginal and we thus refrain from using such a subdivision. Furthermore, computational costs could decrease if the outer MM-region is given point charges but no polarizabilities.134 Test shows that the removal of polarizabilities yields similar spectral trends, even if only five molecules are treated quantum mechanically. This use of non-polarizable force fields did not lead to significant decrease in computational costs, and since the purpose of this study is not to compare different force fields per se, we adopt throughout the well-established Ahlström force field. Force field comparisons have been done previously in the literature—see, e.g., studies by Kongsted and co-workers.106,135 As the MM region lacks Pauli repulsion, it is important to ensure that the naked positive charges do not lead to an artificial increase in charge density at the QM/MM boundary. For the ground state this is unlikely to be a problem, as the boundary molecules all have a double-ζ basis set and thus do not have sufficiently polarizing functions to yield such an effect. However, the delocalized nature of the excited states, especially for those of the post-edge region, is such that this lack of Pauli repulsion could be an issue. As the diffuse functions that penetrate into the MM region will enclose both positive and negative charges it is unlikely, but in Fig. 7c we address this concern directly by comparing a QM cluster of 96 molecules with QM/MM calculations of 64 QM and 32 MM molecules. Adding this MM region leads to a general improvement in spectral features with no unphysical distortions.
While the cluster size dependence of summed spectra has been studied elsewhere for TP-DFT,9,10,61 no such studies have been found at the TDDFT level of theory. In Fig. 7d we investigate the effects of averaging over 10 PIMD structures using clusters of 32 QM molecules, as well as QM/MM calculations of a single QM molecule with a 12 Å MM shell, and 24 or 96 QM molecules in clusters with a radius of 30 Å. The extremal case of a single QM molecule can be compared to a recent development of damped linear response coupled cluster with a polarizable embedding,69 where the performance of this method was demonstrated on water as well as a number of other systems. In that work only a single water molecule was treated quantum mechanically, such that the post-edge could not be resolved, and the resulting spectrum retained much of the gas-phase features. Note that an additional 0.5 eV shift was applied to the pre-edge feature of the TDDFT results reported in Fig. 7d, similar to the shift from the gas-phase to the condensed phase; it is well known that intermolecular orbital interactions are important for the calculation of spectral features.136
In comparison to the results in ref. 69, the more diffuse basis set used in the present work results in a more smeared out spectrum, but tests using an identical basis set show that this is largely an effect of the basis set rather than of the different electronic structure methods. However, the spectral features are in both cases markedly different to the benchmark calculations with 96 QM waters, and the lack of Pauli repulsion is clearly an issue. In view of the more realistic QM/MM calculations, we note that both divisions agree well with each other, as well as with the pure 32 QM calculations. The largest QM cluster exhibits less fluctuations, but all three cluster divisions give the same trends. For lower energies, the 24 QM/30 Å summed spectrum agrees better with that of 96 QM/30 Å than with that of 32 QM, but for higher energies this relation is reversed. Due to the small number of structures, we cannot draw any firm conclusions from this, but it is to be expected that more structures will yield an improved agreement for all energies; note, e.g., the improved agreement between the QM/MM main-edge region in the summed spectra as compared to the single structure in panel (a). We thus expect all three cluster divisions to yield spectral features of similar quality when averaged spectra are determined. We further emphasize the advantages of using the 24 QM/30 Å model, as this can include long-range effects when those are of importance, as well as decrease the computational costs as compared to using 32 QM molecules.
Using clusters of 32 QM molecules, the TP-DFT and TDDFT summed spectra of 100 randomly selected PIMD structures are reported in Fig. 8, compared against experimental measurements on liquid water.18 For TP-DFT, the first nine transition energies were corrected using Slater transition-state calculations to improve the description of the pre-edge region where relaxation effects are more important due to the localized character of the pre-edge transitions.19 It is to be noted that this comparison is primarily aimed towards comparing the relative performance of TP-DFT and TDDFT, not to produce state-of-the-art calculations simulating the spectrum of liquid water. As such, the chosen cluster size is relatively small and the total number of PIMD structures is too small to obtain full spectral convergence. Furthermore, as discussed above, the TDDFT calculations would benefit from using a polarizable embedding as this enables the use of smaller QM regions while increasing the size of the total system by several orders of magnitude. At the TP-DFT level of theory, it is difficult to resolve the different spectral features, but we note a post-edge region of high intensity with a shoulder that could indicate the position of the main-edge feature. However, the energy separation of these two features is smaller than that found in experiment, and the pre-edge feature cannot conclusively be resolved. By using Slater transition states for the first few excitations, the pre-edge feature is improved, with intensity shifted towards lower energies. For TDDFT, the agreement with experiment is remarkably good, showing clearly separated pre-, main-, and post-edges with qualitatively correct relative energetics and intensities. The pre-edge feature is broader than that found in the experiment, which could be an effect of a shifted onset of spectral features due to the small cluster size—the excitation energy of this feature in Fig. 6 (right panels) can be seen to vary by a few tenths of an eV depending on the cluster size, an effect which is expected to broaden the features of the summed spectrum considered here. We also observe the same effect in Fig. 7d, where the 32 QM calculation yields a slightly broader spectral peak as compared to the benchmark calculation. It is also to be noted that the TDDFT spectrum exhibits a fourth spectral feature at approximately 544 eV, a feature which is not resolved in the experimental measurements.
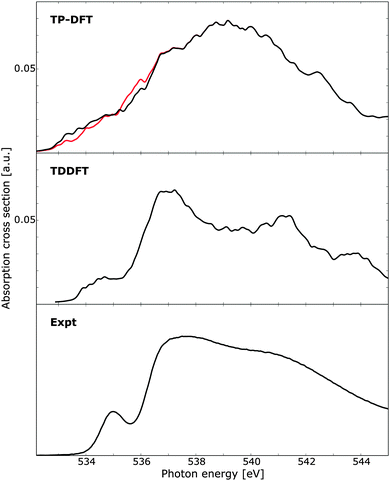 | ||
| Fig. 8 X-ray absorption spectra of 100 water clusters as obtained using transition-potential DFT and time-dependent DFT, compared against experiment.10 For TP-DFT the results have been obtained using standard TP-DFT (red) or the first nine excited states computed using Slater transition states (black). Each cluster consists of 32 water molecules and the TDDFT results have been aligned to the experimental pre-edge by an absolute shift of 14.90 eV. Experimental data obtained at 299 K. | ||
E. Ice
Finally we consider the X-ray absorption spectrum of ice, as calculated for a single model structure. As experimental reference, we consider new measurements of D2O ice grown on hydrophobic BaF2 surfaces and measured at a temperature of 144 K, as this ice structure has been attributed to possess a very low degree of grain boundaries and other defects.18 The resulting spectrum exhibits a very weak pre-edge and a split in the post-edge feature, both characteristic of a highly crystalline ice structure. The remaining pre-edge intensity has been attributed to vibronic effects, as well as beam-induced conversion to HDA ice,18 since it remains stronger than the pre-edge reported for a water monolayer on the Ru(0001) surface.16The calculated spectra are reported in Fig. 9, as compared against experiment. At the TP-DFT level of theory, an intense post-edge feature is observed, with a clear splitting of this feature into two parts for the larger clusters. For the pre-edge, only a very weak response is observed, as the model structure possesses a high degree of coordination with no structural defects. The main-edge intensity is pronounced for the 64 and 96 molecule clusters, but for the 32 molecule cluster this feature is shifted to higher energy. In general, the different cluster sizes yield qualitatively similar spectra, with overestimated intensity difference between the main- and post-edge features and the larger clusters exhibiting a more correct onset of the main-edge feature. These observations are consistent with the summed up spectra reported in an earlier study,10 where it was demonstrated that TP-DFT provides a qualitatively correct ice spectrum even if the main-edge appears more as a bump than a distinct shoulder.
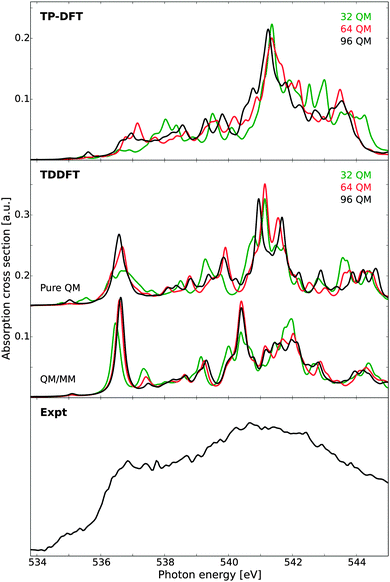 | ||
| Fig. 9 X-ray absorption spectra of a single ice cluster as obtained using transition-potential DFT and time-dependent DFT, compared against experimental measurements on bulk ice.10 Cluster sizes of theoretical calculations vary according to labels, with additional TDDFT results obtained using a polarizable embedding approach such that the total QM/MM cluster spans 30 Å. The TDDFT results have been shifted by 14.90 eV. Experimental data obtained at 144 K. | ||
At the TDDFT level of theory the spectral features are significantly improved, and we especially note the splitting of the post-edge feature which occurs when the cluster size is increased. A weak pre-edge feature at the correct energy position is observed for all cluster sizes, and the main-edge feature is well resolved. For the pure QM calculations, a small splitting of the post-edge feature is observed, which increases when an MM layer is added, and good agreement with experiment is obtained. This is consistent with the identification of a split post-edge as a result of an extended H-bonding network. Further, from experimental measurements a strong shoulder has been observed between 544 and 548 eV, and we note that the TDDFT results of both liquid water and ice exhibit a small feature at an energy of approximately 544 eV. It is particularly gratifying to see all spectral features correctly reproduced in terms of energetics and relative intensities. However, there seems to be intensity lacking between the main-edge and post-edge which might be due to the poor statistics in terms of statistical averaging over several structures.
V. Conclusions
The X-ray absorption spectra of gas-phase water, small water clusters, liquid water, and bulk ice have been studied using TP-DFT, TDDFT, and CC linear response theory.The spectral features obtained using TP-DFT, TDDFT, and CCSD are qualitatively in good agreement for all small complexes considered, while the CC2 results exhibit a compression of the pre-edge region and decreased absorption cross section for the water complexes. For the water dimers and trimers, the effects of H-bond donation can be clearly observed: while H-bond acceptance leaves the spectral features relatively unchanged, H-bond donation yields significant changes due to the rehybridization of the (valence) excited states. It has also been demonstrated that the 4a1 to IP term value of gas-phase water can be estimated within a few tenths of an eV by introducing small changes in the basis set exponents. The current inability of our damped CCSD linear response implementation to provide fully converged results for water trimers is unfortunate, and will be addressed in future implementation of core-valence separation in the excitation space. It is to be noted that the lack of relaxation in TDDFT remains a concern, and that the origin of the observed underestimation of the absorption cross section of CC2 for all but π-conjugated systems66,67,99 remains an open question.
For liquid water, the basis set and cluster size requirements of calculations on a single PIMD structure have been studied, as well as the summed spectra of 100 PIMD structures. It has been demonstrated that a triple-ζ basis set for the solute and first solvation shell gives a good compromise between computational cost and spectrum quality, while convergence in terms of cluster size is more difficult to achieve. We have demonstrated that 170 QM waters for TP-DFT or 96 water molecules for TDDFT are insufficient for converging spectral features of a single spectrum. However, if summed spectra are considered, significantly smaller clusters can be utilized. For TDDFT, it has been demonstrated that a QM/MM approach with a polarizable embedding enables the convergence of spectral features in terms of cluster size, as well as decreasing the computational costs of physically realistic models. An embedding using more than 2000 molecules has been shown to yield converged spectral features for a cluster with 40 QM water molecules. For summed spectra, 32 QM water molecules yield similar features as using 24 or 96 QM water molecules with a MM region extending up to 30 Å from the targeted oxygen atom. In terms of summed spectra, TDDFT is observed to yield very good agreement with experiment, while TP-DFT exhibits difficulties in resolving the different spectral features and gives an overestimated post-edge feature. This latter overestimation is consistent with the results for small water clusters, where TP-DFT is observed to yield high intensities for the high-energy spectral region.
For bulk ice, similar spectral trends as for liquid water are observed, with the TDDFT results showing superior agreement with experiment, as compared to TP-DFT. Here the tetrahedral coordination yields intense post-edge features, while the pre-edge feature is significantly diminished. It is demonstrated that calculations using large clusters yield a splitting of the post-edge feature, in agreement with experimental observations. Furthermore, the TDDFT results of liquid water and bulk ice include a fourth spectral feature, which has experimentally been resolved for bulk ice but not yet for liquid water.
Acknowledgements
Financial support from the Swedish Research Council (Grants No. 621-2014-4646 and No. 621-2011-4223) and Knut and Alice Wallenberg Foundation (Grant No. KAW-2013.0020) is acknowledged as well as grants for computing time from National Supercomputer Centre (NSC) and HPC2N, Sweden.References
- M. F. Chaplin, Water Structure and Science, http://www1.lsbu.ac.uk/water/index.html.
- P. Wernet, D. Nordlund, U. Bergmann, M. Cavalleri, M. Odelius, H. Osagawara, L.-Å. Näslund, T. K. Hirsch, L. Ojamäe, P. Glatzel, L. G. M. Pettersson and A. Nilsson, Science, 2004, 304, 995–999 CrossRef CAS PubMed.
- J. A. Sellberg, C. Huang, T. A. McQueen, N. D. Loh, H. Laksmono, D. Schlesinger, R. G. Sierra, D. Nordlund, C. Y. Hampton, D. Starodub, D. P. DePonte, M. Beye, C. Chen, A. V. Martin, A. Barty, K. T. Wikfeldt, T. M. Weiss, C. Caronna, J. Feldkamp, L. B. Skinner, M. M. Seibert, M. Messerschmidt, G. J. Williams, S. Boutet, L. G. M. Pettersson, M. J. Bogan and A. Nilsson, Nature, 2014, 510, 381–384 CrossRef CAS PubMed.
- A. Nilsson, D. Nordlund, I. Waluyo, H. Ogasawara, S. Kaya, U. Bergmann, L.-Å. Näslund, H. Öström, P. Wernet, K. J. Andersson, T. Schiros and L. G. M. Pettersson, J. Electron Spectrosc. Relat. Phenom., 2010, 177, 99–129 CrossRef CAS.
- J. Stöhr, NEXAFS Spectroscopy, Springer, Berlin, 1992 Search PubMed.
- M. Cavalleri, H. Ogasawara, L. G. M. Pettersson and A. Nilsson, Chem. Phys. Lett., 2002, 364, 363–370 CrossRef CAS.
- J. D. Smith, C. D. Cappa, B. M. Messer, W. S. Drisdell, R. C. Cohen and R. J. Saykally, J. Phys. Chem. B, 2006, 110, 20038–20045 CrossRef CAS PubMed.
- D. Prendergast and G. Galli, Phys. Rev. Lett., 2006, 96, 215502 CrossRef PubMed.
- M. Iannuzzi, J. Chem. Phys., 2008, 128, 204506 CrossRef PubMed.
- M. Leetmaa, M. P. Ljungberg, A. Lyubartsev, A. Nilsson and L. G. M. Pettersson, J. Electron Spectrosc. Relat. Phenom., 2010, 177, 135–157 CrossRef CAS.
- T. D. Kühne and R. Z. Khaliullin, J. Am. Chem. Soc., 2014, 136, 3395–3399 CrossRef PubMed.
- T. Pylkkänen, V. Giordano, J.-C. Chervin, A. Sakko, M. Hakala, J. A. Soininen, K. Hämäläinen, G. Monaco and S. Huotari, J. Phys. Chem. B, 2010, 114, 3804–3808 CrossRef PubMed.
- S. Myneni, Y. Luo, L.-Å. Näslund, M. Cavalleri, L. Ojamäe, H. Ogasawara, A. Pelmenschikov, P. Werner, P. P. Väterlein, C. Heske, Z. Hussain, L. G. M. Pettersson and A. Nilsson, J. Phys.: Condens. Matter, 2002, 14, L213–L219 CrossRef CAS.
- Y. Q. Cai, H.-K. Mao, P. C. Chow, J. S. Tse, Y. Ma, S. Patchkovskii, J. F. Shu, V. Struzhkin, R. J. Hemley, H. Ishii, C. C. Chen, I. Jarrige, C. T. Chen, S. R. Shieh, E. P. Huang and C. C. Kao, Phys. Rev. Lett., 2005, 100, 025502 CrossRef PubMed.
- J. S. Tse, M. Shaw, D. D. Klug, S. Patchkovskii, G. Vankò, G. Monaco and M. Krisch, Phys. Rev. Lett., 2008, 100, 095502 CrossRef PubMed.
- D. Nordlund, H. Ogasawara, K. J. Andersson, M. Tatarkhanov, M. Salmerón, L. G. M. Pettersson and A. Nilsson, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 80, 233404 CrossRef.
- T. Schiros, K. J. Andersson, L. G. M. Pettersson, A. Nilsson and H. Ogasawara, J. Electron Spectrosc. Relat. Phenom., 2010, 177, 85–98 CrossRef CAS.
- J. A. Sellberg, S. Kaya, V. H. Segtnan, C. Chen, T. Tyliszczak, H. Ogasawara, D. Nordlund, L. G. M. Pettersson and A. Nilsson, J. Chem. Phys., 2014, 141, 034507 CrossRef PubMed.
- D. Nordlund, H. Ogasawara, H. Bluhm, M. Takahashi, M. Odelius, M. Nagasono, L. G. M. Pettersson and A. Nilsson, Phys. Rev. Lett., 2007, 99, 217406 CrossRef CAS PubMed.
- T. Pylkkänen, A. Sakko, M. Hakala, K. Hämäläinen, G. Monaco and S. Huotari, J. Phys. Chem. B, 2011, 115, 14544–14550 CrossRef PubMed.
- C. D. Cappa, J. D. Smith, K. R. Wilson, B. M. Messer, M. K. Gilles, R. C. Cohen and R. J. Saykally, J. Phys. Chem. B, 2005, 109, 7046–7052 CrossRef CAS PubMed.
- L.-Å. Näslund, D. C. Edwards, P. Wernet, U. Bergmann, H. Ogasawara, L. G. M. Pettersson, S. Myneni and A. Nilsson, J. Phys. Chem. A, 2005, 109, 5995–6002 CrossRef PubMed.
- O. Fuchs, M. Zharnikov, M. Blum, M. Weigand, Y. Zubavichus, M. Bär, F. Maier, J. D. Denlinger, C. Heske, M. Grunze and E. Umbach, Phys. Rev. Lett., 2008, 100, 027801 CrossRef CAS PubMed.
- K. M. Lange, K. F. Hodeck, U. Schade and E. F. Aziz, J. Phys. Chem. B, 2010, 114, 16997–17001 CrossRef CAS PubMed.
- I. Waluyo, C. Huang, D. Nordlund, U. Bergmann, T. M. Weiss, L. G. M. Pettersson and A. Nilsson, J. Chem. Phys., 2011, 134, 064513 CrossRef PubMed.
- I. Juurinen, T. Pylkkänen, K. O. Ruotsalainen, C. J. Sahle, G. Monaco, K. Hämäläinen, S. Huotari and M. Hakala, J. Phys. Chem. B, 2013, 117, 16506–16511 CrossRef CAS PubMed.
- M. Nagasaka, K. Mochizuki, V. Leloup and N. Kosugi, J. Phys. Chem. B, 2014, 118, 4388–4396 CrossRef CAS PubMed.
- I. Waluyo, D. Nordlund, U. Bergmann, D. Schlesinger, L. G. M. Pettersson and A. Nilsson, J. Chem. Phys., 2014, 140, 244506 CrossRef PubMed.
- L.-Å. Näslund, M. Cavalleri, H. Ogasawara, A. Nilsson, L. G. M. Pettersson, P. Wernet, D. C. Edwards, M. Sandström and S. Myneni, J. Phys. Chem. A, 2003, 107, 6869–6876 CrossRef.
- M. Cavalleri, L.-Å. Näslund, D. C. Edwards, P. Wernet, H. Ogasawara, S. Myneni, L. Ojamäe, M. Odelius, A. Nilsson and L. G. M. Pettersson, J. Chem. Phys., 2006, 124, 194508 CrossRef PubMed.
- C. D. Cappa, J. D. Smith, B. M. Messer, C. R. Cohen and R. J. Saykally, J. Phys. Chem. B, 2006, 110, 1166–1171 CrossRef CAS PubMed.
- C. Chen, C. Huang, I. Waluyo, D. Nordlund, T.-C. Weng, D. Sokaras, T. Weiss, U. Bergmann, L. G. M. Pettersson and A. Nilsson, J. Chem. Phys., 2013, 138, 154506 CrossRef PubMed.
- P. Wernet, D. Testemale, J. L. Hazemann, R. Argoud, P. Glatzel, L. G. M. Pettersson, A. Nilsson and U. Bergmann, J. Chem. Phys., 2005, 123, 154503 CrossRef PubMed.
- I. Waluyo, D. Nordlund, U. Bergmann, L. G. M. Pettersson and A. Nilsson, J. Chem. Phys., 2009, 131, 031103 CrossRef PubMed.
- U. Bergmann, D. Nordlund, P. Wernet, M. Odelius, L. G. M. Pettersson and A. Nilsson, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 76, 024202 CrossRef.
- L. Kong, X. Wu and R. Car, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 86, 134203 CrossRef.
- J. D. Smith, C. D. Cappa, K. R. Wilson, B. M. Messer, R. C. Cohen and R. J. Saykally, Science, 2004, 306, 851–853 CrossRef CAS PubMed.
- J. D. Smith, C. D. Cappa, B. M. Messer, R. C. Cohen and R. J. Saykally, Science, 2005, 308, 793B CrossRef.
- W. Chen, X. Wu and R. Car, Phys. Rev. Lett., 2010, 105, 017802 CrossRef PubMed.
- G. N. I. Clark, C. D. Cappa, J. D. Smith, R. J. Saykally and T. Head-Gordon, Mol. Phys., 2010, 108, 1415–1433 CrossRef CAS.
- J. Vinson, J. J. Kas, F. D. Vila, J. J. Rehr and E. L. Shirley, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 85, 045101 CrossRef.
- A. Nilsson, P. Wernet, D. Nordlund, U. Bergmann, M. Cavalleri, M. Odelius, H. Ogasawara, L.-Å. Näslund, T. K. Hirsch, L. Ojamäe, P. Glatzel and L. G. M. Pettersson, Science, 2005, 308, 793A CrossRef PubMed.
- M. Odelius, M. Cavalleri, A. Nilsson and L. G. M. Pettersson, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 73, 024205 CrossRef.
- M. Leetmaa, M. Ljungberg, H. Ogasawara, M. Odelius, L.-Å. Näslund, A. Nilsson and L. G. M. Pettersson, J. Chem. Phys., 2006, 125, 244510 CrossRef PubMed.
- A. Nilsson, C. Huang and L. G. M. Pettersson, J. Mol. Liq., 2012, 176, 2–16 CrossRef CAS.
- A. Nilsson and L. G. M. Pettersson, Chem. Phys., 2011, 389, 1–34 CrossRef CAS.
- C. Huang, K. T. Wikfeldt, T. Tokushmia, D. Nordlund, Y. Harada, U. Bergmann, M. Niebuhr, T. M. Weiss, Y. Horikawa, M. Leetmaa, M. P. Ljungberg, O. Takahashi, A. Lenz, L. Ojamäe, A. P. Lyubartsev, S. Shin, L. G. M. Pettersson and A. Nilsson, Proc. Natl. Acad. Sci. U. S. A., 2009, 106, 15214–15218 CrossRef CAS PubMed.
- T. Head-Gordon and F. H. Stillinger, J. Chem. Phys., 1993, 98, 3313–3327 CrossRef CAS.
- V. Holten and M. A. Anisimov, Sci. Rep., 2012, 2, 713 CAS.
- J. Russo and H. Tanaka, Nat. Commun., 2014, 5, 3556 Search PubMed.
- K. T. Wikfeldt, A. Nilsson and L. G. M. Pettersson, Phys. Chem. Chem. Phys., 2009, 13, 19918–19924 RSC.
- G. A. Appignanesi, J. A. Rodriguez Friz and F. Sciortino, Eur. Phys. J. E: Soft Matter Biol. Phys., 2009, 29, 305–310 CrossRef CAS PubMed.
- P. G. Debenedetti and F. H. Stillinger, Nature, 2014, 410, 259–267 CrossRef PubMed.
- E. Shiratani and M. Sasai, J. Chem. Phys., 1996, 104, 7671–7680 CrossRef CAS.
- R. H. Henchman and S. J. Cockram, Faraday Discuss., 2013, 167, 529–550 RSC.
- T. D. Kühne and R. Z. Khaliullin, Nat. Commun., 2013, 4, 1450 CrossRef PubMed.
- B. Hetényi, F. D. Angelis, P. Giannozzi and R. Car, J. Chem. Phys., 2004, 120, 8632–8637 CrossRef PubMed.
- G. Brancato, N. Rega and V. Barone, Phys. Rev. Lett., 2008, 100, 107401 CrossRef PubMed.
- M. Leetmaa, K. T. Wikfeldt, M. P. Ljungberg, M. Odelius, J. Swenson, A. Nilsson and L. G. M. Pettersson, J. Chem. Phys., 2008, 129, 084502 CrossRef PubMed.
- L. Triguero, L. G. M. Pettersson and H. Ågren, Phys. Rev. B: Condens. Matter Mater. Phys., 1998, 58, 8097–8110 CrossRef CAS.
- M. Cavalleri, M. Odelius, A. Nilsson and L. G. M. Pettersson, J. Chem. Phys., 2004, 121, 10065–10075 CrossRef CAS PubMed.
- M. Cavalleri, M. Odelius, D. Nordlund, A. Nilsson and L. G. M. Pettersson, Phys. Chem. Chem. Phys., 2005, 7, 2854–2858 RSC.
- R. L. C. Wang, H. J. Kreuzer and M. Grunze, Phys. Chem. Chem. Phys., 2006, 8, 4744–4751 RSC.
- M. E. Casida, in Time-dependent density-functional response theory for molecules, ed. D. P. Chong, Recent Advances in Density Functional Methods Part I, World Scientific, Singapore, 1995 Search PubMed.
- J. Vinson, J. J. Rehr, J. J. Kas and E. L. Shirley, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 83, 115106 CrossRef.
- S. Coriani, O. Christiansen, T. Fransson and P. Norman, Phys. Rev. A: At., Mol., Opt. Phys., 2012, 85, 022507 CrossRef.
- S. Coriani, T. Fransson, O. Christiansen and P. Norman, J. Chem. Theory Comput., 2012, 8, 1616–1628 CrossRef CAS PubMed.
- J. Kauczor, P. Norman, O. Christiansen and S. Coriani, J. Chem. Phys., 2013, 139, 211102 CrossRef PubMed.
- N. H. List, S. Coriani, J. Kongsted and O. Christiansen, J. Chem. Phys., 2014, 141, 244107 CrossRef PubMed.
- M. Nooijen and R. J. Bartlett, J. Chem. Phys., 1995, 102, 6735–6756 CrossRef CAS.
- J. Brabec, K. Bhaskaran-Nair, N. Govind, J. Pittner and K. Kowalski, J. Chem. Phys., 2012, 137, 171101 CrossRef PubMed.
- J. Schirmer, Phys. Rev. A: At., Mol., Opt. Phys., 1982, 26, 2395–2416 CrossRef CAS.
- J. Schirmer, A. B. Trofimov, K. J. Randall, J. Feldhaus, A. M. Bradshaw, Y. Ma, C. T. Chen and F. Sette, Phys. Rev. A: At., Mol., Opt. Phys., 1993, 47, 1136–1147 CrossRef CAS.
- J. Wenzel, M. Wormit and A. Dreuw, J. Comput. Chem., 2014, 35, 1900–1915 CrossRef CAS PubMed.
- K. Kuramoto, M. Ehara and H. Nakatsuji, J. Chem. Phys., 2005, 122, 014304 CrossRef PubMed.
- Y. Ohtsuka and H. Nakatsuji, J. Chem. Phys., 2006, 124, 054110 CrossRef PubMed.
- T. Helgaker, S. Coriani, P. Jørgensen, K. Kristensen, J. Olsen and K. Ruud, Chem. Rev., 2012, 112, 543–631 CrossRef CAS PubMed.
- P. Norman, Phys. Chem. Chem. Phys., 2011, 13, 20519–20535 RSC.
- J. C. Slater, Adv. Quantum Chem., 1972, 6, 1 CrossRef CAS.
- J. C. Slater and K. H. Johnsson, Phys. Rev. B: Solid State, 1972, 5, 844 CrossRef.
- M. Nyberg, Y. Luo, L. Triguero, L. G. M. Pettersson and H. Ågren, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 60, 7956–7960 CrossRef CAS.
- O. Takahashi and L. G. M. Pettersson, J. Chem. Phys., 2004, 121, 10339–10345 CrossRef CAS PubMed.
- C. Kolczewski, R. Püttner, O. Plashkevych, H. Ågren, V. Staemmler, M. Martins, G. Snell, A. S. Schlachter, M. Sant'anna, G. Kaindl and L. G. M. Pettersson, J. Chem. Phys., 2001, 115, 6426–6437 CrossRef CAS.
- R. W. Boyd, Nonlinear Optics, Academic Press, San Diego, 3rd edn, 2008 Search PubMed.
- C. Vahlberg, M. Linares, S. Villaume, P. Norman and K. Uvdal, J. Phys. Chem. C, 2011, 115, 165–175 CAS.
- P. Norman, D. M. Bishop, H. J. Aa. Jensen and J. Oddershede, J. Chem. Phys., 2001, 115, 10323–10334 CrossRef CAS.
- P. Norman, D. M. Bishop, H. J. Aa. Jensen and J. Oddershede, J. Chem. Phys., 2005, 123, 194103 CrossRef PubMed.
- E. R. Davidson, J. Comput. Phys., 1975, 17, 87–94 CrossRef.
- U. Ekström, P. Norman, V. Carravetta and H. Ågren, Phys. Rev. Lett., 2006, 97, 143001 CrossRef PubMed.
- U. Ekström and P. Norman, Phys. Rev. A: At., Mol., Opt. Phys., 2006, 74, 042722 CrossRef.
- J. Kauczor, P. Jørgensen and P. Norman, J. Chem. Theory Comput., 2011, 7, 1610–1630 CrossRef CAS PubMed.
- J. Kauczor and P. Norman, J. Chem. Theory Comput., 2014, 10, 2449–2455 CrossRef CAS PubMed.
- K. Lopata, B. E. Van Kuiken, M. Khalil and N. Govind, J. Chem. Theory Comput., 2012, 8, 3284–3292 CrossRef CAS PubMed.
- N. A. Besley, M. J. G. Peach and D. J. Tozer, Phys. Chem. Chem. Phys., 2009, 11, 10350–10358 RSC.
- N. A. Besley and F. A. Asmuruf, Phys. Chem. Chem. Phys., 2010, 12, 12024–12039 RSC.
- S. T. Skowron and N. A. Besley, Theor. Chem. Acc., 2012, 131, 1267 CrossRef.
- G. Tu, V. Carravetta, O. Vahtras and H. Ågren, J. Chem. Phys., 2007, 127, 174110 CrossRef PubMed.
- G. Tu, Z. Rinkevicius, O. Vahtras, H. Ågren, U. Ekström, P. Norman and V. Carravetta, Phys. Rev. A: At., Mol., Opt. Phys., 2007, 76, 022506 CrossRef.
- T. Fransson, S. Coriani, O. Christiansen and P. Norman, J. Chem. Phys., 2013, 138, 124311 CrossRef PubMed.
- J. Schirmer and A. Dreuw, Phys. Rev. A: At., Mol., Opt. Phys., 2007, 75, 022513 CrossRef.
- J. Schirmer and A. Dreuw, Phys. Rev. A: At., Mol., Opt. Phys., 2008, 78, 056502 CrossRef.
- N. T. Maitra, R. van Leeuwen and K. Burke, Phys. Rev. A: At., Mol., Opt. Phys., 2008, 78, 056501 CrossRef.
- O. Christiansen, H. Koch and P. Jørgensen, Chem. Phys. Lett., 1995, 243, 409–418 CrossRef CAS.
- G. D. Purvis, J. Chem. Phys., 1982, 76, 4 CrossRef.
- O. Christiansen, H. Koch and P. Jørgensen, J. Chem. Phys., 1996, 105, 1451–1459 CrossRef CAS.
- M. Olsen, K. Aidas and J. Kongsted, J. Chem. Theory Comput., 2010, 6, 3721–3734 CrossRef.
- M. N. Pedersen, E. D. Hedegård, J. M. H. Olsen, J. Kauczor, P. Norman and J. Kongsted, J. Chem. Theory Comput., 2014, 10, 1164–1171 CrossRef CAS PubMed.
- K. Sneskov, T. Schwabe, J. Kongsted and O. Christiansen, J. Chem. Phys., 2011, 134, 104108 CrossRef PubMed.
- A. M. Koster, G. Geudtner, P. Calaminici, M. E. Casida, V. D. Dominguez, R. Flores-Moreno, G. U. Gamboa, A. Goursot, T. Heine, A. Ipatov, F. Janetzko, J. M. del Campo, J. U. Reveles, A. Vela, B. Zuniga-Gutierrez and D. R. Salahub, deMon2k, Version 3, The deMon developers, Cinvestav, Mexico City, 2011 Search PubMed.
- K. Hermann, L. G. M. Pettersson, M. E. Casida, C. Daul, A. Goursot, A. Koester, E. Proynov, A. St-Amant, D. R. Salahub, V. Carravetta, A. Duarte, N. Godbout, J. Guan, C. Jamorski, M. Leboeuf, M. Leetmaa, M. Nyberg, L. Pedocchi, F. Sim, L. Triguero and A. Vela, StoBe-deMon version 3.3, 2014 Search PubMed.
- H. Ågren, V. Carravetta, O. Vahtras and L. G. M. Pettersson, Theor. Chem. Acc., 1997, 97, 14–40 CrossRef.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS PubMed.
- DALTON, a molecular electronic structure program, Release DALTON2013.2, 2013, see http://daltonprogram.org Search PubMed.
- K. Aidas, C. Angeli, K. L. Bak, V. Bakken, R. Bast, L. Boman, O. Christiansen, R. Cimiraglia, S. Coriani, P. Dahle, E. K. Dalskov, U. Ekström, T. Enevoldsen, J. J. Eriksen, P. Ettenhuber, B. Fernández, L. Ferrighi, H. Fliegl, L. Frediani, K. Hald, A. Halkier, C. Hättig, H. Heiberg, T. Helgaker, A. C. Hennum, H. Hettema, E. Hjertenæs, S. Høst, I.-M. Høyvik, B. Iozzi, M. F. Jansik, H. J. Aa. Jensen, D. Jonsson, P. Jørgensen, J. Kauczor, S. Kirpekar, T. Kjærgaard, W. Klopper, S. Knecht, R. Kobayashi, H. Koch, J. Kongsted, A. Krapp, K. Kristensen, A. Ligabue, O. B. Lutnæs, J. I. Melo, K. V. Mikkelsen, R. H. Myhre, C. Neiss, C. B. Nielsen, P. Norman, J. Olsen, J. M. H. Olsen, A. Osted, M. J. Packer, F. Pawlowski, T. B. Pedersen, P. F. Provasi, S. Reine, Z. Rinkevicius, T. A. Ruden, K. Ruud, V. Rybkin, P. Salek, C. C. M. Samson, A. Sánchez de Merás, T. Saue, S. P. A. Sauer, B. Schimmelpfennig, K. Sneskov, A. H. Steindal, K. H. Sylvester-Hvid, P. R. Taylor, A. M. Teale, E. I. Tellgren, D. P. Tew, A. J. Thorvaldsen, L. Thøgersen, O. Vahtras, M. A. Watson, D. J. D. Wilson, M. Ziolkowski and H. Ågren, WIREs Comput. Mol. Sci., 2014, 4, 269–284 CrossRef CAS PubMed.
- T. Yanai, D. P. Tew and N. C. Handy, Chem. Phys. Lett., 2004, 393, 51–57 CrossRef CAS.
- W. Kutzelnigg, U. Fleischer and M. Schindler, NMR – Basic Principle and Progress, Springer, Heidelberg, 1990 Search PubMed.
- K. Kaufmann, W. Baumeister and M. Jungen, J. Phys. B: At., Mol. Opt. Phys., 1989, 22, 2233–2240 Search PubMed.
- A. Bergner, M. Dolg, W. Kuechle, H. Stoll and H. Preuss, Mol. Phys., 1993, 80, 1431–1441 CrossRef CAS.
- N. Godbout, D. R. Salahub, J. Andzelm and E. Wimmer, Can. J. Chem., 1992, 70, 560–571 CrossRef CAS.
- L. G. M. Pettersson, U. Wahlgren and O. Gropen, J. Chem. Phys., 1987, 86, 2176–2184 CrossRef CAS.
- P. Ahlström, A. Wallqvist, S. Engström and B. Jönsson, Mol. Phys., 1989, 68, 563–581 CrossRef.
- L. B. Skinner, C. Huang, D. Schlesinger, L. G. M. Pettersson, A. Nilsson and C. J. Benmore, J. Chem. Phys., 2013, 138, 074506 CrossRef PubMed.
- A. Møgelhøj, A. K. Kelkkanen, K. T. Wikfeldt, J. Schiøtz, J. J. Mortensen, L. G. M. Pettersson, B. I. Lundqvist, K. W. Jacobsen, A. Nilsson and J. K. Nørskov, J. Phys. Chem. B, 2011, 115, 14149–14160 CrossRef PubMed.
- G. Kresse and J. Furthmüller, Comput. Mater. Sci., 1996, 6, 15–50 CrossRef CAS.
- G. Kresse and D. Joubert, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758–1775 CrossRef CAS.
- J. Klimeš, D. R. Bowler and A. Michaelides, J. Phys.: Condens. Matter, 2010, 22, 022201 CrossRef PubMed.
- H. C. Andersen, J. Chem. Phys., 1980, 72, 2384–2393 CrossRef CAS.
- J. A. Hayward and J. R. Reimers, J. Chem. Phys., 1997, 106, 1518–1529 CrossRef CAS.
- P. W. Langhoff, Chem. Phys. Lett., 1973, 22, 60–64 CrossRef CAS.
- J.-L. Pascual and L. G. M. Pettersson, Mol. Phys., 2003, 101, 255–265 CrossRef CAS.
- L. G. M. Pettersson, H. Ågren, B. L. Schürmann, A. Lippits and W. E. S. Unger, Int. J. Quantum Chem., 1997, 63, 749–765 CrossRef CAS.
- A. H. Steindal, K. Ruud, L. Frediani, K. Aidas and J. Kongsted, J. Phys. Chem. B, 2011, 115, 3027–3037 CrossRef CAS PubMed.
- M. Dračínský and P. Bouř, J. Chem. Theory Comput., 2010, 6, 288–299 CrossRef PubMed.
- M. T. P. Beerepoot, A. H. Steindal, K. Ruud, J. M. H. Olsen and J. Kongsted, Comput. Theor. Chem., 2014, 1040, 304–311 CrossRef.
- J. M. H. Olsen, N. H. List, K. Kristensen and J. Kongsted, J. Chem. Theory Comput., 2015, 11, 1832–1842 CrossRef CAS PubMed.
- A. Nilsson, H. Ogasawara, M. Cavalleri, D. Nordlund, M. Nyberg, P. Wernet and L. G. M. Pettersson, J. Chem. Phys., 2005, 122, 154505 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: Structures of monomers, dimers, and trimers, CCSD estimate of IP using a smaller basis set, influence of using a basis set for 96 molecules for a calculation with 64 molecules, basis set effects on 1 QM/12 Å calculations, and influence of using a non-polarizable force field in QM/MM calculations. See DOI: 10.1039/c5cp03919c |
| This journal is © the Owner Societies 2016 |