Chalcogens act as inner and outer heteroatoms in borane cages with possible consequences for σ-hole interactions

Abstract

Chalcogen bonds are a subset of σ-hole interactions and the number of their applications has been increasing rapidly. While chalcogen bonding in organic compounds has been intensively studied in the past decade, it is entirely new in boron cluster chemistry. In this paper, we review the remarkable ability of chalcogenated boron clusters to form strong chalcogen bonds. Chalcogen atoms have a unique property to be incorporated in a boron cluster both innerly and outerly. Various molecular shapes (e.g. icosahedral, bicapped-square antiprismatical) have been computationally analyzed and discussed. No general physical trend has been observed and, therefore, it is recommended to tackle each cluster individually.

---

Jindřich Fanfrlík

Jindřich Fanfrlík is a senior research fellow at Institute of Organic Chemistry and Biochemistry (IOCB) of the ASCR, v. v. i. in Prague. He received his PhD from Charles University, Prague in 2008 under the supervision of Pavel Hobza. He spent postdoctoral studies in the group of Antonín Holý at IOCB and Kwang S. Kim at Pohang University of Science and Technology, Republic of Korea. He was also a visiting professor in Puerto Rico for a short time. His main research interests are related to the computational treatment of noncovalent interactions, boron clusters and protein–ligand complexes. He dedicates his spare time to tigers and wildlife.

Drahomír Hnyk

Drahomír Hnyk graduated in organic chemistry from Charles University in Prague. He pursued a PhD course under the supervision of Otto Exner. He was a postdoctoral research fellow with David Rankin in Edinburgh in the area of gas-phase electron diffraction and a DAAD fellow with Paul von Ragué Schleyer in Erlangen-Nürnberg in the area of computational chemistry. His current research interests include molecular structure determinations by gas-phase electron diffraction in the concerted use with computations and studying reaction pathways and noncovalent interactions. He is employed by the Institute of Inorganic Chemistry of the Czech Academy of Sciences, v.v.i. The Czech Academy of Sciences awarded him the scientific degree of Doctor of Science on the basis of the doctoral thesis entitled “Molecular Structure of Free Boron and Gallium Clusters”.

---

Introduction

A chalcogen bond is an attractive interaction between an electrophilic (positive) region associated with a Group VI atom (abbreviated as Y atoms) in a molecular entity and a nucleophilic (negative) region in another, or the same, molecule. Chalcogen bonds have been intensively studied.¹ Particularly, the S⋯O chalcogen bond has been attracting great attention because of its influence on protein structures² and its importance for the biological activities of several organic molecules.³ Interestingly, the same chalcogen atom can simultaneously interact with both positive and negative sites. This ability has been explained in terms of regions of the positive electrostatic potential (ESP) on the outer surfaces of chalcogen atoms.⁴ These regions, called σ-holes, are located along the extensions of their existing covalent bonds.⁵ Chalcogen bonds are thus analogous to other σ-hole interactions, termed halogen bonds, which are of considerable importance in crystal engineering and drug design.⁶ A σ-hole is characterized by its magnitude (V_s,max) and spatial size.⁷V_s,max and the size increase with the atomic number of the chalcogen atom (from S to Te; analogous to that from Cl to I). They can likewise be modulated by changing the chemical environment, i.e. electron-withdrawing groups also increase the σ-hole. It has been demonstrated that the larger the V_s,max value, the stronger the halogen bond.⁷ A modulation of halogen bonds in protein–inhibitor complexes has been used to reduce the IC₅₀ values accordingly.⁸

Partial atomic charges on S atoms usually have negative values in simple organosulfur compounds where the S atoms are covalently bound to C and H atoms. Consequently, such S atoms have very small σ-holes. In some cases, the V_s,max can even have a negative value (e.g. V_s,max for H₂C=S of −3.1 kcal mol⁻¹).^9,10 The V_s,max value increases with the introduction of electron-withdrawing groups as mentioned above (e.g. V_s,max for F₂C=S and S=C=S of 12.6 and 16.0 kcal mol⁻¹, respectively).¹⁰ On the other hand, partial atomic charges on S atoms have positive values when the S atom is bound to highly electronegative atoms (e.g. halogens). Consequently, the S atoms in such compounds have σ-holes with very large V_s,max values (e.g. V_s,max for SCl₂, SCl₄ and SF₄ of 28.6, 38.3 and 51.5 kcal mol⁻¹, respectively). Nziko and Schneier have theoretically studied the N⋯S chalcogen bond between SF₄ and a series of amines. They have demonstrated that this chalcogen bond is very strong. The interaction energies ranged from −7 to −14 kcal mol⁻¹ (for NH₃ and trimethylamine, respectively).¹¹ They also compared tetravalent SF₄ with divalent SF₂ and SHF. They found very small differences between the divalent and tetravalent S complexes.¹¹

Interestingly, there are compounds with very large V_s,max values on the chalcogen atom even though the chalcogen atom is only bound to highly electropositive B atoms (i.e. the substituted boron hydrides that are described below). Closo-1-SB₁₁H₁₁ has five σ-holes with V_s,max values of 28.2 kcal mol⁻¹.⁹Closo-1-SB₁₁H₁₁ has been shown to form strong complexes with trimethylamine and benzene (interaction energy of −6.5 and −6.3 kcal mol⁻¹, respectively) in our computational study.¹² As mentioned above, the strength of chalcogen bonds increases with the atomic number of the chalcogen. Closo-1-SeB₁₁H₁₁ thus forms even stronger chalcogen bonded complexes: the interaction energies of closo-1-SeB₁₁H₁₁ with trimethylamine and benzene are −8.1 and −7.0 kcal mol⁻¹, respectively.¹² These are very strong chalcogen bonds considering that the interaction energies of the benzene⋯Se=CF₂, benzene⋯Se(CF₃)₂, trimethylamine⋯Se=CF₂ and trimethylamine⋯Se(CF₃)₂ complexes possessing the chalcogen bond are −3.5, −4.5, −4.6 and −3.7 kcal mol⁻¹, respectively.¹³

Boron clusters

Boron atoms have a remarkable ability to form molecules of unlimited size by covalently bonding to themselves and other elements. Polyhedral boron clusters (boranes) exhibit an astonishing variety of stable molecular structures due to this ability.¹⁷ Boranes have a broad range of applications including radioactive waste extraction, nanotechnology and medicinal chemistry. Such a wide range of applications are enabled by the unique properties of boranes, which include high stability, low toxicity, hydrophobicity¹⁸ and the ability to form nonclassical noncovalent interactions¹⁹ such as dihydrogen bonds²⁰ and σ-hole interactions.⁹ Although boron is the neighbor of carbon in the periodic table, their chemistries differ dramatically.²¹ Their geometries are not compatible even in the case of simple B₂H₆ and C₂H₆. B₂H₆, possessing the D_2h symmetry, differs from the ethane-like structure of the D_3d symmetry with two-center two-electron bond (2c–2e). Conceivably, B₂H₆ could be fitted to the electron diffraction data only if a hydrogen-bridge-based model with the so-called 3-center 2-electron bond (3c–2e) of the D_2h symmetry were considered.²² Further experimental structural studies have led to the formulation of the unusual bonding principles in boron clusters (the concept multicenter bonding)²³ by W. N. Lipscomb. An important class of boranes comprises closo-B_nH_n²⁻ (n = 5–12) dianions. The systematic replacement of BH (formally neutral) vertices in them by a variety of chalcogens such as S²⁺, Se²⁺, or other heteroatoms (e.g. CH⁺), leads to a broad range of so-called heteroboranes.

As opposed to the electronegativity concept, parent boron hydrides (boranes) are electron deficient and any heteroatom within a cluster framework (endo substituent) acts as if it were an electron donor. Consequently, the heterovertex (or a midpoint of two-heterovertex separation) is a center of a partial positive charge, as evidenced by interpreting experimental dipole moments. Indeed, it is the midpoint of the CC vector that is the center of the partial positive charge in closo-1,2-C₂B₁₀H₁₂, which has been determined experimentally in an unambiguous way.²⁴ The same applies to another closo system, closo-1-SB₁₁H₁₁, where the S atom bears the partially positive charge in the icosahedral cage.²⁵ We have modeled the unsynthesized closo-1-OB₁₁H₁₁ compound²⁶ in order to demonstrate the effect of a boron cluster framework for heteroatoms. V_s,max values were positive even on the highly electronegative O atom (Table 1).

Table 1 The maximum of the electrostatic potential on the surface of the chalcogen atom (V_s,max) in kcal mol⁻¹. For each compound, all the V_s,max values are listed. In general, the number of V_s,max value correlates with the coordination number of the chalcogen atom. Partial atomic charges (q) on the chalcogen atom from RESP are in e⁻. Polarisability (α) in a.u.

Molecule (symmetry)	V s,max HF/cc-pVDZ	q B3LYP/cc-pVTZ	α B3LYP/cc-pVTZ
a Trigonal bipyramidal shape dictated by the so-called quadruple average angle, see. ref. 11b. b A more stable form with Cs symmetry has 2 σ-holes with a Vs,max value of 19.8 kcal mol^−1. c V s,max values were determined on the 0.001 a.u. molecular surface computed at the HF/cc-pVDZ level using the Gaussian 09,^15 Molekel4.3 (ref. 16a and b) and WFA (wavefunction analysis)^16c programs. It has been recently shown that larger basis sets are not needed for these purposes.^16d d It was recently shown that the RESP,^16e in contrast to NBO, represents a method of choice for heteroboranes, as NBO's closely correspond to the picture of localized bonds and lone pairs as basic units of the molecular structure. This is not true for delocalized heteroboranes.^20 e α is the second-order tensor of the dipole polarizability; the reported average polarizability is given by 1/3 (αxx + αyy + αzz).
H2C=S (C2v)	−3.1 (ref. 9)	−0.15	29.5
F2C=S (C2v)	12.6 (ref. 9)	−0.13	30.7
S=C=S (D∞h)	16.0 (ref. 14)	0.05	49.2
SCl2 (C2v)	2 × 28.6	0.07	42.4
SCl4 (C2v)^a	2 × 38.3	0.38	87.3
SF2 (C2v)	2 × 45.5	0.23	18.9
SF4 (C2v)^a	2 × 51.5	0.44	25.5
Closo-1-SB4H4 (C3v)	3 × 16.9	0.04	67.9
Closo-1-SB5H5 (C4v)	4 × 11.1	0.17	77.1
Closo-1-SB9H9 (C4v)	4 × 22.4 (ref. 12)	0.19	122.1
Closo-1-SB6H6 (C5v)	5 × 12.3	0.17	88.4
Closo-1-SB11H11 (C5v)	5 × 28.2 (ref. 12)	0.21	139.7
Closo-1-OB11H11 (C5v)	5 × 11.7	−0.07	126.9
Closo-1-SeB11H11 (C5v)	5 × 29.5 (ref. 12)	0.31	145.8
Closo-1-SB7H7 (C6v)^b	6 × 10.4	0.06	101.3
Closo-1-SB13H13 (C6v)	6 × 22.9	0.15	165.7
12-F-closo-1-SB11H11 (C5v)	5 × 29.2 (ref. 12)	0.22	139.7
1,2-(SH)2-closo-1,2-C2B10H10 (C2v)	16.0	−0.10	169.2
1,2-(SeH)2-closo-1,2-C2B10H10 (C2v)	20.4	0.01	181.7

---

Chalcogens and hydrogenated chalcogens in boron clusters

As mentioned above, BH vertices in closo-B_nH_n²⁻ (n = 5–12) can be replaced by various heterovertices. Several parental heteroboranes with a chalcogen vertex have been synthesized, specifically closo-1-SB₁₁H₁₁,²⁷closo-1-SeB₁₁H₁₁,²⁸closo-1-SB₉H₉ (ref. 29) and closo-1-TeB₁₁H₁₁.³⁰ All these neutral parent icosahedral heteroboranes have been geometrically characterized using gas-phase electron diffraction since their monocrystals are disordered, which prevents them from X-ray diffraction analyses. However, this is not the case of some exo-substituted heteroboranes. We have demonstrated the dominant role of chalcogen bonding in the crystal packing for 12-Ph-closo-1-SB₁₁H₁₀ (Fig. 2).⁹

It would be very tempting to have some guidelines for the relations of physical properties of thiaboranes going from closo-SB_nH_n to closo-SB_n+1H_n+1. In order to obtain deeper insight into thiaborane properties, we have analyzed the NMR chemical shifts and V_s,max values of various thiaboranes. The experimental observation related to a strong downfield ¹¹B NMR chemical shift of the antipodal boron atom in closo-1-SB₉H₉ (a symmetry of C_4v) and closo-1-SB₁₁H₁₁ (a symmetry of C_5v) may, however, lead to unrealistic assumptions.^27,29 Considering the V_s,max values and NMR shifts of closo-1-SB₉H₉ and closo-1-SB₁₁H₁₁ (22.4 and 28.2 kcal mol⁻¹ (ref. 12) and 76 and 18 ppm,^27,29 respectively), we would have expected a larger computed V_max for the hypothetical closo-1-SB₁₃H₁₃ (a symmetry of C_6v,³¹δ(¹¹B(antipodal B13)) = −8.4 ppm) than for closo-1-SB₁₁H₁₁ because this downfield chemical shift decreases with the increasing number of the vertices. However, the V_s,max value of this hypothetical bicapped-hexagon-type antiprismatic thiaborane closo-1-SB₁₃H₁₃ is computed to be “only” 22.9 kcal mol⁻¹. Conceivably, there is no relation between the electrostatic potential, i.e. the partial atomic charge on the S atom, and the ¹¹B chemical shift of the B atom antipodally coupled with the S atom. The same applies to a series of hypothetical bipyramidal thiaboranes with symmetries of C_3v,C_4v, C_5v, and C_6v (see Table 1, the isoelectronic monocarbaboranes are experimentally available^31c). These computational results further support the known fact that there are no relations as to the physical and chemical properties of closo-heteroboranes going from closo-YB_nH_n to closo-YB_n+1H_n+1.³² Each cluster thus must be treated individually, which will also be true for future applications in crystal engineering.

Chalcogen atoms are able to act as both inner and outer heteroatoms in boranes. In the form of YH, they can substitute exopolyhedral hydrogens and in the form of Y BH vertices in them. As an example of exo-chalcogenated carboranes, we can list experimentally known 1,2-(SH)₂-closo-1,2-C₂B₁₀H₁₀,³³ 9,12-(SH)₂-closo-1,2-C₂B₁₀H₁₀,³⁴ 1,2-(SeH)₂-closo-1,2-C₂B₁₀H₁₀ (ref. 35) and still hypothetical 9,12-(SeH)₂-closo-1,2-C₂B₁₀H₁₀.³⁶ The S atom of 9,12-(SH)₂-closo-1,2-C₂B₁₀H₁₀ is bound to the B vertex. It has a negative ESP surface and it does not have a σ-hole (see Fig. 1). Conversely, the S atom of 1,2-(SH)₂-closo-1,2-C₂B₁₀H₁₀ is bound to the C heterovertex of the carborane cage. It has a positive σ-hole along the extension of the S–H bond with the V_s,max value of 16.0 kcal mol⁻¹. There is an even more positive ESP surface along the extension of the S–B bond, but it is impossible to determine its V_s,max value, because the ESP does not have a local maximum here. The ESP continuously becomes more positive towards the H atom (see Fig. 1). There is a clear analogy between carboranes with exopolyhedral chalcogen and halogen atoms. We have recently computed that the σ-hole on Br atoms of brominated carboranes could be highly positive but only if it were bound to a C vertex.^12,37 On the other hand, the V_s,max on the Br atom had a negative value when the Br atom was bound to a B vertex. Interestingly, this observation is also true in dilute solutions of closo-1-Ph-2-X-1,2-C₂B₁₀H₁₀ (for X = F, Cl, Br, I),³⁸ where dipole moments were measured and subsequently interpreted by a simple vector algebra.³⁸ The observed dipole-moment anomaly for X = Br, I in contrast to F, Cl could be accounted for only when an additional vector pointing from the outer surface of bromine and iodine (irrespective of the corresponding electronegativities) towards the negative part of the aromatic quadrupole moment was introduced, which confirmed the anisotropy of heavier halogen atoms.

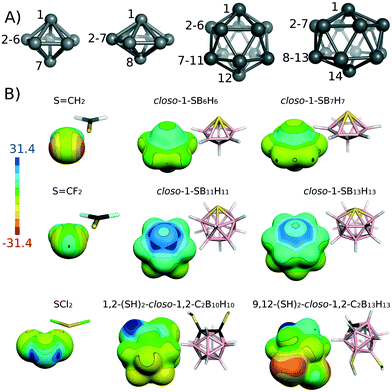Fig. 1 (A) The structure and numbering scheme of 7-, 8-, 12- and 14-vertex cages adopting the symmetries of C_5v, C_6v, C_5v and C_6v, respectively. (B) The molecular diagrams and electrostatic potential (ESP) on the 0.001 a.u. molecular surface computed at the HF/cc-pVDZ level using the Gaussian 09 (ref. 15) and Molekel4.3 (ref. 16a and b) programs for selected S-atom possessing molecules. Color range in kcal mol⁻¹.

Fig. 2 The crystal packing of 12-Ph-closo-1-SB₁₁H₁₀.

A comparison of closo-YB₁₁H₁₁ with the 1,2-(YH)₂-closo-1,2-C₂B₁₀H₁₀ series suggests that the effect of the borane cages is more pronounced (i.e. higher V_s,max values) when the chalcogen atom is an endo substituent (see Table 1). This difference is the most significant when Y = O: the O atom of 1,2-(OH)₂-closo-1,2-C₂B₁₀H₁₀ has a negative ESP surface in contrast to closo-1-OB₁₁H₁₁, where we have computed a positive V_s,max value.

We have recently decomposed several interaction energies of chalcogen bonded complexes in order to establish the nature of chalcogen bonding.¹² The electrostatic and dispersion terms were found to be systematically predominant. The strength of the electrostatic term is predetermined by the V_s,max value on the Y atom, which was discussed above. The strength of the dispersion energy is determined in terms of polarisability. The computed polarisabilities (Table 1) of the studied compounds are large and even comparable to halogenated carboranes.³⁷

It should also be mentioned that the σ-hole interaction can play an important role in reaction mechanisms if chalcogen atoms are involved. We have recently modeled a synthetic route to 1,7-(SCN)₂-closo-B₁₂H₁₀²⁻. We have found that the σ-hole on the elongation of the S–S axis of (SNC)₂ plays a role when approaching the closo-B₁₂H₁₂²⁻ anion.³⁹

Conclusions

The chemistry of chalcogenated boranes is very broad. Chalcogen atoms can replace both BH vertices and exopolyhedral H atoms of boranes and heteroboranes. Due to the electro-deficiency of boron cages, any heterovertex (endo substituent) acts as an e⁻ donor and becomes a center of a partial positive charge. Consequently, any chalcogen atom within a boron cluster framework and any heavier chalcogen atom bound to the C heterovertex of neutral carboranes have highly positive σ-holes. These compounds thus have a remarkable ability to form strong chalcogen bonds,⁴⁰ which makes them attractive for many exciting applications in materials chemistry, crystal engineering as well as in other fields.

Acknowledgements

This work has been supported by the research project RVO 61388963 of the Academy of Sciences of the Czech Republic. We acknowledge the financial support of the Czech Science Foundation (JF: P208/12/G016 and DH: 15-056775).

Notes and references

1. A. Bauza, T. J. Mooibroek and A. Frontera, ChemPhysChem, 2015, 16, 2496.
2. (a) M. Iwaoka, S. Takemoto, M. Okada and S. Tomoda, Chem. Lett., 2001, 132; (b) M. Iwaoka, S. Takamoto and S. Tomoda, J. Am. Chem. Soc., 2002, 124, 10613.
3. Y. Nagao, T. Hirata, S. Goto, S. Sano, A. Kakehi, K. Iizuka and M. Shiro, J. Am. Chem. Soc., 1998, 120, 3104.
4. (a) J. S. Murray, P. Lane, T. Clark and P. Politzer, J. Mol. Model., 2007, 13, 1033; (b) S. Tsuzuki and N. Sato, J. Phys. Chem. B, 2013, 117, 6849.
5. (a) T. Clark, M. Hennemann, J. S. Murray and P. Politzer, J. Mol. Model., 2007, 13, 291; (b) P. Politzer and J. S. Murray, ChemPhysChem, 2013, 14, 278.
6. (a) G. Cavallo, P. Metrangolo, R. Milani, T. Pilati, A. Priimagi, G. Resnati and G. Terraneo, Chem. Rev., 2016, 116, 2478–2601; (b) R. Wilcken, M. O. Zimmermann, A. Lange, A. C. Joerger and F. M. Boeckler, J. Med. Chem., 2013, 56, 1363.
7. (a) K. E. Riley, J. S. Murray, J. Fanfrlík, J. Řezáč, R. J. Sola, M. C. Concha, F. M. Ramos and P. Politzer, J. Mol. Model., 2011, 17, 3309; (b) M. Kolář, J. Hostaš and P. Hobza, Phys. Chem. Chem. Phys., 2014, 16, 9987; (c) M. Kolář, J. Hostaš and P. Hobza, Phys. Chem. Chem. Phys., 2015, 17, 23279.
8. (a) L. A. Herdegger, B. Kuhn, B. Spinnler, L. Anselm, R. Ecabert, M. Stihle, B. Gsell, R. Thoma, J. Diez, J. Benz, J. M. Plancher, G. Hartmann, D. W. Banner, W. Haap and F. Diederich, Angew. Chem., Int. Ed., 2011, 50, 314; (b) J. Fanfrlík, M. Kolář, M. Kamlar, D. Hurny, F. X. Ruiz, A. Cousido-Siah, A. Mitschler, J. Řezáč, E. Munusamy, M. Lepšík, P. Matejicek, J. Vesely, A. Podjarny and P. Hobza, ACS Chem. Biol., 2013, 8, 2484.
9. J. Fanfrlík, A. Přáda, Z. Padělková, A. Pecina, J. Macháček, M. Lepšík, J. Holub, A. Růžička, D. Hnyk and P. Hobza, Angew. Chem., Int. Ed., 2014, 53, 10139.
10. W. Wang, B. Ji and Y. Zhang, J. Phys. Chem. A, 2009, 113, 8132.
11. (a) V. Nziko and S. Scheiner, J. Phys. Chem. A, 2014, 118, 10849; (b) For the molecular structures of molecules with two- and four-coordinated sulfsur see I. Hargittai, The Structure of Volatile Sulphur Compounds, Akadémiai Kiadó, Budapest, 1985.
12. A. Pecina, M. Lepsik, D. Hnyk, P. Hobza and J. Fanfrlík, J. Phys. Chem. A, 2015, 119, 1388.
13. A. Bauza, D. Quinonero, P. M. Deya and A. Frontera, CrystEngComm, 2013, 15, 3137.
14. W. Zierkiewicz, J. Fanfrlík, P. Hobza, D. Michalska and T. Zeegers-Huyskens, Theor. Chem. Acc., 2016, 135, 217.
15. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery Jr., J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, Ö. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian 09, Gaussian, Inc., Wallingford CT, 2009.
16. (a) P. Flűkiger, H. P. Lűthi, S. Portmann and J. Weber, MOLEKEL 4.3, Swiss Center for Scientific Computing, Manno Switzerland, 2000; (b) S. Portmann and H. P. Lűthi, MOLEKEL: CHIMIA, 2007, vol. 28, p. 555; (c) F. A. Bulat, A. Toro-Labbe, T. E. Brinck, J. S. Murray and P. Politzer, J. Mol. Model., 2010, 16, 1679; (d) K. E. Riley, K.-A. Tran, P. Lane, J. S. Murray and P. Politzer, J. Comput. Sci. DOI:10.1016/j.jocs.2016.03.010; (e) C. I. Bayly, P. Cieplak, W. D. Cornell and P. A. Kollman, J. Phys. Chem., 1993, 97, 10269.
17. Borane architecture is based on three-dimensional structures composed of triangular B-B-B and B-H-B units, the latter representing a hydrogen bridge. The unique architectures of binary boron hydrides (stable as dianions, B_nH_n²⁻) stem from the number of boron vertices n (in the basic series n = 5–12) and electrons available – we thus distinguish closed-cage closo-species (2n + 2 electrons) and several open-cage species, derived by the formal removal one (nido-, 2n + 4 electrons), two (arachno-, 2n + 6 electrons) or more (hypho-, 2n + 8 electrons) boron vertices. See e.g. D. Hnyk and D. A. Wann, Boron – the Fifth Element, Challenges and Advances in Computational Chemistry and Physics, ed. D. Hnyk and M. McKee, Springer, Heidelberg, New York, Dordrecht and London, 2015, ch. 2, vol. 20.
18. (a) All such properties and subsequent applications are reviewed in J. Plešek, Chem. Rev., 1992, 92, 269; (b) Boron Science – New Technologies and Applications, ed. N. S. Hosmane, CRC Press, Boca Raton, 2012.
19. R. Sedlak, J. Fanfrlík, A. Pecina, D. Hnyk, P. Hobza and M. Lepšík, Boron – the Fifth Element, Challenges and Advances in Computational Chemistry and Physics, ed. D. Hnyk and M. McKee, Springer, Dordrecht, The Netherlands, 2015, ch. 9, vol. 20.
20. J. Fanfrlík, M. Lepšík, D. Hořínek, Z. Havlas and P. Hobza, ChemPhysChem, 2006, 7, 1100.
21. E. D. Jemmis and E. G. Jaysree, Acc. Chem. Res., 2003, 36, 816.
22. K. Hedberg and V. Schomaker, J. Am. Chem. Soc., 1951, 73, 1482.
23. W. N. Lipscomb, Boron Hydrides, Benjamin, New York, 1963.
24. D. Hnyk, V. Všetečka, L. Drož and O. Exner, Collect. Czech. Chem. Commun., 2001, 66, 1375.
25. J. Fanfrlík, D. Hnyk, M. Lepšík and P. Hobza, Phys. Chem. Chem. Phys., 2007, 9, 2085.
26. The presence of oxygen in a single-cluster borane framework has been achieved once in nido-[OB₁₁H₁₂]⁻, see A. Ouassas, B. Fenet, H. Mongeot, B. Gautheron, E. Bardky and B. Frange, J. Chem. Soc., Chem. Commun., 1995, 1663.
27. The gas-phase electron diffraction structure together with computations of ¹¹B NMR is reported in D. Hnyk, E. Vajda, M. Bühl and P. v. R. Schleyer, Inorg. Chem., 1992, 31, 2464.
28. D. Hnyk, D. A. Wann, J. Holub, M. Bühl, H. E. Robertson and D. W. H. Rankin, Dalton Trans., 2008, 96.
29. Not only the electron diffraction structure but also the mechanism of the antipodal effect is reported in D. Hnyk, D. A. Wann, J. Holub, S. Samdal and D. W. H. Rankin, Dalton Trans., 2011, 40, 5734 . The antipodal effect is based on the occurrence of paramagnetic contributions to the shielding tensor. These contributions arise from the coupling of HOMO and LUMO orbitals that have predominant coefficients on the Y and antipodal atoms. ¹¹B chemical shift were computed using Gaussian 09, ref. 15.
30. The insertion of Te into a boron cluster is mentioned in G. D. Friesen and L. J. Todd, J. Chem. Soc., Chem. Commun., 1978, 349.
31. (a) P. v. R. Schleyer, K. Najafian and A. M. Mebel, Inorg. Chem., 1998, 37, 6765; (b) A. P. M. Robertson, N. A. Beattie, G. Scott, W. Y. Man, J. J. Jones, S. A. Macgregor, G. M. Rosair and A. J. Welch, Angew. Chem., Int. Ed., 2016, 55, 8706; (c) P. v. R. Schleyer and K. Najafian, Inorg. Chem., 1998, 37, 3454.
32. A. J. Stone and M. J. Alderton, Inorg. Chem., 1982, 21, 2297 , and the references therein.
33. T. Baše, Z. Bastl, M. Šlouf, M. Klementová, J. Šubrt, A. Vetushka, M. Ledinský, A. Fejfar, J. Macháček, M. J. Carr and M. G. S. Londesborough, J. Phys. Chem. C, 2008, 112, 14446.
34. D. A. Wann, P. D. Lane, H. E. Roberson, T. Baše and D. Hnyk, Dalton Trans., 2013, 42, 12015.
35. This compound has been recently prepared and structurally characterized in terms of electron diffraction and NMR spectroscopy.
36. This compound has not been synthesized yet.
37. R. Lo, J. Fanfrlik, M. Lepsik and P. Hobza, Phys. Chem. Chem. Phys., 2015, 17, 20814.
38. D. Hnyk, V. Všetečka and L. Drož, J. Mol. Struct., 2010, 978, 246.
39. M. Lepšík, M. Srnec, J. Plešek, M. Buděšínský, B. Klepetářová, D. Hnyk, B. Grüner and L. Rulíšek, Inorg. Chem., 2010, 49, 5040.
40. Not only closo systems but also neutral nido clusters are potential candidates for the examination of σ-hole interactions; for some neutral nido-heteroboranes, see e.g. (a) D. Hnyk, M. Hofmann, P. v. R. Schleyer, M. Bühl and D. W. H. Rankin, J. Phys. Chem., 1996, 100, 3435; (b) B. Štíbr, O. L. Tok, J. Holub, M. Bakardjiev, W. Milius, D. Hnyk and B. Wrackmeyer, Eur. J. Inorg. Chem., 2002, 2320.

---