 Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Optically generated hyperpolarization for sensitivity enhancement in solution-state NMR spectroscopy†
Matthew W.
Dale
 and
Christopher J.
Wedge
and
Christopher J.
Wedge
 *
*
Department of Physics, University of Warwick, Coventry CV4 7AL, UK. E-mail: chris.wedge@chch.oxon.org
First published on 30th September 2016
Abstract
We show that optical excitation of radical triplet pair systems can produce a fourfold NMR signal enhancement in solution, without the need for microwave pumping. Development of optical hyperpolarization methods will significantly impact all NMR user groups by boosting sensitivity and reducing signal averaging times.
Nuclear magnetic resonance (NMR) spectroscopy is a powerful technique for interrogation of the structure and dynamics of molecules with atomic precision, and is widely used throughout chemistry, biochemistry and materials science. Owing to the small energy of the nuclear Zeeman splitting, NMR is however an inherently insensitive technique, relying on the tiny population differences (polarization) of the nuclear spin states at thermal equilibrium. Small improvements in sensitivity have been achieved, for example by increasing the magnetic field strength, the use of cryogenically cooled probes and miniaturization of coils for low sample volumes.1,2 The most promising method for further significant sensitivity improvements is hyperpolarization, the creation of non-equilibrium spin populations, for example by microwave-driven dynamic nuclear polarization (DNP). Whilst the large gains made by application of DNP methods are revolutionizing solid-state NMR,3,4 a method to enhance sensitivity in high-resolution multidimensional NMR of biological macromolecules in liquid solution has proved elusive.1,5–8
In solution, DNP is achieved by the Overhauser effect, whereby the cross-relaxation of an electron–nuclear spin system, mediated by time dependent fluctuations of the coupling between the spins, preferentially populates one nuclear spin state.5–9 This process requires perturbation of the electron spin populations, which is typically achieved by microwave irradiation of the electron spin transition. The Solomon equations describe the relaxation mechanisms of the electron–nuclear system. Their steady state solution under constant microwave irradiation is the well-known Overhauser formula, giving the enhancement factor as:10
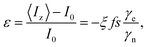 | (1) |
One method to overcome the Boltzmann limit on maximum DNP enhancement, to potentially reach |ε| > 104, is to use photoexcited electronic spin states as a non-equilibrium polarization source.7,8,13 This approach has achieved large enhancements in the solid-state14 but to our knowledge bulk nuclear polarization enhancements in the solution-state have not previously been reported. Among the many mechanisms known to photochemically generate electron spin-polarization,15 the radical–triplet pair mechanism (RTPM)16 stands out in that it is able to polarize a stable radical. Avoiding the generation of transient radicals reduces the risk of unwanted chemical reactions, and ensures that polarization transfer is not in competition with radical decay. The previously reported phenomenon known as photochemically induced dynamic nuclear polarization (photo-CIDNP) is based on the related radical pair mechanism,17,18 and typically achieves enhancements only of certain solvent-exposed aromatic amino acids participating in electron transfer reactions, so is applicable only in special cases.2,19,20 By contrast, our radical–triplet pair based method relies on non-selective Overhauser polarization transfer from a spin-polarized stable radical, creating bulk nuclear hyperpolarization as in microwave-pumped DNP experiments.
The RTPM may be understood by considering a diffusive encounter between a radical (doublet) and photogenerated triplet in solution. The total spin states of such a pair may be described as quartet and doublet manifolds (see ESI†), with mixing between these driven by the zero-field splitting of the triplet species. As only the doublet state of the radical–triplet encounter pair may undergo spin-allowed relaxation to the ground state, selective quenching leads to generation of net electronic hyperpolarization of the radical. While previous work has sought to exploit RTPM electron spin-polarization directly in electron paramagnetic resonance (EPR),21,22 or in construction of an optically pumped maser,23 here we demonstrate its use to boost sensitivity in solution-state NMR.
A recent systematic investigation of the RTPM in water soluble xanthene dyes in combination with nitroxide radicals identified the rose bengal and 2,2,6,6-tetramethylpiperidine 1-oxyl (TEMPO) system as producing electron spin polarization of −150 times the thermal level.24 Encouraged by this large electron spin polarization we sought to detect generation of nuclear spin polarization by the Overhauser effect in the same system. A continuous wave 520 nm laser diode with an output power of 1 W was used to photogenerate the rose bengal triplet whilst NMR spectra were simultaneously recorded at the 1H frequency of 14.6 MHz in a 0.342 T magnetic field. Rose bengal was found to photodegrade and so the solution was flowed continuously through the spectrometer. Dissolved oxygen was particularly detrimental to the generation of nuclear polarization and so solutions were bubbled with nitrogen gas prior to use, and the flow system was purged with nitrogen. Further experimental details can be found in the ESI.†
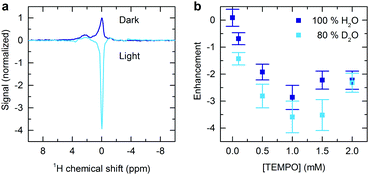
The 1H NMR spectra of a deoxygenated aqueous dye and radical solution is shown in Fig. 1a in the presence and absence of continuous optical illumination. This unresolved low-field (0.342 T) spectrum is dominated by the water peak, but serves to illustrate the effectiveness of the methodology. Upon illumination the NMR signal is inverted and the intensity significantly enhanced, resulting in a fourfold sensitivity increase compared to the dark case. This demonstrates generation of significant emissive nuclear spin polarization. Such an effect is not seen in the absence of radical (Fig. 2), and is significantly reduced without sample deoxygenation (Fig. S4, ESI†), verifying that the effect is not due to an artefact arising from laser induced sample heating.
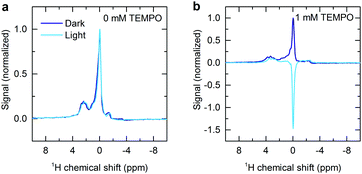 | ||
| Fig. 2 1H NMR spectra showing the effect of illumination on 0.2 mM aqueous solutions of rose bengal (a) without TEMPO and (b) with 1 mM TEMPO. | ||
To further characterize the hyperpolarization mechanism experiments were performed at a range of radical concentrations. The enhancement factors obtained are shown in Fig. 1b. In both fully protonated and partially deuterated solvent the enhancements are maximized for 1 mM radical concentration and reduce significantly at lower concentrations. To rationalize this behaviour we consider the three variable terms ξ, f and s in the Overhauser equation. Whilst derived in the case of continuous perturbation of the electronic magnetization by a saturating microwave field, the solution is also applicable to continuous optical pumping. The coupling factor ξ depends upon modulation of the interactions between electron and nuclear spins by molecular tumbling. From nuclear magnetic resonance dispersion measurements it is known that a value of 0.36 is appropriate for TEMPO in aqueous solution at the magnetic field of 0.34 T and ambient temperature.11,12
The leakage factor may be experimentally determined as f = 1 − T1n/T01n where T1n (T01n) is the nuclear relaxation time measured in the presence (absence) of added radical.10 This value is larger in partially deuterated solvent and increases from 0 to 0.8 as the radical concentration is increased to 2 mM (Fig. 3a), indicating increasing dominance of the radical in determining the nuclear relaxation rate. As radical concentration is increased f will tend towards 1,10 however, as will be shown below, the nuclear polarization obtained is not anticipated to increase further if this change is made in isolation.
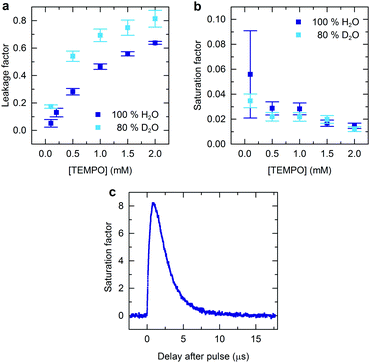 | ||
| Fig. 3 (a) The leakage factor (f) and (b) saturation factor (s), as a function of TEMPO concentration, under continuous illumination. The leakage factor was determined from relaxation measurements using f = 1 − T1n/T01n, and used to calculate the corresponding saturation factor giving rise to the enhancement show in Fig. 1b. (c) Time-evolution of the saturation factor s = (S0 − 〈Sz〉)/S0 after pulsed laser illumination. Electron spin-echo intensity was measured at a variable time relative to a 532 nm laser pulse for a nitrogen purged aqueous solution of 0.2 mM rose bengal and 0.2 mM TEMPO. | ||
The deviation of electronic magnetization from equilibrium is quantified by the saturation factor s = (S0 − 〈Sz〉)/S0 where Sz is the electron polarization with pumping radiation and S0 the thermal equilibrium value. In conventional DNP methods this indicates the degree of microwave saturation, with a maximum possible value of 1. In our work s is determined by the efficiency of the optical polarization mechanism which is not thermally limited hence |s| ≫ 1 is possible.
Using the experimentally determined enhancement and leakage factors an effective saturation factor may be calculated (Fig. 3b). This is found to decrease with increasing radical concentration, and to be independent of partial solvent deuteration within experimental error. This behaviour indicates that the electron spin polarization step is limited by lack of photochemically generated triplet states. Addition of more radicals ought to favour radical quenching over other possible triplet decay pathways, but when radical quenching dominates any further concentration increase has the effect of reducing the proportion of radicals that are polarized leading s to decrease.
The observation of peak nuclear polarization enhancement at 1 mM may therefore be understood as occurring due to interplay of the opposite trends in leakage factor and saturation factor as radical concentration is varied. Higher enhancements are obtained at all TEMPO concentrations in the case of partially deuterated solvent (Fig. 1b) due to the larger leakage factor. In order to maximize the efficiency of polarization transfer to nuclei the leakage factor should be made close to the maximum possible value of 1. Further increase in the level of solvent deuteration will help to achieve this by increasing the intrinsic relaxation time T01n and hence shifting the plateau region of the leakage factor curve to lower radical concentrations (Fig. 3a).
To allow higher radical concentrations to be used to fully maximize the leakage factor it is necessary to increase the electronic saturation factor under these conditions. This requires more radicals to be polarized and hence an increase in the concentration of triplet excited states. The triplet sensitizer concentration may be increased, but is limited by a reduction in the depth of the sample to which light penetrates. Assuming Beer–Lambert behaviour the optical path length could be decreased to maintain a constant absorbance. For strongly absorbing dyes such as rose bengal it may therefore be beneficial to alter the sample geometry to use a uniformly illuminated thin layer of sample. In order to maximize not just the enhancement but also the detection sensitivity the NMR probe design would need to be optimized so as not to compromise the filling factor or spectral resolution.25
The electronic saturation factor in the optical polarization case is also a function of laser power. As in previous microwave DNP experiments11,12 we believe that our current experiment is power limited (Fig. S6, ESI†). An increase in laser intensity should increase the concentration of triplet states and hence the saturation factor, giving significant optical electron polarization in the radical concentration regime in which f is close to unity. Care must be exercised to avoid excessive sample heating through use of high-powered laser sources, necessitating the design of more efficient polarizing agents as discussed below. Moderate heating may, however, improve sensitivity enhancements through an increase in the coupling factor arising from increased molecular motion.26
The absolute value of the electronic saturation factor is small in the present case, being in all cases less than 0.1. In order to out-perform microwave pumped DNP it is necessary to achieve saturation factors in excess of 1. Such values can easily be obtained transiently using pulsed laser excitation as shown by time-resolved EPR (Fig. 3c). In the case of flash-lamp pumped pulsed Nd:YAG lasers, commonly used for time-resolved EPR investigations, the repetition rate is typically limited to <50 Hz. With electron spin-polarization persisting for <20 μs after each laser pulse the time averaged saturation factor will therefore be small and nuclear polarization insignificant when using such sources. Implementation of specialist high repetition rate pulsed lasers, or rapidly chopped continuous-wave laser sources, has the potential to overcome this problem.27,28 By analogy to pulsed microwave DNP optimization of laser repetition rate, relative to the rate of nuclear polarization loss between pulses (1/T1n) and polarization gain per pulse, should enable lower average illumination powers without compromising the NMR enhancement factor.29
The final factor for optimization of photochemically generated nuclear polarization is the dye and radical system. The intrinsic polarization generated per radical quenching event is known to vary with the identity of these species,24 hence searches should be made for optimal partners. Photostability of the dye should also be considered in order to alleviate the need to flow the sample as in our current demonstration system. Quenching efficiency may be significantly enhanced by forming radical–triplet linked systems to increase the quantum yield of radical induced triplet quenching,15,30,31 whilst avoiding an excess of radicals over triplet states, which as we have shown results in a decreased overall saturation factor. The optimal system would therefore combine a high radical polarization per quenching event with absorption characteristics that allow good light penetration to be obtained simultaneously with a high leakage factor. Molecular tumbling of the radical moiety must also be taken into account to avoid compromising the coupling factor ξ.32 Confinement of radical, triplet sensitizer and substrate within a reverse micelle might enable optimization of these parameters without chemically linking the radical and dye, and it is already known that such encapsulation increases polarization transfer to substrate in conventional microwave pumped DNP.33
In conclusion we have established a new method for sensitivity enhancement in solution-state NMR that does not rely on microwave pumping of EPR transitions and whose maximum enhancement is not limited by use of thermalized electrons. The technique has been demonstrated in aqueous solution as will be necessary for application to polarization of biologically relevant macromolecules. As in previous Overhauser DNP studies it was convenient for proof of principle to demonstrate gains on the solvent peak,11,12,34 but Overhauser polarization transfer to water-solubilized substrates is well-known.8,35
Our initial demonstration has been achieved at low magnetic field (0.342 T), but once optimized to realize enhancements above the thermal limit it will be possible to combine with rapid sample transfer to a high-field magnet to obtain sensitivity enhancements in high-resolution NMR spectra.8 Based on the previously determined coupling factor for an aqueous nitroxide radical at ∼0.35 T a saturation factor of only 5 would give an NMR signal enhancement of over 103, which upon shuttling to 14.1 T (for 600 MHz 1H NMR) will incur a 40 fold reduction11 such that a high-field gain of 25 times will be achieved (vs. <5 from microwave pumped shuttle DNP).8 Given transient saturation factors of 8 have already been shown (Fig. 3c), such revolutionary gains are within reach. With the electronic polarization per quenching event reported to be −150 times the thermal level,24 enhancements of 104 (scaling to 250 at 14.1 T) are plausible with optimised sample and photoexcitation conditions. Optically pumped DNP will significantly lower the limit of detection of solution-state NMR and reduce signal averaging times by many orders of magnitude, allowing hitherto unfeasible multidimensional NMR experiments to be completed within a reasonable experimental timeframe.
We thank the Engineering and Physical Sciences Research Council (EPSRC) for financial support (EP/N007875/1), and Bruker UK for an equipment loan. We thank P. J. Hore and M. E. Newton for helpful discussions, and G. W. Morley, P. J. Sadler and J. G. Kempf for commenting on the manuscript.
Notes and references
- J.-H. Ardenkjaer-Larsen, G. S. Boebinger, A. Comment, S. Duckett, A. S. Edison, F. Engelke, C. Griesinger, R. G. Griffin, C. Hilty, H. Maeda, G. Parigi, T. Prisner, E. Ravera, J. van Bentum, S. Vega, A. Webb, C. Luchinat, H. Schwalbe and L. Frydman, Angew. Chem., Int. Ed., 2015, 54, 9162–9185 CrossRef CAS PubMed.
- J. H. Lee, Y. Okuno and S. Cavagnero, J. Magn. Reson., 2014, 241, 18–31 CrossRef CAS PubMed.
- Q. Z. Ni, E. Daviso, T. V. Can, E. Markhasin, S. K. Jawla, T. M. Swager, R. J. Temkin, J. Herzfeld and R. G. Griffin, Acc. Chem. Res., 2013, 46, 1933–1941 CrossRef CAS PubMed.
- A. J. Rossini, A. Zagdoun, M. Lelli, A. Lesage, C. Copéret and L. Emsley, Acc. Chem. Res., 2013, 46, 1942–1951 CrossRef CAS PubMed.
- J. van Bentum, B. van Meerten, M. Sharma and A. Kentgens, J. Magn. Reson., 2016, 264, 59–67 CrossRef CAS PubMed.
- U. L. Günther, Top. Curr. Chem., 2013, 335, 23–69 CrossRef.
- E. Ravera, C. Luchinat and G. Parigi, J. Magn. Reson., 2016, 264, 78–87 CrossRef CAS PubMed.
- C. Griesinger, M. Bennati, H. M. Vieth, C. Luchinat, G. Parigi, P. Höfer, F. Engelke, S. J. Glaser, V. Denysenkov and T. F. Prisner, Prog. Nucl. Magn. Reson. Spectrosc., 2012, 64, 4–28 CrossRef CAS PubMed.
- A. W. Overhauser, Phys. Rev., 1953, 92, 411–415 CrossRef CAS.
- K. H. Hausser and D. Stehlik, Adv. Magn. Reson., 1968, 3, 79–139 CAS.
- M.-T. Turke, I. Tkach, M. Reese, P. Höfer and M. Bennati, Phys. Chem. Chem. Phys., 2010, 12, 5893–5901 RSC.
- P. Höfer, G. Parigi, C. Luchinat, P. Carl, G. Guthausen, M. Reese, T. Carlomagno, C. Griesinger and M. Bennati, J. Am. Chem. Soc., 2008, 130, 3254–3255 CrossRef PubMed.
- K. Tateishi, M. Negoro, A. Kagawa and M. Kitagawa, Angew. Chem., Int. Ed., 2013, 52, 13307–13310 CrossRef CAS PubMed.
- K. Tateishi, M. Negoro, S. Nishida, A. Kagawa, Y. Morita and M. Kitagawa, Proc. Natl. Acad. Sci. U. S. A., 2014, 111, 7527–7530 CrossRef CAS PubMed.
- M. D. E. Forbes, L. E. Jarocha, S. Sim and V. F. Tarasov, Adv. Phys. Org. Chem., 2013, 47, 1–83 CrossRef CAS.
- C. Blättler, F. Jent and H. Paul, Chem. Phys. Lett., 1990, 166, 375–380 CrossRef.
- G. L. Closs and L. E. Closs, J. Am. Chem. Soc., 1969, 91, 4549–4550 CrossRef CAS.
- R. Kaptein and J. L. Oosterhoff, Chem. Phys. Lett., 1969, 4, 195–197 CrossRef CAS.
- K. H. Mok and P. J. Hore, Methods, 2004, 34, 75–87 CrossRef CAS PubMed.
- K. H. Mok, L. T. Kuhn, M. Goez, I. J. Day, J. C. Lin, N. H. Andersen and P. J. Hore, Nature, 2007, 447, 106–109 CrossRef CAS PubMed.
- S. Sim and M. D. E. Forbes, J. Phys. Chem. B, 2014, 118, 9997–10006 CrossRef CAS PubMed.
- A. Kawai, S. Mori, K. Tsuji and K. Shibuya, Appl. Magn. Reson., 2010, 38, 205–216 CrossRef CAS.
- H. Levanon and A. Blank, US Pat., 6515539B1, 2003.
- H. Takahashi, M. Iwama, N. Akai, K. Shibuya and A. Kawai, Mol. Phys., 2014, 112, 1012–1020 CrossRef CAS.
- G. Finch, A. Yilmaz and M. Utz, J. Magn. Reson., 2016, 262, 73–80 CrossRef CAS PubMed.
- E. V. Kryukov, K. J. Pike, T. K. Y. Tam, M. E. Newton, M. E. Smith and R. Dupree, Phys. Chem. Chem. Phys., 2011, 13, 4372–4380 RSC.
- T. Kawahara, S. Sakaguchi, K. Tateishi, T. L. Tang and T. Uesaka, J. Phys. Soc. Jpn., 2015, 84, 044005 CrossRef.
- K. Takeda, T. Yamamura, A. Kagawa and M. Kitagawa, J. Magn. Reson., 2005, 174, 310–313 CrossRef CAS PubMed.
- S. E. Korchak, A. S. Kiryutin, K. L. Ivanov, A. V. Yurkovskaya, Yu. A. Grishin, H. Zimmermann and H.-M. Vieth, Appl. Magn. Reson., 2010, 37, 515–537 CrossRef.
- S. Jockusch, G. Dedola, G. Lem and N. J. Turro, J. Phys. Chem. B, 1999, 103, 9126–9129 CrossRef CAS.
- V. Rane and R. Das, J. Phys. Chem. A, 2015, 119, 5515–5523 CrossRef CAS PubMed.
- N. Enkin, G. Liu, M. d C. Gimenez-Lopez, K. Porfyrakis, I. Tkach and M. Bennati, Phys. Chem. Chem. Phys., 2015, 17, 11144–11149 RSC.
- K. G. Valentine, G. Mathies, S. Bédard, N. V. Nucci, I. Dodevski, M. A. Stetz, T. V. Can, R. G. Griffin and A. J. Wand, J. Am. Chem. Soc., 2014, 136, 2800–2807 CrossRef CAS PubMed.
- P. Neugebauer, J. G. Krummenacker, V. P. Denysenkov, C. Helmling, C. Luchinat, G. Parigi and T. F. Prisner, Phys. Chem. Chem. Phys., 2014, 16, 18781–18787 RSC.
- P. Lottmann, T. Marquardsen, A. Krahn, A. Tavernier, P. Höfer, M. Bennati, F. Engelke and C. Griesinger, Appl. Magn. Reson., 2012, 43, 207–221 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available: Experimental details, energy level diagram, additional data. See DOI: 10.1039/c6cc06651h |
| This journal is © The Royal Society of Chemistry 2016 |

![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
: