Open Access Article
Open Access ArticleThe death of the Job plot, transparency, open science and online tools, uncertainty estimation methods and other developments in supramolecular chemistry data analysis†
D.
Brynn Hibbert
a and
Pall
Thordarson
 *ab
*ab
aSchool of Chemistry, University of New South Wales, Sydney, NSW 2052, Australia
bThe Australian Centre for Nanomedicine and the ARC Centre of Excellence in Convergent Bio-Nano Science and Technology, University of New South Wales, Sydney, NSW 2052, Australia. E-mail: p.thordarson@unsw.edu.au
First published on 25th August 2016
Abstract
Data analysis is central to understanding phenomena in host–guest chemistry. We describe here recent developments in this field starting with the revelation that the popular Job plot method is inappropriate for most problems in host–guest chemistry and that the focus should instead be on systematically fitting data and testing all reasonable binding models. We then discuss approaches for estimating uncertainties in binding studies using case studies and simulations to highlight key issues. Related to this is the need for ready access to data and transparency in the methodology or software used, and we demonstrate an example a webportal (http://supramolecular.org) that aims to address this issue. We conclude with a list of best-practice protocols for data analysis in supramolecular chemistry that could easily be translated to other related problems in chemistry including measuring rate constants or drug IC50 values.
Introduction
Central to scientific research is the cycle of hypothesis, experiment, data analysis, and then verifying, refining or rejecting the hypothesis based on interpretation of the data. Analysis of data is pivotal in this process, making robust data analysis methods critical in the armoury of most scientists. This is no different in supramolecular chemistry, although often, researchers do not seem to place the same value on understanding data analysis methods as, for instance, analytical chemists, or scientists in experimental physics or genomics (bioinformatics). There is, however, an opportunity here as supramolecular chemistry offers a rich collection of interesting challenges in the analysis and interpretation of its data.The three, somewhat linked, key challenges in the analysis of data in supramolecular chemistry concern: (i) determining the stoichiometry of interactions (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, 1
1, 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2, 2
2, 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1,…),1 (ii) picking the most appropriate binding model (non-cooperative, cooperative…)2 and (iii) obtaining values of thermodynamic quantities such as binding constant(s) Ki, with reasonable estimates of measurement uncertainty.1–3 It has been stated by one of us that any analysis without proper information on the reliability of results is useless,4 which highlights the importance of using well-grounded methods to ensure reliability of the information obtained.
1,…),1 (ii) picking the most appropriate binding model (non-cooperative, cooperative…)2 and (iii) obtaining values of thermodynamic quantities such as binding constant(s) Ki, with reasonable estimates of measurement uncertainty.1–3 It has been stated by one of us that any analysis without proper information on the reliability of results is useless,4 which highlights the importance of using well-grounded methods to ensure reliability of the information obtained.
The demand for reliability is now becoming intimately linked to a push for openness and transparency in how the data is handled. Proponents of the Open Science movement have stated its goal as encompassing transparent processes where good practices are characterised by: free, public access to scientific communication, open access to web-based tools that facilitate scientific collaboration and public availability and reusability of data.5 This approach has obvious benefits for improving the reliability of results obtained from data analysis. If both the raw data and the methodology used (e.g., software code) is made accessible and as transparent as possible, then it should be easier to detect and correct any mistakes, even post-publication.
This feature article covers some recent developments in supramolecular chemistry data analysis in terms of the three aforementioned challenges with particular focus on uncertainty estimations. The potential role that open science and online tools have in addressing the challenges will also be discussed. First the paper will discuss the related challenges of stoichiometry and selection of a binding model. After brief comments on accuracy in the software used and on method selection (NMR vs. UV-vis), the paper will examine some different approaches to estimating measurement uncertainties using sample data to illustrate these methods. The paper finishes by discussing the role of open science and online tools for data analysis in supramolecular chemistry. To conclude a suggested best-practice list is offered for the researcher. The work here builds on our earlier discussions on the fundamentals of analysing binding data.1,2 After a brief review of the key equations for 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 and 1
1 and 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 equilibria and quality of fit indicators, we shall frequently refer the reader to these papers for more in-depth descriptions of key principles and concepts.
2 equilibria and quality of fit indicators, we shall frequently refer the reader to these papers for more in-depth descriptions of key principles and concepts.
The availability of sufficient computing power to apply more realistic statistical and mathematical approaches has caused a shift from forced assumptions of linearity, pseudo-first-order processes, and graphical methods, to numerical solutions of non-linear systems yielding models and parameters with GUM-compliant uncertainties.6 We hope that the current article will assist supramolecular chemists in critically evaluating past and present results and planning their future work to obtain more reliable results.
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/h3_char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/h3_char_2009.gif) 1 and 1
1 and 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/h3_char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/h3_char_2009.gif) 2 equilibria and fit indicators
2 equilibria and fit indicators
The basic 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 equilibrium between a host (H – see Chart 1 for abbreviations and symbols used in this review) and a guest (G) is usually described using the equilibrium association constant Ka (or K1):1,2
1 equilibrium between a host (H – see Chart 1 for abbreviations and symbols used in this review) and a guest (G) is usually described using the equilibrium association constant Ka (or K1):1,2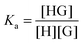 | (1) |
Usually, the concentration of the host–guest complex cannot be obtained directly but it can be related back to the known total concentrations of the host ([H]0) and guest ([G]0) and the equilibrium constant Ka through the following quadratic equation:
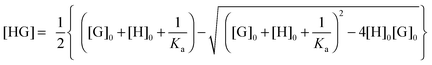 | (2) |
In supramolecular titration experiments, the host is then typically titrated with a solution of guest and the change (ΔY) in some physical quantity that is sensitive to the formation of the host–guest complex is then measured. For UV-vis titration the change in absorbance is measured (i.e. ΔY = ΔA), which is proportional to the concentration of the host–guest complex [HG] from (2) multiplied by the difference between the molar absorptivities of host–guest complex and free host εΔHG = εHG − εH1,2
| ΔY = ΔA = εΔHG([HG]) | (3) |
For NMR titrations the observed change ΔY = Δδ is likewise directly proportional to the change δΔHG in the NMR resonances between the host–guest complex (δHG) and free host (δH) but this time multiplied by the amount fraction of the complex HG:
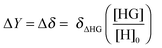 | (4) |
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 equilibria can similarly be described through the step-wise equilibrium constants: K1 for the formation of 1
2 equilibria can similarly be described through the step-wise equilibrium constants: K1 for the formation of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 complex HG, and K2 for the formation of 1
1 complex HG, and K2 for the formation of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 complex HG:1,2
2 complex HG:1,2
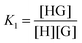 | (5) |
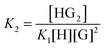 | (6) |
Cooperative 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 systems are characterised by K1 ≠ 4K2 whereas for non-cooperative systems, K1 = 4K2, simplifying the data analysis as discussed below.
2 systems are characterised by K1 ≠ 4K2 whereas for non-cooperative systems, K1 = 4K2, simplifying the data analysis as discussed below.
For systems where the measured physical change (ΔY) depends on the amount fraction, such as in NMR titrations, we can use similar approaches as outlined above for simple 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 equilibria, to obtain:1,2
1 equilibria, to obtain:1,2
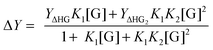 | (7) |
For UV-vis titrations the right-hand side of (7) is multiplied by [H]0. The concentration of free guest [G] cannot usually be obtained directly but it can be related back to the total concentrations of the host, guest and equilibrium constant through the cubic equation analogue of (2) (not shown here).1,2 For other equilibria such as 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, similar approaches are then used to obtain relationships between measurable parameters, a physical change that occurs upon forming the host–guest complex, and the equilibrium constants of interest. For 1
1, similar approaches are then used to obtain relationships between measurable parameters, a physical change that occurs upon forming the host–guest complex, and the equilibrium constants of interest. For 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, 1
1, 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 and 2
2 and 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 host–guest systems straightforward analytical (exact) solutions are available, but for more complex systems, some shortcuts or approximations are necessary.2
1 host–guest systems straightforward analytical (exact) solutions are available, but for more complex systems, some shortcuts or approximations are necessary.2
We now turn our attention to the data fitting process. A general model of the problem such as (3) or (7) for N data (xdata, ydata) with individual observations (xi, yi) can be written as:
| yi = f(xi,β) + ei | (8) |
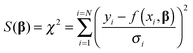 | (9) |
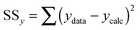 | (10) |
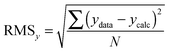 | (11) |
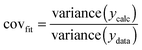 | (12) |
Determining stoichiometry and the best binding model(s)
Supramolecular interactions in host–guest chemistry are usually studied through titration experiments. The data obtained can then be fitted to as few or many binding models as desired to obtain the K-value(s) of interest.1 The data fitting process itself is “blind” and the results obtained have no inherent physical meaning.Picking the correct model is not straightforward. A good fit of a “simple” model does not prove the model as there are usually an (almost) infinite number of other, usually more complicated, models that might fit the experimental data equally well. Traditionally, supramolecular chemists opt for the simplest plausible model (Occam's razor) once the stoichiometry has been determined. However model selection is a mature statistical field and information theory gives approaches (e.g. Bayesian Information Criterion) that could be applied here.10 We describe below simple F-value calculations to aid the choice of model.
To narrow down the number of plausible binding models, knowledge about the host–guest stoichiometry is therefore paramount. Once that has been achieved the more subtle differences between available binding models can then be considered.
The death of the Job plot
The continuous variation method, better known as the Job plot11 has until recently been the most popular method for determining stoichiometry in host–guest chemistry. This is despite concerns raised first by Connors12 and echoed by us1 and others13 about its limitations when more than one complex is present. More recently, Long and Pfeffer14 noted that popular shortcuts to the Job method, such as the MacCarthy modification,15 gave in some instances very different results from the original method. But until very recently the orthodox view in the community appeared to be that the original Job method was in most cases reliable when it came to determining stoichiometry in host–guest chemistry.Recently published work by Jurczak and co-workers16 at the Polish Academy of Sciences challenged this view and, in our opinion, essentially spelled the death of the Job plot as a useful tool in analysing supramolecular binding interactions! Their simulations show that the observed maxima in the Job plot (xmax) for various cases of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 equilibria may or may not give the “expected” xmax ≈ 0.33 for a 1
2 equilibria may or may not give the “expected” xmax ≈ 0.33 for a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 system (Fig. 1). In other words, the observed xmax value is often misleading; of all the 1
2 system (Fig. 1). In other words, the observed xmax value is often misleading; of all the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 cases shown in columns 3–5 in Fig. 1, only 4 out of 12 have xmax ≤ 0.4 and only one is reasonably close xmax ≈ 0.33 (0.36 at the bottom right corner of Fig. 1). What Fig. 1 shows is that the Job plot is more sensitive to the K1/K2 ratio and host concentration than to the real stoichiometry.
2 cases shown in columns 3–5 in Fig. 1, only 4 out of 12 have xmax ≤ 0.4 and only one is reasonably close xmax ≈ 0.33 (0.36 at the bottom right corner of Fig. 1). What Fig. 1 shows is that the Job plot is more sensitive to the K1/K2 ratio and host concentration than to the real stoichiometry.
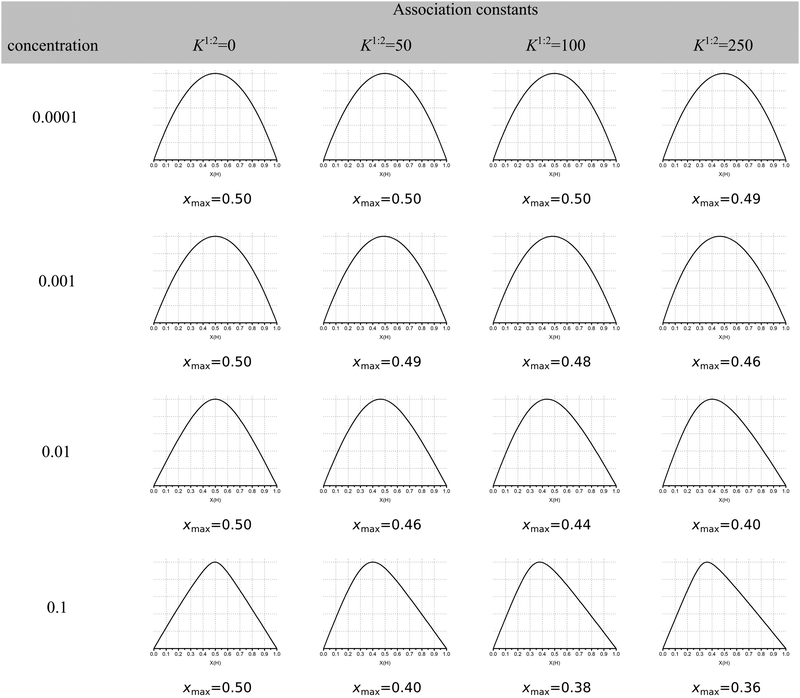 | ||
Fig. 1 Simulated Job Plots for various cases of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 stoichiometry with the exception of the 1 2 stoichiometry with the exception of the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 complexes in column 2 (K2 = 0). In all cases K1 = 1000 M−1 with YHG = 1 and YHG2 = 2 (additive model). The concentration of host in M is shown in column 1. The simulated maxima in the Job plots is shown as xmax. Reproduced with permission from ref. 16. 1 complexes in column 2 (K2 = 0). In all cases K1 = 1000 M−1 with YHG = 1 and YHG2 = 2 (additive model). The concentration of host in M is shown in column 1. The simulated maxima in the Job plots is shown as xmax. Reproduced with permission from ref. 16. | ||
Jurczak and co-workers then go further and show that even at reasonably high host concentration (0.01 M) with a low K1/K2 ratio of 4, corresponding to classical non-cooperative binding, the outcome is highly dependent on the ratio and direction (increasing/decreasing) of the physical (analytical) signal Y from the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 (YHG) and 1
1 (YHG) and 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 (YHG2) complexes formed (Fig. 2).16 In NMR titrations, YHG correspond to the chemical resonance (change) from the 1
2 (YHG2) complexes formed (Fig. 2).16 In NMR titrations, YHG correspond to the chemical resonance (change) from the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 complex (δHG) and YHG2 to the one from the 1
1 complex (δHG) and YHG2 to the one from the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 complex (δHG2) (see also (7) above).
2 complex (δHG2) (see also (7) above).
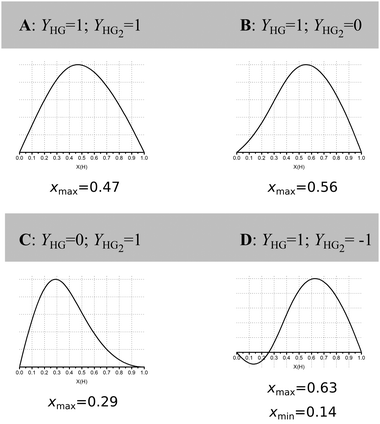 | ||
Fig. 2 Simulated Job Plots for various cases of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 stoichiometry with concentration of host = 0.01 M, K1 = 1000 M−1 and K2 = 250 M−1, i.e. non-cooperative 1 2 stoichiometry with concentration of host = 0.01 M, K1 = 1000 M−1 and K2 = 250 M−1, i.e. non-cooperative 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 binding. Only YHG and YHG2 between cases A–D. The corresponding case for YHG = 1 and YHG2 = 2 is shown in row 4, column 5 of Fig. 1. Reproduced with permission from ref. 16. 2 binding. Only YHG and YHG2 between cases A–D. The corresponding case for YHG = 1 and YHG2 = 2 is shown in row 4, column 5 of Fig. 1. Reproduced with permission from ref. 16. | ||
These simulations show that for a true 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 equilibria, depending on the combinations of YHG and YHG2, the observed xmax may lie anywhere between 0.29 and 0.63, depending on the assumed 1
2 equilibria, depending on the combinations of YHG and YHG2, the observed xmax may lie anywhere between 0.29 and 0.63, depending on the assumed 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2, 1
2, 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 or 2
1 or 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 stoichiometry! The message from the data in Fig. 1 and 2 is that Job plots are exceptionally poor indicators of stoichiometry in supramolecular host–guest chemistry. It is for this reason that we propose to declare the Job method as practically dead as an analytical tool in supramolecular chemistry. Jurczak and co-workers point out that the Job method may still have a valid use in the study of inorganic complexes16 where the Ki's are typically ≫1/host concentration [H]0 (or in other words, the dissociation constant(s) Kd ≪ [H]0) which correspond somewhat to the case in the bottom right corner of Fig. 1. This situation is relatively rare in classical supramolecular host–guest chemistry, particularly the type that is studied by NMR titration where the K's hardly exceed 105 M−1 for practical reasons.1,17 Alternatively, in the case of positive cooperativity, if K2 is comparable or even larger than K1, a Job plot will probably give the correct answer (consider this as an extreme case of the ones shown in the right-most column in Fig. 1).
1 stoichiometry! The message from the data in Fig. 1 and 2 is that Job plots are exceptionally poor indicators of stoichiometry in supramolecular host–guest chemistry. It is for this reason that we propose to declare the Job method as practically dead as an analytical tool in supramolecular chemistry. Jurczak and co-workers point out that the Job method may still have a valid use in the study of inorganic complexes16 where the Ki's are typically ≫1/host concentration [H]0 (or in other words, the dissociation constant(s) Kd ≪ [H]0) which correspond somewhat to the case in the bottom right corner of Fig. 1. This situation is relatively rare in classical supramolecular host–guest chemistry, particularly the type that is studied by NMR titration where the K's hardly exceed 105 M−1 for practical reasons.1,17 Alternatively, in the case of positive cooperativity, if K2 is comparable or even larger than K1, a Job plot will probably give the correct answer (consider this as an extreme case of the ones shown in the right-most column in Fig. 1).
Are Job plots then useful at all? In the limiting cases where either both K1 and K2 are large or K2 is relatively large compared to K1, Job plots still appear to give the “right” answer. However, one can only be certain about this if one has prior knowledge of K1 and K2. In other words, at best, a Job plot can only be used for additional positive confirmation of a binding model about which there is sufficient information, i.e. the values of K1 and K2. It is practically useless as a tool to rule out more complex models or to differentiate between different binding models. In light of our discussion below, the additional time and effort required to obtain a Job plot, would be much better spent on repeat experiments or by performing a titration experiment at a different concentration of the host.
There are, as outlined in our earlier paper,1 other methods than the continuous variation method that can be used to determine stoichiometry in host–guest systems, including the consistency of the model(s) proposed to changes in concentration.1 Jurczak and co-workers point out in their paper that a residual plot is probably most useful.16 A regular sinusoidal distribution of the residual indicates the assumed model is incorrect but unfortunately, such an observation does not direct the researcher to the correct stoichiometry. In essence, this means that if there any ambiguity about the binding model or the correct stoichiometry, the best approach is to fit the raw data to all probable models and then compare the results.
Comparing different binding models
The stoichiometry problem aside, there is often more than one binding model that can be used to fit the data. For instance, even if it is known that the stoichiometry is 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2, there are 4 different binding model variants (Fig. 3B) or flavours of (7) that could be used to fit the data depending whether the 1
2, there are 4 different binding model variants (Fig. 3B) or flavours of (7) that could be used to fit the data depending whether the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 binding interaction cooperative or not and whether the physical quantities ΔY (e.g. δ for the complexes in NMR titration) are additive or not.2,18 So how should one compare these models? We will look at a recent example from our own work and then outline possible best practice for dealing with this problem.
2 binding interaction cooperative or not and whether the physical quantities ΔY (e.g. δ for the complexes in NMR titration) are additive or not.2,18 So how should one compare these models? We will look at a recent example from our own work and then outline possible best practice for dealing with this problem.
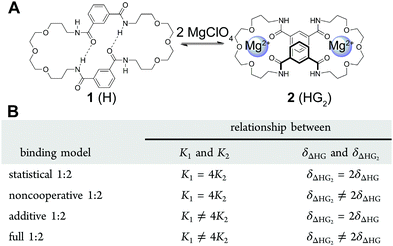 | ||
Fig. 3 (A) The structure of the host (H) 1 and its 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 host–guest (HG2) complex 2. (B) The four different binding models (flavours) based on (7) that can be used to describe a 1 2 host–guest (HG2) complex 2. (B) The four different binding models (flavours) based on (7) that can be used to describe a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 equilibria. Reproduced with permission from ref. 18. 2 equilibria. Reproduced with permission from ref. 18. | ||
The host 1 (Fig. 3A) can bind up to two cations such as Ca2+ or Mg2+ to form the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 complex 2 (1 can also bind two anions). The binding data for Mg2+ and other cations and anions was fitted to all four flavours of the 1
2 complex 2 (1 can also bind two anions). The binding data for Mg2+ and other cations and anions was fitted to all four flavours of the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 equilibria and the results then systematically compared in terms of quality of fit indicators, residual plots vs. number of parameters obtained (Table 1).18
2 equilibria and the results then systematically compared in terms of quality of fit indicators, residual plots vs. number of parameters obtained (Table 1).18
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 binding models used to fit chemical shift data from an NMR titration of 1 with Mg(ClO4)2 in CD3CN/CDCl3 (1
2 binding models used to fit chemical shift data from an NMR titration of 1 with Mg(ClO4)2 in CD3CN/CDCl3 (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, v/v).18 The raw data and the fits are stored at http://supramolecular.org (ESI for URL's)19
1, v/v).18 The raw data and the fits are stored at http://supramolecular.org (ESI for URL's)19
| Binding modela | K 1/M−1 | K 2/M−1 | covfit ratiob | SSy/10−3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) c c |
dfd | Fe | Pf |
|---|---|---|---|---|---|---|---|
a The four different binding models compared (see Fig. 3B).
b Raw covfit from (12) divided by covfit for the statistical model = 3.66 × 10−3.
c Calculated from (10).
d Degrees of freedom = N − k.
e
F-value from (11). In all cases the more complex model (2 in (13)) is the full 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 model.
f
P-value (significance test).20
g The SSy for the Noncoop model is 0.004% greater than for the full model.
h For noncooperative/statistical binding K2 is calculated as K2 = K1/4 from the K1 value obtained.
i The K1 value obtained is physically improbable. If as in ref. 18 no constraints are used the model converges on a negative K2 which is physically impossible. 2 model.
f
P-value (significance test).20
g The SSy for the Noncoop model is 0.004% greater than for the full model.
h For noncooperative/statistical binding K2 is calculated as K2 = K1/4 from the K1 value obtained.
i The K1 value obtained is physically improbable. If as in ref. 18 no constraints are used the model converges on a negative K2 which is physically impossible.
|
|||||||
| Full | 4139 | 1059 | 5.6 | 1.98g | 86 | N/A | N/A |
| Noncoop. | 4252 | 1063h | 5.6 | 1.98g | 87 | 0.004 | 0.95 |
| Additivei | 3 × 106 | 1784 | 0.5 | 7.33 | 90 | 58.1 | 10−23 |
| Statistical | 15986 | 3997h | 1 | 11.17 | 91 | 79.9 | 10−30 |
The most useful indicator used to select a binding model in this study was covfit obtained from (12). The more complex model, and hence the number of parameters fitted, the better the fit generally is. To justify the selection of a more complex model such as the full 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 model over a simpler 1
2 model over a simpler 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 additive model, covfit needs to be at least three to five times better (lower) for the complex model(s).18 For example, in the case of Mg2+ binding, the covfit for both the full and noncooperative 1
2 additive model, covfit needs to be at least three to five times better (lower) for the complex model(s).18 For example, in the case of Mg2+ binding, the covfit for both the full and noncooperative 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 model was 5.6× better (lower) than the simpler 1
2 model was 5.6× better (lower) than the simpler 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 statistical model (Table 1). The additive model was ruled out not only because of the poor covfit, but also as the magnitude of K1 obtained was physically improbable. The conclusion from this work was therefore that both the full and noncooperative 1
2 statistical model (Table 1). The additive model was ruled out not only because of the poor covfit, but also as the magnitude of K1 obtained was physically improbable. The conclusion from this work was therefore that both the full and noncooperative 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 models could be used to describe the binding of Mg2+ to 1.18
2 models could be used to describe the binding of Mg2+ to 1.18
The above process for selecting binding models relies on the subjective assessment of indicators. A greater number of coefficients will usually achieve a better fit, so a means of taking into account the reduced degrees of freedom would lead to comparable figures of merit. A more statistically robust approach is to test the sum-of-squares from each model by an F test at the appropriate degrees of freedom of each model:21
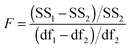 | (13) |
Here, number 1 and 2 refer to the simpler (Noncoop., Additive or Statistical) and more complex (Full) models being compared, respectively, SS1 and SS2 are the SSy values calculated according to (10) and df1 and df2 are degrees of freedom calculated from df = N − k with N = number of data points and k = number of parameters. The probability (P) of finding the observed F-value given the null hypothesis that the sums-of-squares are drawn from the same population, i.e. there is no difference between the models, can be readily calculated.20 Rejecting the null hypothesis at, say, the 95% level (P < 0.05) implies that the more complex model (number 2 in (13)) does fit the data better than the simpler one (number 1 in eqn (13)). This is not same as saying the more complex model is correct if the P-value is low but that the fit of the data is better described by that model.
We analysed the data shown Table 1 using the F-test and calculated the corresponding P-values (Table 1). The results clearly show that we accept the null hypothesis (P > 0.05) between the full and noncooperative 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 binding model, and therefore infer the noncooperative binding model. This is in contrast to the difference between the more complex full model with either the additive or statistical 1
2 binding model, and therefore infer the noncooperative binding model. This is in contrast to the difference between the more complex full model with either the additive or statistical 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 model which give minuscule P-values (<10−23). The sum-of-square test yields the same conclusion as the simple semi-subjective quality of fit comparison but it is quantitative and objective.
2 model which give minuscule P-values (<10−23). The sum-of-square test yields the same conclusion as the simple semi-subjective quality of fit comparison but it is quantitative and objective.
Accuracy in data fitting and the software used
The older literature on fitting data in host–guest chemistry is filled with methods and examples aimed at simplifying the process by taking shortcuts or making approximations to avoid solving the complex fundamental quadratic (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1) or cubic (1
1) or cubic (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2, 2
2, 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1) equations that describe the concentrations of the species of interest. This made sense when computational power was scarce or non-existent, as when linear-transformations such as Benesi–Hildebrand22 or Scatchard23 plots were invented, but these have been shown time and again to be highly inaccurate.21 Amazingly though, they are still being used in the 21st Century with drastic consequences. A recent example concerns the quest for enantioselective hosts for anion guests. Ulatowski and Jurczak showed by NMR competition experiments that a previously claimed record holder for enantioselective anion recognition, which was based on analysis by the Benesi–Hildebrand method,25 did in fact have very limited selectivity.24
1) equations that describe the concentrations of the species of interest. This made sense when computational power was scarce or non-existent, as when linear-transformations such as Benesi–Hildebrand22 or Scatchard23 plots were invented, but these have been shown time and again to be highly inaccurate.21 Amazingly though, they are still being used in the 21st Century with drastic consequences. A recent example concerns the quest for enantioselective hosts for anion guests. Ulatowski and Jurczak showed by NMR competition experiments that a previously claimed record holder for enantioselective anion recognition, which was based on analysis by the Benesi–Hildebrand method,25 did in fact have very limited selectivity.24
The frequent use of approximations in older literature and software programs also raises issues. Many legacy programs that are still quite popular use the method of successive approximation to solve the quadratic eqn (4) for 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 equilibria or the cubic equation that underpins (7) for 1
1 equilibria or the cubic equation that underpins (7) for 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 equilibria. This is no longer necessary as the combination of modern computer processing power and highly sophisticated programs (languages) such as fast and accurate mathematical and statistical algorithms within the open source Python programming language or commercial packages like Matlab solve these polynomials quickly and accurately. Although these legacy programs often get the answer almost right, we have demonstrated previously26 that even in the case of relatively simple 1
2 equilibria. This is no longer necessary as the combination of modern computer processing power and highly sophisticated programs (languages) such as fast and accurate mathematical and statistical algorithms within the open source Python programming language or commercial packages like Matlab solve these polynomials quickly and accurately. Although these legacy programs often get the answer almost right, we have demonstrated previously26 that even in the case of relatively simple 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 NMR models, the binding constants obtained by one popular legacy program differs by a few percent when compared to a Matlab-based program1 that solves (4) directly.
1 NMR models, the binding constants obtained by one popular legacy program differs by a few percent when compared to a Matlab-based program1 that solves (4) directly.
Selecting the appropriate experimental method
For newcomers and experienced users in this field alike, choosing the appropriate experimental method presents a major challenge. As we pointed out previously, there is a risk of letting economical or emotional factors determine whether, for instance, one should use 1H NMR or UV-vis titrations to determine host–guest binding constants in supramolecular chemistry.1 There is no simple answer to the question of selecting a method and in many instances, doing both would be desirable. One of the most powerful ways of testing a stoichiometry model is to carry out the experiment at different concentrations and see if the data fits the originally proposed model.1 For more concentrated solutions, (1H) NMR is usually the best choice, however, if the association constant is K > 105 M−1, NMR is not reliable.1,17 For larger K's, UV-vis is more suitable.The main limitation of UV-vis spectroscopic titrations is not only the need for a suitable chromophore, but that the titration has to be performed within the absorbance range that follows the Beer–Lambert law, limiting the available concentration range. Fluorescence titration can lower the concentration limit for UV-vis (around 10−6 M for strong chromophores), even towards the nM range, but fluorescence titrations are also limited to the relatively narrow concentration range that yields a linear (Beer–Lambert like) response.1,2
Spectroscopic UV-vis or fluorescence titration methods at low concentrations will often “mask” the presence of higher stoichiometries, e.g. in the case of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 host–guest complexes; unless K2 is particularly large, the concentration of the 1
2 host–guest complexes; unless K2 is particularly large, the concentration of the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 host–guest (HG2) complex will be minuscule and not detectable in the data obtained.
2 host–guest (HG2) complex will be minuscule and not detectable in the data obtained.
Uncertainty estimation in host–guest chemistry
Data without any information about their reliability is meaningless.4 A minimum indicator in quantitative analysis is the estimation measurement uncertainty of the measurement result for the target quantity.6 When doing n-repeat measurements, in the absence of bias (neglecting the bias from doing serial additions in titration experiments), the standard uncertainty (u) is taken as the standard deviation of the mean, the sample standard deviation (s) of the n-repeat measurements divided by the square root of n. To obtain a coverage interval about the mean at a desired probability (e.g. 95%) this is multiplied by the Student t-value for the degrees of freedom of the mean (n − 1).3 If replicate, independent measurements of binding constants are available, this approach is recommended if there is no evidence of between-measurement variability (caused by uncorrected biases), as described in a following section. For values obtained from non-linear model fitting, as is the case with determining binding constants, only approximations to true standard errors are obtained analytically from the regression.21 As discussed further below, having access to data from different laboratories allows investigation of inter- and intra-laboratory bias.27,28The “Guide to the expression of uncertainty in measurement” (GUM)6 and its supplements is produced by an international collaboration of eight organisations (including IUPAC), the Joint Committee for Guides on Metrology. It offers guidance on how the uncertainty of a measurement result can be estimated from knowledge of systematic and random factors that influence the result. There are strategies to obtain uncertainties that are not provided by statistical treatment of replicate measurements. Taking the measurement equation, uncertainties in each term are combined by the law of propagation of error. Combination of uncertainty terms in quadrature is correct for the linear case, and is also sufficient for problems that are mildly non-linear. However the use of Monte Carlo methods is recommended for obtaining coverage intervals of many problems where non-linearities do not allow simple error propagation.29 In analytical chemistry, the elimination, or correction for, systematic errors is a major problem in assuring the quality of results. Differences between results reported by laboratories, often in excess of estimated uncertainties, can be attributed to unknown, and uncontrolled bias.30 Error models used to obtain coefficients in supramolecular chemistry always assume the absence of bias, even when no great efforts have been made to demonstrate its absence.
Monte Carlo methods
The Monte Carlo approach to obtaining uncertainties for parameters takes the best fit and resamples the input data about their fitted values using known values of the standard deviation of those data. Each set of the M resampled data is then fitted giving M values of each parameter. These are a numerical approximation of the distribution function for the parameter. The standard uncertainty is the half width of the interval covering 68.3% of the values, and other coverages, e.g. 95%, 99%, are simply obtained by choosing the appropriate fraction of the distribution about the mean.If the 100P% coverage interval is needed (e.g. P = 0.95) it is recommended that considerably more than 1/(1 − P) trials are taken. If M ∼ 104 × 1/(1 − P) the parameters can be expressed to about two significant figures (a relative uncertainty of ∼1%) As each trial to obtain equilibrium parameters requires an iterative, non-linear fit it is not practical with present computing power to run thousands or tens of thousands of trials. It is therefore recommended (Section 7.2.3 of ref. 6)6 that if M = 100 or less, and a Gaussian distribution of the parameter values is assumed, then the mean and standard deviation of the set of M parameter values should be used to construct the coverage interval. In the simulations discussed below, M = 200 which means the relative uncertainty on the uncertainty values obtained is closer to 10% than ∼1%, e.g. for a reported uncertainty value below of 8%, the uncertainty on that number is in the order of ±0.8% (rounded to ±1%).
In host–guest titration data analysis one would include the uncertainties of the input concentrations ([H]0 and [G]0) and the “best” fitted physical values (ycalc in eqn (8)). To estimate the correct variances for these inputs, an uncertainty budget estimation3 on the concentration of the solutions prepared and the precision of the observed signal (e.g. chemical shift in NMR) should be made.
Estimating the uncertainties of parameters s
To deliver a set of parameters with GUM-compatible uncertainties depends on the quality of the fit, but also the view of the distribution of parameter estimates. For normally distributed parameter estimates, various linear assumptions give the following for the standard error of a parameter βi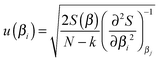 | (14) |
It is stressed that the standard uncertainty given by (14) has many assumptions, and delivers a symmetrical interval, also called the asymptotic error.21
An alternative approach uses the ‘profile likelihood’ or ‘model comparison’21 method in which keeping k − 1 parameters constant at their optimised values, varies the kth to construct a coverage interval of 100 − α% based on a likelihood ratio that is at the α/2 limit of significance, as determined by an F-test using21
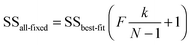 | (15) |
Reproducibility and combining uncertainties
As with any experiments to establish the value of a particular parameter sufficient independent replicates should be performed to give some confidence in the results. It is dangerous to report results based on a single experiment. There is much advice on how to combine independent data with uncertainties, arising from several campaigns to certify reference materials based on data from National Measurement Institutes (NMIs).The value of the binding constant(s) (K) should be the arithmetic average ![[K with combining macron]](https://www.rsc.org/images/entities/i_char_004b_0304.gif) of the N results Ki, or, if it is thought that the different data could have significantly different measurement uncertainties, the weighted mean (
of the N results Ki, or, if it is thought that the different data could have significantly different measurement uncertainties, the weighted mean (![[K with combining macron]](https://www.rsc.org/images/entities/i_char_004b_0304.gif) w).
w).
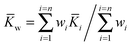 | (16) |
| (wi = 1/ui2) | (17) |
The associated combined uncertainty is more difficult to determine. Duewer32 gives eleven ways of combining the individual quoted uncertainties and the standard deviation of the means. The two recommended here as practical and easily implemented are the simple sample standard deviation of the mean (s(![[K with combining macron]](https://www.rsc.org/images/entities/i_char_004b_0304.gif) )) calculated from the data with no regard to the individual standard uncertainties (the assumption is the variability between values reflects the internal variability)
)) calculated from the data with no regard to the individual standard uncertainties (the assumption is the variability between values reflects the internal variability)
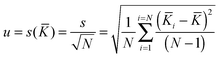 | (18) |
![[K with combining macron]](https://www.rsc.org/images/entities/i_char_004b_0304.gif) w) where the individual standard uncertainties are scaled to 1/n:
w) where the individual standard uncertainties are scaled to 1/n: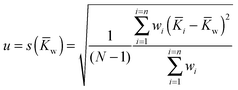 | (19) |
Estimating uncertainty on binding constants – case studies
We now apply the above discussion on uncertainty estimation to the binding data discussed above (Fig. 3 and Table 1). We start by noting that best practice would be to perform multiple repeats of this experiment as discussed further below. It is, however, quite common to find it impractical to perform multiple experiments. We start therefore by looking at the different methods to estimate the uncertainty on the parameters obtained from a single (n = 1) fitting process (the fitting error).The fit of the data to the full 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 binding model was analysed (Table 2 and Fig. 4) using standard uncertainties of the binding constant values (u(Ki)) from (14) (asymptotic errors), the profile likelihood or model comparison based on (15), and from Monte Carlo simulations (M = 200) based on random sampling from distributions of the input concentration data for the host ([H]0) and guest ([G]0), and the ideal calculated fit data (ycalc). The relative standard deviations of the distributions were 2% for [H]0, 1% for [G]0 and 0.5% for ycalc. The difference in relative standard deviations for [H]0 and [G]0 can be rationalised based on the fact that the concentration of the guest solution used in supramolecular titration is generally greater than that of the host. Modern NMR (and UV-vis) instruments are also highly accurate making the 0.5% estimation of relative standard deviation conservative.
2 binding model was analysed (Table 2 and Fig. 4) using standard uncertainties of the binding constant values (u(Ki)) from (14) (asymptotic errors), the profile likelihood or model comparison based on (15), and from Monte Carlo simulations (M = 200) based on random sampling from distributions of the input concentration data for the host ([H]0) and guest ([G]0), and the ideal calculated fit data (ycalc). The relative standard deviations of the distributions were 2% for [H]0, 1% for [G]0 and 0.5% for ycalc. The difference in relative standard deviations for [H]0 and [G]0 can be rationalised based on the fact that the concentration of the guest solution used in supramolecular titration is generally greater than that of the host. Modern NMR (and UV-vis) instruments are also highly accurate making the 0.5% estimation of relative standard deviation conservative.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, v/v) to the full 1
1, v/v) to the full 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 model (see also Table 1)17
2 model (see also Table 1)17
| Binding constant analysed | Type of limit | u(Ki)a | Model comparisonb | Monte Carlo methodc | ||
|---|---|---|---|---|---|---|
| ±Limit (%) | Lower limit (%) | Higher limit (%) | Lower limit (%) | Higher limit (%) | ||
| a Relative standard uncertainty or asymptotic error21 from (14). b Based on (15),21 also sometime also referred to as the profile likelihood method (see Fig. 4 for illustration). c From Monte Carlo (M = 200) simulation using 2% relative uncertainty on [H]0, 1% relative uncertainty on [G]0 and 0.5% relative uncertainty on ycalc. The uncertainty values obtained from Monte Carlo have themselves approximately ±10% relative uncertainty. d Standard deviation = standard uncertainty according to (16) (calculated using de Levie's method)31 or 68.3% confidence interval (P-value or α = 0.317) for the Model Comparison and Monte Carlo methods. e The 95% coverage interval (CI with P-value or α = 0.05). For the standard uncertainty method, the value obtained from (16) is multiplied by the t-value at α = 0.05 and divided by √N. | ||||||
| K 1 | u | ±4.1 | −12 | 14 | −9 | 9 |
| U 95% | ±8.2 | −15 | 18 | −16 | 24 | |
| K 2 | u | ±5.2 | −14 | 18 | −4 | 3 |
| U 95% | ±10 | −19 | 24 | −7 | 6 | |
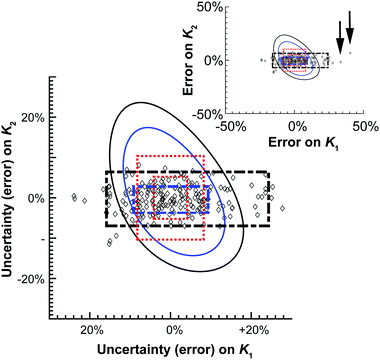 | ||
| Fig. 4 Graphical representation of the data shown in Table 2. The diamonds represent one of the M = 200 simulated results from the Monte Carlo calculations. The 68.3% or one standard deviation (blue) and 95% (black) confidence intervals for both the Monte Carlo (broken thick lines) and Model Comparison (solid thin lines) or Profile Likelihood methods. The symmetrical standard uncertainty (inner dotted red line box) or asymptotic error from (15) (calculated using de Levie's method)31 limits are also shown together with the corresponding 95% confidence interval on the standard uncertainty value (outer dotted red line box). The insert shows two of the outliers (arrows) from the Monte Carlo simulations. | ||
The differences between these methods are most readily seen when they are plotted graphically as a function of relative (%) error of K1 and K2 (Fig. 4). The scatter pattern that the 200 Monte Carlo simulations, and the corresponding confidence limits (broken black and blue lines) are clearly not symmetrical around the “best fit” K1 and K2 values (0%). The Monte Carlo results show more spread or up to 50% from the best fit K1 value along the K1 axis, but at the most only about 10% away from best fit K2 value. The Model Comparison (Profile Likelihood) method is not symmetrical either but has a distinctly different shape than the Monte Carlo with the uncertainty being larger along the K2 axis. In contrast, the standard uncertainty or asymmetric error is symmetrical, unlike the raw Monte Carlo scatter.
These results demonstrate the approximate nature of estimating standard uncertainty by eqn (14) or asymptotic error methods. Monte Carlo and Model Comparison (Profile likelihood) methods also give quite different results. The scatter in the Monte Carlo simulations suggests there is better information (smaller uncertainty) on K2 than K1 in this system. This makes good sense; the ratio of K1/K2 suggests noncooperative binding (see also Table 1) and the calculated amount fractions (see unique URL from http://supramolecular.org19 and Fig. S3 in ESI†) shows that the maximum amount fraction for the formation of the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 complex is 0.5, where the 1
1 complex is 0.5, where the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 complex reaches a amount fraction of 0.9 at the end of the titration. This means the NMR data obtained from this experiment “sees” the 1
2 complex reaches a amount fraction of 0.9 at the end of the titration. This means the NMR data obtained from this experiment “sees” the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 complex better than the 1
2 complex better than the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 complex, resulting in a smaller uncertainty on K2. In line with best practice recommendation in the GUM,29 the Monte Carlo results appear to give the best presentation of the underlying uncertainties in host–guest binding studies.
1 complex, resulting in a smaller uncertainty on K2. In line with best practice recommendation in the GUM,29 the Monte Carlo results appear to give the best presentation of the underlying uncertainties in host–guest binding studies.
Encouraged by these results, we carried out a large number of Monte Carlo simulations for NMR titrations for both the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 and 1
1 and 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 binding equilibria, using a range of binding constants (Ki). In all cases the chemical shifts are assumed to be additive (see Fig. 3B), the total host concentration was fixed at [H]0 = 10−3 M which is typical for NMR titrations and the final guest concentration at [G]0 = 0.035 M (35 equivalents). The results for the 1
2 binding equilibria, using a range of binding constants (Ki). In all cases the chemical shifts are assumed to be additive (see Fig. 3B), the total host concentration was fixed at [H]0 = 10−3 M which is typical for NMR titrations and the final guest concentration at [G]0 = 0.035 M (35 equivalents). The results for the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 binding equilibria are shown in Fig. 5.
1 binding equilibria are shown in Fig. 5.
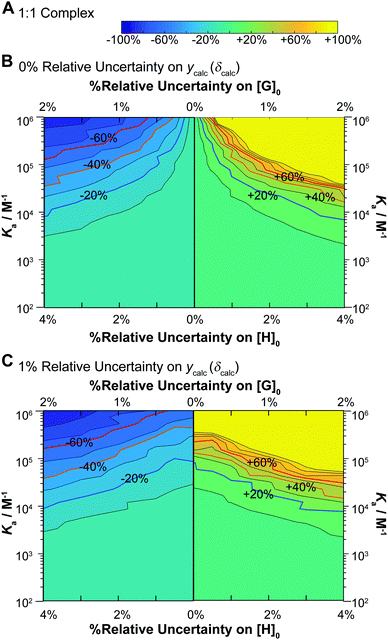
The results give valuable insight into factors that affect uncertainty in determining binding constants from host–guest titrations with some interesting but expected trends clearly evident. In terms of the lower limits (Fig. 5, left panels) and the higher limits (Fig. 5, right panel) on the uncertainties on the expected Ka, they are not quite symmetrical with slightly larger uncertainties on the higher limits for a given relative standard deviation of [H]0, [G]0 and ycalc (δcalc). For Ka > 5 × 103 M−1 the uncertainties do not exceed 10% regardless of the variance. As the Ka get larger, the variance has a more pronounced effect on the estimated uncertainty. At Ka > 105 M−1, which in any case is close to the limit achievable by NMR,1,17 meaningful Ka (uncertainty <40%) estimate can only be obtained with the noise (errors) on [H]0, [G]0 and ycalc (δcalc) are vanishingly small or 0%.
The results from our simulations for NMR titrations for 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 equilibria are shown in Fig. 6. These simulations were carried out under conditions where K2 = 0.1 × K1 or in other words, mild negative cooperativity (interaction parameter12,33α = 0.4). These simulations start by assuming that the chemical shift changes are additive (δHG = 0.5 ppm and δHG2 = 1 ppm).
2 equilibria are shown in Fig. 6. These simulations were carried out under conditions where K2 = 0.1 × K1 or in other words, mild negative cooperativity (interaction parameter12,33α = 0.4). These simulations start by assuming that the chemical shift changes are additive (δHG = 0.5 ppm and δHG2 = 1 ppm).
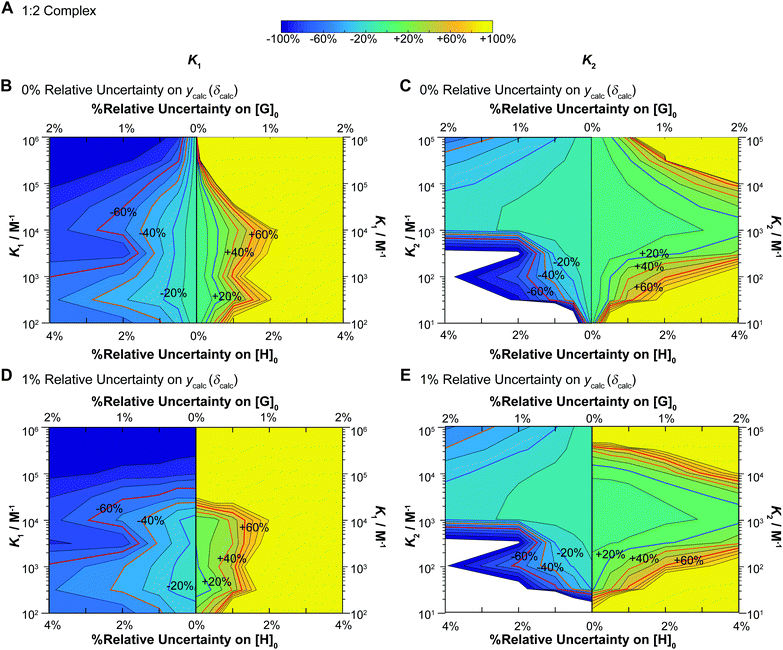 | ||
Fig. 6 Monte Carlo simulations (M = 200) for NMR titrations with underlying 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 equilibria (full model). In all cases [H]0 = 10−3 M, [G]0 is spread unevenly across 49 data points between [G]0 = 0–0.035 M, with δHG = 0.5 ppm and δHG2 = 1 ppm (as in the additive model – Fig. 3B) as the starting values in the “ideal” datasets used at the start of these simulations. The data was fitted with K1 between 102–106 M−1 and K2 between 10–105 M−1 with K2 always fixed at K2 = 0.1 × K1 (mild negative cooperativity). The variance is either 0% or 1% on ycalc (δcalc), 0–2% on [G]0 and 0–4% on [H]0. In each case the variance of [H]0 is 2× that of [G]0. The contour plot is coloured according to relative (%) the Monte Carlo uncertainty on the expected K1 (left column) and K2 (right column) values at the 95% confidence interval level (95% CI). (A) The colour scheme used in the contour plots between −100% and +100% of the expected K1 or K2 values. (B) Contour plot of the calculated Monte Carlo 95% CI on K1 assuming uncertainty of 0% for ycalc (δcalc). The lines indicate steps of 10%. The ±20% (blue) ±40% (orange) and ±60% (red) levels are highlighted with bold lines and labels. The y-axis represents changes in K1. Starting from the central vertical line, the x-axis represents increasing noises in [H]0 and [G]0 for the lower limit (left side panel) and higher limit (right side panel) of the expected K1. (C) Same as (B) except for K2 instead of K1 including the y-axis which shows K2. (D) Same as (B) except with additional 1% relative standard deviation on ycalc (δcalc). (E) Same as (D) except for K2 instead of K1 including the y-axis which shows K2. Note the order of magnitude difference in the y-axis between the left (K1) and right (K2) columns. 2 equilibria (full model). In all cases [H]0 = 10−3 M, [G]0 is spread unevenly across 49 data points between [G]0 = 0–0.035 M, with δHG = 0.5 ppm and δHG2 = 1 ppm (as in the additive model – Fig. 3B) as the starting values in the “ideal” datasets used at the start of these simulations. The data was fitted with K1 between 102–106 M−1 and K2 between 10–105 M−1 with K2 always fixed at K2 = 0.1 × K1 (mild negative cooperativity). The variance is either 0% or 1% on ycalc (δcalc), 0–2% on [G]0 and 0–4% on [H]0. In each case the variance of [H]0 is 2× that of [G]0. The contour plot is coloured according to relative (%) the Monte Carlo uncertainty on the expected K1 (left column) and K2 (right column) values at the 95% confidence interval level (95% CI). (A) The colour scheme used in the contour plots between −100% and +100% of the expected K1 or K2 values. (B) Contour plot of the calculated Monte Carlo 95% CI on K1 assuming uncertainty of 0% for ycalc (δcalc). The lines indicate steps of 10%. The ±20% (blue) ±40% (orange) and ±60% (red) levels are highlighted with bold lines and labels. The y-axis represents changes in K1. Starting from the central vertical line, the x-axis represents increasing noises in [H]0 and [G]0 for the lower limit (left side panel) and higher limit (right side panel) of the expected K1. (C) Same as (B) except for K2 instead of K1 including the y-axis which shows K2. (D) Same as (B) except with additional 1% relative standard deviation on ycalc (δcalc). (E) Same as (D) except for K2 instead of K1 including the y-axis which shows K2. Note the order of magnitude difference in the y-axis between the left (K1) and right (K2) columns. | ||
These results immediately demonstrate that the estimated uncertainty is highly sensitive to the relative standard deviation on both the total host and guest concentrations and the calculated ycalc (δcalc) values. The higher limit on K1 is particularly vulnerable to any variance; if the relative standard deviation of [G]0 exceeds 0.5 (relative standard deviation on [H]0 < 1%), a meaningful estimate on the upper limit of K1 cannot be obtained (Fig. 6B and D). The uncertainty of K1 is on the other hand fairly insensitive to variance on the calculated ycalc (δcalc) values, or the expected measured analytical signal. This suggests that researchers need to take particular care at preparing host–guest solutions when a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 equilibria is suspected to minimize the resulting uncertainty.
2 equilibria is suspected to minimize the resulting uncertainty.
Interestingly, the simulations also suggest a region of stability where one expects fairly accurate K2 values, i.e. when K2 > 103 M−1. In contrast if K2 < 103 M−1, it appears that it would be very hard to obtain a meaningful estimate on K2. This does make sense as with a low K2 there would little “information” about the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 complex on the expected binding isotherm whereas for high K2 the opposite is true (a high K2 and a 10× higher K1 would be beyond the practical limit for NMR).1,17
2 complex on the expected binding isotherm whereas for high K2 the opposite is true (a high K2 and a 10× higher K1 would be beyond the practical limit for NMR).1,17
Up to this point we have only discussed how the uncertainty on binding constant(s) obtained from host–guest titration studies could be estimated from a single experiment (n = 1). This is, however, not the ideal situation – if possible, an experiment needs to be repeated several times and the uncertainty then estimated from these n-repeats. The uncertainty of each individual fit then becomes incorporated in the uncertainty or variations across the multiple repeat, allowing us, as we show below, to largely ignore the estimated uncertainty on individual fits. At the very minimum, one should perform the experiment in triplicate (n = 3) but we strongly recommend that titration experiments should be carried out in quadruplicate (n = 4) as the results for n = 4 are significantly more statistically robust than for n = 3. Compared with three repeats, four repeats will improve the ratio of the t-values multiplied with the ratio of the square root of n (see (18)) by 36% and going from n = 4 to n = 5 improves that number by 21%.
The next question is how to estimate the uncertainty on the arithmetic or weighted mean values we obtain. To answer this we return to our Mg2+ titration of 1 example (Fig. 3 and Table 1) but this time looking at three repeats of this experiments (n = 3) with the results summarised in Table 3.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, v/v) to the full 1
1, v/v) to the full 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 model (see also Table 1). The raw data and the fits are stored at http://supramolecular.org (ESI for URL's)19
2 model (see also Table 1). The raw data and the fits are stored at http://supramolecular.org (ESI for URL's)19
| K 1 value/M−1 | Uncertaintya | K 2 value/M−1 | Uncertaintya | |||
|---|---|---|---|---|---|---|
| −sb/−M−1 | +sc/M−1 | −sb/M−1 | +sc/M−1 | |||
| a Standard deviation (68.3% confidence interval, CI) limit on Ki obtained from Monte Carlo (parameters the same as in Table 2 and as M = 200, these uncertainty values themselves also have a relatively uncertainty of ±10%). b The lower 68.3% CI limit from Monte Carlo. c The upper 68.3% CI limit from Monte Carlo. d Mean = sum of Ki values/n. e Calculated standard deviation of the mean from (18). f Weighted mean from (16); lower value calculated from lower Monte Carlo limits (−s) and higher value from the higher Monte Carlo limits (+s). g Weighted standard deviation from the mean calculated with (19) and based on the lower (−s) and higher (+s) Monte Carlo uncertainties. | ||||||
| Experiment 1 | 4139 | −378 | 386 | 1059 | −40 | 30 |
| Experiment 2 | 4832 | −480 | 545 | 907 | −38 | 32 |
| Experiment 3 | 3840 | −372 | 490 | 667 | −28 | 32 |
![[K with combining macron]](https://www.rsc.org/images/entities/i_char_004b_0304.gif) (mean)d (mean)d |
4271 M−1 | 878 M−1 | ||||
±s(![[K with combining macron]](https://www.rsc.org/images/entities/i_char_004b_0304.gif) )e )e |
±293 M−1 | ±114 M−1 | ||||
(Relative s(![[K with combining macron]](https://www.rsc.org/images/entities/i_char_004b_0304.gif) ), %) ), %) |
(±6.9%) | (±13%) | ||||
![[K with combining macron]](https://www.rsc.org/images/entities/i_char_004b_0304.gif) w
w
|
4185 M−1–4216 M−1 | 823 M−1–1050 M−1 | ||||
±s(![[K with combining macron]](https://www.rsc.org/images/entities/i_char_004b_0304.gif) w)g w)g |
−275 M−1, +261 M−1 | −122 M−1, +114 M−1 | ||||
(Relative s(![[K with combining macron]](https://www.rsc.org/images/entities/i_char_004b_0304.gif) w), %) w), %) |
(−6.6%, +6.2%) | (−14.9%, +10.9%) | ||||
Apart from calculating the (normal) mean ![[K with combining macron]](https://www.rsc.org/images/entities/i_char_004b_0304.gif) and (normal) standard deviation of the mean s(
and (normal) standard deviation of the mean s(![[K with combining macron]](https://www.rsc.org/images/entities/i_char_004b_0304.gif) ) from (19), we also include here the weighted mean
) from (19), we also include here the weighted mean ![[K with combining macron]](https://www.rsc.org/images/entities/i_char_004b_0304.gif) w(16) and weighted standard deviation of the mean s(
w(16) and weighted standard deviation of the mean s(![[K with combining macron]](https://www.rsc.org/images/entities/i_char_004b_0304.gif) w) (19). And as the Monte Carlo uncertainties are not symmetrical, this result in different lower and upper limit estimated of
w) (19). And as the Monte Carlo uncertainties are not symmetrical, this result in different lower and upper limit estimated of ![[K with combining macron]](https://www.rsc.org/images/entities/i_char_004b_0304.gif) w and s(
w and s(![[K with combining macron]](https://www.rsc.org/images/entities/i_char_004b_0304.gif) w). Interestingly, the weighted
w). Interestingly, the weighted ![[K with combining macron]](https://www.rsc.org/images/entities/i_char_004b_0304.gif) w and s(
w and s(![[K with combining macron]](https://www.rsc.org/images/entities/i_char_004b_0304.gif) w) do not seem to differ much from the normal
w) do not seem to differ much from the normal ![[K with combining macron]](https://www.rsc.org/images/entities/i_char_004b_0304.gif) and s(
and s(![[K with combining macron]](https://www.rsc.org/images/entities/i_char_004b_0304.gif) ) values even though only the former incorporates the uncertainty (here Monte Carlo) estimates from the individual fits. We conclude from this that in most cases, the normal (unweighted) process for calculating the mean and standard deviation of the mean is perfectly acceptable.
) values even though only the former incorporates the uncertainty (here Monte Carlo) estimates from the individual fits. We conclude from this that in most cases, the normal (unweighted) process for calculating the mean and standard deviation of the mean is perfectly acceptable.
There are two key lessons to take from this last example; firstly, by doing n-repeats and assigning the (normal) standard deviation of the mean of these repeats to the standard uncertainty, one can almost ignore the problem of estimating the uncertainty on the parameters in each experiment! We put the qualifier almost here, as it would still be prudent to estimate these, even if it just done with the simple standard uncertainty (asymptotic error) method using (15) to check how realistic the obtained Ki's are. The other interesting lesson is that for this experiment, the relative standard deviation of the mean is greater (13%) for K2 than for K1 (6.9%) – opposite from the estimation of the uncertainties from the individual fits according to Tables 2 and 3! The reason for this becomes evident if one compares the results from Experiment 3 to the others in Table 3 as the K2 value appears to be an outlier resulting in a large standard deviation of the mean for K2.
Open science and online tools
The above examples indicate the importance of transparent processes and show that with access to raw data from previous publication(s), it is sometimes possible to refine (or reject!) previously published findings. On a more philosophical level, it stands to reason that, when practical, data should be accessible to the public and the processes used to analyse them be as transparent as possible – principles that perfectly align with the ethos of the Open Science movement.5 Open Science encourages the free-of-charge universal sharing of good transparent practices, open access to scientific publications, scientific collaboration through open access web-based tools and open access and reusability of data.Open access to publications is now quite common but researchers in host–guest chemistry, and to some extent in chemistry at large, have been relatively slow to adopt other important Open Science tools. Depositing raw data with manuscripts is the exception and until now, there has not been any open access database for host–guest complexation data. Contrast this with single crystal X-ray crystallography where for 50 years the Cambridge Crystallographic Data Centre (CCDC) has allowed researchers both to deposit raw data and then search and retrieve any other deposited data for further analysis.34
One of us (Thordarson) has now established the web-portal OpenDataFit35 which includes the site http://supramolecular.org.19 This site provides data deposition and storage, and offers the community a free (open) access web-tool to fit their data to a range of binding models. The software code is open source (Python) and available online for scrutiny and further improvements (Fig. S1, ESI†).
The website is built around the concept of end-users uploading their input data (host and guest concentrations and the measured physical signal such as NMR resonance) in a simple spreadsheet format. The user then selects between various binding models and sets parameters such as initial guesses of the binding constant(s) being sought. After fitting the data and examining the results, which include residual and mole-fraction (speciation) plots, the user either refines the binding process further or saves the results. The archiving step includes an opportunity to add metadata such as which host and guest were used, solvent, temperature and other useful information. The user is then given a unique URL that can be used to access the data later as well as the option of downloading all the results in a spreadsheet for further analysis and plotting (Fig. 7 and Fig. S1–S4, ESI†).
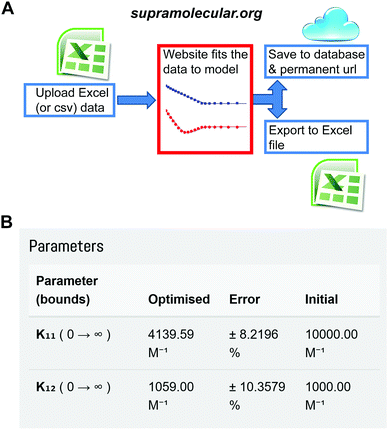 | ||
Fig. 7 The Open Access website http://supramolecular.org19 for data analysis and archiving in host–guest supramolecular chemistry. (A) Flow diagram of how data is processed on the website. (B) Snapshot from the website showing the result window from data archived at the unique url: http://app.supramolecular.org/bindfit/view/8a658114-0b28-4c63-92c0-09a7a976f0be which was fitted to 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 NMR binding data. Additional screenshots are provided in ESI† (Fig. S2–S5). 2 NMR binding data. Additional screenshots are provided in ESI† (Fig. S2–S5). | ||
The website offers inter alia, global36 fitting of host–guest titration data to 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, 1
1, 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 and 2
2 and 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 binding models, including the various 1
1 binding models, including the various 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 (and corresponding 2
2 (and corresponding 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1) flavours mentioned above. Users can also choose between the robust Nelder–Mead37 (Simplex) algorithm and the L-BFGS-B38,39 (limited (L) memory quasi-Newton Broyden–Fletcher–Goldfarb–Shanno simple box (B) constraints), which allows constraint of the search space. The site also returns the standard uncertainty21 (asymptotic error – see above) of the estimated binding constants. Users can also simulate binding data to help design their experiments. Planned additions include Monte Carlo estimation of uncertainty (see above). For the 1
1) flavours mentioned above. Users can also choose between the robust Nelder–Mead37 (Simplex) algorithm and the L-BFGS-B38,39 (limited (L) memory quasi-Newton Broyden–Fletcher–Goldfarb–Shanno simple box (B) constraints), which allows constraint of the search space. The site also returns the standard uncertainty21 (asymptotic error – see above) of the estimated binding constants. Users can also simulate binding data to help design their experiments. Planned additions include Monte Carlo estimation of uncertainty (see above). For the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, 1
1, 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 and 2
2 and 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 binding models, the fitting processes are based on the exact solutions (no approximations) of the equations used to describe these binding equilibria, e.g., (4) in the case of the 1
1 binding models, the fitting processes are based on the exact solutions (no approximations) of the equations used to describe these binding equilibria, e.g., (4) in the case of the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 NMR model.
1 NMR model.
The database function should in time, allow for systematic investigation of inter- and intra-laboratory biases by comparing data from different laboratories. Data mining might also allow investigators to do more systematic investigations into methods for comparing models, answering questions such as how robust the F-value (13) calculation method really is with a large set of real data.
It is our hope that the http://supramolecular.org website might also provide a catalyst for the supramolecular chemistry community for setting minimum standards for publishing data, along the lines of what is already common practice in the crystallography community. Other data-intensive fields have also established community-based “minimum information criteria” for publishing data, with proteomics being a prime example.40
Conclusions
In this article we have shown a few recent examples that illustrate how data analysis in host–guest chemistry experiments can be improved. We focused on the three key challenges as we see them; choosing the right model and stoichiometry, access to data and methods to analyse data and most importantly, methods to estimate uncertainties on the results obtained using case studies and simulations to explore the problem. We will now draw our conclusions together in a list of our suggestion for the start of a best-practice protocol for data analysis in supramolecular chemistry.Draft for best-practice protocol for data analysis in supramolecular chemistry
(1) Following Jurczak and co-workers15 work it is now clear that Job plots should not be used in ordinary host–guest titration experiments.41 At the very best it can only be used as an “after the fact” verification once the K's have been established with confidence based on titration experiment data. Given that constructing Job plots is quite time consuming, researchers should focus instead on repeat experiments or performing titration studies at different concentrations to test the robustness of the assumed binding model(s).(2) If more than one stoichiometry or binding model is suspected, fit the data to all models and systematically compare results to eliminate those that do not fit based on criteria's such as shape (scatter) of the residual plot16 and the sum-of-squares F-test19 (eqn (13)).
(3) If certain binding constants in multi-species equilibria are very low, e.g. K2 in the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 host–guest equilibria, the information content associated with that complex is inherently very limited. No method, no matter how sophisticated is likely to yield any reliable estimate of that binding constant (they will have large uncertainties).
2 host–guest equilibria, the information content associated with that complex is inherently very limited. No method, no matter how sophisticated is likely to yield any reliable estimate of that binding constant (they will have large uncertainties).
(4) Reviewers should without hesitation request for a revision of any papers that still use outdated and inaccurate linear-transformation methods such as Benesi–Hildebrand.
(5) When possible, the program used to fit the data should calculate the concentrations of the species involved using the exact mathematical expression for the equilibria of interest. For simple 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, 1
1, 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 and 2
2 and 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 binding model this should be mandatory and legacy programs that use the method of successive approximation should not be allowed.
1 binding model this should be mandatory and legacy programs that use the method of successive approximation should not be allowed.
(6) Best practice for estimating uncertainties clearly involves repeating the experiment at least 3, ideally 4 or more, times. The estimated uncertainty on the fit in individual experiments should be checked for signs of very poor fit. This can be done with the simple standard uncertainty method (asymptotic error) using (14) but Monte Carlo is desirable.42 If the individual fits are not unreasonable, they can subsequently be ignored and the uncertainties of binding constants and other parameter then simply estimated from the standard deviation of the mean s(![[x with combining macron]](https://www.rsc.org/images/entities/i_char_0078_0304.gif) ) from the n-repeat experiment.
) from the n-repeat experiment.
(7) If n-repeat measurements cannot be performed for practical reasons, we strongly recommend that the estimation of the uncertainty on the fitted parameters should, as recommended by the GUM Supplement 1,6,29 be performed by Monte Carlo simulations42 and reported at the 95% confidence interval level.
(8) Data should be made accessible (Open Access)5 and the software code used available and transparent to ensure others can verify and analyse further the experimental data.19
Repeating once again the message that “data without any information about its reliability is meaningless”4 we hope that this article and the list above will provide the host–guest supramolecular chemistry community with the necessary tools to make their results even more reliable. This will reduce mistakes and confusion in the field and accelerate further the rapid progress of host–guest supramolecular chemistry. We note also that the above approach could easily be adopted in other fields of chemistry, e.g. when determining rate constants or measuring drug potency via experiments to measure IC50 or EC50.
Acknowledgements
We acknowledge the Australian Research Council for an ARC Centre of Excellence Grant (CE140100036) and a Future Fellowship to PT (FT120100101) to P. T.References
- P. Thordarson, Chem. Soc. Rev., 2011, 40, 1305–1323 RSC.
- P. Thordarson, in Supramolecular Chemistry: From Molecules to Nanomaterials, ed. P. A. Gale and J. W. Steed, John Wiley & Sons, Chichester, UK, 2012, vol. 2, pp. 239–274 Search PubMed.
- D. B. Hibbert and J. J. Gooding, Data Analysis for Chemistry, Oxford University Press, New York, 2006 Search PubMed.
- D. B. Hibbert, Quality Assurance for the Analytical Chemistry Laboratory, Oxford University Press, New York, 2007 Search PubMed.
- http://www.openscience.org/blog/?p=269 (accessed 9th May 2016).
- Joint Committee for Guides in Metrology, Evaluation of measurement data – Guide to the expression of uncertainty in measurement. In JCGM 100, BIPM: Sèvres, http://www.bipm.org/utils/common/documents/jcgm/JCGM_100_2008_E.pdf, 2008 (accessed 9th May 2016).
- D. A. Vander Griend, D. K. Bediako, M. J. DeVries, N. A. Dejong and L. P. Heeringa, Inorg. Chem., 2008, 47, 656–662 CrossRef CAS PubMed.
- http://www.calvin.edu/˜dav4/Sivvu.htm (accessed 9th May 2016).
- P. Thordarson, E. J. A. Bijsterveld, J. A. A. W. Elemans, P. Kasák, R. J. M. Nolte and A. E. Rowan, J. Am. Chem. Soc., 2003, 125, 1186–1187 CrossRef CAS PubMed.
- G. Schwarz, Ann. Stat., 1978, 6, 461–464 CrossRef.
- P. Job, Anal. Chim. Appl., 1928, 9, 113–203 CAS.
- K. A. Connors, in Comprehensive Supramolecular Chemistry, ed. J. L. Atwood, J. E. D. Davies, D. D. MacNicol and F. Vögtle, Pergamon, Oxford, 1996, vol. 3, ch. 6, pp. 205–241 Search PubMed.
- H.-J. Schneider and A. Yatsimirsky, Principles and Methods in Supramolecular Chemistry, John Wiley & Sons, Chichester, 2000, p. 149 Search PubMed.
- B. M. Long and F. M. Pfeffer, Supramol. Chem., 2015, 27, 136–140 CrossRef CAS.
- P. MacCarthy, Anal. Chem., 1978, 50, 2165 CrossRef CAS.
- F. Ulatowski, K. Dabrowa, T. Balakier and J. Jurczak, J. Org. Chem., 2016, 81, 1746–1756 CrossRef CAS PubMed.
- C. S. Wilcox, in Frontier in Supramolecular Organic Chemistry and Photochemistry, ed. H.-J. Schneider and H. Dürr, VCH, Weinheim, 1991, pp. 123–144 Search PubMed.
- E. N. W. Howe, M. Bhadbhade and P. Thordarson, J. Am. Chem. Soc., 2014, 136, 7505–7516 CrossRef CAS PubMed.
- http://supramolecular.org (accessed 9th May 2016).
- In Excel for instance, one can calculate the P-value using this formula: P = FDIST((F,df1,df2),df2).
- H. J. Motulsky and A. Christopoulos, Fitting models to biological data using linear and nonlinear regression. A practical guide to curve fitting, GraphPad Software Inc., San Diego, CA, 2003 Search PubMed.
- H. Benesi and J. Hildebrand, J. Am. Chem. Soc., 1949, 71, 2703–2707 CrossRef CAS.
- G. Scatchard, Ann. N. Y. Acad. Sci., 1949, 51, 660–672 CrossRef CAS.
- F. Ulatowski and J. Jurczak, J. Org. Chem., 2015, 80, 4235–4243 CrossRef CAS PubMed.
- Y. K. Kim, H. N. Lee, N. J. Singh, H. J. Choi, J. Y. Xue, K. S. Kim, J. Yoon and M. H. Hyun, J. Org. Chem., 2008, 73, 301–304 CrossRef CAS PubMed.
- A. J. Lowe, F. M. Pfeffer and P. Thordarson, Supramol. Chem., 2012, 24, 585–594 CrossRef CAS.
- J. L. Sessler, D. E. Gross, W.-S. Cho, V. M. Lynch, F. P. Schmidtchen, G. W. Bates, M. E. Light and P. A. Gale, J. Am. Chem. Soc., 2006, 128, 12281–12288 CrossRef CAS PubMed.
- G. E. O'Donnell and D. B. Hibbert, Analyst, 2013, 138, 3673–3678 RSC.
- Joint Committee for Guides in Metrology, Evaluation of measurement data – Supplement 1 to the “Guide to the expression of uncertainty in measurement” – Propagation of distributions using a Monte Carlo method. In JCGM 101, http://www.bipm.org/utils/common/documents/jcgm/JCGM_101_2008_E.pdf ed.; BIPM; IEC; IFCC; ISO; IUPAC; IUPAP; OIML, Eds. BIPM: Sèvres, 2008 (accessed 9th May 2016).
- M. Thompson and S. Ellison, Accredit. Qual. Assur., 2011, 16, 483–487 CrossRef.
- R. de Levie, J. Chem. Educ., 1999, 76, 1594–1598 CrossRef CAS.
- D. L. A. Duewer, A robust approach for the determination of CCQM key comparison reference values and uncertainties, BIPM: Sevres, Paris, 2004, pp. 1–25 Search PubMed.
- K. A. Connors, A. Paulson and D. Toledo-Velasquaz, J. Org. Chem., 1988, 53, 2023–2026 CrossRef CAS.
- http://www.ccdc.cam.ac.uk (accessed 9th May 2016).
- http://opendatafit.org (accessed 9th May 2016).
- J. M. Beechem, Methods Enzymol., 1992, 210, 37–54 CAS.
- J. A. Nelder and R. Mead, Computer J., 1965, 7, 308–313 CrossRef.
- R. H. Byrd, P. Lu, J. Nocedal and C. Zhu, SIAM J. Sci. Comput., 1995, 16, 1190–1208 CrossRef.
- C. Zhu, R. H. Byrd, P. H. Lu and J. Nocedal, ACM Trans. Math. Software, 1997, 23, 550–560 CrossRef.
- C. F. Taylor, et al. , Nat. Biotechnol., 2007, 25, 887–893 CrossRef CAS PubMed.
- A. L. Chun, B. Le Bailly, A. Moscatelli and G. Prando, Nat. Nanotechnol., 2016, 11, 308 CrossRef.
- User-friendly access to Monte Carlo methods remains a challenge (the Matlab code for the Monte Carlo simulations used in this paper are in the ESI†). The authors hope that Monte Carlo options will become available in the future on the http://supramolecular.org website.
Footnote |
| † Electronic supplementary information (ESI) available: Unique URL's for key data, Matlab m-files for Uncertainty Estimations, additional website screenshots. See DOI: 10.1039/c6cc03888c |
| This journal is © The Royal Society of Chemistry 2016 |