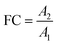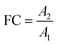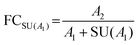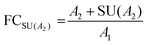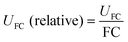Uncertainty budgeting in fold change determination and implications for non-targeted metabolomics studies in model systems†
Karin
Ortmayr
ab,
Verena
Charwat
c,
Cornelia
Kasper
c,
Stephan
Hann
 b and
Gunda
Koellensperger
*a
b and
Gunda
Koellensperger
*a
aInstitute of Analytical Chemistry, University of Vienna, Faculty of Chemistry, Waehringer Strasse 38, 1090 Vienna, Austria. E-mail: gunda.koellensperger@univie.ac.at; Fax: +431 42779523; Tel: +43 664 6027752303
bDepartment of Chemistry, University of Natural Resources and Life Sciences (BOKU) Vienna, Muthgasse 18, 1190 Vienna, Austria
cDepartment of Biotechnology, University of Natural Resources and Life Sciences (BOKU) Vienna, Muthgasse 18, 1190 Vienna, Austria
First published on 30th September 2016
Abstract
The p-value is the most prominent established metric for statistical significance in non-targeted metabolomics. However, its adequacy has repeatedly been the subject of discussion criticizing its uncertainty and its dependence on sample size and statistical power. These issues compromise non-targeted metabolomics in model systems, where studies typically investigate 5–10 samples per group. In this paper we propose a different approach for assessing the relevance of fold change (FC) data, where the FC is treated as a quantitative value and is validated by uncertainty budgeting. For the purpose of large-scale application in non-targeted metabolomics, we present a simplified approach for uncertainty propagation using experimental standard deviations of metabolite intensities as type A-summarized standard uncertainties. The resulting expanded FC uncertainty can be used to derive a minimum relevant FC as a complementary criterion in metabolomics data evaluation. This concept overcomes the need for a uniform p-value cut-off for all metabolites by considering the experimental uncertainty for each metabolite individually. The proposed procedure is part of analytical method validation, however the concept has not previously been applied to non-targeted metabolomics. A case study on mesenchymal stem cells cultured in normoxia and hypoxia demonstrates the practical value of this approach, in particular for studies with a small sample size. An online two-dimensional LC method coupled to mass spectrometry was crucial in providing both broad metabolome coverage and excellent experimental precision (<8% CV for peak areas, on average 0.5% CV for retention times) that was required for sensitive differential analysis as low as FC 1.1.
1 Introduction
Non-targeted approaches in metabolomics have contributed to the field's rapid evolution and spread into different research areas, including metabolic engineering in biotechnology,1–5 human health6–8 and biomarker discovery.9–11 In fact, the metabolic network is an important regulatory level in cellular physiology, as it allows the cell to adapt to sudden changes in its environment.12 Since the environmental trigger for these changes might only be transient, and extensive metabolic re-arrangements are costly for the cell, the metabolome is a highly dynamic system. This entails challenges for metabolome analysis, with changes either occurring too fast even for modern methods to capture, or the effects leveling off after a short adaptation phase. These considerations result in specific requirements for non-targeted metabolomics methods, in that they must be sensitive to small changes in order to allow in-depth studies of cellular metabolism. This, on the other hand, implies the necessity for tight experimental control and investigation of as many aspects as possible in order to avoid artefacts and analytical blind-spots.Non-targeted metabolomics entails the comprehensive analysis of the metabolome, and is typically undertaken using a differential approach aiming to elucidate global changes in biological systems in response to a specific perturbation. As such, non-targeted metabolomics is treated as a relative quantification technique, where the fold change (FC) serves as a measure for the relative change in a given metabolite's concentration in the different conditions under investigation. FC values are calculated relative to a given reference sample based on averaged raw signal intensities. While some typical analytical challenges associated with the absolute quantification of cellular metabolites are mitigated by the differential approach, care must be taken in the quantitative interpretation of these intensity ratios. Several pitfalls in the generation and interpretation of non-targeted metabolomics data remain, including aspects of experimental setup and control, analysis of biological samples and data evaluation.
Following measurement, differential MS-based metabolomics addresses quantitative relative fold changes between different experimental groups, using null-hypothesis significance testing (NHST) and the p-value as a metric for judgements about the significance of observations in a study. This (in addition to multivariate approaches13–15) is still the preferred approach within the community, in spite of a long-standing debate over the universal adequacy of NHST and the importance attributed to the p-value.16–20 Indeed, wide-spread misinterpretations of the p-value have been highlighted by many authors.16,18,20–23 Most recently, the uncertainty of the p-value and its dependence on statistical power has been discussed.23,24 With a low number of biological replicates and limited statistical power, the p-value is fraught with high uncertainty, leading to poor reproducibility of once significant findings, implying that p can be unreliable.23 Moreover, a uniform p-value cut off for all measured entities may not be ideal. It is exactly this situation which compromises non-targeted metabolomics in model systems as typical studies include a limited number of biological replicates per group, typically 5 to 10. Moreover, the effects under investigation are in many cases very minor (i.e. low FC).
The magnitude of the observed effect is the focus point of alternative approaches to NHST. The use of effect sizes has been encouraged by many,17,19,22,25 but was met with considerable resistance in the scientific community.16,23,26 However, NHST investigates only whether the observed differences have a trivial cause or reflect an effect caused by the respective treatment. In a recent commentary on this topic, Claridge-Chang and Assam promote the use of point estimates and confidence intervals19 to assess the magnitude and relevance of observed effects. Unlike the p-value (an abstract statistic) these point estimates use the same units and scale as measurement data and are therefore more intuitive and easier to interpret. In the light of the wide sample-to-sample variability of the p-value, the interpretation of effect sizes overcomes several concerns and paves the way for meta-analysis and cumulative knowledge generation.19,25
In this paper we propose a different approach for judging the relevance of FC-based findings. We treat the fold change as a quantitative value, and firstly assess the quantification task of untargeted metabolomics by uncertainty budgeting according to the official Guide to the Expression of Uncertainty in Measurement (GUM).27 Although most comprehensive, stringent uncertainty budgeting is complex and time-consuming when applied on a large scale. We therefore propose the use of the experimental standard deviation of metabolite intensities as type A-summarized standard uncertainties. The Kragten method28 for error propagation calculations allows the relatively simple handling of error propagation calculations even on a large scale, and is ideally suited for automatization and integration into non-targeted metabolomics data analysis workflows. The resulting expanded FC uncertainty allows the derivation of a minimum FC value to be considered relevant for each metabolite, given the observed data variation. The concept hence circumvents the selection criterion of a uniform p-value cut-off for all metabolites. The procedure is an integral part of analytical method validation as described in the Eurachem guideline “Fitness for Purpose of Analytical Methods”.29 Method validation strategies in the context of non-targeted metabolomics have been addressed30 alongside with a series of initiatives to establish common standards in metabolomics,31–36 but have so far not included uncertainty budgeting for “omics” methods and the concept of FC uncertainty.
The practical value of the proposed approach is demonstrated in a case study on human mesenchymal stem cells cultivated under normoxia and hypoxia. An online two-dimensional LC-MS method, used for the first time in MS-based non-targeted metabolomics, proved invaluable in providing both broad selectivity (i.e. metabolome coverage) and high repeatability precision, which was manifested as low FC uncertainty. In combination with efficient sample-level normalization via total protein content, the method thus meets several important requirements for the generation of high-quality non-targeted metabolomics data sets.
2 Materials and methods
2.1 Calculation of total combined measurement uncertainty
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 iterations were run, and the mean FC and standard deviation (as a measure for FC uncertainty) was calculated across the simulation results. Given the approximately normally distributed FC simulation results, a coverage factor of 2 (k = 2) was applied to the standard deviation estimate to derive the expanded uncertainty, UFC, with a 95% coverage probability for the fold change value within this error interval.
000 iterations were run, and the mean FC and standard deviation (as a measure for FC uncertainty) was calculated across the simulation results. Given the approximately normally distributed FC simulation results, a coverage factor of 2 (k = 2) was applied to the standard deviation estimate to derive the expanded uncertainty, UFC, with a 95% coverage probability for the fold change value within this error interval.
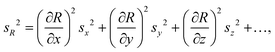 | (1) |
2.2 Adipose-derived mesenchymal stem cells
Adipose-derived human mesenchymal stem cells (adMSC) were derived from healthy adipose tissue obtained from abdominoplasty following written informed consent by the patient. The study was approved by the Ethics Committee of the Medical University Vienna and the General Hospital Vienna (EK no. 1949/2012). αMEM (12000-063, Gibco, Thermo Fisher Scientific, Waltham, MA, USA) supplemented with 2.5% human platelet lysate (hPL, PLS-100.01, PL BioScience GmbH, Aachen, Germany), 1 U ml−1 heparin (5394.00.00, Ratiopharm, Ulm, Germany) and 0.5% gentamicin sulfate (BE02-012E, Lonza, Basel, Switzerland) was used as growth medium. Cells at passage number 2 were seeded into 6-well plates at a density of approximately 24![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cells per cm2 and 1.5 ml growth medium per well. Analysis was performed after 48 h incubation under either “normoxic” (21% oxygen) or “hypoxic” (5% oxygen) conditions in a standard cell culture incubator (HERAcell 240i, Thermo Scientific, Waltham, MA, USA). Cell numbers were determined by particle counting using ImageJ software (V 1.49f) on fluorescence images of ethanol fixated and DAPI (D8417, Sigma-Aldrich, St Louis, MO, USA) stained cell layers. Data was averaged from n = 3 individual wells and 6 images per well. The concentration of D-glucose and L-lactate in the culture supernatants was measured from n = 3 individual wells using the YSI 2700 Select Biochemistry Analyzer (YSI Incorporated, Yellow Springs, OH, USA).
000 cells per cm2 and 1.5 ml growth medium per well. Analysis was performed after 48 h incubation under either “normoxic” (21% oxygen) or “hypoxic” (5% oxygen) conditions in a standard cell culture incubator (HERAcell 240i, Thermo Scientific, Waltham, MA, USA). Cell numbers were determined by particle counting using ImageJ software (V 1.49f) on fluorescence images of ethanol fixated and DAPI (D8417, Sigma-Aldrich, St Louis, MO, USA) stained cell layers. Data was averaged from n = 3 individual wells and 6 images per well. The concentration of D-glucose and L-lactate in the culture supernatants was measured from n = 3 individual wells using the YSI 2700 Select Biochemistry Analyzer (YSI Incorporated, Yellow Springs, OH, USA).
The harvesting and metabolite extraction procedure for adherently growing cells was adapted from Dettmer et al., 2011.37 At the time point of sampling, the medium was aspirated and the cell layer washed three times with 1 mL of a PBS solution (4 °C). Finally, the cells were scraped in 2 mL ice-cold methanol (80% v/v methanol, 20% v/v water) with a cell scraper. The methanolic cell extracts were transferred to separate sample tubes and centrifuged at 4 °C and 20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000g for 5 min. The pellet, containing precipitated cellular protein and cell debris, was used for the determination of total protein content using 2-D Quant Kit (GE Healthcare, Little Chalfont, UK). For analysis by RPLC, aliquots of 400 μL of the methanolic extracts were dried in a GeneVac EZ-2 vacuum concentrator (GeneVac, Suffolk, UK) and reconstituted in 50 μL of LC-MS grade water prior to injection.
000g for 5 min. The pellet, containing precipitated cellular protein and cell debris, was used for the determination of total protein content using 2-D Quant Kit (GE Healthcare, Little Chalfont, UK). For analysis by RPLC, aliquots of 400 μL of the methanolic extracts were dried in a GeneVac EZ-2 vacuum concentrator (GeneVac, Suffolk, UK) and reconstituted in 50 μL of LC-MS grade water prior to injection.
2.3 RP-PGC-TOFMS
A two-dimensional liquid chromatography method coupled to time-of-flight mass spectrometry that provides both polar and non-polar selectivity38 (Table S2, ESI†) was the method of choice for the analysis of stem cell extracts, employing reversed-phase (RP-)LC in the first, and a porous graphitized carbon (PGC-) column in the second dimension. Analysis was carried out as described previously,38 with a minor modification: PGC column dimensions were 2.1 × 150 mm and 3 μm particle size. Samples were kept at 6 °C until injection and were analyzed in randomized order with intermittent injections of a standard-based quality control sample containing 90 intracellular metabolites. TOFMS analysis was performed on an Agilent 6230 LC-TOFMS system equipped with an Agilent Jet Stream interface. Ionization parameters were set as follows: 250 °C drying gas temperature, 12 L min−1 drying gas flow, 45 psig nebulizer pressure, 350 °C sheath gas temperature, 11 L min−1 sheath gas flow, 3500 V capillary voltage, 110 V fragmentor voltage. The TOF detector was operated in the low mass range (≤1700 m/z) in 2 GHz extended dynamic range mode with an acquisition rate of 3 spectra per second (4469 TOF transients per spectrum). Spectral data were recorded over a mass range of 50–1000 m/z.2.4 Data evaluation
TOFMS data of stem cell extracts was evaluated in a typical non-targeted workflow. Feature finding was performed via batch-recursive Molecular Feature Extraction (rMFE) in MassHunter Profinder (Agilent Technologies). The feature finding step also included the alignment of features across different samples via retention time and accurate mass. Furthermore, features were grouped into compounds considering chemical information (i.e. isotopologue signals, Na+ adducts and doubly-charged species). Further data filtering was performed in MassProfiler Professional 13.1 (Agilent Technologies, Santa Clara, CA, USA). After sample-specific scaling of all peak areas to the total protein content, only compounds occurring in 100% of samples in at least one experimental group with a coefficient of variation (CV) of less than 15% were considered for statistical analysis. Fold changes were calculated relative to samples from normoxic culture condition. A moderated t-test was performed in MassProfiler Professional 13.1 (Agilent Technologies). Scripts for bootstrap resampling and a Mann–Whitney U test were written in the statistical computing software R.3 Results and discussion
3.1 Measurement uncertainty in fold change determination
In non-targeted metabolomics, the quantity to be measured is the fold change (FC), a quantitative measure for changes in metabolite concentrations relative to a reference group. The fold change is calculated for a given metabolite as a simple ratio of group-averaged peak areas (metabolite intensities) A in two sample groups 1 and 2: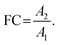 | (2) |
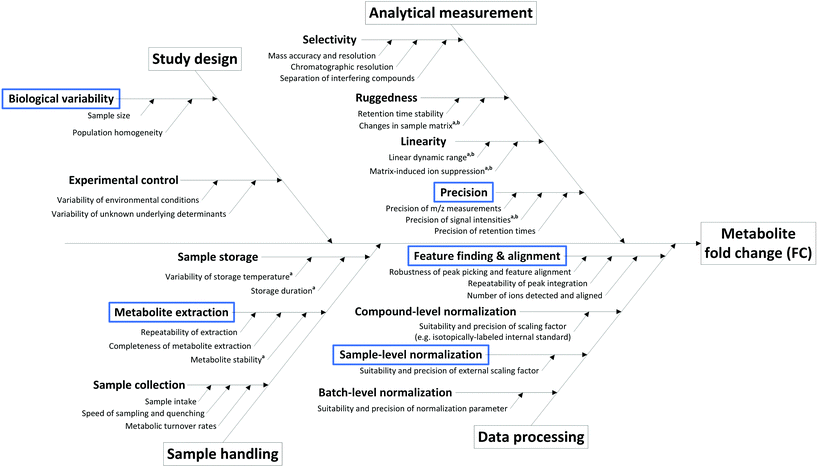
The sources of variation (and hence uncertainty) are manifold in metabolomics studies, arising from study design, sample collection and pre-treatment, sample storage, analytical measurement and even data processing (Fig. 1). Many of these critical aspects are assessed during the development and validation of methods suitable for metabolome analysis, where the minimization of their impact is the primary goal. Overall, only methods and procedures that fulfill important robustness criteria are suitable for application in non-targeted metabolomics as described here, and the following considerations are valid under the assumption that only such methods are employed. As such, we assume an ideal measurement according to the following criteria:
1. Chromatographic selectivity: resolution of interfering compounds and isobaric overlaps, separation from matrix compounds.
2. Retention time stability: max. 1% variation of retention times within a measurement series.
3. High-resolution mass spectrometry: >20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 mass resolution (FWHM), <5 ppm mass bias, mass axis stability.
000 mass resolution (FWHM), <5 ppm mass bias, mass axis stability.
4. Linear dynamic range: sufficient for the observed magnitude of changes in metabolite signals (typically 4–5 orders of magnitude).
State-of-the-art methods in non-targeted metabolomics routinely fulfill these criteria, so that the contribution of many factors shown in Fig. 1 can be omitted in uncertainty considerations based on the experimental conditions assumed here. However, additional factors intrinsic to the experimental layout contribute to uncertainty in the context of non-targeted metabolomics that do not originate from the measurement process. These aspects include the measured peak area (a), the use of an external scalar (s, e.g. the total protein content in the sample) for sample-specific normalization of peak areas, peak integration (i), recovery in metabolite extraction (r), and biological variability (b), and hence have to be considered in the estimation of the uncertainty of a fold change result, i.e. uncertainty budgeting.
Uncertainty budgeting is an essential part of analytical method validation and takes all sources of uncertainty within a given analytical workflow into account and expresses a total combined uncertainty for the final reported result value. Guidance on the evaluation of measurement uncertainty and the steps to be followed is available from the Joint Committee for Guides in Metrology (JCGM) in the Guide to the Expression of Uncertainty in Measurement (GUM).27 The initial steps include the definition of the quantity to be measured and a suitable model equation for its determination. Subsequently, all possible sources of uncertainty are identified and each input quantity is associated with the appropriate standard uncertainty. Finally, error propagation calculations based on the model equation are used to determine the combined uncertainty acting on the quantity to be measured, and the contributions of all input quantities are calculated. Applying an additional coverage factor, k, one can further state an expanded uncertainty with which the result is to be reported. A typical value for k is 2, and approximates a coverage probability of 95% for a single FC value under repeatability conditions.27
The standard uncertainties associated to each contributor included in the model equation are in practice derived from repeatability data (type A uncertainty), or reference data and known performance characteristics (type B uncertainty). In the context of metabolomics, appropriate repeatability data that allows the separate evaluation of a single contributor is in many instances difficult to obtain. Here, the standard uncertainties associated with extraction recovery (metabolite-specific), peak integration (manual or automated), total protein content determination and general biological variability are therefore estimated from typical observations and experience (Table 2). The model equation for FC calculation is formulated as follows, with the contributors i, r, and b considered as factors with a value of 1:
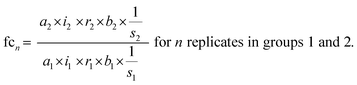 | (3) |
| Abbr. | Input quantity | Input type | Standard uncertainty | Distribution |
|---|---|---|---|---|
| a | Peak area | Measured data | — | Poisson |
| i | Peak integration | Factor | 3% | Triangular |
| r | Extraction recovery | Factor | 5% | Normal |
| s | External scalar | Measured data | 5% | Normal |
| b | Biological variability | Factor | 15% | Normal |
The final fold change value is then calculated as the average across n replicate observations:
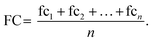 | (4) |
The Monte-Carlo simulation method was used for the calculation of the total combined uncertainty, as described in Appendix E.3 of the Eurachem guide Quantifying Uncertainty in Analytical Measurement (QUAM).39 This approach allows the propagation of uncertainties with an associated probability density function (PDF, e.g. normal, triangular or rectangular distribution), by random sampling of a single value for each input quantity from its PDF. When repeated for a large number of iterations (105–106), a set of simulated results for the quantity to be measured is obtained. From the frequency distribution of these results, the mean and standard deviation can be derived as estimates of the quantity to be measured and its total combined uncertainty. Notably, this process only takes random errors into account. Fig. 2 shows the uncertainty budget and simulation results for the amino acid arginine as a model compound and a fold change determined across two differently-treated sample groups with 5 biological replicates each. The mean of the output distribution (Fig. 2a) is an estimate for the fold change, and its standard deviation is the corresponding total combined uncertainty. The expanded uncertainty UFC is then derived using a coverage factor k = 2, as an approximation of the 95% confidence interval given a normal distribution of FC simulation results (Fig. 2a). As such, the FC for arginine can be reported as 1.20 ± 0.26 (21.7% relative expanded uncertainty).
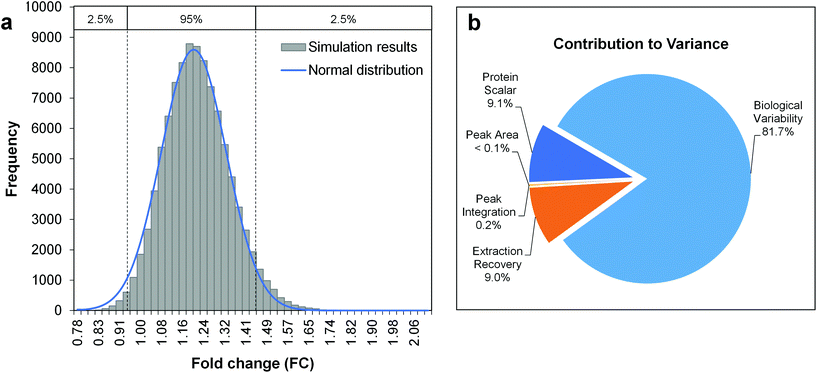 | ||
Fig. 2 Uncertainty budgeting using Monte Carlo simulations for the estimation of the total combined uncertainty of a metabolite fold change (model metabolite arginine). The model equation is given by eqn (3) and (4), considering the input quantities given in Table 2. a. Histogram of Monte Carlo simulation results (100![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 iterations), b. Pie chart with the relative contributions of the individual input quantities to the overall variance in simulation results. 000 iterations), b. Pie chart with the relative contributions of the individual input quantities to the overall variance in simulation results. | ||
Although uncertainty budgeting as an exhaustive approach provides a comprehensive view on the final quantity result, it also becomes relatively complex and time-consuming when multiple calculations need to be performed. The latter is the case in non-targeted metabolomics, where individual fold change values need to be calculated for several hundreds of metabolites, which essentially requires automatization.
3.2 Simplified uncertainty propagation calculations for large-scale application
Stringent uncertainty budgeting and a separation of uncertainty contributions as described above is comprehensive, but also relatively time-consuming when applied in the analysis of large data sets. As an alternative, the approach can be simplified by treating the experimental standard deviation of metabolite intensities within a group as a type A-summarized standard uncertainty. In this concept, the standard uncertainty can contain contributions from several sources of uncertainty, allowing a reduction in the number of individual input quantities in the model equation. As such, the model equation for FC determination can be simplified to the initial form of eqn (2) as a simple ratio of group-averaged metabolite intensities, each with an associated standard uncertainty (approximated by the experimental standard deviation) that is considered to contain contributions from all factors described in Table 2. Furthermore, the numerical implementation of uncertainty estimation can be simplified using the Kragten spreadsheet method28 (Table 1), based on classical error propagation (eqn (1)). The results are stated as an expanded uncertainty UFC, considering a coverage factor k of 2 to reflect a coverage probability of approximately 95%.27 Overall, UFC can be derived as follows using only two inputs: group-averaged metabolite intensities A and their standard uncertainties SU(A) approximated by the experimentally observed within-group standard deviations: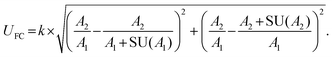 | (5) |
Applying this approach to the above-described example of the amino acid arginine, an expanded uncertainty of 0.25 is calculated, and the fold change for arginine can be reported as 1.20 ± 0.25 (20.8% relative expanded uncertainty). The fact that this is in very good agreement with the expanded uncertainty estimated by uncertainty budgeting (see above) demonstrates the validity of the simplified uncertainty propagation approach based on type A-summarized standard uncertainties. Thus, the approach is ideally suited for large-scale implementation in non-targeted metabolomics, as the calculations are easily automatized using eqn (5) in a spreadsheet layout and can be readily implemented in standard data analysis pipelines.
3.3 Verifying the relevance of FC findings via minimum relevant fold changes
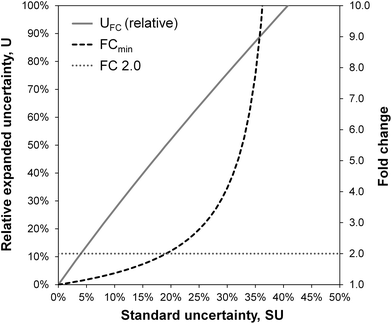
The uncertainty of fold changes is a direct result of experimental precision and within-group variation (Fig. 3). Notably, FC uncertainty is independent of the actual size of the FC. This implies that error propagation affects small FC values to a greater extent than large FC values, and that the detection of small fold changes requires a much lower level of within-group variation (resulting from biological and technical variability).The actual question at hand in statistical differential analysis in non-targeted metabolomics is to determine whether a given observed effect in the form of an FC value is significantly different from a FC of 1 (indicating no change). To this end, the expanded relative uncertainty UFC can be used to derive a minimum FC value (FCmin) that can be distinguished from FC = 1 within uncertainty. In other words, FCmin represents a minimum factor by which a metabolite's signal intensity must change from one group to another in order to be recognized as a relevant difference, given a certain degree of data variation. This value of FCmin can be determined from the relative expanded uncertainty using the following simple equation, where UFC is the expanded uncertainty relative to the FC:
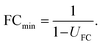 | (6) |
The resulting minimum relevant fold changes rapidly increase with higher observed standard uncertainty of the group-averaged metabolite intensities (Fig. 3), so that the commonly used fold change threshold of 2 only holds true when the within-group variation is below 20%.
The information obtained from determining FCmin is somewhat complementary to traditional significance testing such as t-test procedures, where the p-value expresses the probability that an effect with a t statistic of this magnitude or greater could have occurred, assuming that there is no difference in the two sample groups (null-hypothesis significance testing). In contrast to classical statistical differential analysis, our uncertainty propagation approach focuses on the size of the observed effect, and aims to support decision-making regarding its relevance. As such, FCmin is probably most useful as an additional parameter with a message complementary to p-value-based statistical significance decisions. The p-value alone, being an abstract statistical metric with a very specific meaning, does not provide information on whether a fold change of a given magnitude exceeds within-group data variation – an aspect that is especially important given the often high noise level in metabolomics data. Alternative parameters with a better reflection of data reality are therefore needed. To this end, FC uncertainty propagation and FCmin validate effect magnitude with respect to the observed data variation, and serve directly as a basis for determining the relevance of a given observation. Importantly, using FCmin as a threshold value is possible for each compound individually within minimal calculation times, thereby overcoming concerns associated with the use of global metabolome-wide cut-offs. Nevertheless, global FC cut-offs for a given data set can be defined using the average of observed within-group variations and serve as the basis for early decisions about the quality of a data set.
To date, the variability of fold changes in large data sets is estimated using bootstrap resampling.40 In this approach, a large number of samples (typically 103) are generated from replicate data points by random sampling with replacement. The fold change is then calculated from each of these bootstrap samples. The resulting population of fold change values can then be used to derive an estimate for the FC from the mean, and its error interval from the 95% confidence interval of the PDF underlying the population of bootstrapped FC values. When a large number of samples is available, this approach indeed provides a good coverage of the apparent variability in the data set. When the number of samples is small, however, this approach is unreliable, as the random sampling with replacement allows repetitions of the same value in the same bootstrap sample, which becomes more likely with decreasing sample size. Furthermore, this procedure samples from a discrete population of observations which, in combination with the repetition problem, leads to an underestimation of FC variability in small data sets. This is demonstrated in a direct comparison of 95% confidence intervals derived by bootstrap resampling and the expanded uncertainty as derived by the herein proposed uncertainty propagation method in Fig. S1 (ESI†). In contrast to bootstrap resampling, uncertainty propagation approximates the sample data by a continuous distribution described by the average metabolite intensities as the group means and the corresponding experimental standard uncertainties as standard deviations. This implies that a PDF is imposed on the sample data (here: normal distribution), which can be difficult to define for such small sample sizes. However, this procedure provides a better reflection of data reality and – at least for small samples – more meaningful error intervals.
3.4 Case study on the intracellular metabolome of mesenchymal stem cells
Non-targeted metabolomics applications are as diverse as the metabolome itself, but the underlying general concepts addressed in this paper apply independent of the specific application. The following case study represents a typical example for a cell culture-based metabolomics study with a small sample size.Adipose-derived human mesenchymal stem cells show promise in tissue engineering for regenerative medicine applications,41,42 and extensive research is ongoing with respect to controlling culture conditions as similar as possible to actual physiological conditions. In this proof-of-concept study, adherent stem cell cultures were subjected to either normoxic or hypoxic culture condition (n = 5, each) for 48 h before sampling, and the cell extracts were analyzed by RP-PGC-TOFMS.38 In a previous study, this online two-dimensional LC method was shown to provide excellent retention time repeatability precision and broad coverage of both polar and non-polar metabolites without the use of ion pairing reagents (Table S2, ESI†). Due to the extended selectivity of this approach, less matrix interference and co-elution can be expected, and high repeatability precision for retention times and peak areas is routinely achieved. The samples were further characterized by several parameters related to cell culture (Table S3, ESI†), all of which reflect the tightly controlled experimental conditions. Overall, all methods in use have been characterized with respect to repeatability precision and fitness for purpose. A QC sample (standard-based, containing 90 intracellular metabolites) was analyzed repeatedly throughout the total measurement time of 16 h, and the observed peak areas were stable within on average less than 10% RSD, hence verifying the stability of the analytical system and appropriate sample storage. After feature finding, alignment and normalization to the total protein content per sample, the resulting positive mode MS data set comprised 248 compounds with a coefficient of variation (CV) below 15% (n = 5). The fold changes observed for these compounds were small, with maximum values of −1.49 for down-regulated, and +1.48 for up-regulated compounds. The detection of such relatively small changes in metabolite levels is in practice complicated by the often high variability in metabolomics data resulting from many sources of uncertainty (Fig. 1), and careful evaluation is necessary.
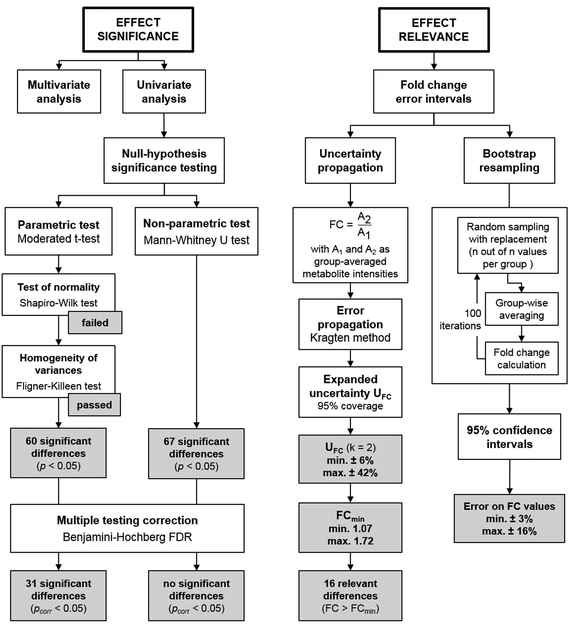
Fig. 4 gives an overview on typical data analysis strategies in non-targeted metabolomics, targeting either effect significance or effect relevance, and selected results from the case study. A moderated t-test revealed a significant outcome (pcorr < 0.05) for 31 compounds, although the underlying assumption of normally distributed data could not be verified in a prior test (Shapiro–Wilk test). In contrast, the Mann–Whitney U test, the non-parametric alternative that does not assume normal distribution, found no compounds with a significant difference between the two sample groups after correction for multiple hypotheses testing (Benjamini–Hochberg FDR, pcorr < 0.05). However, the power of statistical tests on this data set may be limited due to the small sample size. The aspect of effect relevance is best viewed from the perspective of the fold change as a point estimate, complemented by an error interval reflecting its uncertainty. The commonly used method of bootstrap resampling revealed comparably small error intervals for the FC values in this data set (±3–±16%). As discussed above, the bootstrap resampling process is of limited power for such small data sets, as it simulates an erroneously narrow population. This becomes apparent in a direct comparison of bootstrap resampling with the herein proposed approach of uncertainty propagation for the compounds in the case study data set (Fig. S1, ESI†). Uncertainty propagation revealed relative expanded uncertainties of between ±6% and ±42%. Accordingly, the compound-specific minimum relevant fold changes FCmin lie between 1.07 and 1.72. This threshold value is exceeded for a total of 16 compounds. Interestingly, 15 of these compounds were also found statistically significant in the moderated t-test with pcorr < 0.05.
Strikingly, a comparison between FCmin and the observed FC values for the 31 compounds identified to be statistically significant in the moderated t-test reveals that 16 out of the 31 compounds do not exceed the FCmin threshold (Table S4, ESI†). Thus, these should not be considered relevant findings, despite their statistical significance as judged by the p-value. This is not surprising, since the p-value was not designed to provide information on this aspect. Hence, this represents yet another argument on why the p-value alone is not a suitable metric to describe and judge findings in non-targeted metabolomics when sample sizes are small, as is often the case in studies on model systems. However, despite all its shortcomings the p-value can still be considered a very useful parameter when used in combination with valid test procedures (e.g. parametric vs. non-parametric tests). Rather than intending to dismiss statistical significance testing, we therefore suggest that uncertainty propagation is implemented as a complementary tool in data evaluation.
Whether the combined information described above indicates a significant and relevant difference in intracellular metabolic profiles of mesenchymal stem cells, induced specifically by the change in oxygen tension, remains to be elucidated by further experiments that were not within the scope of demonstrating the technical feasibility in this study. Despite this and other examples for well-controlled metabolomics data sets, we emphasize that thorough investigations of non-targeted metabolomics practice are needed to allow the high expectations for the generation of biological knowledge to be met reliably.
4 Conclusion
The here-in presented concept circumvents several concerns associated with common null-hypothesis significance testing and data interpretation based on p-values, especially in the case of studies with a small sample size. The FC value itself qualifies as a point estimate of the difference in the investigated populations. The proposed approach of uncertainty propagation adds to this by delivering an expanded uncertainty for each FC value that approximates a 95% coverage probability given the within-group variation of measured metabolite intensities. Thus, this concept is in line with the recently promoted use of estimation statistics in the interpretation of differential studies19 and adds to the ongoing debate over the use of p-values and confidence intervals.44–46 Instead of reducing study findings to dichotomous scale, the focus on the FC and its uncertainty is a better reflection of modern quantitative biology, in that it addresses and validates the magnitude of the observed effects. A similar motivation gave rise to a method proposed by Jung et al. for the assessment of the biological relevance of selected genes in microarray experiments, where FC values are associated with an adjusted confidence interval and further classified based on the location of this confidence interval relative to a relevance threshold in order to assist biological interpretation.47The quantification of FC uncertainty is not only helpful for the immediate interpretation of FC data, but also offers the necessary information for relevance decisions. FC uncertainty considerations are also relevant for guiding the choice and improvement of methods for non-targeted metabolomics studies by allowing the definition of a target uncertainty43 that the method needs to comply with in order to allow finding effects of the expected magnitude.
To our knowledge, it is the first time that error propagation and fold change uncertainty in non-targeted metabolomics are systematically assessed based on available official guidelines. The practical relevance for routine non-targeted metabolomics is demonstrated using the example of mesenchymal stem cells. The observed differences between the sample groups from normoxic and hypoxic culture were minor, and high-precision methods were necessary in order to obtain useful information. While technically feasible, it is ultimately up to the operator to decide whether small effect sizes are considered biologically relevant. However, due to the highly dynamic nature and quick adaptation of cellular metabolism, subtle changes can contain information of high biological relevance and might be overlooked when fold change uncertainty is not considered and optimized.
Acknowledgements
This work was funded by the European Association of National Metrology Institutes (EURAMET, Project HLT05-REG4) and the Austrian Science Fund (FWF): FWF P26603 and FWF W1224 Doctoral Program BioToP – Biomolecular Technology of Proteins. Wirtschaftsagentur Wien and EQ BOKU VIBT GmbH are gratefully acknowledged for funding mass spectrometry instrumentation.References
- N. Guan, J. Li, H. Shin, J. Wu, G. Du, Z. Shi, L. Liu and J. Chen, Metabolomics, 2014, 11, 1106–1116 CrossRef.
- M. G. López, M. I. Zanor, G. R. Pratta, G. Stegmayer, S. B. Boggio, M. Conte, L. Bermúdez, C. C. Leskow, G. R. Rodríguez, L. A. Picardi, R. Zorzoli, A. R. Fernie, D. Milone, R. Asís, E. M. Valle and F. Carrari, Metabolomics, 2015, 11, 1416–1431 CrossRef.
- C. A. Sellick, A. S. Croxford, A. R. Maqsood, G. Stephens, H. V. Westerhoff, R. Goodacre and A. J. Dickson, Biotechnol. Bioeng., 2011, 108, 3025–3031 CrossRef PubMed.
- B. Wang, J. Liu, H. Liu, D. Huang and J. Wen, J. Ind. Microbiol. Biotechnol., 2015, 42, 949–963 CrossRef PubMed.
- M. Xia, D. Huang, S. Li, J. Wen, X. Jia and Y. Chen, Biotechnol. Bioeng., 2013, 110, 2717–2730 CrossRef PubMed.
- R. González-Domínguez, T. García-Barrera, J. Vitorica and J. L. Gómez-Ariza, Metabolomics, 2015, 11, 1175–1183 CrossRef.
- S. F. Graham, O. P. Chevallier, C. T. Elliott, C. Hölscher, J. Johnston, B. McGuinness, P. G. Kehoe, A. P. Passmore and B. D. Green, PLoS One, 2015, 10, e0119452 Search PubMed.
- B. Li, B. Qiu, D. S. M. Lee, Z. E. Walton, J. D. Ochocki, L. K. Mathew, A. Mancuso, T. P. F. Gade, B. Keith, I. Nissim and M. C. Simon, Nature, 2014, 513, 251–255 CrossRef PubMed.
- E. G. Armitage and C. Barbas, J. Pharm. Biomed. Anal., 2014, 87, 1–11 CrossRef PubMed.
- Y. Lu, C. Huang, L. Gao, Y.-J. Xu, S. E. Chia, S. Chen, N. Li, K. Yu, Q. Ling, Q. Cheng, M. Zhu, M. Chen and C. N. Ong, Metabolomics, 2015, 1–13 Search PubMed.
- J. Xia, D. I. Broadhurst, M. Wilson and D. S. Wishart, Metabolomics, 2012, 9, 280–299 CrossRef PubMed.
- H. Link, T. Fuhrer, L. Gerosa, N. Zamboni and U. Sauer, Nat. Methods, 2015, 12, 1091–1097 Search PubMed.
- I. Martínez-Arranz, R. Mayo, M. Pérez-Cormenzana, I. Mincholé, L. Salazar, C. Alonso and J. M. Mato, J. Proteomics, 2015, 127(Part B), 275–288 CrossRef PubMed.
- P. S. Gromski, H. Muhamadali, D. I. Ellis, Y. Xu, E. Correa, M. L. Turner and R. Goodacre, Anal. Chim. Acta, 2015, 879, 10–23 CrossRef PubMed.
- E. Saccenti, H. C. J. Hoefsloot, A. K. Smilde, J. A. Westerhuis and M. M. W. B. Hendriks, Metabolomics, 2013, 10, 361–374 Search PubMed.
- J. Cohen, Am. Psychol., 1994, 49, 997–1003 CrossRef.
- R. E. Kirk, Educ. Psychol. Meas., 2001, 61, 213–218 CrossRef.
- R. S. Nickerson, Psychol. Methods, 2000, 5, 241–301 CrossRef PubMed.
- A. Claridge-Chang and P. N. Assam, Nat. Methods, 2016, 13, 108–109 CrossRef PubMed.
- R. L. Wasserstein and N. A. Lazar, Am. Stat., 2016, 70, 129–133 CrossRef.
- J. J. Vaske, J. A. Gliner and G. A. Morgan, Hum. Dimens. Wildl., 2002, 7, 287–300 CrossRef.
- G. M. Sullivan and R. Feinn, J. Grad. Med. Educ., 2012, 4, 279–282 CrossRef PubMed.
- L. G. Halsey, D. Curran-Everett, S. L. Vowler and G. B. Drummond, Nat. Methods, 2015, 12, 179–185 CrossRef PubMed.
- L. C. Lazzeroni, Y. Lu and I. Belitskaya-Lévy, Nat. Methods, 2016, 13, 107–108 CrossRef PubMed.
- F. L. Schmidt, Am. Psychol., 1992, 47, 1173–1181 CrossRef.
- B. Thompson, J. Psychol., 1999, 133, 133–140 CrossRef.
- JCGM 100:2008, Evaluation of measurement data – Guide to the expression of uncertainty in measurement (GUM), Bureau International des Poids et Mesures (BIPM), 2010, http://www.bipm.org Search PubMed.
- J. Kragten, Analyst, 1994, 119, 2161–2165 RSC.
- B. Magnusson and U. Örnemark, Eurachem Guide: The Fitness for Purpose of Analytical Methods - A Laboratory Guide to Method Validation and Related Topics, Eurachem guide MV, 2014 Search PubMed.
- S. Naz, M. Vallejo, A. García and C. Barbas, J. Chromatogr. A, 2014, 1353, 99–105 CrossRef PubMed.
- R. Goodacre, D. Broadhurst, A. K. Smilde, B. S. Kristal, J. D. Baker, R. Beger, C. Bessant, S. Connor, G. Capuani, A. Craig, T. Ebbels, D. B. Kell, C. Manetti, J. Newton, G. Paternostro, R. Somorjai, M. Sjöström, J. Trygg and F. Wulfert, Metabolomics, 2007, 3, 231–241 CrossRef.
- O. Fiehn, D. Robertson, J. Griffin, M. van der Werf, B. Nikolau, N. Morrison, L. W. Sumner, R. Goodacre, N. W. Hardy, C. Taylor, J. Fostel, B. Kristal, R. Kaddurah-Daouk, P. Mendes, B. van Ommen, J. C. Lindon and S.-A. Sansone, Metabolomics, 2007, 3, 175–178 CrossRef.
- R. M. Salek, S. Neumann, D. Schober, J. Hummel, K. Billiau, J. Kopka, E. Correa, T. Reijmers, A. Rosato, L. Tenori, P. Turano, S. Marin, C. Deborde, D. Jacob, D. Rolin, B. Dartigues, P. Conesa, K. Haug, P. Rocca-Serra, S. O'Hagan, J. Hao, M. van Vliet, M. Sysi-Aho, C. Ludwig, J. Bouwman, M. Cascante, T. Ebbels, J. L. Griffin, A. Moing, M. Nikolski, M. Oresic, S.-A. Sansone, M. R. Viant, R. Goodacre, U. L. Günther, T. Hankemeier, C. Luchinat, D. Walther and C. Steinbeck, Metabolomics, 2015, 11, 1587–1597 CrossRef PubMed.
- D. Trutschel, S. Schmidt, I. Grosse and S. Neumann, Metabolomics, 2014, 11, 851–860 CrossRef.
- J.-C. Martin, M. Maillot, G. Mazerolles, A. Verdu, B. Lyan, C. Migné, C. Defoort, C. Canlet, C. Junot, C. Guillou, C. Manach, D. Jabob, D. J.-R. Bouveresse, E. Paris, E. Pujos-Guillot, F. Jourdan, F. Giacomoni, F. Courant, G. Favé, G. L. Gall, H. Chassaigne, J.-C. Tabet, J.-F. Martin, J.-P. Antignac, L. Shintu, M. Defernez, M. Philo, M.-C. Alexandre-Gouaubau, M.-J. Amiot-Carlin, M. Bossis, M. N. Triba, N. Stojilkovic, N. Banzet, R. Molinié, R. Bott, S. Goulitquer, S. Caldarelli and D. N. Rutledge, Metabolomics, 2014, 1–15 Search PubMed.
- P. Rocca-Serra, R. M. Salek, M. Arita, E. Correa, S. Dayalan, A. Gonzalez-Beltran, T. Ebbels, R. Goodacre, J. Hastings, K. Haug, A. Koulman, M. Nikolski, M. Oresic, S.-A. Sansone, D. Schober, J. Smith, C. Steinbeck, M. R. Viant and S. Neumann, Metabolomics, 2015, 12, 1–13 Search PubMed.
- K. Dettmer, N. Nürnberger, H. Kaspar, M. A. Gruber, M. F. Almstetter and P. J. Oefner, Anal. Bioanal. Chem., 2011, 399, 1127–1139 CrossRef PubMed.
- K. Ortmayr, S. Hann and G. Koellensperger, Analyst, 2015, 140, 3465–3473 RSC.
- Eurachem/CITAC guide: Quantifying Uncertainty in Analytical Measurement, ed. S. L. R. Ellison and A. Williams, 3rd edn, 2012, ISBN 978-0-948926-30-3. Available from http://www.eurachem.org Search PubMed.
- J. Carpenter and J. Bithell, Stat. Med., 2000, 19, 1141–1164 CrossRef PubMed.
- A. Hilfiker, C. Kasper, R. Hass and A. Haverich, Langenbecks Arch. Surg., 2011, 396, 489–497 CrossRef PubMed.
- L.-P. Kamolz, M. Keck and C. Kasper, Stem Cell Res. Ther., 2014, 5, 62 CrossRef PubMed.
- R. Bettencourt da Silva and A. Williams, Eurachem/CITAC Guide: Setting and Using Target Uncertainty in Chemical Measurement, Eurachem/CITAC guide STMU, 2015 Search PubMed.
- W. Huber, Nat. Methods, 2016, 13, 607–607 CrossRef PubMed.
- L. G. Halsey, D. Curran-Everett and G. B. Drummond, Nat. Methods, 2016, 13, 606–606 CrossRef PubMed.
- J. van Helden, Nat. Methods, 2016, 13, 605–606 CrossRef PubMed.
- K. Jung, T. Friede and T. Beißbarth, BMC Bioinf., 2011, 12, 288 CrossRef PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c6an01342b |
| This journal is © The Royal Society of Chemistry 2017 |