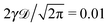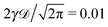Anomalous diffusion in time-fluctuating non-stationary diffusivity landscapes
Received
8th May 2016
, Accepted 8th August 2016
First published on 8th August 2016
Abstract
We investigate the ensemble and time averaged mean squared displacements for particle diffusion in a simple model for disordered media by assuming that the local diffusivity is both fluctuating in time and has a deterministic average growth or decay in time. In this study we compare computer simulations of the stochastic Langevin equation for this random diffusion process with analytical results. We explore the regimes of normal Brownian motion as well as anomalous diffusion in the sub- and superdiffusive regimes. We also consider effects of the inertial term on the particle motion. The investigation of the resulting diffusion is performed for unconfined and confined motion.
I. Introduction
The diffusion of a tracer particle is typically characterised in terms of the mean squared displacement (MSD)| | 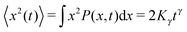 | (1) |
corresponding to the second moment of the probability density function P(x,t) to find the particle at position x at time t. When the exponent γ = 1 the law (1) describes normal Brownian diffusion, otherwise we speak of anomalous diffusion. In the latter case, the generalised diffusion coefficient Kγ has the physical dimensions cm2 s−γ, and we distinguish subdiffusion (0 < γ < 1) and superdiffusion (γ > 1) depending on the value of the anomalous diffusion exponent γ.1
Following a surge in microscopic techniques, diffusive phenomena of passive tracer particles can now be monitored at unprecedented resolution.2 Thus, for instance, the hydrodynamic backflow effects of a Brownian particle could be directly probed.3 Even more remarkable is the rapidly growing number of experimental evidence for anomalous diffusion in dense fluids4 as well as in living biological cells.5–10 The motion of various endogenous and artificial tracers in live cells was shown to be subdiffusive.11–13 However, when active dynamics such as driving by molecular motors or cytoplasmic streaming are involved, superdiffusion may also be observed.14 Massive computer simulations of pure and protein-crowded lipid bilayer membranes demonstrate transient anomalous diffusion of both lipids and proteins, the crossover to normal diffusion being delayed with increasing disorder.15,16 In the membranes of living cells anomalous diffusion is even observed on macroscopic time scales.17–19 As a general physical principle for anomalous diffusion various form of crowding of the environment are considered.20–22 We note that anomalous diffusion also occurs on the level of entire organisms, such as the subdiffusion of bacteria cells in biofilms23 or the superdiffusion of hydra or protozoa.24
Several additional studies of crowded in vitro systems demonstrate the existence of non-Fickian and/or non-Gaussian motion, for instance the glassy dynamics in membrane domains,25 confined diffusion of water molecules in soft environments,26 polymer diffusion on nanopillar-structured surfaces,27 intermittent molecular hopping on solid–liquid interfaces,28 diffusion of colloidal spheres in dense crowded suspensions29 and glasses,30,31 particle diffusion in porous media with heterogeneous and position-dependent mobilities,32 and the transport of contaminants in porous and fractured geological formations.33 Concurrently the existence of anomalous yet Brownian diffusion—a linear time dependence of the MSD (1) accompanied by significantly non-Gaussian (exponential or stretched exponential) probability density P(x,t)—was demonstrated for the motion of colloidal beads along linear phospholipid bilayer tubes,34,35 particle dynamics in hard sphere colloidal suspensions,36 and the diffusion of nanoparticles in nanopost arrays.37
Brownian motion is bound to the Gaussian shape of the probability density function by the spell of the central limit theorem and thus fully characterised by the second moment (1). In contrast, anomalous diffusion dynamics is inherently non-universal, and therefore a large variety of anomalous diffusion models exists (also with non-Gaussian probability densities), depending on the exact physical circumstances defining the dynamics.1,5,7–10 To name but a few of these anomalous diffusion processes we recall continuous time random walks with scale free trapping time distributions38 and a potential additional noise source,39 general trapping models,40 correlated diffusion processes,41,42 fractional Brownian motion43 and generalised Langevin equation motion,43–46 as well as diffusion in disordered media and on fractal structures.47–49
Here we focus on models based on randomly and/or deterministically varying diffusion coefficients which have recently been under intense study. We show that when the diffusion coefficient varies randomly such that its distribution has a finite width, normal diffusion emerges in the long time limit. We analyse these random diffusion processes (RDPs) in terms of the MSD and time averaged MSD (typically evaluated in single particle tracking and simulations studies), for both unconfined and confined diffusion. In addition, we quantify the degree of randomness between different individual trajectories.
In Section II we provide a concise overview of heterogeneous diffusion processes, followed by a definition of the various observables in Section III. In Section IV we present the details of the specific model investigated here and the numerical scheme used to simulate the RDPs. We then present the main results of our calculations for the ensemble averaged MSD, time averaged MSD, probability distribution function P(x,t), and the ergodicity breaking parameter of RDPs in Sections V and VI, respectively, for massless and massive particles. We consider the situation both in the absence and in the presence of an external confinement. Section VII summaries our findings and discusses their possible applications and generalisations.
II. Heterogeneous mobility: models and examples
A. Random diffusivity models
For massless particles the study of normal and anomalous diffusion in the presence of random diffusivity fields recently attracted considerable attention.19,50–53 Several models assume that the instantaneous diffusion coefficient D is governed by a steady state distribution p(D) in an annealed fashion, that is, the instantaneous value of D is independent of the actual particle position x. Particular attention received the idea of a diffusing diffusivity introduced by Chubynsky and Slater.51 They assume an exponential distribution| | p(D) = D0−1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp[−D/D0] exp[−D/D0] | (2) |
and weigh the standard Gaussian P(x,D,t) = (4πDt)−1/2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−x2/[4Dt]) with this function,
exp(−x2/[4Dt]) with this function, 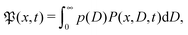 to obtain the exponential probability distribution function (PDF)
to obtain the exponential probability distribution function (PDF)| | 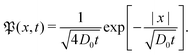 | (3) |
The characteristic decay length of this PDF grows with the diffusion time as ≃t1/2,51 but the MSD grows linearly with time, that is, follows eqn (1) with γ = 1 and Kγ = D0.51 Other than exponential diffusivity distributions—for instance, power-law forms of p(D)—were shown to lead to subdiffusive and non-ergodic MSD behaviour.50 After the current manuscript was submitted, the authors became aware of the simulation-based study54 of particle diffusion in rough energy landscapes with both Gaussian and Gamma distributed local energy values.
Dynamical heterogeneities—as reflected in the above assumption of a random diffusivity—are considered a characteristic property of systems such as supercooled or glassy liquids.52,55–58 Quite broad distributions of particle diffusivities were detected in a number of living systems, for instance, for the motion of pathogen receptors on two dimensional cell membranes19 (see also ref. 59), the motion of Cajal bodies in eukaryotic nuclei,60 one dimensional diffusion of repressor proteins on the DNA,61 and for the motion of proteins along the corrugated landscape created by the DNA sequence.62,63 In these systems, the inherent stochasticity of the diffusive properties of a tracer particle as well as the heterogeneities of its environment contribute to the observed distribution of diffusivities subsumed in the distribution p(D).
The reader is particularly referred to the characterisation of the dynamical spreading of a population of nematode worms, both in homogeneous and heterogeneous environments.64 Other examples of living systems with diffusing individuals obeying non-Gaussian distributions of diffusivities, speeds of motion v, or turning angles are also mentioned in this study. Hapca et al.64 state that the anomalous diffusion monitored in the heterogeneous populations of worms can be solely due to fat-tailed, e.g., Gamma distributed65 forms of diffusivities, while the motion of each individual remains Brownian. This study served as a strong biological motivation for us in trying to unveil the properties of particle diffusion with a given time dependent form of p(D,t).
Also note that fat-tailed leptokurtic distribution of particle mobilities—often occurring in population of individuals of a species—can ensure a facilitation of their colonial invasion,64 as compared to the standard Brownian diffusion law of spreading. Such skewed distributions p(D) or p(v) (of the particle speeds) can originate from medium heterogeneities when the organisms explore different regions of space with different mobilities. The notion of fat-tailed distributions and faster than standard front propagation emerges also in long-distance dispersal of plants66,67 and pollen,68 in patterns of fish movements,69 as well as in rare event driven spreading of plant pathogens.70
B. Deterministic variation of the diffusivity with position or time
Following experimental observations of deterministic gradients of the local diffusivity in both pro- and eukaryotic cells71,72 and the existence of thermal gradient conditions,73 the model of heterogeneous diffusion processes (HDPs) with a power-law, exponential, and logarithmic form for D(x) was recently introduced by the authors;74–76 see also ref. 77–80. These Markovian processes based on a Langevin description with multiplicative noise exhibit anomalous diffusion and weak ergodicity breaking.74–76 The latter emerges due to the fact that even in the limit of long trajectories time and ensemble averages of physical observables do not coincide,6,8 see below. Models with a power-law time dependenceof the diffusivity exist, the so-called scaled Brownian motion (SBM).8,81–87 SBM was originally introduced by Batchelor in the description of Richardson turbulence.88 Note that in the context of such highly non-stationary processes the degree of ergodicity breaking is controlled via introducing a time- or length-dependent scale into the problem.45,89 A combined space-time diffusivity dependence of the form D(x,t) ≃ |x|βtα−1 was also investigated.90–92 Aged and confined versions of these processes were recently considered as well.76,93 Here ageing refers to the explicit dependence of the process on the overall time span of its evolution, as expected for non-stationary processes. The limiting cases with scaling exponent β → 2 for HDPs and α → 0 for SBM were shown to lead, respectively, to an ultrafast (exponential) and ultraslow (logarithmic) MSD growth with time.94–96
C. Massless versus massive particles
For massive particles, the situation in anomalous diffusion is often less clear. While the underdamped limit of standard Brownian motion97 and of fractional Langevin equation motion46 are well understood, for other anomalous diffusion processes these limits and general solutions are just emerging. In particular, for SBM it was recently shown that the long time limit of underdamped motion (including the inertia term) in general does not correspond to the overdamped limit of the same motion.98 Also, the recent study99 addresses a giant particle diffusion in the underdamped limit with a temperature dependent diffusion coefficient and in the presence of a bias.
One purpose of the current study is to investigate RDPs for massive and massless particles. A growing interest in the diffusive behaviour of tracked particles combined with the unprecedented precision of experimental observations, in particular, at short times for the diffusion of small particles in living cells,100 pose a need for the development of new and more flexible models of stochastic processes. Thus, a larger pool of theoretical models is necessary for quantitative descriptions of these systems, with possibly fewer number of model parameters.
Some implications of a finite particle mass for diffusion processes with position dependent diffusivity of the form D(x) ≃ |x|β were recently examined.101 The reader is also referred to the studies102,103 regarding the inertial Langevin dynamics in media with space inhomogeneous friction, and conventions of how to interpret the associated multiplicative stochastic equation as well as the existence of fluctuation–dissipation relations for such systems. In what follows, we refer to the diffusion coefficient D as to local variable in space and time, rather as to a long time asymptote of the Einstein relation, see the discussion in ref. 103.
III. Observables of diffusion processes
Anomalous diffusion processes can be classified by the MSD diffusion exponent γ. In single particle tracking and simulations studies garnering few but long individual time series x(t) of the particle position the time averaged MSD6,8| | 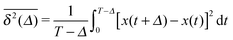 | (5) |
is typically employed. Here T is the total length of the trajectory (observation time) and Δ is the lag time. Note that while the ensemble averaged MSD (1) is a spatial average at a particular time instant t, the time averaged MSD (5) for any given lag time Δ is taken over the entire history of the trajectory x(t). As usual, ensemble averaging is denoted hereafter by angular brackets, while time averaging is indicated by the overline. To obtain smoother curves for the time averaged MSD an additional average is taken over N trajectories, defining the mean time averaged MSD6,8| | 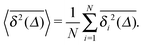 | (6) |
Ergodicity in the Boltzmann–Khinchin sense typically assumed in equilibrium statistical mechanics would imply the equivalence of ensemble and time averaged MSD in the limit of long measurement times, 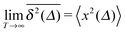 . Following Bouchaud104 the breakdown of this relation is referred to as weak ergodicity breaking,5,8,105–108
. Following Bouchaud104 the breakdown of this relation is referred to as weak ergodicity breaking,5,8,105–108
| | 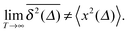 | (7) |
Continuous time random walks and HDPs are known to be weakly non-ergodic,
8 while diffusion on fractals is ergodic on the infinite cluster but not on the entirety of all clusters.
49 In contrast, other diffusive processes such as fractional Brownian motion and SBM are only marginally non-ergodic.
8,81,86,87,109–113
A distinctive measure of non-reproducibility of individual time averaged MSD traces is the ergodicity breaking parameter108
based on the dimensionless ratio
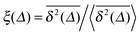
quantifying the spread of individual time averaged MSDs about their mean
(6). Typically EB of a weakly non-ergodic process decays to zero with increasing trace length slower than for the standard Brownian motion,
46,112| | 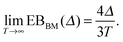 | (9) |
Or, EB may even attain a finite value as
Δ/
T → 0, for instance, for HDPs and continuous times random walks.
8,74,106,108,114 Often, also the ratio of the time and ensemble averaged MSDs
115| | 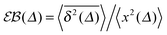 | (10) |
provides additional information about the ergodic properties of the diffusion process.
IV. The random diffusivity model
In this section we describe the details of RDPs. As a generalisation of eqn (2), the instantaneous value of the diffusion coefficient on each simulation step is independently chosen from the Rayleigh distribution| | 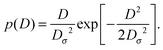 | (11) |
The mean particle diffusivity is then given by| | 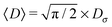 | (12) |
and the diffusivity variance is 〈(D− 〈D〉)2〉 = (2 − π/2)Dσ2. Independence of successive values of the diffusion coefficient indicates no temporal correlations in its fluctuations. Our system is thus out of equilibrium (the temperature is not fixed) and the fluctuation dissipation theorem does not hold.
The PDF (11) is a smooth function in the range from D = 0 to D = ∞ and it vanishes on the boundaries of this interval. This distribution p(D) is used instead of a Gaussian distributed diffusion coefficient to avoid non-physical negative D values. The distribution (11) is thus physically different from the exponential p(D) form given by eqn (2) used by Chubynsky and Slater.51 When the mean diffusivity stays constant over time, in the long time limit the particle diffuses normally. However, when the mean diffusivity is allowed to vary in addition deterministically as a powerlaw,
the resulting process is reminiscent of SBM. Physically, such an increase of the mean diffusivity could be due to a diffusing diffusivity of the form 〈
D(
ti)〉 = |〈
D(
ti−1)〉 +
ζD(
ti−1)|, where
ζD(
ti) is an incremental change. This is analogous to the power-law growth of the waiting times in the correlated continuous time random walks.
42
We consider below both massless and massive particles diffusing in both unconfined and a confined environments. We implement the same algorithms for the iterative computation of the particle displacement x(t) as developed for HDPs74 and combined HDP-SBM motion.92 First, we simulate the one dimensional overdamped Langevin equation
| | 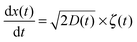 | (14) |
driven by zero-mean and unit-variance Gaussian noise
ζ(
t). At step
i + 1 the particle displacement is given by
| | 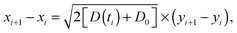 | (15) |
where (
yi+1 −
yi) are the increments of the Wiener process. Unit time intervals separate consecutive steps. To avoid possible particle stalling we regularise
D by adding a small constant
D0 = 10
−3.
75,76 This does not affect the intermediate- and long-time diffusive behaviour. The particle's initial position is
x0 =
x(
t = 0) = 0.1. In the second part of the paper, we simulate the underdamped Langevin equation for a particle of mass
m,
| | 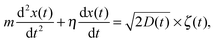 | (16) |
with the unit damping coefficient set below to
η = 1. At a step
i + 1 the particle displacement is found from the iteration scheme
| | 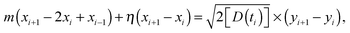 | (17) |
where the instantaneous diffusivity is taken from
eqn (11) with the mean
(13).
V. Results: overdamped motion
A. Free diffusion
We start with the diffusion of massless particles with a fluctuating diffusivity and time invariant mean. As naively expected, we find that due to friction the MSD in the long time limit is Brownian,| | | 〈x2(t)〉 ∼ x02 + 2〈D(t)〉t. | (18) |
The MSD and the time averaged MSD are nearly identical after a fast relaxation of the starting position x0 of the particle and the ergodicity is approximately fulfilled at all times (results not shown here).
Now we address the more interesting case of RDPs with instantaneous diffusivity chosen from the distribution (11) with a time dependent mean (13). Namely, the most likely diffusivity Dσ(t) at simulation step i is
| | 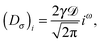 | (19) |
where the prefactor is chosen for convenience and the coefficient
![[scr D, script letter D]](https://www.rsc.org/images/entities/char_e523.gif)
tunes the magnitude of the diffusivity. From
eqn (14) we straightforwardly compute
| | 〈x2(t)〉 = x02 + 2![[scr D, script letter D]](https://www.rsc.org/images/entities/char_e523.gif) tγ, tγ, | (20) |
with
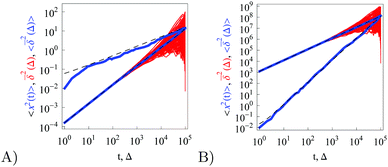
Fig. 1 depicts the case of ω = 1/2 or the MSD diffusion exponent γ = 3/2. As can be seen from the simulations the time averaged MSD grows linearly with the lag time Δ, as in the Brownian case. This process also reveals a quite moderate amplitude spread of individual traces  , see the thin red curves in Fig. 1. Obviously when the lag time approaches the observation time, Δ ∼ T, the amplitude scatter increases due to the deteriorating statistic of
, see the thin red curves in Fig. 1. Obviously when the lag time approaches the observation time, Δ ∼ T, the amplitude scatter increases due to the deteriorating statistic of 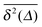 .8 Varying
.8 Varying ![[scr D, script letter D]](https://www.rsc.org/images/entities/char_e523.gif) in Fig. 1 we demonstrate that, as expected, larger initial diffusivities give rise to a faster approach of the MSD to the theoretical asymptote. In contrast, for rather small diffusivities (smaller
in Fig. 1 we demonstrate that, as expected, larger initial diffusivities give rise to a faster approach of the MSD to the theoretical asymptote. In contrast, for rather small diffusivities (smaller ![[scr D, script letter D]](https://www.rsc.org/images/entities/char_e523.gif) values) the system needs more time to approach the long time asymptote, Fig. 1. A diminished magnitude of the MSD at smaller
values) the system needs more time to approach the long time asymptote, Fig. 1. A diminished magnitude of the MSD at smaller ![[scr D, script letter D]](https://www.rsc.org/images/entities/char_e523.gif) values inevitably leads to a decrease in the magnitude of the time averaged MSD, see below. At intermediate to long times the superdiffusive MSD regime with γ = 3/2 emerges. Finally, towards the very end of the trace the MSD and the time averaged MSD coincide, as they should.8
values inevitably leads to a decrease in the magnitude of the time averaged MSD, see below. At intermediate to long times the superdiffusive MSD regime with γ = 3/2 emerges. Finally, towards the very end of the trace the MSD and the time averaged MSD coincide, as they should.8
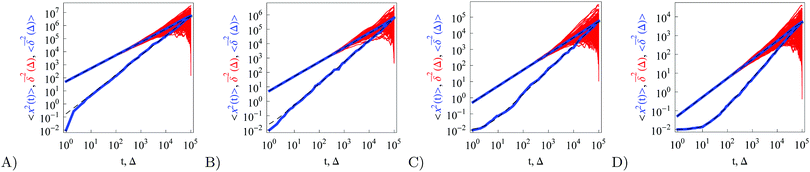 |
| | Fig. 1 MSD 〈x2(t)〉 and time averaged MSD 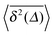 (thick blue curves) as well as individual time traces (thick blue curves) as well as individual time traces 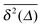 (red curves) for overdamped RDPs. The asymptotes (20) and (22) for the MSD and the time averaged MSD are shown by the dashed curves. The asymptotes often superimpose with the results of simulations. Parameters: the scaling exponent is ω = 1/2, the trace length is T = 105, and number of traces used for the averaging is N = 150. The starting position is x0 = 0.1 and the parameter (red curves) for overdamped RDPs. The asymptotes (20) and (22) for the MSD and the time averaged MSD are shown by the dashed curves. The asymptotes often superimpose with the results of simulations. Parameters: the scaling exponent is ω = 1/2, the trace length is T = 105, and number of traces used for the averaging is N = 150. The starting position is x0 = 0.1 and the parameter 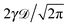 takes the values 10−1, 10−2, 10−3, and 10−4 for the panels from left to right. takes the values 10−1, 10−2, 10−3, and 10−4 for the panels from left to right. | |
Analytically, we obtain for the time averaged MSD from eqn (14) for x(t) and after averaging over the noise ζ(t) and diffusion coefficient realisations p(D) the result
| | 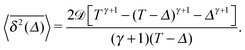 | (22) |
This expression nicely agrees with the results of computer simulations for all
ω and
![[scr D, script letter D]](https://www.rsc.org/images/entities/char_e523.gif)
values investigated, see
Fig. 1 and 8. It is not surprising that both MSD and time averaged MSD are proportional to
![[scr D, script letter D]](https://www.rsc.org/images/entities/char_e523.gif)
determining the basal value of the particle diffusivity,
eqn (19). In the limit of short lag times,
Δ ≪
T, from
eqn (22) we recover the scaling behaviour
| | 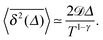 | (23) |
Thus, for superdiffusive RDPs with
γ > 1 the magnitude of the time averaged MSD is a growing function of the trace length
T, while for subdiffusive RDPs
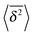
magnitude decreases with
T, in agreement with
Fig. 9. In the limit
Δ→
T the ensemble and time averaged MSDs coincide,
8 as it is easy to check from
eqn (20) and (22) and corroborated in
Fig. 1. The non-equivalence of the time averaged MSD
(22) and the time averaged MSD
(20) demonstrates that the system is weakly non-ergodic. The scaling behaviour
(23)—regarding the magnitude of the time averaged MSD in terms of the power law of the trace length
T and the linearity in the lag time—is analogous to that obtained for subdiffusive continuous time random walks
13,106,108,116 and their correlated version
42 as well as for HDPs
74,75,92 and SBM;
87,93 see also
ref. 8 for an overview.
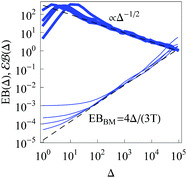
For RDPs the ergodicity breaking parameter EB computed from simulations tends to follow the asymptote (9) for Brownian motion at intermediate and long times, Fig. 2. We observe that the initial relaxation of EB to this asymptote is relatively fast. As we show in Fig. 2, after this relaxation time the parameter 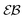 (10) becomes a power-law function of the lag time Δ,
(10) becomes a power-law function of the lag time Δ,
| | 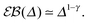 | (24) |
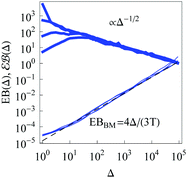 |
| | Fig. 2 Ergodicity breaking parameter EB and the parameter 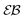 versus lag time Δ for overdamped RDPs. The curves are computed for the parameters of Fig. 1 with ω = 1/2. The curves for versus lag time Δ for overdamped RDPs. The curves are computed for the parameters of Fig. 1 with ω = 1/2. The curves for 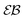 from top to bottom correspond to from top to bottom correspond to 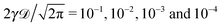 , respectively. The asymptote (9) of Brownian motion and the relation (24) are the dashed lines. , respectively. The asymptote (9) of Brownian motion and the relation (24) are the dashed lines. | |
Diffusivity distributions p(D) whose mean diffusivity grows with time may be viewed to correspond to an effectively increasing temperature in the system. The opposite case of a temporally shrinking width may stem from a cooling of the system in the course of time. In this respect the current process is reminiscent of SBM.81,87,93 An important example for the latter are granular gases with a relative velocity dependent restitution coefficient.85
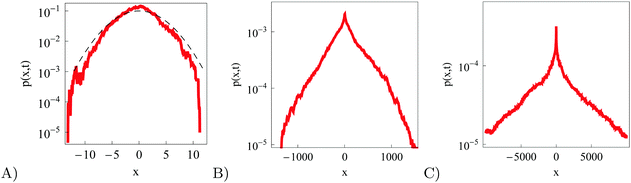
The particle spreading for very subdiffusive RDPs can be compared to the PDF of SBM, identical to that of fractional Brownian motion for x0 = 0 for natural boundary conditions of a vanishing PDF of diffusing particles at |x| → ∞.83,87 Namely, after the substitution of the corresponding MSD (20) this produces
| | 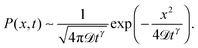 | (25) |
Fig. 10 compares the conjecture
(25) with the result from simulations of RDPs. We see, however, that as the MSD scaling exponent increases a distinct cusp of the PDF starts to develop at the origin. The PDF of superdiffusive RDPs becomes pronouncedly non-Gaussian. This spike however cannot be described by a convolution of the diffusivity distribution
(11) with the kernels of Brownian motion and SBM motion. A more detailed investigation is required to understand this spike at short times and possibly exponential forms of the PDF tails at long times. This generally non-Gaussian and
γ-dependent shape of the PDF is one important distinction of RDPs with time dependent and in addition fluctuating diffusivities, as compared to the SBM process with the deterministic value of the diffusion coefficient at each step,
D(
t) = 〈
D(
t)〉.
B. Confined diffusion
We now turn to confined RDPs on an interval −L < x < L. Such confined motion is important especially for the understanding of diffusion processes in biological cells. In cells—due to their external confinement by the plasma membrane and internal compartmentalisation—a diffusing tracer frequently collides with boundaries. As expected, after an initial free diffusion the MSD converges to the stationary plateau8| | 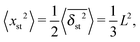 | (26) |
as demonstrated in Fig. 3. The time averaged MSD, by virtue of its definition (5), approaches twice the value of the MSD in the long time limit.
The existence of a plateau is similar to that of standard Brownian motion, and interval-confined SBM and HDPs.76,92 Note that SBM confined by an external potential has a time dependent thermal value of the MSD.87,93 The behaviour of confined continuous time random walks is strikingly different, there confinement leads to a crossover to a second power-law regime in the time averaged MSD.13,116 The PDF of confined RDPs approaches a uniform distribution of particles on the interval.
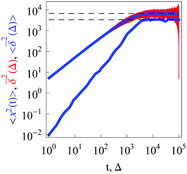 |
| | Fig. 3 Same as in Fig. 1 but for confined overdamped RDPs. The box size is L = 102, ω = 1/2, and 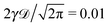 . The asymptote (26) and twice this value are the dashed lines. . The asymptote (26) and twice this value are the dashed lines. | |
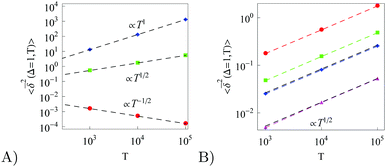
At more severe confinement the ergodicity breaking parameter EB at large lag times Δ values starts to deviate form the Brownian asymptote (9), see Fig. 4. In addition, we find that for a fixed width of the confining interval and varying trace length T the EB parameter follows the scaling relation
as illustrated in
Fig. 11A and B. This is a standard decrease of the EB parameter for longer trajectories, a property ubiquitous among a number of both ergodic and non-ergodic stochastic processes.
8 The decrease of EB with
T indicates a progressively more ergodic diffusion for longer particle traces.
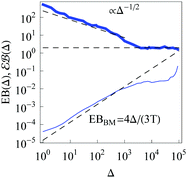 |
| | Fig. 4 Parameters EB and  for confined overdamped RDPs for the parameters of Fig. 3. The Brownian asymptote (9) and the plateau for confined overdamped RDPs for the parameters of Fig. 3. The Brownian asymptote (9) and the plateau 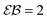 are shown as the dashed lines. are shown as the dashed lines. | |
VI. Results: underdamped motion
A. Free diffusion
In this section, we study the diffusion of massive particles in the same time dependent random diffusivity scenario (19) based on the underdamped Langevin equation. In particular, we explore to what extent inertia effects modify the long time behaviour of the MSD and the time averaged MSD, as compared to the overdamped RDPs considered above. The general solution for the particle MSD follows from the standard procedure for the Brownian motion of massive particles.97 Namely, we obtain| | 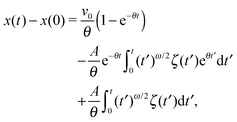 | (28) |
where we defined θ = η/m and A2 = 2γ![[scr D, script letter D]](https://www.rsc.org/images/entities/char_e523.gif) /m2. Moreover, v0 is the initial particle velocity. Then the MSD of the particles after averaging over the noise ζ can formally be written as
/m2. Moreover, v0 is the initial particle velocity. Then the MSD of the particles after averaging over the noise ζ can formally be written as| | 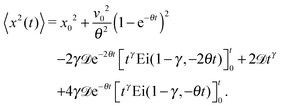 | (29) |
Here 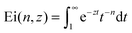 denotes the generalised exponential integral.
denotes the generalised exponential integral.
For zero initial velocity of the particles v0 = 0, as in the computer simulations performed here, the inertial term in the Langevin equation gives rise to the initial MSD scaling of the form 〈x2(t)〉 ∼ tγ+2. It is due to progressively accelerating (heating) particles. Explicitly, for the MSD at short times we get
| | 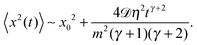 | (30) |
This faster than ballistic MSD regime often called hyperdiffusion is known to emerge, for instance, for a power-law like transient heating of particles with temperature variation of the form
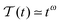
.
117 This superballistic behaviour emerges for RDPs with fluctuating diffusivities and time dependent mean, in analogy with a faster than linear short time ballistic regime in Brownian motion.
97
Note that the short time MSD regime (30)—with the scaling exponent by one larger than the long time MSD exponent—is absent in the model of underdamped SBM elucidated by us recently in ref. 85. The reason is that the damping coefficient is set to be temperature independent in the current model, whereas in the model of underdamped SBM η(t) is coupled to the diffusivity variations via the generalised time-local Einstein relation85
| | | D(t) = kBT(t)/(mη(t)). | (31) |
So, the fluctuation–dissipation theorem is valid, contrary to the current approach. For the underdamped SBM process, the relation
η(
t) ∼
T1/2(
t) is consistent with the physical picture of elastically colliding and relaxing particles in a bath with a deterministically varying temperature.
98 The reader is also referred to
ref. 118 for studying different relationships between the friction coefficient and velocity for passive and active
119 particles, including nonlinear forms.
Note that the diffusive and ergodic properties of underdamped SBM were recently considered as well.98 It was demonstrated that inertial effects relax rather quickly in the course of particle diffusion for superdiffusive (γ > 1) situations. This follows from comparing the magnitudes of the acceleration and friction terms in the Langevin equation. Conversely, for small positive values of γ a finite particle mass yields an extensive intermediate regime, both for the MSD and the time averaged MSD growth behaviour with time. Interestingly, in the case of ultraslow logarithmic SBM motion—realised for the limiting value γ = 0—the overdamped limit of particle diffusion96 is not reached at long times, independent on the total measurement time.98
The time averaged MSD of underdamped RDPs follows from eqn (28) and (5),
| | 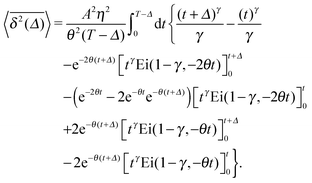 | (32) |
This integral expression can be evaluated numerically. In the limit of short lag times
Δ ≪
T we can evaluate the integral and find
| | 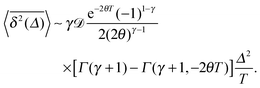 | (33) |
Here
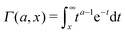
is the generalised incomplete Gamma function and
Γ(
a,0) =
Γ(
a) is the Gamma function. The short time asymptotes of both the MSD and the time averaged MSD are plotted as the dot-dashed curves in
Fig. 5 showing nice agreement with the results of computer simulations of
eqn (15).
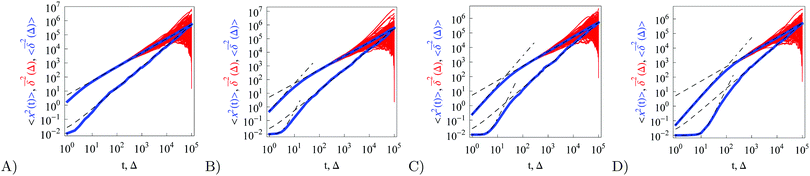 |
| | Fig. 5 Ensemble averaged MSD, individual time averaged MSDs, and mean time averaged MSD, with the same notation as in Fig. 1, evaluated for underdamped RDPs with particle mass m = 1, 5, 10, and 50, for panels from left to right. N ∼ 102 traces are shown. The long time asymptotes (20) and (22) are the dashed lines. The dot-dashed lines are the asymptotes for the short time regimes, eqn (30) and (34). Parameters: 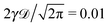 , ω = 1/2, and T = 105. , ω = 1/2, and T = 105. | |
Expanding the Gamma functions in the corresponding limit we find from expression (33) for light particles or high friction in the system—that is for θT ≪ 1—that
| | 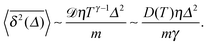 | (34) |
This has the form of the short time MSD behaviour of standard Brownian motion.
97 All particle masses in this study guarantee the validity of
eqn (34) as the short time expansion for the time averaged MSD in this underdamped limit. Comparing the
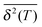
-variation with
eqn (34) in
Fig. 9B further supports this validity regarding the dependence on the length of particle trajectory
T. In the opposite limit of
θT ≪ 1—very massive particles or low friction for the particle motion—we find
| | 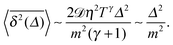 | (35) |
Let us now describe the results of our computer simulations and compare them with these analytical predictions. We observe that in the particle displacement the initial condition of zero particle velocity (v0 = 0) relaxes within several initial diffusion steps. Naturally, it takes for the system longer to accelerate heavier particles, as shown in Fig. 5, in agreement with eqn (30). The initial slow acceleration of heavy particles yields slowly growing MSD that gets in turn reflected in small amplitudes of the time averaged MSD at short lag times Δ. The MSD follows eqn (30) for short times and then crosses over to the long time scaling (20). Note that the same initial quadratic regime was observed in ref. 98 for the short time behaviour of the time averaged MSD of the standard underdamped SBM process. For the time averaged MSD the heavier particles feature a longer ballistic regime, see Fig. 5. The magnitude of 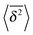 decreases with the particle mass, in agreement with eqn (34). At longer times the MSD and time averaged MSD approach the results expected for the overdamped RDP motion, shown as the long time asymptotes in Fig. 5. As expected, apart from the initial ballistic regime of the time averaged MSD described by eqn (34), the analytical solution for the overdamped limit (22) describes the long time behaviour of the results of our computer simulations.
decreases with the particle mass, in agreement with eqn (34). At longer times the MSD and time averaged MSD approach the results expected for the overdamped RDP motion, shown as the long time asymptotes in Fig. 5. As expected, apart from the initial ballistic regime of the time averaged MSD described by eqn (34), the analytical solution for the overdamped limit (22) describes the long time behaviour of the results of our computer simulations.
Similar to the overdamped situation, at short lag times the magnitudes of 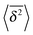 follow the relation (23), see Fig. 9B. We also observe that for underdamped RDPs the spread of individual
follow the relation (23), see Fig. 9B. We also observe that for underdamped RDPs the spread of individual 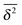 traces is similar to that of standard Brownian motion. This small spread is consistent with the observation that the EB parameter for this underdamped RDP motion does not deviate strongly from the Brownian asymptote (9) at intermediate and long times, see Fig. 6. In the region of short Δ the deviations are quite substantial, particularly for massive particles exhibiting a ballistic initial growth of
traces is similar to that of standard Brownian motion. This small spread is consistent with the observation that the EB parameter for this underdamped RDP motion does not deviate strongly from the Brownian asymptote (9) at intermediate and long times, see Fig. 6. In the region of short Δ the deviations are quite substantial, particularly for massive particles exhibiting a ballistic initial growth of 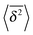 and a nonlinear growth of the MSD, see Fig. 5. The auxiliary parameter
and a nonlinear growth of the MSD, see Fig. 5. The auxiliary parameter 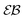 —again after the initial particle acceleration—follows the asymptote (24), see the thick curves in Fig. 6. The deviations of EB and
—again after the initial particle acceleration—follows the asymptote (24), see the thick curves in Fig. 6. The deviations of EB and 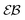 at short lag times from the Brownian asymptote is more evident for massive particles.
at short lag times from the Brownian asymptote is more evident for massive particles.
 |
| | Fig. 6 Parameters EB and 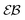 versus lag time Δ for underdamped RDPs. The Brownian asymptote (9) and eqn (24) are the dashed lines. The curves correspond to varying particle mass, m = 1, 5, 10, 50; the other parameters are the same as in Fig. 5. versus lag time Δ for underdamped RDPs. The Brownian asymptote (9) and eqn (24) are the dashed lines. The curves correspond to varying particle mass, m = 1, 5, 10, 50; the other parameters are the same as in Fig. 5. | |
B. Confined diffusion
We complete the analysis of RDPs with the study of the underdamped motion in a confining box. We observe that at short time the MSD develops similar to the unconfined scenario. Once the boundary of the confined region is reached, the plateaus start to develop at the same levels as for the overdamped RDP case both for the MSD and time averaged MSD, see eqn (26) and Fig. 7. Towards the very end of the trajectory at Δ = T, the MSD and the time averaged MSD coincide, as they should.8 The longer the entire trajectory, however, the narrower the range of lag times where this convergence takes place, and thus the more precise should be the Δ-sampling in this region—that is often computationally costly. This effect was studied in detail for the pure SBM motion confined in harmonic potentials87 and for HDPs confined between hard walls.76,92
 |
| | Fig. 7 Analogue of Fig. 5 for confined underdamped RDPs with particle mass m = 1, 5, 10, and 50, from left to right. We show N = 150 traces for each set of parameters and the interval width is L = 102. The asymptotes for the confined motion (26) are the dashed lines. | |
 |
| | Fig. 8 Same as in Fig. 1 but at ω = −1/2 (A) and ω = 1 (B) computed for 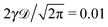 and N = 150. The asymptotes for the MSD and time averaged MSD are shown as the dashed lines. and N = 150. The asymptotes for the MSD and time averaged MSD are shown as the dashed lines. | |
 |
| | Fig. 9 Time averaged MSD versus trace length T for (A) non-confined overdamped RDPs for ω = −1/2, 1/2, 1 (for data points from bottom to top) and for (B) non-confined underdamped RDPs for m = 1, 5, 10, 50 (for data points from top to bottom) and ω = 1/2. Other parameters are the same as in Fig. 1 and 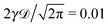 . Dashed lines indicate the scaling relation (23) in panel (A) and eqn (34) in panel (B). . Dashed lines indicate the scaling relation (23) in panel (A) and eqn (34) in panel (B). | |
 |
| | Fig. 10 PDF of the overdamped RDPs for ω = −1/2, 1/2, and 1 (from left to right). Other parameters are the same as in Fig. 1 with 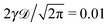 and N = 300. The PDF asymptote for subdiffusive SBM (25) is shown as the dashed curve. and N = 300. The PDF asymptote for subdiffusive SBM (25) is shown as the dashed curve. | |
 |
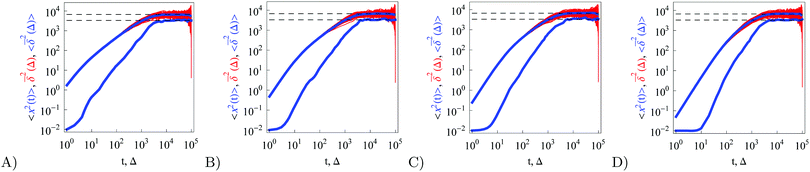
| | Fig. 11 EB parameter at Δ = 1 computed for free and confined overdamped RDPs (panels (A) and (B)) and for free and confined underdamped RDPs (panels (C) and (D)). Parameters: for all the panels ω = 1/2,  and (panel (A): free overdamped process) m = 0, L = ∞; (panel (B): confined overdamped process) m = 0, L = 102; (panel (C): free underdamped process) m = 50, L = ∞; (panel (D): confined underdamped process) m = 50, L = 102. and (panel (A): free overdamped process) m = 0, L = ∞; (panel (B): confined overdamped process) m = 0, L = 102; (panel (C): free underdamped process) m = 50, L = ∞; (panel (D): confined underdamped process) m = 50, L = 102. | |
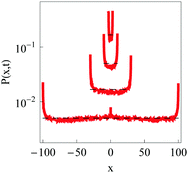
The PDFs of confined underdamped RDPs at varying box width L is presented in Fig. 12. We observe that for wide intervals the particles are nearly uniformly distributed on the interval (see the dashed lines in Fig. 12), with only insignificant increase in the particle occupancies near the box boundaries due to reflections. Note that the particle starting position at x = x0 is still slightly visible in the PDF for a weak confinement. As the confinement becomes more severe, the particle accumulation near the interval boundaries occupies a larger fraction of space available for diffusion.
 |
| | Fig. 12 PDF of underdamped confined RDPs for L = 3, 10, 30, and 100 (from top to bottom), computed for ω = 1/2, 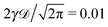 , T = 105, m = 50. Dashed lines designate the uniform distribution of particles on the interval. , T = 105, m = 50. Dashed lines designate the uniform distribution of particles on the interval. | |
The EB parameter for massive particles deviates progressively from the Brownian law (9) at both short and long lag times Δ (not shown). This is due to slow particle acceleration at short times (MSD plateau) and particle confinement at long times, respectively. For free and confined underdamped RDPs—similarly to the overdamped situation—the EB parameter follows the asymptote (27) with the trajectory length T, see Fig. 11C and D. As the confinement becomes less severe, the EB parameter approaches the value for the free underdamped RDP motion. Fig. 13 illustrates this EB evolution with the width of the confining interval.
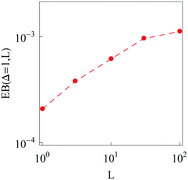 |
| | Fig. 13 EB parameter at Δ = 1 for underdamped RDPs with varying degree of confinement L. Parameters are the same as in Fig. 12: ω = 1/2, 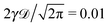 , T = 105, m = 50. , T = 105, m = 50. | |
VII. Conclusions
We examined the ensemble and time averaged characteristics of random diffusion processes. The randomness of the diffusion coefficient D was implemented in the model via a non-stationary distribution p(D). RDPs are not thermalised, that is, the motion of the particles is inherently out of equilibrium. The distribution of the diffusion coefficient reflects individual variations of particle diffusivities and heterogeneities of the environment. For typical out-of-equilibrium systems such as biological cells this does not pose any restrictions to our model. RDPs represent a quite flexible model to study asymptotically Brownian and anomalous diffusive systems with a locally fluctuating diffusion coefficient to model physical situations in many complex systems.
We rationalised both by computer simulations and analytically the MSD, the time averaged MSD, and the ergodicity breaking parameter of RDPs. Unconfined and interval-confined motion was examined. We found that in terms of these standard characteristics subdiffusive RDPs appear similar to subdiffusive SBM with a deterministic diffusivity variation in time. For superdiffusive RDPs the fluctuations grow with time. Concurrently, the average diffusion coefficient 〈D(t)〉 grows with time together with the spread of its values. These features reflect an increasing temperature and more pronounced fluctuations of the medium in the course of particle diffusion. The properties of ageing overdamped and underdamped RDPs will be considered elsewhere and compared to the ageing properties of SBM,93 HDPs,76 and continuous time random walks.114
Living cells feature heterogeneous and densely crowded environments established by a “melange” of various macromolecules and (importantly) a rather viscoelastic solution between them. This often leads to a broadening in the distribution of diffusion coefficients and subdiffusive exponents, as observed for obstructed diffusion of various tracers.12,59,120,121 In particular, some extensions of the standard diffusion models to account for these effects—similar to our p(D) distribution for the SBM like diffusion model presented above—appear necessary e.g. for a quantitative fit of fluorescence recovery after photobleaching curves.120 The models of SBM type—with the diffusivity formally decaying in time according to the power law (13)—are often implemented to describe the subdiffusive MSD behaviour (1) of the tracer particles in cells. This anomalous MSD scaling was observed e.g. via fitting the shape of the autocorrelation curves of fluorescence correlation spectroscopy measurements.12,122,123
In single particle tracking measurements in biological cells some time dependent scatter of the diffusion coefficients was also detected.59,124 It is necessary in theoretical models i.a. to distinguish between the normal, restricted, and fully trapped populations of the tracers. In fact, a Gamma distribution similar to the Rayleigh distribution (11) used above was proposed in ref. 59 to characterise the scatter of the MSD distribution of the diffusing particles. On the level of diffusing simple organisms, Gamma like diffusivity distributions were documented for the motion of nematode worms.64 The latter also exhibit non-Gaussian PDFs of the particle displacements with a “spike” at the origin,64,125 similar to some of our findings. Also, the recent study126 of anomalous and non-ergodic dynamics of particles within a predator-prey model with a broad distribution of diffusion coefficients of interacting partners needs to be mentioned here.
The current study with its preset functional form of the diffusivity distribution and a deterministic law (13) represents a first step into the terrain of stochastic processes with fluctuating and time varying diffusivities. A more general consideration would correspond to a system of coupled stochastic differential equations for the particle position and its diffusivity. The first equation is the standard Langevin equation, while the second equation involves an additional, generally decoupled noise source governing D(t) variation. The correlation function and other noise properties—not necessarily Gaussian—determine then both the ensemble and the time averaged MSDs of diffusing particles.127
Appendix
In this Appendix we present several additional figures (Fig. 8–13) supporting the claims in the main text of the manuscript.
References
- J.-P. Bouchaud and A. Georges, Phys. Rep., 1990, 195, 127 CrossRef CAS; R. Metzler and J. Klafter, Phys. Rep., 2000, 339, 1 CrossRef; R. Metzler and J. Klafter, J. Phys. A: Math. Gen., 2004, 37, R161 CrossRef.
-
C. Bräuchle, D. C. Lamb and J. Michaelis, Single Particle Tracking and Single Molecule Energy Transfer, Wiley-VCH, Weinheim, Germany, 2012 CrossRef CAS PubMed; X. S. Xie, P. J. Choi, G.-W. Li, N. K. Lee and G. Lia, Annu. Rev. Biophys., 2008, 37, 417 CrossRef CAS PubMed.
- T. Franosch, M. Grimm, M. Belushkin, F. M. Mor, G. Foffi, L. Forro and S. Jeney, Nature, 2011, 478, 7367 CrossRef PubMed.
- D. S. Banks and C. Fradin, Biophys. J., 2005, 89, 2960 CrossRef CAS PubMed; G. Guigas, C. Kalla and M. Weiss, Biophys. J., 2007, 93, 316 CrossRef PubMed; J. Szymanski and M. Weiss, Phys. Rev. Lett., 2009, 103, 038102 CrossRef PubMed; W. Pan, L. Filobelo, N. D. Q. Pham, O. Galkin, V. V. Uzunova and P. G. Vekilov, Phys. Rev. Lett., 2009, 102, 058101 CrossRef PubMed; J.-H. Jeon, N. Leijnse, L. B. Oddershede and R. Metzler, New J. Phys., 2013, 15, 045011 CrossRef.
- S. Burov, J.-H. Jeon, R. Metzler and E. Barkai, Phys. Chem. Chem. Phys., 2011, 13, 1800 RSC.
- E. Barkai, Y. Garini and R. Metzler, Phys. Today, 2012, 65(8), 29 CrossRef CAS.
- F. Höfling and T. Franosch, Rep. Prog. Phys., 2013, 76, 046602 CrossRef PubMed.
- R. Metzler, J.-H. Jeon, A. G. Cherstvy and E. Barkai, Phys. Chem. Chem. Phys., 2014, 16, 24128 RSC.
- Y. Meroz and I. M. Sokolov, Phys. Rep., 2015, 573, 1 CrossRef.
- C. Manzo and M. F. Garcia-Parajo, Rep. Prog. Phys., 2015, 78, 124601 CrossRef PubMed.
- A. Caspi, R. Granek and M. Elbaum, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2002, 66, 011916 CrossRef CAS PubMed; G. Seisenberger,
et al.
, Science, 2001, 294, 1929 CrossRef PubMed; I. Golding and E. C. Cox, Phys. Rev. Lett., 2006, 96, 098102 CrossRef PubMed; I. Bronstein, Y. Israel, E. Kepten, S. Mai, Y. Shav-Tal, E. Barkai and Y. Garini, Phys. Rev. Lett., 2009, 103, 018102 CrossRef PubMed; S. M. A. Tabei, S. Burov, H. Y. Kim, A. Kuznetsov, T. Huynh, J. Jureller, L. H. Philipson, A. R. Dinner and N. F. Scherer, Proc. Natl. Acad. Sci. U. S. A., 2013, 110, 4911 CrossRef PubMed.
- M. Weiss, M. Elsner, F. Kartberg and T. Nilsson, Biophys. J., 2004, 87, 3518 CrossRef CAS PubMed.
- J.-H. Jeon, V. Tejedor, S. Burov, E. Barkai, C. Selhuber-Unkel, K. Berg-Sorensen, L. Oddershede and R. Metzler, Phys. Rev. Lett., 2011, 106, 048103 CrossRef PubMed.
- A. Caspi, R. Granek and M. Elbaum, Phys. Rev. Lett., 2000, 85, 5655 CrossRef CAS PubMed; N. Gal and D. Weihs, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2010, 81, 020903(R) CrossRef PubMed; D. Robert, T. H. Nguyen, F. Gallet and C. Wilhelm, PLoS One, 2010, 4, e10046 Search PubMed; J. F. Reverey, J.-H. Jeon, H. Bao, M. Leippe, R. Metzler and C. Selhuber-Unkel, Sci. Rep., 2015, 5, 11690 CrossRef PubMed.
- G. R. Kneller, K. Baczynski and M. Pasienkewicz-Gierula, J. Chem. Phys., 2011, 135, 141105 CrossRef CAS PubMed; T. Akimoto, E. Yamamoto, K. Yasuoka, Y. Hirano and M. Yasui, Phys. Rev. Lett., 2011, 107, 178103 CrossRef PubMed; J.-H. Jeon, H. Martinez-Seara Monne, M. Javanainen and R. Metzler, Phys. Rev. Lett., 2012, 109, 188103 CrossRef PubMed; M. Javanainen, H. Hammaren, L. Monticelli, J.-H. Jeon, R. Metzler and I. Vattulainen, Faraday Discuss., 2013, 161, 397 RSC; S. Stachura and G. R. Kneller, J. Chem. Phys., 2014, 40, 245 Search PubMed; E. Yamamoto, A. C. Kalli, T. Akimoto, K. Yasuoka and M. S. P. Sansom, Sci. Rep., 2015, 5, 18245 CrossRef PubMed.
- J.-H. Jeon, M. Javanainen, H. Martinez-Seara, R. Metzler and I. Vattulainen, Phys. Rev. X, 2016, 6, 021006 Search PubMed.
- A. V. Weigel, B. Simon, M. M. Tamkun and D. Krapf, Proc. Natl. Acad. Sci. U. S. A., 2011, 108, 6438 CrossRef CAS PubMed; D. Krapf, Curr. Top. Membr., 2015, 75, 167 Search PubMed; D. Krapf, G. Campagnola, K. Nepal and O. B. Peersen, Phys. Chem. Chem. Phys., 2016, 18, 12633 RSC.
- R. Metzler, J.-H. Jeon and A. G. Cherstvy, Biochim. Biophys. Acta, 2016, 1858, 2451 CrossRef PubMed.
- C. Manzo, J. A. Torreno-Pina, P. Massignan, G. J. Lapeyre, Jr., M. Lewenstein and M. F. Garcia Parajo, Phys. Rev. X, 2015, 5, 011021 Search PubMed.
- H. Berry and H. A. Soula, Front. Physiol., 2014, 5, 437 Search PubMed; H. Berry and H. Chate, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2014, 89, 022708 CrossRef CAS PubMed; F. Trovato and V. Tozzini, Biophys. J., 2014, 107, 2579 CrossRef PubMed; M. Weiss, Int. Rev. Cell Mol. Biol., 2014, 307, 383 Search PubMed; M. J. Saxton, J. Phys. Chem. B, 2014, 118, 12805 CrossRef PubMed; D. S. Banks, C. Tressler, R. D. Peters, F. Höfling and C. Fradin, Soft Matter, 2016, 12, 4190 RSC; T. Sentjabrskaja, E. Zaccarelli, C. De Michele, F. Sciortino, P. Tartaglia, F. Höfling and T. Franosch, Phys. Rev. Lett., 2007, 98, 140601 CrossRef PubMed; S. Leitmann and T. Franosch, Phys. Rev. Lett., 2013, 111, 190603 CrossRef PubMed; T. Voigtmann, S. U. Egelhaaf and M. Laurati, Nat. Commun., 2016, 7, 11133 CrossRef PubMed.
- S. K. Ghosh, A. G. Cherstvy and R. Metzler, Phys. Chem. Chem. Phys., 2015, 17, 472 Search PubMed.
- S. Ghosh, A. G. Cherstvy, D. S. Grebenkov and R. Metzler, New J. Phys., 2016, 16, 013027 CrossRef.
- S. S. Rogers, C. van der Walle and T. A. Weigh, Langmuir, 2008, 24, 13549 CrossRef CAS PubMed.
- A. Upadhyaya, J.-P. Rieu, J. A. Glazier and Y. Sawada, Physica A, 2001, 293, 549 CrossRef; L. G. A. Alves, D. B. Scariot, R. R. Guimaraes, C. V. Nakamura, R. S. Mendes and H. V. Ribeiro, PLoS One, 2016, 11, e0152092 Search PubMed.
- I. Munguira, I. Casuso, H. Takahashi, F. Rico, A. Miyagi, M. Chami and S. Scheuring, ACS Nano, 2016, 10, 2584 CrossRef CAS PubMed.
- S. Hanot, S. Lyonnard and S. Mossa, Nanoscale, 2016, 8, 3314 RSC.
- D. Wang, C. He, M. P. Stoykovich and D. K. Schwartz, ACS Nano, 2015, 9, 1656 CrossRef CAS PubMed.
- M. J. Skaug, J. Mabry and D. K. Schwartz, Phys. Rev. Lett., 2013, 110, 256101 CrossRef PubMed.
- G. Kwon, B. J. Sung and A. Yethiraj, J. Phys. Chem. B, 2014, 118, 8128 CrossRef CAS PubMed.
- E. R. Weeks, J. C. Crocker, A. C. Levitt, A. Schofield and D. A. Weitz, Science, 2000, 287, 627 CrossRef CAS PubMed.
- P. Charbonneau, Y. Jin, G. Parisi and F. Zamponi, Proc. Natl. Acad. Sci. U. S. A., 2014, 111, 15025 CrossRef CAS PubMed.
- M. J. Skaug, L. Wang, Y. Ding and D. K. Schwartz, ACS Nano, 2015, 9, 2148 CrossRef CAS PubMed; M. J. Skaug and D. K. Schwartz, Ind. Eng. Chem. Res., 2015, 54, 4414 CrossRef.
- B. Berkowitz, A. Cortis, M. Dentz and H. Scher, Rev. Geophys., 2006, 44, RG2003 CrossRef.
- B. Wang, S. M. Anthony, S. C. Bae and S. Granick, Proc. Natl. Acad. Sci. U. S. A., 2009, 106, 15160 CrossRef CAS PubMed.
- B. Wang, J. Kuo, S. C. Bae and S. Granick, Nat. Mater., 2012, 11, 481 CrossRef CAS PubMed.
- J. Guan, B. Wang and S. Granick, ACS Nano, 2014, 8, 3331 CrossRef CAS PubMed.
- K. He, F. B. Khorasani, S. T. Retterer, D. K. Thomas, J. C. Conrad and R. Krishnamoorti, ACS Nano, 2013, 7, 5122 CrossRef CAS PubMed.
- E. W. Montroll and G. H. Weiss, J. Math. Phys., 1965, 6, 167 CrossRef CAS; H. Scher and E. W. Montroll, Phys. Rev. B: Solid State, 1975, 12, 2455 CrossRef.
- J.-H. Jeon, E. Barkai and R. Metzler, J. Chem. Phys., 2013, 139, 121916 CrossRef PubMed.
- T. Akimoto and E. Barkai, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2013, 87, 032915 CrossRef CAS; T. Akimoto, Phys. Rev. Lett., 2012, 108, 164101 CrossRef PubMed; T. Geisel and S. Thomae, Phys. Rev. Lett., 1984, 52, 1936 CrossRef; T. Geisel, J. Nierwetberg and A. Zacherl, Phys. Rev. Lett., 1985, 54, 616 CrossRef PubMed; M. W. Deem and D. Chandler, J. Stat. Phys., 1994, 76, 911 CrossRef; C. Monthus and J.-P. Bouchaud, J. Phys. A: Math. Gen., 1996, 29, 3847 CrossRef; E. Bertin and J.-P. Bouchaud, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2003, 67, 026128 CrossRef PubMed; S. Burov and E. Barkai, Phys. Rev. Lett., 2007, 98, 250601 CrossRef PubMed; M. Dentz,
et al.
, Adv. Water Resour., 2012, 49, 13 CrossRef;
T. Akimoto, E. Barkai and K. Saito, 2016, arXiv:1604.06175.
- M. M. Meerschaert, E. Nane and Y. Xiao, Stat. Probab. Lett., 2009, 79, 1194 CrossRef; A. V. Chechkin, M. Hofmann and I. M. Sokolov, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2009, 80, 031112 CrossRef PubMed; J. H. P. Schulz, A. V. Chechkin and R. Metzler, J. Phys. A: Math. Theor., 2013, 46, 475001 CrossRef.
- V. Tejedor and R. Metzler, J. Phys. A: Math. Theor., 2010, 43, 082002 CrossRef; M. Magdziarz, R. Metzler, W. Szczotka and P. Zebrowski, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2012, 85, 051103 CrossRef PubMed.
- B. B. Mandelbrot and J. W. van Ness, SIAM Rev., 1968, 10, 422 CrossRef.
- R. Kubo, Rep. Prog. Phys., 1966, 29, 255 Search PubMed; P. Hänggi, Z. Phys. B: Condens. Matter Quanta, 1978, 31, 407 CrossRef CAS; P. Hänggi and F. Mojtabai, Phys. Rev. E, 1982, 26, 1168 CrossRef; S. C. Kou, Ann. Appl. Stat., 2008, 2, 501 CrossRef; I. Goychuk, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2009, 80, 046125 CrossRef PubMed; I. Goychuk, Adv. Chem. Phys., 2012, 150, 187 CrossRef.
-
G. Pagnini, D. Molina-Garcia, T. M. Pham, C. Manzo and P. Paradisi, 2015, E-print arXiv:1508.01361.
- W. Deng and E. Barkai, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2009, 79, 011112 CrossRef PubMed.
- J. W. Haus and K. W. Kehr, Phys. Rep., 1987, 150, 263 CrossRef CAS; S. Havlin and D. Ben-Avraham, Adv. Phys., 1987, 36, 695 CrossRef;
G. C. Papanicolaou, “Diffusion in random media”, Surveys in applied mathematics, Plenum Press, New York, 1995, pp. 205–253 CrossRef; G. M. Zaslavsky, Phys. Rep., 2002, 371, 461 CrossRef; J. P. Bouchaud, A. Comtet, A. Georges and P. le Doussal, Ann. Phys., 1990, 201, 285 Search PubMed.
- A. J. Bray, S. N. Majumdar and G. Schehr, Adv. Phys., 2013, 62, 225 CrossRef CAS.
- Y. Mardoukhi, J.-H. Jeon and R. Metzler, Phys. Chem. Chem. Phys., 2015, 17, 30134 RSC.
- P. Massignan,
et al.
, Phys. Rev. Lett., 2014, 112, 150603 CrossRef CAS PubMed.
- M. V. Chubynsky and G. W. Slater, Phys. Rev. Lett., 2014, 113, 098302 CrossRef PubMed.
- T. Uneyama, T. Miyaguchi and T. Akimoto, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2015, 92, 032140 CrossRef PubMed.
- R. Jain and K. L. Sebastian, J. Phys. Chem. B, 2016, 120, 3988 CrossRef CAS PubMed.
- J. Bewerunge, I. Ladadwa, F. Platten, C. Zunke, A. Heuer and S. Egelhaaf, Phys. Chem. Chem. Phys., 2016, 18, 18887 RSC.
- W. Gotze and L. Sjogren, Rep. Prog. Phys., 1992, 55, 241 CrossRef.
- R. Yamamoto and A. Onuki, Phys. Rev. Lett., 1998, 81, 4915 CrossRef CAS.
- R. Richert, J. Phys.: Condens. Matter, 2002, 14, R703 CrossRef CAS.
- L. Berthier and G. Biroli, Rev. Mod. Phys., 2011, 83, 587 CrossRef CAS.
- M. J. Saxton, Biophys. J., 1997, 72, 1744 CrossRef CAS PubMed.
- M. Platani, I. Goldberg, A. I. Lamond and J. R. Swedlow, Nat. Cell Biol., 2002, 4, 502 CrossRef CAS PubMed.
- Y. M. Wang, R. H. Austin and E. C. Cox, Phys. Rev. Lett., 2006, 97, 048302 CrossRef CAS PubMed.
- I. Goychuk and V. O. Kharchenko, Phys. Rev. Lett., 2014, 113, 100601 CrossRef PubMed.
- M. Bauer, E. S. Rasmussen, M. A. Lomholt and R. Metzler, Sci. Rep., 2015, 5, 10072 CrossRef PubMed.
- S. Hapca, J. W. Crawford and L. M. Young, J. R. Soc., Interface, 2009, 6, 111 CrossRef PubMed.
- K. Yamamura, Popul. Ecol., 2002, 44, 93 CrossRef.
- J. S. Clark, Am. Nat., 1998, 152, 204 CrossRef CAS PubMed.
- R. Nathan, Science, 2006, 313, 786 CrossRef CAS PubMed.
- K. Yamamura, Popul. Ecol., 2004, 46, 87 CrossRef.
- G. T. Skalski and J. F. Gilliam, Ecology, 2000, 81, 1685 CrossRef.
- J. K. M. Brown and M. S. Hovmoller, Sci. Transl. Med., 2002, 297, 537 CAS.
- T. Kühn, T. O. Ihalainen, J. Hyvaluoma, N. Dross, S. F. Willman, J. Langowski, M. Vihinen-Ranta and J. Timonen, PLoS One, 2011, 6, e22962 Search PubMed.
- B. P. English, V. Hauryliuk, A. Sanamrad, S. Tankov, N. H. Dekker and J. Elf, Proc. Natl. Acad. Sci. U. S. A., 2011, 108, E365 CrossRef CAS PubMed.
- C. B. Mast, S. Schink, U. Gerland and D. Braun, Proc. Natl. Acad. Sci. U. S. A., 2013, 110, 8030 CrossRef CAS PubMed.
- A. G. Cherstvy, A. V. Chechkin and R. Metzler, New J. Phys., 2013, 15, 083039 CrossRef CAS; A. G. Cherstvy and R. Metzler, Phys. Chem. Chem. Phys., 2013, 15, 20220 RSC.
- A. G. Cherstvy, A. V. Chechkin and R. Metzler, Soft Matter, 2014, 10, 1591 RSC.
- A. G. Cherstvy, A. V. Chechkin and R. Metzler, J. Phys. A: Math. Theor., 2014, 47, 485002 CrossRef.
- K. S. Fa and E. K. Lenzi, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2003, 67, 061105 CrossRef PubMed.
- K. S. Fa, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2005, 72, 020101(R) CrossRef PubMed.
- M. Burgis,
et al.
, New J. Phys., 2011, 13, 043031 CrossRef.
-
M. Heidernätsch, On the diffusion in inhomogeneous systems, PhD thesis, TU Chemnitz, 2015 Search PubMed.
- H. Safdari, A. G. Cherstvy, A. V. Chechkin, F. Thiel, I. M. Sokolov and R. Metzler, J. Phys. A: Math. Theor., 2015, 48, 375002 CrossRef.
-
E. Geneston, R. Tuladhar, M. T. Beig, M. Bologna and P. Grigolini, 2015, arXiv:1601.02879.
- S. C. Lim and S. V. Muniandy, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2002, 66, 021114 CrossRef CAS PubMed.
- R. Friedrich, J. Peinke, M. Sahimi and M. R. R. Tabar, Phys. Rep., 2011, 506, 87 CrossRef.
- A. Bodrova, A. V. Chechkin, A. G. Cherstvy and R. Metzler, Phys. Chem. Chem. Phys., 2015, 17, 21791 RSC.
- F. Thiel and I. M. Sokolov, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2014, 89, 012115 CrossRef PubMed.
- J.-H. Jeon, A. V. Chechkin and R. Metzler, Phys. Chem. Chem. Phys., 2014, 16, 15811 RSC.
- G. K. Batchelor, Math. Proc. Cambridge Philos. Soc., 1952, 48, 345 CrossRef.
- A. G. Cherstvy and R. Metzler, J. Chem. Phys., 2015, 142, 144105 CrossRef PubMed.
- A. Fulinski, J. Chem. Phys., 2013, 138, 021101 CrossRef CAS PubMed; A. Fulinski, Acta Phys. Pol., 2013, 44, 1137 CrossRef.
- A. Fulinski, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2011, 83, 061140 CrossRef CAS PubMed.
- A. G. Cherstvy and R. Metzler, J. Stat. Mech.: Theory Exp., 2015, P05010 CrossRef.
- H. Safdari, A. V. Chechkin, G. R. Jafari and R. Metzler, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2015, 91, 042107 CrossRef PubMed.
- A. G. Cherstvy and R. Metzler, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2014, 90, 012134 CrossRef CAS PubMed.
- A. W. C. Lau and T. C. Lubensky, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2007, 76, 011123 CrossRef CAS PubMed.
- A. Bodrova, A. V. Chechkin, A. G. Cherstvy and R. Metzler, New J. Phys., 2015, 17, 063038 CrossRef.
- G. E. Uhlenbeck and L. S. Ornstein, Phys. Rev., 1930, 36, 823 CrossRef CAS.
- A. Bodrova, A. V. Chechkin, A. G. Cherstvy, H. Safdari, I. M. Sokolov and R. Metzler, Sci. Rep., 2016, 6, 30520 CrossRef PubMed.
- B. Lindner and I. M. Sokolov, Phys. Rev. E, 2016, 93, 042106 CrossRef PubMed.
- C. Di Rienzo, V. Piazza, E. Gratton, F. Beltram and F. Cardarelli, Nat. Commun., 2014, 5, 5891 CrossRef CAS PubMed.
-
S. Regev, N. Gronbech-Jensen and O. Farago, 2016, arXiv:1606.08632.
- O. Farago and N. Gronbech-Jensen, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2014, 89, 013301 CrossRef PubMed.
- O. Farago and N. Gronbech-Jensen, J. Stat. Phys., 2014, 156, 1093 CrossRef.
- J.-P. Bouchaud, J. Phys. I, 1992, 2, 1705 CrossRef.
- G. Bel and E. Barkai, Phys. Rev. Lett., 2005, 94, 240602 CrossRef CAS; A. Rebenshtok and E. Barkai, Phys. Rev. Lett., 2007, 99, 210601 CrossRef PubMed.
- A. Lubelski, I. M. Sokolov and J. Klafter, Phys. Rev. Lett., 2008, 100, 250602 CrossRef PubMed.
- S. Burov, R. Metzler and E. Barkai, Proc. Natl. Acad. Sci. U. S. A., 2010, 107, 13228 CrossRef CAS PubMed.
- Y. He, S. Burov, R. Metzler and E. Barkai, Phys. Rev. Lett., 2008, 101, 058101 CrossRef CAS PubMed.
- J.-H. Jeon and R. Metzler, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2010, 81, 021103 CrossRef PubMed.
- J.-H. Jeon, N. Leijnse, L. B. Oddershede and R. Metzler, New J. Phys., 2013, 15, 045011 CrossRef.
-
M. Schwarzl, A. Godec, E. Barkai and R. Metzler, unpublished.
- A. Andreanov and D. S. Grebenkov, J. Stat. Mech.: Theory Exp., 2012, P07001 Search PubMed.
- J. Kursawe, J. Schulz and R. Metzler, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2013, 88, 062124 CrossRef PubMed.
- J. H. P. Schulz, E. Barkai and R. Metzler, Phys. Rev. Lett., 2013, 110, 020602 CrossRef PubMed; J. H. P. Schulz, E. Barkai and R. Metzler, Phys. Rev. X, 2014, 4, 011028 Search PubMed.
- A. Godec and R. Metzler, Phys. Rev. Lett., 2013, 110, 020603 CrossRef PubMed.
- J.-H. Jeon and R. Metzler, J. Phys. A: Math. Theor., 2010, 43, 252001 CrossRef.
- P. Siegle, I. Goychuk and P. Hänggi, Phys. Rev. Lett., 2010, 105, 100602 CrossRef CAS PubMed.
- B. Lindner, New J. Phys., 2007, 9, 136 CrossRef; B. Lindner, J. Stat. Phys., 2008, 130, 523 CrossRef; B. Lindner, New J. Phys., 2010, 12, 063026 CrossRef.
- P. Romanczuk, M. Bär, W. Ebeling, B. Lindner and L. Schimansky-Geier, Eur. Phys. J.: Spec. Top., 2012, 202, 1 CrossRef CAS.
- M. J. Saxton, Biophys. J., 2001, 81, 2226 CrossRef CAS PubMed.
- T. J. Feder, I. Brust-Mascher, J. P. Slattery, B. Baird and W. W. Webb, Biophys. J., 1996, 70, 2767 CrossRef CAS PubMed.
- P. Schwille, J. Korlach and W. W. Webb, Cytometry, 1999, 36, 176 CrossRef CAS PubMed.
- M. Weiss, H. Hashimoto and T. Nilsson, Biophys. J., 2003, 84, 4043 CrossRef CAS PubMed.
- A. Kusumi, Y. Sako and M. Yamamoto, Biophys. J., 1993, 65, 2021 CrossRef CAS PubMed.
- S. Hapca, J. W. Crawford, K. MacMillan, M. J. Wilson and I. M. Young, J. Theor. Biol., 2007, 248, 212 CrossRef PubMed.
-
C. Charalambous, G. Munoz-Gil, A. Celi, M. F. Garcia-Parajo, M. Lewenstein, C. Manzo and M. A. Garca-March, 2016, arXiv:1607.00189.
-
A. G. Cherstvy, A. V. Chechkin and R. Metzler, unpublished.
|
| This journal is © the Owner Societies 2016 |
Click here to see how this site uses Cookies. View our privacy policy here.  Open Access Article
Open Access Article *
*
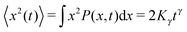
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp[−D/D0]
exp[−D/D0]![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−x2/[4Dt]) with this function,
exp(−x2/[4Dt]) with this function, 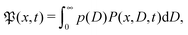 to obtain the exponential probability distribution function (PDF)
to obtain the exponential probability distribution function (PDF)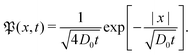
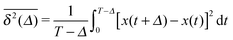
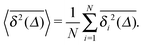
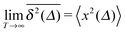 . Following Bouchaud104 the breakdown of this relation is referred to as weak ergodicity breaking,5,8,105–108
. Following Bouchaud104 the breakdown of this relation is referred to as weak ergodicity breaking,5,8,105–108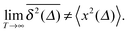
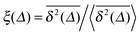 quantifying the spread of individual time averaged MSDs about their mean (6). Typically EB of a weakly non-ergodic process decays to zero with increasing trace length slower than for the standard Brownian motion,46,112
quantifying the spread of individual time averaged MSDs about their mean (6). Typically EB of a weakly non-ergodic process decays to zero with increasing trace length slower than for the standard Brownian motion,46,112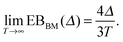
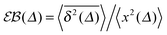
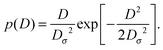
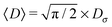
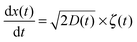
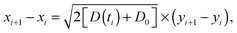
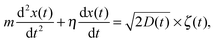
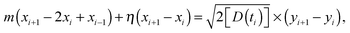
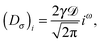
![[scr D, script letter D]](https://www.rsc.org/images/entities/char_e523.gif) tunes the magnitude of the diffusivity. From eqn (14) we straightforwardly compute
tunes the magnitude of the diffusivity. From eqn (14) we straightforwardly compute![[scr D, script letter D]](https://www.rsc.org/images/entities/char_e523.gif) tγ,
tγ,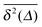 , see the thin red curves in Fig. 1. Obviously when the lag time approaches the observation time, Δ ∼ T, the amplitude scatter increases due to the deteriorating statistic of
, see the thin red curves in Fig. 1. Obviously when the lag time approaches the observation time, Δ ∼ T, the amplitude scatter increases due to the deteriorating statistic of 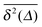 .8 Varying
.8 Varying ![[scr D, script letter D]](https://www.rsc.org/images/entities/char_e523.gif) in Fig. 1 we demonstrate that, as expected, larger initial diffusivities give rise to a faster approach of the MSD to the theoretical asymptote. In contrast, for rather small diffusivities (smaller
in Fig. 1 we demonstrate that, as expected, larger initial diffusivities give rise to a faster approach of the MSD to the theoretical asymptote. In contrast, for rather small diffusivities (smaller ![[scr D, script letter D]](https://www.rsc.org/images/entities/char_e523.gif) values) the system needs more time to approach the long time asymptote, Fig. 1. A diminished magnitude of the MSD at smaller
values) the system needs more time to approach the long time asymptote, Fig. 1. A diminished magnitude of the MSD at smaller ![[scr D, script letter D]](https://www.rsc.org/images/entities/char_e523.gif) values inevitably leads to a decrease in the magnitude of the time averaged MSD, see below. At intermediate to long times the superdiffusive MSD regime with γ = 3/2 emerges. Finally, towards the very end of the trace the MSD and the time averaged MSD coincide, as they should.8
values inevitably leads to a decrease in the magnitude of the time averaged MSD, see below. At intermediate to long times the superdiffusive MSD regime with γ = 3/2 emerges. Finally, towards the very end of the trace the MSD and the time averaged MSD coincide, as they should.8
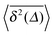 (thick blue curves) as well as individual time traces
(thick blue curves) as well as individual time traces 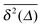 (red curves) for overdamped RDPs. The asymptotes (20) and (22) for the MSD and the time averaged MSD are shown by the dashed curves. The asymptotes often superimpose with the results of simulations. Parameters: the scaling exponent is ω = 1/2, the trace length is T = 105, and number of traces used for the averaging is N = 150. The starting position is x0 = 0.1 and the parameter
(red curves) for overdamped RDPs. The asymptotes (20) and (22) for the MSD and the time averaged MSD are shown by the dashed curves. The asymptotes often superimpose with the results of simulations. Parameters: the scaling exponent is ω = 1/2, the trace length is T = 105, and number of traces used for the averaging is N = 150. The starting position is x0 = 0.1 and the parameter 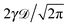 takes the values 10−1, 10−2, 10−3, and 10−4 for the panels from left to right.
takes the values 10−1, 10−2, 10−3, and 10−4 for the panels from left to right.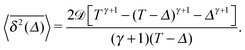
![[scr D, script letter D]](https://www.rsc.org/images/entities/char_e523.gif) values investigated, see Fig. 1 and 8. It is not surprising that both MSD and time averaged MSD are proportional to
values investigated, see Fig. 1 and 8. It is not surprising that both MSD and time averaged MSD are proportional to ![[scr D, script letter D]](https://www.rsc.org/images/entities/char_e523.gif) determining the basal value of the particle diffusivity, eqn (19). In the limit of short lag times, Δ ≪ T, from eqn (22) we recover the scaling behaviour
determining the basal value of the particle diffusivity, eqn (19). In the limit of short lag times, Δ ≪ T, from eqn (22) we recover the scaling behaviour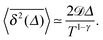
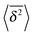 magnitude decreases with T, in agreement with Fig. 9. In the limit Δ→T the ensemble and time averaged MSDs coincide,8 as it is easy to check from eqn (20) and (22) and corroborated in Fig. 1. The non-equivalence of the time averaged MSD (22) and the time averaged MSD (20) demonstrates that the system is weakly non-ergodic. The scaling behaviour (23)—regarding the magnitude of the time averaged MSD in terms of the power law of the trace length T and the linearity in the lag time—is analogous to that obtained for subdiffusive continuous time random walks13,106,108,116 and their correlated version42 as well as for HDPs74,75,92 and SBM;87,93 see also ref. 8 for an overview.
magnitude decreases with T, in agreement with Fig. 9. In the limit Δ→T the ensemble and time averaged MSDs coincide,8 as it is easy to check from eqn (20) and (22) and corroborated in Fig. 1. The non-equivalence of the time averaged MSD (22) and the time averaged MSD (20) demonstrates that the system is weakly non-ergodic. The scaling behaviour (23)—regarding the magnitude of the time averaged MSD in terms of the power law of the trace length T and the linearity in the lag time—is analogous to that obtained for subdiffusive continuous time random walks13,106,108,116 and their correlated version42 as well as for HDPs74,75,92 and SBM;87,93 see also ref. 8 for an overview.
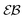 (10) becomes a power-law function of the lag time Δ,
(10) becomes a power-law function of the lag time Δ,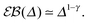

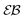 versus lag time Δ for overdamped RDPs. The curves are computed for the parameters of Fig. 1 with ω = 1/2. The curves for
versus lag time Δ for overdamped RDPs. The curves are computed for the parameters of Fig. 1 with ω = 1/2. The curves for 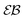 from top to bottom correspond to
from top to bottom correspond to 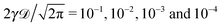 , respectively. The asymptote (9) of Brownian motion and the relation (24) are the dashed lines.
, respectively. The asymptote (9) of Brownian motion and the relation (24) are the dashed lines.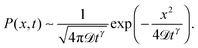
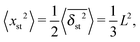

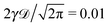 . The asymptote (26) and twice this value are the dashed lines.
. The asymptote (26) and twice this value are the dashed lines.
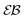 for confined overdamped RDPs for the parameters of Fig. 3. The Brownian asymptote (9) and the plateau
for confined overdamped RDPs for the parameters of Fig. 3. The Brownian asymptote (9) and the plateau 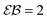 are shown as the dashed lines.
are shown as the dashed lines.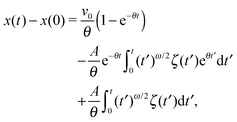
![[scr D, script letter D]](https://www.rsc.org/images/entities/char_e523.gif) /m2. Moreover, v0 is the initial particle velocity. Then the MSD of the particles after averaging over the noise ζ can formally be written as
/m2. Moreover, v0 is the initial particle velocity. Then the MSD of the particles after averaging over the noise ζ can formally be written as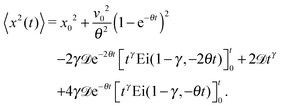
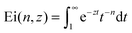 denotes the generalised exponential integral.
denotes the generalised exponential integral.
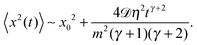
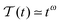 .117 This superballistic behaviour emerges for RDPs with fluctuating diffusivities and time dependent mean, in analogy with a faster than linear short time ballistic regime in Brownian motion.97
.117 This superballistic behaviour emerges for RDPs with fluctuating diffusivities and time dependent mean, in analogy with a faster than linear short time ballistic regime in Brownian motion.97
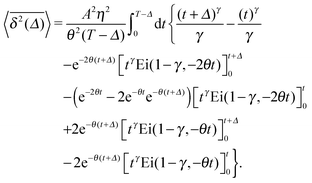
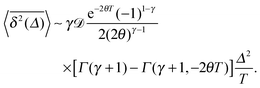
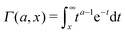 is the generalised incomplete Gamma function and Γ(a,0) = Γ(a) is the Gamma function. The short time asymptotes of both the MSD and the time averaged MSD are plotted as the dot-dashed curves in Fig. 5 showing nice agreement with the results of computer simulations of eqn (15).
is the generalised incomplete Gamma function and Γ(a,0) = Γ(a) is the Gamma function. The short time asymptotes of both the MSD and the time averaged MSD are plotted as the dot-dashed curves in Fig. 5 showing nice agreement with the results of computer simulations of eqn (15).

 , ω = 1/2, and T = 105.
, ω = 1/2, and T = 105.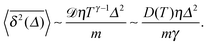
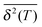 -variation with eqn (34) in Fig. 9B further supports this validity regarding the dependence on the length of particle trajectory T. In the opposite limit of θT ≪ 1—very massive particles or low friction for the particle motion—we find
-variation with eqn (34) in Fig. 9B further supports this validity regarding the dependence on the length of particle trajectory T. In the opposite limit of θT ≪ 1—very massive particles or low friction for the particle motion—we find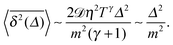
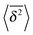 decreases with the particle mass, in agreement with eqn (34). At longer times the MSD and time averaged MSD approach the results expected for the overdamped RDP motion, shown as the long time asymptotes in Fig. 5. As expected, apart from the initial ballistic regime of the time averaged MSD described by eqn (34), the analytical solution for the overdamped limit (22) describes the long time behaviour of the results of our computer simulations.
decreases with the particle mass, in agreement with eqn (34). At longer times the MSD and time averaged MSD approach the results expected for the overdamped RDP motion, shown as the long time asymptotes in Fig. 5. As expected, apart from the initial ballistic regime of the time averaged MSD described by eqn (34), the analytical solution for the overdamped limit (22) describes the long time behaviour of the results of our computer simulations.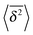 follow the relation (23), see Fig. 9B. We also observe that for underdamped RDPs the spread of individual
follow the relation (23), see Fig. 9B. We also observe that for underdamped RDPs the spread of individual 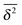 traces is similar to that of standard Brownian motion. This small spread is consistent with the observation that the EB parameter for this underdamped RDP motion does not deviate strongly from the Brownian asymptote (9) at intermediate and long times, see Fig. 6. In the region of short Δ the deviations are quite substantial, particularly for massive particles exhibiting a ballistic initial growth of
traces is similar to that of standard Brownian motion. This small spread is consistent with the observation that the EB parameter for this underdamped RDP motion does not deviate strongly from the Brownian asymptote (9) at intermediate and long times, see Fig. 6. In the region of short Δ the deviations are quite substantial, particularly for massive particles exhibiting a ballistic initial growth of 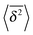 and a nonlinear growth of the MSD, see Fig. 5. The auxiliary parameter
and a nonlinear growth of the MSD, see Fig. 5. The auxiliary parameter 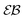 —again after the initial particle acceleration—follows the asymptote (24), see the thick curves in Fig. 6. The deviations of EB and
—again after the initial particle acceleration—follows the asymptote (24), see the thick curves in Fig. 6. The deviations of EB and 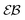 at short lag times from the Brownian asymptote is more evident for massive particles.
at short lag times from the Brownian asymptote is more evident for massive particles.
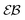 versus lag time Δ for underdamped RDPs. The Brownian asymptote (9) and eqn (24) are the dashed lines. The curves correspond to varying particle mass, m = 1, 5, 10, 50; the other parameters are the same as in Fig. 5.
versus lag time Δ for underdamped RDPs. The Brownian asymptote (9) and eqn (24) are the dashed lines. The curves correspond to varying particle mass, m = 1, 5, 10, 50; the other parameters are the same as in Fig. 5.

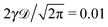 and N = 150. The asymptotes for the MSD and time averaged MSD are shown as the dashed lines.
and N = 150. The asymptotes for the MSD and time averaged MSD are shown as the dashed lines.
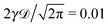 . Dashed lines indicate the scaling relation (23) in panel (A) and eqn (34) in panel (B).
. Dashed lines indicate the scaling relation (23) in panel (A) and eqn (34) in panel (B).
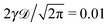 and N = 300. The PDF asymptote for subdiffusive SBM (25) is shown as the dashed curve.
and N = 300. The PDF asymptote for subdiffusive SBM (25) is shown as the dashed curve.
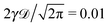 , T = 105, m = 50.
, T = 105, m = 50.