Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Thermal fluctuations in chemically cross-linked polymers of cyclodextrins
Barbara
Rossi
*ab,
Valentina
Venuti
c,
Alessandro
Paciaroni
d,
Andrea
Mele
e,
Stéphane
Longeville
f,
Francesca
Natali
g,
Vincenza
Crupi
c,
Domenico
Majolino
c and
Francesco
Trotta
h
aElettra – Sincrotrone Trieste, Strada Statale 14 km 163.5, Area Science Park, 34149 Trieste, Italy
bDepartment of Physics University of Trento, via Sommarive 14, 38123 Povo, Trento, Italy. E-mail: rossi@science.unitn.it; Fax: +39 0461281690; Tel: +39 0461282940
cDepartment of Physics and Earth Sciences, University of Messina, Viale Ferdinando Stagno D'Alcontres 31, 98166 Messina, Italy
dDepartment of Physics, University of Perugia, Via A. Pascoli, 06123 Perugia, Italy
eDepartment of Chemistry, Materials and Chemical Engineering, G. Natta, Politecnico di Milano, Piazza L. da Vinci 32, 20133, Milano, Italy
fLaboratoire Léon Brillouin (CEA/CNRS), CEA Saclay, 91191 Gif-sur-Yvette Cedex, France
gCNR-IOM, c/o ILL, 71 avenue des Martyrs, CS 20156-38042, Grenoble, France
hDepartment of Chemistry, University of Torino, Via Pietro Giuria 7, 10125 Torino, Italy
First published on 9th January 2015
Abstract
The extent and nature of thermal fluctuations in the innovative class of cross-linked polymers called cyclodextrin nanosponges (CDNS) are investigated, on the picosecond time scale, through elastic and quasielastic neutron scattering experiments. Nanosponges are complex 3D polymer networks where covalent bonds connecting different cyclodextrin (CD) units and intra- and inter-molecular hydrogen-bond interactions cooperate to define the molecular architecture and fast dynamics of the polymer. The study presented here aims to clarify the nature of the conformational rearrangements activated by increasing temperature in the nanosponge polymer, and the constraints imposed by intra- and inter-molecular hydrogen-bond patterns on the internal dynamics of the macromolecule. The results suggest a picture, in which conformational rearrangements involving the torsion of the OH groups around the C–O bonds dominate the internal dynamics of the polymer over the picosecond time scale. Moreover, the estimated values of mean square displacements reveal that the motions of the hydrogen atoms in the nanosponges are progressively hampered as the cross-linking degree of the polymer is increased. Finally, the study of the molecular relaxations suggests a dynamical rearrangement of the hydrogen-bond networks, which is characterized by a jump diffusion motion of the more mobile hydrogen atoms belonging to the OH groups of the CD units. All these findings add further contribution to the rational comprehensive view of the dynamics of these macromolecules, which may be particularly beneficial in designing new drug-delivery systems with tuneable inclusion/release properties.
Introduction
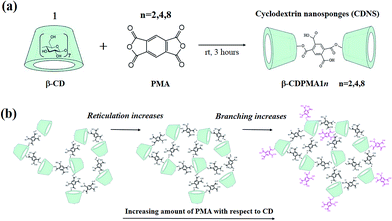
The use of cross-linked polymers for smart applications in the technological fields of high social impact is presently attracting great attention.1 As a matter of fact, cross-linked polymers have been shown to be superior in uses requiring resistance to high temperatures and high mechanical performance.1 Polymeric networks of molecules are considered to be a very versatile class of materials having tailored properties at different length scales, and they have been proposed for use in the fast-growing fields of drug delivery, tissue engineering, and regenerative medicine.2–4In this framework, cyclodextrin nanosponges (CDNS) play a relevant role in the design and development of new delivery systems adapted to the physicochemical features of the active species and to the therapeutic demands of pathology.5,6 In particular, they offer interesting possibility to selectively encapsulate and release both hydrophobic and hydrophilic active ingredients.5–12
Nanosponges are prepared by poly-condensation between cyclodextrins (CD), which are cyclic oligomers of amylose and well known for their ability to form inclusion complexes with a large variety of guest molecules,13,14 and suitable cross linking agents (CL) such as carbonyldiimidazole (CDI),15,16 pyromellitic anhydride (PMA)17–23 or activated derivatives of ethylenediaminetetraacetic acid (EDTA).24–26 The polymerization reaction leads to the formation of a three-dimensional network of CD units showing both hydrophilic and hydrophobic nano-sized cavities (Fig. 1(a)). X-ray diffraction18 and low-frequency inelastic light17 and neutron23 scattering measurements indicate that cyclodextrin nanosponges are, in the majority of cases, completely amorphous; therefore, thorough structural characterization is still an open field of investigation.
These polymers are safe and biodegradable materials with negligible toxicity on cell cultures, and they are considered to exhibit superior inclusion ability with respect to native CD by incorporating a large class of molecules within their structures.5
Few types of CDNS exhibit marked swelling behaviour in the presence of aqueous solution, giving rise to the formation of gel-like dispersions.20–22,25–27 This ability to absorb a large amount of water is particularly intriguing in view of the possible use of these polymeric matrices as efficient water nano-containers.27 Moreover, the hydrogels obtained by swelling CDNS polymers seem to be good candidates as stimuli-responsive systems for the entrapment/release of bio-active compounds. It has been shown that their physical state can be modified in a controlled way22,25–27 and that they can pass progressively from a rigid gel to a liquid suspension upon gradual increase of the hydration level of CDNS in water.
The functional features of CDNS, such as their water holder capacity and inclusion/release capabilities, are intimately related to the molecular structure and conformational rearrangements of the chemical groups within the cross-linked network. In this sense, a full explanation of the relationship existing between the molecular architecture and polymer dynamics of CDNS, and their corresponding macroscopic physical properties is still an ambitious objective to be reached.
In recent years, many efforts have been devoted to explore the structural features of nanosponges over different length scales by implementing a broad repertoire of experimental and computational techniques. In particular, in the case of ester-bridged CDNS,17–26 previous results indicate that a crucial contribution to the molecular architecture and rigidity of the entire polymer network comes from the complex interplay between covalent bonds and non-covalent interactions, which are typically hydrogen-bonds (HB) that connect the CD units within the polymer.20,23 The connectivity patterns of these chemical–physical interactions have been explored in depth by a detailed analysis of the vibrational dynamics of CDNS performed in different frequency regimes17,19,21,24,25 and by exploiting the different sensitivities of complementary techniques such as inelastic light and neutron scattering.23 All the experimental results clearly indicate that the polymeric structure and the physical–chemical properties of CDNS can be successfully modulated by varying (i) the chemical structure of CL,17 (ii) the type of CD28 and (iii) the relative amount of CL17,19,23,24,28 with respect to the monomer (i.e. n = the molar ratio between the cross-linking agent and CD). Among these factors, the molar ratio n mainly influences the degree of reticulation of the polymer during its synthesis, as demonstrated in our previous study.17–20,23,24,28 In these studies, an interpretation of the effect of the increasing amount of cross linking agent with respect to the monomer cyclodextrin on CDNS structure was proposed (Fig. 1(b)). The cross-linking degree of the polymer increases with increasing molar ratio n up to a critical value, beyond which a further excess of CL results in branching the CD units rather than grafting them together, which can reasonably be attributed to steric crowding.
In this study, we report the results of an extensive investigation on the dynamics of ester-bridged nanosponges over picosecond temporal windows, by exploiting the potentiality of incoherent neutron scattering. As a matter of fact, elastic (ENS) and quasielastic (QENS) neutron scattering are among the most powerful experimental techniques to finely estimate the extent of the thermal fluctuations due to the molecular motions and the relaxational features in complex macromolecules. In particular, due to the energy resolution of the neutron scattering spectrometers employed in the present study, attention will be focussed on the dynamical processes involving the fluctuation of the hydrogen-bond networks formed inside a single CD molecule (intra-molecular HB) and among different CD units (inter-molecular HB). The dynamics of PMA-nanosponges obtained by the polymerization of CD with pyromellitic anhydride at different values of molar ratio n were investigated as a function of temperature, and the results were compared with the characteristic internal motions of the monomeric unit β-cyclodextrin.
Interestingly, a general increase of the cyclodextrin OH group mobility is observed when CD units are assembled into the polymeric network of CDNS. Moreover, the analysis of the elastic incoherent structure factor suggests a model of atomic motion, which is well described by a random jump diffusion of hydrogen atoms into the HB patterns involving the OH groups of CD.
These results add a further contribution to the rational comprehensive view of the fast dynamics of CD assembled into CDNS networks and could be particularly beneficial in designing new stimuli-responsive CDNS hydrogels with tuneable inclusion/release properties.
Materials and methods
A The synthesis and purification of nanosponges
Ester-bridged cyclodextrin nanosponges based on pyromellitic anhydride were obtained by following the synthetic procedure already described in an Italian patent, with minor modifications.29–31In order to obtain the β-CDPMA1n polymers (for the notation see Fig. 1(a)), the reactions of polymerization between β-CD and the cross-linking agent pyromellitic dianhydride (PMA) at β-CD![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) PMA molar ratios of 1
PMA molar ratios of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) n (with n = 2, 4, 8) were conducted by dissolving the reagents in dimethyl sulfoxide (DMSO) in the presence of triethylamine and allowing them to react at room temperature for 3 hours. Once the reaction was complete, the obtained solid was broken up with a spatula and washed with acetone in a Soxhlet apparatus for 24 hours. This process ensures the complete removal of unreacted reagents and the purification of the final polymer product. The pale yellow solid material was finally dried under vacuum for about 24 hours, which is generally a sufficient time to achieve a constant weight of the product. After the drying procedure, no further water is present or can be removed. The chemical and thermal stability of the nanosponges were previously evaluated,5 and the results indicate that a degradation of the material is observed only at high temperature values (>60 °C) in acidic conditions.
n (with n = 2, 4, 8) were conducted by dissolving the reagents in dimethyl sulfoxide (DMSO) in the presence of triethylamine and allowing them to react at room temperature for 3 hours. Once the reaction was complete, the obtained solid was broken up with a spatula and washed with acetone in a Soxhlet apparatus for 24 hours. This process ensures the complete removal of unreacted reagents and the purification of the final polymer product. The pale yellow solid material was finally dried under vacuum for about 24 hours, which is generally a sufficient time to achieve a constant weight of the product. After the drying procedure, no further water is present or can be removed. The chemical and thermal stability of the nanosponges were previously evaluated,5 and the results indicate that a degradation of the material is observed only at high temperature values (>60 °C) in acidic conditions.
B Neutron scattering experiments
Quasi elastic neutron scattering experiments were performed at Laboratoire Léon Brillouin (LLB, Saclay, France) using the time-of-flight (TOF) spectrometer MIBEMOL.Measurements were carried out at temperatures of 150 and 300 K using neutrons with an incident wavelength of 6 Å, with a Q-independent experimental elastic energy resolution of 92.7 μeV (defined as the full-width half-maximum, FWHM, of a vanadium standard). The Q-range covered was from 0.49 Å−1 to 1.73 Å−1. The recorded spectra were organized into 10 groups to improve the counting statistics. The explored energy range was from −45 meV to about 1.4 meV. In all of the figures reported herein, the sign of the energy transfer has been reversed for the sake of simplicity. A standard, indium sealed, flat aluminum cell with a thickness of 0.2 mm internal spacing was used as a sample holder. For each measurement, the sample holder was placed at an angle of 135° with respect to the incident beam direction. The time of data acquisition was about 8 hours. A transmission of ∼96% was estimated for all the investigated samples. The measured time-of-flight spectra were analyzed with the QENSH data treatment program, available at LLB, which allows, inter alia, the correction of the detector efficiency by normalization to vanadium spectra, the correction for the empty cell, the transformation of the TOF spectra into energy spectra, and the data grouping to improve the corresponding signal/noise ratio.
Elastic scattering scans were performed using a high-energy resolution, wide momentum transfer backscattering spectrometer IN13 at the Institute Laue-Langevin (ILL, Grenoble, France). An energy resolution of 9 μeV FWHM, corresponding to an incident neutron wavelength of 2.23 Å, was achieved in the Q range 0.2–4.6 Å−1. A standard, indium sealed, flat aluminium cell with a thickness of 0.3 mm was used as a sample holder for all the examined samples. The temperatures explored ranged from 130 to 310 K, and the acquisition time varied between 1 and 2 hours depending on the type of nanosponge. The acquired data were corrected in order to take into account the incident flux, cell scattering, self-shielding, and detector responses. The elastic intensity of each sample relative to a given temperature was then normalized with respect to the corresponding lowest measured temperature (T = 20 K). A transmission of about 90% was measured for β-CDPMA12, 88% for β-CDPMA14 and 88.5% for β-CDPMA18. The data have not been corrected by the multiple scattering contributions, which is estimated to be below 10% on the elastic peak and affects all the analysed samples in a very similar way.
C Theoretical background
In a typical neutron scattering experiment, the molecular motions of the atoms were investigated by measuring the so-called dynamical structure factor S(Q, E), which gives the probability that an incident neutron is scattered by the sample with an energy E and an exchanged momentum Q. The functional dependence of S(Q, E) on E and Q provides information, respectively, on the characteristic time scales and the geometry of the molecular motions that contribute to the revealed signal, respectively. The dynamical structure factor includes both coherent and incoherent contributions, which arise from the inter- or self-particle correlations of collective or individual atomic motions, respectively.However, in the case of the samples under investigation in our experiment, the dominant contribution to the revealed signal is due to the large amount of hydrogen atoms, which is characterized by a very large, almost exclusively incoherent neutron cross section.32 Therefore, the neutron scattering experiment allows us to study the self-particle dynamics of the hydrogen atoms, which can be considered as a probe of the thermal fluctuations of the whole molecule.33–36
In the incoherent approximation, the intensity of scattered neutrons can be written, at a given temperature T, as:
| S(Q, E) = e−2W(Q,T){A0(Q)δ(ω) + [1 − A0(Q)]SQE(Q, ω) + SINEL(Q, ω)}⊗R(Q, ω) | (1) |
The term A0(Q)δ(ω) in eqn (1) represents the elastic response of the system due to those scattering events, which do not involve changes in energy, whereas the function SQE(Q, ω) is the quasielastic scattering contribution, which gives information about the diffusive and relaxational motions of the system. Finally, the term SINEL(Q, ω) represents the inelastic scattering portion of the spectra, which is usually much less intense than the quasielastic contribution, and is modelled with a flat background. All the internal motions are convoluted with the experimental resolution function R(Q, ω).
The energy dependence of the elastic signal is described by a delta function (δ(u)), whereas the modulation as a function of Q is provided by the elastic incoherent structure factor (EISF) A0(Q), which is the space-Fourier transform of the scatterers distributions taken at infinite time, and averaged over all the possible initial positions. The Q-behaviour of the factor A0(Q) provides information on the geometry and the types of motions of the scattering centres. As we will see below, the measured elastic intensity shows a non-Gaussian Q-dependence, which is more and more visible as the temperature increases, whereas the quasielastic linewidths display a Q-independent trend. This behaviour suggests that the neutron scattering signal originates from anharmonic dynamics, which possibly involves random jump confined motions. A quite reasonable model to describe these dynamical features is the so-called double-well model,38 extensively applied to picosecond proton dynamics in several types of disordered systems.39,40 It provides an over-simplified description of the energy landscape by taking into account the deviation of the elastic intensity from the Gaussian behaviour. In spite of this approximation, one can obtain, as explained in the following, a quantitative estimation of the mean square displacements. In this framework, the protons are considered dynamically equivalent, and their motions are schematized as jumps between two distinct sites with a free energy difference ΔG.
On the basis of the double-well jump model, the corresponding EISF can be written as:41
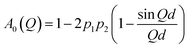 | (2) |
In the harmonic approximation, the temperature-dependence of 〈u2〉 in the Debye–Waller factor can be described by using the Einstein model of independent quantized oscillators:34
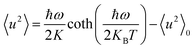 | (3) |
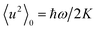 provides the zero-point mean square displacements.
provides the zero-point mean square displacements.
However, since the measured elastic intensity has been normalized with respect to the lowest temperature (as indicated below), the zero-point mean square displacements have been subtracted in the right side of eqn (3).
Finally, a quantitative measurement of the average hydrogen mobility is given by the total MSD 〈u2〉tot, which can be derived from eqn (1), with A0(Q) given by eqn (2) and 〈u2〉 given by eqn (3), through the relationship:37
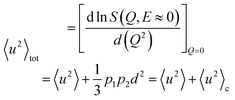 | (4) |
In the above equation, 〈u2〉 is the aforementioned harmonic vibrational MSD term, whereas 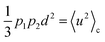 represents the conformational contribution to the total MSD,40 which describes the proton mobility due to jumping between the two energetic sites.
represents the conformational contribution to the total MSD,40 which describes the proton mobility due to jumping between the two energetic sites.
It is thus more useful to model the term SQE(Q, ω) through a phenomenological function described as a sum of Lorentzians curves:42,43
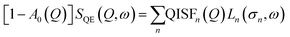 | (5) |
Results and discussion
A Conformational mobility of OH groups
In Fig. 2(a) and (b), the incoherent elastic neutron scattering intensities measured for β-CDPMA12 and β-CDPMA14 nanosponges are shown, as a function of Q2, at three different values of temperature T. The experimental profiles are reported after the usual standard corrections and normalization (see Materials and Methods section).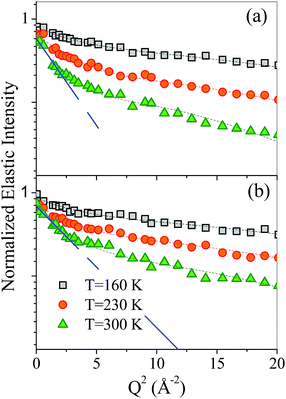 | ||
| Fig. 2 Normalized incoherent elastic intensities as a function of Q2 for (a) β-CDPMA12 and (b) β-CDPMA14 nanosponges at three different temperatures. Experimental data (open symbols) are reported along with the fit (dashed line) according to eqn (6) (see text for details). The blue lines highlight the change of slope typical of non-Gaussian behaviour. The error bars (less than 15%) are not reported for the sake of clarity. | ||
The logarithmic scale in Fig. 2 allows us to point out that the experimental elastic intensities exhibit a Q2 dependence that tends to slightly depart from the Gaussian-like behaviour of the Debye–Waller factor. This effect, which becomes more and more pronounced as the temperature increases, has previously been observed in other systems such as hydrated protein powders44,45 and cyclodextrin inclusion complexes.46 In these systems, the departure from the Gaussian dependence has been interpreted as originating from anharmonic motions, involving the re-orientational dynamics of small molecular groups, and described in terms of the double-well model.38 We may expect that a similar dynamical activation can be the basis of the behaviour found in the present systems, due to the significant contribution from the re-orientations of OH groups belonging to both cyclodextrin and the cross-linking agent. This is why we chose to describe the experimental elastic intensities by using the double-well model,38,41,44,46 according to the equation:
| S(Q, ω ≈ 0) ∝ e−〈u2〉GQ2[A0(Q)δ(ω)]⊗R(Q, ω) | (6) |
Eqn (6) provides an excellent fit to the data, as shown in Fig. 2, with a jump distance d equal to 1.7 ± 0.2 Å for all the analysed samples of nanosponges, which are independent of temperature.
Since the measured elastic intensity reflects the dynamical contribution of the motions of atoms of CDNS that are accessible in the experimental energy and momentum transfer range, the double-well jump model may provide only an average description of the internal dynamics of the polymers. In this context, our experimental data seem to suggest the existence of hydrogen atom motions, which are characterized by a spatial distance, d. This internal dynamic may be related to the reorientational degrees of freedom, involving the hydrogen atoms of the several OH groups present in the polymeric framework, which easily undergo conformational rearrangements due to the torsion around the C–(OH) chemical bonds.
As a matter of fact, the value of the d parameter is consistent with the characteristic distance explored by the hydrogen atoms of the OH groups during their reorientational motions. The temperature independence of this parameter also suggests that as the temperature increases, the extent of these torsional motions stays the same, whereas the number of mobile OH groups progressively increases as can be witnessed from the trend of the MSD shown in the next section. We can speculate that the increasing mobility on increasing the temperature and decreasing the cross-linking degree could be related to improved effectiveness for particular purposes such as the inclusion of small molecules.
B Effect of hydrogen-bonds on internal polymer dynamics
As previously specified, quantitative information on the average proton dynamics of the system can be provided from the temperature-behaviour of the total mean square displacements 〈u2〉tot. The total MSD as obtained from eqn (4) (upper part) for the three different types of examined β-CDPMA1n nanosponges and for pure β-CD46 are reported in Fig. 3 as a function of temperature.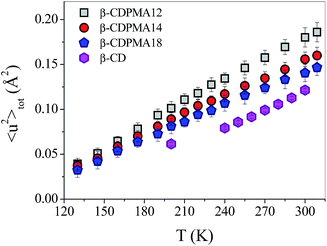 | ||
| Fig. 3 Total mean square displacements 〈u2〉tot as a function of temperature T for β-CDPMA1n nanosponges (n = 2, 4 and 8) and β-CD [data from ref. 46]. | ||
It is noteworthy that over the whole range of temperatures explored, the proton mobility of the nanosponges is significantly higher than that of the monomeric unit β-CD. As we expect that a large contribution to the measured MSD comes from the OH groups of the cyclodextrins, this finding strongly suggests that the assembly of CD units into the polymeric network of CDNS gives rise to a general increase of the OH group degrees of freedom. To explain this effect, a picture can be proposed where the average mobility at a local level is increased due to the perturbation of the strongly interconnected intra-molecular hydrogen-bond (HB) network, involving the 2- and 3-OH groups around the bottom rim of the cyclodextrin, as a result of the distortions of the CD macro-ring brought about by the polymerization process. This interpretation is consistent with the finding previously reported by 13C CP-MAS NMR spectroscopy16 that the primary OH groups of CD are the principal reactive sites for the ester formation, thus leaving majority of the OH groups at position 2 and 3 of the glucose units unreacted.
The findings described above can be related to the results of the inspection of the vibrational band observed in the IR spectra of CDNS in the high-wavenumber region, and assigned to the stretching modes of the OH groups of the polymer.19 The analysis of the spectral features of this complex band gives important information on the connectivity pattern of the HB network of the system. Recent IR measurements performed on CDNS in a dry state19 evidenced a disruption of the intra-molecular H-bond network at the larger rim of the CD units, which was related to the increased steric hindrance of the entire system with the growing cross-linking degree of the nanosponges. This effect on the OH group populations of the polymeric matrix was found to be largely dependent on the chemical nature of the cross-linker as shown by the analysis of the vibrational spectra of the CDI-based nanosponges.15
As a general trend, the mobility increase of the hydrogen atoms is observed for all three types of β-CDPMA1n nanosponges with increasing temperature (Fig. 3). This finding seems to be consistent with our previous IR measurements,15,19 which give evidence of a characteristic destructuring effect on the HB scheme in CDNS when the temperature of the polymer increases.
The comparison between the temperature-behaviour exhibited by the total MSD for the monomeric unit β-CD46 and the nanosponge polymers (Fig. 3) deserves some specific comments. The trend shown by the 〈u2〉tot of β-CDPMA12 nanosponges looks similar to that observed for pure β-CD, whereas the temperature-dependence of MSD seems to change when passing from n = 2 to 8. This behaviour suggests that the polymeric systems become less temperature-responsive as the molar ratio n increases, which is in agreement with the increasing constraint experienced by the OH groups in the nanosponge network. This finding also appears to be of particular interest in view of the potential applications of nanosponges as stimuli-responsive systems.
C Mobility versus elastic constants
The values of MSD reported in Fig. 3 also point to a general hindering of the proton mobility of CDNS as the molar ratio n increases from 2 to 8. This result suggests that the parameter n strongly affects the internal polymer dynamics of CDNS on the picosecond time scale.The behaviour found for MSD is fully consistent with the attenuation of the intensity of the vibrational modes of the CDNS polymer, which is observed in the inelastic neutron scattering spectra.23 The vibrational density of states estimated for β-CDPMA1n nanosponges shows that the hydrogen atoms tend to exhibit vibrational motions of smaller amplitude when they are inserted in a more interconnected pattern of cross-links.
A more quantitative description of this effect can be provided by the estimation of the average rigidity of the samples in the high-temperature regime, where large structural fluctuations take place and the systems become less and less stable. It may be argued that, as the systems approach the instability region, the double-well method would lose its validity as the atoms will tend to explore most of the conformational space accessible to them. In this approximation, we can consider that in the high-T range, and the energy landscape accessible to the hydrogen atoms will resemble a confining harmonic potential well:40
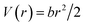 | (7) |
This approximation holds, provided that the experimental time-window is quite large, in such a way that the atoms have the time to explore the conformational landscape. Moreover, we are confident that eqn (7) may be applied for temperatures such that 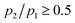 , i.e. above 280 K, where the conformational landscape is rather homogeneously populated. Under these conditions, the configurational mean square displacements 〈u2〉c can be described by the relation:41
, i.e. above 280 K, where the conformational landscape is rather homogeneously populated. Under these conditions, the configurational mean square displacements 〈u2〉c can be described by the relation:41
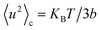 | (8) |
It is noteworthy that a similar approach has already been exploited to describe the dynamic features of proteins in terms of an effective force constant.47,48
The fit of the experimental 〈u2〉c performed by using eqn (8) in the high-T range allows us to obtain a direct measurement of b for the three different samples of nanosponges under investigation, as reported in Table 1.
| Type of nanosponge | b (N m−1) |
|---|---|
| β-CDPMA12 | 0.96 ± 0.02 |
| β-CDPMA14 | 1.02 ± 0.02 |
| β-CDPMA18 | 1.12 ± 0.02 |
| β-CD | 0.70 ± 0.03 |
The stiffness of nanosponges, as quantified by the b parameter, increases from n = 2 to n = 8. This estimation of the average rigidity of CDNS polymers can be related to the qualitative evolution of the low-frequency vibrational modes observed in the inelastic light17,18,24,28 and neutron scattering23 spectra of nanosponges. In previous studies, the modifications revealed in the frequency position of the Boson peak (BP) for different types of CDNS and as a function of molar ratio n were found to be consistent with the trend observed for the Brillouin sound velocity measured on the same samples.17 We remark that both the BP and Brillouin peaks are spectroscopic features related to the transformation of the elastic constants of the material, the former on a mesoscopic length-scale and the latter on a wider scale, extending up to hundreds of nanometers. The analysis of the inelastic light and neutron spectra of PMA-nanosponges17,23 clearly shows that the BP shifts toward higher wavenumbers when the parameter n changes from 2 to 8. This behaviour was explained by considering a general increase of the average rigidity (stiffness) of the CDNS polymer matrix, which is in full agreement with the estimated values of the parameter b reported in Table 1.
These results strongly confirm the hypothesis that the extent of the covalent network, which is controlled by the cross-linking agent/cyclodextrin molar ratio n, induces a general modification of the elastic properties of nanosponge polymers.
This finding appears to be of particular interest given that the functional properties of CDNS, such as their swelling ability and inclusion/release performances, are expected to be strongly affected by the rigidity of the three-dimensional polymeric matrix.
D Relaxational dynamics: reorganization of HB network
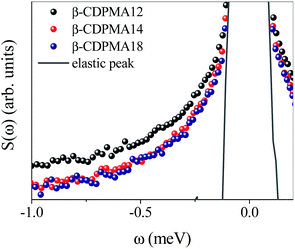
Further information on the polymer dynamics of CDNS can be obtained by the analysis of the relaxational processes of the system as provided by quasielastic neutron scattering signals.No quasielastic contribution has been revealed for all the investigated nanosponge polymers at T = 150 K, while at T = 300 K the quasielastic signal can be immediately recognized in the experimental profiles of Fig. 4 as a broadening of the elastic peak.
The presence of the quasielastic contribution in the spectra of nanosponges suggests the existence of internal dynamics that can be related to the relaxation of the hydrogen-bond pattern involving the OH groups of the CD units49 in the polymer network of CDNS.
By inspection of the spectra in Fig. 4, it can be seen that the intensity of the quasielastic wings seems to decrease on passing from the n = 2 to the n = 4, 8 values. The same qualitative behaviour was observed in the low-frequency Raman spectra of nanosponges,24,28 where the quasielastic contribution to the total experimental profiles varies passing from its maximum intensity at n = 2 to the minimum intensity for high values of n. This trend is also consistent with the spectral modifications of BP observed in the inelastic light and neutron scattering spectra,17,23,24,28 and with the estimation of the rigidity of the polymer matrix of CDNS reported in Table 1.
The trend shown in Fig. 4 could be due to either the narrowing of the quasielastic contribution (i.e. slower characteristic time) or the decrease of the quasielastic intensity (i.e. fewer mobile groups) on increasing the cross-linking molar ratio. To differentiate between these alternative situations, and to obtain quantitative information we analysed the spectra by the model described in the “Theoretical background” section. The experimental quasielastic signal can be well described as a sum of Lorentzian functions convoluted with the instrumental resolution function.
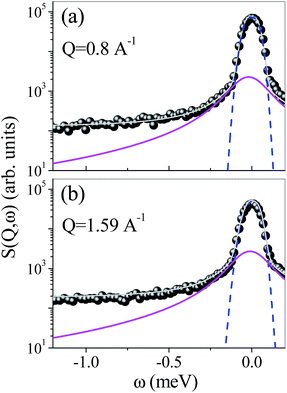
In particular, the spectra of CDNS have been adequately reproduced using only one Lorentzian component, L(σ, ω) with linewidth σ, describing the sub-meV broadening of the elastic peak and a flat background.49 In Fig. 5, a typical example of the best fitting procedure of SQE(Q, ω) is shown for β-CDPMA12 at two different values of exchanged momentum Q.
The Q-dependence of the line width σ of the Lorentzian function used to reproduce the quasielastic signal gives information on the dynamic of the atoms inside the volume explored by the moving protons.
In Fig. 6, the line widths obtained by the fitting procedure of the experimental quasielastic contribution are reported as a function of Q for β-CDPMA1n nanosponges.
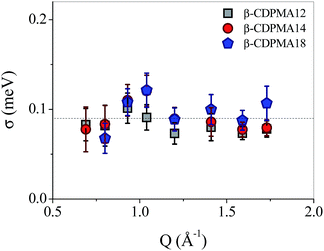 | ||
| Fig. 6 Linewidth (FWHM) σ of the Lorentzian contribution of quasielastic neutron scattering as a function of Q for β-CDPMA1n nanosponges (n = 2, 4 and 8) at T = 300 K. | ||
The characteristic time of the motions, which give rise to the quasi-elastic signal is found to be quite similar for all the three types of examined polymers and it is about 7.3 ps.
The independence on Q of the half-width of L(σ, ω) (see Fig. 6) suggests that the hydrogen atoms of the polymer network of nanosponges explore a finite volume, i.e. their dynamics are confined.49,50 Indeed, this signature of a confined motion holds in the experimental accessible timescale that is estimated as the inverse of the energy resolution, corresponding to about 15 ps. In fact, a more detailed treatment of confined motions, accounting also for the dynamical behaviour over a longer timescale may even give rise to Q-dependent splitting.51
More detailed information on the geometry of the proton motions of the system is provided by the calculated elastic incoherent structure factor A0(Q), which shows a different Q-behaviour for the three β-CDPMA1n nanosponges as shown in Fig. 7.
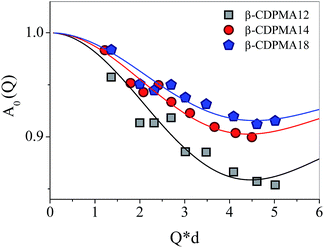 | ||
| Fig. 7 Q-dependence of A0(Q) for β-CDPMA1n nanosponges (n = 2, 4 and 8) at T = 300 K. The error bars (less than 5%) are not reported for the sake of clarity. | ||
In order to obtain more quantitative details on the dynamics of the three different samples of nanosponges, the experimental profiles of A0(Q) can be well described using the same double-well jump model previously adopted for the analysis of elastic intensities (eqn (2)).
Consistently with the Q-independent behaviour of the linewidths σ, we assume that most of the diffusing hydrogen atoms belong to the OH groups of CD, and that they can perform a random jump diffusion motion between two sites separated by the characteristic distance d. Based on these assumptions, the elastic incoherent structure factor A0(Q) can be well reproduced by using eqn (2), as shown in Fig. 7 for the three different types of examined nanosponges.
The fitting procedure of A0(Q) provides the estimation of the parameter f = 1 − 4p1p2, which represents the fraction of atoms that move too slowly to be resolved in the experiment.
The values obtained for the “immobile” atoms f are reported in Table 2 along with those found for the characteristic distance d between the sites, among which the mobile hydrogens diffuse by random jump (Table 2).
| Type of nanosponge | f | d (Å) |
|---|---|---|
| β-CDPMA12 | 0.768 ± 0.04 | 2.9 ± 0.03 |
| β-CDPMA14 | 0.840 ± 0.04 | 2.6 ± 0.02 |
| β-CDPMA18 | 0.861 ± 0.04 | 2.9 ± 0.03 |
The increase of the fraction f of immobile hydrogens in CDNS at high values of the parameter n is fully consistent with the hypothesis that the molecular dynamics of nanosponges are mainly driven by the motion of the hydrogen atoms belonging to the OH groups of CD. As a matter of fact, these groups are expected to be those involved in the polymerization reaction with the cross-linking agent during the formation of the CD polymer network.
The characteristic distance of the jump diffusion motion is found to be quite similar for all the β-CDPMA1n nanosponges, and corresponds to an average value of 2.8 Å. This estimated value is consistent with the diffusion by jump motion from one OH group to another over the hydrogen-bond pattern established inside the polymer network of the nanosponge.
Conclusions
The thermal fluctuations occurring in an innovative class of chemically cross-linked polymers of cyclodextrins have been investigated, on the picosecond timescale, through elastic and quasi elastic neutron scattering experiments. A comparative assessment of the fast molecular dynamics of hydrogen atoms in CD-polymers and in the single monomeric unit β-cyclodextrin has been performed with the aim of understanding the balance between covalent bonds and hydrogen-bonds in defining the molecular architecture and rigidity of the whole polymer network.As a main result, the extent of the thermal fluctuations in the nanosponges were found to be noticeably broader than those estimated in cyclodextrin alone, revealing the establishment, in the polymer, of a characteristic inter-molecular HB network at the expense of the more strongly interconnected intra-molecular HB formed among the OH groups on the rims of the macrocycle.
This finding along with the description of the molecular diffusion dynamics in the polymer network provided by the analysis of the elastic incoherent structure factor, suggests a picture, in which the jump diffusion motion of more mobile hydrogen atoms over the hydrogen-bond network of nanosponges dominates the dynamics of the system over the picosecond temporal window.
Finally, the molecular rigidity of CDNS related to the hampering of the picosecond time scale dynamics can be of great interest in order to optimize the design and synthesis of cyclodextrin-based polymers with tuneable inclusion/release properties for specific technological applications.
Acknowledgements
The authors gratefully acknowledge PRIN 2010–2011 NANOMED prot. 2010 FPTBSH for financial support, and the reviewers for thorough and accurate revision of our paper and suggestions.Notes and references
- R. A. Dickie, S. S. Labana and R. S. Bauer, Cross-Linked Polymers: Chemistry, Properties, and Applications, Acs Symposium Series, American Chemical Society, 2nd edn, 1988 Search PubMed.
- K. Sakurada, F. M. McDonald and F. Shimada, Angew. Chem., Int. Ed., 2008, 47(31), 5718 CrossRef CAS PubMed.
- A. Atala, R. P. Lanza, J. A. Thomson and R. M. Nerem, Principles of Regenerative Medicine, Academic Press, Burlington, MA, 2008 Search PubMed.
- B. V. Slaughter, S. S. Khurshid, O. Z. Fisher, A. Khademhosseini and N. A. Peppas, Adv. Mater., 2009, 21, 3307 CrossRef CAS PubMed.
- F. Trotta, M. Zanetti and R. Cavalli, Beilstein J. Org. Chem., 2012, 8, 2091 CrossRef CAS PubMed.
- S. Subramanian, A. Singireddy, K. Krishnamoorthy and M. Rajappan, J. Pharm. Pharm. Sci., 2012, 15(1), 103 CAS.
- D. Lembo, S. Swaminathan, M. Donalisio, A. Civra, L. Pastero, D. Aquilano, P. Vavia, F. Trotta and R. Cavalli, Int. J. Pharm., 2013, 443, 262 CrossRef CAS PubMed.
- R. Minelli, R. Cavalli, L. Ellis, P. Pettazzoni, F. Trotta, E. Ciamporcero, G. Barrera, R. Fantozzi, C. Dianzani and R. Pili, Eur. J. Pharm. Sci., 2012, 47, 686 CrossRef CAS PubMed.
- S. J. Torne, K. A. Ansari, P. R. Vavia, F. Trotta and R. Cavalli, Drug Delivery, 2010, 17, 419 CrossRef CAS PubMed.
- D. Li and M. Ma, Clean Products and Processes, 2000, 2, 112 CrossRef.
- S. Swaminathan, L. Pastero, L. Serpe, F. Trotta, P. R. Vavia, D. Aquilano, M. Trotta, G. Zara and R. Cavalli, Eur. J. Pharm. Biopharm., 2010, 74(2), 193 CrossRef CAS PubMed.
- E. Memisoglu-Bilensoy, I. Vural, A. Bochot, J. M. Renoir, D. Duchene and A. A. Hincal, J. Controlled Release, 2005, 104, 489 CrossRef CAS PubMed.
- J. Szejtli, Chem. Rev., 1998, 98, 1743 CrossRef CAS PubMed.
- M. L. Bender and M. Komiyama, Cyclodextrin Chemistry, Springer-Varlag, New York, 1978 Search PubMed.
- F. Castiglione, V. Crupi, D. Majolino, A. Mele, B. Rossi, F. Trotta and V. Venuti, J. Phys. Chem. B, 2012, 116(43), 13133 CrossRef CAS PubMed.
- F. Castiglione, V. Crupi, D. Majolino, A. Mele, W. Panzeri, B. Rossi, F. Trotta and V. Venuti, J. Inclusion Phenom. Macrocyclic Chem., 2013, 75(3–4), 247 CrossRef CAS.
- B. Rossi, S. Caponi, F. Castiglione, S. Corezzi, A. Fontana, M. Giarola, G. Mariotto, A. Mele, C. Petrillo, F. Trotta and G. Viliani, J. Phys. Chem. B, 2012, 116(17), 5323 CrossRef CAS PubMed.
- A. Mele, F. Castiglione, L. Malpezzi, F. Ganazzoli, G. Raffaini, F. Trotta, B. Rossi, A. Fontana and G. Giunchi, J. Inclusion Phenom. Macrocyclic Chem., 2011, 69, 403 CrossRef CAS.
- F. Castiglione, V. Crupi, D. Majolino, A. Mele, B. Rossi, F. Trotta and V. Venuti, J. Phys. Chem. B, 2012, 116(27), 7952 CrossRef CAS PubMed.
- V. Crupi, D. Majolino, A. Mele, B. Rossi, F. Trotta and V. Venuti, Soft Matter, 2013, 9, 6457 RSC.
- F. Castiglione, V. Crupi, D. Majolino, A. Mele, B. Rossi, F. Trotta and V. Venuti, J. Raman Spectrosc., 2013, 44(10), 1463 CrossRef CAS.
- V. Crupi, A. Fontana, D. Majolino, A. Mele, L. Melone, C. Punta, B. Rossi, F. Rossi, F. Trotta and V. Venuti, J. Inclusion Phenom. Macrocyclic Chem., 2014, 80, 69 CrossRef CAS.
- V. Crupi, A. Fontana, M. Giarola, S. Longeville, D. Majolino, G. Mariotto, A. Mele, A. Paciaroni, B. Rossi, F. Trotta and V. Venuti, J. Phys. Chem. B, 2014, 118(2), 624 CrossRef CAS PubMed.
- V. Crupi, A. Fontana, M. Giarola, D. Majolino, G. Mariotto, A. Mele, L. Melone, C. Punta, B. Rossi, F. Trotta and V. Venuti, J. Raman Spectrosc., 2013, 44(10), 1457 CrossRef CAS.
- V. Crupi, D. Majolino, A. Mele, L. Melone, C. Punta, B. Rossi, F. Toraldo, F. Trotta and V. Venuti, Soft Matter, 2014, 10, 2320 RSC.
- F. Castiglione, V. Crupi, D. Majolino, A. Mele, L. Melone, W. Panzeri, C. Punta, B. Rossi, F. Trotta and V. Venuti, J. Inclusion Phenom. Macrocyclic Chem., 2014, 80, 77 CrossRef CAS PubMed.
- W. Liang, C. Yang, D. Zhou, H. Haneoka, M. Nishijima, G. Fukuhara, T. Mori, F. Castiglione, A. Mele, F. Caldera, F. Trotta and Y. Inoue, Chem. Commun., 2013, 49, 3510 RSC.
- B. Rossi, A. Fontana, M. Giarola, G. Mariotto, A. Mele, C. Punta, L. Melone, F. Toraldo and F. Trotta, J. Non-Cryst. Solids, 2014, 401, 73 CrossRef CAS PubMed.
- F. Trotta and W. Tumiatti, Cross-linked polymers based on cyclodextrin for removing polluting agents, Patent WO 03/085002, 2003.
- F. Trotta, W. Tumiatti, R. Cavalli, O. Zerbinati, C. M. Roggero and R. Vallero, Ultrasound-assisted synthesis of cyclodextrin-based nanosponges, Patent number WO 06/002814, 2006.
- F. Trotta, V. Tumiatti, R. Cavalli, C. Rogero, B. Mognetti and G. Berta, Cyclodextrin-based nanosponges as a vehicle for antitumoral drugs, Patent number WO 09/003656 A1, 2009.
- R. Lefort, D. Morineau, R. Guégan, C. Ecolivet, M. Guendouz, J. M. Zanotti and B. Frick, Phys. Chem. Chem. Phys., 2008, 10, 2993 RSC.
- J. C. Q. Smith, Annu. Rev. Biophys., 1991, 24, 1 Search PubMed.
- K. Wood, A. Frolich, A. Paciaroni, M. Moulin, M. Hartlein, G. Zaccai, D. J. Tobias and M. Weik, J. Am. Chem. Soc., 2008, 130, 4586 CrossRef CAS PubMed.
- M. Plazanet, M. Dean, M. Merlini, A. Huller, H. Emerich, C. Meneghini, M. R. Johnson and H. P. Trommsdorff, J. Chem. Phys., 2006, 125, 154504 CrossRef CAS PubMed.
- F. Sonvico, M. T. Di Bari, L. Bove, A. Deriu, F. Cavatorta and G. Albanese, Phys. B, 2006, 385–386, 725 CrossRef CAS PubMed.
- A. Stoeckli, A. Furrer, C. Schoenenberger, B. H. Meier, R. R. Ernst and I. Anderson, Phys. B, 1986, 136, 161 CrossRef CAS.
- W. Doster, S. Cusack and W. Petry, Nature, 1989, 337, 754 CrossRef CAS PubMed.
- B. Frick and D. Richter, Science, 1995, 267, 1939 CAS.
- P. W. Fenimore, H. Frauenfelder, B. H. McMahon and R. D. Young, Proc. Natl. Acad. Sci. U. S. A., 2004, 101, 14408 CrossRef CAS PubMed.
- M. Bée, Quasielastic Neutron Scattering, Adam Hilger, Bristol, UK, 1988 Search PubMed.
- J. Fitter, R. E. Lechner and N. A. Dencher, Biophys. J., 1997, 73, 2126 CrossRef CAS.
- T. Springer, Quasielastic Neutron Scattering for the Investigation of Diffusive Motions in Solids and Liquids, Springer Tracts in Modern Physics, Springer, Berlin, 1972 Search PubMed.
- A. Paciaroni, S. Cinelli and G. Onori, Biophys. J., 2002, 83, 1157 CrossRef CAS.
- S. Magazù, G. Maisano, F. Migliardo and A. Benedetto, J. Phys. Chem. B, 2008, 112, 8936 CrossRef PubMed.
- V. Crupi, D. Majolino, A. Paciaroni, R. Stancanelli and V. Venuti, J. Phys. Chem. B, 2009, 113, 11032 CrossRef CAS PubMed.
- G. Zaccai, Science, 2000, 288, 1604 CrossRef CAS.
- D. G. Bicout and G. Zaccai, Biophys. J., 2001, 80, 1115 CrossRef CAS.
- V. Crupi, G. Guella, S. Longeville, D. Majolino, I. Mancini, A. Paciaroni, B. Rossi and V. Venuti, J. Phys. Chem. B, 2013, 117, 11466 CrossRef CAS PubMed.
- V. F. Sears, Can. J. Phys., 1967, 45, 237 CrossRef CAS PubMed.
- T. Bickel and C. M. Marques, Eur. Phys. J. E, 2002, 9, 349 CrossRef CAS PubMed.
Footnote |
| † Actually, the latter expression and the relationship for the double-well model mean square displacements describe one dimensional system motions. To pass to a 3D system one has to multiply the resulting MSD values by a factor of 3. |
| This journal is © The Royal Society of Chemistry 2015 |